Effect of Soil Reinforcement on Tunnel Deformation as a Result of Stress Relief
Abstract
:1. Introduction
2. Material and Methods
2.1. Description of the Simulated Centrifuge Test
2.2. Finite Element Analysis
2.2.1. Finite Element Mesh and Boundary Conditions
2.2.2. Constitutive Model and Model Parameters
2.2.3. Numerical Modeling Procedure
- Establish the initial stress conditions using K0 = 0.5. Apply the same amount of vertical and horizontal pressure as that in the centrifuge test to the formation level and diaphragm wall, respectively.
- Increment the gravitational acceleration of the entire model from 1 g to 60 g. Simultaneously, apply pressure to the formation level and wall.
- Decrease the amount of vertical and horizontal pressure gradually in each excavation stage to simulate excavation up to a depth of 9 m.
2.2.4. Numerical Modeling Scheme
3. Results and Analysis
3.1. Effect of Reinforced Soil’s Young’s Modulus on Tunnel Heave
3.2. Effect of Reinforced Soil’s Young’s Modulus on Tunnel Diameter Change
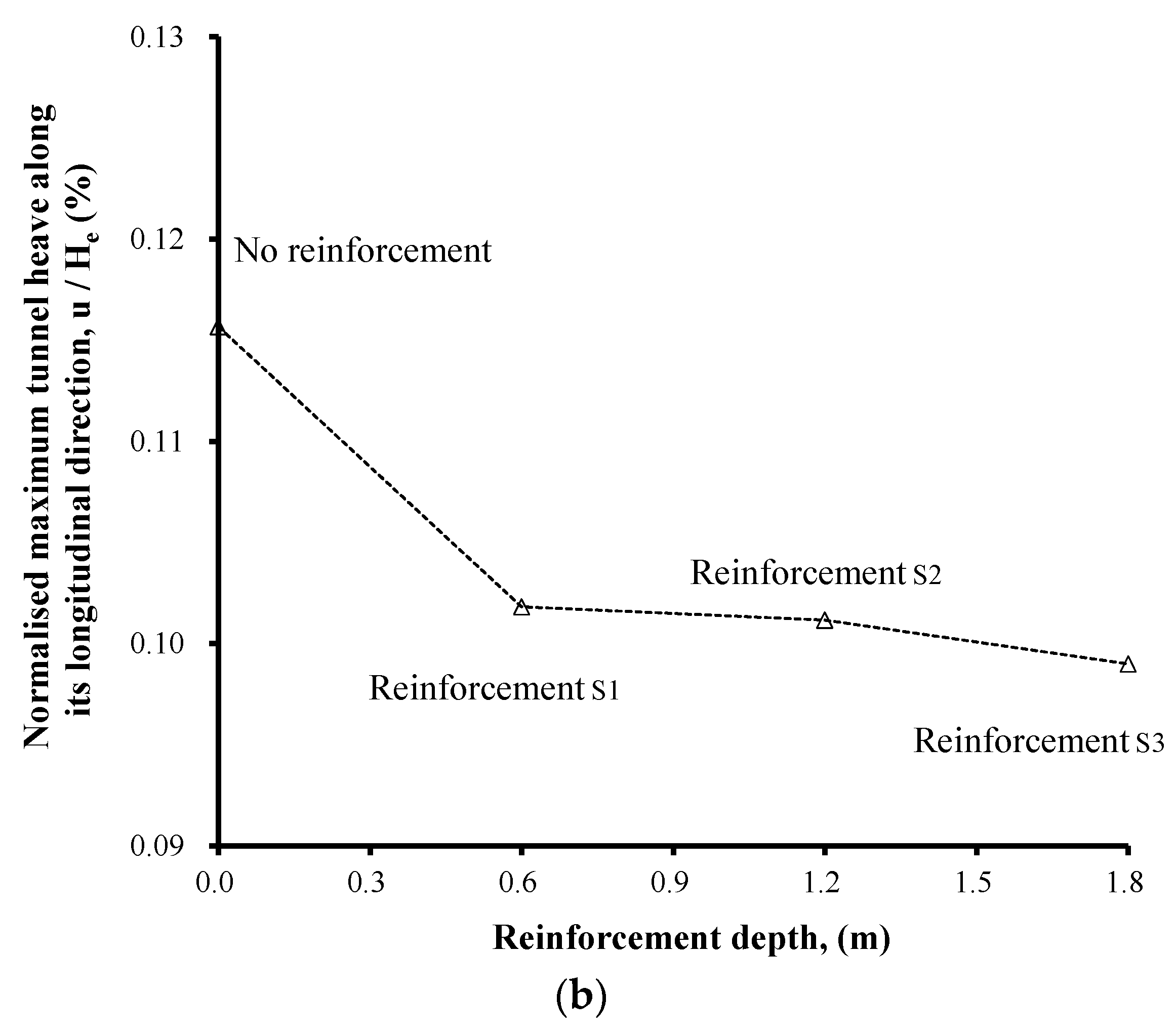
3.3. Effect of Reinforcement Depth on Tunnel Heave
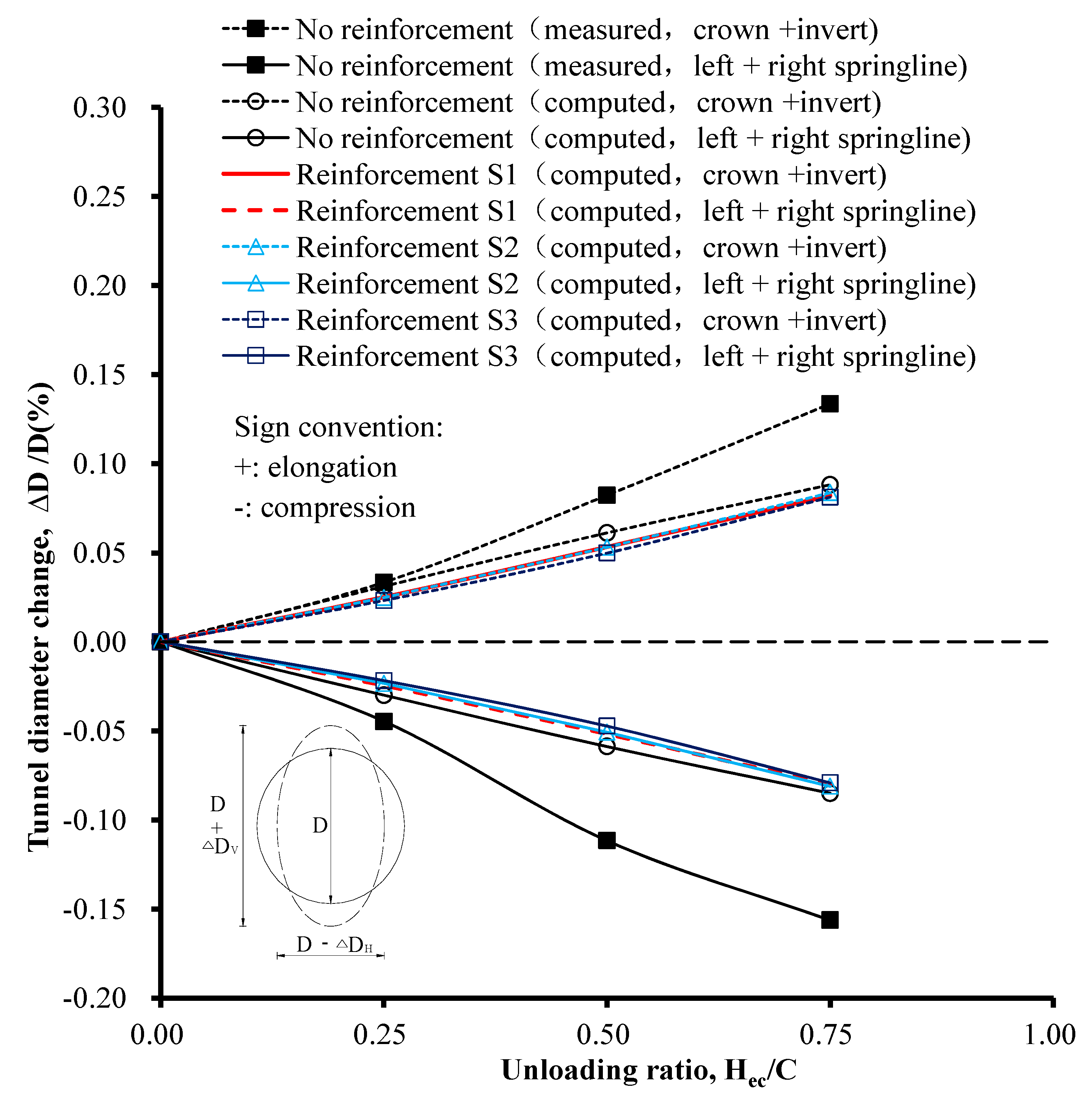
3.4. Effect of Reinforcement Depth on Tunnel Diameter Change
3.5. Analyses of Soil Responses Caused by Excavation
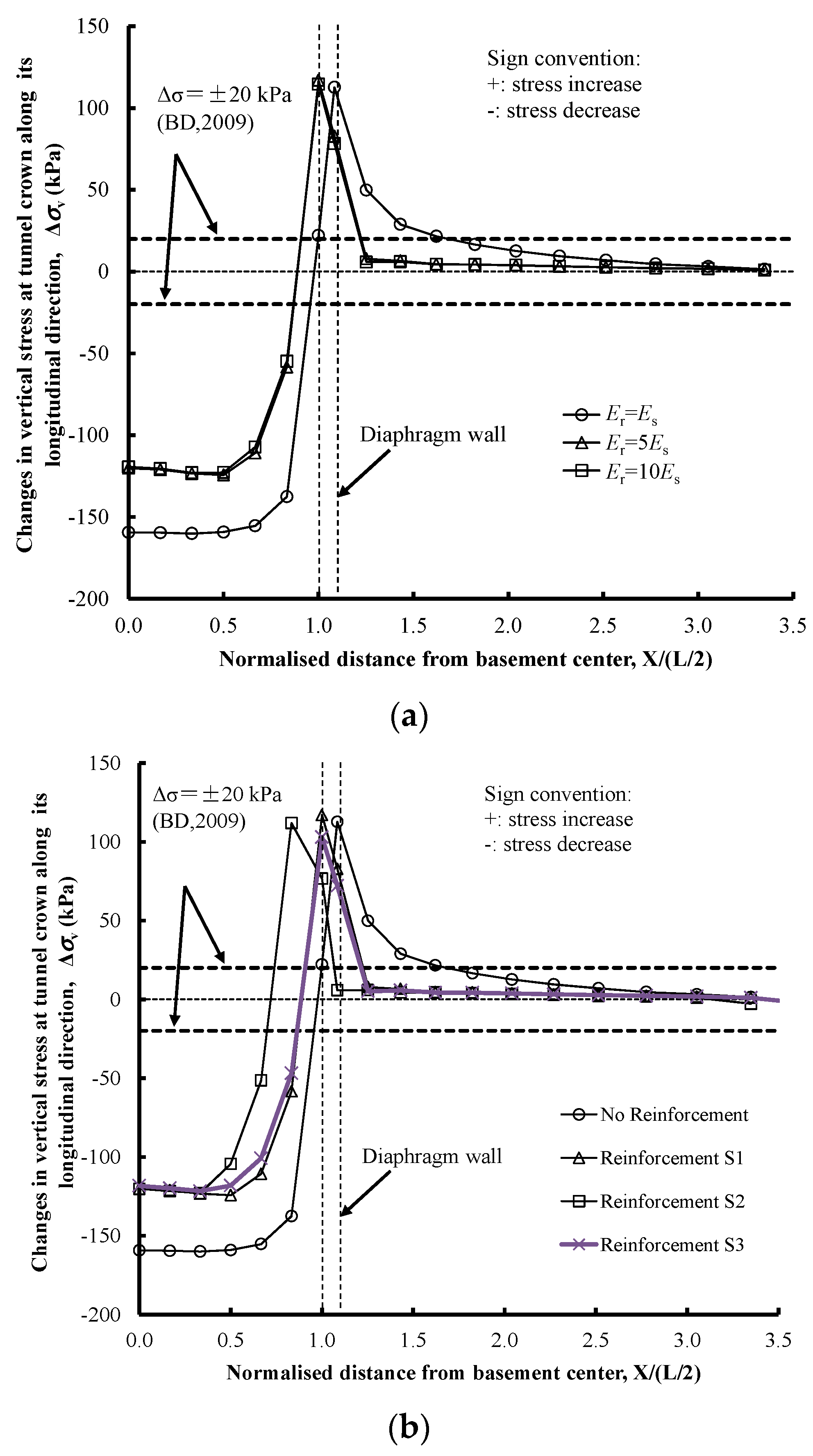
3.5.1. Stress Distributions of Soil Elements in the Tunnel’s Longitudinal Direction
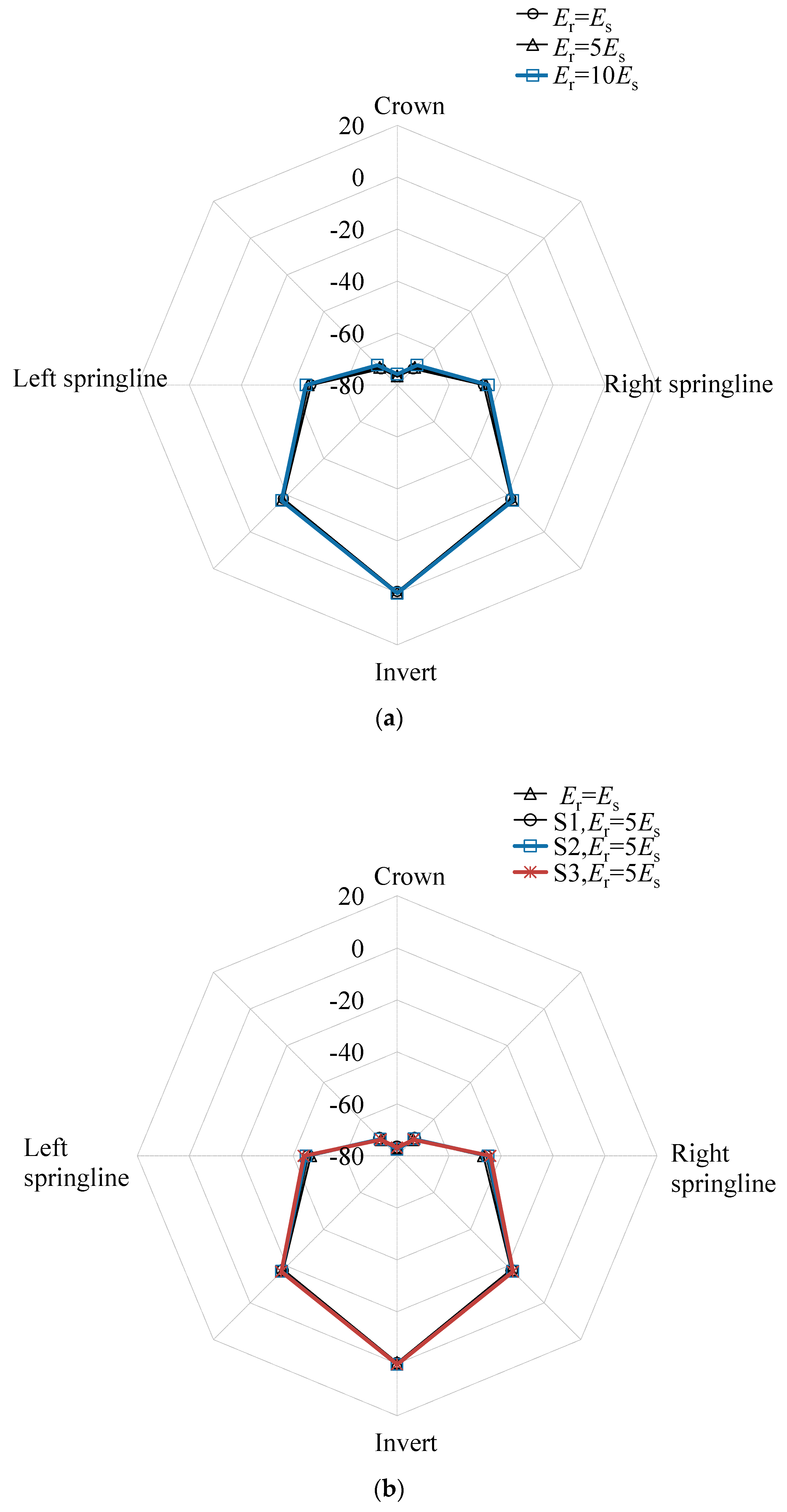
3.5.2. Stress Distributions of Soil Elements in the Tunnel’s Transverse Direction
4. Conclusions
- (a)
- As a result of the stress relief caused by the basement excavation, tunnel heave was observed for the tunnel underneath the basement excavation. The heave was greatly reduced by improving the basement bottom soil’s Young’s modulus. When a specific soil area S1 was reinforced with a Young’s modulus that varied from Es to 5Es, the computed tunnel heave decreased by 18%. This was because the reinforced soil blocked the stress transfer and thus reduced the tunnel heave caused by excavation unloading. A further increase of the reinforced soil’s Young’s modulus did not significantly reduce the tunnel heave. This can be attributed to the fact that obvious stress changes were not observed when the reinforced soil’s Young’s modulus increased from 5Es to 10Es.
- (b)
- When the reinforcement depth was 0.6 m, the computed tunnel heave decreased by 15% in comparison with the non-reinforced case. However, significant changes were not observed when the reinforcement depth increased further. The further increase of reinforcement depth had no effect and would therefore be uneconomical.
- (c)
- As the reinforced soil’s Young’s modulus varied from Es to 5Es, the maximum elongation of the tunnel lining in the circumferential direction changed by 9%. Significant changes were not observed when the reinforced soil’s Young’s modulus increased from 5Es to 10Es. Significant changes were not observed when the reinforcement depth increased further. Thus, it was concluded that the reinforced soil’s Young’s modulus and the reinforcement depth exerted only a slight influence on the diameter change of the tunnel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability Statement
References
- Burford, D. Heave of tunnels beneath the Shell Centre. London, 1959–1986. Géotechnique 1988, 38, 135–137. [Google Scholar] [CrossRef]
- Chang, C.-T.; Sun, C.-W.; Duann, S.; Hwang, R.N. Response of a Taipei Rapid Transit System (TRTS) tunnel to adjacent excavation. Tunn. Undergr. Space Technol. 2001, 16, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Simpson, B.; Vardanega, P.J. Results of monitoring at the British Library excavation. Proc. Inst. Civ. Eng.—Geotech. Eng. 2014, 167, 99–116. [Google Scholar] [CrossRef] [Green Version]
- Ng, C.W.; Shi, J.; Hong, Y. Three-dimensional centrifuge modelling of basement excavation effects on an existing tunnel in dry sand. Can. Geotech. J. 2013, 50, 874–888. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Zhang, D. Centrifuge modelling of deep excavation over existing tunnels. Proc. Inst. Civ. Eng.—Geotech. Eng. 2014, 167, 3–18. [Google Scholar] [CrossRef]
- Ng, C.; Shi, J.; Lei, G.; Mašín, D.; Sun, H. Influence of sand density and retaining wall stiffness on three-dimensional responses of tunnel to basement excavation. Can. Geotech. J. 2015, 52, 1811–1829. [Google Scholar] [CrossRef]
- Lo, K.; Ramsay, J. The effect of construction on existing subway tunnels—A case study from Toronto. Tunn. Undergr. Space Technol. 1991, 6, 287–297. [Google Scholar] [CrossRef]
- Doležalová, M. Tunnel complex unloaded by a deep excavation. Comput. Geotech. 2001, 28, 469–493. [Google Scholar] [CrossRef]
- Sharma, J.S.; Hefny, A.M.; Zhao, J.; Chan, C.W. Effect of large excavation on displacement of adjacent MRT tunnels. Tunn. Undergr. Space Technol. 2001, 16, 93–98. [Google Scholar] [CrossRef]
- Hu, Z.F.; Yue, Z.Q.; Zhou, J.; Tham, L.G. Design and construction of a deep excavation in soft clay adjacent to the shanghai metro tunnels. Can. Geotech. J. 2003, 40, 933–948. [Google Scholar] [CrossRef]
- Zheng, G.; Wei, S.W. Numerical analysis of influence of overlying pit excavation on existing tunnels. J. Cent. South Univ. Technol. 2008, 15, 69–75. [Google Scholar] [CrossRef]
- Liu, H.L.; Li, P.; Liu, J.Y. Numerical investigation of underlying tunnel heave during a new tunnel construction. Tunn. Undergr. Space Technol. 2011, 26, 276–283. [Google Scholar] [CrossRef]
- Huang, X.; Schweiger, H.F.; Huang, H.W. Influence of deep excavations on nearby existing tunnels. Int. J. Geomech. ASCE 2013, 13, 170–180. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Sun, H.S.; Lei, G.H.; Shi, J.W.; Mašín, D. Ability of three different soil constitutive models to predict a tunnel’s response to basement excavation. Can. Geotech. J. 2015, 52, 1685–1698. [Google Scholar] [CrossRef]
- Shi, J.; Ng, C.W.W.; Chen, Y. Three-dimensional numerical parametric study of the influence of basement excavation on existing tunnel. Comput. Geotech. 2015, 63, 146–158. [Google Scholar] [CrossRef]
- Zhang, J.F.; Chen, J.J.; Wang, J.H.; Zhu, Y.F. Prediction of tunnel displacement induced by adjacent excavation in soft soil. Tunn. Undergr. Space Technol. 2013, 36, 24–33. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Wang, W. Evaluation of deformation response for adjacent tunnels due to soil unloading in excavation engineering. Tunn. Undergr. Space Technol. 2013, 38, 244–253. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M.; Zhao, Q. A simplified analysis for deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays. Arab. J. Geosci. 2015, 8, 1–15. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Space Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Zheng, G.; Du, Y.M.; Diao, Y. Influenced zones for deformation of existing tunnels adjacent to excavations. Chin. J. Geotech. Eng. 2016, 38, 599–612. [Google Scholar]
- Ng, C.W.W.; Van Laak, P.A.; Tang, W.H.; Li, X.S.; Zhang, L.M. The Hong Kong geotechnical centrifuge. In Proceedings of the 3rd International Conference on Soft Soil Engineering, Hong Kong, China, 6–8 December 2001; pp. 225–230. [Google Scholar]
- Ng, C.W.W.; Van Laak, P.A.; Zhang, L.M.; Tang, W.H.; Zong, G.H.; Wang, Z.L.; Xu, G.M.; Liu, S.H. Development of a four-axis robotic manipulator for centrifuge modeling at HKUST. In Proceedings of the International Conference on Physical Modelling in Geotechnics, St John’s, NL, Canada, 10–12 July 2002; pp. 71–76. [Google Scholar]
- Ng, C.W.W. The state-of-the-art centrifuge modelling of geotechnical problems at hkust. J. Zhejiang Univ. A 2014, 15, 1–21. [Google Scholar] [CrossRef]
- ABAQUS, Inc. ABAQUS User’s and Theory Manuals; Version 6.17; ABAQUS, Inc.: Providence Rhode Island, RI, USA, 2017. [Google Scholar]
- LTA. Code of Practice for Railway Protection; Development & Building Control Department, Land Transport Authority (LTA): Singapore, 2000.
- BTS. Specification for Tunnelling; British Tunnelling Society (BTS): Thomas Telford, London, UK, 2000. [Google Scholar]
- BD. Practice Note for Authorized Persons APP-24. Technical Notes for Guidance in Assessing the Effects of Civil Engineering Construction/Building Development on Railway Structures and Operations; Building Department of the Government of HKSAR (BD): Hongkong, China, 2009.
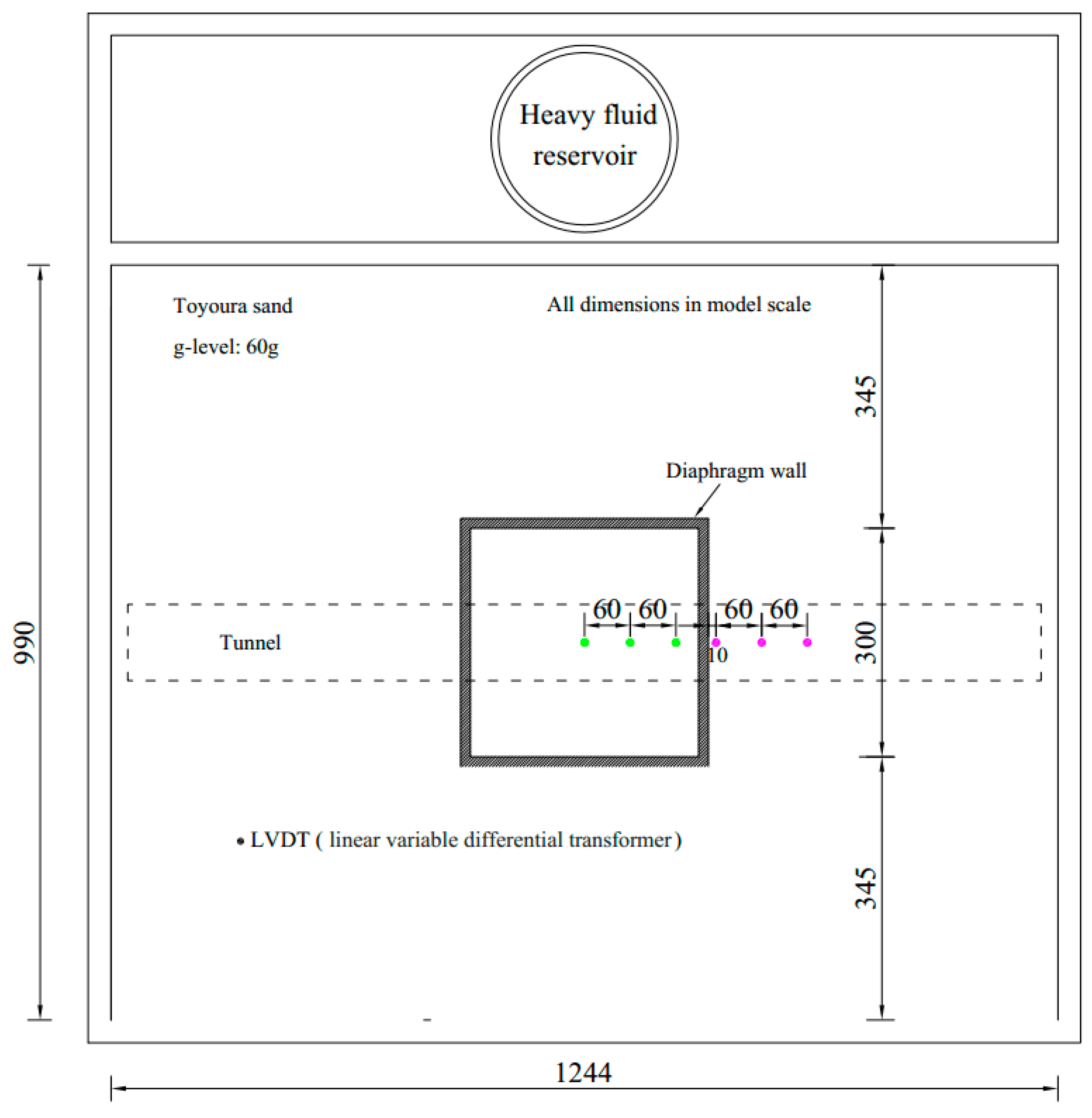
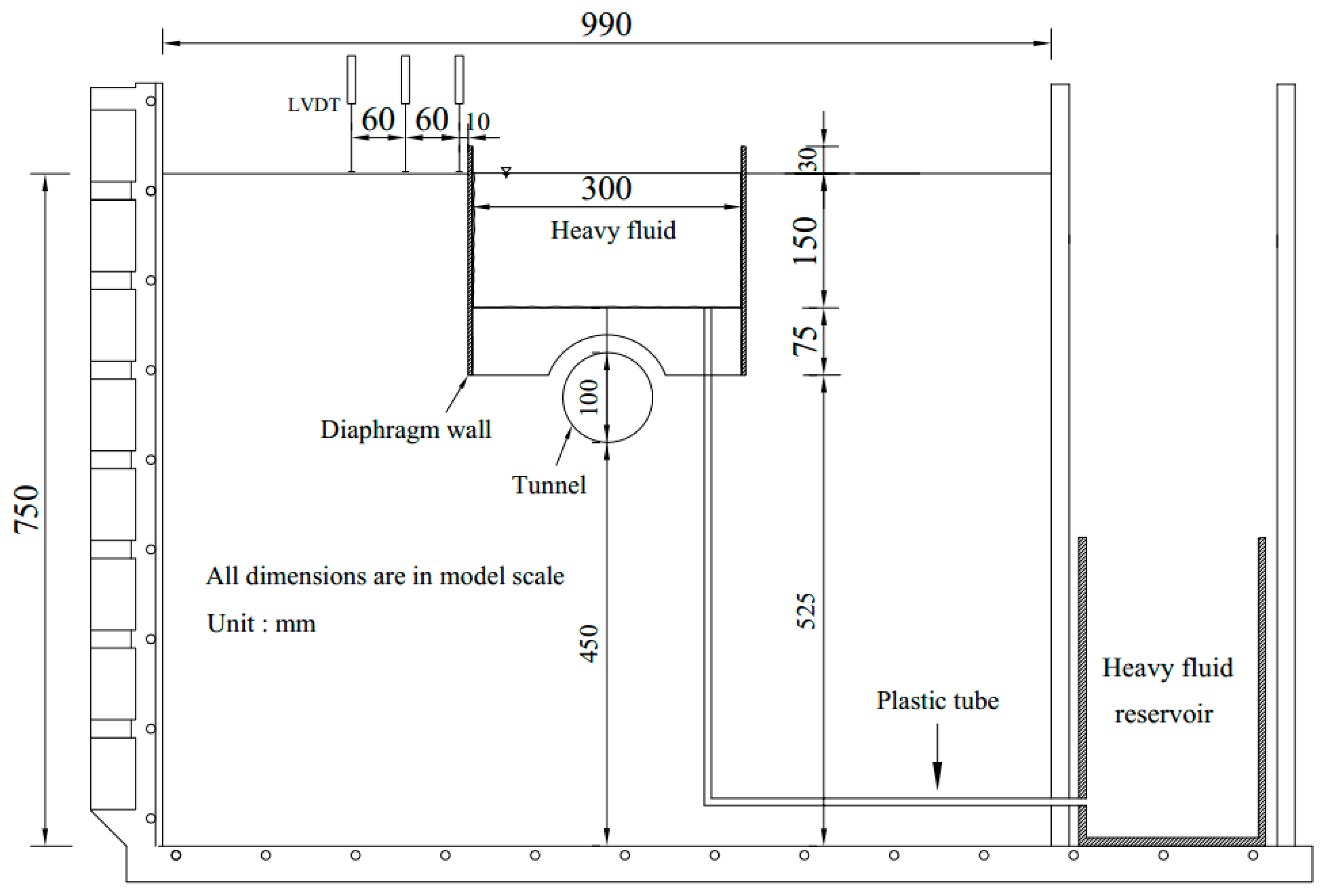
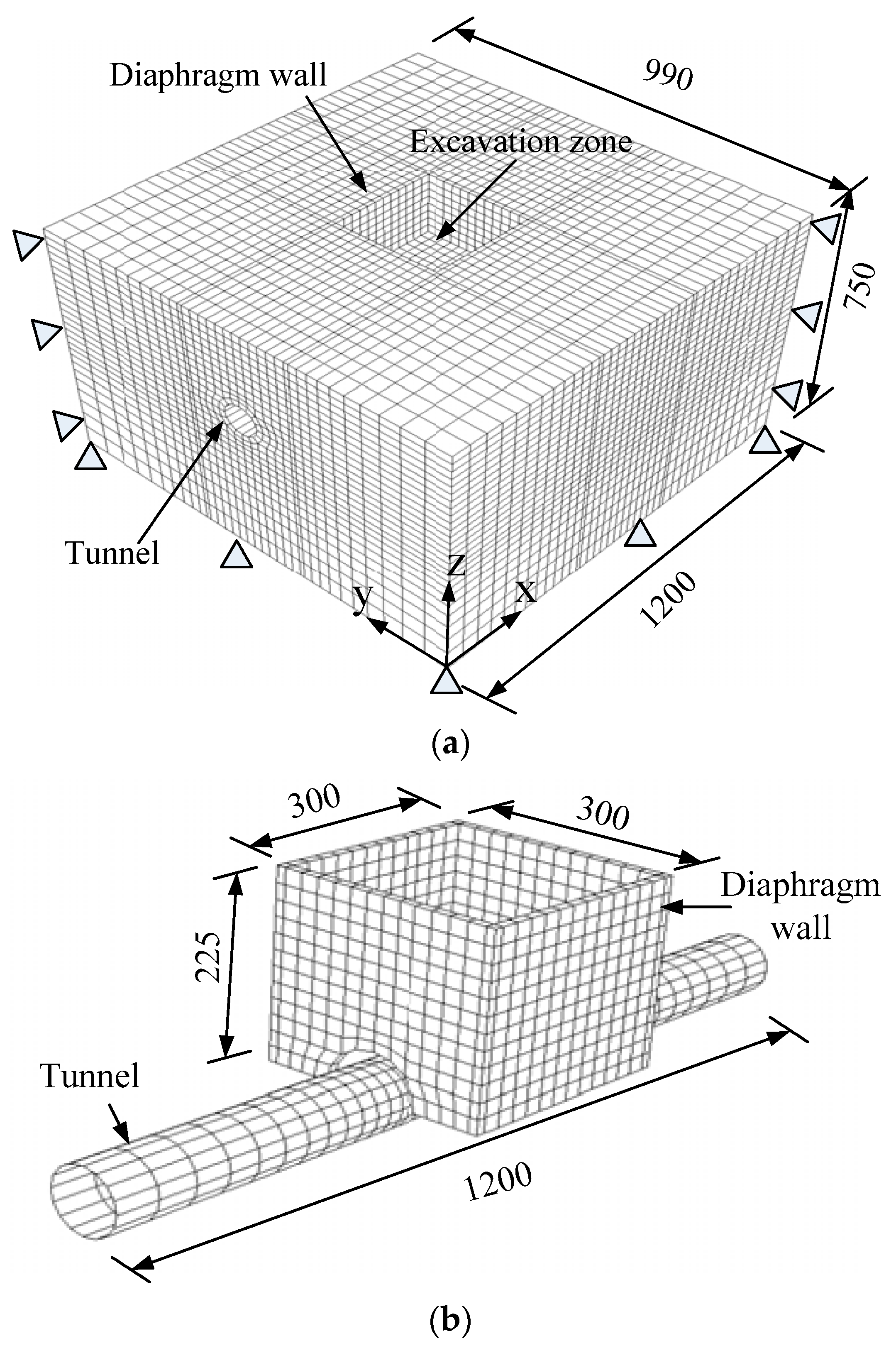
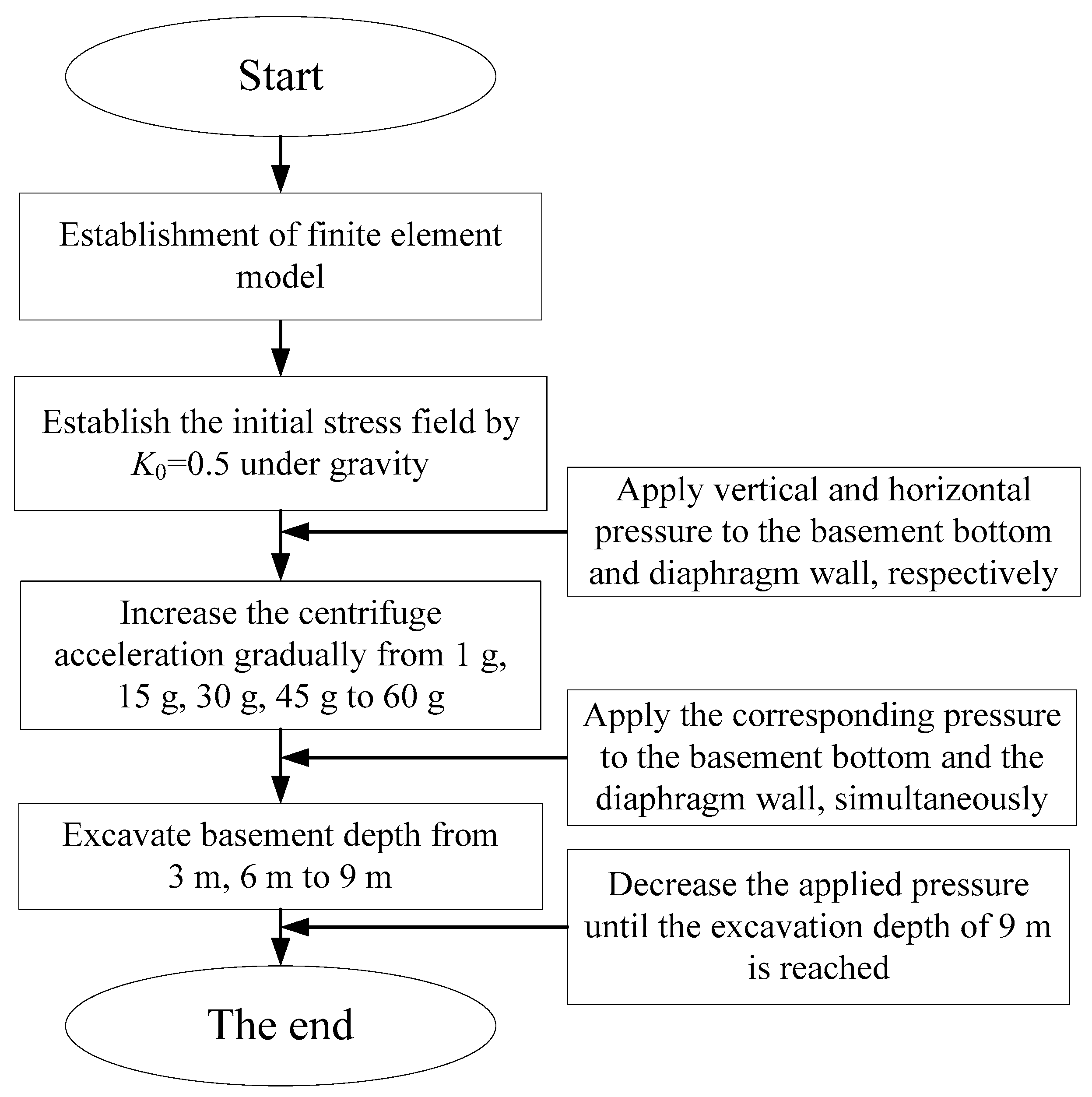
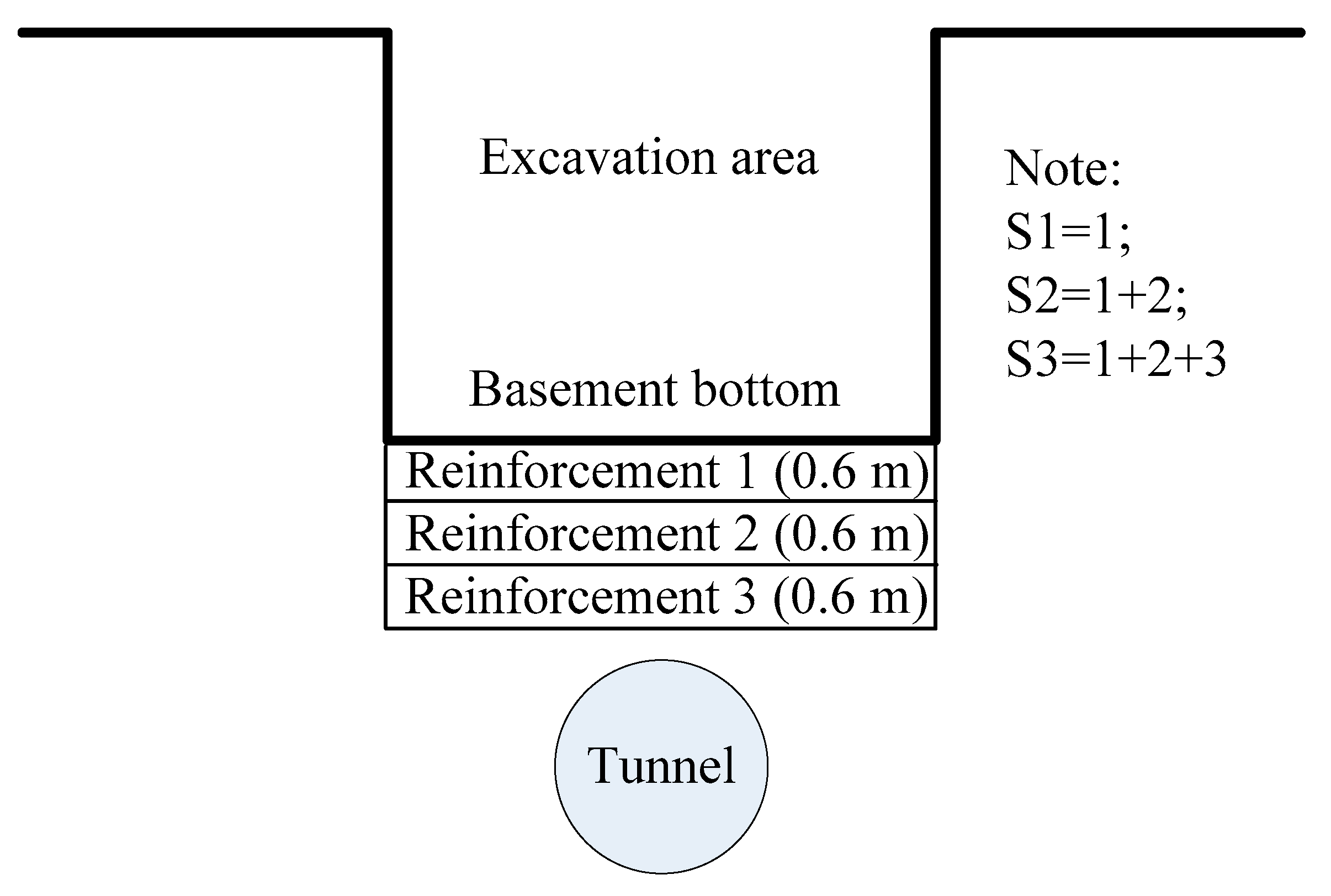
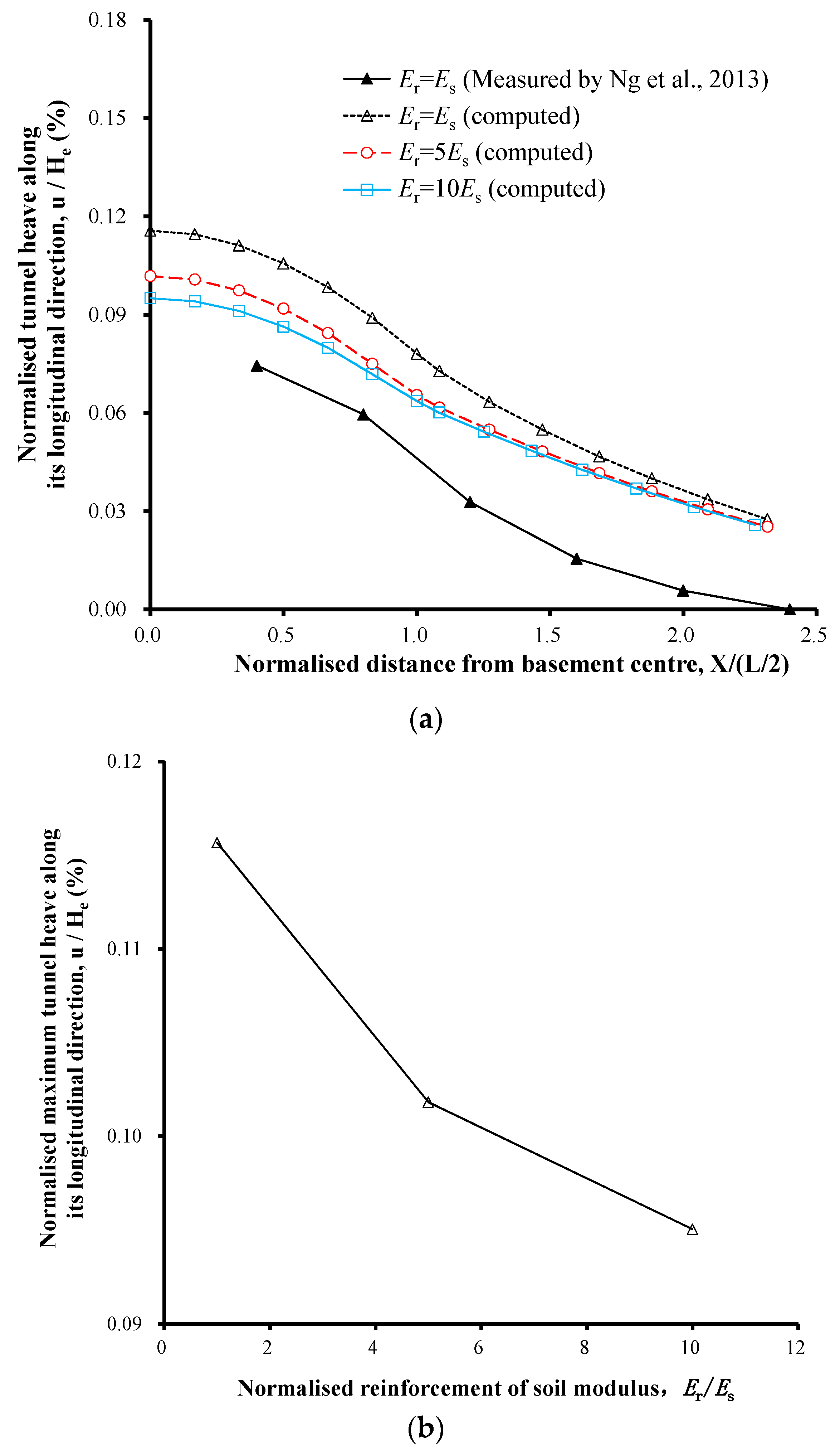
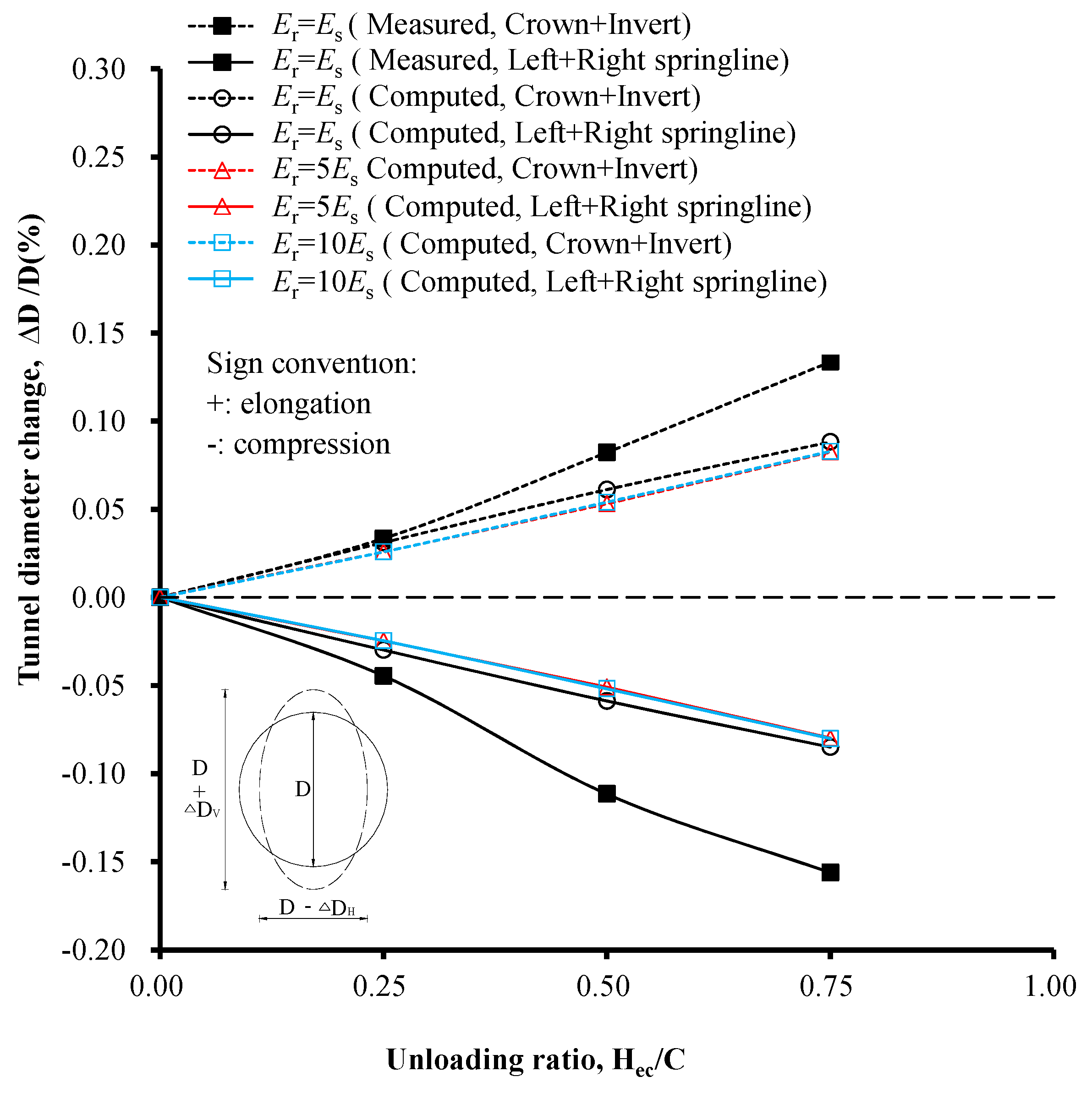
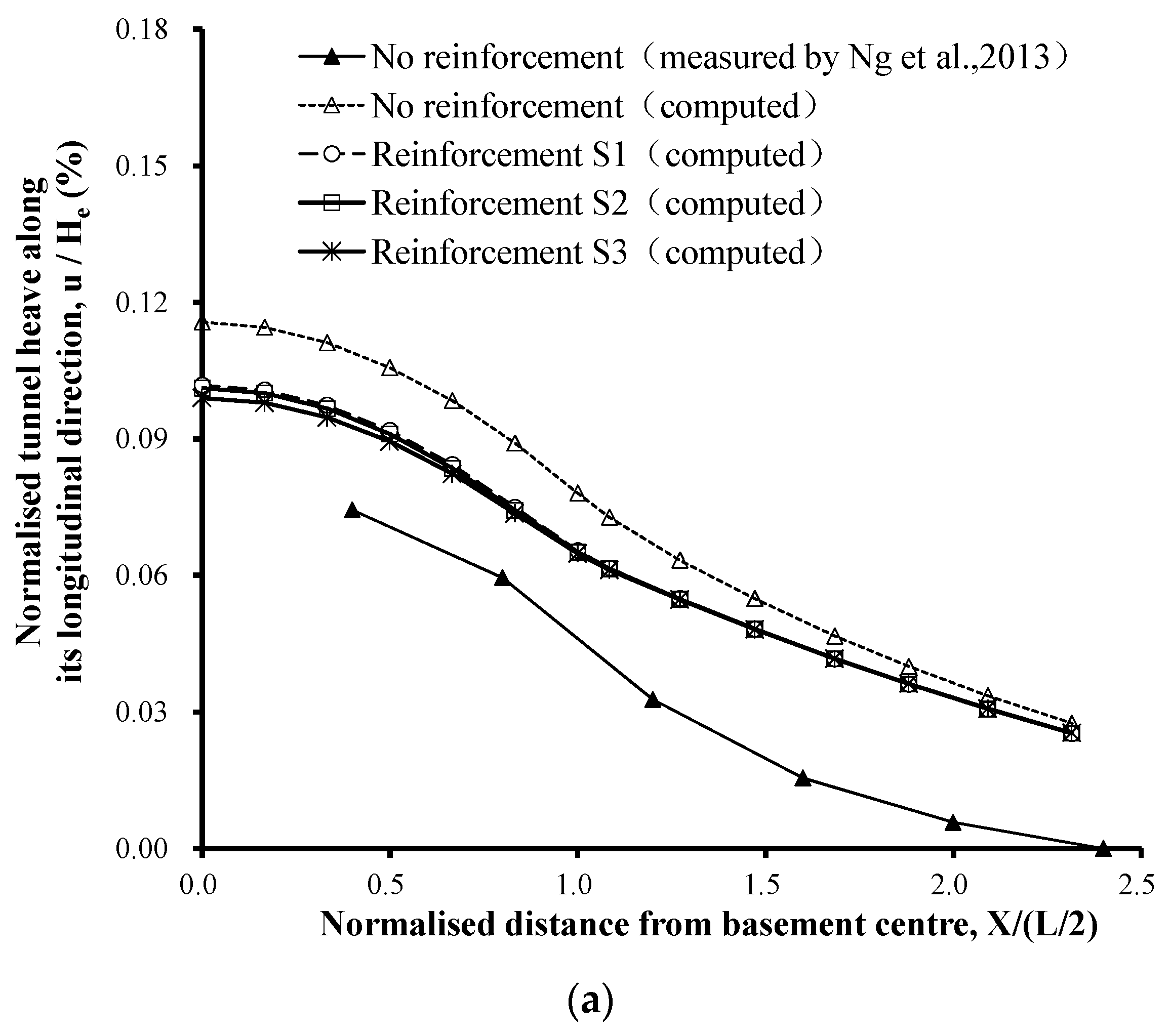
| Soil Parameters | Values |
|---|---|
| Young’s modulus, Es | 117 MPa |
| Poisson’s ratio, ν | 0.3 |
| Peak friction angle, φp | 35° |
| Critical friction angle, φc | 30° |
| Cohesion, c | 2 kPa |
| Dilatancy angle, ψ | 6° |
| Cases | Young’s Modulus of Reinforced Soil, Er | Max. Tunnel Heave | Max. Change in Tunnel Diameter |
|---|---|---|---|
| No reinforcement | Er = Es | +50% | −35% |
| Reinforcement S1 | Er = 5Es | +32% | −39% |
| Reinforcement S1 | Er = 10Es | +23% | −39% |
| Reinforcement S2 | Er = 5Es | +31% | −39% |
| Reinforcement S3 | Er = 5Es | +28% | −40% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Sun, W. Effect of Soil Reinforcement on Tunnel Deformation as a Result of Stress Relief. Appl. Sci. 2019, 9, 1420. https://doi.org/10.3390/app9071420
Sun H, Sun W. Effect of Soil Reinforcement on Tunnel Deformation as a Result of Stress Relief. Applied Sciences. 2019; 9(7):1420. https://doi.org/10.3390/app9071420
Chicago/Turabian StyleSun, Huasheng, and Wenbin Sun. 2019. "Effect of Soil Reinforcement on Tunnel Deformation as a Result of Stress Relief" Applied Sciences 9, no. 7: 1420. https://doi.org/10.3390/app9071420
APA StyleSun, H., & Sun, W. (2019). Effect of Soil Reinforcement on Tunnel Deformation as a Result of Stress Relief. Applied Sciences, 9(7), 1420. https://doi.org/10.3390/app9071420





