Channel Estimation Based on IOTA Filter in OFDM/OQPSK and OFDM/OQAM Systems
Abstract
:Featured Application
Abstract
1. Introduction
2. Related Work
3. OFDM/OQPSK System Model
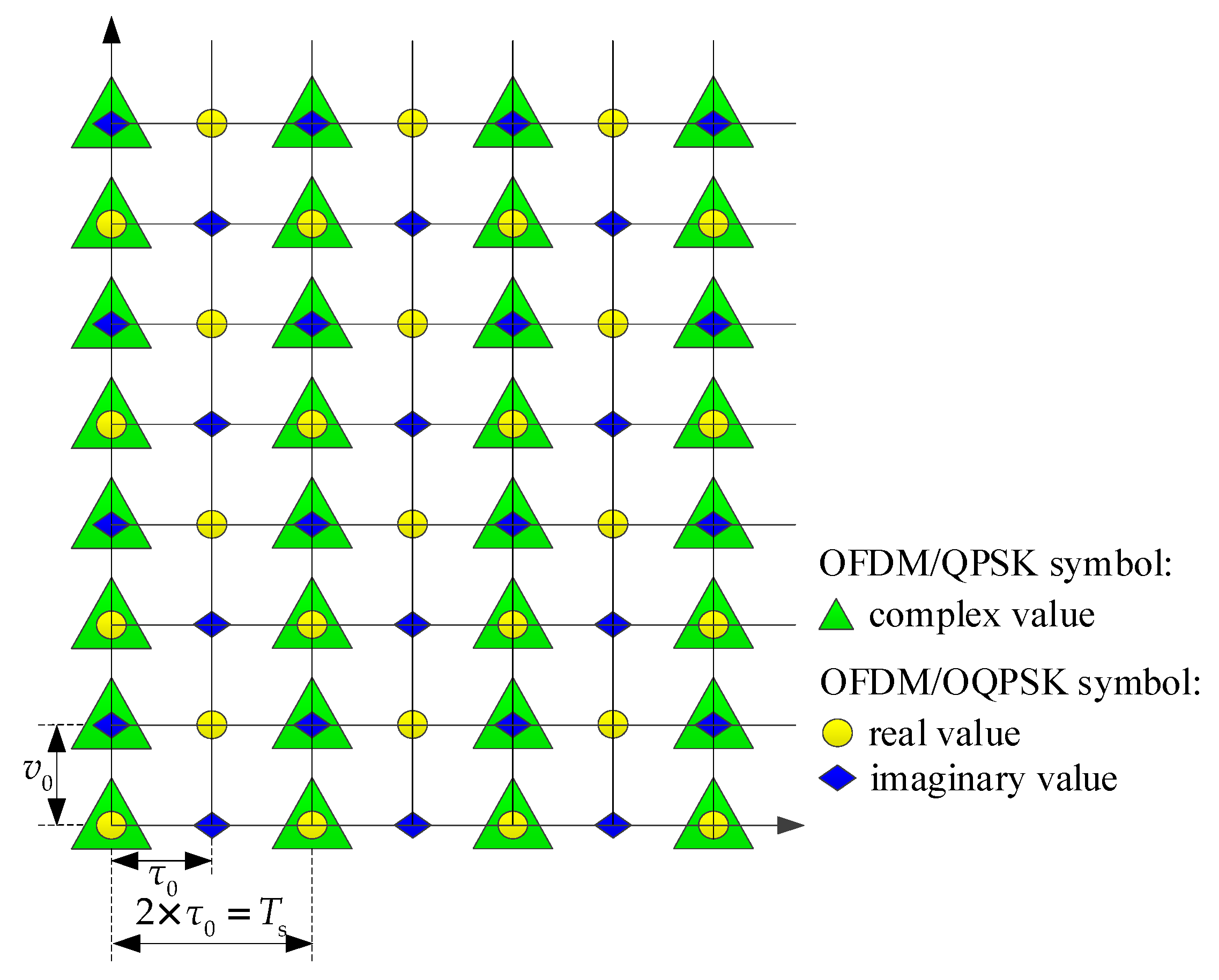
3.1. OFDM/OQPSK Symbols
3.2. Design of the IOTA Filter
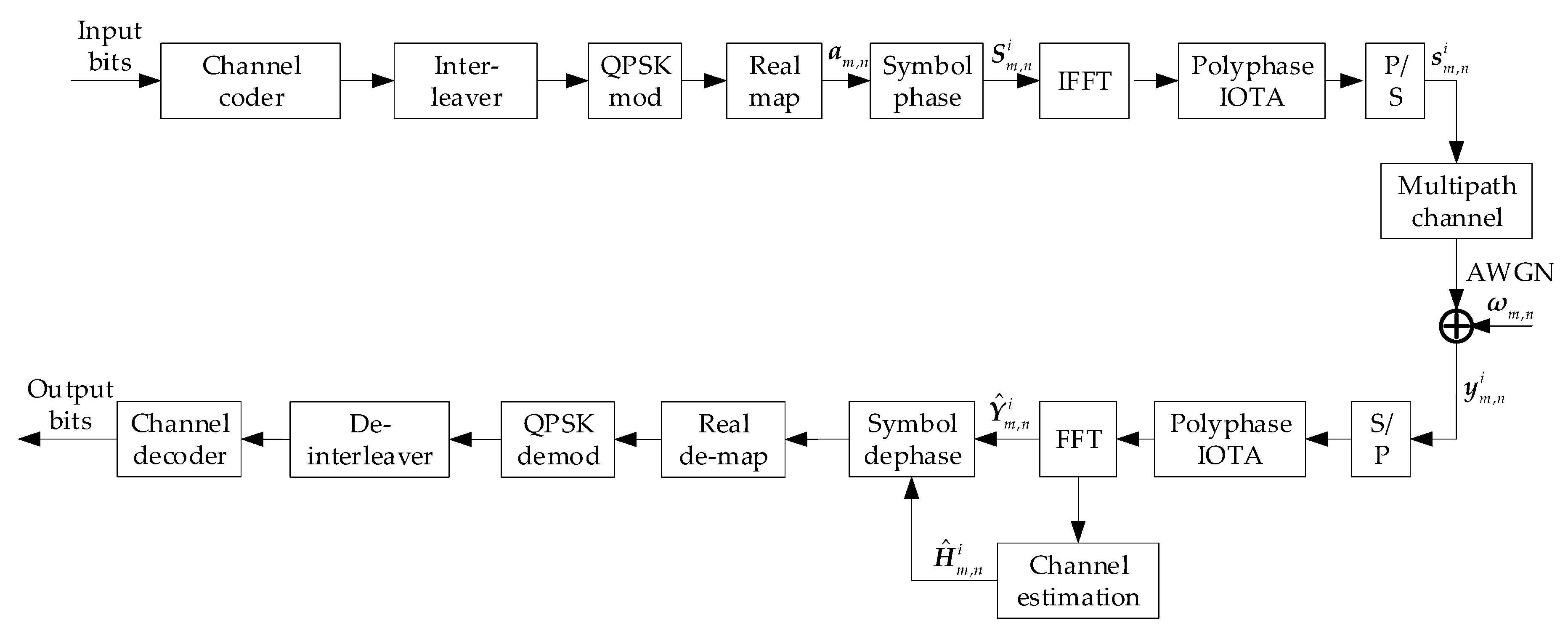
3.3. OFDM-IOTA System Model
4. Channel Coding
4.1. Time Diversity in Jakes Model
4.2. Convolutional Encoder and Viterbi Decoder
5. Simulation Results
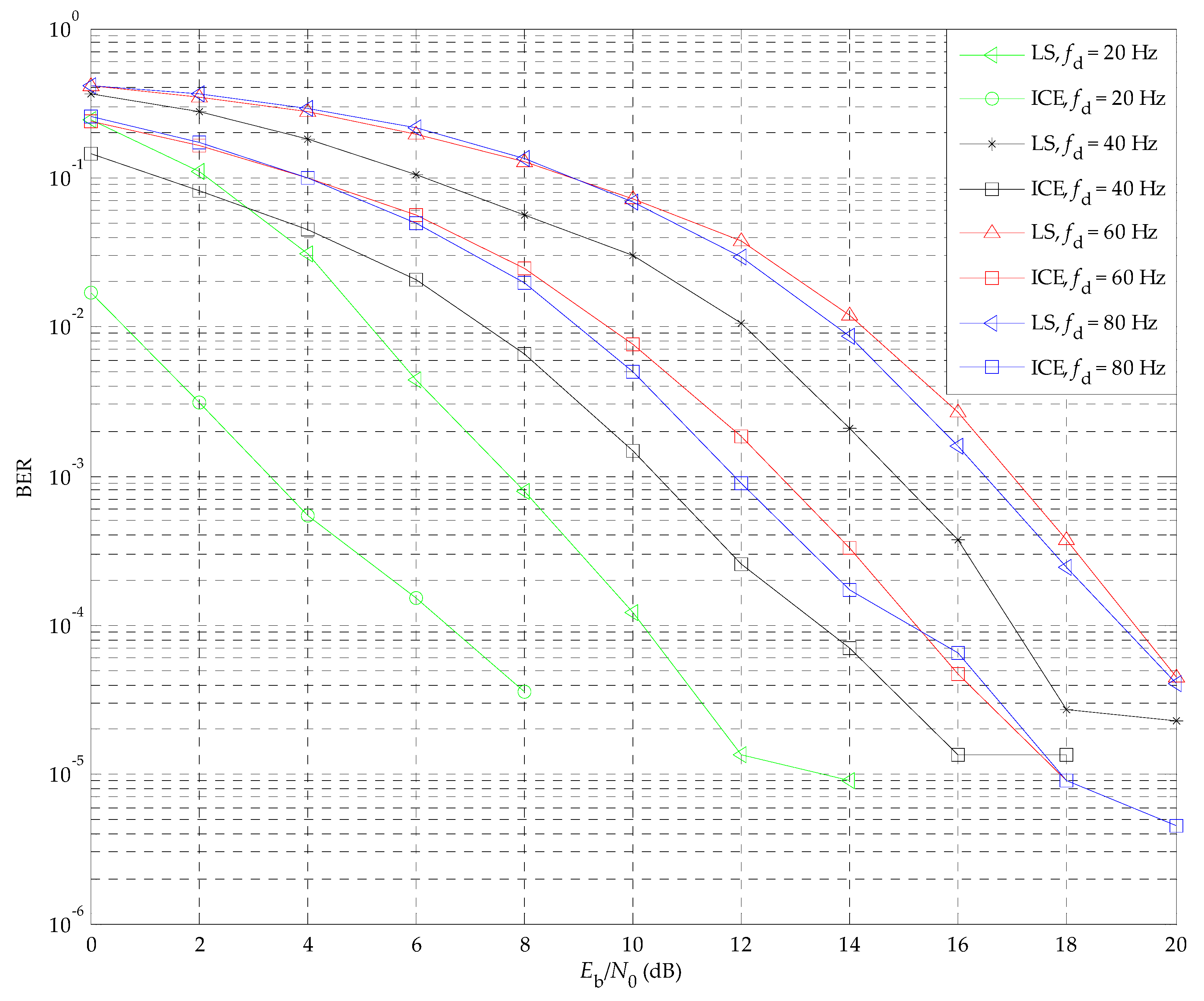
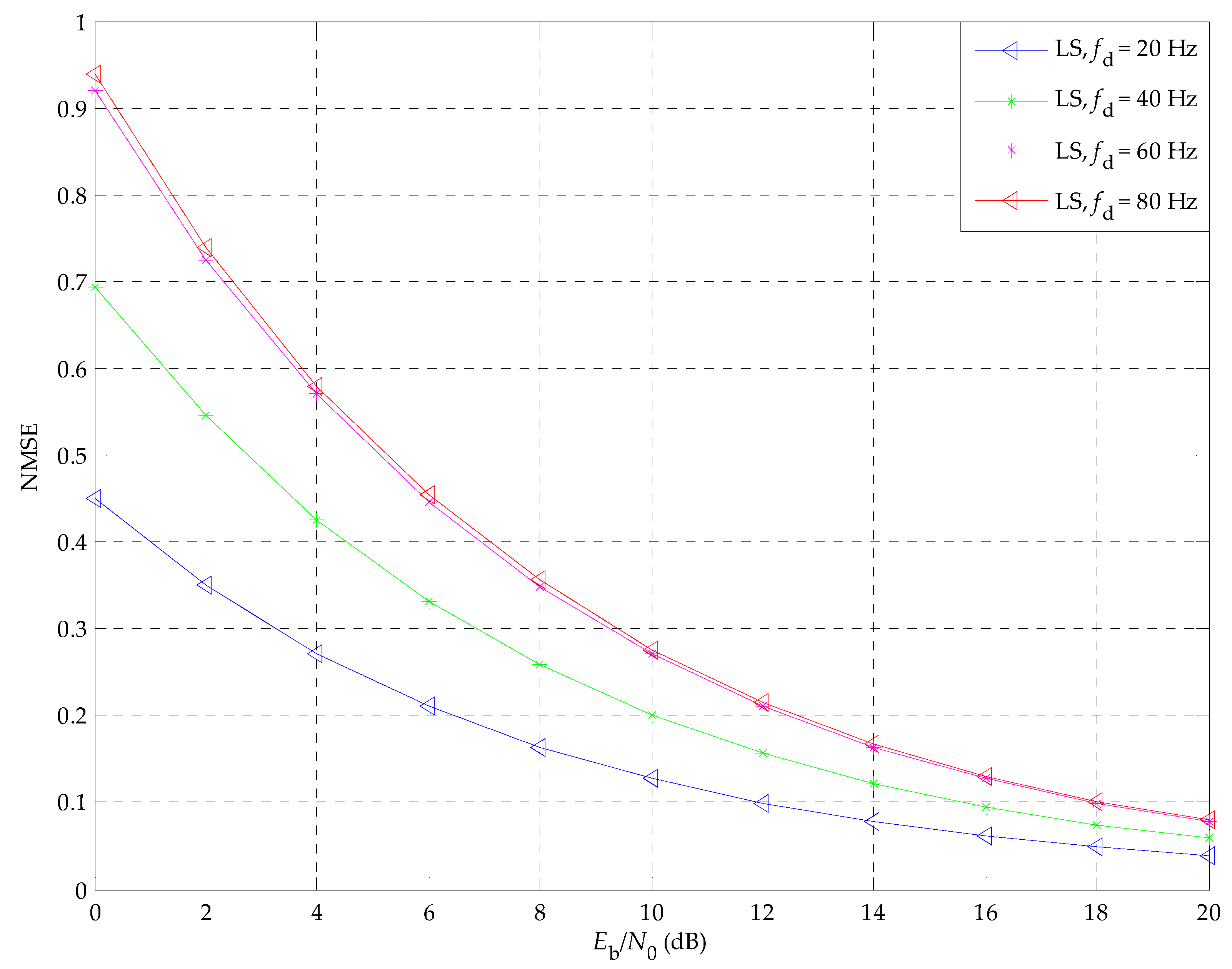
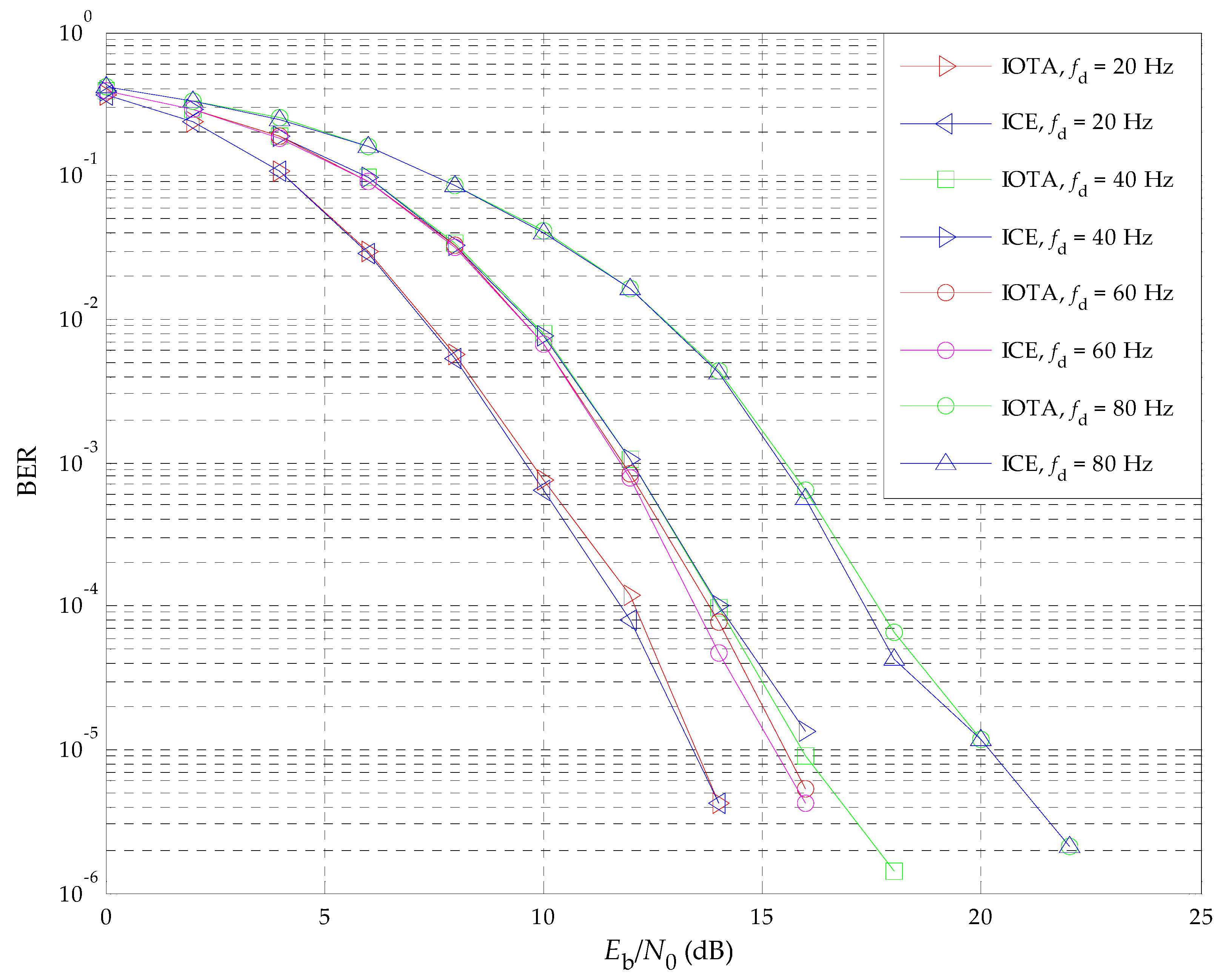
5.1. The Performance of the OFDM/OQPSK System
5.2. The Performance of the OFDM/QPSK System
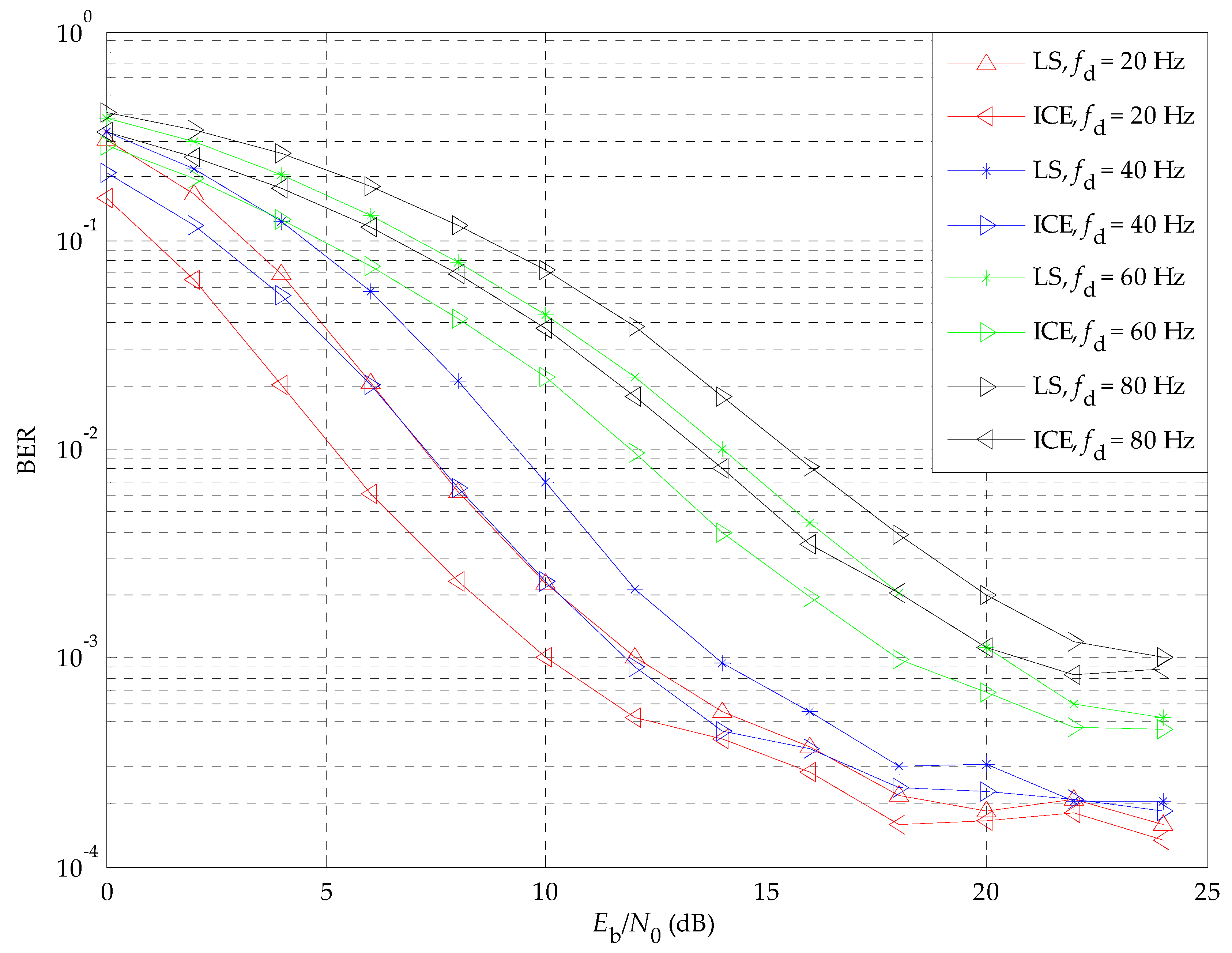
5.3. The Performance of the OFDM/OQAM System
5.4. The Performance of the OFDM/16-QAM System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Galande, N.A.; Shah, A.M. Implementation of OFDM by using wavelet for optimization of wireless communication system. In Proceedings of the IEEE International Conference on Recent Trends in Electronics, Information and Communication Technology, Bangalore, India, 20–21 May 2016; pp. 451–455. [Google Scholar] [CrossRef]
- Du, J.F.; Signell, S. Time frequency localization of pulse shaping filters in OFDM/OQAM systems. In Proceedings of the 6th International Conference on Information, Communications and Signal Processing, Singapore, Singapore, 10–13 December 2007; pp. 1–5. [Google Scholar] [CrossRef]
- Sheela, M.S.; Surekha, T.P.; Arjun, K.R. Analysis of BER in OFDM using wavelet and FFT based method. In Proceedings of the International Conference on Current Trends in Computer, Electrical, Electronics and Communication, Mysore, India, 8–9 September 2017; pp. 473–476. [Google Scholar] [CrossRef]
- Yoo, T.W.; Im, S.B.; Hwang, S.H.; Choi, H.J. Pilot structure for high data rate in OFDM/OQAM-IOTA system. In Proceedings of the 68th IEEE Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Kongara, K.P.; Smith, P.J.; Mann, S. A comparison of CP-OFDM with IOTA-OFDM under typical system imperfections. In Proceedings of the IET Seminar on Wideband and Ultrawideband Systems and Technologies, London, UK, 6 November 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Mehmood, S.; Dasalukunte, D.; Öwall, V. Hardware architecture of IOTA pulse shaping filters for multicarrier systems. IEEE Trans. Circuits Syst. Regul. Pap. 2013, 60, 733–742. [Google Scholar] [CrossRef]
- Du, J.; Xiao, P.; Wu, J.; Chen, Q. Design of isotropic orthogonal transform algorithm based multicarrier systems with blind channel estimation. IET Commun. 2012, 6, 2695–2704. [Google Scholar] [CrossRef]
- Kurt, T.; Siala, M.; Yongaçoglu, A. Multi-carrier signal shaping employing Hermite functions. In Proceedings of the 13th European Signal Processing Conference, Antalya, Turkey, 4–8 September 2005; pp. 2026–2029. [Google Scholar]
- Razavi, R.; Xiao, P.; Tafazolli, R. Information theoretic analysis of OFDM/OQAM with utilized intrinsic interference. IEEE Signal Process. Lett. 2015, 22, 618–622. [Google Scholar] [CrossRef]
- Kol, V.K.; Mishra, A. Discrete wavelet transform based OFDM-IDMA system with AWGN channel. In Proceedings of the Students Conference on Engineering and Systems, Allahabad, India, 12–14 April 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Abdullah, K.; Al-Hinai, N.; Sadik, A.Z.; Hussain, Z.M. Circular 16-QAM modulation scheme for wavelet and Fourier based OFDM systems. In Proceedings of the 5th GCC Conference and Exhibition, Kuwait City, Kuwait, 17–19 March 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Bader, F.; Shaat, M.; Medjahdi, Y. New opportunities for spectrum coexistence using advanced multicarrier scheme. In Proceedings of the Military Communications and Information Systems Conference, Saint Malo, France, 7–9 October 2013; pp. 1–6. [Google Scholar]
- Suma, M.N.; Narasimhan, S.V.; Kanmani, B. The OFDM system based on discrete cosine harmonic wavelet transform. In Proceedings of the National Conference on Communications, Kharagpur, India, 3–5 February 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Siohan, P.; Roche, C. Cosine-modulated filterbanks based on extended Gaussian functions. IEEE Trans. Signal Process. 2000, 48, 3052–3061. [Google Scholar] [CrossRef]
- Zhou, X.; Ye, Z.; Liu, X.X.; Wang, C.Y. Channel estimation based on linear filtering least square in OFDM systems. J. Commun. 2016, 11, 1005–1011. [Google Scholar] [CrossRef]
- Zhou, X.; Ye, Z.; Liu, X.X.; Wang, C.Y. Chi-square distribution-based confidence measure channel estimation method in OFDM Systems. IETE J. Res. 2017, 63, 662–670. [Google Scholar] [CrossRef]
- Jacob, N.; Sripati, U. Bit error rate of coded OFDM for digital audio broadcasting system, employing parallel concatenated convolutional turbo codes. In Proceedings of the IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems, Calicut, India, 19–21 February 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Verma, S.; Sharma, P.; Ahuja, S.; Hajela, P. Partial transmit sequence with convolutional codes for reducing the PAPR of the OFDM signal. In Proceedings of the 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; pp. 70–73. [Google Scholar] [CrossRef]
- Khan, K.; Sheikh, S.A. PAPR reduction of OFDM signals using convolutional codes. In Proceedings of the IEEE Student Conference on Research and Development, Serdang, Malaysia, 16–18 November 2009; pp. 26–28. [Google Scholar] [CrossRef]
- Ahmad, N.; S-Yusof, S.K.; Fisal, N. Analysis of recursive systematic convolutional turbo codes in MB-OFDM UWB with channel estimation. In Proceedings of the International Conference on Computer Applications and Industrial Electronics, Kuala Lumpur, Malaysia, 5–8 December 2010; pp. 137–141. [Google Scholar] [CrossRef]
- Cho, S.C.; Kim, J.U.; Lee, K.T.; Cho, K.R. Convolutional turbo coded OFDM/TDD mobile communication system for high speed multimedia services. In Proceedings of the Advanced Industrial Conference on Telecommunications/Service Assurance with Partial and Intermittent Resources Conference/E-Learning on Telecommunications Workshop, Lisbon, Portugal, 17–20 July 2005; pp. 244–248. [Google Scholar] [CrossRef]
- Tang, R.G.; Zhou, X.; Wang, C.Y. A Haar wavelet decision feedback channel estimation method in OFDM systems. Appl. Sci. 2018, 8, 877. [Google Scholar] [CrossRef]
- Ben Mabrouk, M.; Chafii, M.; Louet, Y.; Bader, F. Low-PAPR condition for 5G-candidate waveforms. In Proceedings of the General Assembly and Scientific Symposium of the International Union of Radio Science, Montreal, QC, Canada, 19–26 August 2017; pp. 1–4. [Google Scholar] [CrossRef]





| 0 | 1 | 0.75 | 1.6406 | 2.6367 | 4.6529 | 6.9749 | 11.5368 | 16.8193 |
| 1 | −1 | −1.875 | −3.4219 | −5.9131 | −9.8831 | −15.7769 | −24.8536 | 0 |
| 2 | 0.75 | 1.1875 | 3.0176 | 4.7681 | 9.0985 | 14.0379 | 23.4937 | 0 |
| 3 | −0.625 | −0.9609 | −2.2354 | −4.2567 | −7.3957 | −12.2028 | 0 | 0 |
| 4 | 0.5469 | 0.8320 | 1.9036 | 3.4279 | 6.6095 | 10.3934 | 0 | 0 |
| 5 | −0.4922 | −0.7451 | −1.6937 | −3.0167 | −5.6268 | 0 | 0 | 0 |
| 6 | 0.4512 | 0.6812 | 1.5433 | 2.7365 | 5.0687 | 0 | 0 | 0 |
| 7 | −0.4189 | −0.6314 | −1.4279 | −2.526 | 0 | 0 | 0 | 0 |
| 8 | 0.3928 | 0.5913 | 1.3356 | 2.3594 | 0 | 0 | 0 | 0 |
| 9 | −0.3709 | −0.558 | −1.2594 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0.3524 | 0.5299 | 1.1951 | 0 | 0 | 0 | 0 | 0 |
| 11 | −0.3364 | −0.5056 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0.3224 | 0.4843 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | −0.31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0.2989 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameters | Specifications |
|---|---|
| 15 | |
| 8 | |
| Parameters | Specifications |
|---|---|
| Symbol duration | QPSK: 1/6000 s, 16-QAM: 1/3000 s |
| Symbol rate | 12 kbit/s |
| Guard interval (GI) length | OFDM-IOTA: 0, CP-OFDM: 128 symbols |
| System model | OFDM-IOTA / CP-OFDM |
| The length of FFT | 512 |
| Carrier frequency | 2 GHz |
| Fast fading model | Jakes spectrum |
| Number of multi-paths | 6 |
| Code rate | 1/2 |
| 0.995 | |
| Inter-leaver | Block inter-leaver (300 OFDM symbols) |
| Doppler spread | 20, 40, 60, 80 Hz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, C.; Tang, R. Channel Estimation Based on IOTA Filter in OFDM/OQPSK and OFDM/OQAM Systems. Appl. Sci. 2019, 9, 1454. https://doi.org/10.3390/app9071454
Zhou X, Wang C, Tang R. Channel Estimation Based on IOTA Filter in OFDM/OQPSK and OFDM/OQAM Systems. Applied Sciences. 2019; 9(7):1454. https://doi.org/10.3390/app9071454
Chicago/Turabian StyleZhou, Xiao, Chengyou Wang, and Ruiguang Tang. 2019. "Channel Estimation Based on IOTA Filter in OFDM/OQPSK and OFDM/OQAM Systems" Applied Sciences 9, no. 7: 1454. https://doi.org/10.3390/app9071454
APA StyleZhou, X., Wang, C., & Tang, R. (2019). Channel Estimation Based on IOTA Filter in OFDM/OQPSK and OFDM/OQAM Systems. Applied Sciences, 9(7), 1454. https://doi.org/10.3390/app9071454







