Seismic Response of Aeolian Sand High Embankment Slopes in Shaking Table Tests
Abstract
:1. Introduction
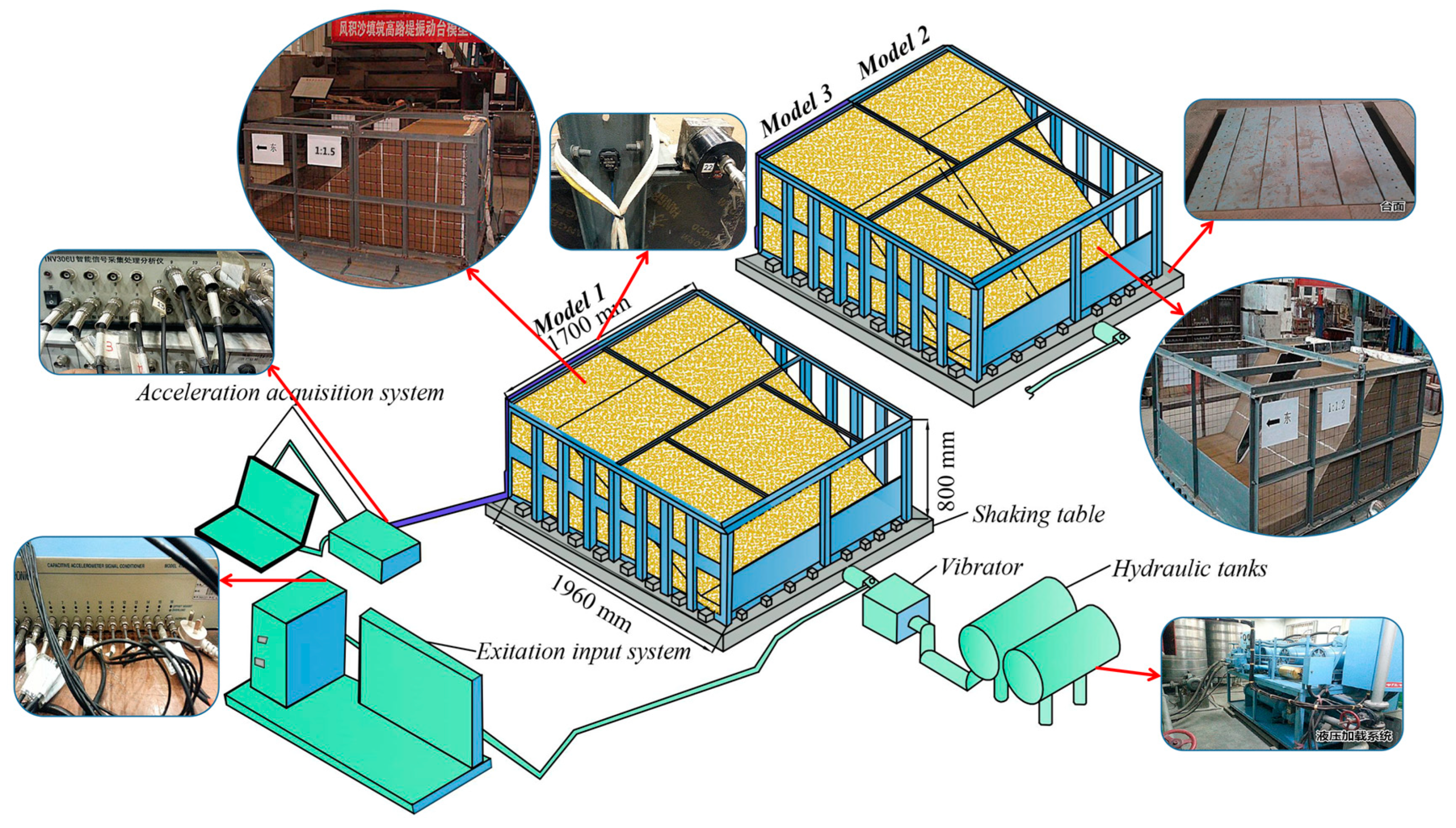
2. Shaking Table Tests
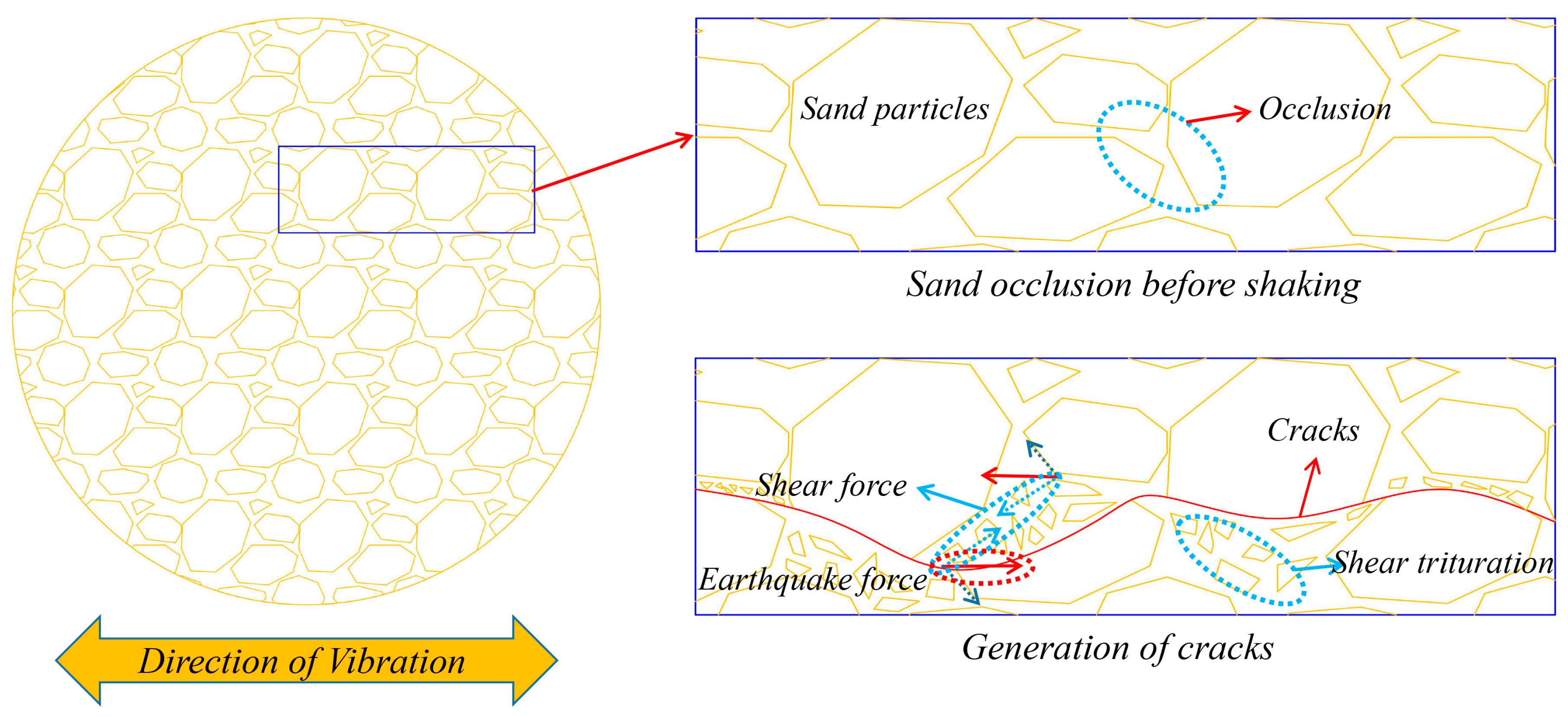
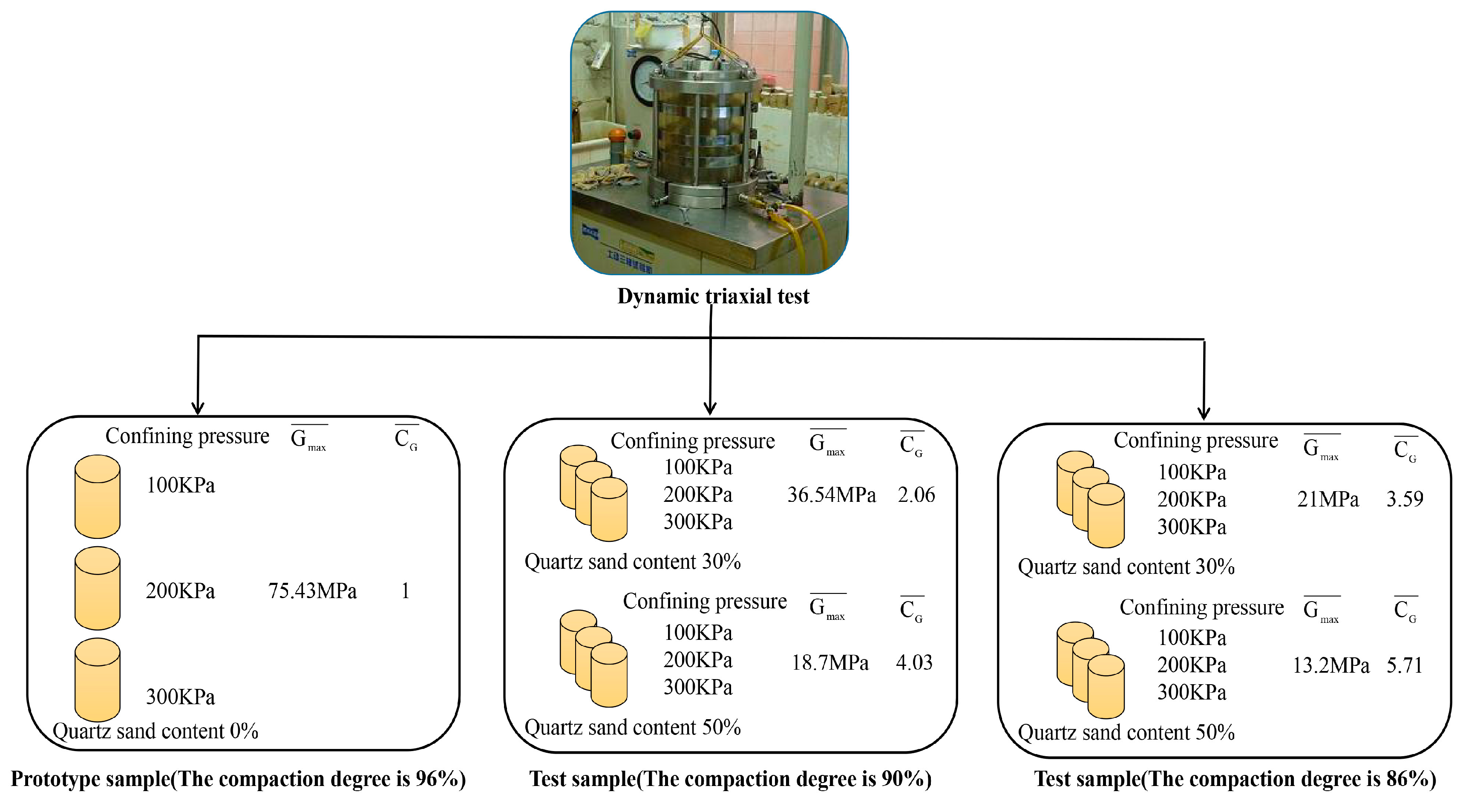
2.1. Mechanical Properties and Microcosmic Shear Failure Mechanism of Prototype Sand
2.2. Similarity Laws and Materials
2.3. Test Cases
2.4. Boundary Effect and Loading Method
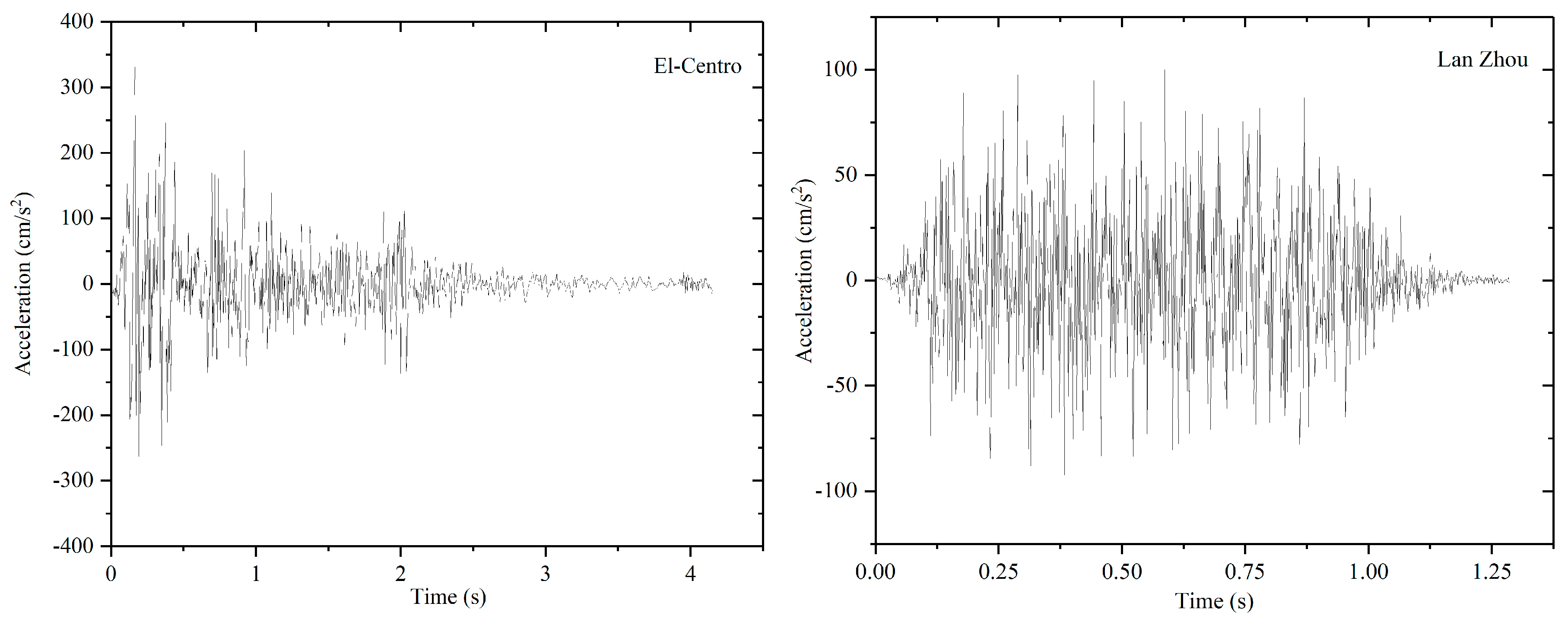
2.5. Rationality of the Earthquake Excitations
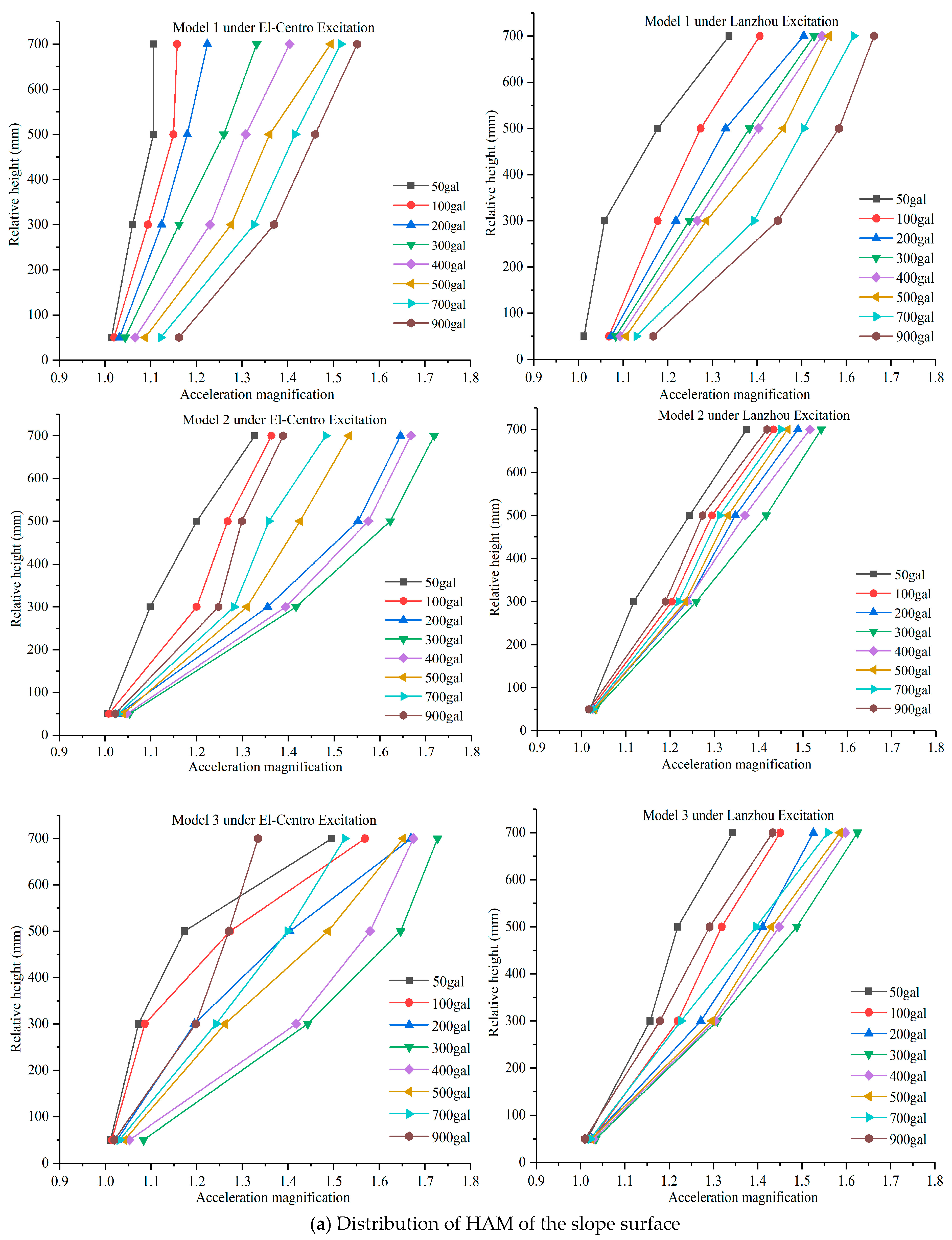
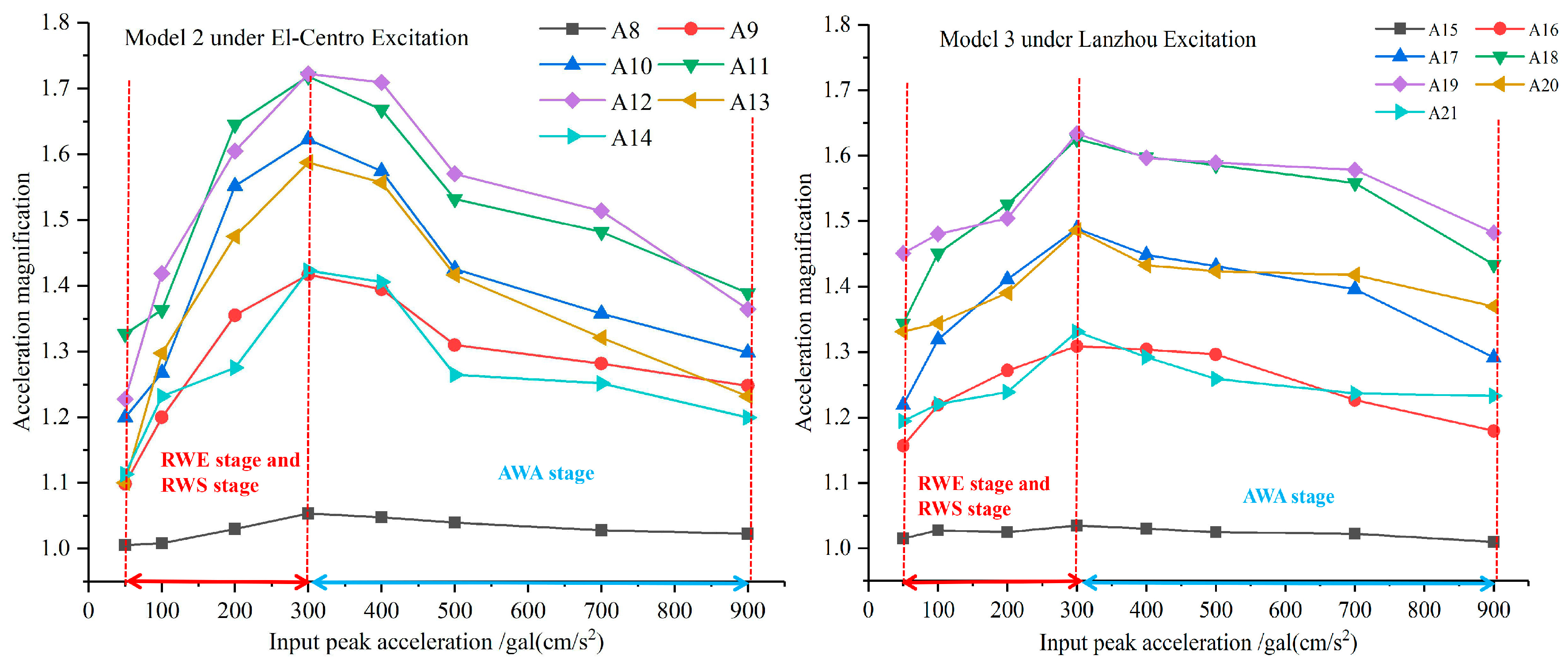
3. Horizontal Acceleration Response Results and Discussion
4. Failure Mode Analysis of Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, C.; Zhang, J.; Wang, Z.; Hou, J.; Si, C. Model test of failure modes of high embankment and aseismic measures for buried strike-slip fault movement. Environ. Earth Sci. 2018, 77, 233. [Google Scholar] [CrossRef]
- Li, Y.; Xu, S.; Liu, H.; Ma, E.; Wang, L. Displacement and stress characteristics of tunnel foundation in collapsible loess ground reinforced by jet grouting columns. Adv. Civ. Eng. 2018, 1–16. [Google Scholar] [CrossRef]
- Lee, J.S.; Santamarina, J.C. Seismic monitoring short-duration events: Liquefaction in 1g models. Can. Geotech. J. 2007, 44, 659–672. [Google Scholar] [CrossRef]
- Lai, J.; He, S.; Qiu, J.; Chen, J.; Wang, L.; Wang, K.; Wang, J. Characteristics of Seismic Disasters and Aseismic Measures of Tunnels in Wenchuan Earthquake. Environ. Earth Sci. 2017, 76, 94. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, X.; He, S.; Liu, H.; Lai, J.; Wang, L. The Catastrophic Landside in Maoxian County, Sichuan, SW China, on June 24, 2017. Nat. Hazards 2017, 89, 1485–1493. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, S.; Kong, X.; Lei, J.; Liu, T. Optimization analysis of settlement parameters for postgrouting piles in loess area of Shaanxi, China. Adv. Civ. Eng. 2019, 1–16. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Z.; Lai, J.; Wang, H.; Wang, K.; Zan, W. Settlement characteristics of jacked box tunneling underneath a highway embankment. J. Perform. Constr. Facil. 2019, 33, 04019005. [Google Scholar] [CrossRef]
- Qin, C.B.; Chian, S.C. Seismic Ultimate Bearing Capacity of a Hoek-Brown Rock Slope Using Discretization-Based Kinematic Analysis and Pseudodynamic Methods. Int. J. Geomech. 2018, 18, 04018054. [Google Scholar] [CrossRef]
- Shukha, R.; Baker, R. Design implications of the vertical pseudo-static coefficient in slope analysis. Comput. Geotech. 2008, 35, 86–96. [Google Scholar] [CrossRef]
- Basha, B.; Babu, G. Seismic Rotational Displacements of Gravity Walls by Pseudodynamic Method with Curved Rupture Surface. Int. J. Geomech. 2010, 10, 93–105. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Chugh, A.K. Dynamic displacement analysis of embankment dams. Geotechnique 1995, 45, 295–299. [Google Scholar] [CrossRef]
- Crespellani, T.; Facciorusso, J.; Madiai, C.; Vannucchi, G. Influence of uncorrected accelerogram processing techniques on Newmark’s rigid block displacement evaluation. Soil Dyn. Earthq. Eng. 2003, 23, 415–424. [Google Scholar] [CrossRef]
- Al-Defae, A.H.; Knappett, J.A. Newmark sliding block model for pile-reinforced slopes under earthquake loading. Soil Dyn. Earthq. Eng. 2015, 75, 265–278. [Google Scholar] [CrossRef] [Green Version]
- Shinoda, M.; Miyata, Y. Regional landslide susceptibility following the Mid NIIGATA prefecture earthquake in 2004 with NEWMARK’S sliding block analysis. Landslides 2017, 14, 1887–1889. [Google Scholar] [CrossRef]
- Kyren, R. Seismic displacement of gently-sloping coastal and marine sediment under multidirectional earthquake loading. Eng. Geol. 2017, 227, 84–92. [Google Scholar]
- Rodriguez-Peces, M.J.; Perez-Garcia, J.L.; Garcia-Mayordomo, J.; Azanón, J.M.; Insua-Arévalo, J.M.; Delgado-García, J. Applicability of Newmark method at regional, sub-regional and site scales: Seismically induced Bullas and La Paca rock-slide cases (Murcia, SE Spain). Nat. Hazards 2011, 59, 1109–1124. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes-A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Nakata, N.; Stehman, M. Substructure shake table test method using a controlled mass: Formulation and numerical simulation. Earthq. Eng. Struct. Dyn. 2012, 41, 1977–1988. [Google Scholar] [CrossRef]
- Yakut, A.; Kazaz, I.; Gulkan, P. Numerical simulation of dynamic shear wall tests: A benchmark study. Comput. Struct. 2006, 84, 549–562. [Google Scholar] [CrossRef]
- Akcelyan, S.; Lignos, D.G.; Hikino, T. Adaptive numerical method algorithms for nonlinear viscous and bilinear oil damper models subjected to dynamic loading. Soil Dyn. Earthq. Eng. 2018, 113, 488–502. [Google Scholar] [CrossRef]
- Nurhan, E. Simulation of seismic liquefaction: 1-g model testing system and shaking table tests. Eur. J. Environ. Civ. Eng. 2013, 17, 899–919. [Google Scholar] [Green Version]
- Goldgruber, M.; Shahriari, S.; Zenz, G. Dynamic Sliding Analysis of a Gravity Dam with Fluid-Structure-Foundation Interaction Using Finite Elements and Newmark’s Sliding Block Analysis. Rock Mech. Rock Eng. 2015, 48, 2405–2419. [Google Scholar] [CrossRef]
- Luo, X.; Li, D.; Yang, Y.; Zhang, S. Spatiotemporal Traffic Flow Prediction with KNN and LSTM. J. Adv. Transp. 2019, 1–10. [Google Scholar] [CrossRef]
- Zhou, Z.; Ren, C.; Xu, G.; Zhan, H.; Liu, T. Dynamic failure mode and dynamic response of high slope using shaking table test. Shock Vib. 2019, 1–19. [Google Scholar] [CrossRef]
- Teymur, B.; Madabhushi, S.P.G. Experimental study of boundary effects in dynamic centrifuge modelling. Geotechnique 2003, 53, 655–663. [Google Scholar] [CrossRef]
- Rayhani, M.M.; Naggar, E.L. Centrifuge modeling of seismic response of layered soft clay. Bull. Earthq. Eng. 2007, 5, 571–589. [Google Scholar] [CrossRef]
- Torisu, S.; Sato, J.; Towhata, I.; Honda, T. 1-G model tests and hollow cylindrical torsional shear experiments on seismic residual displacements of fill dams from the viewpoint of seismic performance-based design. Soil Dyn. Earthq. Eng. 2010, 30, 423–437. [Google Scholar] [CrossRef]
- Qiu, J.; Qin, Y.; Lai, J.; Wang, K.; Niu, F.; Wang, H.; Zhang, G. Structural response of the metro tunnel under local dynamic water environment in loess strata. Geofluids 2019, 1–16. [Google Scholar] [CrossRef]
- Dashti, S.; Hashash, Y.M.A.; Gillis, K.; Musgrove, M.; Walker, M. Development of dynamic centrifuge models of underground structures near tall buildings. Soil Dyn. Earthq. Eng. 2016, 86, 89–105. [Google Scholar] [CrossRef] [Green Version]
- Balci, M.C.; Kayabali, K.; Asadi, R. Miniature Centrifuge Modeling for Conventional Consolidation Test. Geotech. Test. J. 2018, 41, 590–600. [Google Scholar] [CrossRef]
- Ziotopoulou, K. Seismic response of liquefiable sloping ground: Class A and C numerical predictions of centrifuge model responses. Soil Dyn. Earthq. Eng. 2018, 113, 744–757. [Google Scholar] [CrossRef]
- Sadrekarimi, A. Dynamic Behavior of Granular Soils at Shallow depths from 1 g shaking table tests. J. Earthq. Eng. 2013, 17, 227–252. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.; Weng, X.; Xie, Y. A new soil-water characteristic curve model for unsaturated loess based on wetting-induced pore deformation. Geofluids 2019, 1–14. [Google Scholar] [CrossRef]
- Guler, E.; Selek, O. Reduced-Scale Shaking Table Tests on Geosynthetic-Reinforced Soil Walls with Modular Facing. J. Geotech. Geonvironmental Eng. 2014, 140, 04014015. [Google Scholar] [CrossRef]
- Lai, J.; Wang, X.; Qiu, J.; Chen, J.; Hu, Z.; Wang, H. Extreme deformation characteristics and countermeasures for a tunnel in difficult grounds in southern Shaanxi, China. Environ. Earth Sci. 2018, 77, 1–14. [Google Scholar] [CrossRef]
- Yazdandoust, M. Seismic performance of soil-nailed walls using a 1g shaking table. Can. Geotech. J. 2018, 55, 1–18. [Google Scholar] [CrossRef]
- Profession Standard of the People’s Republic of China. Test Methods of Soils for Highway Engineering (JTG E40-2007); Ministry of Communications of the PRC: Beijing, China, 2007.
- Iai, S.; Tobita, T.; Nakahara, T. Generalized scaling relations for dynamic centrifuge tests. Geotechnique 2005, 55, 355–362. [Google Scholar] [CrossRef]
- Park, H.J.; Kim, D.S. Centrifuge modelling for evaluation of seismic behaviour of stone masonry structure. Soil Dyn. Earthq. Eng. 2013, 53, 187–195. [Google Scholar] [CrossRef] [Green Version]
- Dezi, F.; Morici, M.; Carbonari, S.; Leoni, G. Higher order model for the seismic response of bridge embankments. Soil Dyn. Earthq. Eng. 2012, 43, 186–201. [Google Scholar] [CrossRef]
- Hardin, B.O. Vibration modulus of normally consolidated clay. J. Soil Mech. Found. Div. 1968, 94, 353–370. [Google Scholar]
- Qiu, J.; Wang, X.; Lai, J.; Zhang, Q.; Wang, J. Response characteristics and preventions for seismic subsidence of loess in Northwest China. Nat. Hazards 2018, 92, 1909–1935. [Google Scholar] [CrossRef]
- Lai, J.; Wang, K.; Qiu, J.; Niu, F.; Wang, J.; Chen, J. Vibration response characteristics of the cross tunnel structure. Shock Vib. 2016, 1–16. [Google Scholar] [CrossRef]
- Huang, R. Some catastrophic landslides since the twentieth centuryin the southwest of China. Landslides 2009, 6, 69–81. [Google Scholar] [CrossRef]
- Wang, X.; Lai, J.; Garnes, R. On the Support System for Tunnelling in Squeezing Ground of Qingling-Daba Mountainous Area: Case Study from Soft Rock Tunnels. Adv. Civ. Eng. 2019, 1–14. [Google Scholar] [CrossRef]
- Burjanek, J.V.; Gischig, J.; Moore, R.; Fah, D. Ambient vibration characterization and monitoring of a rock slope close to collapse. Geophys. J. Int. 2018, 212, 297–310. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, Z.; Tao, L.; Cui, J.; Yan, Q. Model tests on longitudinal surface settlement caused by shield tunnelling in sandy soil. Sustain. Cities Soc. 2019, 47, 101504. [Google Scholar] [CrossRef]
- Lai, J.; Qiu, J.; Fan, H.; Zhang, Q.; Hu, Z.; Wang, J.; Chen, J. Fiber bragg grating sensors-based in-situ monitoring and safety assessment of loess tunnel. J. Sens. 2016, 1–10. [Google Scholar] [CrossRef]



| Physical Quantity | Similarity Law | Similarity Constants | Remark |
|---|---|---|---|
| Geometry () | 30 | Control variable | |
| Mass density () | 1.02 | Control variable | |
| Gravity acceleration | 1.0 | Control variable | |
| Stress | 30.6 | ||
| Strain | 5.53 | ||
| Shear modulus | 5.53 | ||
| Displacement | 165.95 | ||
| Velocity | 12.88 | ||
| Input acceleration () | 1.0 | Input control | |
| Time | 12.88 | Input control | |
| Frequency | 1/12.88 | ||
| Damping ratio | 1.0 | ||
| Internal friction angle | 1.0 |
| Serial Number | Seismic Wave | Peak Acceleration/gal(cm/s2) |
|---|---|---|
| 1 | WN1 | 30 |
| 2 | E0.5 | 50 |
| 3 | L0.5 | 50 |
| 4 | WN2 | 30 |
| 5 | E1 | 100 |
| 6 | L1 | 100 |
| 7 | WN3 | 30 |
| 8 | E2 | 200 |
| 9 | L2 | 200 |
| 10 | WN4 | 30 |
| 11 | E3 | 300 |
| 12 | L3 | 300 |
| 13 | WN5 | 30 |
| 14 | E4 | 400 |
| 15 | L4 | 400 |
| 16 | WN6 | 30 |
| 17 | E5 | 500 |
| 18 | L5 | 500 |
| 19 | WN7 | 30 |
| 20 | E6 | 600 |
| 21 | L6 | 600 |
| 22 | WN8 | 30 |
| 23 | E7 | 700 |
| 24 | L7 | 700 |
| 25 | WN9 | 30 |
| 26 | E8 | 800 |
| 27 | L8 | 800 |
| 28 | WN10 | 30 |
| 29 | E9 | 900 |
| 30 | L9 | 900 |
| 31 | WN11 | 30 |
| 32 | E10 | 1000 |
| 33 | L10 | 1000 |
| 34 | WN12 | 30 |
| 35 | S1 (4 Hz) | 1200 |
| 36 | WN13 | 30 |
| 37 | S2 (4 Hz) | 1500 |
| Magnifications under E3 Condition | Magnifications under L3 Condition | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Relative Height/mm | Inside | Surface | Difference | Average | Inside | Surface | Difference | Average | |
| Model 1 | 300 | 1.080 | 1.162 | 0.082 | 0.0723 | 1.159 | 1.249 | 0.09 | 0.0810 |
| 500 | 1.174 | 1.260 | 0.086 | 1.310 | 1.383 | 0.073 | |||
| 700 | 1.332 | 1.381 | 0.049 | 1.448 | 1.528 | 0.08 | |||
| Model 2 | 300 | 1.423 | 1.417 | 0.006 | 0.0147 | 1.243 | 1.259 | 0.016 | 0.0090 |
| 500 | 1.588 | 1.622 | 0.034 | 1.415 | 1.417 | 0.002 | |||
| 700 | 1.722 | 1.718 | 0.004 | 1.550 | 1.541 | 0.009 | |||
| Model 3 | 300 | 1.449 | 1.443 | 0.006 | 0.0030 | 1.331 | 1.309 | 0.022 | 0.0110 |
| 500 | 1.648 | 1.647 | 0.001 | 1.486 | 1.488 | 0.002 | |||
| 700 | 1.726 | 1.728 | 0.002 | 1.634 | 1.625 | 0.009 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Lei, J.; Shi, S.; Liu, T. Seismic Response of Aeolian Sand High Embankment Slopes in Shaking Table Tests. Appl. Sci. 2019, 9, 1677. https://doi.org/10.3390/app9081677
Zhou Z, Lei J, Shi S, Liu T. Seismic Response of Aeolian Sand High Embankment Slopes in Shaking Table Tests. Applied Sciences. 2019; 9(8):1677. https://doi.org/10.3390/app9081677
Chicago/Turabian StyleZhou, Zhijun, Jiangtao Lei, Shaobo Shi, and Tong Liu. 2019. "Seismic Response of Aeolian Sand High Embankment Slopes in Shaking Table Tests" Applied Sciences 9, no. 8: 1677. https://doi.org/10.3390/app9081677
APA StyleZhou, Z., Lei, J., Shi, S., & Liu, T. (2019). Seismic Response of Aeolian Sand High Embankment Slopes in Shaking Table Tests. Applied Sciences, 9(8), 1677. https://doi.org/10.3390/app9081677





