Joint Operation of Renewable Energy and Battery Switch Station Considering the Benefits of Different Subjects
Abstract
:1. Introduction
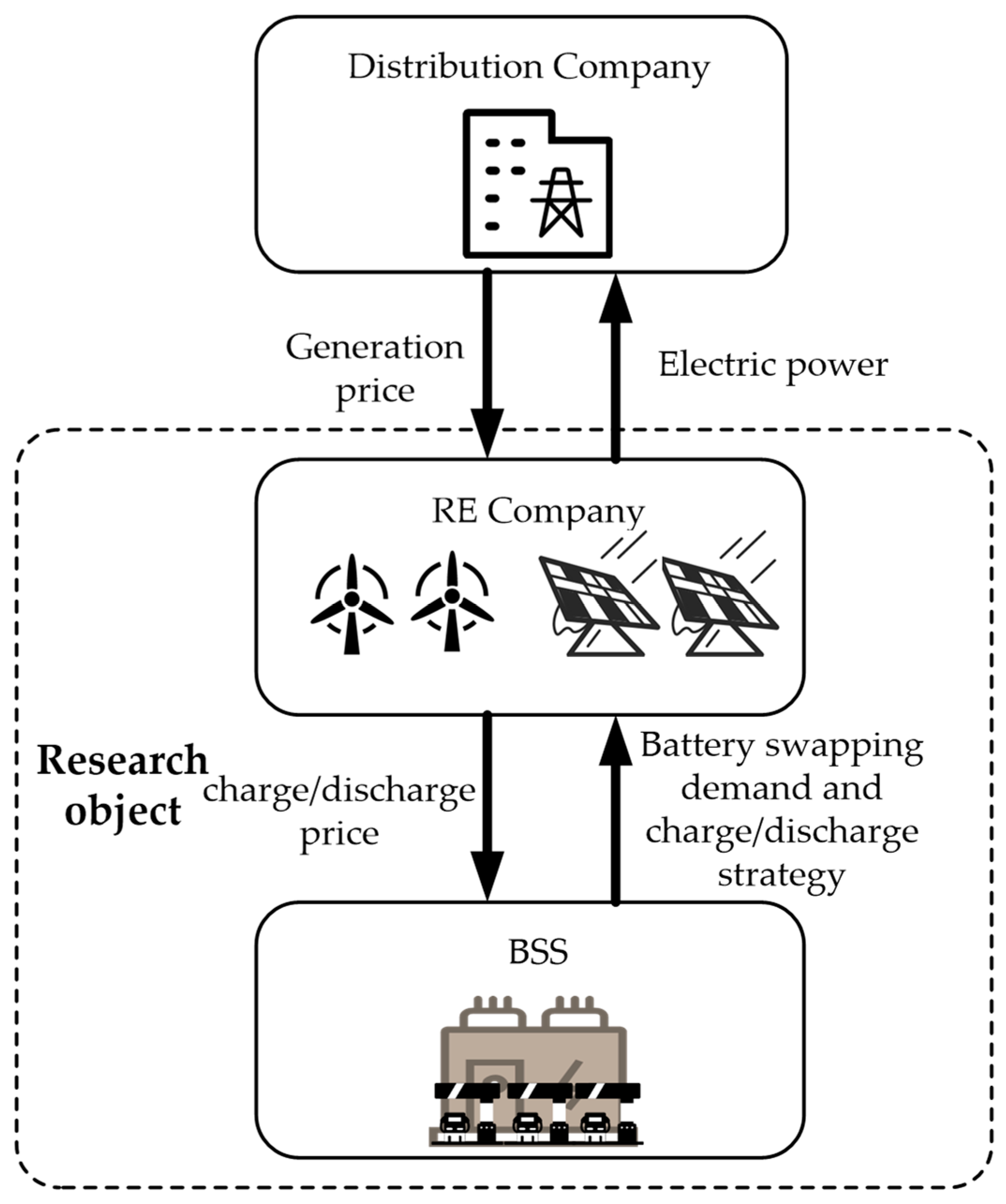
2. Operation Mode of Renewable Energy (RE) and Battery Switch Station (BSS)
2.1. Independent Operation Mode
2.2. Joint Operation Mode
3. Mathematical Modeling
3.1. Leader (RE Company) Model
3.2. Follower (BSS) Model
3.3. Stackelberg Game Model
4. Stackelberg Equilibrium
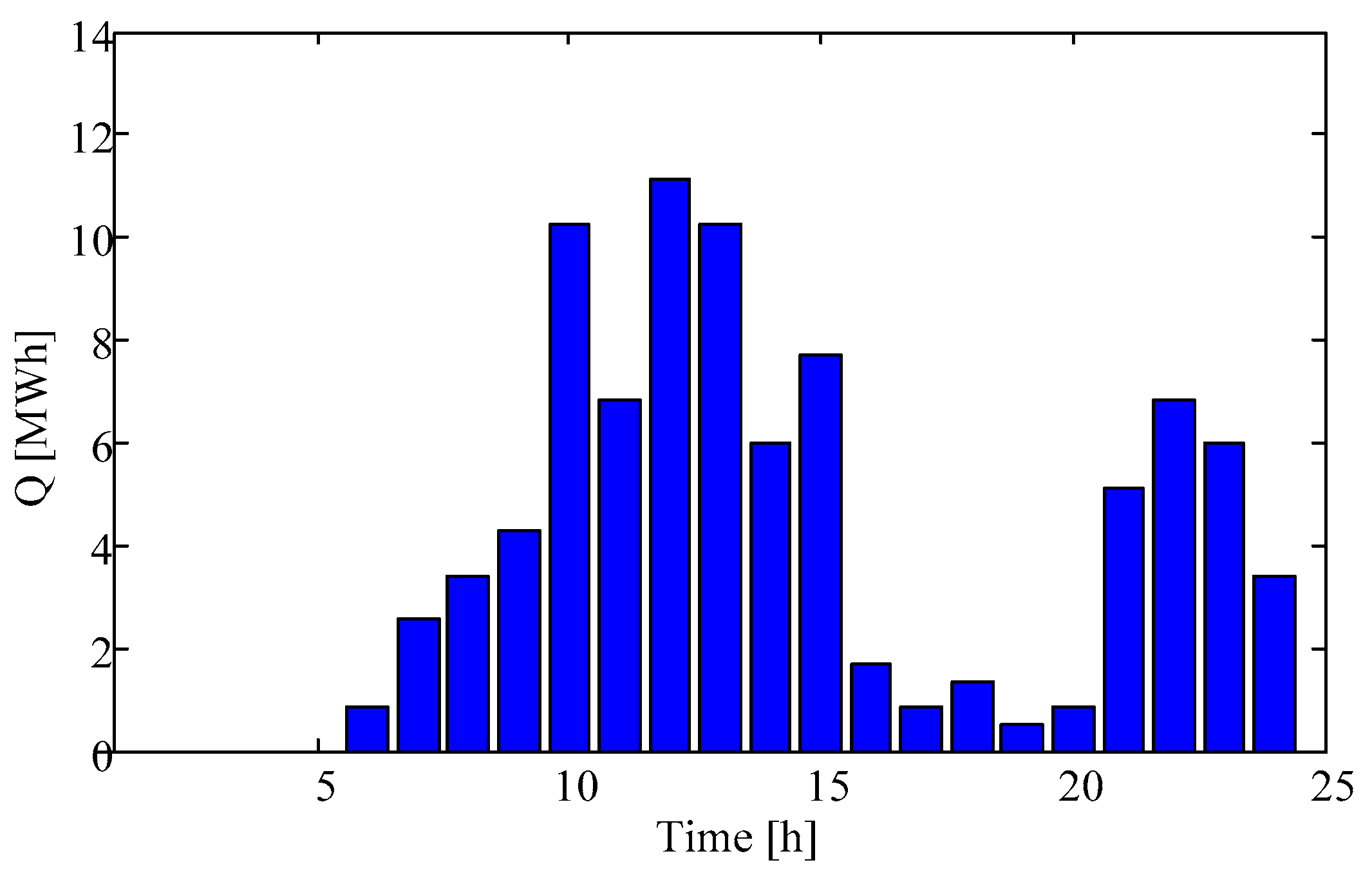
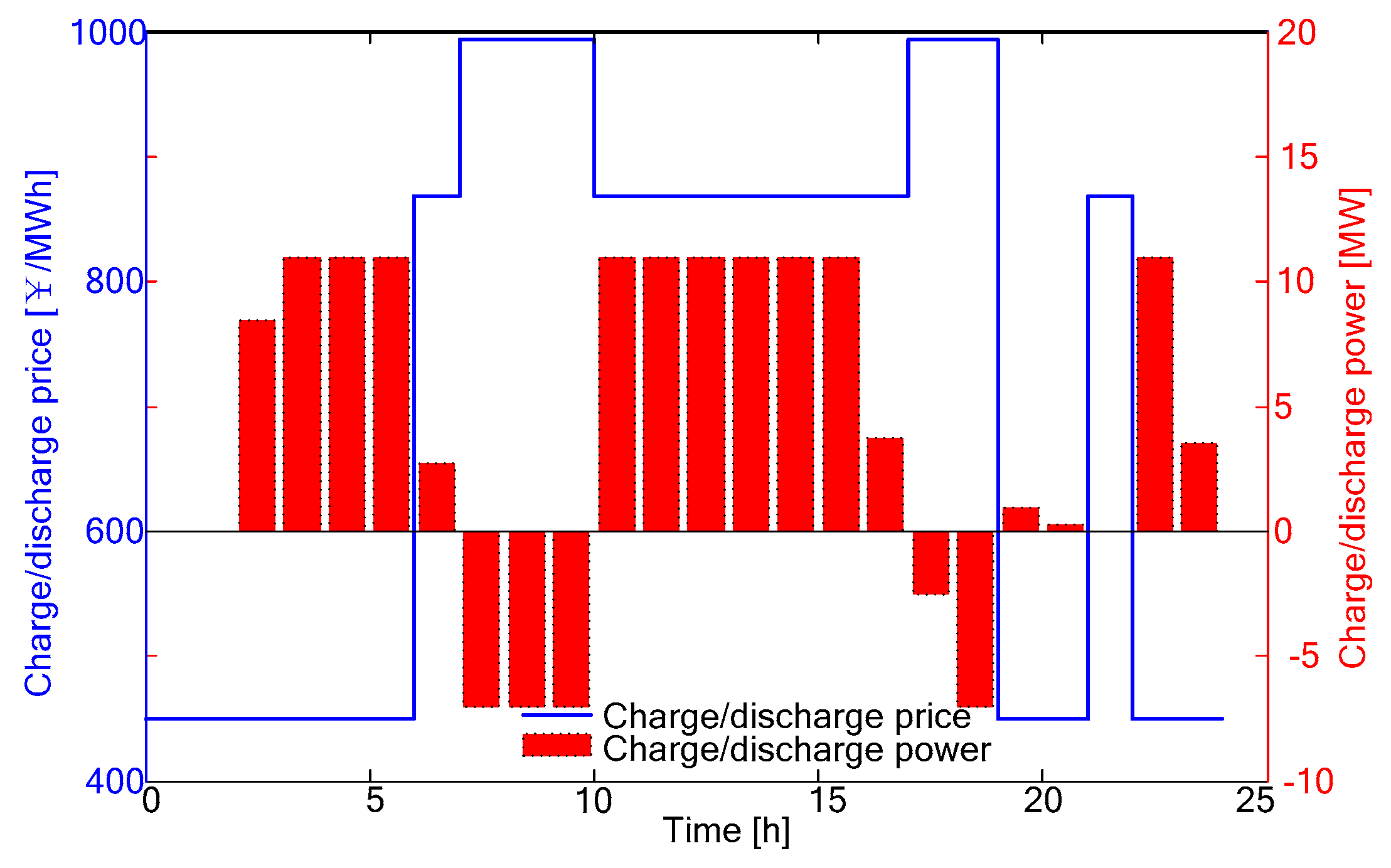
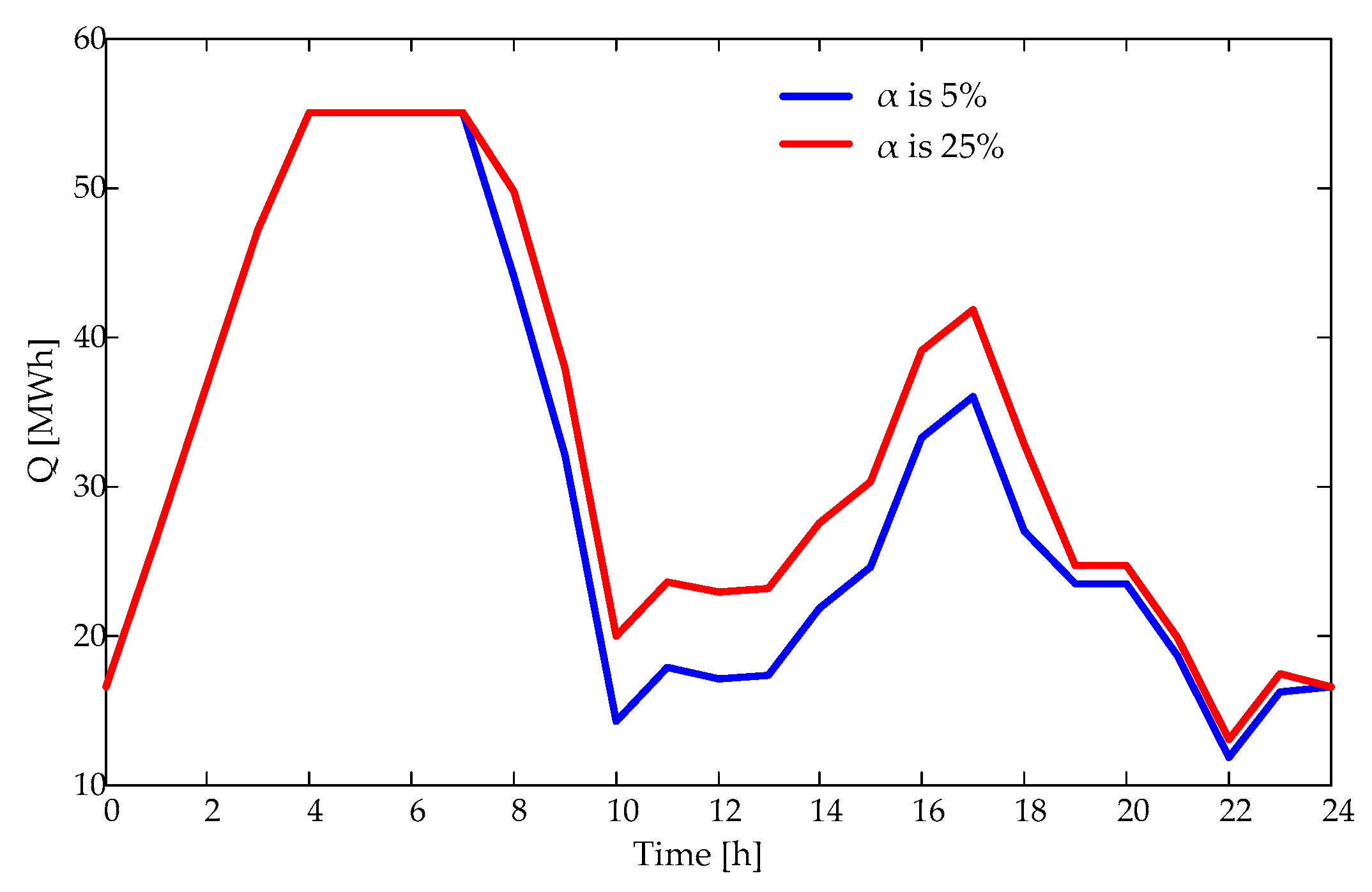
5. Simulation Analysis
5.1. Simulation Parameter Setting
5.2. Optimization Result Analysis
6. Conclusions
- (1)
- A Stackelberg game model with the RE company as leader and BSS as follower is proposed, which can effectively simulate the interaction between the RE company and BSS. On the one hand, the RE company does not need to directly control the charge/discharge behavior of the BSS, but only needs to optimize the charge/discharge price of each period to guide the charge/discharge behavior of the BSS. On the other hand, the BSS is not only a passive recipient of the price. The BSS could affect the revenue of the RE company by adjusting its own charge/discharge strategy, so as to urge the RE company to adjust the charge/discharge price.
- (2)
- The proposed model no longer requires that the RE company and BSS belong to a same interest subject, and there is no need for unified coordinated control between them. While pursuing the maximization of their own interests, the RE company and the BSS could automatically realize the optimal allocation of resources, and a win-win situation is achieve as well.
- (3)
- The comparative analysis of the two Stackelberg equilibriums shows that the weak Stackelberg equilibrium is more in line with the cooperation mechanism proposed in this paper. In addition, the simulation results show that the revenue of the RE company and BSS in the model proposed in this paper is higher than their revenue when they operate alone, which proves that both of them have the motivation to participate in the game.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Nt | Number of time intervals |
| Length of a single time interval | |
| Active power output of renewable energy at time t | |
| Pool purchase price of RE generation at time t | |
| Charging power of BSS at time t | |
| Discharging power of BSS at time t | |
| Charge/discharge price of BSS at time t | |
| Minimum Charge/discharge price of BSS at time t | |
| Maximum Charge/discharge price of BSS at time t | |
| Average Charge/discharge price | |
| Contract price for the direct charging of BSS from the distribution company | |
| s | Unit price of battery swapping |
| Battery swapping demand at time t | |
| Maximum charging power of BSS | |
| Maximum discharging power of BSS | |
| Energy storage of BSS at time t | |
| Rated capacity of BSS | |
| Minimum energy storage of the BSS | |
| Initial energy storage of BSS | |
| Energy storage at the end of a decision-making cycle | |
| Charge efficiency of BSS | |
| Discharge efficiency of BSS | |
| Reserve ratio of the battery swapping demand |
References
- Min, C.-G. Analyzing the impact of variability and uncertainty on power system flexibility. Appl. Sci. 2019, 9, 561. [Google Scholar] [CrossRef]
- Golovanov, N.; Lazaroiu, G.C.; Roscia, M.; Zaninelli, D. Power quality assessment in small scale renewable energy sources supplying distribution systems. Energies 2013, 6, 634–645. [Google Scholar] [CrossRef]
- Bizuayehu, A.; Nieta, A.; Contreras, J.; Catalao, J. Impacts of stochastic wind power and storage participation on economic dispatch in distribution systems. IEEE Trans. Sustain. Energy 2017, 7, 1336–1345. [Google Scholar] [CrossRef]
- Lu, S.-D.; Wang, M.-H.; Kuo, M.-T.; Tsou, M.-C.; Liao, R.-M. Optimal unit commitment by considering high penetration of renewable energy and ramp rate of thermal units-a case study in Taiwan. Appl. Sci. 2019, 9, 421. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Rasmussen, C. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- Torres-Moreno, J.L.; Gimenez-Fernandez, A.; Perez-Garcia, M.; Rodriguez, F. Energy management strategy for micro-grids with PV-battery systems and electric vehicles. Energies 2018, 11, 522. [Google Scholar] [CrossRef]
- Chan, K.; Luo, X.; Qin, M.; Wu, T.; Chung, C. Optimal planning and operation of energy storage systems in radial networks for wind power integration with reserve support. IET Gener. Transm. Distrib. 2016, 10, 2019–2025. [Google Scholar]
- Barton, J.; Infield, D. Energy storage and its use with intermittent renewable energy. IEEE Trans. Energy Convers. 2004, 19, 441–448. [Google Scholar] [CrossRef]
- Hu, X.; Wang, K.; Liu, X.; Sun, Y.; Guo, S. Energy management for EV charging in software-defined green vehicle-to-grid network. IEEE Commun. Mag. 2018, 56, 156–163. [Google Scholar] [CrossRef]
- Xue, F.; Lei, X.; Zhang, Y.; Liu, H.; Gao, C. A brand-new approach of connecting electrical vehicles with smart grid from vehicle-to-grid mode to battery-to-grid mode. Power Syst. Technol. 2012, 36, 29–34. [Google Scholar]
- Jiang, Z.; Han, X.; Li, Z.; Li, W. Dependent chance goal programming of wind-EVBSS considering its multiple benefits. Power Syst. Technol. 2016, 40, 1134–1139. [Google Scholar]
- Miao, Y.; Jiang, Q.; Cao, Y. Operation strategy for battery swap station of electric vehicles based on microgrid. Autom. Electr. Power Syst. 2012, 36, 33–38. [Google Scholar]
- Liu, F.; Yang, X.; Shi, S.; Zhang, M.; Deng, H.; Guo, P. Economic operation of microgrid containing charging-swapping-storage integrated station under uncertain factors of wind farm and photovoltaic generation. Power Syst. Technol. 2015, 39, 669–676. [Google Scholar]
- Tian, Y.; Liao, Q.; Xue, Y.; Chen, Y. Multi-scenario coordinated planning method of EV battery-swapping station and distributed generation based on coordinated charging strategy. Electr. Power Autom. Equip. 2017, 37, 62–69. [Google Scholar]
- Fu, H.; Liu, M.; Chen, Z. Multi-objective optimization of battery swapping station with wind photovoltaic and energy storage. In Proceedings of the CSU-EPSA, Brussels, Belgium, 23–25 June 2016; Volume 28, pp. 38–43. [Google Scholar]
- Chen, Z.; Liu, N.; Xiao, X.; Zhang, J. Energy exchange model of PV-based battery switch stations based on battery swap service and power distribution. In Proceedings of the IEEE Energytech Conference, Cleveland, OH, USA, 21–23 May 2013. [Google Scholar]
- Liu, N.; Chen, Q.; Lu, X.; Liu, J.; Zhang, J. A charging strategy for pv-based battery switch stations considering service availability and self-consumption of PV energy. IEEE Trans. Ind. Electr. 2015, 62, 4878–4889. [Google Scholar] [CrossRef]
- Jiang, Z.; Han, X.; Li, Z.; Wang, M.; Liu, G.; Wang, M.; Li, W.; Ollis, T.B. Capacity optimization of a centralized charging station in joint operation with a wind farm. Energies 2018, 11, 1164. [Google Scholar] [CrossRef]
- Jiang, Z.; Han, X.; Li, Z.; Li, W.; Wang, M.; Wang, M. Two-stage multi-objective collaborative scheduling for wind farm and battery switch station. Energies 2016, 9, 886. [Google Scholar] [CrossRef]
- Suo, L.; Xiang, C.; Tang, W.; Liu, Z.; Zhao, H. Multi-objective Bi-level programming of centralized charging station considering benefits balance for different subjects. Autom. Electr. Power Syst. 2016, 40, 100–107. [Google Scholar]
- Wang, K.; Ouyang, Z.; Krishnan, R.; Shu, L.; He, L. A game theory based energy management system using price elasticity for smart grids. IEEE Trans. Ind. Inform. 2015, 11, 1607–1616. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, L.; Mei, S. Typical applications and prospects of game theory in power System. Proc. CSEE 2014, 34, 5009–5017. [Google Scholar]
- Schneider, I.; Roozbehani, M. Energy market design for renewable resources: Imbalance settlements and efficiency-robustness tradeoffs. IEEE Trans. Power Syst. 2017, 3757–3767. [Google Scholar] [CrossRef]
- Mei, S.; Wang, Y.; Liu, F.; Zhang, X.; Sun, Z. Game approaches for hybrid power system planning. IEEE Trans. Sustain. Energy 2012, 3, 506–517. [Google Scholar]
- Wang, Z.; Yuan, Y.; An, B.; Li, M.; Wang, F. An overview of security games. J. Command Control 2015, 1, 121–149. [Google Scholar]
- Leitmann, G. On generalized Stackelberg strategies. J. Optim. Theory Appl. 1978, 26, 637–643. [Google Scholar] [CrossRef]
- Breton, M.; Alj, A.; Haurie, A. Sequential stackelberg equilibria in two-person games. J. Optim. Theory Appl. 1988, 59, 71–97. [Google Scholar] [CrossRef]
- Wei, W.; Chen, Y.; Liu, F.; Mei, S.; Tian, F.; Zhang, X. Stackelberg game based retailer pricing scheme and EV charging management in smart residential area. Power Syst. Technol. 2015, 39, 939–945. [Google Scholar]
- Anandalingam, G.; White, D. A solution method for the linear static stackelberg problem using penalty functions. IEEE Trans. Autom. Control 1990, 35, 1170–1173. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J. Multi-objective cuckoosearch algorithm for Bi-level programming problems. Oper. Res. Manag. Sci. 2017, 26, 1–10. [Google Scholar]


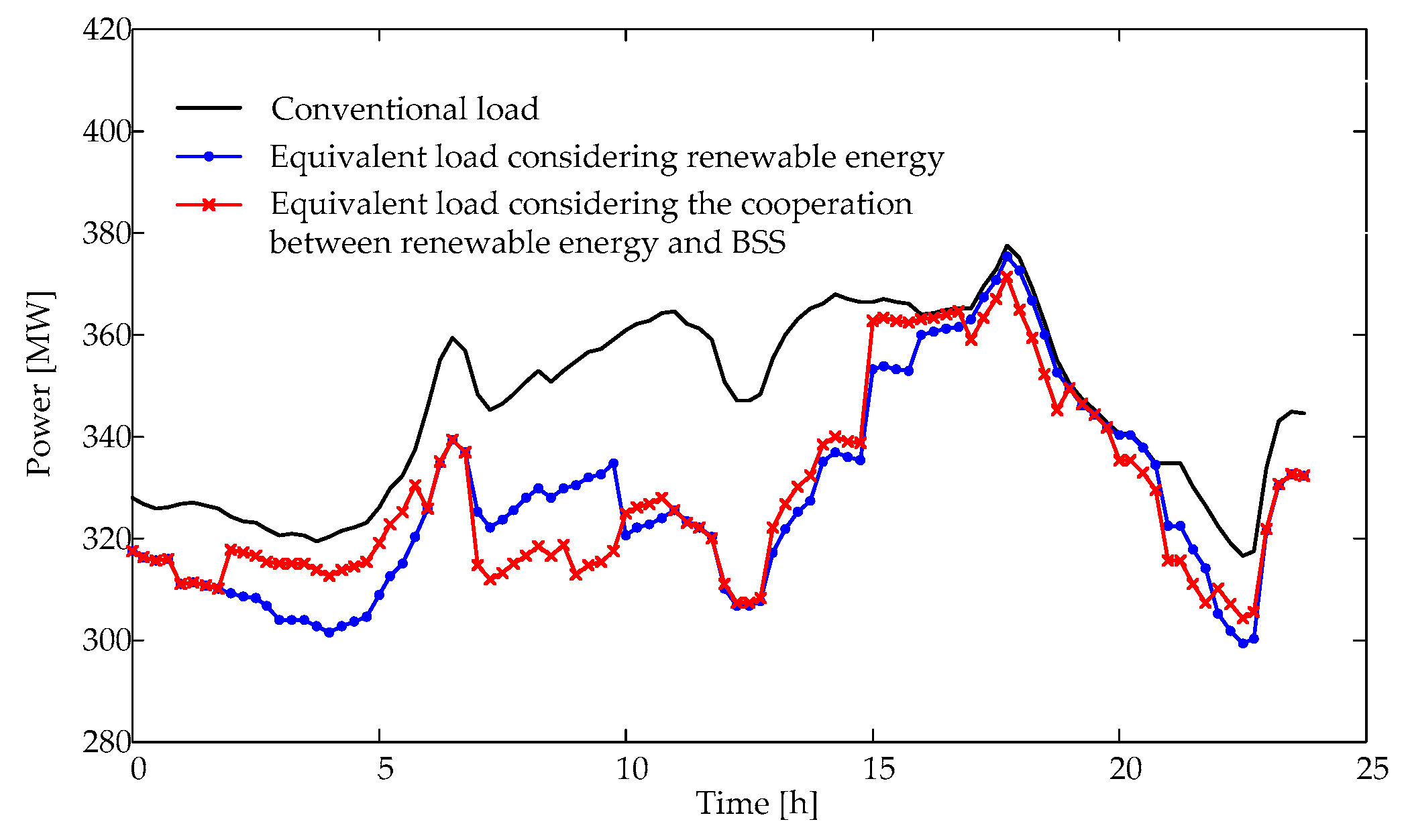
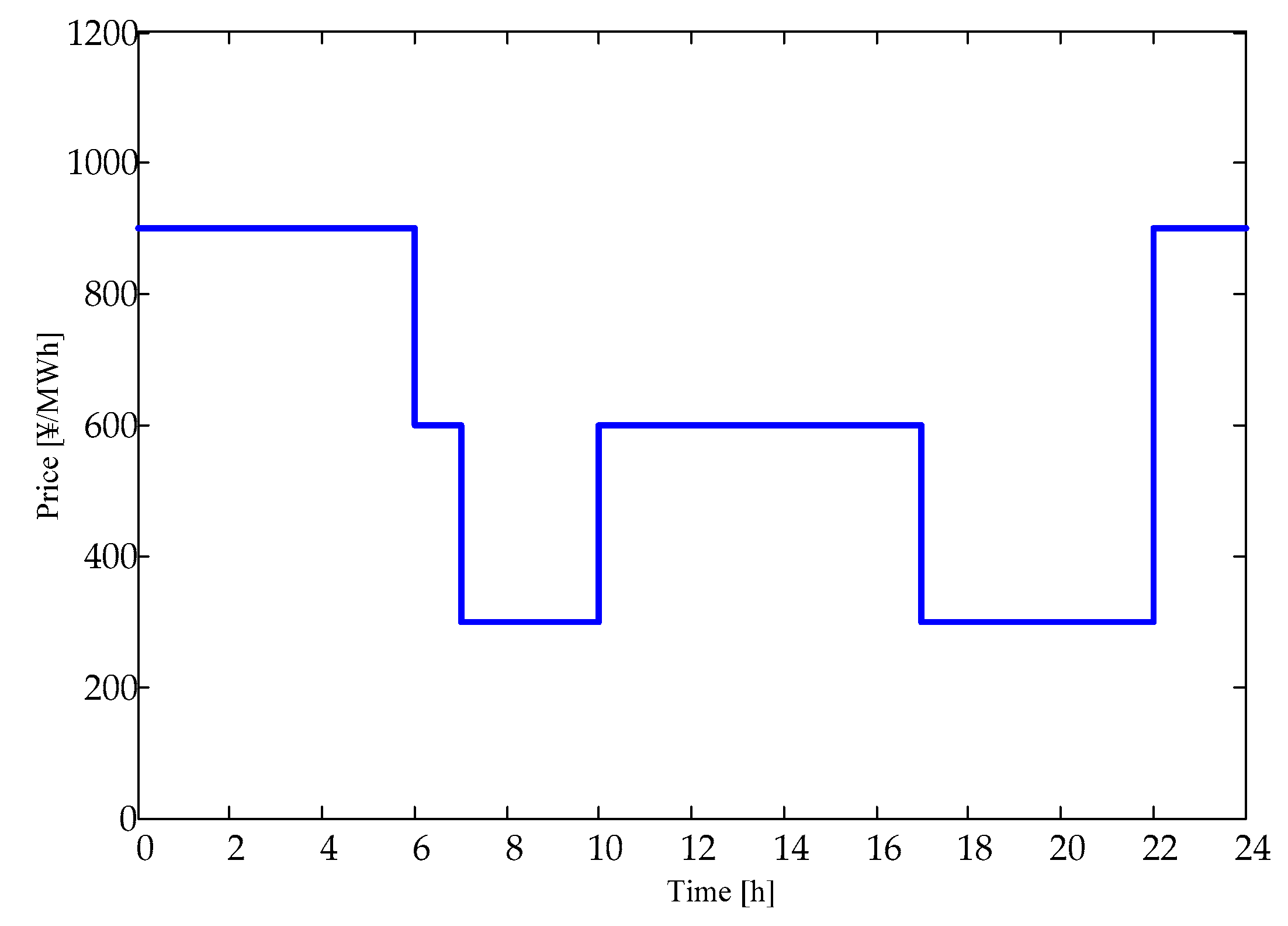

| No. | Parameters | Quantity |
|---|---|---|
| 1 | 55 MWh | |
| 2 | 5.5 MWh | |
| 3 | 16.5 MW | |
| 4 | 16.5 MW | |
| 5 | 11 MW | |
| 6 | 7 MW | |
| 7 | s | 1300 ¥/MWh |
| 8 | 95% | |
| 9 | 92% | |
| 10 | 10% |
| Scenario | RE Company | BSS |
|---|---|---|
| Cooperative scenario | ¥276,480 | ¥58,671 |
| Non-cooperative scenario | ¥252,054 | ¥52,200 |
| Revenue increase | 9.7% | 12.4% |
| Average Charge/Discharge Price ¥/MWh | RE Company ¥ | BSS ¥ | Total Revenue ¥ |
|---|---|---|---|
| 750 | 277,911 | 57,240 | 335,151 |
| 720 | 276,480 | 58,671 | 335,151 |
| 650 | 272,196 | 62,955 | 335,151 |
| 600 | 269,136 | 66,015 | 335,151 |
| 550 | 266,076 | 69,075 | 335,151 |
| α | RE Company ¥ | BSS ¥ |
|---|---|---|
| 5% | 276,502 | 58,803 |
| 10% | 276,480 | 58,671 |
| 15% | 276,458 | 58,539 |
| 20% | 276,437 | 58,407 |
| 25% | 276,415 | 58,276 |
| Qmax MWh | RE Company Revenue ¥ | BSS Revenue ¥ | Discharged Energy of BSS MWh |
|---|---|---|---|
| 55 | 276,480 | 58,671 | 30.5 |
| 60 | 276,819 | 60,872 | 35.0 |
| 65 | 276,973 | 63,300 | 39.7 |
| Swapping Demand MWh | BSS Revenue ¥ | Discharged Energy of BSS MWh |
|---|---|---|
| Case 1 | 51,851 | 45.1 |
| Case 2 | 58,671 | 30.5 |
| Case 3 | 58,539 | 14.0 |
| Scenario | Cooperative Scenario | Non-Cooperative Scenario | ||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 1 | Case 2 | |
| Revenue of the RE company | ¥276,480 | ¥286,791 | ¥252,054 | ¥262,467 |
| Revenue of the BSS | ¥58,671 | ¥60,100 | ¥52,200 | ¥52,200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Li, W.; Ma, C.; Ma, L.; Zhang, B.; Lu, K.; Li, W. Joint Operation of Renewable Energy and Battery Switch Station Considering the Benefits of Different Subjects. Appl. Sci. 2019, 9, 1679. https://doi.org/10.3390/app9081679
Jiang Z, Li W, Ma C, Ma L, Zhang B, Lu K, Li W. Joint Operation of Renewable Energy and Battery Switch Station Considering the Benefits of Different Subjects. Applied Sciences. 2019; 9(8):1679. https://doi.org/10.3390/app9081679
Chicago/Turabian StyleJiang, Zhe, Wendong Li, Changhui Ma, Linlin Ma, Bing Zhang, Kuan Lu, and Wenbo Li. 2019. "Joint Operation of Renewable Energy and Battery Switch Station Considering the Benefits of Different Subjects" Applied Sciences 9, no. 8: 1679. https://doi.org/10.3390/app9081679





