Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory
Abstract
:Featured Application
Abstract
1. Introduction
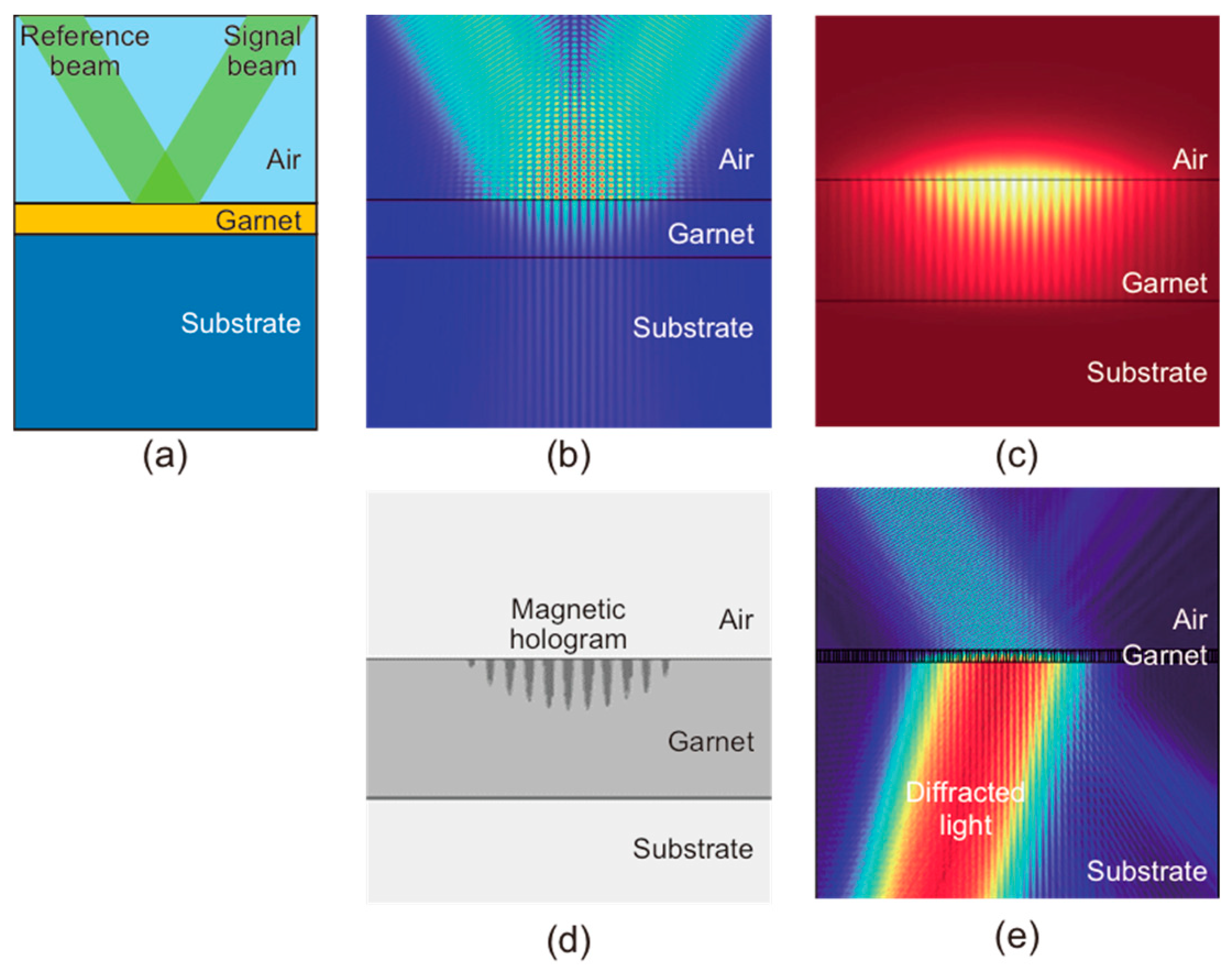
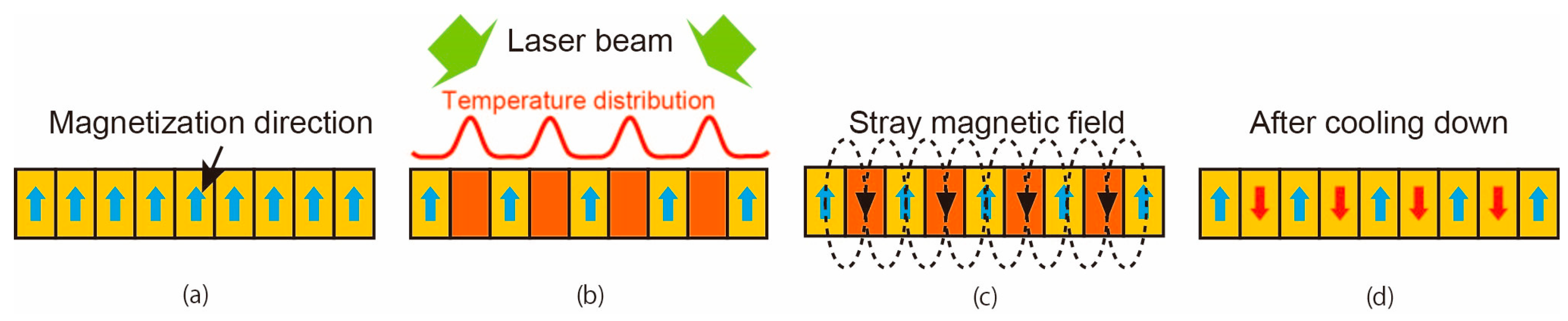
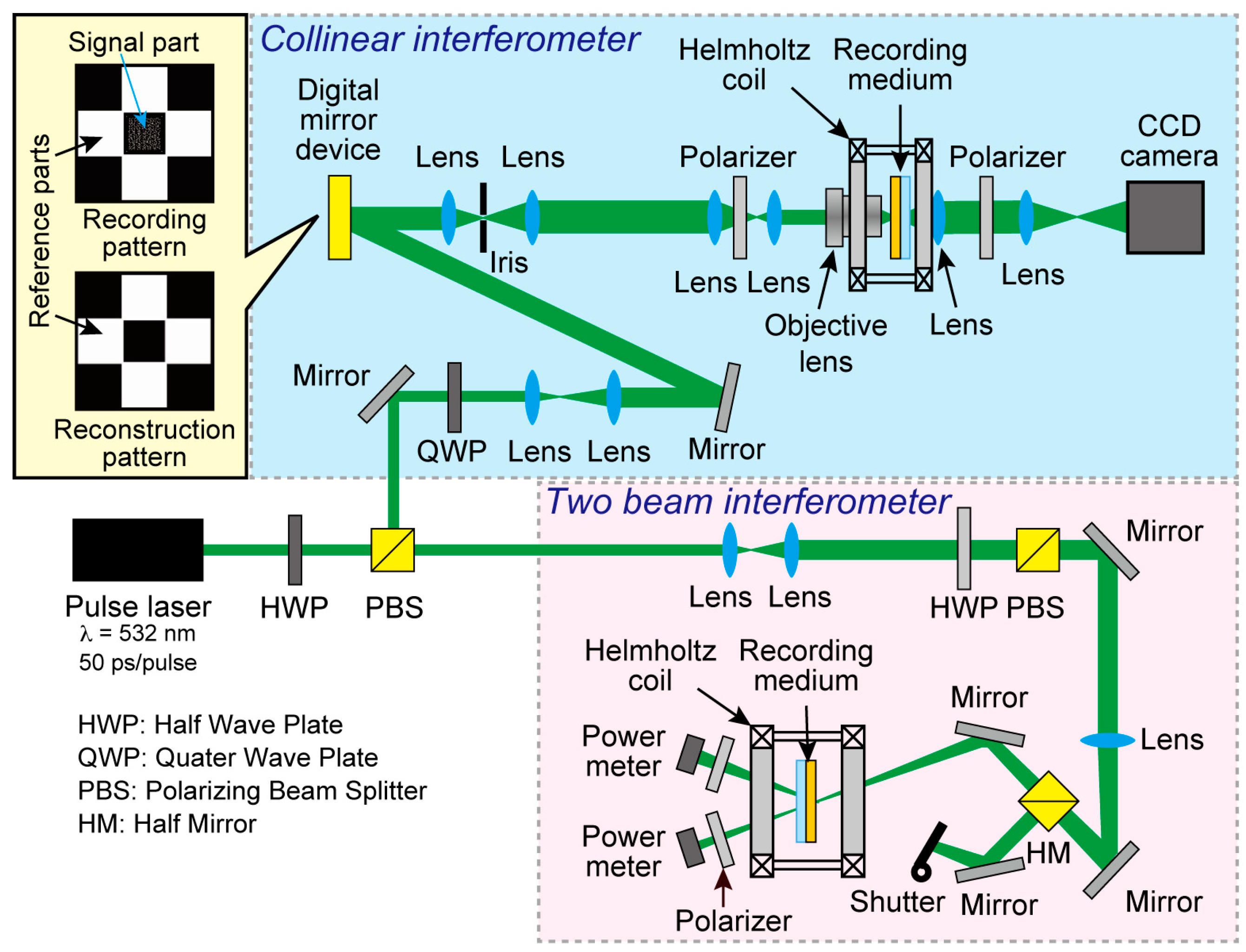
2. Materials and Methods
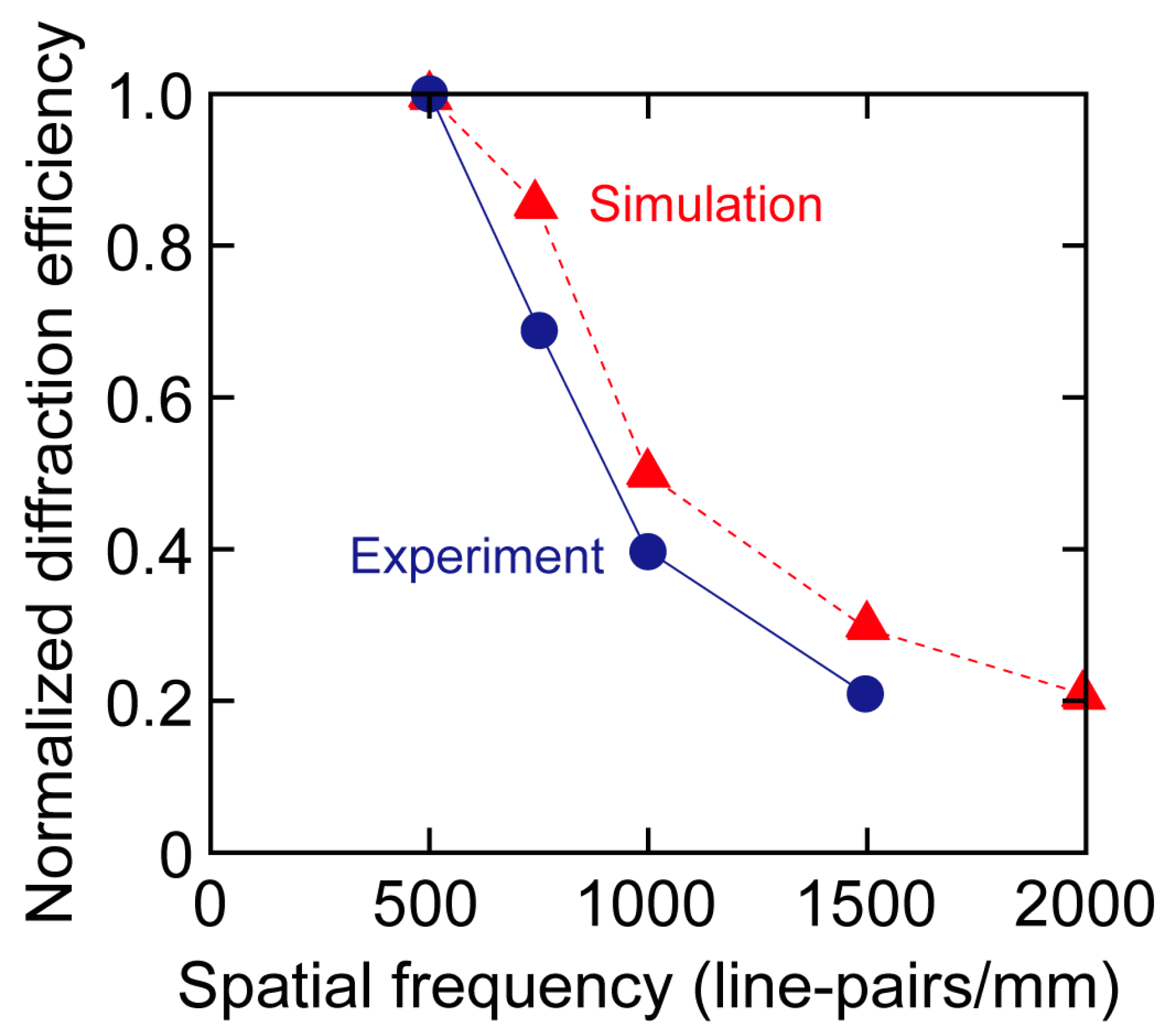
3. Results and Discussion
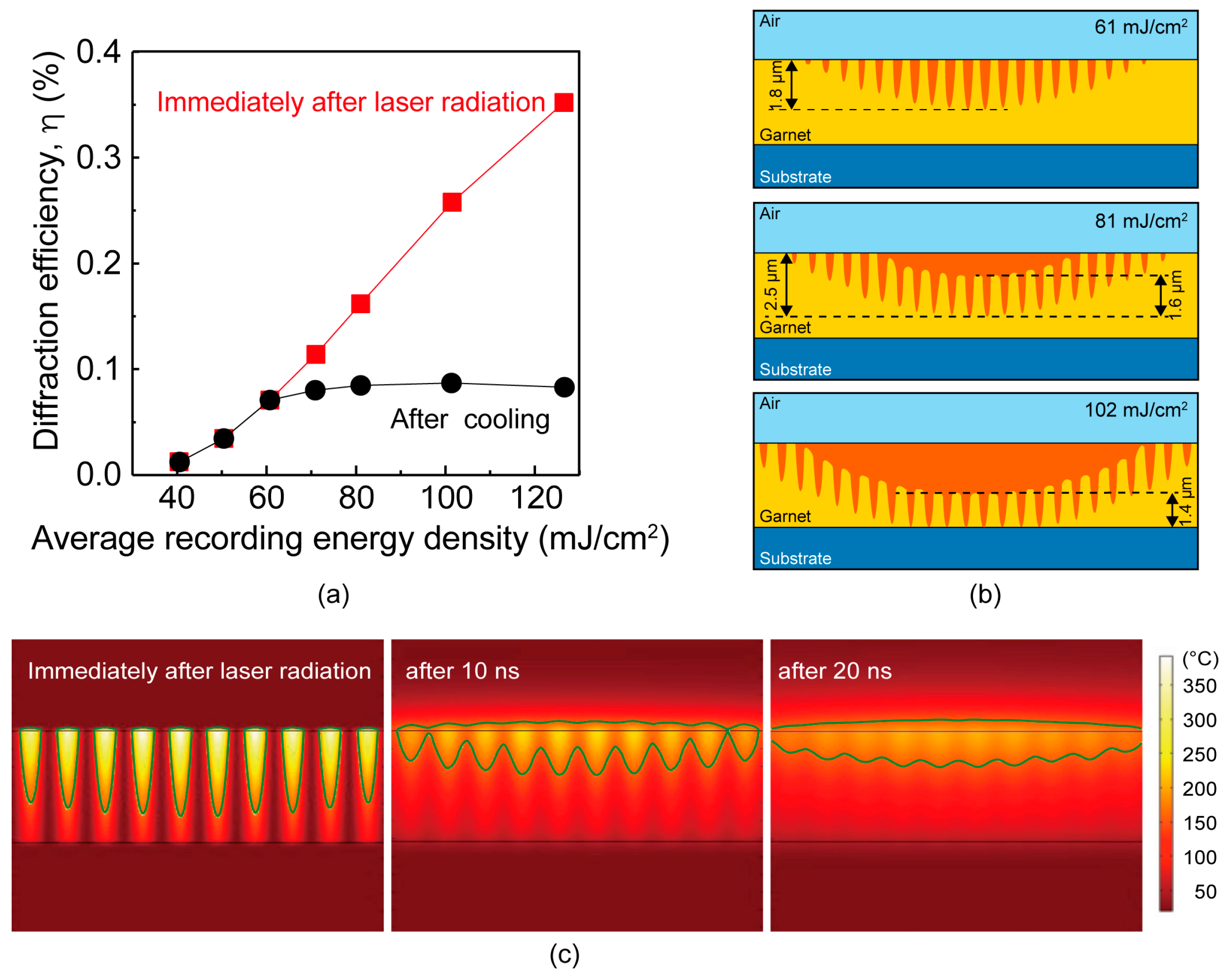
3.1. Garnet Film Morphology and Magnetic Fringe Shape
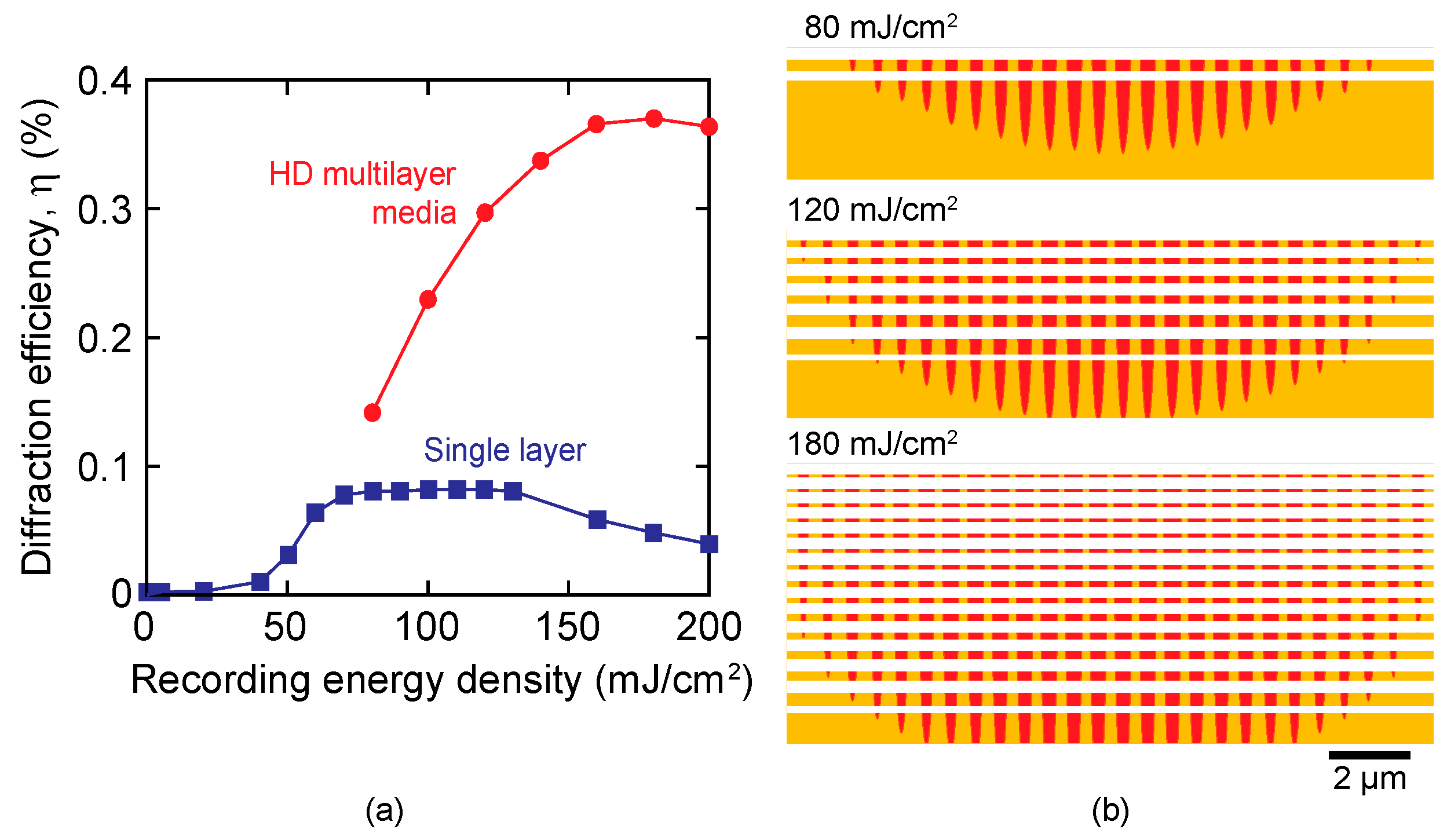
3.2. Effect of Recording Energy
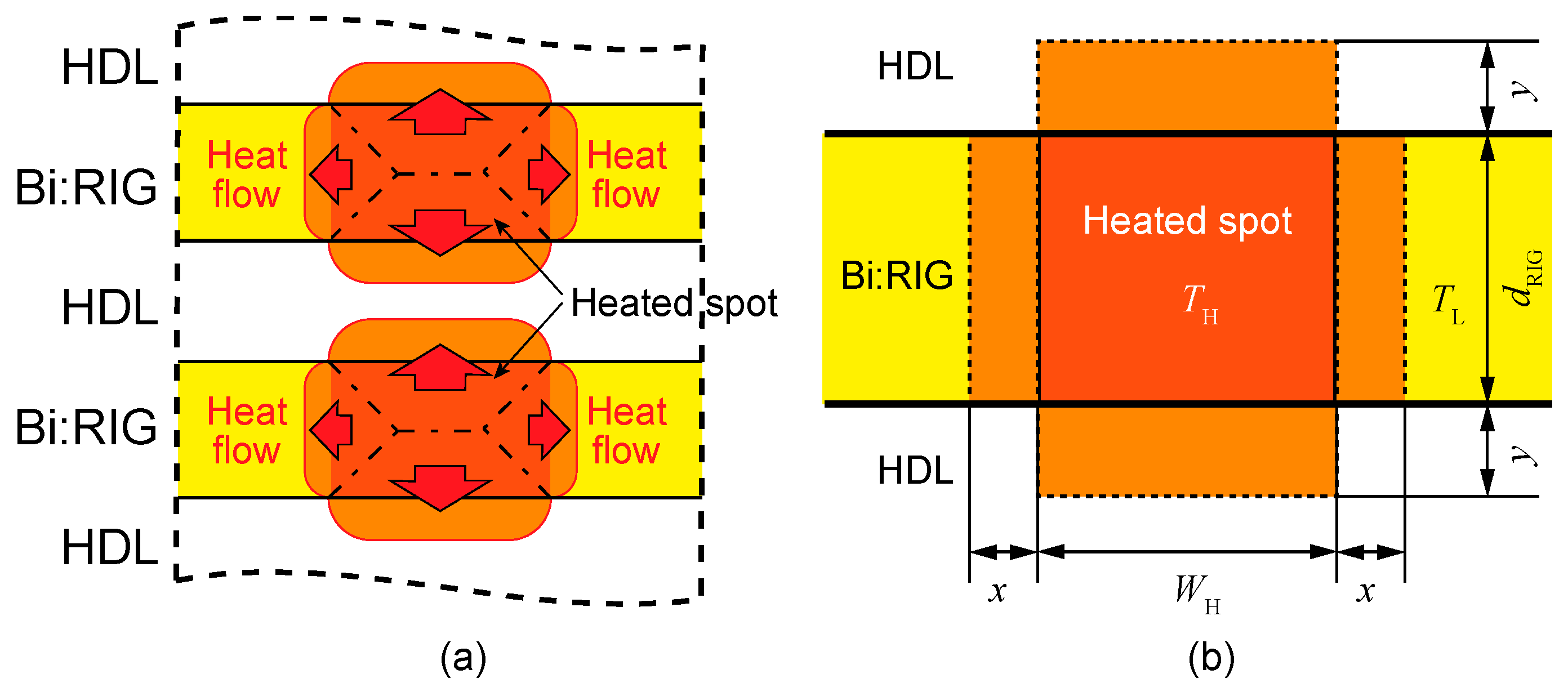
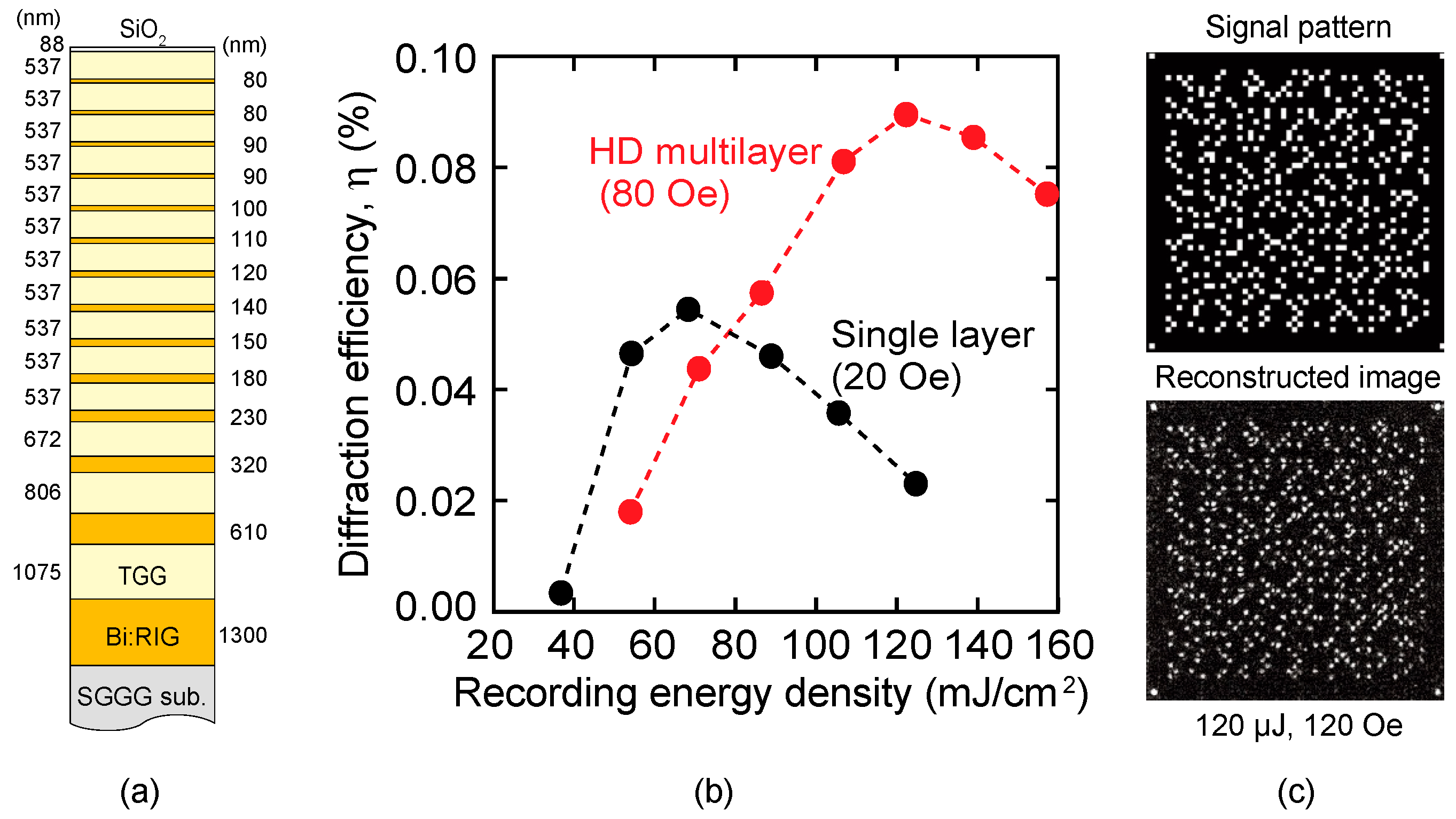
3.3. Design and Properties of HD Multilayer Media
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rajchman, J.A. Holographic Optical Memory An Optical Read-Write Mass Memory. Appl. Opt. 1970, 9, 2269–2271. [Google Scholar] [CrossRef]
- Mikaeliane, A.L.; Bobrinev, V.I. Holographic Memory Devices. Opto-Electronics 1970, 2, 193–199. [Google Scholar] [CrossRef]
- Sakaguchi, M.; Nishida, N.; Nemoto, T. A New Associative Memory System Utilizing Holography. IEEE Trans. Comput. 1970, 19, 1174–1181. [Google Scholar] [CrossRef]
- Takeda, Y. Hologram Memory with High Quality and High Information Storage Density -Hologram Memory-. Jpn. J. Appl. Phys. 1972, 11, 656–665. [Google Scholar] [CrossRef]
- D’Auria, L.; Huignard, J.P.; Spitz, E. Holographic read-write memory and capacity enhancement by 3-D storage. IEEE Trans. Magn. 1973, 9, 83–94. [Google Scholar] [CrossRef]
- Curtis, K.; Pu, A.; Psaltis, D. Method for holographic storage using peristrophic multiplexing. Opt. Lett. 1994, 19, 993–994. [Google Scholar] [CrossRef]
- Hong, J.H.; McMichael, I.C.; Chang, T.Y.; Christian, W.R.; Paek, E.G. Volume holographic memory systems: techniques and architectures. Opt. Eng. 1995, 34, 2193–2203. [Google Scholar] [CrossRef]
- Breuckmann, B.; Thieme, W. Computer-aided analysis of holographic interferograms using the phase-shift method. Appl. Opt. 1985, 24, 2145–2149. [Google Scholar] [CrossRef] [PubMed]
- Rakuljic, G.A.; Leyva, V.; Yariv, A. Optical data storage by using orthogonal wavelength-multiplexed volume holograms. Opt. Lett. 1992, 17, 1471–1473. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-Y.S.; Psaltis, D. Three-dimensional holographic disks. Appl. Opt. 1994, 33, 3764–3774. [Google Scholar] [CrossRef] [PubMed]
- Psaltis, D.; Levene, M.; Pu, A.; Barbastathis, G.; Curtis, K. Holographic storage using shift multiplexing. Opt. Lett. 1995, 20, 782–784. [Google Scholar] [CrossRef]
- Horimai, H.; Tan, X.; Li, J. Collinear holography. Appl. Opt. 2005, 44, 2575–2579. [Google Scholar] [CrossRef]
- Horimai, H.; Tan, X. Advanced collinear holography. Opt. Rev. 2005, 12, 90–92. [Google Scholar] [CrossRef]
- Horimai, H.; Tan, X. Holographic information storage system: today and future. IEEE Trans. Magn. 2007, 43, 943–947. [Google Scholar] [CrossRef]
- Mezrich, R.S. Curie-point writing of magnetic holograms on MnBi. Appl. Phys. Lett. 1969, 14, 132–134. [Google Scholar] [CrossRef]
- Mezrich, R.S. Reconstruction effects in magnetic holography. IEEE Trans. Magn. 1970, 6, 537–541. [Google Scholar] [CrossRef]
- Mezrich, R.S. Magnetic holography. Appl. Opt. 1970, 9, 2275–2279. [Google Scholar] [CrossRef] [PubMed]
- Haskal, H.M. Polarization and efficiency in magnetic holography. IEEE Trans. Magn. 1970, 6, 542–545. [Google Scholar] [CrossRef]
- Nakamura, Y.; Takagi, H.; Lim, P.B.; Inoue, M. Effect of recording condition on the diffraction efficiency of magnetic hologram with magnetic garnet films. J. Appl. Phys. 2014, 116, 103106. [Google Scholar] [CrossRef]
- Tanaka, M.; Ito, T.; Nishimura, Y. Diffraction efficiency of magnetic hologram. IEEE Trans. Magn. 1972, 8, 523–525. [Google Scholar] [CrossRef]
- Nakamura, Y.; Takagi, H.; Lim, P.B.; Inoue, M. Magnetic volumetric hologram memory with magnetic garnet. Opt. Express 2014, 22, 16439–16444. [Google Scholar] [CrossRef]
- Isogai, R.; Sagara, N.; Goto, T.; Nakamura, Y.; Lim, P.B.; Inoue, M. Diffraction efficiency of volumetric magnetic holograms with magnetophotonic crystals. J. Magn. Soc. Jpn. 2014, 38, 119–122. [Google Scholar] [CrossRef]
- Isogai, R.; Goto, T.; Takagi, H.; Nakamura, Y.; Lim, P.B.; Inoue, M. Effect of structure and properties of magnetic material on diffraction efficiency of magnetophotonic crystal media for magnetic volumetric holography. J. Magn. Soc. Jpn. 2015, 39, 33–36. [Google Scholar] [CrossRef]
- Isogai, R.; Suzuki, S.; Nakamura, K.; Nakamura, Y.; Takagi, H.; Goto, T.; Lim, P.B.; Inoue, M. Collinear volumetric magnetic holography with magnetophotonic microcavities. Opt. Express 2015, 23, 13153–13158. [Google Scholar] [CrossRef]
- Isogai, R.; Nakamura, Y.; Takagi, H.; Goto, T.; Lim, P.B.; Inoue, M. Thermomagnetic writing into magnetophotonic microcavities controlling thermal diffusion for volumetric magnetic holography. Opt. Express 2016, 24, 522–527. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, Y.; Shirakashi, Z.; Takagi, H.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Error-free reconstruction of magnetic hologram via improvement of recording conditions in collinear optical system. Opt. Express 2017, 25, 15349–15357. [Google Scholar] [CrossRef]
- Shirakashi, Z.; Goto, T.; Takagi, H.; Nakamura, Y.; Lim, P.B.; Uchida, H.; Inoue, M. Reconstruction of non-error magnetic hologram data by magnetic assist recording. Sci. Rep. 2017, 7, 12835. [Google Scholar] [CrossRef] [PubMed]
- Mito, S.; Sakurai, H.; Takagi, H.; Baryshev, A.V.; Inoue, M. Polycrystalline magnetic garnet films comprising weakly coupled crystallites for piezoelectrically-driven magneto-optic spatial light modulators. J. Appl. Phys. 2012, 111, 07A519. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, Y.; Lim, P.B.; Goto, T.; Uchida, H.; Inoue, M. Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory. Appl. Sci. 2019, 9, 1738. https://doi.org/10.3390/app9091738
Nakamura Y, Lim PB, Goto T, Uchida H, Inoue M. Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory. Applied Sciences. 2019; 9(9):1738. https://doi.org/10.3390/app9091738
Chicago/Turabian StyleNakamura, Yuichi, Pang Boey Lim, Taichi Goto, Hironaga Uchida, and Mitsuteru Inoue. 2019. "Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory" Applied Sciences 9, no. 9: 1738. https://doi.org/10.3390/app9091738
APA StyleNakamura, Y., Lim, P. B., Goto, T., Uchida, H., & Inoue, M. (2019). Development of Heat Dissipation Multilayer Media for Volumetric Magnetic Hologram Memory. Applied Sciences, 9(9), 1738. https://doi.org/10.3390/app9091738




