A Size-Dependent Cost Function to Solve the Inverse Elasticity Problem
Abstract
:1. Introduction
2. Methods
2.1. Forward Problem
2.2. Inverse Problem
3. Results
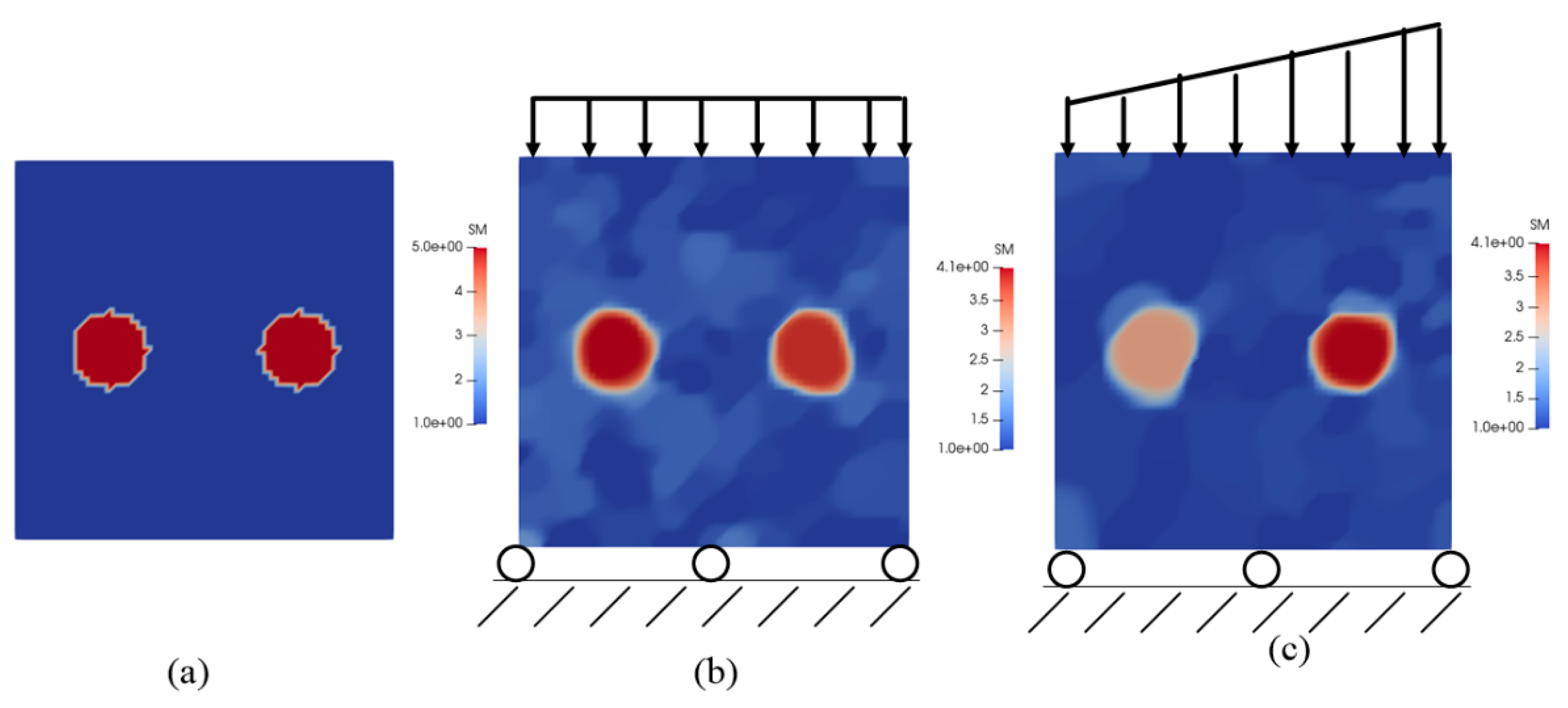
3.1. Modulus Reconstruction Acquired by Simulated Data
3.2. Modulus Reconstruction by a One-Dimensional Coupled Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rossi, M.; Cortese, L.; Genovese, K.; Lattanzi, A.; Nalli, F.; Pierron, F. Evaluation of volume deformation from surface DIC measurement. Exp. Mech. 2018, 58, 1181–1194. [Google Scholar] [CrossRef]
- Dufour, J.-E.; Beaubier, B.; Hild, F.; Roux, S. CAD-based displacement measurements with stereo-DIC. Exp. Mech. 2015, 55, 1657–1668. [Google Scholar] [CrossRef]
- Passieux, J.-C.; Bugarin, F.; David, C.; Périé, J.-N.; Robert, L. Multiscale Displacement Field Measurement Using Digital Image Correlation: Application to the Identification of Elastic Properties. Exp. Mech. 2015, 55, 121–137. [Google Scholar] [CrossRef]
- Avril, S.; Huntley, J.; Pierron, F.; Steele, D. 3D heterogeneous stiffness reconstruction using MRI and the virtual fields method. Exp. Mech. 2008, 48, 479–494. [Google Scholar] [CrossRef]
- Pierron, F.; Grédiac, M. The Virtual Fields Method: Extracting Constitutive Mechanical Parameters from Full-Field Deformation Measurements; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Nguyen, T.T.; Huntley, J.M.; Ashcroft, I.A.; Ruiz, P.D.; Pierron, F. A Fourier-series-based virtual fields method for the identification of 2-D stiffness distributions. Int. J. Numer. Methods Eng. 2014, 98, 917–936. [Google Scholar] [CrossRef] [Green Version]
- Oberai, A.A.; Gokhale, N.H.; Feijóo, G.R. Solution of inverse problems in elasticity imaging using the adjoint method. Inverse Probl. 2003, 19, 297. [Google Scholar] [CrossRef]
- Goenezen, S.; Barbone, P.; Oberai, A.A. Solution of the nonlinear elasticity imaging inverse problem: The incompressible case. Comput. Methods Appl. Mech. Eng. 2011, 200, 1406–1420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mei, Y.; Goenezen, S. Spatially weighted objective function to solve the inverse problem in elasticity for the elastic property distribution. In Computational Biomechanics for Medicine: New Approaches and New Applications; Doyle, B.J., Miller, K., Wittek, A., Nielson, P.M.F., Eds.; Springer: New York, NY, USA, 2015; Volume 6. [Google Scholar]
- Mei, Y.; Tajderi, M.; Goenezen, S. Regularizing biomechanical maps for partially known material properties. Int. J. Appl. Mech. 2017, 9, 1750020. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. L-BFGS-B: FORTRAN Subroutines for Large Scale Bound Constrained Optimization; Tech. Report, NAM-11; EECS Department, Northwestern University: Evanston, IL, USA, 1994. [Google Scholar]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. L-BFGS-B: A Limited Memory FORTRAN Code for Solving Bound Constrained Optimization Problems; Tech. Report, NAM-11; EECS Department, Northwestern University: Evanston, IL, USA, 1994. [Google Scholar]
- Maniatty, A.M.; Liu, Y.; Klaas, O.; Shephard, M.S. Higher order stabilized finite element method for hyperelastic finite deformation. Comput. Methods Appl. Mech. Eng. 2002, 191, 1491–1503. [Google Scholar] [CrossRef]
- Pan, X.; Liu, K.; Bai, J.; Luo, J. A regularization-free elasticity reconstruction method for ultrasound elastography with freehand scan. Biomed. Eng. Online 2014, 13, 132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mei, Y.; Stover, B.; Kazerooni, N.A.; Srinivasa, A.; Hajhashemkhani, M.; Hematiyan, M.; Goenezen, S. A comparative study of two constitutive models within an inverse approach to determine the spatial stiffness distribution in soft materials. Int. J. Mech. Sci. 2018, 140, 446–454. [Google Scholar] [CrossRef]
- Mei, Y.; Kuznetsov, S.; Goenezen, S. Reduced boundary sensitivity and improved contrast of the regularized inverse problem solution in elasticity. J. Appl. Mech. 2016, 83, 031001. [Google Scholar] [CrossRef]
- Gerbig, D.; Bower, A.; Savic, V.; Hector, L.G. Coupling digital image correlation and finite element analysis to determine constitutive parameters in necking tensile specimens. Int. J. Solids Struct. 2016, 97, 496–509. [Google Scholar] [CrossRef]
- Mei, Y.; Wang, S.; Shen, X.; Rabke, S.; Goenezen, S. Mechanics Based Tomography: A Preliminary Feasibility Study. Sensors 2017, 17, 1075. [Google Scholar] [CrossRef] [PubMed]
- Avril, S.; Pierron, F.; Sutton, M.A.; Yan, J. Identification of elasto-visco-plastic parameters and characterization of Luders behavior using digital image correlation and the virtual fields method. Mech. Mater. 2008, 40, 729–742. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Sun, Y.; Mei, Y. A Size-Dependent Cost Function to Solve the Inverse Elasticity Problem. Appl. Sci. 2019, 9, 1799. https://doi.org/10.3390/app9091799
Zhao X, Sun Y, Mei Y. A Size-Dependent Cost Function to Solve the Inverse Elasticity Problem. Applied Sciences. 2019; 9(9):1799. https://doi.org/10.3390/app9091799
Chicago/Turabian StyleZhao, Xinbo, Yanli Sun, and Yue Mei. 2019. "A Size-Dependent Cost Function to Solve the Inverse Elasticity Problem" Applied Sciences 9, no. 9: 1799. https://doi.org/10.3390/app9091799
APA StyleZhao, X., Sun, Y., & Mei, Y. (2019). A Size-Dependent Cost Function to Solve the Inverse Elasticity Problem. Applied Sciences, 9(9), 1799. https://doi.org/10.3390/app9091799



