Study on the Wellbore Flow for Carbon Dioxide Fracturing
Abstract
:1. Introduction
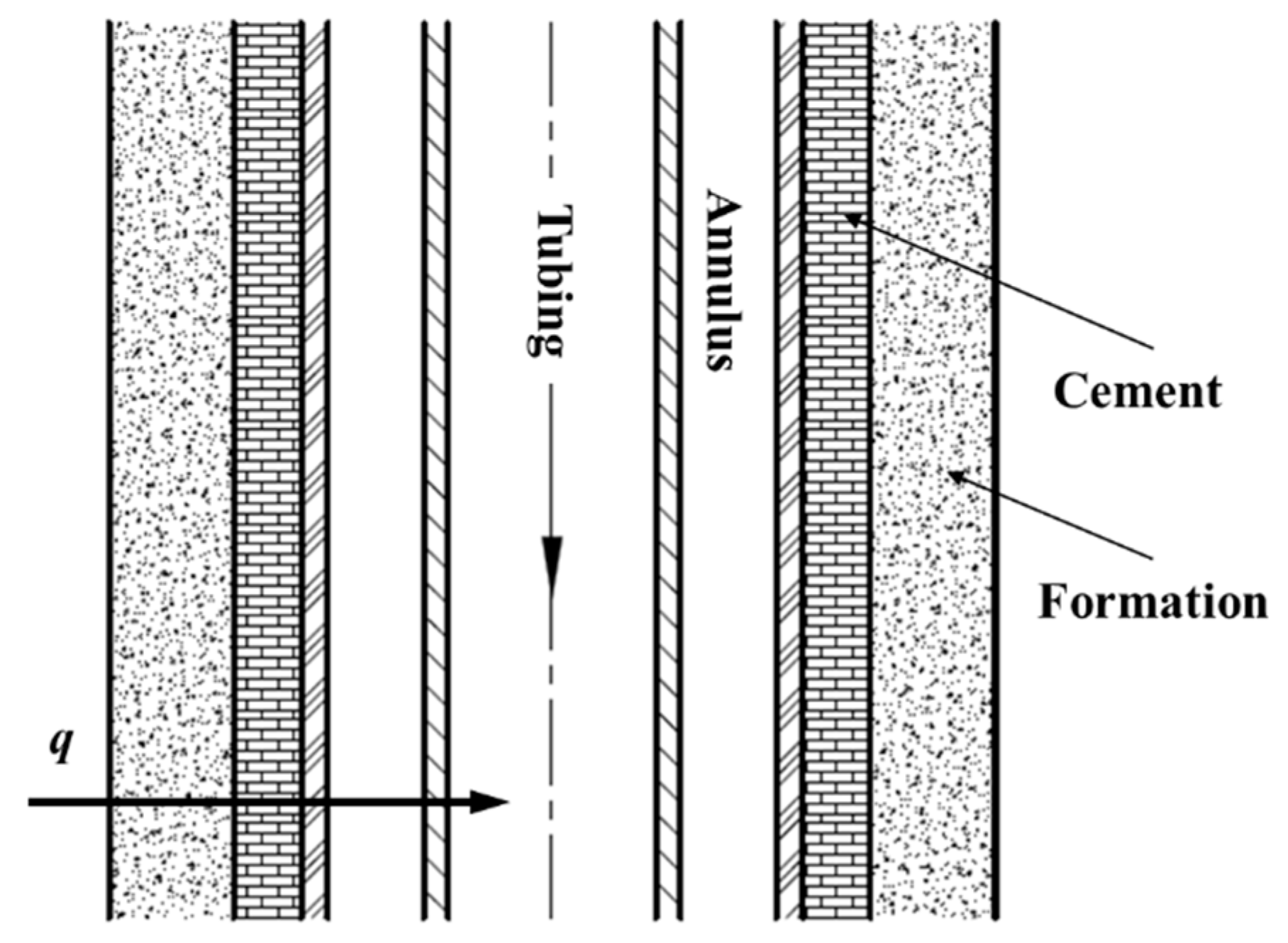
2. Mathematic Model of Wellbore Flow
2.1. Temperature Field Model
2.2. Pressure Field Model
3. Solution Procedure
3.1. Physical Properties of CO2
3.2. Coupling Computation Methodology
4. Results and Discussion
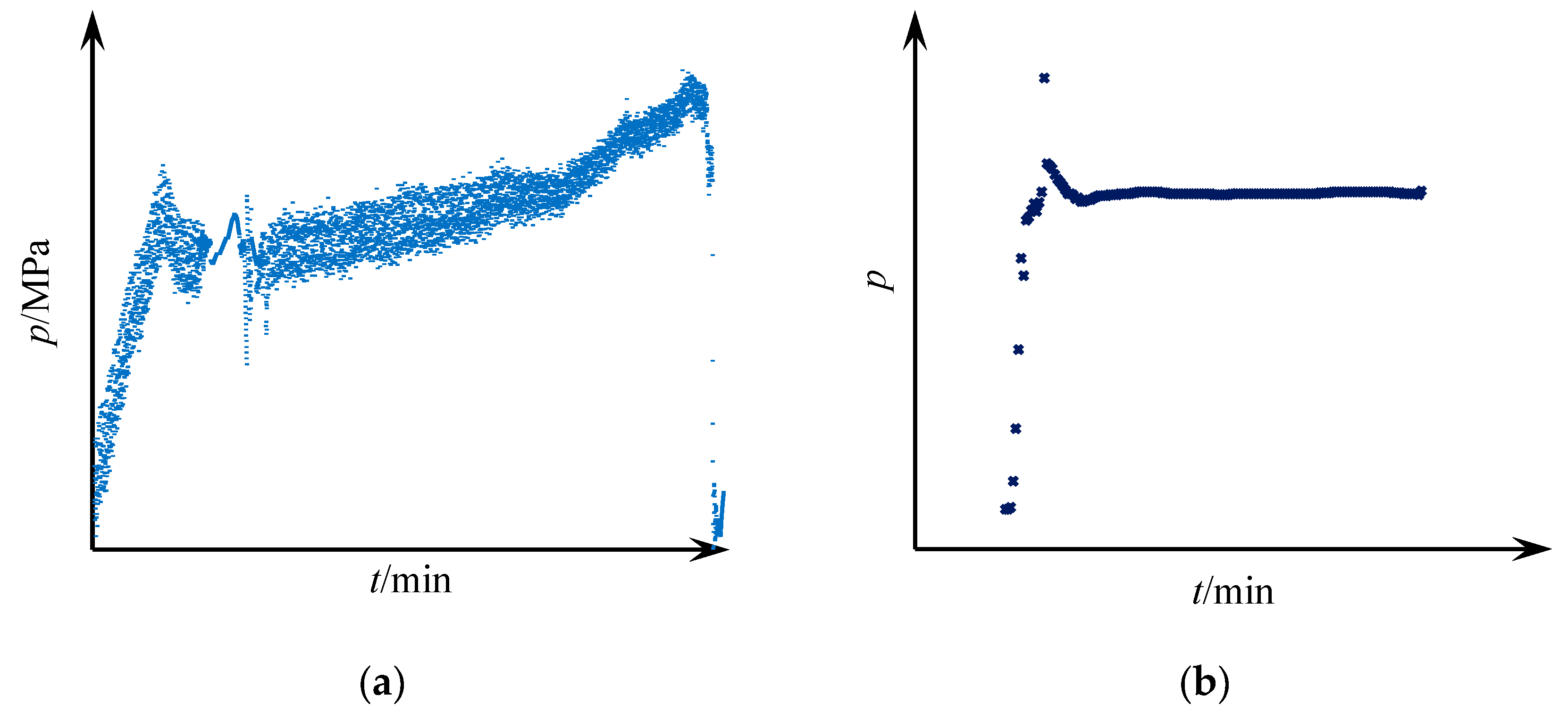
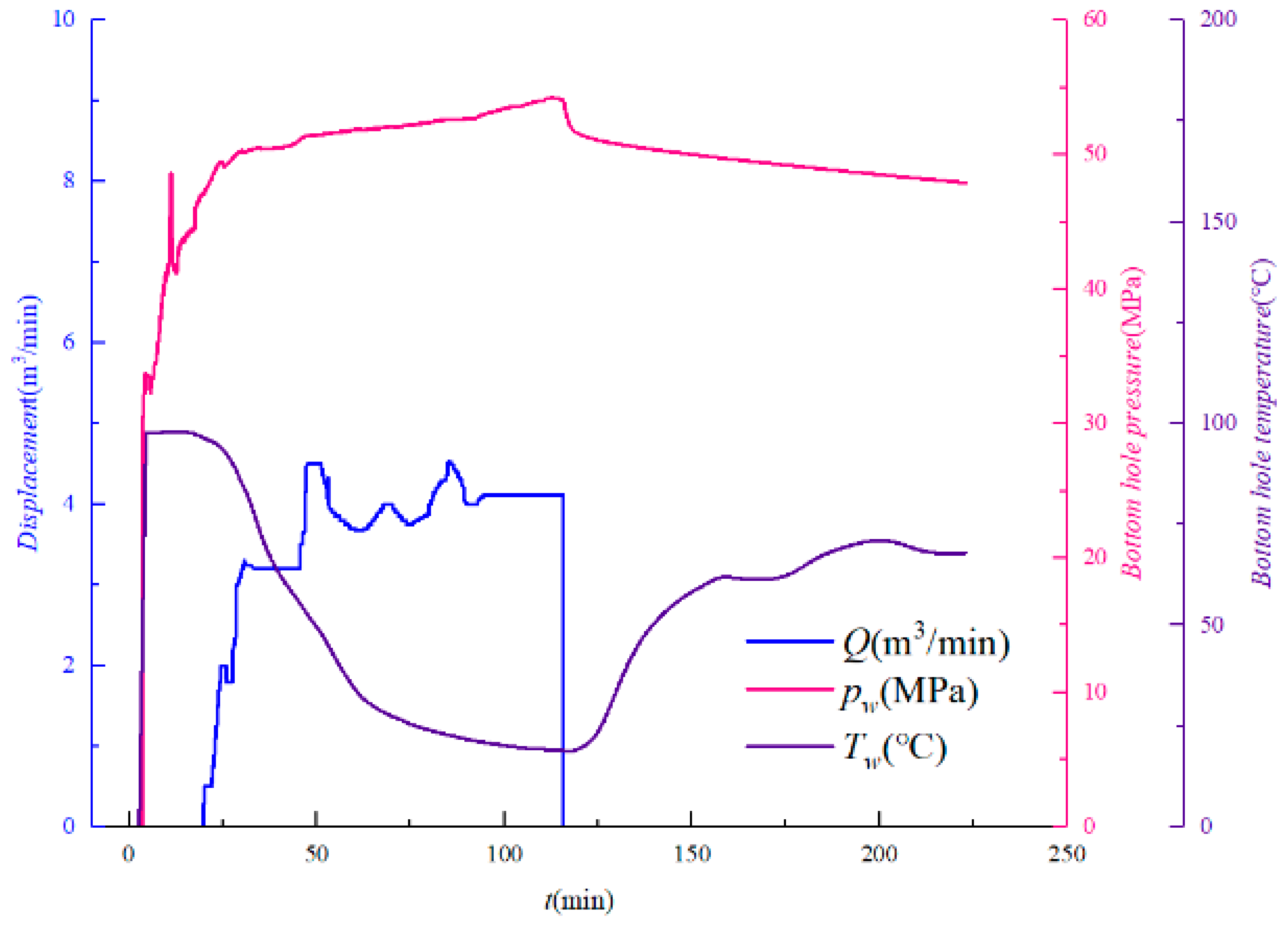
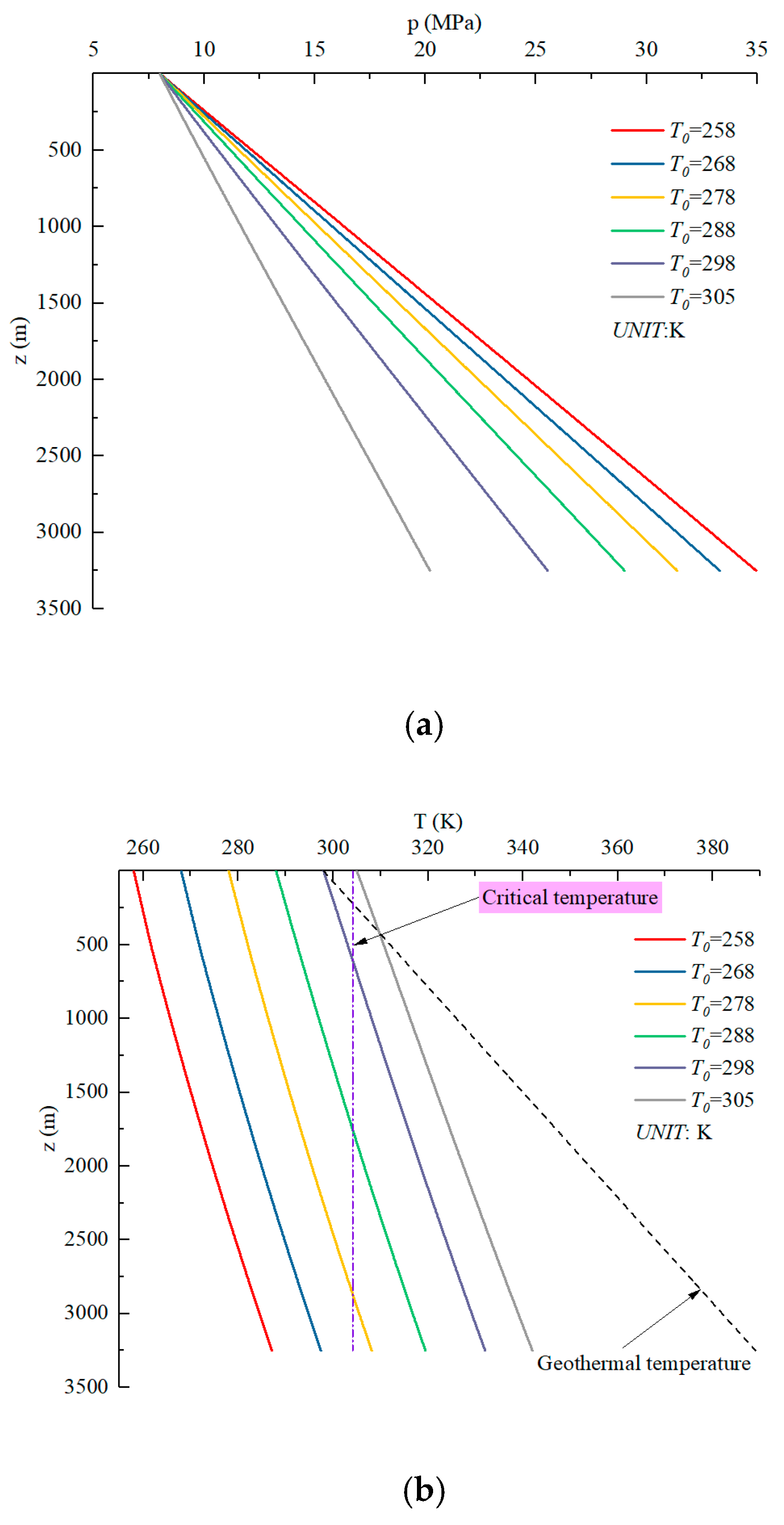
4.1. Model Validation and Wellbore Temperature–Pressure Distribution
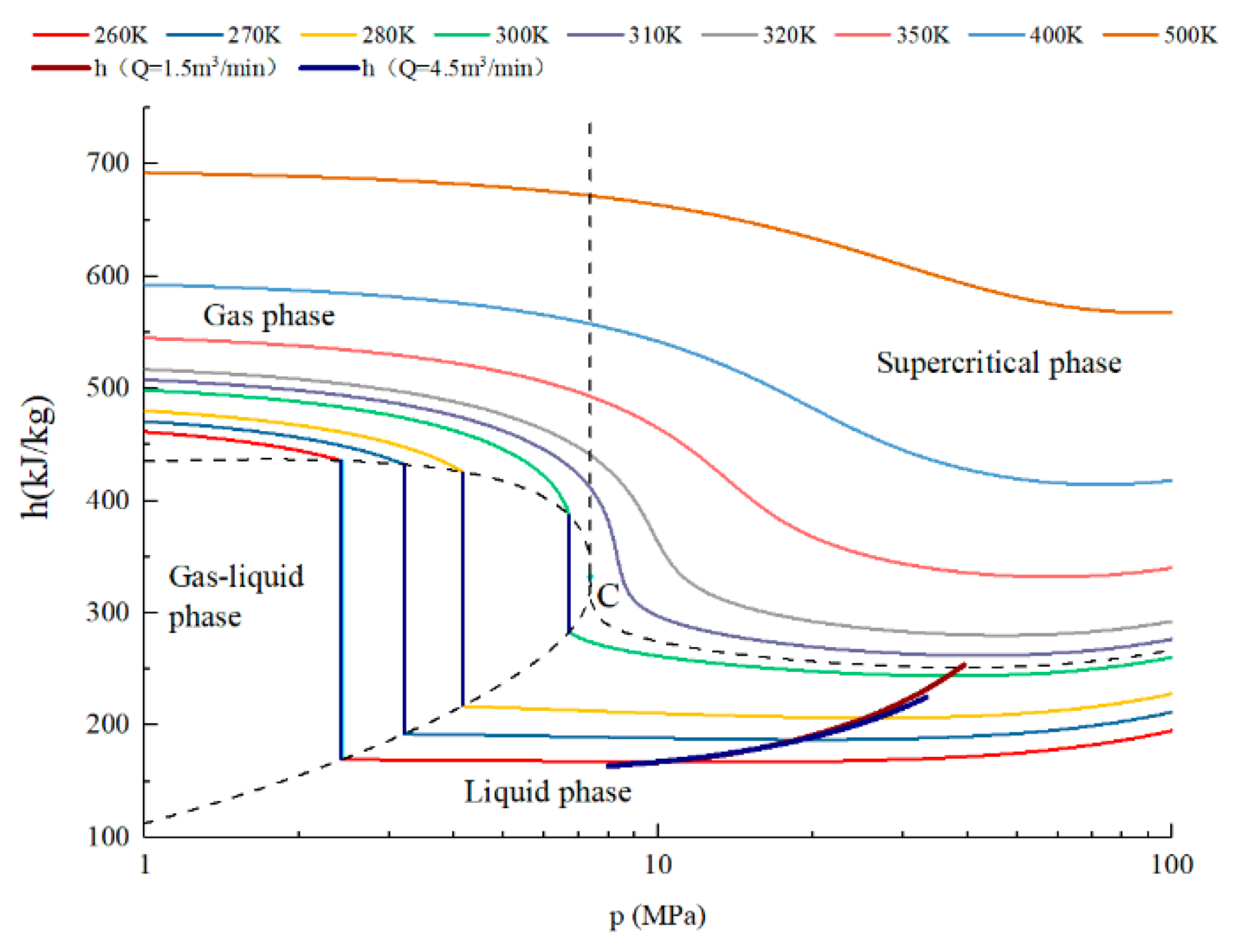
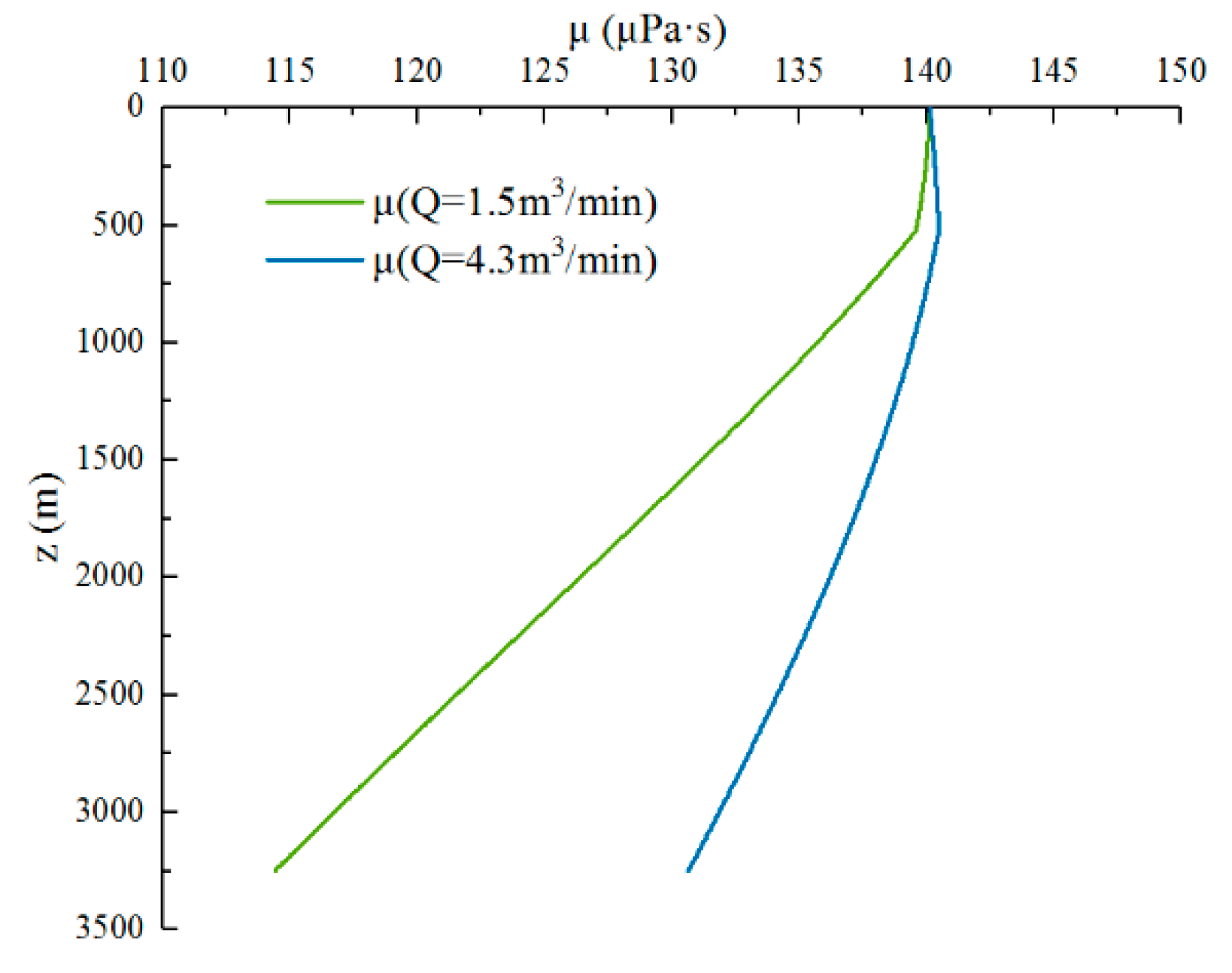
4.2. CO2 Phase State and Physical Properties Distribution
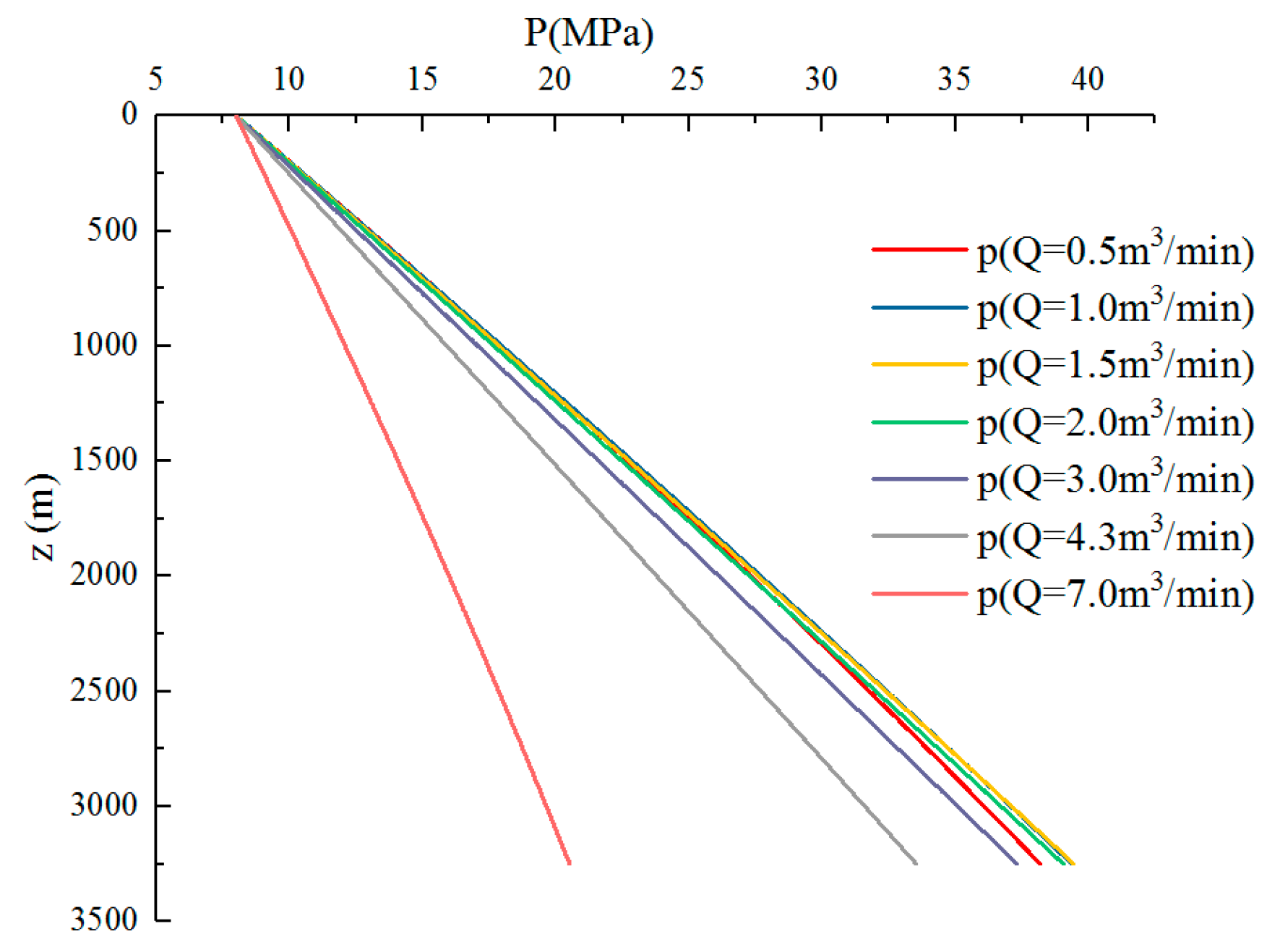
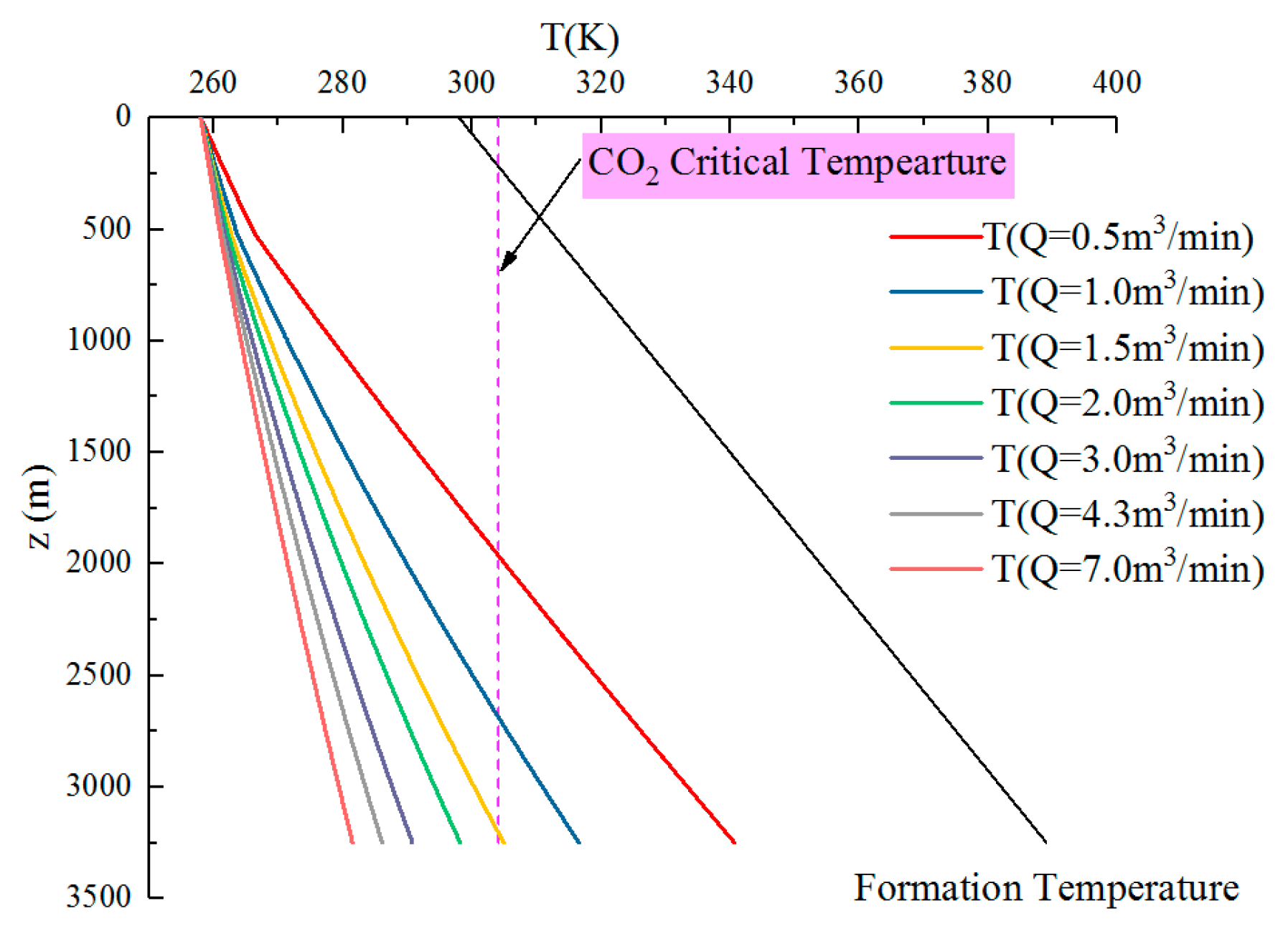
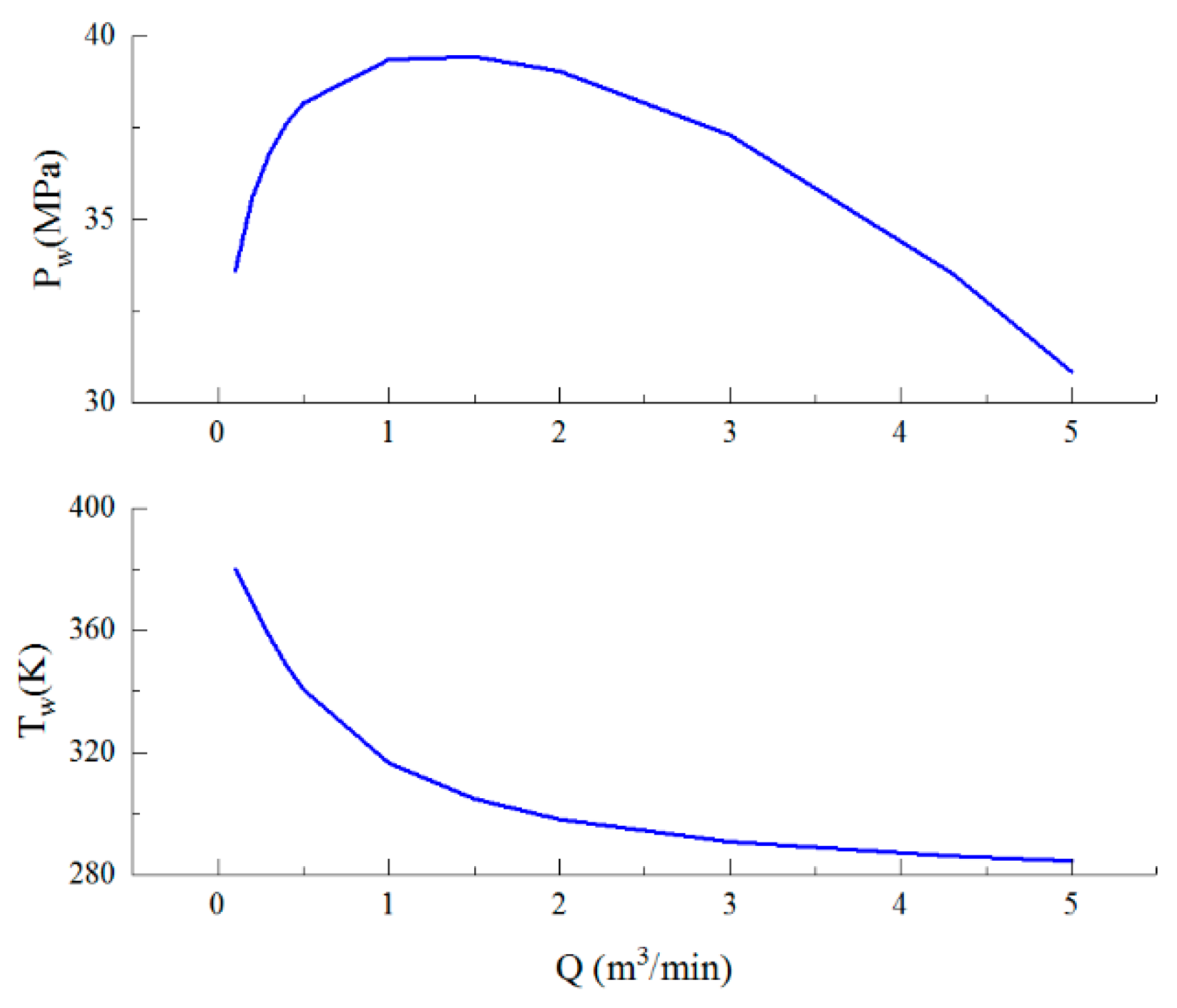
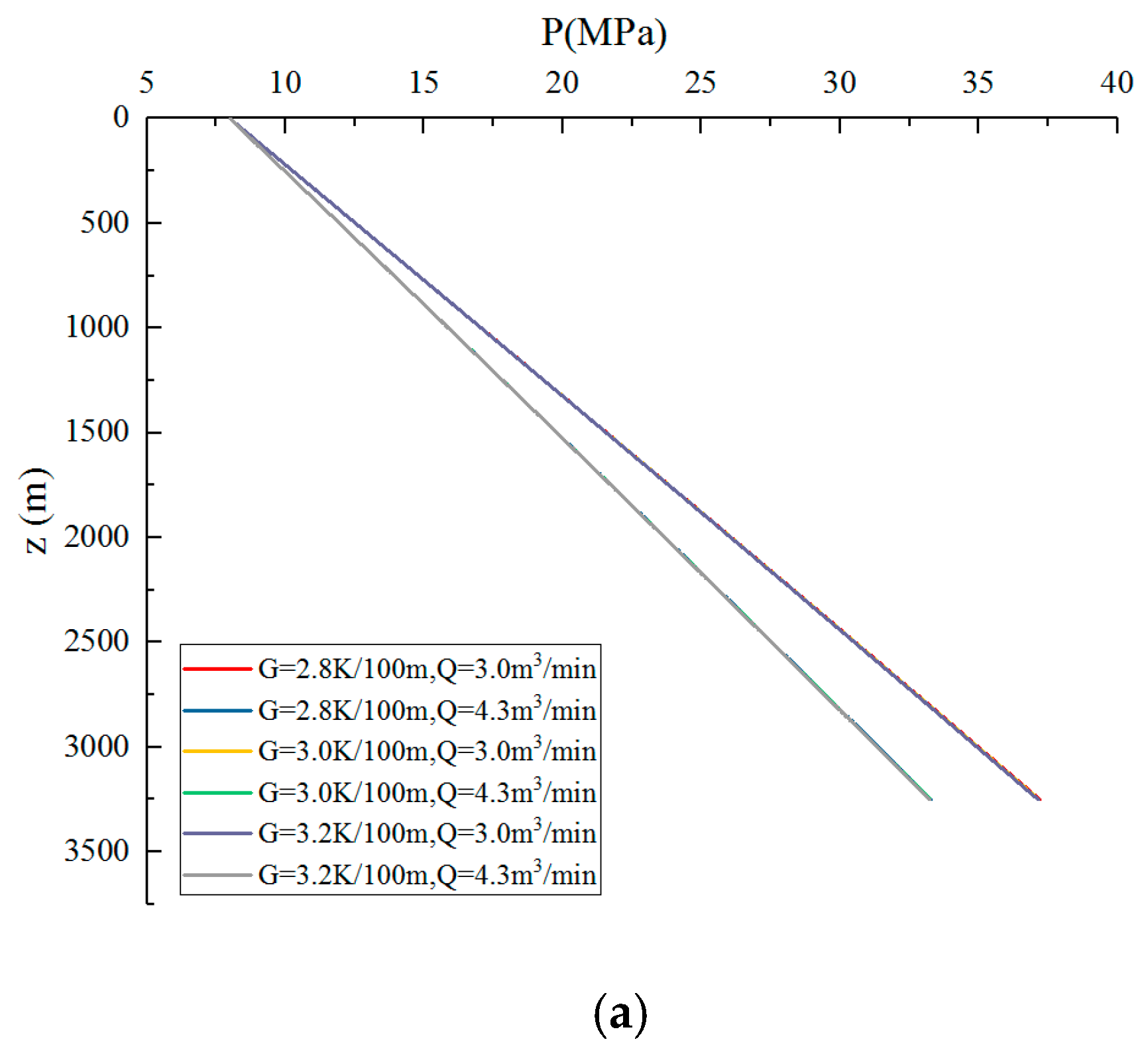
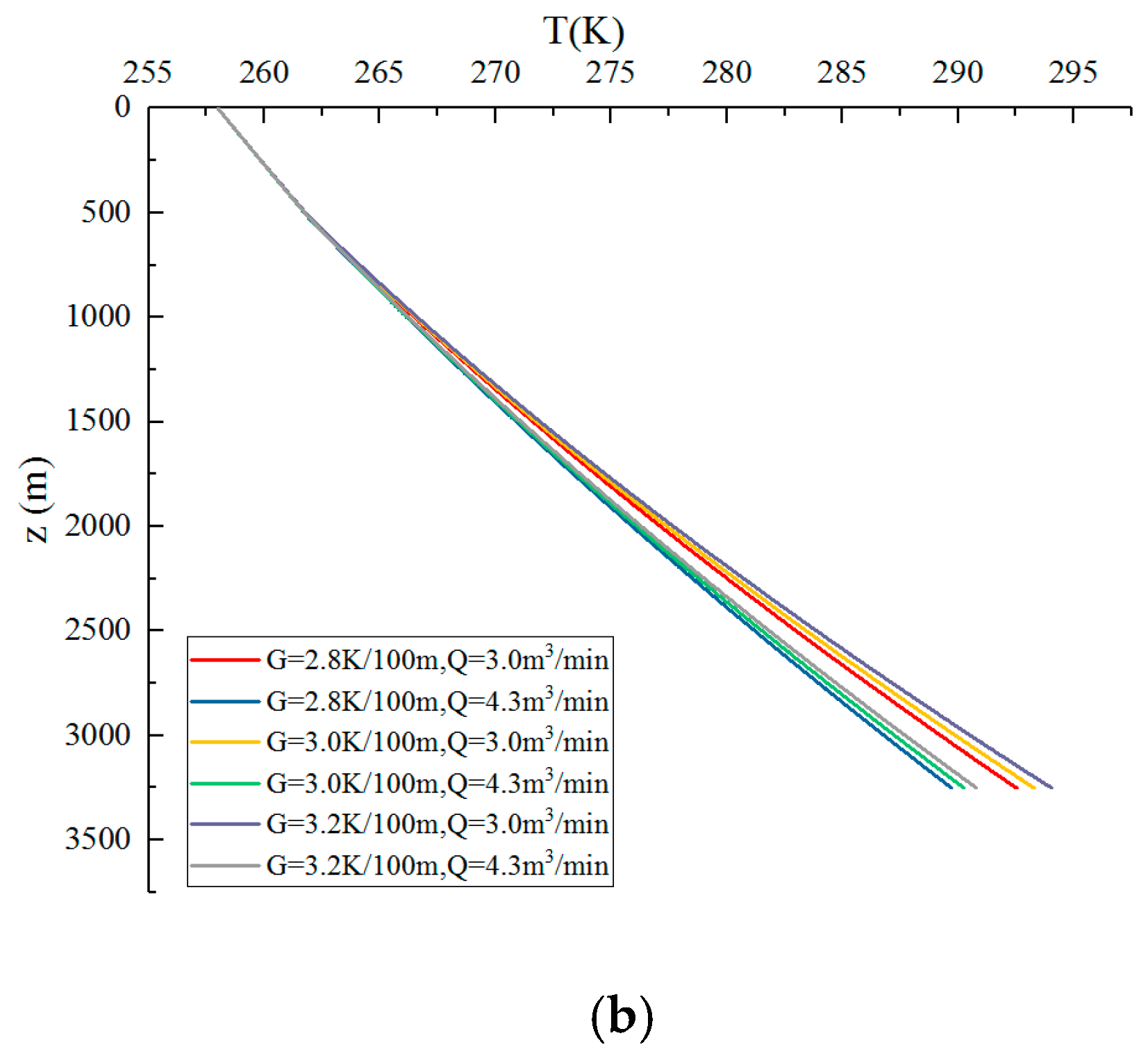
4.3. Sensitivity Analyses on Controlling Factors for CO2 Fracturing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Semianalytical Method for Formation Heat Transfer
Appendix B. Thermal Resistance of Wellbore
References
- Bullen, R.S.; Lillies, A.T. Carbon Dioxide Fracturing Process and Apparatus. U.S. Patent 4,374,545, 22 February 1983. [Google Scholar]
- Mazza, R.L. Liquid-Free CO2/Sand Stimulations: An Overlooked Technology-Production Update. In Proceedings of the SPE Eastern Regional Meeting, Canton, OH, USA, 17–19 October 2001. [Google Scholar]
- Middleton, R.; Viswanathan, H.; Currier, R.; Gupta, R. CO2 as a fracturing fluid: Potential for commercial-scale shale gas production and CO2 sequestration. Energy Procedia 2014, 63, 7780–7784. [Google Scholar] [CrossRef]
- Asadi, M.; Scharmach, W.; Jones, T.; Sampayo, A.; Chesney, E.; Unruh, D. Water-Free Fracturing: A Case History. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 13–15 October 2015. [Google Scholar]
- Li, M.; Ni, H.; Wang, R.; Xiao, C. Comparative simulation research on the stress characteristics of supercritical carbon dioxide jets, nitrogen jets and water jets. Eng. Appl. Comput. Fluid Mech. 2017, 11, 357–370. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Li, G.; Shen, Z. A feasibility analysis on shale gas exploitation with supercritical carbon dioxide. Energy Sources Part A 2012, 34, 1426–1435. [Google Scholar] [CrossRef]
- Chung, F.T.H.; Jones, R.A.; Burchfield, T.E. Recovery of viscous oil under high pressure by CO2 displacement: A laboratory study. In Proceedings of the International Meeting on Petroleum Engineering, Tianjin, China, 1–4 November 1988. [Google Scholar]
- Zhang, L.; Ezekiel, J.; Li, D.; Pei, J.; Ren, S. Potential assessment of CO2 injection for heat mining and geological storage in geothermal reservoirs of China. Appl. Energy 2014, 122, 237–246. [Google Scholar] [CrossRef]
- Wang, J.; Lv, K.; Bian, Y.; Cheng, Y. Energy efficiency and marginal carbon dioxide emission abatement cost in urban China. Energy Policy 2017, 105, 246–255. [Google Scholar] [CrossRef]
- Dai, Z.; Middleton, R.; Viswanathan, H.; Fessenden-Rahn, J.; Bauman, J.; Pawar, R.; Lee, S.Y.; McPherson, B. An integrated framework for optimizing CO2 sequestration and enhanced oil recovery. Environ. Sci. Technol. Lett. 2014, 1, 49–54. [Google Scholar] [CrossRef]
- Dai, Z.; Viswanathan, H.; Middleton, R.; Pan, F.; Ampomah, W.; Yang, C.; Jia, W.; Xiao, T.; Lee, S.Y.; McPherson, B.; et al. CO2 accounting and risk analysis for CO2 sequestration at enhanced oil recovery sites. Environ. Sci. Technol. Lett. 2016, 50, 7546–7554. [Google Scholar] [CrossRef]
- Balch, R.; McPherson, B. Integrating enhanced oil recovery and carbon capture and storage projects: a case study at farnsworth field, Texas. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 23–26 May 2016; Society of Petroleum Engineers. [Google Scholar]
- Ampomah, W.; Balch, R.S.; Rose-Coss, D.; Will, R.; Cather, M.; Dai, Z.; Soltanian, M.R. Optimal Design of CO2 Storage and Oil Recovery under Geological Uncertainty. Appl. Energy 2017, 195, 80–92. [Google Scholar] [CrossRef]
- Ramey, H.J. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Raymond, L.R. Temperature distribution in a circulating drilling fluid. J. Pet. Technol. 1969, 21, 333–341. [Google Scholar] [CrossRef]
- Eickmeier, J.R.; Ersoy, D.; Ramey, H.J. Wellbore temperatures and heat losses during production or injection operations. J. Pet. Technol. 1970, 9. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Aspects of wellbore heat transfer during two-phase flow. SPE Prod. Facil. 1994, 9, 211–216. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Wellbore heat-transfer modeling and applications. J. Pet. Technol. 2012, 86, 127–136. [Google Scholar] [CrossRef]
- Kabir, C.S.; Hasan, A.R.; Kouba, G.E.; Ameen, M. Determining circulating fluid temperature in drilling, workover, and well-control operations. SPE Drill. Complet. 1996, 11, 74–79. [Google Scholar] [CrossRef]
- Gao-Feng, W.; Yong-Le, H.U.; Zhi-Ping, L.I.; Wei, Y.; Yu-Wei, J. Modification and Application of Ramey’s Wellbore Heat Transmission. J. Southwest Pet. Univ. 2011, 33, 5. [Google Scholar]
- Cronshaw, M.B.; Bolling, J.D. A numerical model of the non-isothermal flow of carbon dioxide in wellbores. In Proceedings of the SPE California Regional Meeting, San Francisco, CA, USA, 24–26 March 1982. [Google Scholar]
- Gupta, A.P.; Langlinais, J. Feasibility of supercritical carbon dioxide as a drilling fluid for deep underbalanced drilling operating. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Al-Adwani, F.; Langlinais, J.; Hughes, R. Modeling of an underbalanced-drilling operation using supercritical carbon dioxide. SPE Prod. Facil. 2009, 24, 599–610. [Google Scholar] [CrossRef]
- Wang, H.; Shen, Z.; Li, G. A wellbore flow model of coiled tubing drilling with supercritical carbon dioxide. Energy Sources Part A 2012, 34, 1347–1362. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, B.; Sun, X.; Li, H.; Wang, J. Phase state variations for supercritical carbon dioxide drilling. Greenh. Gases Sci. Technol. 2016, 6, 83–93. [Google Scholar] [CrossRef]
- Lindeberg, E. Modelling pressure and temperature profile in a CO2 injection well. Energy Procedia 2011, 4, 3935–3941. [Google Scholar] [CrossRef]
- Song, W.; Ni, H.; Wang, R.; Sun, B.; Shen, Z. Pressure transmission in the tubing of supercritical carbon dioxide fracturing. J. CO2 Util. 2017, 21, 467–472. [Google Scholar] [CrossRef]
- Anderson, J.D.; Wendt, J. Computational Fluid Dynamics; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Wang, Z.; Sun, B.; Wang, J.; Hou, L. Experimental study on the friction coefficient of supercritical carbon dioxide in pipes. Int. J. Greenh. Gas Control 2014, 25, 151–161. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Vesovic, A.; Wakeham, W.A. The transport properties of carbon dioxide. J. Phys. Chem. Ref. Data 1990, 19, 763–808. [Google Scholar] [CrossRef]
- Fenghour, A.; Wakeham, W.A. The viscosity of carbon dioxide. J. Phys. Chem. Ref. Data 1998, 27, 31–44. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat transfer during two-Phase flow in Wellbores; Part I—Formation temperature. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiator of the tubular type. Int. Commun. Heat Mass Transf. 1930, 12, 3–22. [Google Scholar] [CrossRef]



| No. | Variables | Symbol | Value | Unit |
|---|---|---|---|---|
| 1 | Well depth | H | 3250 | m |
| 2 | Borehole diameter | dw | 0.121 | m |
| 3 | Formation pore pressure | ppo | 28.16 | MPa |
| 4 | Surface temperature | Teo | 298 | K |
| 5 | Injection temperature | T0 | 258 | K |
| 6 | Injection pressure | p0 | 8 | MPa |
| 7 | Geothermal gradient | G | 2.8 | K/100m |
| 8 | Initial breakdown pressure | pf | 66.02 | MPa |
| 9 | Initial formation compressible strength | σc | 135.077 | MPa |
| 10 | Tensile strength | σt | σc/12 | MPa |
| 11 | Initial elastic modulus | E | 18.7070 | GPa |
| 12 | Thermal expansion coefficient of rock | σm | 3 × 10−5 | K−1 |
| 13 | Initial Poisson ratio | ν | 0.242 | - |
| 14 | Porosity | φ | 0.05 | - |
| 15 | Maximum horizontal in situ stress gradient | σH | 1.9 | g/cm3 |
| 16 | Minimum horizontal in situ stress gradient | σh | 1.45 | g/cm3 |
| 17 | Overburden gradient | σv | 2.3 | g/cm3 |
| 18 | Biot’s parameter | α | 1.0 | - |
| Q (m3/min) | Comparison Items | Measured Values | Calculated Values | Error (%) |
|---|---|---|---|---|
| 4.0 | Bottom hole temperature (K) | 288.75 | 287.10 | 0.57 |
| Bottom hole pressure (MPa) | 52.81 | 53.22 | 0.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Xiao, C.; Mu, C.; Zheng, L. Study on the Wellbore Flow for Carbon Dioxide Fracturing. Appl. Sci. 2019, 9, 1864. https://doi.org/10.3390/app9091864
Bai J, Xiao C, Mu C, Zheng L. Study on the Wellbore Flow for Carbon Dioxide Fracturing. Applied Sciences. 2019; 9(9):1864. https://doi.org/10.3390/app9091864
Chicago/Turabian StyleBai, Jianwen, Caiyun Xiao, Chunguo Mu, and Lihui Zheng. 2019. "Study on the Wellbore Flow for Carbon Dioxide Fracturing" Applied Sciences 9, no. 9: 1864. https://doi.org/10.3390/app9091864
APA StyleBai, J., Xiao, C., Mu, C., & Zheng, L. (2019). Study on the Wellbore Flow for Carbon Dioxide Fracturing. Applied Sciences, 9(9), 1864. https://doi.org/10.3390/app9091864




