A Microcrack Location Method Based on Nonlinear S0 Mode Lamb Wave and Probability Scan Positioning Imaging Matrix
Abstract
:Featured Application
Abstract
1. Introduction
2. Theory and Analysis
2.1. Probability Hypothesis
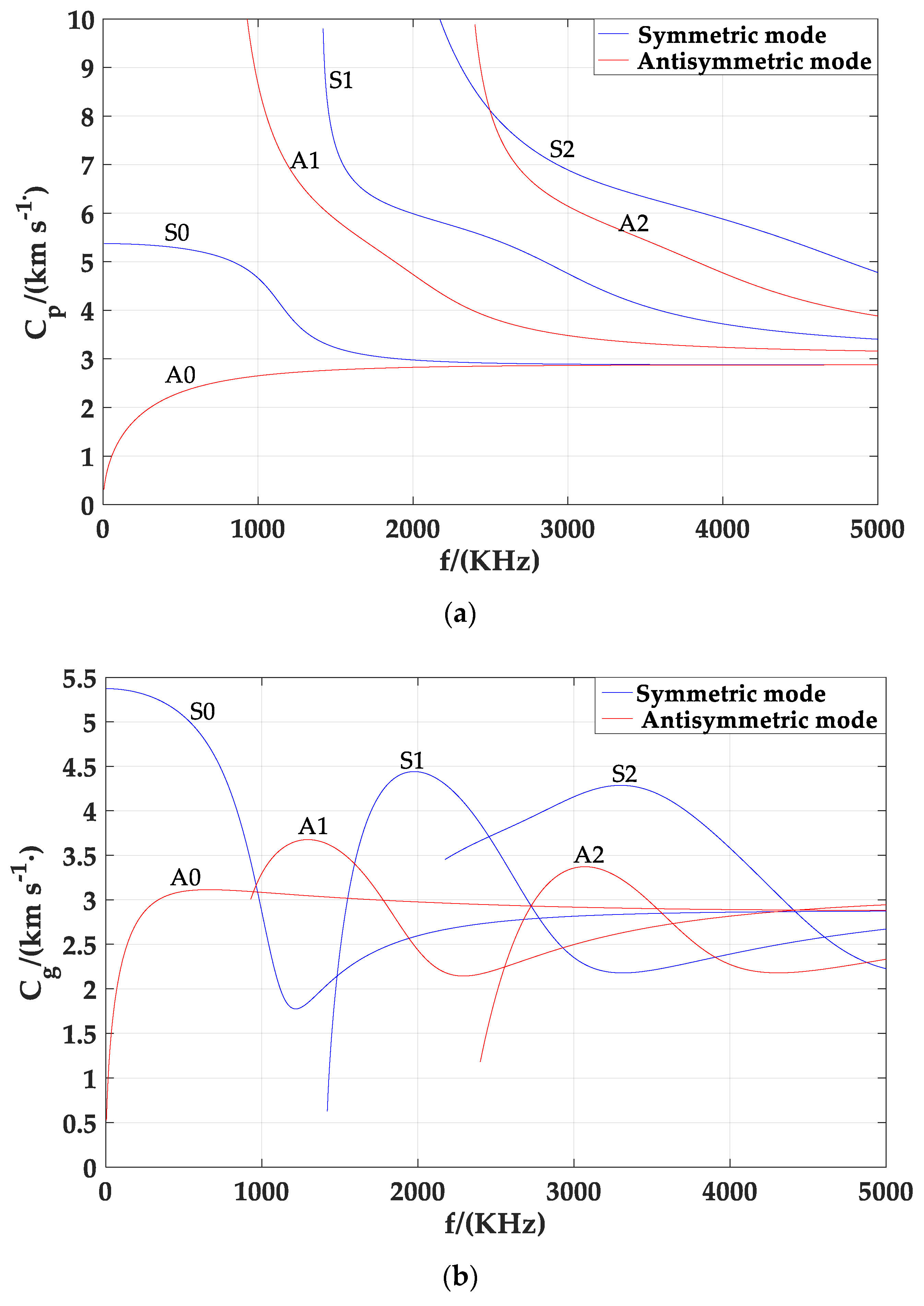
2.2. Lamb Excitation
2.3. Nonlinear Coefficient
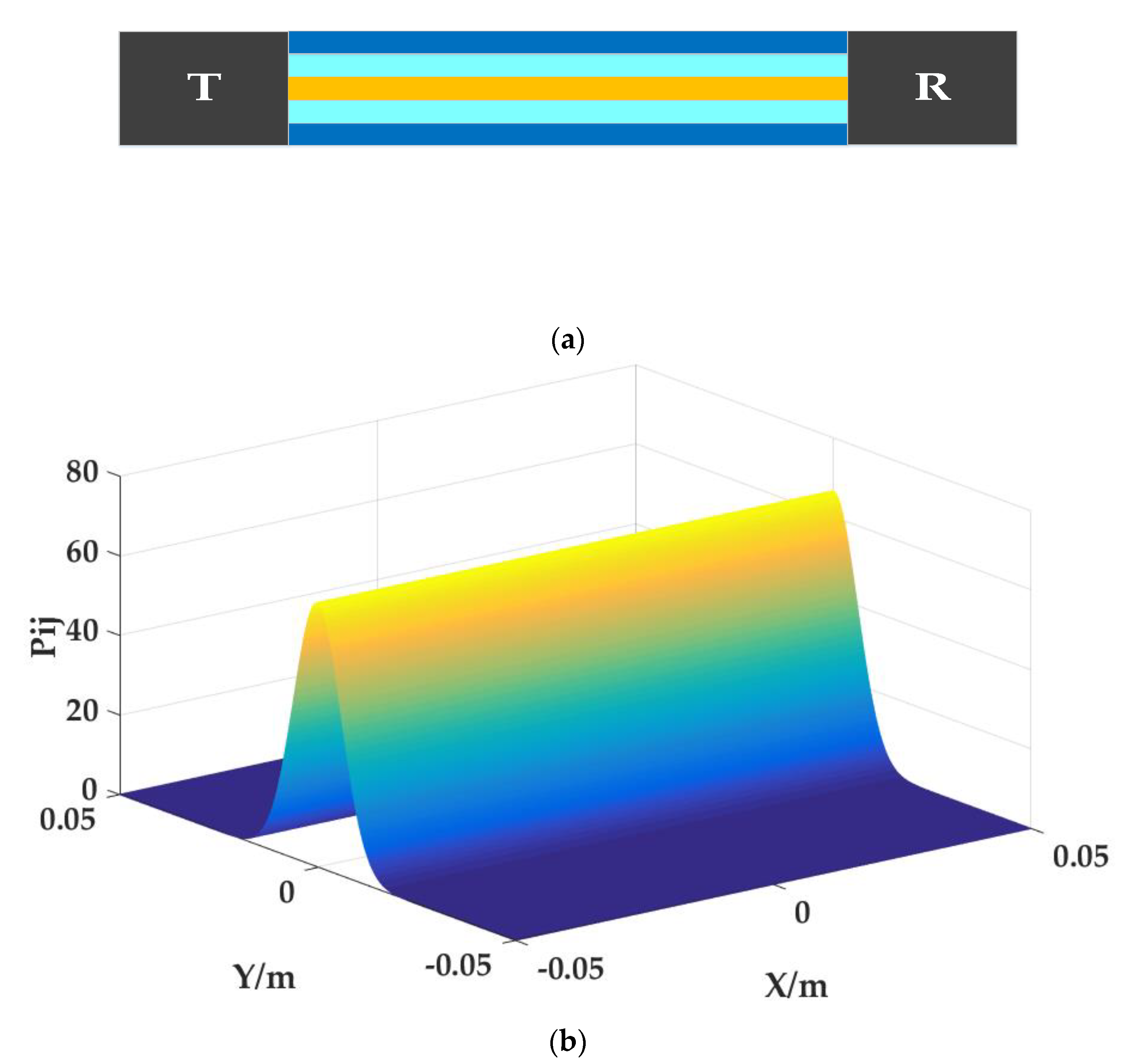
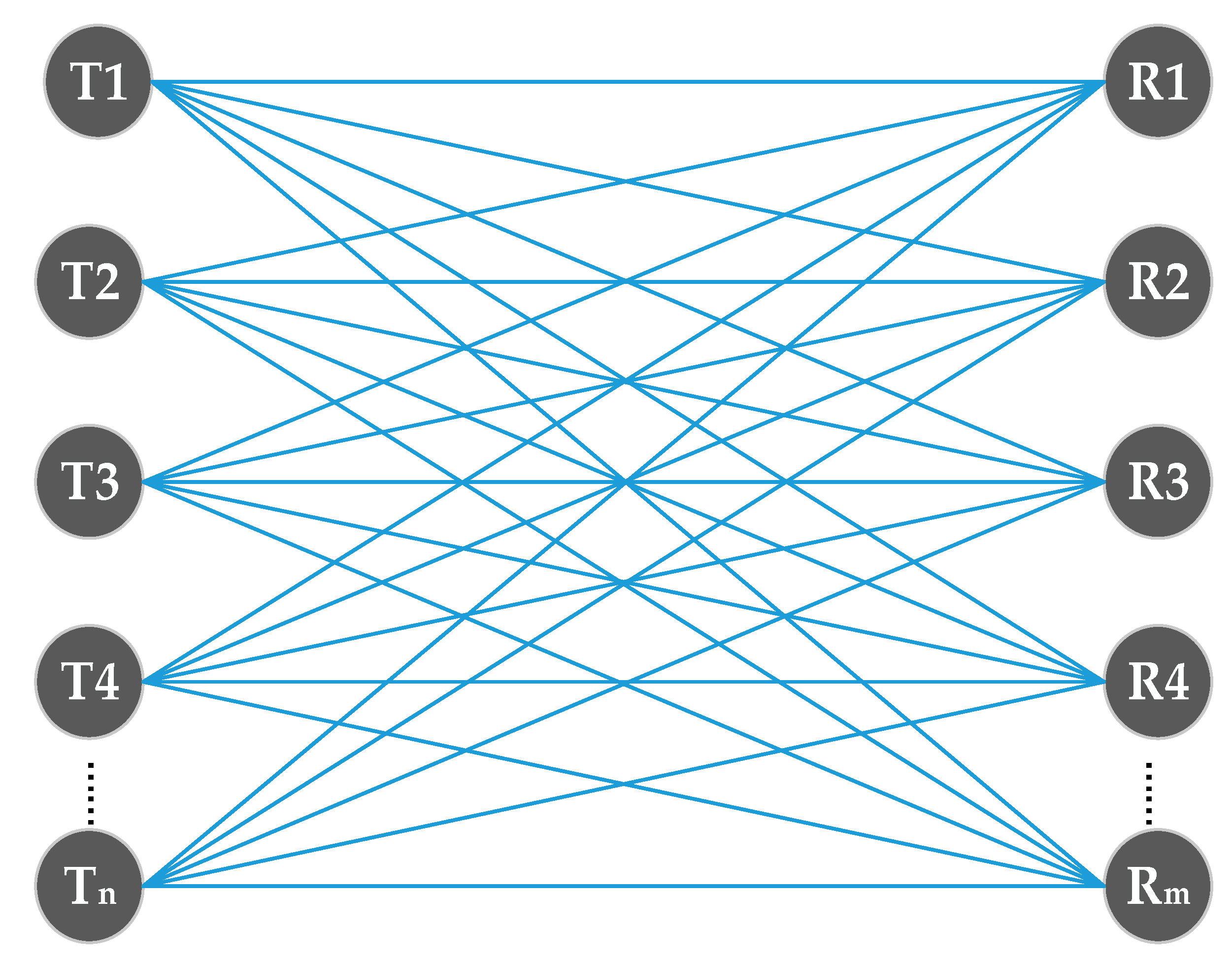
2.4. Probability Scan Matrix
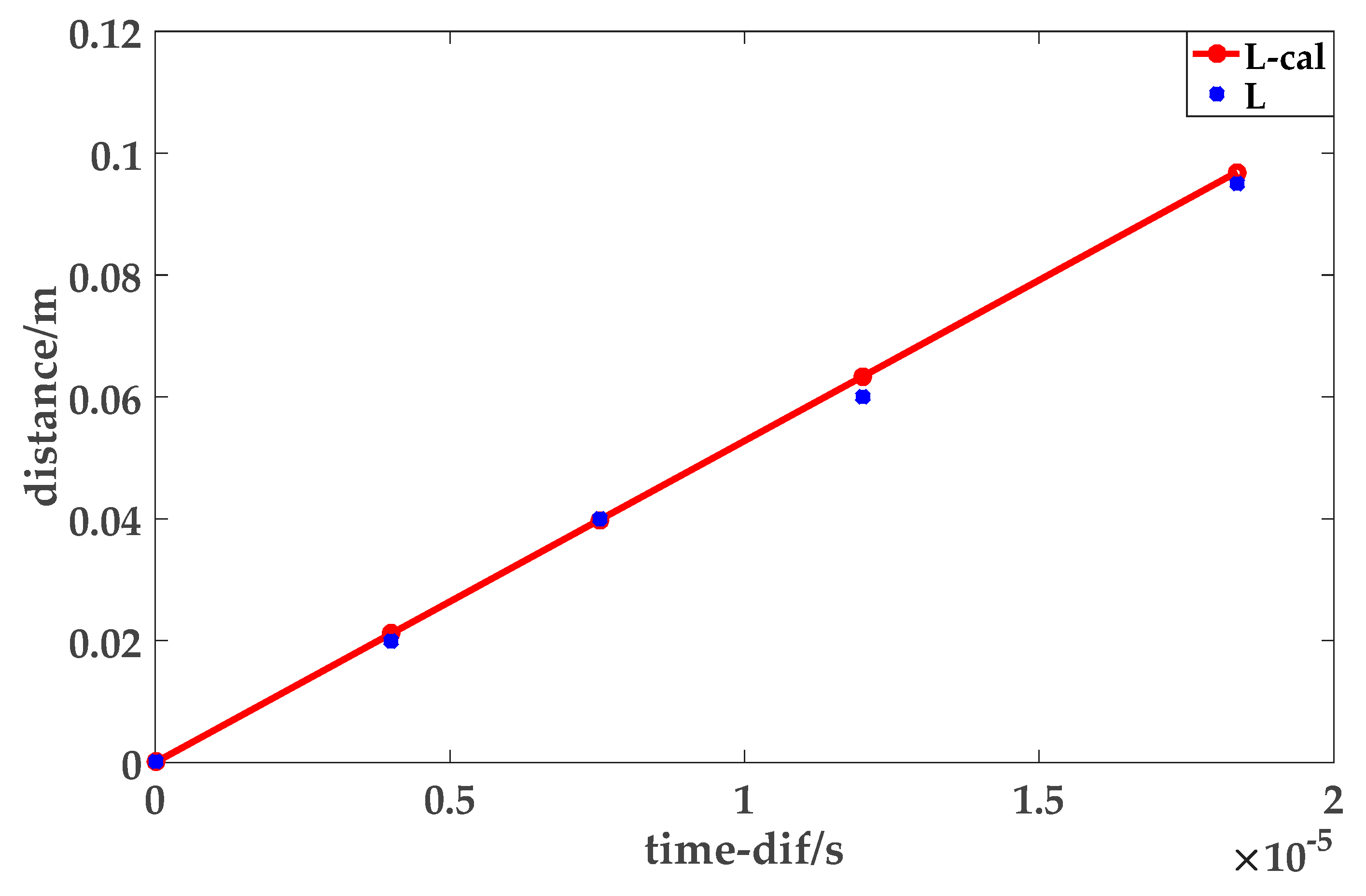
2.5. Result Evaluation
3. Three-Dimensional Finite Element Simulation
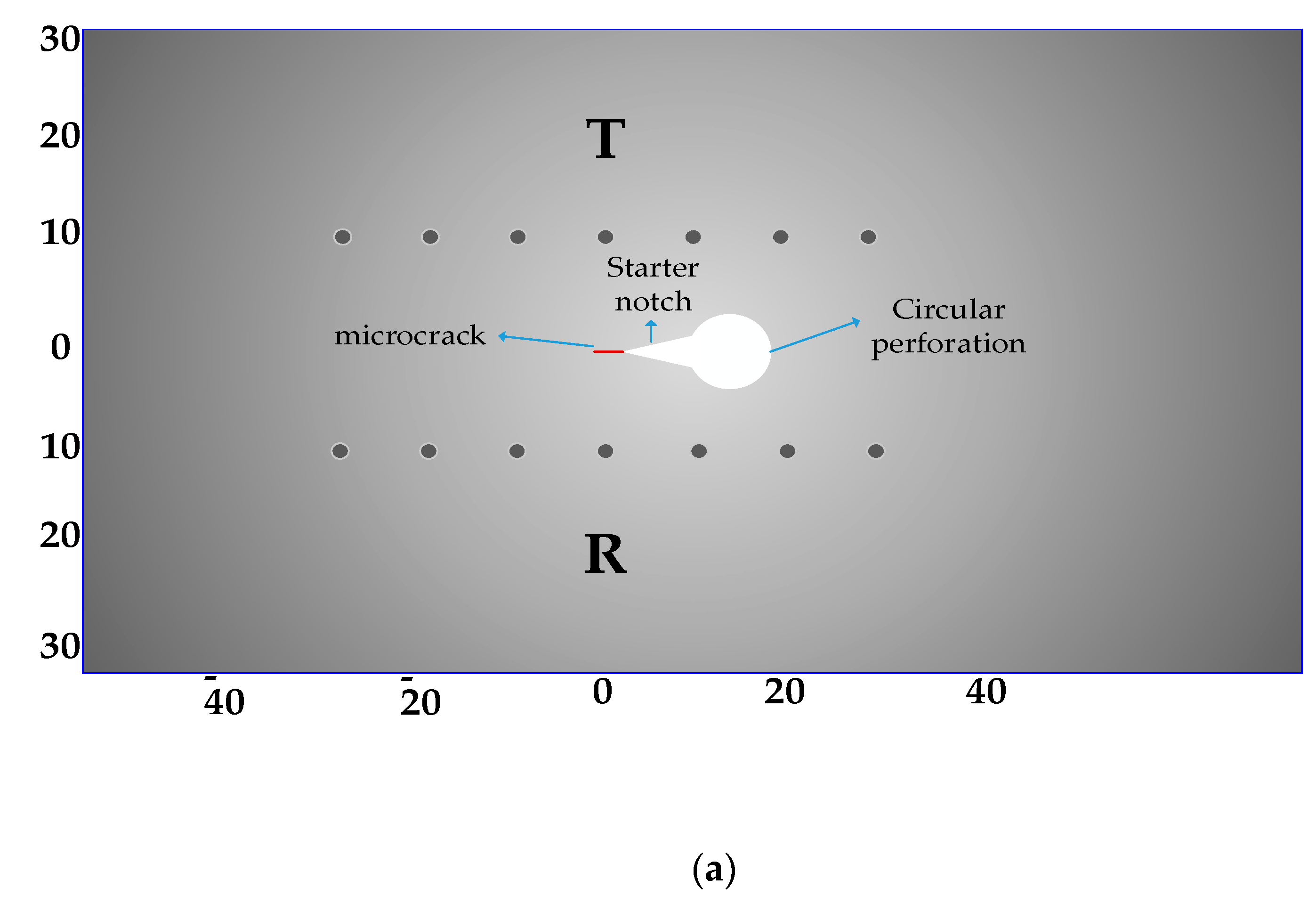
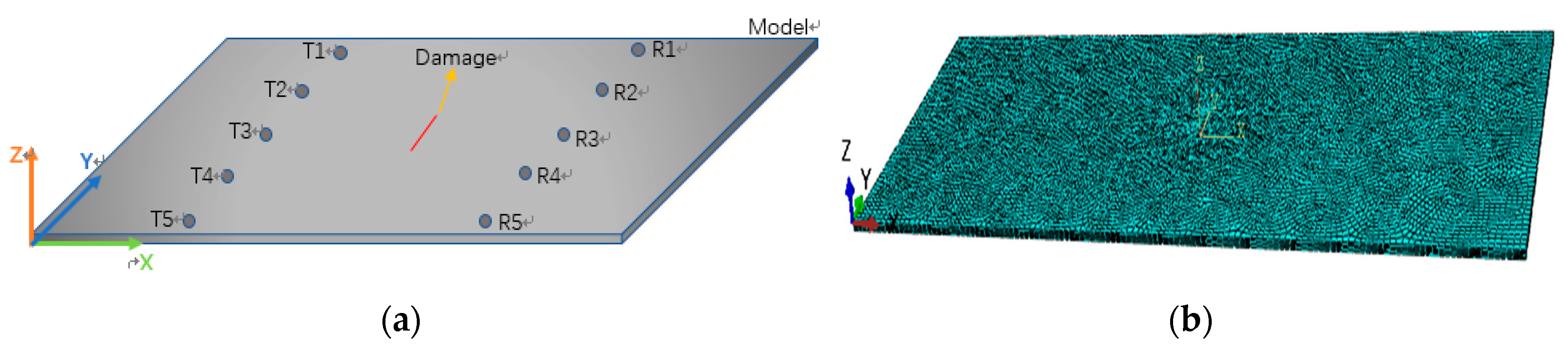
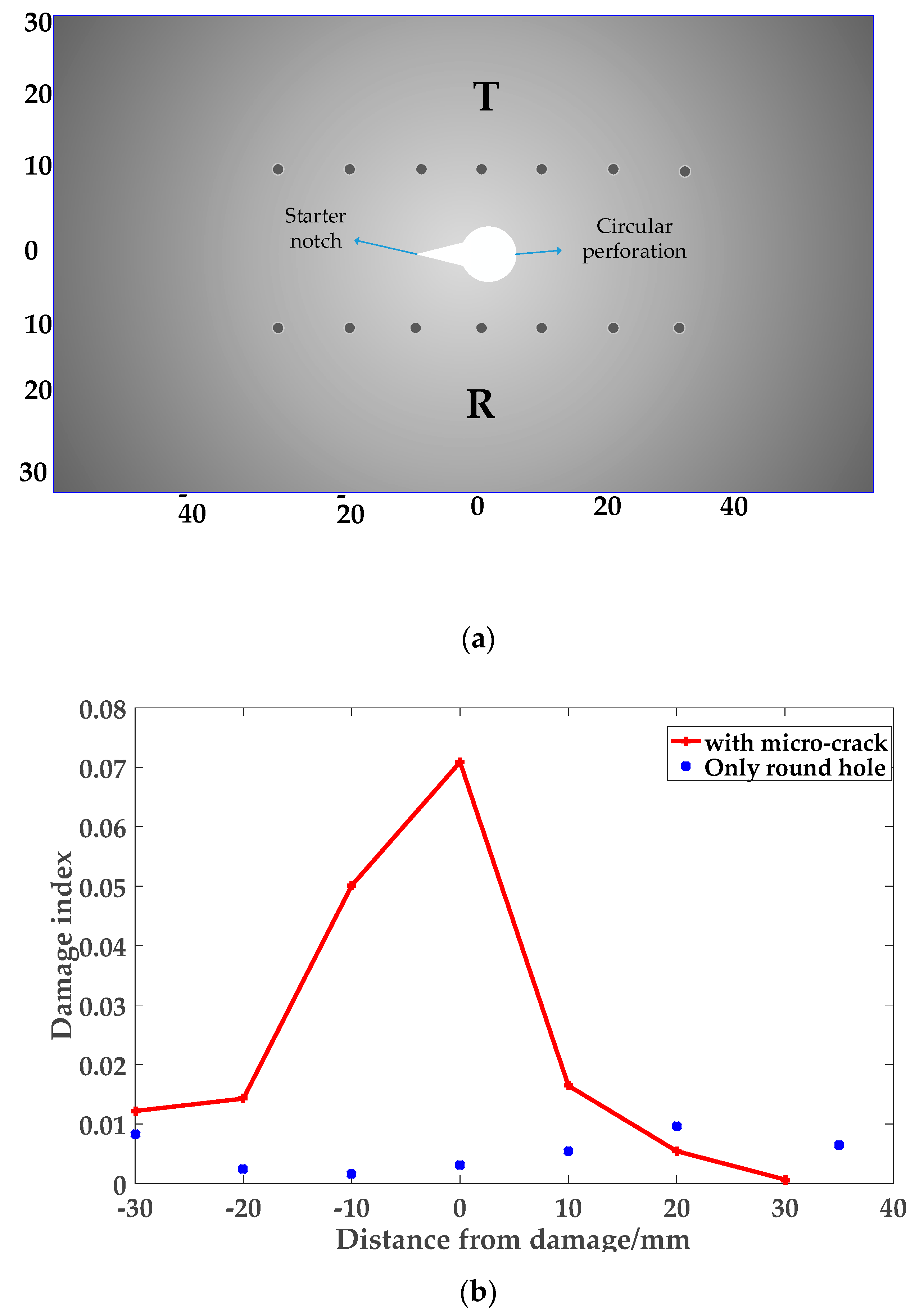
3.1. Model Establishment
3.2. Results and Analysis of Simulation
4. Experimental Verification
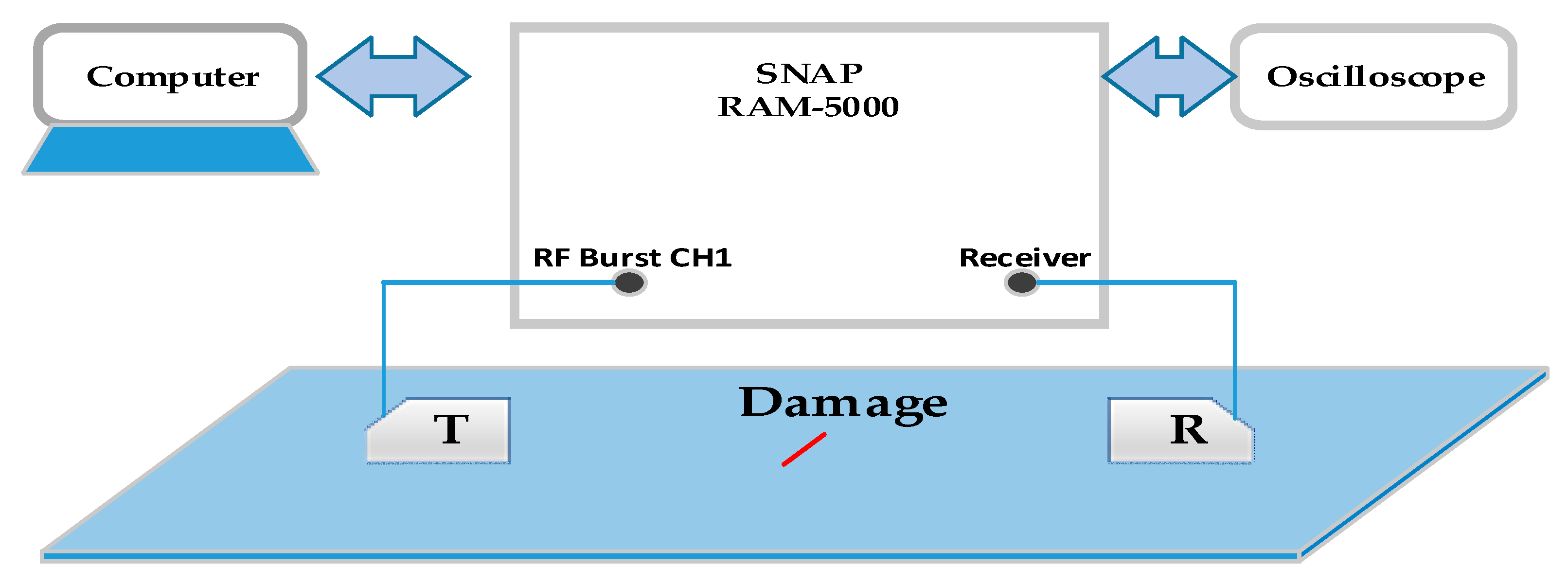
4.1. Construction of Experimental System
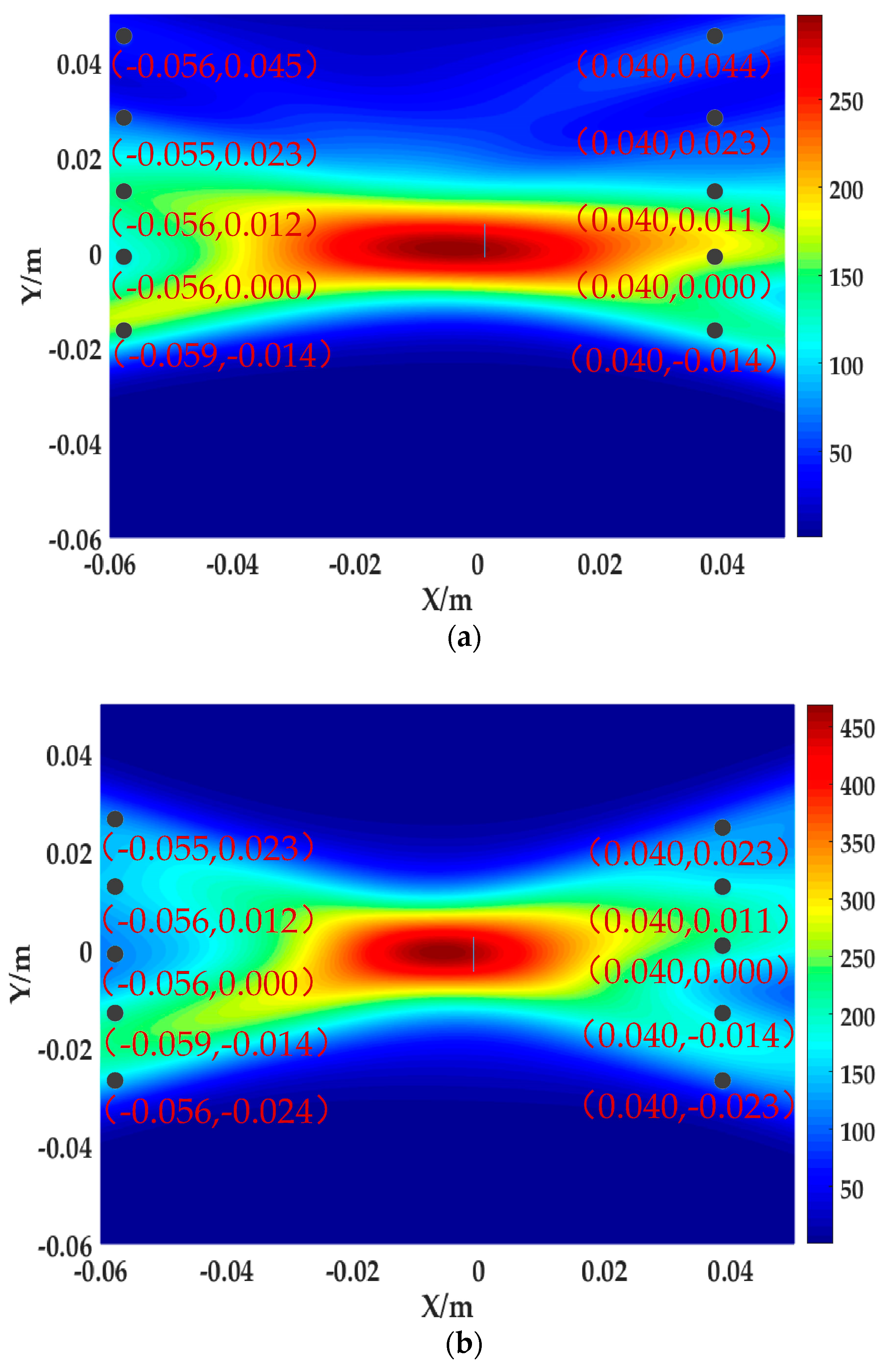
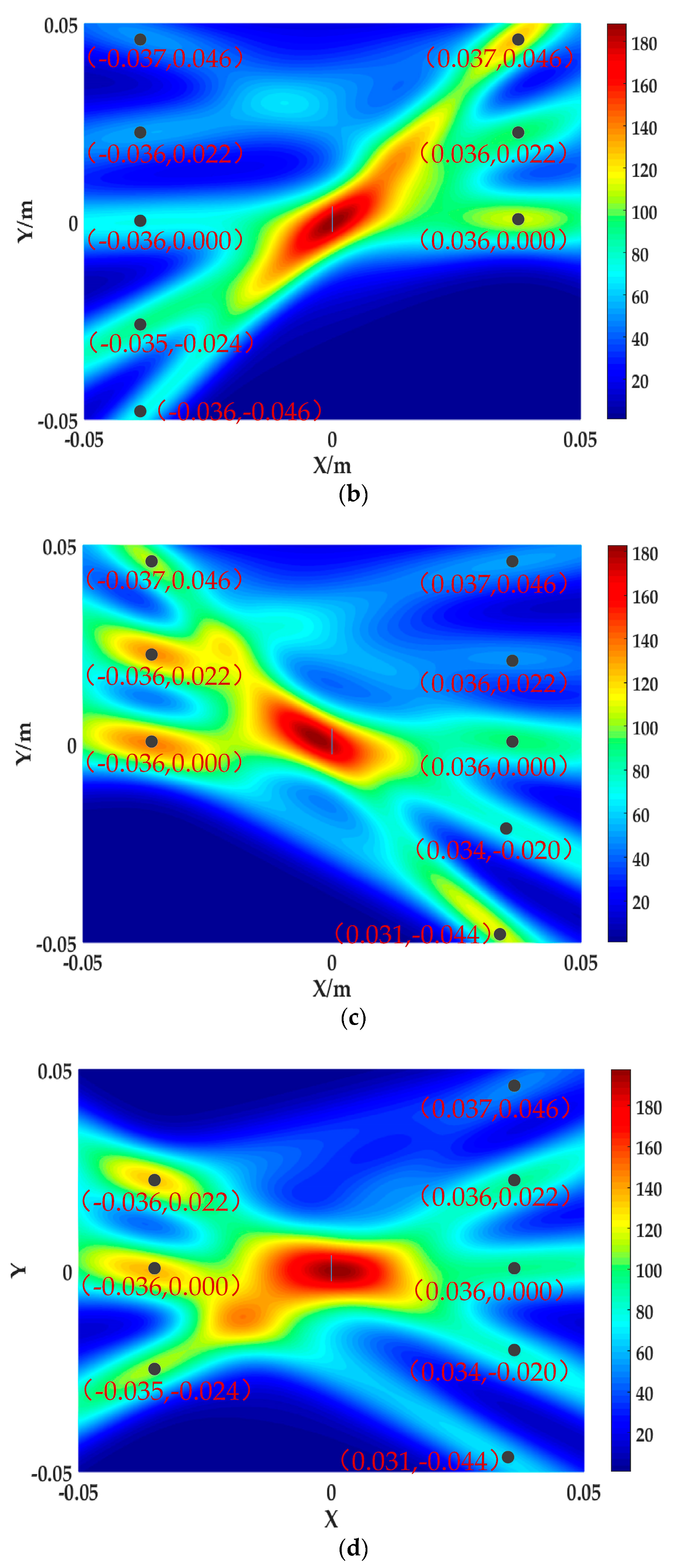
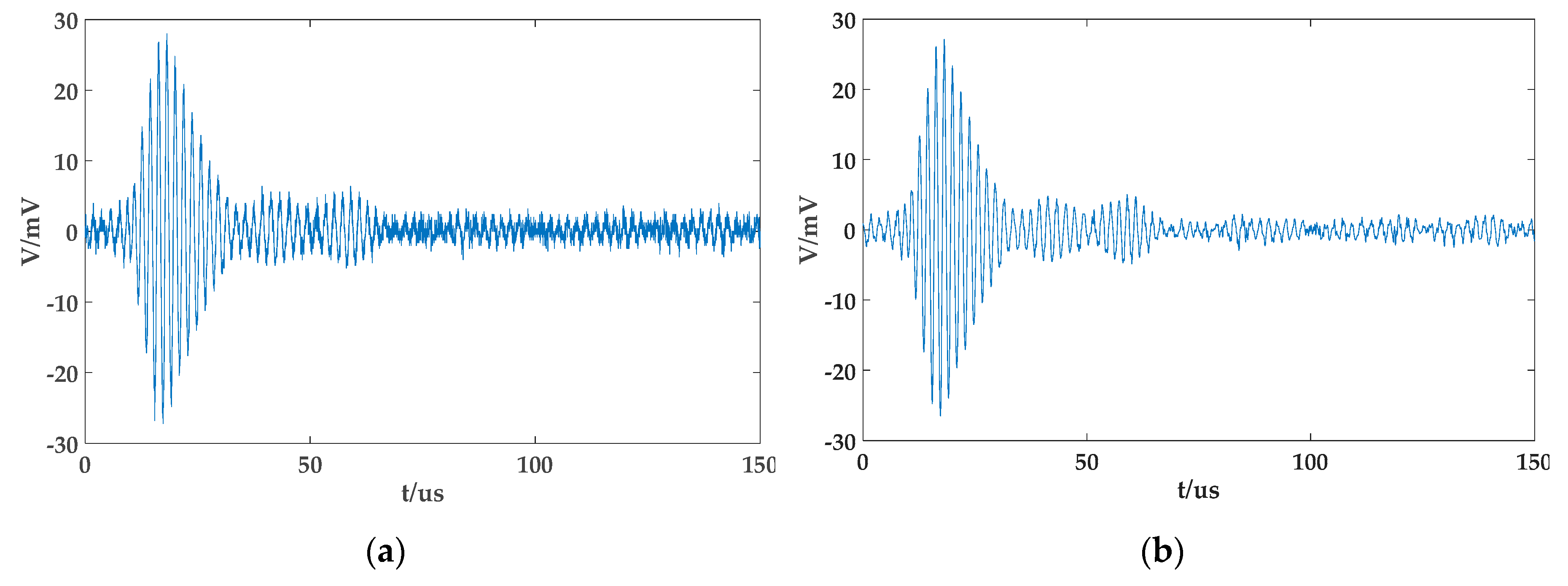
4.2. Results and Analysis of Experiment
4.3. Discussion
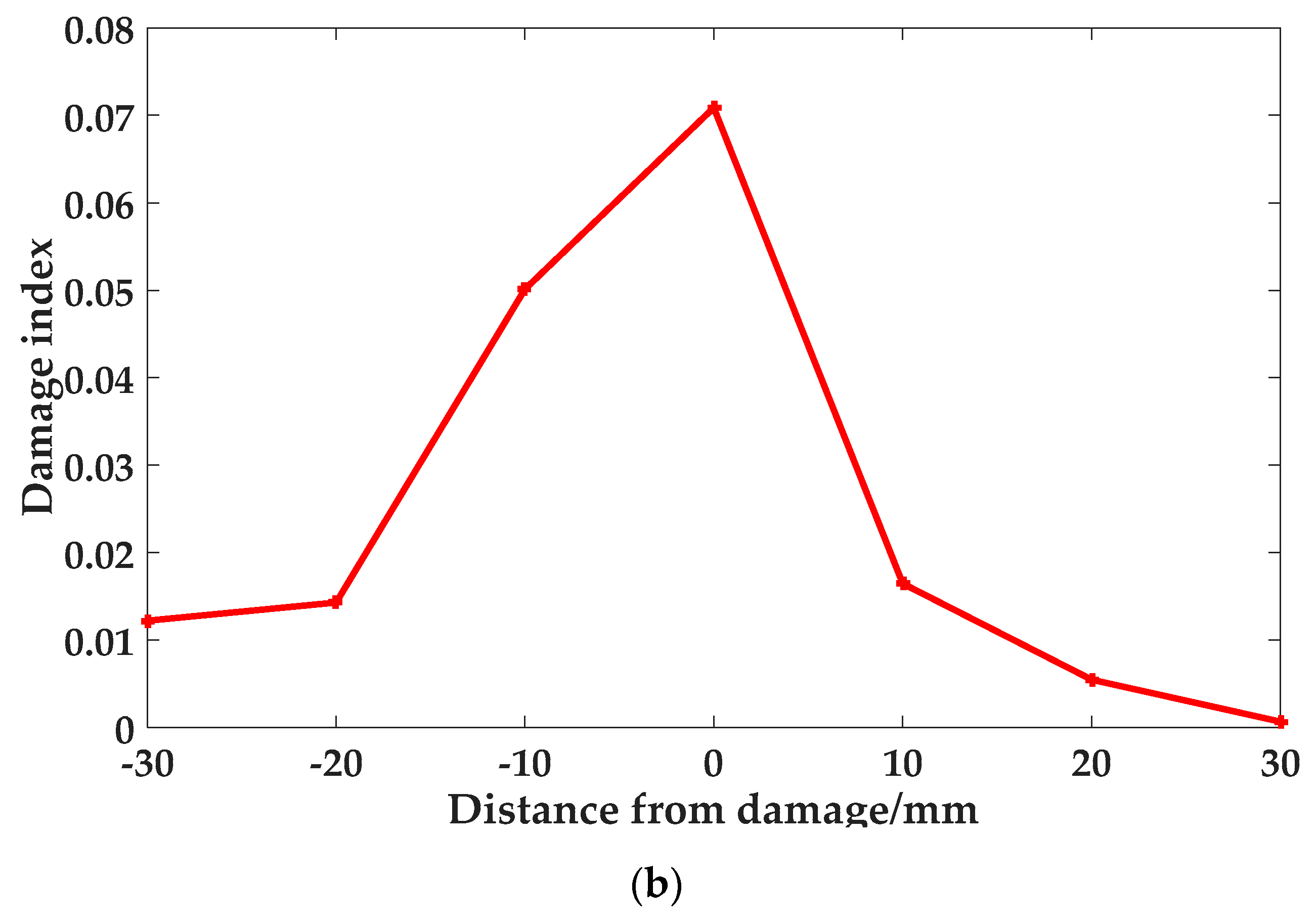
- The above results show that when the S0 single-mode lamb wave is used as the detection fundamental wave, the method of using the probability scan matrix to locate the microcrack can effectively locate and image the microcrack. This method has good robustness and accuracy, and is only sensitive to microcracks.
- The limitation of the method in this paper is that a microcrack can be effectively positioned only when two or more scanning centerlines pass through it, although there is an error when the microcrack is not at the focus. However, by moving the scan matrix and comparing the amplitude of the imaging core, it can still accurately locate the microcrack.
- In order to better solve the above shortcomings, for small area detection, the array can be set closer and the scanning path can be increased. For wide area detection, this method can be used as a qualitative test method, as long as the possibility of microcrack is detected within the area, further narrowing the range for secondary scanning.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, L. Research on Nonlinear Ultrasonic Testing of Fatigue Damage of Aluminum Alloy Welded Joints. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2012. [Google Scholar]
- Liu, D.; Pons, D. Crack propagation mechanisms for creep fatigue: a consolidated explanation of fundamental behaviours from initiation to failure. Metals 2018, 8, 623. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, F.; Xiang, Y. Evaluation of material damage using nonlinear ultrasonic wave. Sci. Bull. 2016, 61, 1536–1550. [Google Scholar]
- Meyendorf, N.G.H.; Rösner, H.; Kramb, V.; Sathish, S. Thermo-acoustic fatigue characterization. Ultrasonics 2002, 40, 427–434. [Google Scholar] [CrossRef]
- Cantrell, J.H. Substructural organization, dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals. Proc. Phys. Soc. Lond. Sect. A 2004, 460, 757–780. [Google Scholar] [CrossRef]
- Carpinteri, A.; Accornero, F. Multiple snap-back instabilities in progressive microcracking coalescence. Eng. Fract. Mech. 2018, 187, 272–281. [Google Scholar] [CrossRef]
- Lei, Y.; Ding, G.; Bao, H. Non-Destructive Testing Technology Q & A; China Petrochemical Press: Beijing, China, 2013; pp. 1–5. [Google Scholar]
- Liu, S.; Sun, Y.; Gu, M.; Liu, C.; He, L.; Kang, Y. Review and analysis of three representative electromagnetic NDT methods. Insight Non Destr. Test. Cond. Monit. 2017, 59, 176–183. [Google Scholar] [CrossRef]
- Duchene, P.; Chaki, S.; Ayadi, A.; Krawczak, P. A review of non-destructive techniques used for mechanical damage assessment in polymer composites. J. Mater. Sci. 2018, 53, 7915–7938. [Google Scholar] [CrossRef]
- Zhou, Z.; Sun, G. New progress of the study and application of advanced ultrasonic testing technology. J. Mech. Eng. 2017, 53, 1–10. [Google Scholar] [CrossRef]
- Li, G.; Zhang, G. Laser ultrasonic technology and its applications in nondestructive testing in solids. Proc. SPIE Int. Soc. Opt. Eng. 2005, 5638, 804–812. [Google Scholar]
- Masurkar, F.A.; Yelve, N.P. Optimizing location of damage within an enclosed area defined by an algorithm based on the Lamb wave response data. Appl. Acoust. 2017, 120, 98–110. [Google Scholar] [CrossRef]
- Zeng, L.; Lin, J. Structural damage imaging approaches based on lamb waves: A review. In Proceedings of the 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (ICQR2MSE 2011), Xi’an, China, 17–19 June 2011. [Google Scholar]
- Chimenti, D.E. Guided Waves in Plates and Their Use in Materials Characterization. Appl. Mech. Rev. 1997, 50, 247–284. [Google Scholar] [CrossRef]
- Wilcox, P.; Lowe, M.; Cawley, P. The effect of dispersion on long-range inspection using ultrasonic guided waves. NDT E Int. 2001, 34, 1–9. [Google Scholar] [CrossRef]
- Cawley, P.; Alleyne, D. The use of Lamb waves for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiu, Y.; Jacobs, L.J.; Qu, J. Frequency-dependent tensile and compressive effective moduli of elastic solids with distributed penny-shaped microcracks. Acta Mech. 2016, 227, 1–21. [Google Scholar] [CrossRef]
- Accornero, F.; Lacidogna, G.; Carpinteri, A. Evolutionary fracture analysis of masonry arches: Effects of shallowness ratio and size scale. Comptes Rendus Mécanique 2016, 344, 623–630. [Google Scholar] [CrossRef]
- Müller, M.F.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. 2010, 127, 2141. [Google Scholar] [CrossRef]
- Deng, M.; Xiang, Y.; Liu, L. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation. J. Appl. Phys. 2011, 109, 1829–1836. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, F.; Cao, P.; Liu, Y.; Zhang, J.Y.; Fu, S.; Zhang, J.; Hu, N. Generation mechanism of nonlinear ultrasonic Lamb waves in thin plates with randomly distributed micro-cracks. Ultrasonics 2017, 79, 60–67. [Google Scholar] [CrossRef] [Green Version]
- Deng, M. Characterization of surface properties of a solid plate using nonlinear Lamb wave approach. Ultrasonics 2006, 44, 1157–1162. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Fierro, G.P.M.; Meo, M. Nonlinear elastic imaging of barely visible impact damage in composite structures using a constructive nonlinear array sweep technique. Ultrasonics 2018, 90, 125–143. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Liu, Y.; Zhang, J.; Hu, N.; Fu, S.; Deng, M. Detection of micro-cracks using nonlinear lamb waves based on the Duffing-Holmes system. J. Sound Vib. 2017, 405, 175–186. [Google Scholar] [CrossRef]
- Masurkar, F.; Tse, P.W.; Yelve, N. Investigating the critical aspects of evaluating the material nonlinearity in metal plates using Lamb waves: Theoretical and numerical approach. Appl. Acoust. 2018, 140, 301–314. [Google Scholar] [CrossRef]
- Singh, A.K.; Chen, B.Y.; Tan, V.B.; Tay, T.E.; Lee, H.P. Finite element modeling of nonlinear acoustics/ultrasonics for the detection of closed delaminations in composites. Ultrasonics 2016, 74, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Zhao, Y.; Hu, N.; Liu, Y.; Zhang, J.; Deng, M. Experimental and numerical study of nonlinear Lamb waves of a low-frequency S0 mode in plates with quadratic nonlinearity. Materials 2018, 11, 2096. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhong, X.; Dong, T.; He, C.; Wu, B. Delamination detection in composite plates by synthesizing time-reversed Lamb waves and a modified damage imaging algorithm based on RAPID. Struct. Control Health Monit. 2016, 24, 1919. [Google Scholar] [CrossRef]
- Lu, G.; Li, Y.; Wang, T.; Xiao, H.; Huo, L.; Song, G. A multi-delay-and-sum imaging algorithm for damage detection using piezoceramic transducers. J. Intell. Mater. Syst. Struct. 2017, 28, 1150–1159. [Google Scholar] [CrossRef]
- Gu, J.; Zhou, C.; Luo, Y.; Wang, Z.; Xu, C. Time reversal multiple signal classification algorithm for imaging of CS damage. Electron. Sci. Technol. 2015. [Google Scholar] [CrossRef]
- Liu, G.; Xiao, Y.; Zhang, H.; Ren, G. Elliptical ring distribution probability-based damage imaging method for complex aircraft structures. J. Vibroeng. 2017, 19, 4936–4952. [Google Scholar] [CrossRef]
- Yanyu, M.; Shi, Y. Thin plate Lamb propagation rule and dispersion curve drawing based on wave theory. Surf. Rev. Lett. 2018. [Google Scholar] [CrossRef]
- Wan, X.; Tse, P.W.; Xu, G.H.; Tao, T.F.; Zhang, Q. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes. Smart Mater. Struct. 2016, 25. [Google Scholar] [CrossRef]

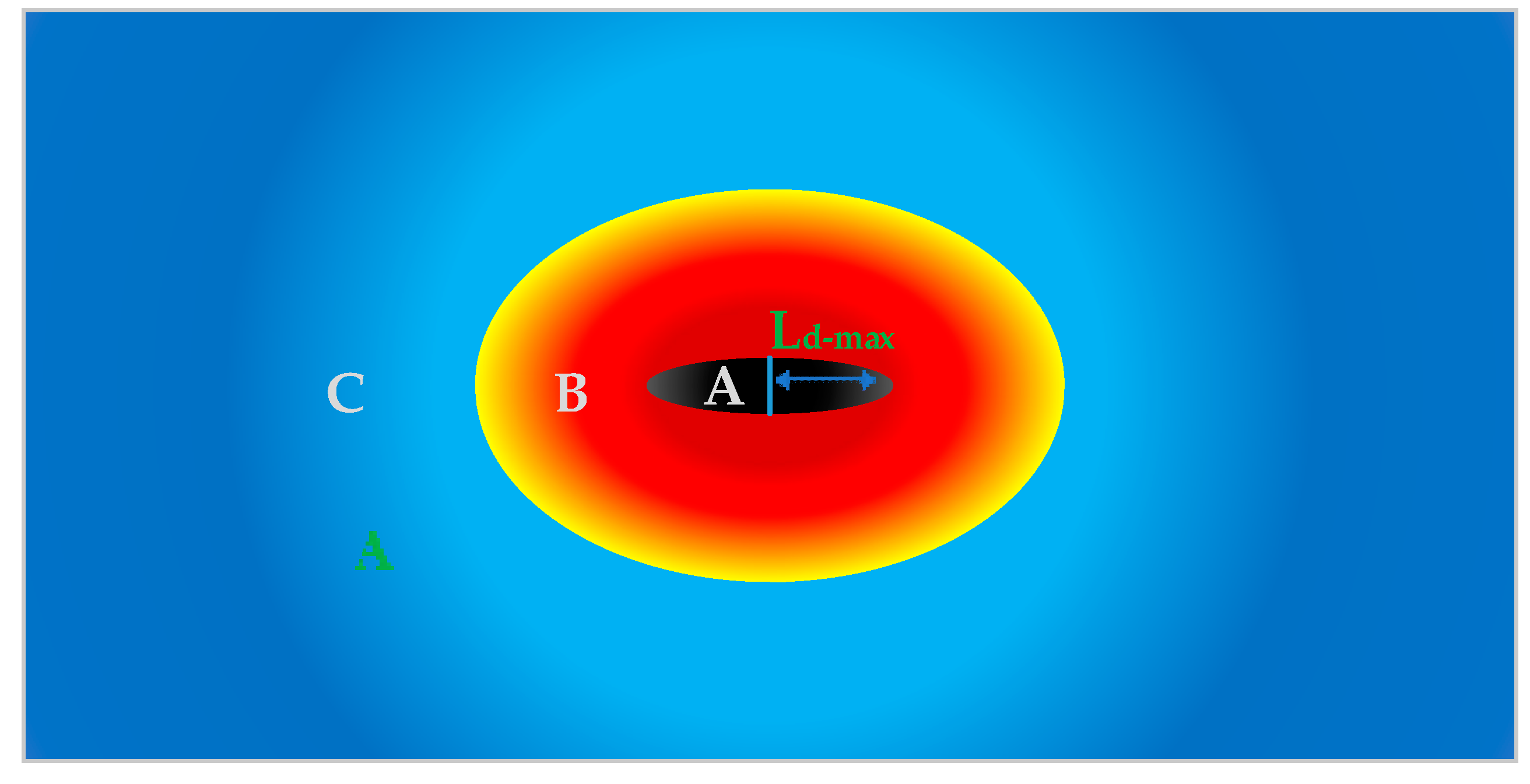

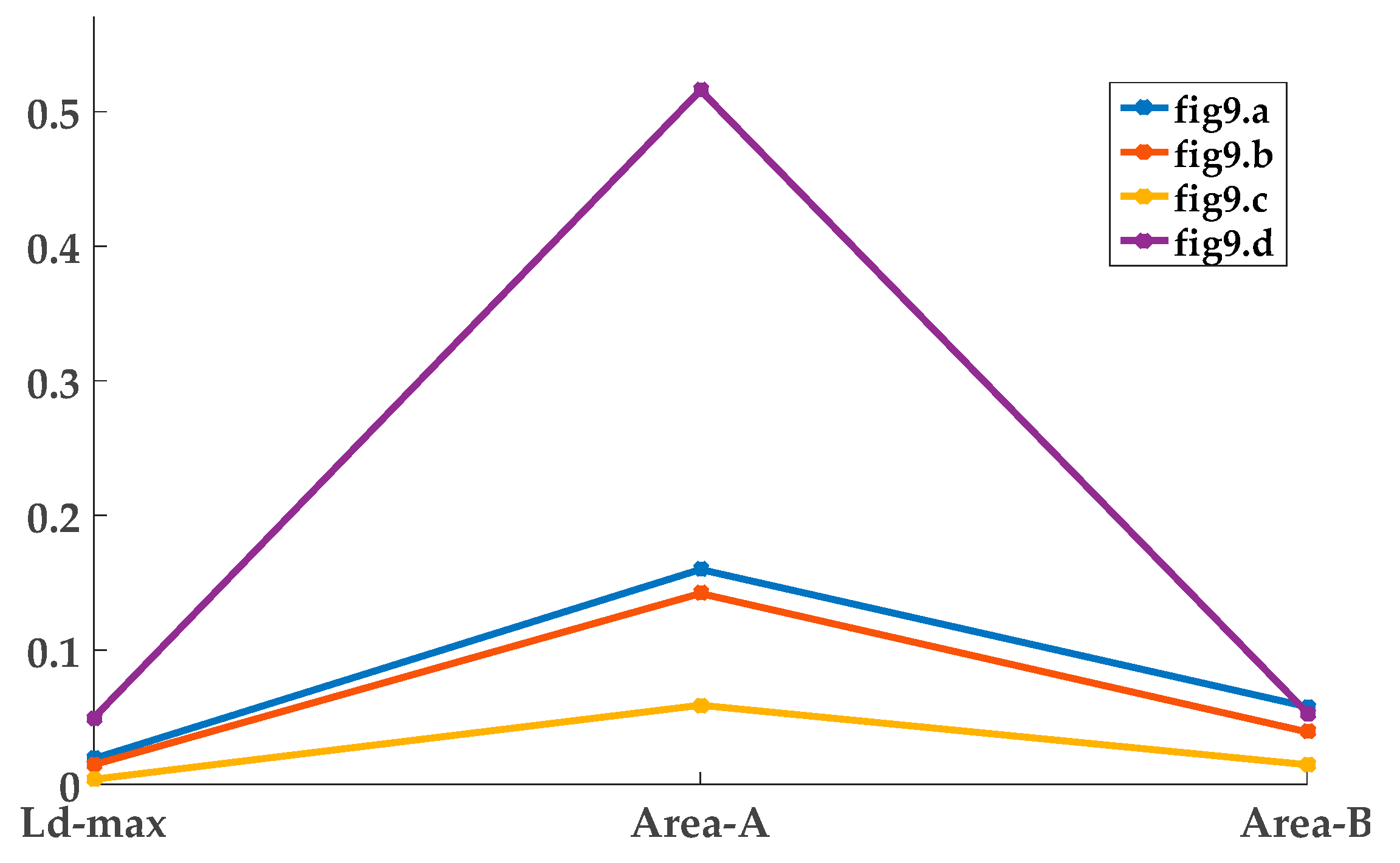


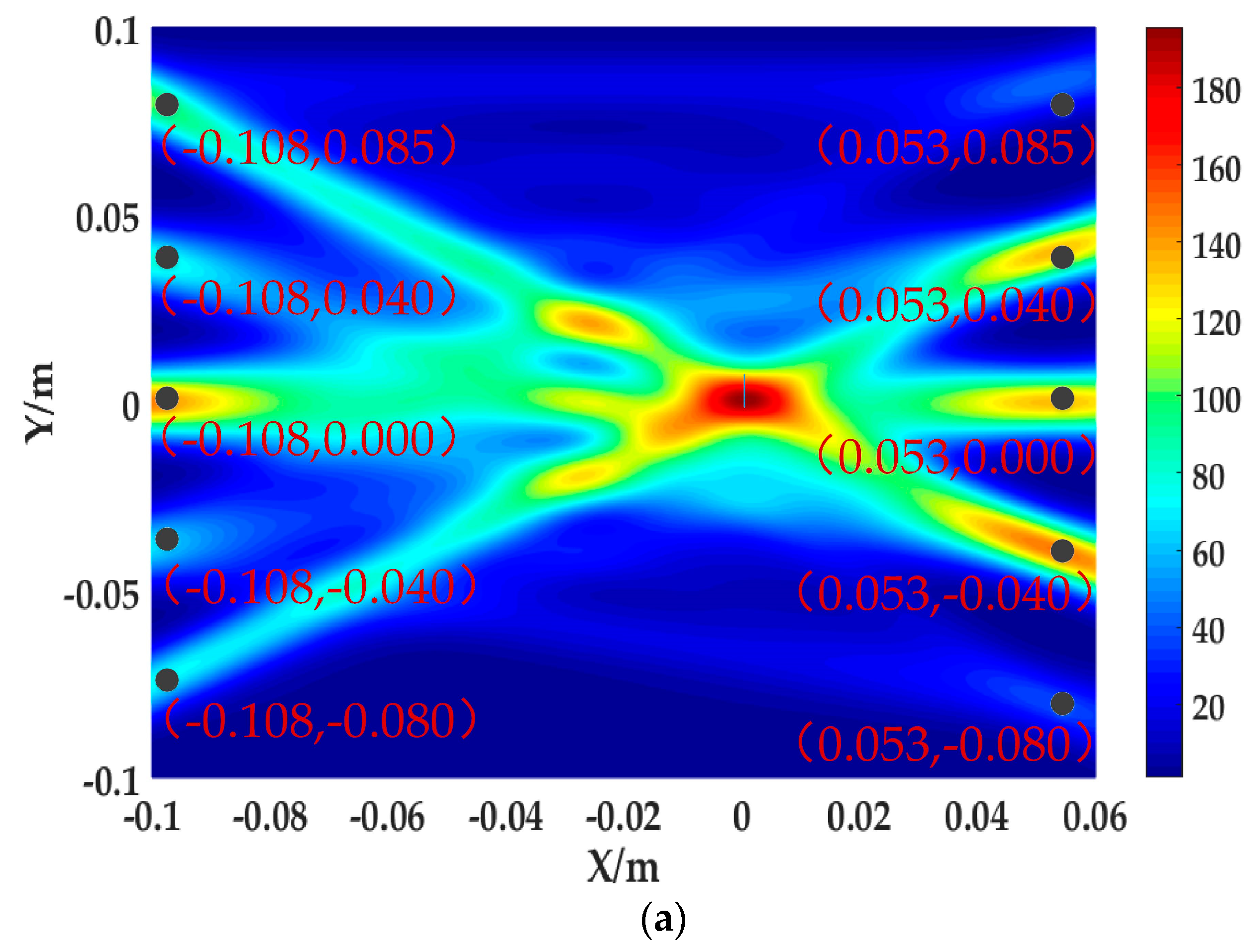
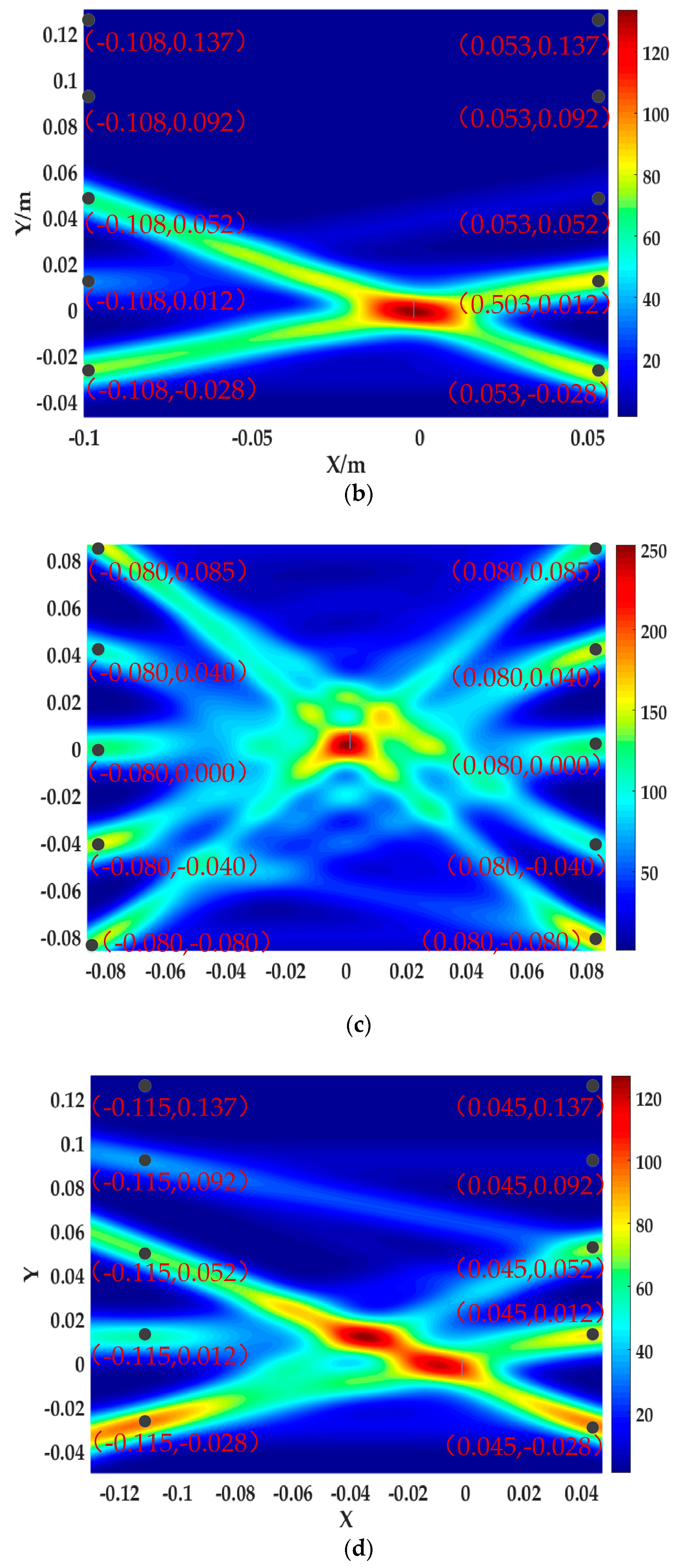
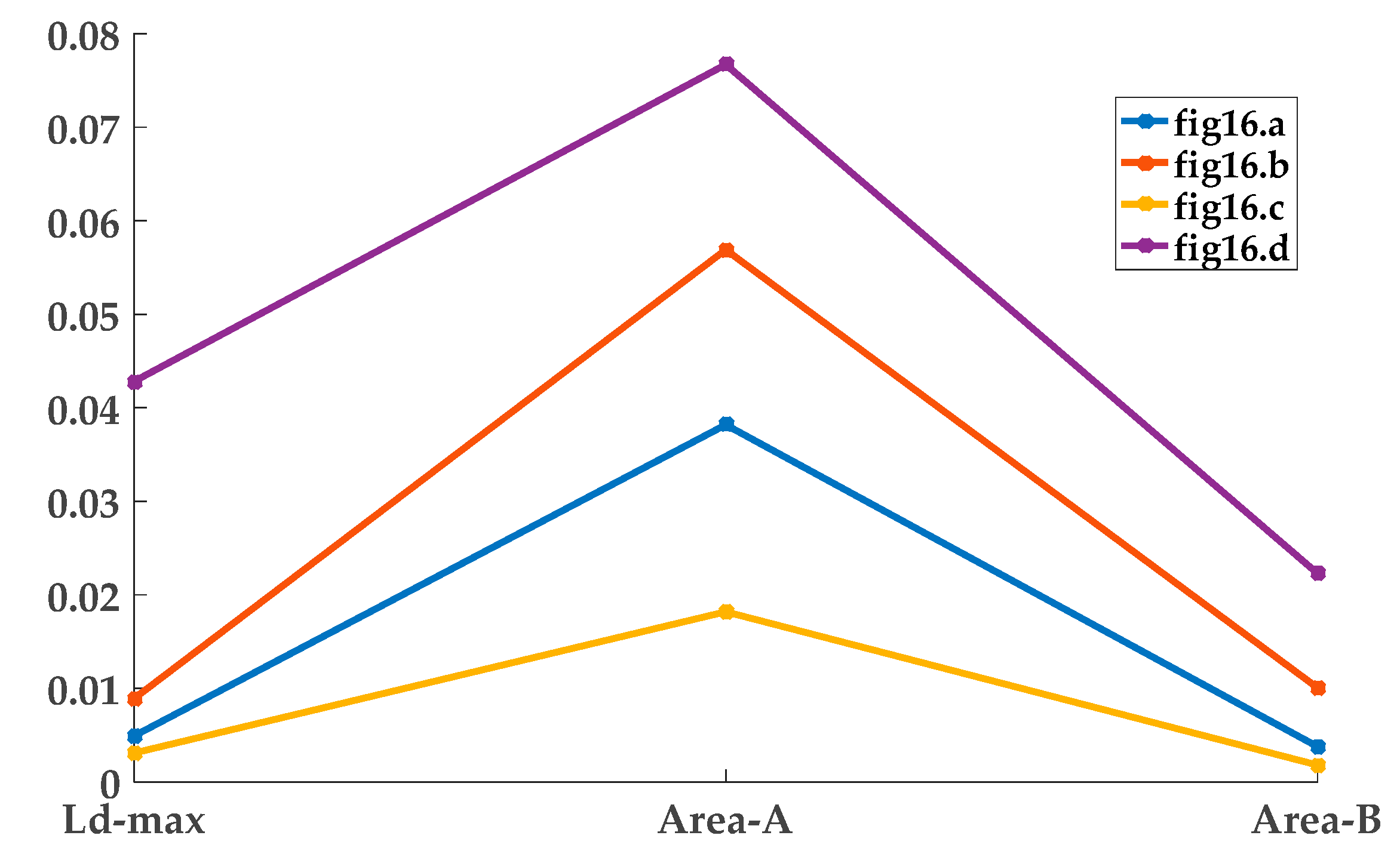
| Figure | Ld-max | Area-A | Area-B |
|---|---|---|---|
| (m) | % | % | |
| (a) | 0.019 | 0.060 | 0.160 |
| (b) | 0.015 | 0.039 | 0.142 |
| (c) | 0.004 | 0.015 | 0.059 |
| (d) | 0.050 | 0.053 | 0.516 |
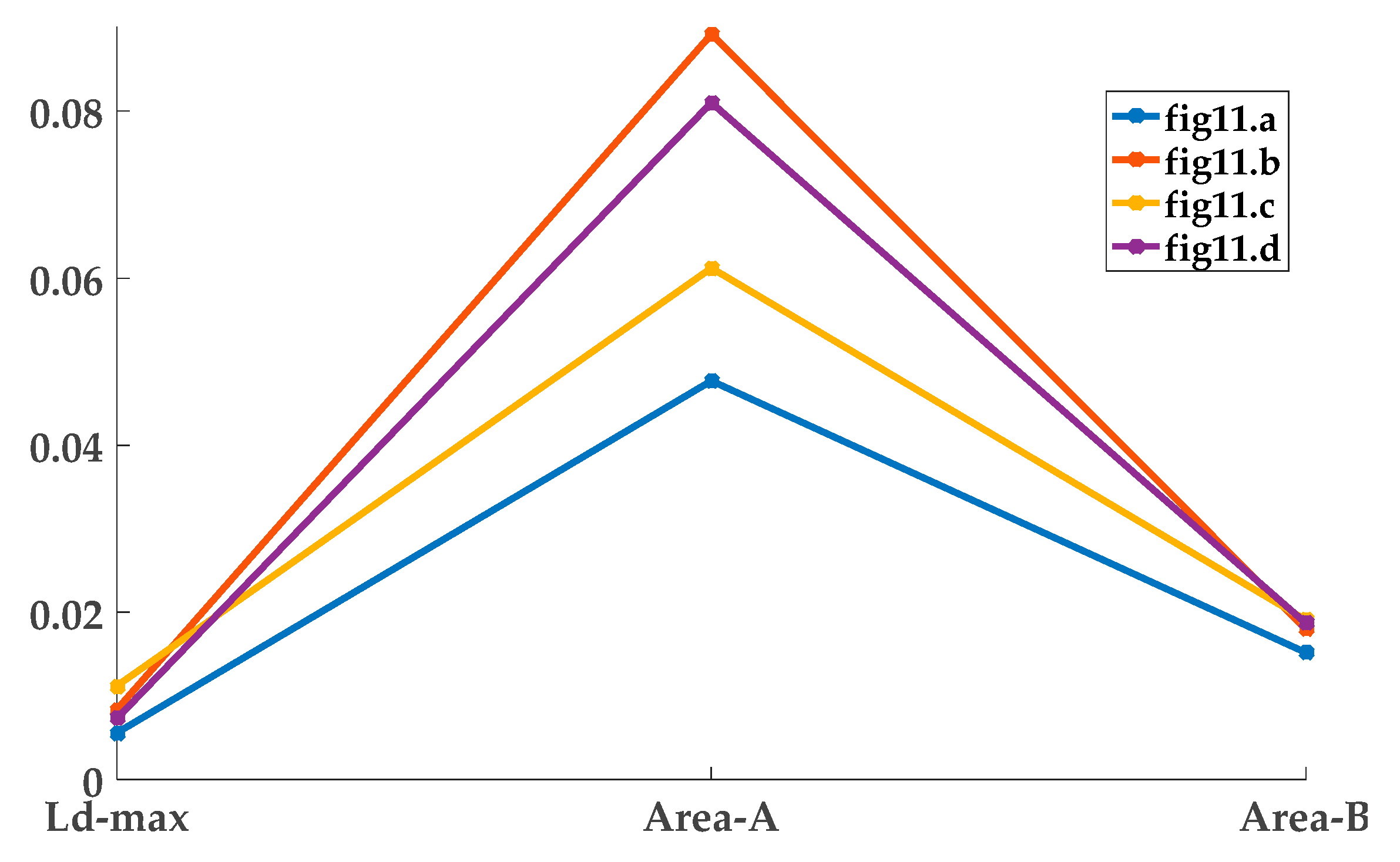
| Figure | Ld-max | Area-A | Area-B |
|---|---|---|---|
| (m) | % | % | |
| (a) | 0.006 | 0.015 | 0.048 |
| (b) | 0.008 | 0.018 | 0.089 |
| (c) | 0.011 | 0.019 | 0.061 |
| (d) | 0.007 | 0.018 | 0.081 |
| Figure | Ld-max | Area-A | Area-B |
|---|---|---|---|
| (m) | % | % | |
| (a) | 0.005 | 0.004 | 0.038 |
| (b) | 0.009 | 0.010 | 0.057 |
| (c) | 0.003 | 0.002 | 0.018 |
| (d) | 0.043 | 0.022 | 0.077 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, S.; Rui, X.; Ma, C.; Yang, Z. A Microcrack Location Method Based on Nonlinear S0 Mode Lamb Wave and Probability Scan Positioning Imaging Matrix. Appl. Sci. 2019, 9, 1874. https://doi.org/10.3390/app9091874
Li Y, Zhang S, Rui X, Ma C, Yang Z. A Microcrack Location Method Based on Nonlinear S0 Mode Lamb Wave and Probability Scan Positioning Imaging Matrix. Applied Sciences. 2019; 9(9):1874. https://doi.org/10.3390/app9091874
Chicago/Turabian StyleLi, Yibo, Shuo Zhang, Xiaobo Rui, Chang Ma, and Zi Yang. 2019. "A Microcrack Location Method Based on Nonlinear S0 Mode Lamb Wave and Probability Scan Positioning Imaging Matrix" Applied Sciences 9, no. 9: 1874. https://doi.org/10.3390/app9091874
APA StyleLi, Y., Zhang, S., Rui, X., Ma, C., & Yang, Z. (2019). A Microcrack Location Method Based on Nonlinear S0 Mode Lamb Wave and Probability Scan Positioning Imaging Matrix. Applied Sciences, 9(9), 1874. https://doi.org/10.3390/app9091874





