3D Photoacoustic Tomography System Based on Full-View Illumination and Ultrasound Detection
Abstract
1. Introduction
2. Methods
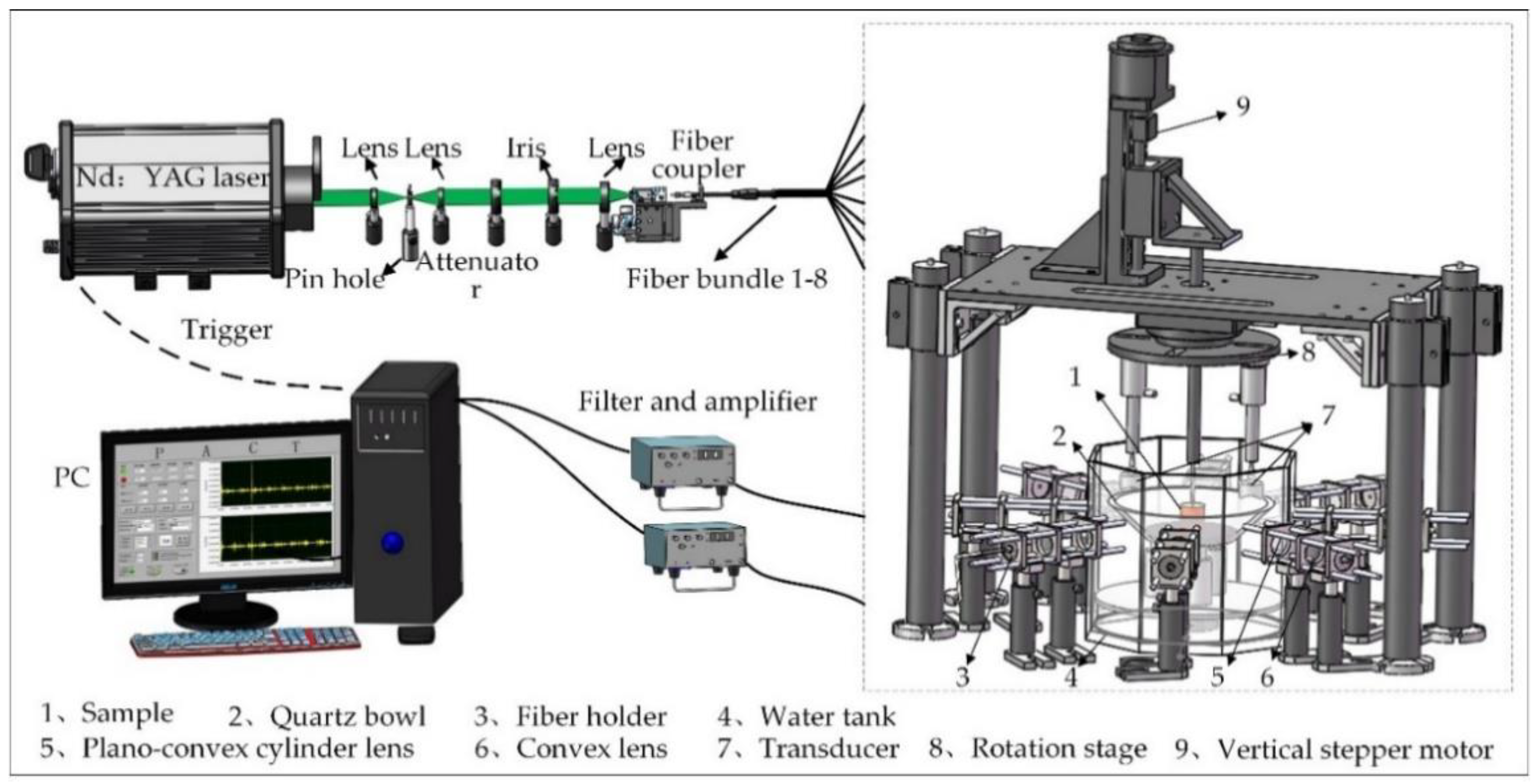
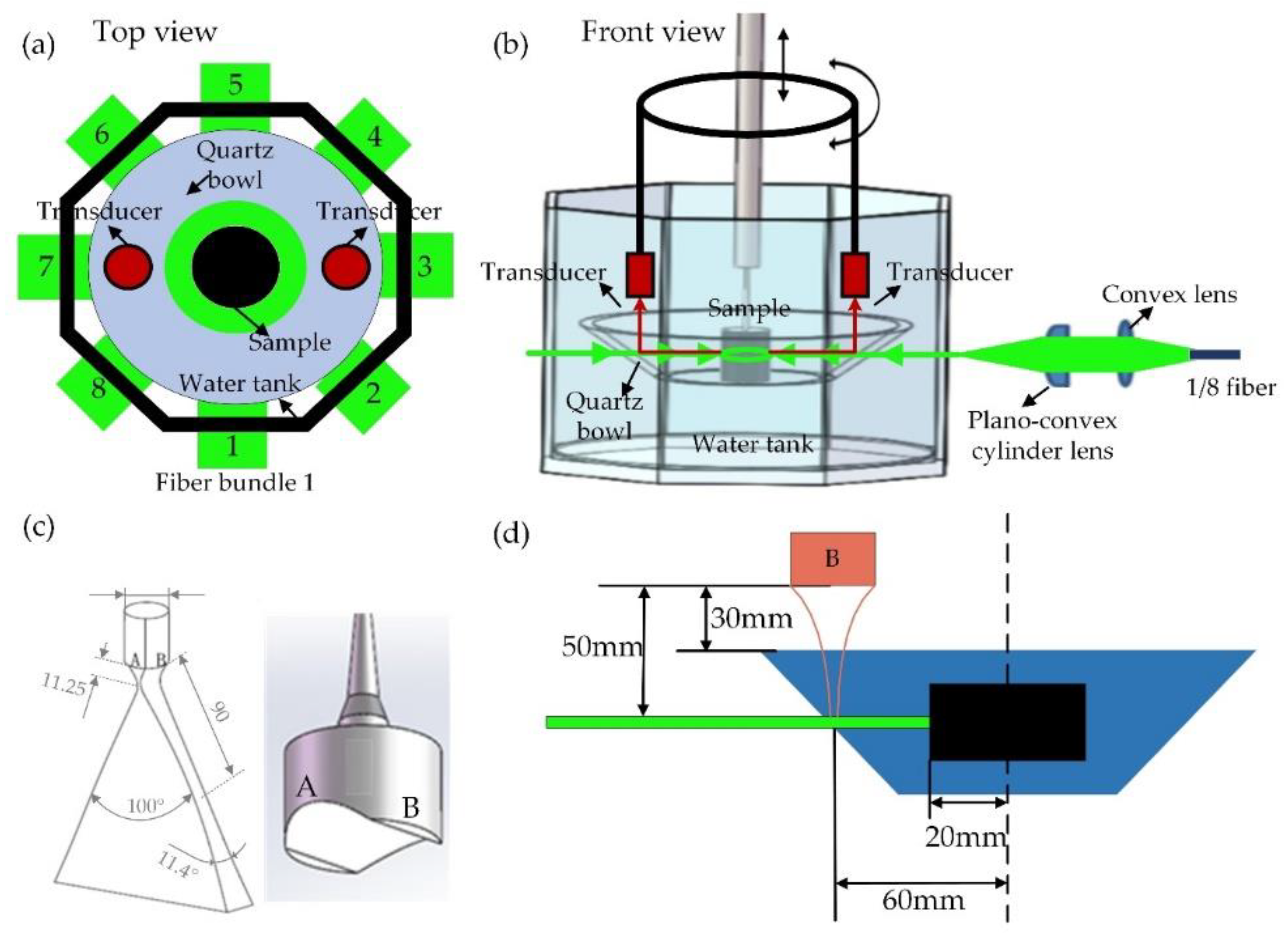
2.1. Introduction to the 3D-PACT System
2.2. The Reconstruction Algorithm of the 3D-PACT System
3. Results
3.1. Performance Test of the 3D-PACT
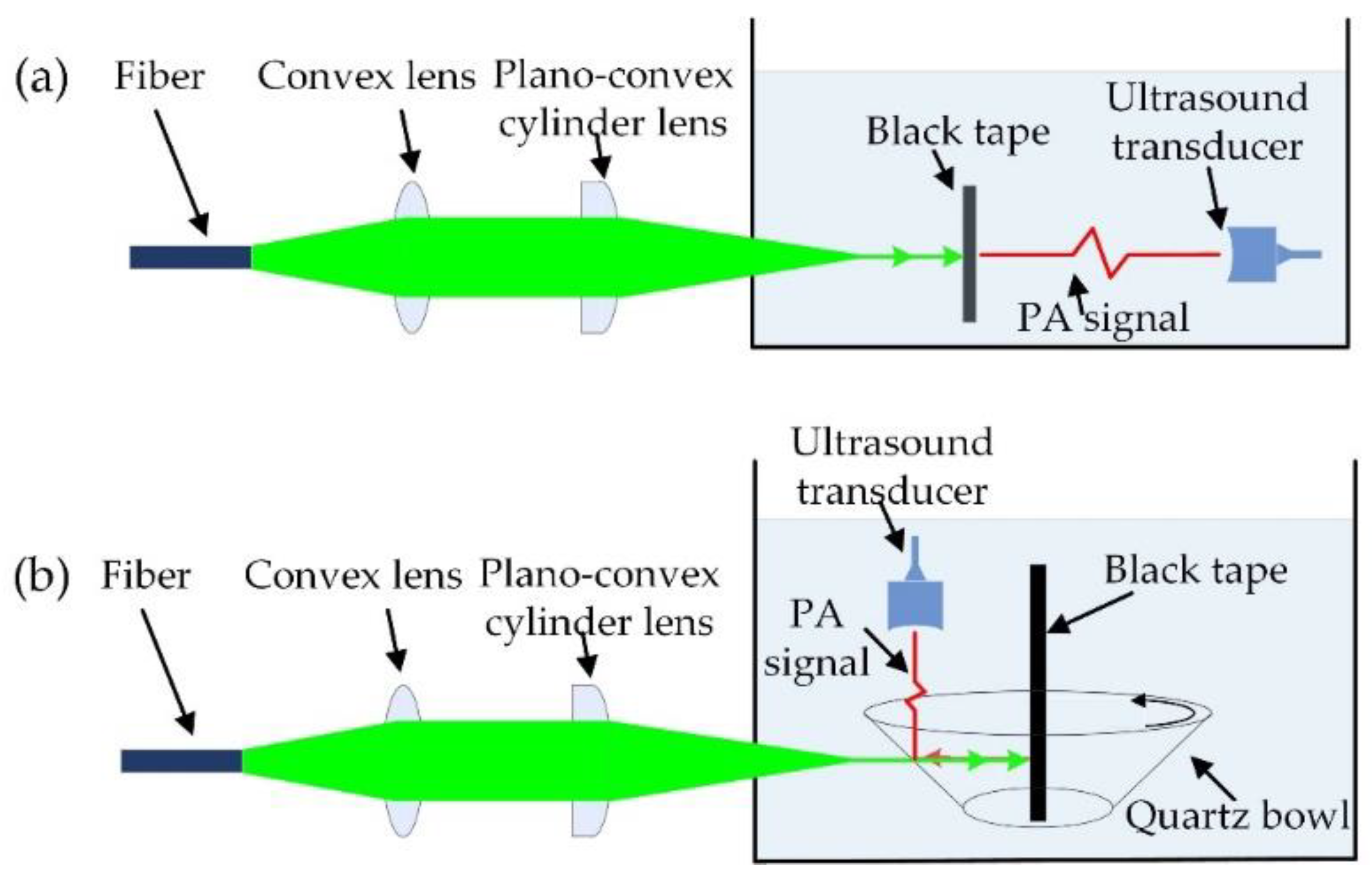
3.1.1. Feasibility Verification of Quartz Bowl in the System
3.1.2. Resolution Test of the System
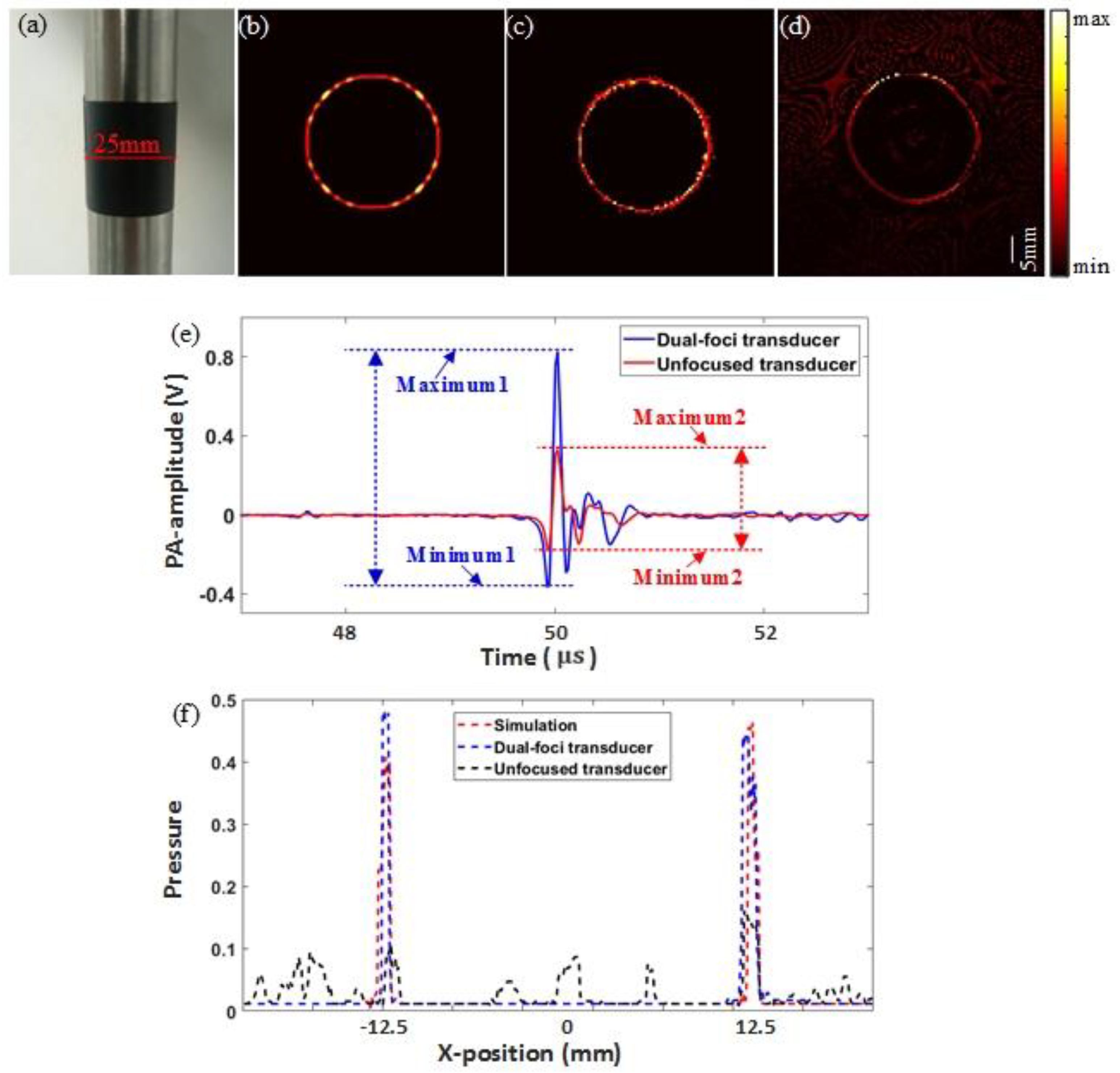
3.1.3. The Superiority of Photoacoustic Coplanar Configuration and Virtual Point Detection
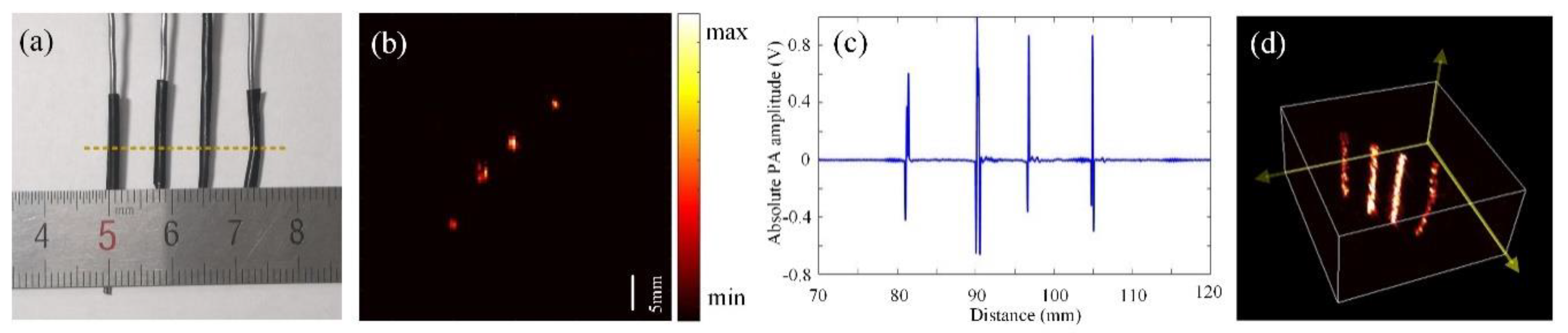
3.1.4. Verification Experiment on Large-Scale Imaging
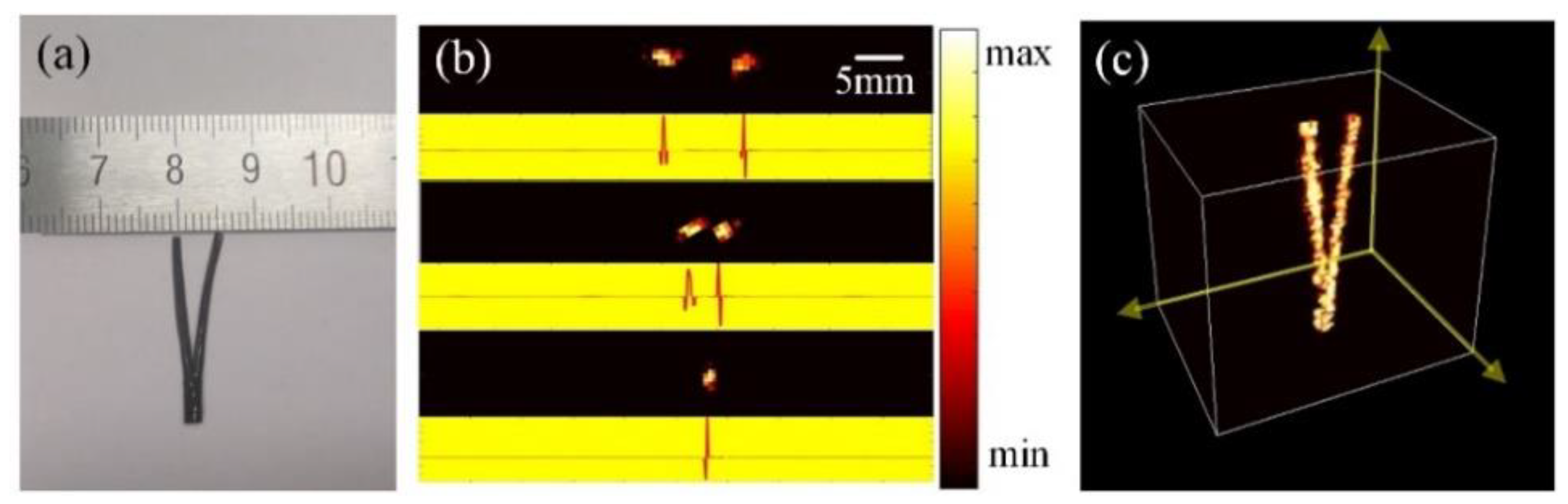
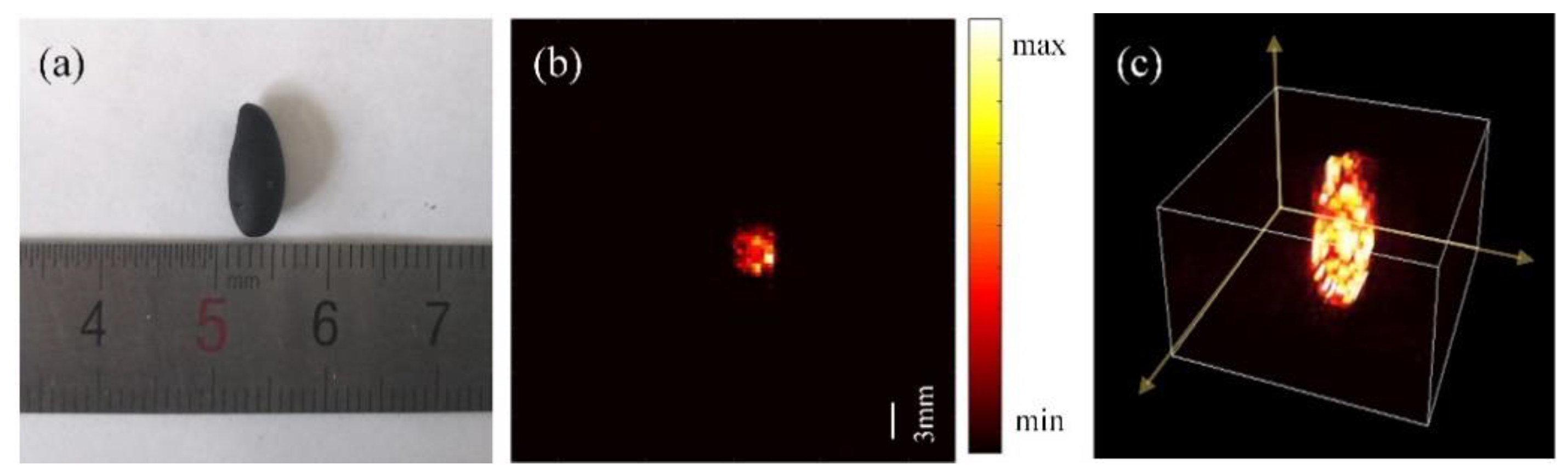
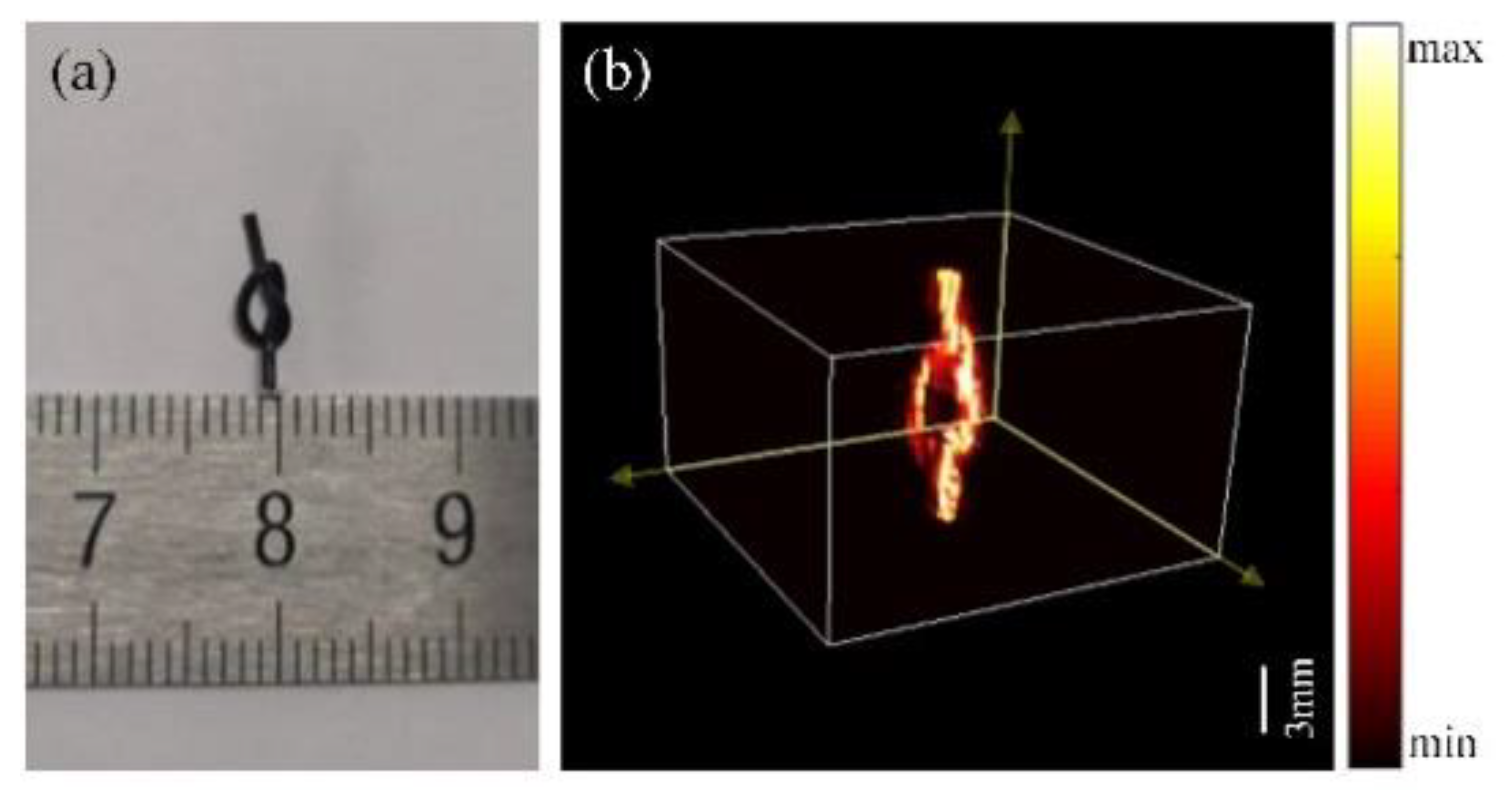
3.2. Photoacoustic Experiments of Different Kinds of Phantoms
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 41101. [Google Scholar] [CrossRef]
- Wang, L.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef]
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602. [Google Scholar] [CrossRef]
- Wang, L.V.; Wu, H. Biomedical optics: Principles and imaging. J. Biomed. Opt. 2008, 13, 049902. [Google Scholar] [CrossRef]
- Liu, T.; Sun, M.; Feng, N.; Wu, Z.; Shen, Y. Multiscale Hessian filter-based segmentation and quantification method for photoacoustic microangiography. Chin. Opt. Lett. 2015, 13, 091701. [Google Scholar]
- Lin, X.; Sun, M.; Feng, N.; Hu, D.; Shen, Y. Monte Carlo light transport-based blood vessel quantification using linear array photoacoustic tomography. Chin. Opt. Lett. 2017, 15, 111701. [Google Scholar]
- Wang, X.; Pang, Y.; Ku, G.; Xie, X.; Stoica, G.; Wang, L.V. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain. Nat. Biotechnol. 2003, 21, 803–806. [Google Scholar] [CrossRef]
- Wang, L.V.; Yao, J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods 2016, 13, 627–638. [Google Scholar] [CrossRef]
- Kruger, R.A.; Lam, R.B.; Reinecke, D.R.; Rio, S.P. Photoacoustic angiography of the breast. Med. Phys. 2010, 37, 6096–6100. [Google Scholar] [CrossRef]
- Wang, S.; Lin, J.; Wang, T.; Chen, X.; Huang, P. Recent Advances in Photoacoustic Imaging for Deep-Tissue Biomedical Applications. Theranostics 2016, 6, 2394–2413. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Gong, X.; Hu, D.; Lin, R.; Sheng, Z.; Zheng, C.; Yan, M.; Chen, J.; Cai, L.; et al. In vivo photoacoustic molecular imaging of breast carcinoma with folate receptor-targeted indocyanine green nanoprobes. Nanoscale 2014, 6, 14270–14279. [Google Scholar] [CrossRef]
- Cao, M.; Yuan, J.; Du, S.; Xu, G.; Wang, X.; PL, C.; Liu, X. Full-view photoacoustic tomography using asymmetric distributed sensors optimized with compressed sensing method. Biomed. Signal Process. Control 2015, 21, 19–25. [Google Scholar] [CrossRef]
- Wang, X.; Roberts, W.W.; Carson, P.L.; Wood, D.P.; Fowlkes, J.B. Photoacoustic tomography: A potential new tool for prostate cancer. Biomed. Opt. Express 2010, 1, 1117. [Google Scholar] [CrossRef]
- Wurzinger, G.; Nuster, R.; Schmitner, N.; Gratt, S.; Meyer, D.; Paltauf, G. Simultaneous three-dimensional photoacoustic and laser-ultrasound tomography. Biomed. Opt. Express 2013, 4, 1380. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, C.; Chen, S.L.; Ling, T. 3D high resolution photoacoustic imaging based on pure optical photoacoustic microscopy with microring resonator. In Proceedings of the SPIE 8943, Photons Plus Ultrasound: Imaging and Sensing 2014; International Society for Optics and Photonics: Bellingham, WA, USA, 2014. [Google Scholar]
- Moradi, H.; Honarvar, M.; Tang, S.; Salcudean, S.E. Iterative photoacoustic image reconstruction for three-dimensional imaging by conventional linear-array detection with sparsity regularization. In Proceedings Volume 10064, Photons Plus Ultrasound: Imaging and Sensing; International Society for Optics and Photonics: Bellingham, WA, USA, 2017. [Google Scholar]
- Tan, Y.; Xia, K.; Ren, Q.; Li, C. Three-dimensional photoacoustic imaging via scanning a one dimensional linear unfocused ultrasound array. Opt. Express 2017, 25, 8022–8028. [Google Scholar] [CrossRef]
- Vaithilingam, S.; Ma, T.J.; Furukawa, Y.; Wygant, I.O.; Zhuang, X.; De La Zerda, A.; Oralkan, O.; Kamaya, Y.; Gambhir, S.S.; Jeffrey, R.B.; et al. Three-dimensional photoacoustic imaging using a two-dimensional CMUT array. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2411–2419. [Google Scholar] [CrossRef]
- Paltauf, G.; Nuster, R.; Burgholzer, P.; Haltmeier, M. Three-dimensional photoacoustic tomography using acoustic line detectors. Proc. SPIE 2007, 6437, 64370N. [Google Scholar]
- Ermolayev, V.; Dean-Ben, X.L.; Mandal, S.; Ntziachristos, V.; Razansky, D. Simultaneous visualization of tumour oxygenation, neovascularization and contrast agent perfusion by real-time three-dimensional optoacoustic tomography. Eur. Radiol. 2016, 26, 1843–1851. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, L.; Jiang, M.S.; Yang, J.; Zhang, Q.; Carney, P.R.; Jiang, H. Photoacoustic tomography system for noninvasive real-time three-dimensional imaging of epilepsy. Biomed. Opt. Express 2012, 3, 1427–1432. [Google Scholar] [CrossRef]
- Hui, L.; Yu, C.; Hongbo, L.; Dong, P.; Yukun, Z.; Kun, W.; Jie, T. High-speed and 128-channel multi-spectral photoacoustic tomography system for small animal. Laser Technol. 2017, 41, 669–674. [Google Scholar]
- Razansky, D.; Buehler, A.; Ntziachristos, V. Volumetric real-time multispectral optoacoustic tomography of biomarkers. Nat. Protoc. 2011, 6, 1121–1129. [Google Scholar] [CrossRef]
- Xia, J.; Chatni, M.R.; Maslov, K.; Guo, Z.; Wang, K.; Anastasio, M.; Wang, L.V. Whole-body ring-shaped confocal photoacoustic computed tomography of small animals in vivo. J. Biomed. Opt. 2012, 17, 050506. [Google Scholar] [CrossRef]
- Wong, T.T.; Zhang, R.; Zhang, C.; Hsu, H.C.; Maslov, K.I.; Wang, L.; Shi, J.; Chen, R.; Shung, K.K.; Zhou, Q.; et al. Label-free automated three-dimensional imaging of whole organs by microtomy-assisted photoacoustic microscopy. Nat. Commun. 2017, 8, 1386. [Google Scholar] [CrossRef]
- Paltauf, G.; Hartmair, P.; Kovachev, G.; Kovachec, G.; Nuster, R. Piezoelectric line detector array for photoacoustic tomography. Photoacoustics 2017, 8, 28–36. [Google Scholar] [CrossRef]
- Li, C.; Aguirre, A.; Gamelin, J.; Maurudis, A.; Zhou, Q.; Wang, L.V. Real-time photoacoustic tomography of cortical hemodynamics in small animals. J. Biomed. Opt. 2010, 15, 010509. [Google Scholar] [CrossRef]
- Xia, J.; Chatni, M.; Maslov, K.; Wang, L.V. Anatomical and metabolic small-animal whole-body imaging using ring-shaped confocal photoacoustic computed tomography. In Proceedings of the Photons Plus Ultrasound: Imaging & Sensing; International Society for Optics and Photonics: Bellingham, WA, USA, 2013. [Google Scholar]
- Ku, G.; Wang, X.; Stoica, G.; Wang, L.V. Multiple-bandwidth photoacoustic tomography. Phys. Med. Biol. 2004, 49, 1329–1338. [Google Scholar] [CrossRef]
- Kruger, R.A.; Liu, P.Y.; Fang, Y.R.; Appledorn, C.R. Photoacoustic ultrasound (PAUS)—Reconstruction tomography. Med. Phys. 1995, 22, 1605–1609. [Google Scholar] [CrossRef]
- Ma, R.; Taruttis, A.; Ntziachristos, V.; Razansky, D. Multispectral optoacoustic tomography (MSOT) scanner for whole-body small animal imaging. Opt. Express 2009, 17, 21414–21426. [Google Scholar] [CrossRef]
- Pramanik, M.; Ku, G.; Wang, L.V. Tangential resolution improvement in thermoacoustic and photoacoustic tomography using a negative acoustic lens. J. Biomed. Opt. 2009, 14, 024028. [Google Scholar] [CrossRef]
- Li, C.; Ku, G.; Wang, L.V. Negative lens concept for photoacoustic tomography. Phys. Rev. E 2008, 78, 021901. [Google Scholar] [CrossRef]
- Perekatova, V.V.; Kirillin, M.Y.; Turchin, I.V.; Subochev, P.V. Combination of virtual point detector concept and fluence compensation in acoustic resolution photoacoustic microscopy. In Proceedings of the the 6th International Symposium on Topical Problems of Biophotonics (TPB), St Petersburg, Russia, 28 July–3 August 2017. [Google Scholar]
- Nie, L.; Guo, Z.; Wang, L.V. Photoacoustic tomography of monkey brain using virtual point ultrasonic transducers. J. Biomed. Opt. 2011, 16, 076005. [Google Scholar] [CrossRef]
- Zhang, H.F.; Menglin, L.; Konstantin, M.; Stocia, G.; Wang, L.V. Three-dimensional photoacoustic imaging of subcutaneous microvasculature in vivo. Proc. SPIE 2006, 6086, 60861E. [Google Scholar]
- Minghua, X.; Wang, L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71 1 Pt 2, 016706. [Google Scholar]
- Xu, M.; Wang, L.V. Pulsed-microwave-induced thermoacoustic tomography: Filtered backprojection in a circular measurement configuration. Med. Phys. 2002, 29, 1661–1669. [Google Scholar] [CrossRef] [PubMed]
- Duoduo, H.; Zheng, S.; Yuan, Y. Reconstruction of Intravascular Photoacoustic Images Based on Filtered Back-projection Algorithm. Chin. J. Biomed. Eng. 2016, 35, 9–19. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multi-scale structural similarity for image quality assessment. In Proceedings of the IEEE Asilomar Conference on Signals, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Mandal, S.; Sudarshan, V.P.; Nagaraj, Y.; Dean-Ben, X.L.; Razansky, D. Multiscale edge detection and parametric shape modeling for boundary delineation in optoacoustic images. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 2015, Milan, Italy, 25–29 August 2015; pp. 707–710. [Google Scholar]
- Kazakeviciute, A.; Ho CJ, H.; Olivo, M. Multispectral Photoacoustic Imaging Artifact Removal and Denoising Using Time Series Model-Based Spectral Noise Estimation. IEEE Trans. Med. Imaging 2016, 35, 2151–2163. [Google Scholar] [CrossRef]



| Areas | E (μJ) | Mean of Signal Amplitude P (V) | Gref = P/E (V/μJ) | H = Gref/Gtrm |
|---|---|---|---|---|
| Q1 | 88.7614 | 2.236 | 0.02519 | 204.46% |
| Q2 | 88.3206 | 2.214 | 0.02507 | 203.49% |
| Q3 | 88.0611 | 2.183 | 0.02480 | 201.30% |
| Q4 | 88.1574 | 2.195 | 0.02490 | 202.11% |
| Q5 | 88.2163 | 2.222 | 0.02520 | 204.54% |
| Q6 | 88.0742 | 2.156 | 0.02448 | 198.70% |
| Q7 | 88.0688 | 2.174 | 0.02469 | 200.41% |
| Q8 | 88.3672 | 2.229 | 0.02522 | 204.71% |
| Index | PSNR (dB) | MSE | SSIM |
|---|---|---|---|
| PA image (c) (Dual-foci transducer) | 35.9379 | 0.0051 | 0.9995 |
| PA image (d) (Unfocused transducer) | 15.2504 | 0.0350 | 0.9174 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Hu, D.; Zhou, W.; Liu, Y.; Qu, Y.; Ma, L. 3D Photoacoustic Tomography System Based on Full-View Illumination and Ultrasound Detection. Appl. Sci. 2019, 9, 1904. https://doi.org/10.3390/app9091904
Sun M, Hu D, Zhou W, Liu Y, Qu Y, Ma L. 3D Photoacoustic Tomography System Based on Full-View Illumination and Ultrasound Detection. Applied Sciences. 2019; 9(9):1904. https://doi.org/10.3390/app9091904
Chicago/Turabian StyleSun, Mingjian, Depeng Hu, Wenxue Zhou, Yang Liu, Yawei Qu, and Liyong Ma. 2019. "3D Photoacoustic Tomography System Based on Full-View Illumination and Ultrasound Detection" Applied Sciences 9, no. 9: 1904. https://doi.org/10.3390/app9091904
APA StyleSun, M., Hu, D., Zhou, W., Liu, Y., Qu, Y., & Ma, L. (2019). 3D Photoacoustic Tomography System Based on Full-View Illumination and Ultrasound Detection. Applied Sciences, 9(9), 1904. https://doi.org/10.3390/app9091904






