Evidence of Chaos in Electroencephalogram Signatures of Human Performance: A Systematic Review
Abstract
1. Introduction
2. Materials and Methods
2.1. Review Standards
2.2. Research Questions
- RQ1: What mental processes have been studied by nonlinear EEG analysis?
- RQ2: What are the major chaotic measures used to characterize various brain functions?
- RQ3: For non-medical purposes, what are the findings of EEG studies that have used chaos theory measures for analysis?
2.3. Search Strategy
2.4. Inclusion and Exclusion Criteria
2.5. Data Collection and Summary of Measures
2.6. Data Extraction and Synthesis
3. Results
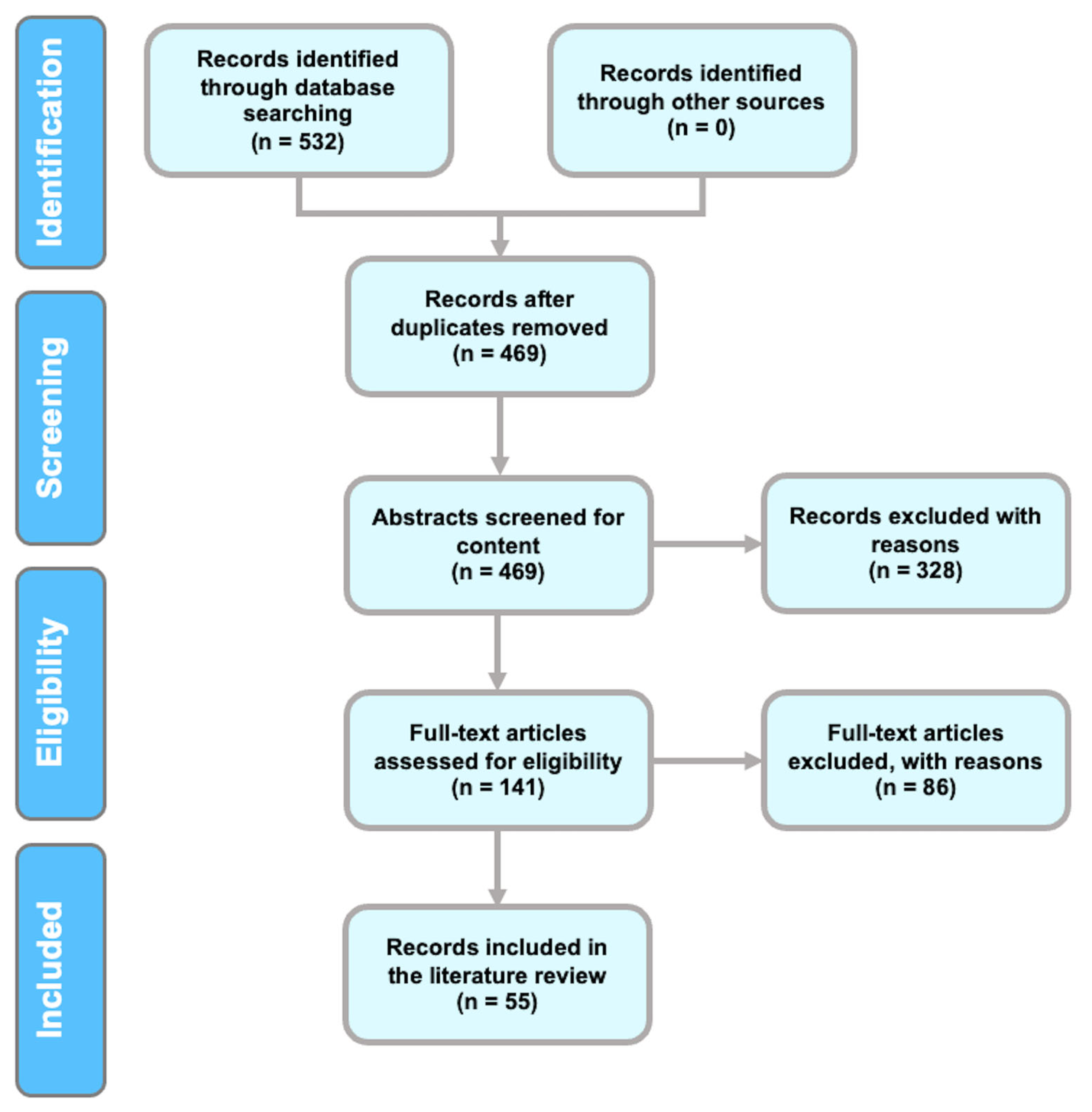
3.1. Literature Search
3.2. Chaos Theory: Applications for EEG Analysis of Mental Processes
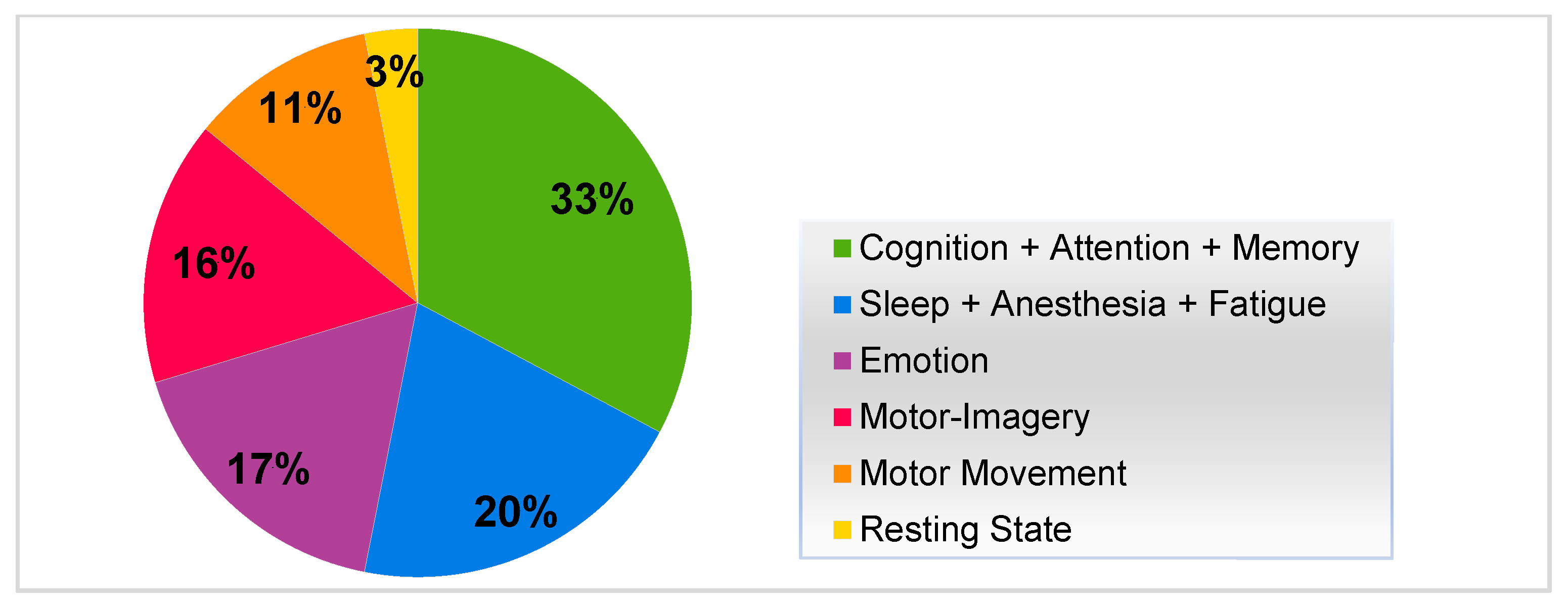
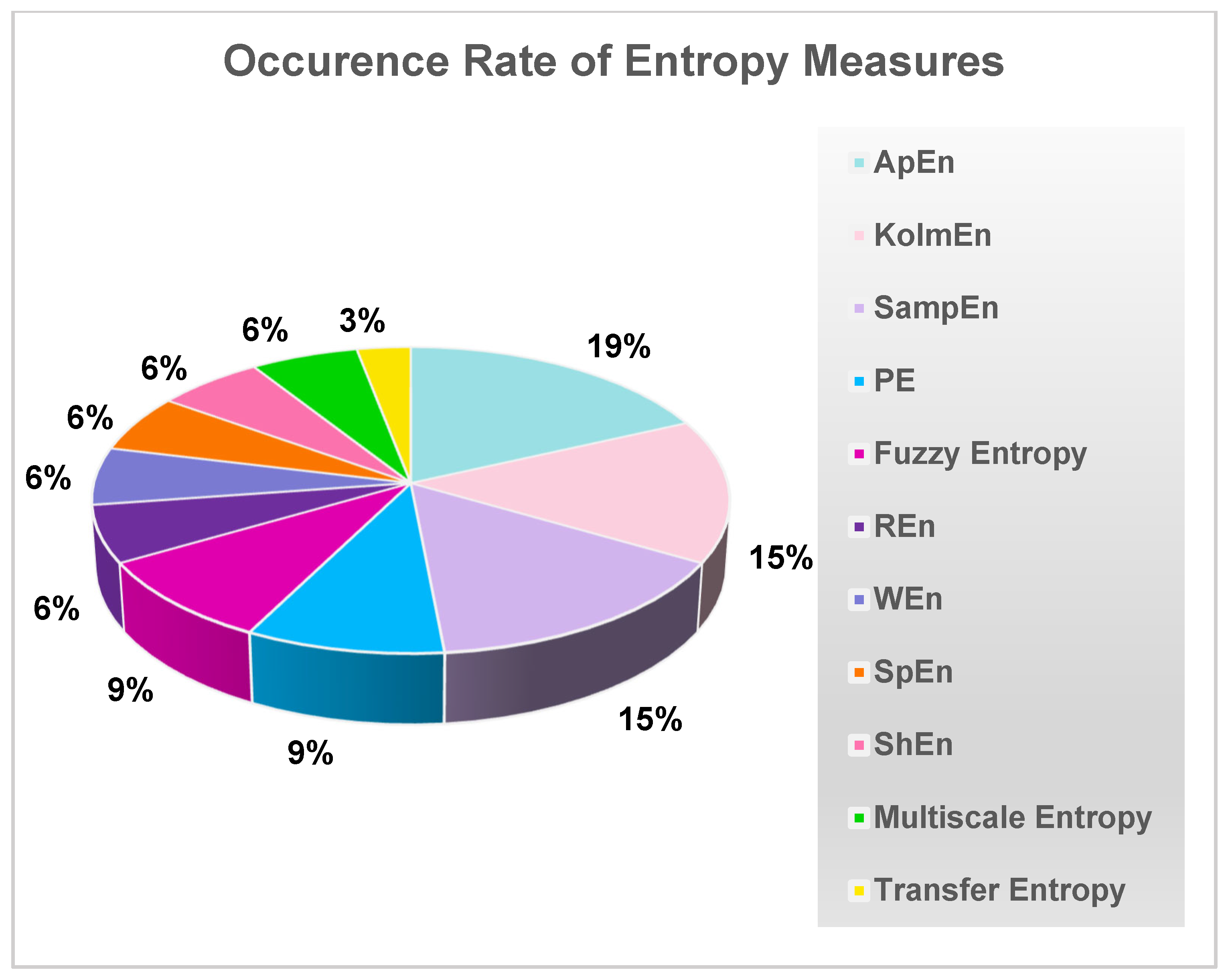
3.3. Chaotic Measures of Various Brain Functions
4. Discussion
4.1. Nonlinear Dynamical Studies on Cognitive Functions
4.1.1. Cognition
4.1.2. Attention
4.1.3. Memory
4.2. Nonlinear Dynamical Studies on Sleep, Anesthesia, and Fatigue
4.3. Nonlinear Dynamical Studies on Emotion
4.4. Nonlinear Dynamical Studies on Motor-Imagery
4.5. Nonlinear Dynamical Studies on Motor Movement
4.6. Nonlinear Dynamical Studies on Resting State
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pakkenberg, B. Aging and the human neocortex. Exp. Gerontol. 2003, 38, 95–99. [Google Scholar] [CrossRef]
- Herculano-Houzel, S. The human brain in numbers: A linearly scaled-up primate brain. Front. Hum. Neurosci. 2009, 3, 31. [Google Scholar] [CrossRef]
- McKenna, T.M.; McMullen, T.A.; Shlesinger, M.F. The brain as a dynamic physical system. Neuroscience 1994, 60, 587–605. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Meng, J.; Tan, G.; Zou, L. Research on the relation of EEG signal chaos characteristics with high-level intelligence activity of human brain. Nonlinear Biomed. Phys. 2010, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, G.C.; Tewarie, P.; Vidaurre, D.; Liuzzi, L.; Woolrich, M.W.; Brookes, M.J. Dynamics of large-scale electrophysiological networks: A technical review. NeuroImage 2018, 180 Pt B, 559–576. [Google Scholar] [CrossRef]
- Ismail, L.E.; Karwowski, W. A Graph Theory-Based Modeling of Functional Brain Connectivity Based on EEG: A Systematic Review in the Context of Neuroergonomics. IEEE Access 2020, 8, 155103–155135. [Google Scholar] [CrossRef]
- Reijneveld, J.C.; Ponten, S.C.; Berendse, H.W.; Stam, C.J. The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 2007, 118, 2317–2331. [Google Scholar] [CrossRef]
- Al-Fahoum, A.S.; Al-Fraihat, A.A. Methods of EEG Signal Features Extraction Using Linear Analysis in Frequency and Time-Frequency Domains. ISRN Neurosci. 2014, 2014, 730218. [Google Scholar] [CrossRef]
- Pritchard, W.S.; Duke, D.W. Measuring Chaos in the Brain—A Tutorial Review of EEG Dimension Estimation. Brain Cogn. 1995, 27, 353–397. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, K.; Acharya, U.R.; Alias, F.; Tiboleng, T.; Puthusserypady, S.K. Nonlinear analysis of EEG signals at different mental states. BioMed. Eng. OnLine 2004, 3, 7. [Google Scholar] [CrossRef]
- Oestreicher, C. A history of chaos theory. Dialogues Clin. Neurosci. 2007, 9, 279–289. [Google Scholar] [CrossRef]
- Justin, M.; Boudoue Hubert, M.; Betchewe, G.; Yamigno Doka, S.; Timoleon Crepin, K. Chaos in Human Brain Phase Transition. In Research Advances in Chaos Theory; IntechOpen: Vienna, Austria, 2020. [Google Scholar] [CrossRef]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef]
- Rodriguez-Bermudez, G.; Garcia-Laencina, P.J. Analysis of EEG signals using nonlinear dynamics and chaos: A review. Appl. Math. Inf. Sci. 2015, 9, 2309. [Google Scholar]
- Hernan Diaz, M.; Cordova, F.M.; Canete, L.; Palominos, F.; Cifuentes, F.; Sanchez, C.; Herrera, M. Order and chaos in the brain: Fractal time series analysis of the EEG activity during a cognitive problem solving task. Procedia Comput. Sci. 2015, 55, 1410–1419. [Google Scholar] [CrossRef]
- Stankova, E.P.; Myshkin, I.Y. Association between individual EEG characteristics and the level of intelligence. Mosc. Univ. Biol. Sci. Bull. 2016, 71, 256–261. [Google Scholar] [CrossRef]
- Shan, P.; Pei, J. Cognition and Education Management Method of Withdrawal Reaction for Students with Internet Addiction Based on EEG Signal Analysis*. Kuram Uygul. Egit. Bilim. 2018, 18, 2235–2246. [Google Scholar] [CrossRef]
- Popivanov, D.; Janyan, A.; Andonova, E.; Stamenov, M. Common dynamic properties of biosignals during cognition: Self-similarity and chaotic dynamics of both response times and EEG during movement imagery. Nonlinear Dyn. Psychol. Life Sci. 2003, 7, 315–328. [Google Scholar] [CrossRef]
- Micheloyannis, S.; Papanikolaou, E.; Bizas, E.; Stam, C.J.; Simos, P.G. Ongoing electroencephalographic signal study of simple arithmetic using linear and non-linear measures. Int. J. Psychophysiol. 2002, 44, 231–238. [Google Scholar] [CrossRef]
- Ramanand, P.; Nampoori, V.P.; Sreenivasan, R. Complexity quantification of dense array EEG using sample entropy analysis. J. Integr. Neurosci. 2004, 3, 343–358. [Google Scholar] [CrossRef] [PubMed]
- Parbat, D.; Chakraborty, M. A novel methodology to study the cognitive load induced EEG complexity changes: Chaos, fractal and entropy based approach. Biomed. Signal Process. Control 2021, 64, 102277. [Google Scholar] [CrossRef]
- Müller, V.; Lindenberger, U. Lifespan differences in nonlinear dynamics during rest and auditory oddball performance. Dev. Sci. 2012, 15, 540–556. [Google Scholar] [CrossRef] [PubMed]
- Ke, Y.; Chen, L.; Fu, L.; Jia, Y.; Li, P.; Zhao, X.; Qi, H.; Zhou, P.; Zhang, L.; Wan, B. Visual attention recognition based on nonlinear dynamical parameters of EEG. Bio-Med. Mater. Eng. 2014, 24, 349–355. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Hramov, A.E.; Grubov, V.V.; Nedaivozov, V.O.; Makarov, V.V.; Pisarchik, A.N. Nonlinear effect of biological feedback on brain attentional state. Nonlinear Dyn. 2019, 95, 1923–1939. [Google Scholar] [CrossRef]
- Azarnoosh, M.; Nasrabadi, A.M.; Mohammadi, M.R.; Firoozabadi, M. Investigation of mental fatigue through EEG signal processing based on nonlinear analysis: Symbolic dynamics. Chaos Solitons Fractals 2011, 44, 1054–1062. [Google Scholar] [CrossRef]
- Behzadfar, N.; Firoozabadi, S.M.; Badie, K. Low-Complexity Discriminative Feature Selection From EEG Before and After Short-Term Memory Task. Clin. EEG Neurosci. 2016, 47, 291–297. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J. Brain dynamics in theta and alpha frequency bands and working memory performance in humans. Neurosci. Lett. 2000, 286, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Zarjam, P.; Epps, J.; Lovell, N.H.; Chen, F. Characterization of memory load in an arithmetic task using non-linear analysis of EEG signals. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 3519–3522. [Google Scholar]
- Lalitha, V.; Eswaran, C. Automated detection of anesthetic depth levels using chaotic features with artificial neural networks. J. Med. Syst. 2007, 31, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Liang, Z.; Li, X.; Voss, L.J.; Sleigh, J.W. Permutation Lempel-Ziv complexity measure of electroencephalogram in GABAergic anaesthetics. Physiol. Meas. 2015, 36, 2483–2501. [Google Scholar] [CrossRef]
- Liang, Z.; Li, D.; Ouyang, G.; Wang, Y.; Voss, L.J.; Sleigh, J.W.; Li, X. Multiscale rescaled range analysis of EEG recordings in sevoflurane anesthesia. Clin. Neurophysiol. 2012, 123, 681–688. [Google Scholar] [CrossRef]
- Bolaños, J.D.; Vallverdú, M.; Caminal, P.; Valencia, D.F.; Borrat, X.; Gambús, P.L.; Valencia, J.F. Assessment of sedation-analgesia by means of poincaré analysis of the electroencephalogram. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6425–6428. [Google Scholar]
- Joo, P.; Kim, S.; Noh, G.J.; Choi, B.M. A robust complexity measure for noisy EEG time series under dynamic transitions during anesthesia. J. Korean Phys. Soc. 2022, 80, 68–73. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.S.; Kim, D.J.; Kim, S.Y.; Chae, J.H.; Go, H.J.; Kim, K.S. Effect of total sleep deprivation on the dimensional complexity of the waking EEG. Sleep 2001, 24, 197–202. [Google Scholar]
- Li, D.; Ruan, Y.; Zheng, F.; Su, Y.; Lin, Q. Fast Sleep Stage Classification Using Cascaded Support Vector Machines with Single-Channel EEG Signals. Sensors 2022, 22, 9914. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Khare, S.K.; Bajaj, V.; Ansari, I.A. Improving the separability of drowsiness and alert EEG signals using analytic form of wavelet transform. Appl. Acoust. 2021, 181, 108164. [Google Scholar] [CrossRef]
- Gao, Z.-K.; Li, Y.-L.; Yang, Y.-X.; Ma, C. A recurrence network-based convolutional neural network for fatigue driving detection from EEG. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 113126. [Google Scholar] [CrossRef]
- Kalauzi, A.; Vuckovic, A.; Boji, T. New complexity measures reveal that topographic loops of human alpha phase potentials are more complex in drowsy than in wake. Med. Biol. Eng. Comput. 2018, 56, 967–978. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.; Zheng, C. EEG-based estimation of mental fatigue by using KPCA–HMM and complexity parameters. Biomed. Signal Process. Control 2010, 5, 124–130. [Google Scholar] [CrossRef]
- Bahari, F.; Janghorbani, A. EEG-based emotion recognition using Recurrence Plot analysis and K nearest neighbor classifier. In Proceedings of the 2013 20th Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 18–20 December 2013; pp. 228–233. [Google Scholar]
- Fan, M.; Chou, C. Recognizing affective state patterns using regularized learning with nonlinear dynamical features of EEG. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 137–140. [Google Scholar]
- Gao, Z.; Cui, X.; Wan, W.; Zheng, W.; Gu, Z. Long-range correlation analysis of high frequency prefrontal electroencephalogram oscillations for dynamic emotion recognition. Biomed. Signal Process. Control 2022, 72, 103291. [Google Scholar] [CrossRef]
- Guodong, G.; Yahan, G. Multi feature fusion EEG emotion recognition. In Proceedings of the 2021 7th International Conference on Big Data and Information Analytics (BigDIA), Chongqing, China, 29–31 October 2021; pp. 280–284. [Google Scholar]
- Xi, X.; Tao, Q.; Li, J.; Kong, W.; Zhao, Y.-B.; Wang, H.; Wang, J. Emotion-movement relationship: A study using functional brain network and cortico-muscular coupling. J. Neurosci. Methods 2021, 362, 109320. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Subasi, A. A new fractal pattern feature generation function based emotion recognition method using EEG. Chaos Solitons Fractals 2021, 144, 110671. [Google Scholar] [CrossRef]
- Khodabakhshi, M.B.; Saba, V. A nonlinear dynamical approach to analysis of emotions using EEG signals based on the Poincare map function and recurrence plots. Biomed. Eng./Biomed. Tech. 2020, 65, 507–520. [Google Scholar] [CrossRef]
- Li, X.; Song, D.; Zhang, P.; Zhang, Y.; Hou, Y.; Hu, B. Exploring EEG features in cross-subject emotion recognition. Front. Neurosci. 2018, 12, 162. [Google Scholar] [CrossRef]
- Yang, Y.-X.; Gao, Z.-K.; Wang, X.-M.; Li, Y.-L.; Han, J.-W.; Marwan, N.; Kurths, J. A recurrence quantification analysis-based channel-frequency convolutional neural network for emotion recognition from EEG. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 085724. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J. Performance comparison of machine learning algorithms for EEG-signal-based emotion recognition. In Proceedings of the Artificial Neural Networks and Machine Learning–ICANN 2017: 26th International Conference on Artificial Neural Networks, Alghero, Italy, 11–14 September 2017; Proceedings, Part I 26. pp. 208–216. [Google Scholar]
- Maity, A.K.; Pratihar, R.; Mitra, A.; Dey, S.; Agrawal, V.; Sanyal, S.; Banerjee, A.; Sengupta, R.; Ghosh, D. Multifractal detrended fluctuation analysis of alpha and theta EEG rhythms with musical stimuli. Chaos Solitons Fractals 2015, 81, 52–67. [Google Scholar] [CrossRef]
- Diaz, M.H.; Rivas, G.; Cordova, F.M.; Palominos, F.; Canete, L.; Troncoso, N. Specialized brains performing specialized tasks: Beta/gamma EEG non-linear analysis reveals discriminative differences between the chaos/no-chaos content of specialized brain’s dynamics. Procedia Comput. Sci. 2016, 91, 813–822. [Google Scholar] [CrossRef]
- Roy, R.; Sikdar, D.; Mahadevappa, M. Chaotic behaviour of EEG responses with an identical grasp posture. Comput. Biol. Med. 2020, 123, 39–48. [Google Scholar] [CrossRef]
- Díaz, H.; Maureira, F.; Cohen, E.; Córdova, F.; Palominos, F.; Otárola, J.; Cañete, L. Individual Differences in the Order/Chaos Balance of the Brain Self-Organization. Ann. Data Sci. 2015, 2, 421–438. [Google Scholar] [CrossRef]
- Elbaz, A.M.; Ahmed, A.T.; Mohamed, A.M.; Oransa, M.A.; Sayed, K.S.; Eldeib, A.M. Motor imagery based brain computer interface using transform domain features. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC 2016), Orlando, FL, USA, 16–20 August 2016; pp. 6421–6424. [Google Scholar]
- Kai, Z.; Guanghua, X.; Chenghang, D.; Yongchen, W.; Xiaowei, Z.; Sicong, Z.; Chengcheng, H.; Renhao, L.; Ruiquan, C. Weak Feature Extraction and Strong Noise Suppression for SSVEP-EEG Based on Chaotic Detection Technology. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 862–871. [Google Scholar] [CrossRef]
- Baravalle, R.; Rosso, O.A.; Montani, F. Discriminating imagined and non-imagined tasks in the motor cortex area: Entropy-complexity plane with a wavelet decomposition. Phys. A Stat. Mech. Its Appl. 2018, 511, 27–39. [Google Scholar] [CrossRef]
- Chea-Yau, K.; Ponnambalam, S.G.; Chu-Kiong, L. Binary and multi-class motor imagery using Renyi entropy for feature extraction. Neural Comput. Appl. 2017, 28, 2051–2062. [Google Scholar] [CrossRef]
- Hosni, S.M.I.; Borgheai, S.B.; McLinden, J.; Zhu, S.; Huang, X.; Ostadabbas, S.; Shahriari, Y. Graph-based Recurrence Quantification Analysis of EEG Spectral Dynamics for Motor Imagery-based BCIs. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC 2021), Virtual, 1–5 November 2021; Volume 2021, pp. 6453–6457. [Google Scholar] [CrossRef]
- Khare, S.K.; Gaikwad, N.; Bokde, N.D. An Intelligent Motor Imagery Detection System Using Electroencephalography with Adaptive Wavelets. Sensors 2022, 22, 8128. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Pavlov, A.; Runnova, A.E.; Nedaivozov, V.; Grubov, V.; Koronovslii, A.; Pchelintseva, S.V.; Pitsik, E.; Pisarchik, A.N.; Hramov, A.E. Nonlinear analysis of brain activity, associated with motor action and motor imaginary in untrained subjects. Nonlinear Dyn. 2018, 91, 2803–2817. [Google Scholar] [CrossRef]
- Dushanova, J. Does the Kolmogorov entropy give more information about the organization of the voluntary movement? Acta Physiol. Pharm. Bulg. 2001, 26, 93–96. [Google Scholar]
- Dushanova, J.; Popivanov, D. Nonlinear dynamics estimation of EEG signals accompanying self-paced goal-directed movements. Nonlinear Dyn. Psychol. Life Sci. 2001, 5, 325–344. [Google Scholar] [CrossRef]
- Hung, T.M.; Haufler, A.J.; Lo, L.C.; Mayer-Kress, G.; Hatfield, B.D. Visuomotor expertise and dimensional complexity of cerebral cortical activity. Med. Sci. Sport. Exerc. 2008, 40, 752–759. [Google Scholar] [CrossRef]
- Kranczioch, C.; Athanassiou, S.; Shen, S.; Gao, G.; Sterr, A. Short-term learning of a visually guided power-grip task is associated with dynamic changes in EEG oscillatory activity. Clin. Neurophysiol. 2008, 119, 1419–1430. [Google Scholar] [CrossRef]
- Yargholi, E.; Nasrabadi, A.M. Chaos–chaos transition of left hemisphere EEGs during standard tasks of Waterloo-Stanford Group Scale of hypnotic susceptibility. J. Med. Eng. Technol. 2015, 39, 281–285. [Google Scholar] [CrossRef] [PubMed]
- Usakli, A.B. Modeling of movement-related potentials using a fractal approach. J. Comput. Neurosci. 2010, 28, 595–603. [Google Scholar] [CrossRef]
- Shaw, S.B.; Dhindsa, K.; Reilly, J.P.; Becker, S. Capturing the forest but missing the trees: Microstates inadequate for characterizing shorter-scale EEG dynamics. Neural Comput. 2019, 31, 2177–2211. [Google Scholar] [CrossRef]
- Zhao, Q.; Peng, H.; Hu, B.; Li, L.; Qi, Y.; Liu, Q.; Liu, L. Towards an efficient and accurate EEG data analysis in EEG-based individual identification. In Proceedings of the Ubiquitous Intelligence and Computing: 7th International Conference, UIC 2010, Xi’an, China, 26–29 October 2010; Proceedings 7. pp. 534–547. [Google Scholar]
- Zhang, J. Cognitive functions of the brain: Perception, attention and memory. arXiv 2019, arXiv:1907.02863. [Google Scholar]
- Lucia, S.; Bianco, V.; Di Russo, F. Specific effect of a cognitive-motor dual-task training on sport performance and brain processing associated with decision-making in semi-elite basketball players. Psychol. Sport Exerc. 2023, 64, 102302. [Google Scholar] [CrossRef]
- Georgopoulos, A.P.; Pellizzer, G. The mental and the neural: Psychological and neural studies of mental rotation and memory scanning. Neuropsychologia 1995, 33, 1531–1547. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Lopes da Silva, F.H. Event-related EEG/MEG synchronization and desynchronization: Basic principles. Clin. Neurophysiol. 1999, 110, 1842–1857. [Google Scholar] [CrossRef] [PubMed]
- Klimesch, W. EEG alpha and theta oscillations reflect cognitive and memory performance: A review and analysis. Brain Res. Rev. 1999, 29, 169–195. [Google Scholar] [CrossRef]
- Dentico, D.; Ferrarelli, F.; Riedner, B.A.; Smith, R.; Zennig, C.; Lutz, A.; Tononi, G.; Davidson, R.J. Short meditation trainings enhance non-REM sleep low-frequency oscillations. PLoS ONE 2016, 11, e0148961. [Google Scholar] [CrossRef] [PubMed]
- Rees, B.; Travis, F.; Shapiro, D.; Chant, R. Significant Reductions in Posttraumatic Stress Symptoms in Congolese Refugees Within 10 days of Transcendental Meditation Practice. J. Trauma. Stress 2014, 27, 112–115. [Google Scholar] [CrossRef] [PubMed]
- Gilden, D.L. Cognitive Emissions of 1/f Noise. Psychol. Rev. 2001, 108, 33–56. [Google Scholar] [CrossRef]
- Kelly, A.; Heathcote, A.; Heath, R.; Longstaff, M. Response-time dynamics: Evidence for linear and low-dimensional nonlinear structure in human choice sequences. Q. J. Exp. Psychol. A Hum. Exp. Psychol. 2001, 54, 805–840. [Google Scholar] [CrossRef]
- İskender, M.; Akin, A. Social self-efficacy, academic locus of control, and internet addiction. Comput. Educ. 2010, 54, 1101–1106. [Google Scholar] [CrossRef]
- Dong, G.; Zhou, H. Is impulse-control ability impaired in people with internet addiction disorder: Electrophysiological evidence from ERP studies. Int. J. Psychophysiol. 2010, 77, 334–335. [Google Scholar] [CrossRef]
- Aamir Saeed, M.; Hafeez Ullah, A. Chapter 8—Visual and Cognitive Fatigue during Learning; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 123–135. [Google Scholar] [CrossRef]
- Huettel, S.A.; McCarthy, G. What is odd in the oddball task?: Prefrontal cortex is activated by dynamic changes in response strategy. Neuropsychologia 2004, 42, 379–386. [Google Scholar] [CrossRef]
- Paas, F.; Tuovinen, J.E.; Tabbers, H.; Van Gerven, P.W.M. Cognitive Load Measurement as a Means to Advance Cognitive Load Theory. Educ. Psychol. 2003, 38, 63–71. [Google Scholar] [CrossRef]
- Stipacek, A.; Grabner, R.H.; Neuper, C.; Fink, A.; Neubauer, A.C. Sensitivity of human EEG alpha band desynchronization to different working memory components and increasing levels of memory load. Neurosci. Lett. 2003, 353, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Harmony, T.A.; Fernández, T.A.; Silva, J.; Bosch, J.; Valdés, P.; Fernández-Bouzas, A.; Galán, L.d.; Aubert, E.; Rodréguez, D. Do specific EEG frequencies indicate different processes during mental calculation? Neurosci. Lett. 1999, 266, 25–28. [Google Scholar] [CrossRef]
- Zhang, X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans Biomed Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, C. A New Method to Monitor Depth of Anesthesia Based on the Autocorrelation EEG Signals. In Proceedings of the 2005 First International Conference on Neural Interface and Control, Wuhan, China, 28–26 May 2005; pp. 123–126. [Google Scholar] [CrossRef]
- Krkic, M.; Roberts, S.J.; Rezek, I.; Jordan, C. EEG-based assessment of anaesthetic depth using neural networks. In Proceedings of the IEE Colloquium on Artificial Intelligence Methods for Biomedical Data Processing, London, UK, 26 April 1996. [Google Scholar] [CrossRef]
- Jeong, J.; Chae, J.H.; Kim, S.Y.; Han, S.H. Nonlinear Dynamic Analysis of the EEG in Patients with Alzheimer’s Disease and Vascular Dementia. J. Clin. Neurophysiol. 2001, 18, 58–67. [Google Scholar] [CrossRef]
- Steriade, M.; McCormick, D.A.; Sejnowski, T.J. Thalamocortical oscillations in the sleeping and aroused brain. Science 1993, 262, 679–685. [Google Scholar] [CrossRef]
- Mashour, G.A.M.D.P.; Pal, D.P. Interfaces of Sleep and Anesthesia. Anesthesiol. Clin. 2012, 30, 385–398. [Google Scholar] [CrossRef]
- Antognini, J.F.; Carstens, E.E.; Raines, D.E. Neural Mechanisms of Anesthesia; Humana Press: Totowa, NJ, USA, 2002. [Google Scholar]
- Nelson, L.E.; Guo, T.Z.; Lu, J.; Saper, C.B.; Franks, N.P.; Maze, M. The sedative component of anesthesia is mediated by GABAA receptors in an endogenous sleep pathway. Nat. Neurosci. 2002, 5, 979–984. [Google Scholar] [CrossRef]
- Lu, J.; Nelson, L.E.; Franks, N.; Maze, M.; Chamberlin, N.L.; Saper, C.B. Role of endogenous sleep-wake and analgesic systems in anesthesia. J. Comp. Neurol. 2008, 508, 648–662. [Google Scholar] [CrossRef] [PubMed]
- Khosrowabadi, R.; Wahab bin Abdul Rahman, A. Classification of EEG correlates on emotion using features from Gaussian mixtures of EEG spectrogram. In Proceeding of the 3rd International Conference on Information and Communication Technology for the Moslem World (ICT4M), Jakarta, Indonesia, 13–14 December 2010; pp. E102–E107. [Google Scholar]
- Mi, L.; Liu, X.; Ren, F.; Araki, H. Characteristics of Event-related Potentials in Recognition Processes of Japanese Kanji and Sentences for Chinese Bilinguals. J. Physiol. Anthropol. 2009, 28, 191–197. [Google Scholar] [CrossRef]
- Hakamata, A.; Ren, F.; Tsuchiya, S. Human emotion model based on discourse sentence for expression generation of conversation agent. In Proceedings of the 2008 International Conference on Natural Language Processing and Knowledge Engineering, Beijing, China, 19–22 October 2008; pp. 1–8. [Google Scholar]
- Horlings, R.; Datcu, D.; Rothkrantz, L. Emotion recognition using brain activity. In Proceedings of the 9th International Conference on Computer Systems and Technologies and Workshop for PhD Students in Computing, Gabrovo, Bulgaria, 12–13 June 2008; p. II.1–1. [Google Scholar]
- Schalk, G.; McFarland, D.J.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J.R. BCI2000: A general-purpose brain-computer interface (BCI) system. IEEE Trans. Biomed. Eng. 2004, 51, 1034–1043. [Google Scholar] [CrossRef]
- Sharma, N.; Simmons, L.H.; Jones, P.S.; Day, D.J.; Carpenter, T.A.; Pomeroy, V.M.; Warburton, E.A.; Baron, J.-C. Motor Imagery After Subcortical Stroke: A Functional Magnetic Resonance Imaging Study. Stroke 2009, 40, 1315–1324. [Google Scholar] [CrossRef]
- Johnson, S.H.; Sprehn, G.; Saykin, A.J. Intact Motor Imagery in Chronic Upper Limb Hemiplegics: Evidence for Activity-Independent Action Representations. J. Cogn. Neurosci. 2002, 14, 841–852. [Google Scholar] [CrossRef]
- Johnson, S.H. Imagining the impossible: Intact motor representations in hemiplegics. Neuroreport 2000, 11, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Birbaumer, N. Brain–computer-interface research: Coming of age. Clin. Neurophysiol. 2006, 117, 479–483. [Google Scholar] [CrossRef] [PubMed]
- Blankertz, B.; Losch, F.; Krauledat, M.; Dornhege, G.; Curio, G.; Muller, K.-R. The Berlin Brain-Computer Interface: Accurate performance from first-session in BCI-naive subjects. IEEE Trans. Biomed. Eng. 2008, 55, 2452–2462. [Google Scholar] [CrossRef]
- Wolpaw, J.R.; Birbaumer, N.; McFarland, D.J.; Pfurtscheller, G.; Vaughan, T.M. Brain–computer interfaces for communication and control. Clin. Neurophysiol. 2002, 113, 767–791. [Google Scholar] [CrossRef] [PubMed]
- Wolpaw, J.R.; Birbaumer, N.; Heetderks, W.J.; McFarland, D.J.; Peckham, P.H.; Schalk, G.; Donchin, E.; Quatrano, L.A.; Robinson, C.J.; Vaughan, T.M. Brain-computer interface technology: A review of the first international meeting. IEEE Trans. Rehabil. Eng. 2000, 8, 164–173. [Google Scholar] [CrossRef]
- Schalk, G.; Mellinger, J. Practical Guide to Brain-Computer Interfacing with BCI2000: General-Purpose Software for Brain-Computer Interface Research, Data Acquisition, Stimulus Presentation, and Brain Monitoring; Springer London, Limited: London, UK, 2010. [Google Scholar] [CrossRef]
- Rosso, O.A.; Masoller, C. Detecting and quantifying stochastic and coherence resonances via information-theory complexity measurements. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79 Pt 1, 040106. [Google Scholar] [CrossRef]
- Boostani, R.; Moradi, M.H. A new approach in the BCI research based on fractal dimension as feature and Adaboost as classifier. J. Neural Eng. 2004, 1, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Brunner, C.; Billinger, M.; Vidaurre, C.; Neuper, C. A comparison of univariate, vector, bilinear autoregressive, and band power features for brain–computer interfaces. Med. Biol. Eng. Comput. 2011, 49, 1337–1346. [Google Scholar] [CrossRef] [PubMed]
- Zheng Yang, C.; Kai Keng, A.; Cuntai, G.; Chuanchu, W.; Haihong, Z. Filter Bank Feature Combination (FBFC) Approach for Brain-Computer Interface. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1352–1357. [Google Scholar] [CrossRef]
- Li, Y.; Koike, Y. A real-time BCI with a small number of channels based on CSP. Neural Comput. Appl. 2010, 20, 1187–1192. [Google Scholar] [CrossRef]
- Floyer-Lea, A.; Matthews, P.M. Changing Brain Networks for Visuomotor Control with Increased Movement Automaticity. J. Neurophysiol. 2004, 92, 2405–2412. [Google Scholar] [CrossRef] [PubMed]
- Vaillancourt, D.E.; Thulborn, K.R.; Corcos, D.M. Neural Basis for the Processes That Underlie Visually Guided and Internally Guided Force Control in Humans. J. Neurophysiol. 2003, 90, 3330–3340. [Google Scholar] [CrossRef]
- Roelfsema, P.R.; Engel, A.K.; König, P.; Singer, W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 1997, 385, 157–161. [Google Scholar] [CrossRef]
- Classen, J.; Gerloff, C.; Honda, M.; Hallett, M. Integrative Visuomotor Behavior Is Associated with Interregionally Coherent Oscillations in the Human Brain. J. Neurophysiol. 1998, 79, 1567–1573. [Google Scholar] [CrossRef]
- Sadaghiani, S.; Hesselmann, G.; Friston, K.J.; Kleinschmidt, A. The relation of ongoing brain activity, evoked neural responses, and cognition. Front. Syst. Neurosci. 2010, 4, 20. [Google Scholar] [CrossRef]
- Michel, C.M.; Koenig, T. EEG microstates as a tool for studying the temporal dynamics of whole-brain neuronal networks: A review. NeuroImage 2018, 180 Pt B, 577–593. [Google Scholar] [CrossRef]
- Albano, A.; Rapp, P. On the reliability of dynamical measures of EEG signals. In Proceedings of the 2nd Annual Conference on Nonlinear Dynamics Analysis of the EEG, Houston, TX, USA, 3–4 April 1992; pp. 117–139. [Google Scholar]


| Article | Chaos Metric | Domain | Number of EEG Channels | Number of Participants | Summary of Experiments | Summary of Findings |
|---|---|---|---|---|---|---|
| [16] | HE | Cognition | 14 EEG channels | 12 | Raven’s test was performed. | Observed HE had a lower value in alpha bands, thus indicating higher unpredictability. The HE values increased the delta frequencies associated with cognitive mental processing, thus suggesting that fundamental processes attract the system to more organized, self-similar, less chaotic, and more predictable conditions. |
| [17] | CD | Cognition | 18 EEG channels | 77 | A domino test was performed, in which participants identified the correct piece corresponding to the previous patterns of dominos. | Intelligence levels and the degree of intelligence levels were positively correlated. Data suggested that participants with highly oscillating signals scored higher on intelligence tests than those with more periodic oscillations. Thus, intelligent participants appeared to have a more complex and chaotic EEG structure. |
| [18] | CD and KolmEn | Cognition | 64 EEG channels | 6 | Resting state EEG was examined. | A comparison of the chaotic features of internet-addicted students and controls of typical students indicated that the former have higher levels of neuronal activity and higher chaotic behaviors of EEG signals in the prefrontal cortex at rest. |
| [19] | FD and CD | Cognition | 9 EEG channels | 42: male = 20, female = 22 | Participants were asked to listen to 25 verb-and-object sentences and to understand and imagine the action indicated. | The response times and EEG records of participants visualizing a series of MI tasks clearly demonstrated self-similarity and chaotic behaviors, thus explaining how the nervous system is a self-organizing mechanism. |
| [20] | CD | Cognition | 28 EEG channels | 2: male = 1, female = 1 | Participants were presented with stimuli on an LCD screen in the categories of arithmetic, language, and symbol processing and were asked to determine whether the stimulus was in the correct or incorrect domain. | The CD method indicated that the right side of the brain exhibited more prominent engagement during an arithmetic task. This finding would have been missed by the spectral analysis method. |
| [21] | SampEn | Cognition, working memory, attention | 128 EEG channels | 6: male = 3, female = 3 | The following were examined: first, a passive state with eyes closed; second, performance of a mental task; and last, performance of the same mental task followed by a fatigue-causing physical task. | SampEn was diminished during the arithmetic task in the prefrontal and occipital regions with respect to the recorded baseline relaxed state, thus indicating less chaos. When fatigue factors were present, diminished SampEn in the central, temporal, and parietal regions associated with performing motor actions was observed. Fatigue changes the dynamics of the brain in the motor cortex areas. |
| [22] | LE, FD, and SampEn | Cognition (attention, memory), attention | 19 EEG channels | 4 | EEG signals in response to four categories of cognitive tasks were investigated—focus, problem solving, memory, and emotion recognition. Cognitive load was assessed using the NASA Task Load Index sheet. The EEG session was designed with the eyes open condition, and a qualitative assessment was performed to determine the difficulty level of executing the task. | This study established a spatiotemporal descriptor for perceiving changes in the properties of the EEG signal, which occurs in response to cognitive load. The study used three different nonlinear parameters to analyze the EEG signals, LE, FD, and SampEn. The researchers used these findings to create a classification model that can identify different states of the brain based on the changes in the EEG signal. |
| [23] | CD and two coupling measures: pointwise trans-information and pointwise conditional coupling divergence (PCCD) | Attention | 58 EEG channels | 9 | Participants with eyes closed listened to two types of tones: a constant 1000-Hz tone as the standard stimulus and an intermittent 800-Hz tone as the deviant stimulus. Participants were asked to count the number of deviant tones and provide feedback. | In the deviant stimulus experiment, nonlinear coupling increased with age, while CD/complexity decreased. |
| [24] | ApEn, SampEn, multi-scale entropy | Visual Attention | 19 EEG Channels | 14: male = 7, female = 0 | Participants were required to maintain their gaze fixed on the center of a computer monitor. Although the time courses of the two experiments were the same, the difference between them was in the action phase: Experiment 1 displayed a cartoon character playing ball, while Experiment 2 showed a cartoon character walking. | The findings indicate that SampEn fared very well among the dynamical parameters, with accuracies of 76.19% and 85.24% in recognizing the three levels of attention for the two experiments, respectively. SampEn also outperformed theta/beta power ratio. These results suggest that nonlinear dynamical parameters may be essential for developing a reliable system for attention recognition. |
| [25] | EEG algorithm | Attention | 5 EEG channels | 12 | A visual task that incorporates perception and primary processing of visual information. | The results obtained suggest that cognitive resources are finite, and to sustain optimal performance over an extended period, the brain needs to operate under a “safe-mode” regime. |
| [26] | Symbolic dynamics | Attention and Mental Fatigue | 11 EEG channels | 20: male = 20, female = 0 | Continuous performance task (CPT) algorithm-based task called “Sustained Attention Dots.” Participants were asked to respond in a certain way where there was a 4-dot pattern. There were a total of 600 patterns and 4 trials. | The findings indicated that, using nonlinear analysis of reaction time, as well as EEG signals from the frontal and central lobes of the brain, it was possible to distinguish between attention and the onset of mental fatigue during trials. Furthermore, the changes in entropy over time demonstrated a decrease in the complexity of mental activity as fatigue set in. |
| [27] | WEn, ApEn, PE, FD | Short-term memory | 2 EEG channels | 16 | Participants were shown 12 black and white pictures for 10 s and then asked to close their eyes for 2 min and provide the names of the pictures that they could remember. | PE increased significantly for FD, ApEn, root mean square, and waveform length in the frontal lobe and the occipital lobe, thus improving the effectiveness of memory-based neurological systems assessing feedback. |
| [28] | CD | Working memory | 21 EEG channels | 21: male = 9, female = 12 | Participants recalled any of the 12 black and white pictures shown to them within 1 min of their eyes closing. | Working memory conditions increased the lower alpha band’s dimension. A correlation was observed between greater working memory capacity and a smaller theta band dimension in women during the no-task condition. Lower band alpha complexity is associated with attention functions. Higher chaotic behavior and desynchronization in women are closely associated with task performance. |
| [29] | CD, HE, ApEn | Working memory | 32 EEG channels | 1: male = 0, female = 1 | An arithmetic task with seven levels of difficulty, from very low to extremely difficult, was shown on a computer display. Participants were asked to select the correct answer using a mouse button. | The decrease in the HE suggests that the random behavior of the brain signals vanishes, and a structured oscillation forms in response to the difficulty of the arithmetic task. |
| [30] | CD, LE, HE | Anesthesia | N/A | 5 | After premedication with morphine and atropine, five participants underwent anesthesia with propofol intravenously, followed by a thiopentone injection. | By combining nonlinear chaotic measures and neural network classifiers, anesthetic depth levels based on EEG signals can be identified. Using the LE with Elman networks (feedback model) detects the optimum depth of anesthesia with 99% accuracy. |
| [31] | Permutation Lempel-Ziv complexity (PLZC) | Anesthesia | 3 EEG channels | 20: male = 10, female = 10 | Sevoflurane gas was administered to participants for 2 min at 3%, followed by 7% in group 1, and intravenous propofol was delivered to group 2. | A permutation Lempel-Ziv complexity test (PLZC) surpassed all other indices in differentiating between awake and deep anesthesia and in predicting the anesthetic drug’s effect. |
| [32] | HE | Anesthesia | 3 EEG channels | 16: male = 0, female = 16 | During the first 2 min of sevoflurane administration, the vaporizer delivered 3% of the inspired concentration to participants, followed by 7%. | The novel method maximal overlap discrete wavelet transformation (MODWT) based on HE analysis was used to describe the effects of sevoflurane on the brain. HE of low-frequency bands (HEOLFB) tracked sevoflurane concentration best and was less susceptible to artifacts than the other methods examined. |
| [33] | Poincaré map (phase-space), SpEn | Anesthesia | 3 EEG channels | 110 | Ultrasonographic endoscopy was performed under sedation-analgesia. | The Poincaré plot model is effective in estimating sedation–analgesia levels. The ratio of the ellipse’s width in the Poincaré plot to its length in a band frequency of 30–110 Hz showed promising results for determining sedation levels, owing to high prediction probability. |
| [34] | Lumped PE | Anesthesia | 2 EEG channels | 16 | During general anesthesia, subjects were administered propofol continuously and its plasma concentration was measured at preset intervals. The EEG states of awake, sedative, and deep anesthesia were identified and the loss and regain of consciousness were determined through verbal commands. As the propofol infusion ended, the plasma concentration decreased gradually, leading to the subject regaining consciousness. | The study investigated the complexity of EEG signals during propofol-induced general anesthesia using three different entropy measures. The authors found that local pattern entropy (LPE) was the best measure to track changes in EEG complexity during anesthesia, showing a stronger and more robust correlation with propofol concentration. The study suggests that LPE could be used for real-time monitoring of anesthesia. |
| [35] | Composite multi-scale permutation entropy (CMSPE) | Anesthesia | 3 EEG channels | 18 | EEG data were collected from patients under sevoflurane anesthesia. | Composite multi-scale permutation entropy (CMSPE) was able to track minor transitions between light and deep anesthesia. The results indicate that CMSPE is superior to the raw single-scale PE in demonstrating the effects of sevoflurane on the central nervous system. |
| [36] | CD | Sleep | 16 EEG channels | 32: male = 16, female = 16 | Participants’ EEG was recorded after 8 h of nighttime sleep at 7:00 AM. Participants were then subjected to 24 h of sleep deprivation, and their EEGs were re-recorded at 7:00 AM. | CDs measured under sleep deprivation conditions were lower than those measured under normal sleep conditions. The decrease in the dimensionality of EEGs in sleep-deprived states indicated decreased chaotic behavior. |
| [37] | REn, LZC, multi-scale entropy, SpEn, SampEn, fuzzy entropy | Sleep | 2 EEG channels | Sleep-EDF database (8 subjects) | Each recording in the database is typically 8 h long and contains information about the sleep stages of the individual. The recordings are divided into 30-s epochs, and each epoch is labeled with the corresponding sleep stage. The sleep stages are Wake, Non-REM (NREM) Stage 1, NREM Stage 2, NREM Stage 3, and REM (Rapid Eye Movement) sleep. | The study aimed to develop an accurate and efficient method for sleep stage classification using single-channel EEG signals. The proposed method used a cascaded SVM model that improved the overall average classification accuracy, and the study analyzed different nonlinear dynamics features and found that fuzzy entropy, LZC, SampEn, and multi-scale entropy contributed significantly to the improvement of accuracy. However, these factors required more time to be calculated than other features. |
| [38] | Flexible analytic wavelet transform (FAWT) | Sleep (Drowsiness) | 32 EEG channels | 16: male = 16, female = 0 | Collected from MIT/BIH dataset of physiobank—no explanation of the experiment. | This study proposes a flexible analytic wavelet transform (FAWT)-based method for detecting drowsiness using EEG signals, which achieved high accuracy, sensitivity, and specificity in distinguishing between alert and drowsy states. The developed FAWT-extreme learning machine-based system was shown to be effective, robust, and accurate, and it could be used to model a real-time drowsiness detection system. |
| [39] | Recurrence network-based | Sleep (fatigue) | 40 EEG channels | 10: male = 8, female = 2 | Simulated driving experiment | The study aimed to develop a method for detecting driver fatigue using EEG signals. They collected EEG signals during a simulated driving experiment and used a recurrence network and a convolutional neural network to extract features and classify the data as alert or fatigued. The results demonstrated high accuracy with an average accuracy of 92.95%, and the proposed method outperformed existing methods, indicating that it was effective in detecting driver fatigue. |
| [40] | FD, circular complexity, longitudinal complexity, intersecting complexity | Sleep (Drowsiness) | 14 EEG channels | 10: male = 7, female = 3 | No task, eyes closed in a dark room | This study looked at the patterns of brain activity, specifically alpha waves, in people when they were awake and drowsy. They found that the patterns of brain activity were more complex when the person was drowsy compared to when he or she was awake, and the traditional way of measuring complexity, called FD, was not able to detect these differences. Instead, the researchers used three new measures of complexity that they developed and were able to show that the differences in brain activity patterns were statistically significant. |
| [41] | ApEn, Kolmogorov complexity (Kc) | Sleep (fatigue) | 32 EEG channels | 50 | Three experimental tasks: Vigilance task—participants had to click the right mouse when an odd number appeared on the screen. Addition and subtraction arithmetic calculation of four one-digit numbers Simple switch task | ApEn and Kolmogorov complexity (Kc) are useful measures of the dynamic complexity of EEG and have a strong association with mental fatigue. Complexity measures decrease as mental fatigue increases. Additionally, KPCA (kernel principal component analysis)-HMM (hidden Markov model) was proven to be a potentially effective model for estimating mental fatigue. |
| [42] | RQA | Emotion | 32 EEG channels | 10 | A total of 40 videos were presented to the participants in each trial, and self-assessment tests were performed | Feature extraction and detection of the emotion through recurrence plot analysis and k-NN classification had accuracy of 64.56%, 58.05%, and 67.42% in all three categories of scaling—values much higher than the accuracy achieved with linear (spectral analysis) methods. |
| [43] | RQA | Emotion | 32 EEG channels | Group 1: 19; Group 2: 10 | Participants scored each video that they were shown on a scale of 0 to 9 in four dimensions: arousal, valence, liking, and dominance. | With RQA, better classification performance was achieved over feature extraction works based on spectral analysis methods in emotion recognition. The proposed method with selected RQA feature extraction resulted in test accuracy of 75.7%. The findings may be used to identify the neurophysiology of human emotions. |
| [44] | Multi-order detrended fluctuation analysis (MODFA), fuzzy entropy | Emotion | 9 EEG channels | 87: male = 31, female = 56 | The study involved a baseline period during which participants had their eyes open and closed while gazing at a white cross displayed on a black screen. Participants then watched six video clips with different emotional themes, including neutral, fear, sadness, happiness, anger, and disgust. The videos were used to elicit emotional responses and were entitled “World Heritage in China”, “The Conjuring”, “Nuan Chun”, “Top Funny Comedian”, “Never Talk to Strangers”, and “The Fly”. | The study proposed a novel algorithm called multi-order detrended fluctuation analysis (MODFA), which improved the accuracy of EEG-based emotion recognition by measuring the homeostasis of prefrontal cortex neural activity. The results showed that MODFA outperformed conventional measures, such as fuzzy entropy and power spectral density with the best binary classification accuracy of 96.81%, the best ternary classification accuracy of 76.39%, and the best six-classification accuracy of 42.17%. The findings also suggested that arousal had a far greater impact than valence on emotion recognition. |
| [45] | Fuzzy entropy | Emotion | 32 EEG channels | 32 | EEG and peripheral physiological signals were recorded after participants watched 40 1-min music video clips. | The results of the experiment demonstrated that combining multiple features extracted from emotional EEG signals through multi-feature fusion produced better outcomes than using a single-feature extraction method. Using a long short-term memory neural network, the proposed method achieved high classification accuracy in emotion recognition. The method’s performance was better than other traditional artificial design feature-based methods that utilized SVM or DBM. |
| [46] | SampEn, transfer entropy, mutual information | Emotion | 64 EEG channels | 24: male = 10, female = 14 | 20 neutral, 20 happy, and 20 sad movie clips were displayed for subjects in three sessions according to the emotions portrayed. During each session, the subjects performed 15 grip strength trials and five no-grip strength trials while watching the video clips. | Researchers investigated the relationship between emotions and movement in the brain using various analysis methods, such as SampEn, transfer entropy, and mutual information. The study found that different emotions cause changes in the SampEn of the frontal lobe, and happiness and sadness can promote the transmission of information between the cerebral cortex and muscle nerves. Additionally, mutual information analysis showed that different emotions can promote the exchange of information in specific brain regions. |
| [47] | Fractal Firat pattern (FFP), tunable Q-factor wavelet transform (TQWT) | Emotion | 14 EEG channels | 28 | The experiment involved four different types of games: funny, boring, horror, and calm. Each game was recorded for 5 min, resulting in a total recording time of 20 min for all four games combined. | The study proposed an automated EEG-based emotion recognition method using fractal Firat pattern (FFP) and tunable Q-factor wavelet transform (TQWT) signal decomposition technique. A multilevel feature generator was developed using FFP and TQWT, and an improved iterative selector was utilized for feature selection. The proposed framework achieved 99.82% accuracy with the SVM classifier, indicating that FFP and TQWT-based feature generation can be successful in emotion recognition using EEG signals. |
| [48] | Poincaré map function, recurrence plots (RPs) | Emotion | 32 EEG channels | 32 | Participants watched 40 one-minute videos and rated each video on arousal, valence, liking, dominance, and familiarity. | The study compared the effectiveness of recurrence plot (RP) features and Poincaré map function in analyzing EEG data and identifying emotional states. The results showed that RP features were more statistically significant in distinguishing emotional ratings, particularly in identifying levels of dominance, in more EEG electrodes. The study also found that nonlinear analysis using an RP-based approach was more effective in identifying emotional states and showed significant correlations over a wider area of the cortex compared to the analysis of EEG power bands. |
| [49] | CD, KolmEn, ShEn | Emotion | 32 EEG channels, 62 EEG channels | Group 1: 32, Group 2: 15 | The experiment utilized two publicly available datasets, DEAP and SEED, to analyze EEG data from human subjects. DEAP consisted of data from 32 subjects who watched one-minute-long music video clips and rated their emotional experiences on a two-dimensional scale of arousal and valence. SEED included data from 15 subjects who watched 15 film clips to induce emotions with three classes of emotions (positive, neutral, negative) evaluated, and each class had five corresponding film clips. | The individual beta rhythm achieved the best performance, and the higher-frequency beta rhythm and gamma rhythm bands performed better than the lower-frequency theta rhythm and alpha rhythm bands. Using linear features outperformed the use of non-linear features in each frequency band. |
| [50] | RQA | Emotion | 40 EEG channels | 5 | This experiment involved participants watching eight movie clips while their emotions were recorded. Each clip was preceded by guiding words displayed on the screen for 5 s, after which the clip was played, and participants were asked to concentrate on it. After each clip, participants were asked to report their true emotional state and rate the intensity of their emotions on a 10-point scale. | The study aimed to design an emotion-classification system for affective computing that could improve communication between humans and machines. The researchers induced three emotions in participants, measured corresponding EEG signals, and proposed an RQA-based channel-frequency convolutional neural network (CFCNN) recognition system for distinguishing emotion states. They found that the system achieved high accuracy and stability, outperforming traditional methods, and they observed a strong correlation between emotional processing and gamma frequency band activities, suggesting potential for research in affective human-machine interaction systems and EEG signal identification in other areas. |
| [51] | Wavelet transform, WEn, ApEn, SampEn | Emotion | 32 EEG channels | 32 | Subjects watched 40 clips from music videos as emotional stimuli. | The authors compared two cases using wavelet transform and entropy measures for feature extraction to improve the accuracy of emotion classification. They found that considering baseline data features improved the accuracy of classification, with nonlinear dynamic features leading to higher accuracy than wavelet-derived features. The most salient features were found to be a combination of ApEn and SampEn, with EEG gamma-band features being more important than other frequency bands. |
| [52] | Wavelet transform, multifractal detrended fluctuation analysis (MFDFA), and HE | Emotion | 19 EEG channels | 10: male = 6, female = 4 | Subjects listened to the sound of a tempura drone generated by software. | This study investigated the effect of a simple acoustical drone stimulus on the human brain using EEG data. Nonlinear dynamical analysis techniques, such as empirical mode decomposition and multifractal detrended fluctuation analysis (MFDFA), were used to analyze the EEG data. The findings suggest that the input of drones enhances the complexity of alpha and theta waves, and this study has potential applications in cognitive music therapy. |
| [53] | HE | MI, cognition | 14 EEG channels | Group 1 (pilots): male = 10 female = 2; group 2 (dancers): male = 3 female = 7 | Dancers mentally visualized and imagined a series of steps and choreographed moves. Pilots were asked to solve a short version of Ravens’ test. | When a skill is learned through repeated practice and specialization or during memory consolidation, professionals within that specialized field may share a structure of ordered trends or “fingerprints”. |
| [54] | CD | MI | 29 EEG channels | 18: male = 10, female = 8 | Participants visualized the grasping of a specific object. Six objects were selected for this experiment: a can, a box, a cup, a ball, a lid, and an egg. | The grasp pattern of a cylindrical or spherical object was identified, and the combination of CD and a SVM achieved 80.6% accuracy in classifying the grasp pattern. |
| [55] | HE | MI | 14 EEG channels | 20: male = 20, female = 0 | Nine professional dancers imagined performing a choreographed dance, and EEG data were recorded for 2 min | The long-term timescales in the resting state demonstrated anti-persistence and similar HEs. This finding suggests that the brain modulated its active tasks differently between the two timescales. |
| [56] | Wavelet transform | MI | 3 EEG channels | 1: male = 0, female = 1 | Subjects were seated on a chair with armrests while imagining left- and right-hand motions. | The maximum accuracy achieved was 90.7%, and the maximum mutual information was 0.76 bits, with the distance series features outperforming other state-of-the-art algorithms. |
| [57] | Spectrum symmetry of chaotic system (SSCS), based on chaos | MI | 8 EEG channels | 32: male = 16, female = 16 | Visual stimulation was performed. | Conventional methods for analyzing EEG data tend to filter out noise, which can result in the loss of valuable information. However, a new approach based on chaos theory, called the spectrum symmetry of a chaotic system, was used to analyze SSVEP data frequencies. This method is particularly advantageous for detecting target frequencies in BCI-illiterate participants since it is sensitive to weak signals and immune to noise |
| [58] | ShEn | MI | 64 EEG channels | 87 | The experiment consists of a one-minute baseline run with eyes open and another one-minute baseline run with eyes closed. This step is followed by three 2-min runs of four different tasks. Two pairs of tasks, one run performing the physical task and the next run imagining performing the same task. | The authors were able to distinguish between motor movements and imagined movements. The authors note that the entropy measures and complexity measures are concepts that complement each other. The entropy-complexity plane provides a global metric that illustrates a variety of characteristics typically associated with the dynamical behavior of motor and envisioned movements. |
| [59] | REn | MI | Group 1: 3; group 2: 64; group 3: 118; group 4: 118; group 5: 22 | Group 1: 1, group 2: 1, group 3: 5, group 4: 1, group 5: 9 | Participants were given visual cues and stimuli for each dataset and asked to perform a specific MI task | Among the chaotic feature extraction methods used in this study, REn had the highest classification accuracy. Furthermore, the accuracy and convenience of REn make it a suitable tool for feature extraction in MI systems. |
| [60] | RQA | MI | 13 EEG channels | 6 | Subjects had two sessions in which EEG data were recorded for MI tasks and periods of rest. Each session had three runs, with each run consisting of 40 trials of either MI or rest, based on visual cues on a screen. The MI task required participants to imagine moving their left or right hand, and each trial lasted for 10 s, followed by a rest period. | The study investigated the use of graph-based RQA and complex network theory to analyze the nonlinear recurrence patterns in the mu and beta spectral bands of EEG signals during MI tasks. The graph-based features outperformed traditional linear spectral features, achieving an average accuracy of approximately 80%. The study concluded that the proposed nonlinear features could potentially improve MI-based brain-computer interface performance by exploiting the nonlinear neural dynamics embedded in MI neural responses beyond the classical linear spectral characteristics. |
| [61] | TQWT | MI | 118 EEG channels | 5 | Subjects performed MI tasks with their right foot (RF) and right hand (RH). | The study proposes a new method for accurately classifying different mental tasks using EEG signals and a brain-computer interface. The method involves using the TQWT technique with automatically selected tuning parameters and then selecting important features from the resulting signals using a least squares SVM classifier. The proposed method achieved high accuracy of 99.78%, which is superior to other state-of-the-art techniques using the same database. |
| [62] | Multifractal analysis, wavelet transform | Motor movement, MI | 19 EEG channels | 12: male = 9, female = 8 | Participants were instructed to perform two types of tasks, lift their right hand slowly in the shoulder joint, and imagine such a movement during a given time interval. The experiment lasted approximately 30 min and was split into 10 sessions, with each session containing 20 identical events. There were five sessions of real movements followed by five sessions of imaginary movements. | Researchers have identified specific frequency bands in EEG signals that can be used to extract features of brain activity associated with motor execution and imagination in untrained individuals. During motor execution, there was a decrease in mu/alpha-band and an increase in delta-band activity in different areas of the brain. During motor imagination, there was an increase in mu/alpha-band activity and a significant decrease in delta-band activity in certain areas of the brain. The researchers developed a real-time algorithm to extract motor execution or motor imaginary events from EEG signals, which demonstrated high accuracy in detecting these events in experimental sessions with subjects. |
| [63] | KolmEn | Motor movement | 9 EEG channels | 12 | Participants performed thumb movements. | Supplementary motor and motor cortex areas exhibit activation approximately 2 s after the initial movement is executed. The EEG patterns in the supplementary motor, premotor, and motor areas of the brain are synchronized in a nonlinear, chaotic manner and are associated with the stages of preparation, intention, decision-making, and the initiation of voluntary movements. |
| [64] | CD, KolmEn, and LE | Motor movement | 9 EEG channels | 19 | A screen with targets was presented to the participants. To reach the target, participants maneuvered a control device and pressed a switch after reaching the target. | According to the results of this study, EEG signals analyzed with chaos metrics show three distinct periods of high complexity that can be interpreted as phases of movement organization. |
| [65] | CD | Motor movement | 10 EEG channels | 11: male = 3, female = 8 | Rifle shooting experts and amateur shooters fired 40 shots in the standard standing position while EEGs were recorded. | Experts showed less reliance on complex brain activities during shooting, owing to a refinement of cognitive processes, whereas greater complexity due to higher CD was associated with better performance in amateurs. |
| [66] | Coherence analysis | Motor movement | 64 EEG channels | 11 | Participants used a power handle to track a target force by applying varying forces. The participants were provided with ongoing force output feedback on a screen. The participants were required to continuously adjust their exerted force to meet the target force level. | Motor performance learning and advancement are coupled with different coherence patterns in different stages of motor performance. |
| [67] | RQA | Motor movement, attention, and memory | 19 EEG channels | 32: male = 32, female = 0 | The tasks that followed involved ideomotor responses, hallucinations, motor challenges, memory recall, and post-hypnotic suggestion. Therefore, the experiment was designed to assess the participants’ hypnotic susceptibility and how it affected different cognitive processes. | This study found that certain brain regions, particularly those on the left side of the brain, were more efficient at distinguishing between hypnotizability levels. Finally, the researchers found that brain wave patterns in people performing the same type of task were similar across different brain regions, suggesting that there may be common patterns of brain activity associated with specific types of tasks. |
| [68] | Variance fractal dimension (VFD) | Motor movement | 64 EEG channels | 1: male = 1, female = 0 | Three tasks: Right foot up Lip pursing Combination of the first two tasks | The results of the experiments and performance tests demonstrate that the suggested modeling approach is efficient in the context of movement-related potentials, particularly for binary brain-computer interfaces intended to aid severely disabled individuals, such as those with amyotrophic lateral sclerosis, in communicating or controlling devices. |
| [69] | FD, phase-space, and LE | Resting state | 62 EEG channels | 12 | Resting state EEG was examined. | The traditional view of microstate analysis was investigated. The notions that microstate regions compete and the simple view in which one microstate is active while the others are at rest are incorrect. The complex dynamics in the phase space, the high FD, and the positive LE support this finding. |
| [70] | ApEn, LE, CD | Resting state | 1 EEG channel | 10: male = 6, female = 4 | Data were collected when participants had their eyes closed and their heads still. | The accuracy of classification reached 97.29% using linear features, whereas it is only 44.14% with nonlinear dynamic features. Based on the experiment’s results, it appears that the linear features of EEG, such as center frequency, max power, power ratio, average peak-to-peak value, and coefficients of the autoregressive model, may perform better in individual identification than the nonlinear dynamic parameters of EEG. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kargarnovin, S.; Hernandez, C.; Farahani, F.V.; Karwowski, W. Evidence of Chaos in Electroencephalogram Signatures of Human Performance: A Systematic Review. Brain Sci. 2023, 13, 813. https://doi.org/10.3390/brainsci13050813
Kargarnovin S, Hernandez C, Farahani FV, Karwowski W. Evidence of Chaos in Electroencephalogram Signatures of Human Performance: A Systematic Review. Brain Sciences. 2023; 13(5):813. https://doi.org/10.3390/brainsci13050813
Chicago/Turabian StyleKargarnovin, Shaida, Christopher Hernandez, Farzad V. Farahani, and Waldemar Karwowski. 2023. "Evidence of Chaos in Electroencephalogram Signatures of Human Performance: A Systematic Review" Brain Sciences 13, no. 5: 813. https://doi.org/10.3390/brainsci13050813
APA StyleKargarnovin, S., Hernandez, C., Farahani, F. V., & Karwowski, W. (2023). Evidence of Chaos in Electroencephalogram Signatures of Human Performance: A Systematic Review. Brain Sciences, 13(5), 813. https://doi.org/10.3390/brainsci13050813






