Understanding Altered Dynamics in Cocaine Use Disorder Through State Transitions Mediated by Artificial Perturbations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants and MRI Data Acquisition
2.2. Diffusion and Functional MRI Pre-Processing
2.3. Leading Eigenvector Dynamics Analysis
2.4. Whole-Brain Computational Model
2.5. Empirical Fitting of the Whole-Brain Model
2.6. Optimization of the Whole-Brain Model
2.7. Artificial Perturbation Protocol
2.8. Statistical Analysis
3. Results
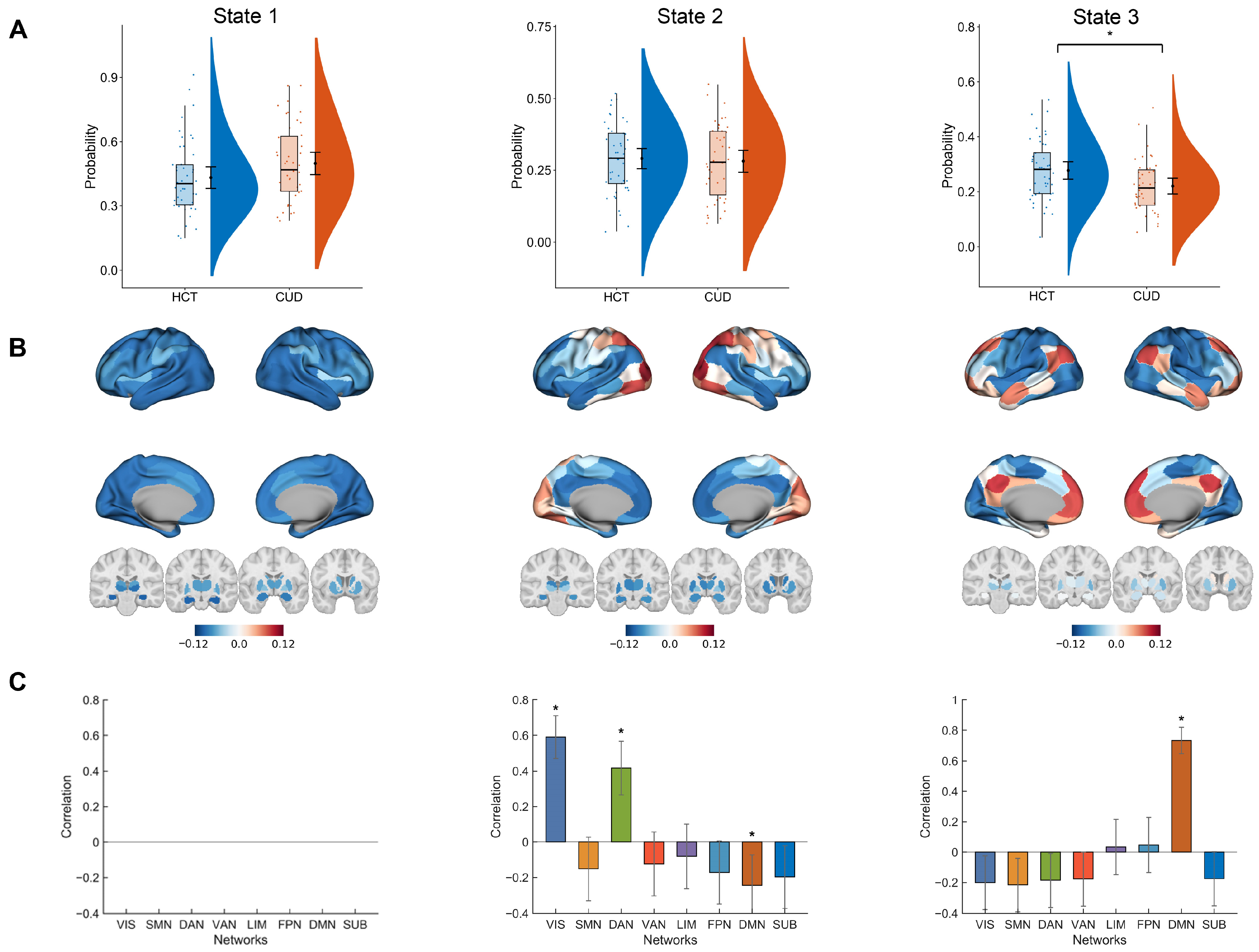
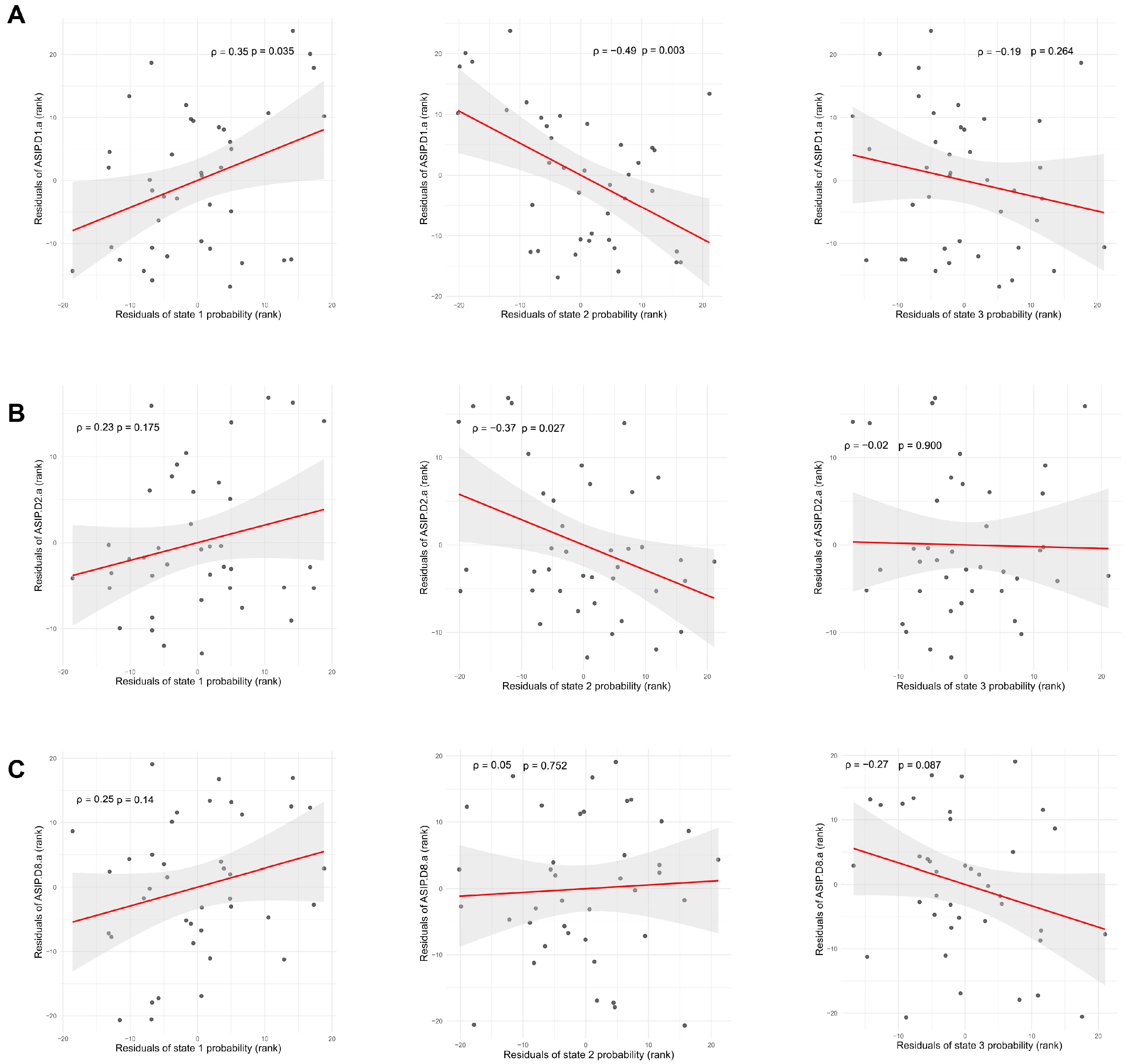
3.1. Empirical Analysis
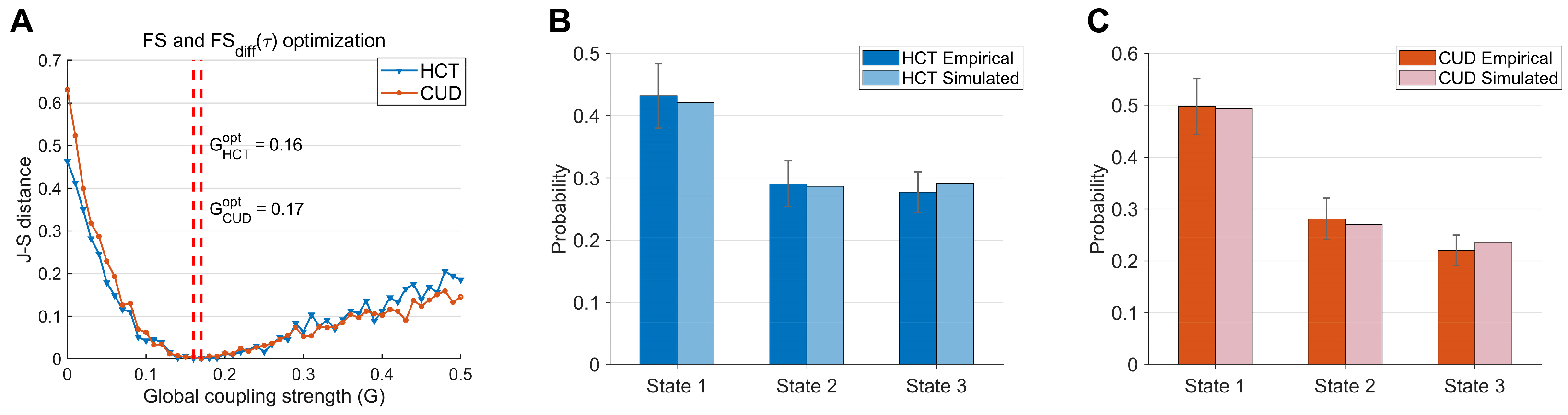
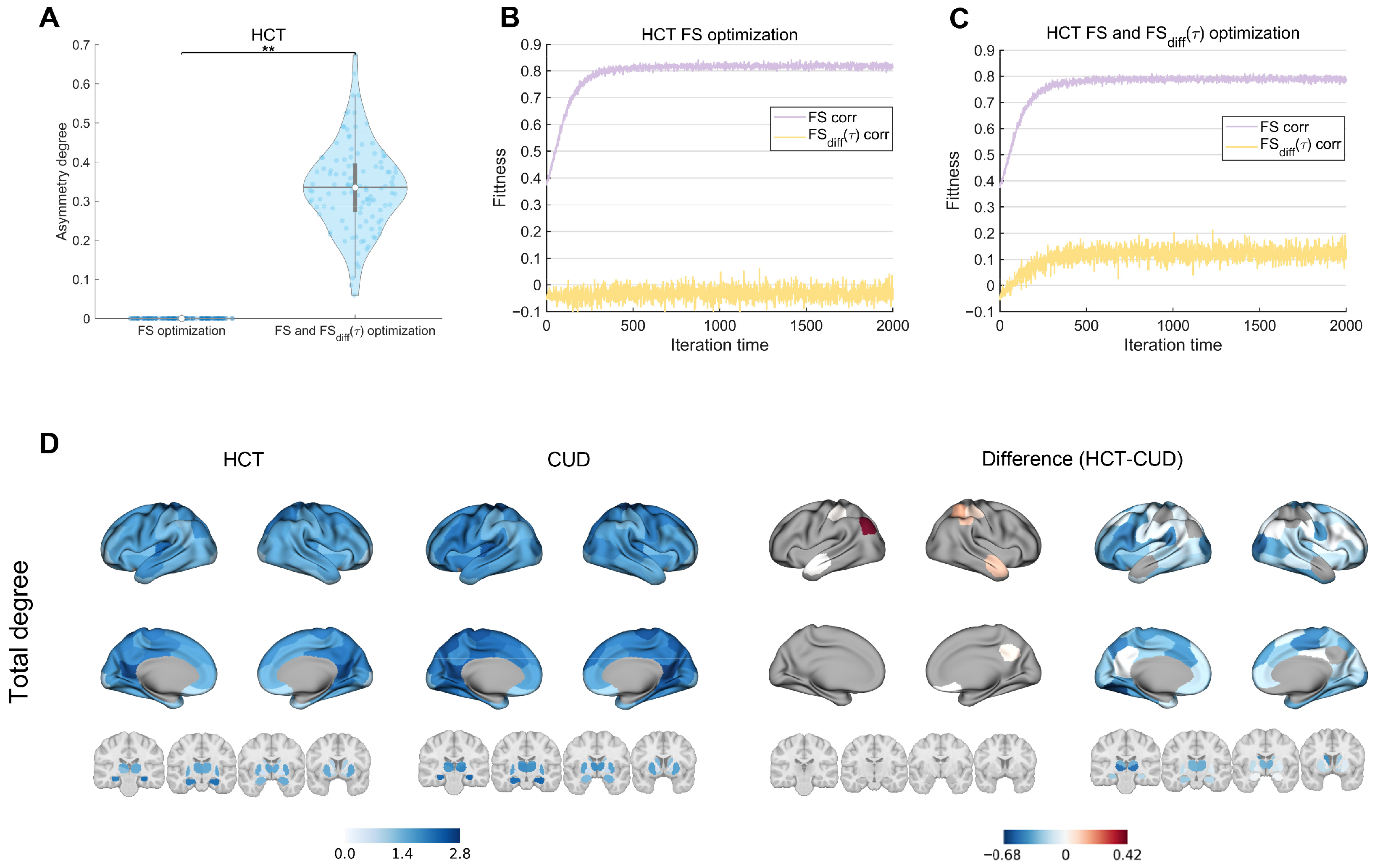
3.2. Model Fitting and Optimization
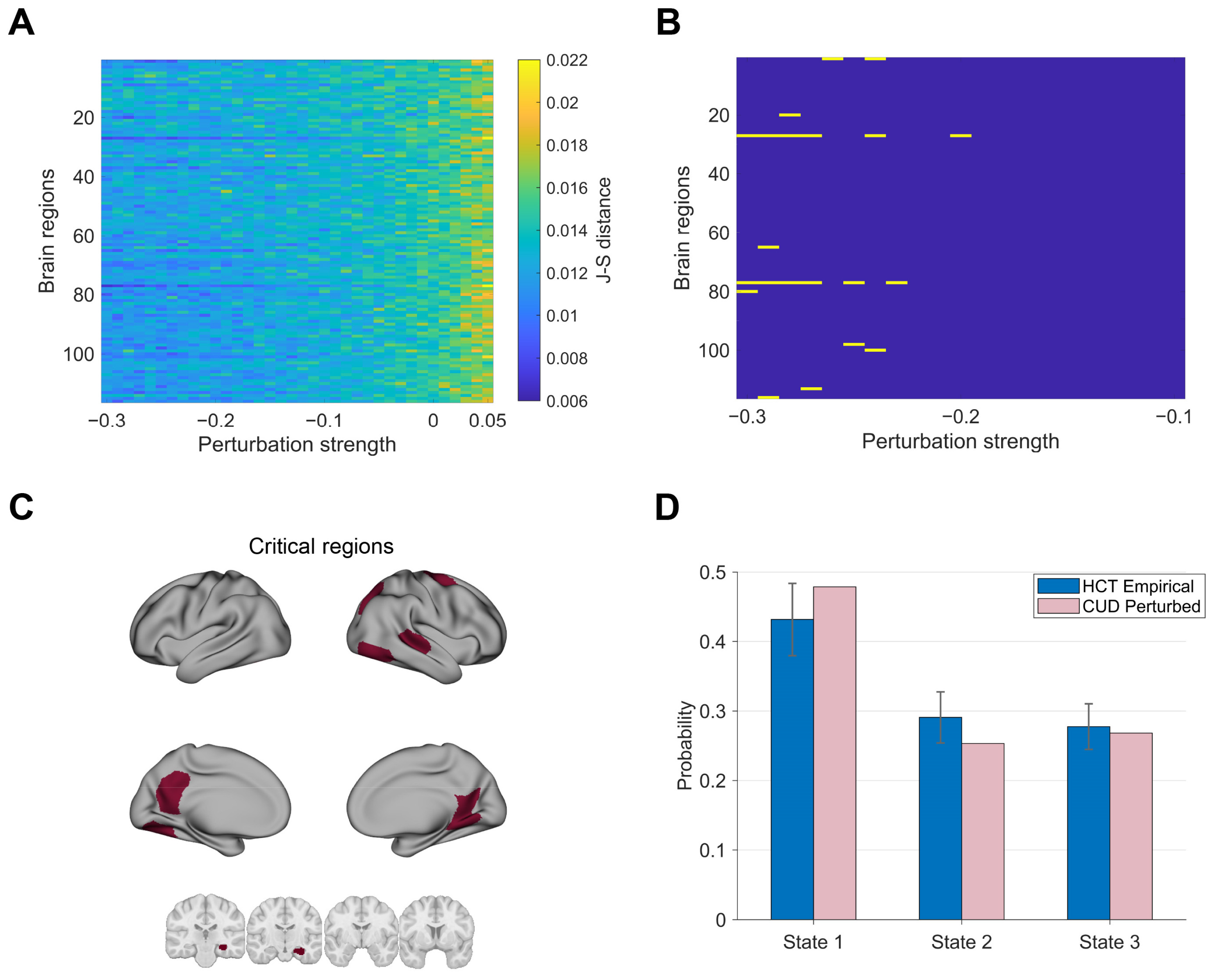
3.3. Mediating Transitions from HCT to CUD Through Perturbations
3.4. Promoting Transitions from CUD to HCT Using Perturbations
4. Discussion
5. Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morelos-Santana, E.; Islas-Preciado, D.; Alcalá-Lozano, R.; González-Olvera, J.; Estrada-Camarena, E. Peripheral neurotrophin levels during controlled crack/cocaine abstinence: A systematic review and meta-analysis. Sci. Rep. 2024, 14, 1410. [Google Scholar] [CrossRef] [PubMed]
- World Drug Report 2023. Available online: https://www.unodc.org/unodc/en/data-and-analysis/world-drug-report-2023.html (accessed on 15 December 2024).
- Dalley, J.W.; Everitt, B.J.; Robbins, T.W. Impulsivity, Compulsivity, and Top-Down Cognitive Control. Neuron 2011, 69, 680–694. [Google Scholar] [CrossRef]
- Koob, G.F.; Volkow, N.D. Neurobiology of addiction: A neurocircuitry analysis. Lancet Psychiatry 2016, 3, 760–773. [Google Scholar] [CrossRef]
- Fu, L.; Bi, G.; Zou, Z.; Wang, Y.; Ye, E.; Ma, L.; Ming-Fan; Yang, Z. Impaired response inhibition function in abstinent heroin dependents: An fMRI study. Neurosci. Lett. 2008, 438, 322–326. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.Z.; Volkow, N.D. Dysfunction of the prefrontal cortex in addiction: Neuroimaging findings and clinical implications. Nat. Rev. Neurosci. 2011, 12, 652–669. [Google Scholar] [CrossRef]
- Kübler, A.; Murphy, K.; Garavan, H. Cocaine dependence and attention switching within and between verbal and visuospatial working memory. Eur. J. Neurosci. 2005, 21, 1984–1992. [Google Scholar] [CrossRef]
- Koob, G.F. A Role for Brain Stress Systems in Addiction. Neuron 2008, 59, 11–34. [Google Scholar] [CrossRef] [PubMed]
- Ricard, J.A.; Labache, L.; Segal, A.; Dhamala, E.; Cocuzza, C.V.; Jones, G.; Yip, S.W.; Chopra, S.; Holmes, A.J. A shared spatial topography links the functional connectome correlates of cocaine use disorder and dopamine D2/3 receptor densities. Commun. Biol. 2024, 7, 1178. [Google Scholar] [CrossRef]
- Hu, Y.; Salmeron, B.J.; Gu, H.; Stein, E.A.; Yang, Y. Impaired Functional Connectivity within and between Frontostriatal Circuits and Its Association with Compulsive Drug Use and Trait Impulsivity in Cocaine Addiction. JAMA Psychiatry 2015, 72, 584–592. [Google Scholar] [CrossRef]
- Zhang, R.; Volkow, N.D. Brain default-mode network dysfunction in addiction. NeuroImage 2019, 200, 313–331. [Google Scholar] [CrossRef]
- Hutchison, R.M.; Womelsdorf, T.; Allen, E.A.; Bandettini, P.A.; Calhoun, V.D.; Corbetta, M.; Della Penna, S.; Duyn, J.H.; Glover, G.H.; Gonzalez-Castillo, J.; et al. Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 2013, 80, 360–378. [Google Scholar] [CrossRef] [PubMed]
- Preti, M.G.; Bolton, T.A.; Van De Ville, D. The dynamic functional connectome: State-of-the-art and perspectives. NeuroImage 2017, 160, 41–54. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Vidaurre, D.; Marques, P.; Magalhães, R.; Silva Moreira, P.; Miguel Soares, J.; Deco, G.; Sousa, N.; Kringelbach, M.L. Cognitive performance in healthy older adults relates to spontaneous switching between states of functional connectivity during rest. Sci. Rep. 2017, 7, 5135. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.A.S. Multistability and metastability: Understanding dynamic coordination in the brain. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 906–918. [Google Scholar] [CrossRef]
- Deco, G.; Kringelbach, M.L.; Jirsa, V.K.; Ritter, P. The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Sci. Rep. 2017, 7, 3095. [Google Scholar] [CrossRef]
- Tognoli, E.; Kelso, J.A.S. The Metastable Brain. Neuron 2014, 81, 35–48. [Google Scholar] [CrossRef]
- Kurtin, D.L.; Scott, G.; Hebron, H.; Skeldon, A.C.; Violante, I.R. Task-based differences in brain state dynamics and their relation to cognitive ability. NeuroImage 2023, 271, 119945. [Google Scholar] [CrossRef]
- Escrichs, A.; Biarnes, C.; Garre-Olmo, J.; Fernández-Real, J.M.; Ramos, R.; Pamplona, R.; Brugada, R.; Serena, J.; Ramió-Torrentà, L.; Coll-De-Tuero, G.; et al. Whole-Brain Dynamics in Aging: Disruptions in Functional Connectivity and the Role of the Rich Club. Cereb. Cortex 2021, 31, 2466–2481. [Google Scholar] [CrossRef]
- Deco, G.; Cruzat, J.; Cabral, J.; Tagliazucchi, E.; Laufs, H.; Logothetis, N.K.; Kringelbach, M.L. Awakening: Predicting external stimulation to force transitions between different brain states. Proc. Natl. Acad. Sci. USA 2019, 116, 18088–18097. [Google Scholar] [CrossRef]
- Lord, L.-D.; Expert, P.; Atasoy, S.; Roseman, L.; Rapuano, K.; Lambiotte, R.; Nutt, D.J.; Deco, G.; Carhart-Harris, R.L.; Kringelbach, M.L.; et al. Dynamical exploration of the repertoire of brain networks at rest is modulated by psilocybin. NeuroImage 2019, 199, 127–142. [Google Scholar] [CrossRef]
- Figueroa, C.A.; Cabral, J.; Mocking, R.J.T.; Rapuano, K.M.; van Hartevelt, T.J.; Deco, G.; Expert, P.; Schene, A.H.; Kringelbach, M.L.; Ruhé, H.G. Altered ability to access a clinically relevant control network in patients remitted from major depressive disorder. Hum. Brain Mapp. 2019, 40, 2771–2786. [Google Scholar] [CrossRef] [PubMed]
- Zhai, T.; Gu, H.; Salmeron, B.J.; Stein, E.A.; Yang, Y. Disrupted Dynamic Interactions Between Large-Scale Brain Networks in Cocaine Users Are Associated with Dependence Severity. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2023, 8, 672–679. [Google Scholar] [CrossRef] [PubMed]
- Klugah-Brown, B.; Yao, X.; Yang, H.; Wang, P.; Biswal, B.B. Altered Dynamics and Characterization of Functional Networks in Cocaine Use Disorder: A Coactivation Pattern Analysis of Resting-State fMRI data. medRxiv 2024. medRxiv: 2024.06.18.24309063. [Google Scholar]
- Cong, Z.; Yang, L.; Zhao, Z.; Zheng, G.; Bao, C.; Zhang, P.; Wang, J.; Zheng, W.; Yao, Z.; Hu, B. Disrupted dynamic brain functional connectivity in male cocaine use disorder: Hyperconnectivity, strongly-connected state tendency, and links to impulsivity and borderline traits. J. Psychiatr. Res. 2024, 176, 218–231. [Google Scholar] [CrossRef]
- Polanía, R.; Nitsche, M.A.; Ruff, C.C. Studying and modifying brain function with non-invasive brain stimulation. Nat. Neurosci. 2018, 21, 174–187. [Google Scholar] [CrossRef] [PubMed]
- Krack, P.; Hariz, M.I.; Baunez, C.; Guridi, J.; Obeso, J.A. Deep brain stimulation: From neurology to psychiatry? Trends Neurosci. 2010, 33, 474–484. [Google Scholar] [CrossRef]
- Okun, M.S. Deep-Brain Stimulation for Parkinson’s Disease. N. Engl. J. Med. 2012, 367, 1529–1538. [Google Scholar] [CrossRef]
- Laxton, A.W.; Lozano, A.M. Deep Brain Stimulation for the Treatment of Alzheimer Disease and Dementias. World Neurosurg. 2013, 80, S28.e1–S28.e8. [Google Scholar] [CrossRef]
- DeGiorgio, C.M.; Krahl, S.E. Neurostimulation for Drug-Resistant Epilepsy. Contin. Lifelong Learn. Neurol. 2013, 19, 743. [Google Scholar] [CrossRef]
- Oberman, L.M.; Rotenberg, A.; Pascual-Leone, A. Use of Transcranial Magnetic Stimulation in Autism Spectrum Disorders. J. Autism Dev. Disord. 2015, 45, 524–536. [Google Scholar] [CrossRef]
- Osoegawa, C.; Gomes, J.S.; Grigolon, R.B.; Brietzke, E.; Gadelha, A.; Lacerda, A.L.T.; Dias, Á.M.; Cordeiro, Q.; Laranjeira, R.; de Jesus, D.; et al. Non-invasive brain stimulation for negative symptoms in schizophrenia: An updated systematic review and meta-analysis. Schizophr. Res. 2018, 197, 34–44. [Google Scholar] [CrossRef]
- Shen, Y.; Ward, H.B. Transcranial magnetic stimulation and neuroimaging for cocaine use disorder: Review and future directions. Am. J. Drug Alcohol. Abus. 2021, 47, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Beynel, L.; Powers, J.P.; Appelbaum, L.G. Effects of repetitive transcranial magnetic stimulation on resting-state connectivity: A systematic review. NeuroImage 2020, 211, 116596. [Google Scholar] [CrossRef]
- Papadopoulos, L.; Lynn, C.W.; Battaglia, D.; Bassett, D.S. Relations between large-scale brain connectivity and effects of regional stimulation depend on collective dynamical state. PLoS Comput. Biol. 2020, 16, e1008144. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Tang, S.; Zheng, H.; Wang, X.; Liu, L.; Yang, Y.; Zhen, Y.; Zheng, Z. Noise improves the association between effects of local stimulation and structural degree of brain networks. PLoS Comput. Biol. 2023, 19, e1010866. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Fonzo, G.A.; Xie, H.; Oathes, D.J.; Keller, C.J.; Carlisle, N.B.; Etkin, A.; Garza-Villarreal, E.A.; Zhang, Y. Discriminative functional connectivity signature of cocaine use disorder links to rTMS treatment response. Nat. Ment. Health 2024, 2, 388–400. [Google Scholar] [CrossRef]
- Hsu, L.-M.; Cerri, D.H.; Lee, S.-H.; Shnitko, T.A.; Carelli, R.M.; Shih, Y.-Y.I. Intrinsic Functional Connectivity between the Anterior Insular and Retrosplenial Cortex as a Moderator and Consequence of Cocaine Self-Administration in Rats. J. Neurosci. 2024, 44, e1452232023. [Google Scholar] [CrossRef]
- Muldoon, S.F.; Pasqualetti, F.; Gu, S.; Cieslak, M.; Grafton, S.T.; Vettel, J.M.; Bassett, D.S. Stimulation-Based Control of Dynamic Brain Networks. PLoS Comput. Biol. 2016, 12, e1005076. [Google Scholar] [CrossRef]
- Gollo, L.L.; Roberts, J.A.; Cocchi, L. Mapping how local perturbations influence systems-level brain dynamics. NeuroImage 2017, 160, 97–112. [Google Scholar] [CrossRef]
- Kato, A.; Shimomura, K.; Ognibene, D.; Parvaz, M.A.; Berner, L.A.; Morita, K.; Fiore, V.G. Computational models of behavioral addictions: State of the art and future directions. Addict. Behav. 2023, 140, 107595. [Google Scholar] [CrossRef]
- Liu, S.; Dolan, R.J.; Heinz, A. Translation of Computational Psychiatry in the Context of Addiction. JAMA Psychiatry 2020, 77, 1099–1100. [Google Scholar] [CrossRef]
- Dayan, P. Dopamine, Reinforcement Learning, and Addiction. Pharmacopsychiatry 2009, 42, S56–S65. [Google Scholar] [CrossRef]
- Schwartenbeck, P.; FitzGerald, T.H.B.; Mathys, C.; Dolan, R.; Wurst, F.; Kronbichler, M.; Friston, K. Optimal inference with suboptimal models: Addiction and active Bayesian inference. Med. Hypotheses 2015, 84, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Nelson, A.B.; Kreitzer, A.C. Reassessing Models of Basal Ganglia Function and Dysfunction. Annu. Rev. Neurosci. 2014, 37, 117–135. [Google Scholar] [CrossRef] [PubMed]
- Lapish, C.C.; Balaguer-Ballester, E.; Seamans, J.K.; Phillips, A.G.; Durstewitz, D. Amphetamine Exerts Dose-Dependent Changes in Prefrontal Cortex Attractor Dynamics during Working Memory. J. Neurosci. 2015, 35, 10172–10187. [Google Scholar] [CrossRef]
- Escrichs, A.; Sanz Perl, Y.; Martínez-Molina, N.; Biarnes, C.; Garre-Olmo, J.; Fernández-Real, J.M.; Ramos, R.; Martí, R.; Pamplona, R.; Brugada, R.; et al. The effect of external stimulation on functional networks in the aging healthy human brain. Cereb. Cortex 2023, 33, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wen, H.; Qiu, S.; Xie, P.; Qiu, J.; He, H. Driving brain state transitions in major depressive disorder through external stimulation. Hum. Brain Mapp. 2022, 43, 5326–5339. [Google Scholar] [CrossRef]
- Mana, L.; Vila-Vidal, M.; Köckeritz, C.; Aquino, K.; Fornito, A.; Kringelbach, M.L.; Deco, G. Using in silico perturbational approach to identify critical areas in schizophrenia. Cereb. Cortex 2023, 33, 7642–7658. [Google Scholar] [CrossRef]
- Dagnino, P.C.; Escrichs, A.; López-González, A.; Gosseries, O.; Annen, J.; Perl, Y.S.; Kringelbach, M.L.; Laureys, S.; Deco, G. Re-awakening the brain: Forcing transitions in disorders of consciousness by external in silico perturbation. PLoS Comput. Biol. 2024, 20, e1011350. [Google Scholar] [CrossRef]
- Angeles-Valdez, D.; Rasgado-Toledo, J.; Issa-Garcia, V.; Balducci, T.; Villicaña, V.; Valencia, A.; Gonzalez-Olvera, J.J.; Reyes-Zamorano, E.; Garza-Villarreal, E.A. The Mexican magnetic resonance imaging dataset of patients with cocaine use disorder: SUDMEX CONN. Sci. Data 2022, 9, 133. [Google Scholar] [CrossRef]
- Angeles-Valdez, D.; Rasgado-Toledo, J.; Villicaña, V.; Davalos-Guzman, A.; Almanza, C.; Fajardo-Valdez, A.; Alcala-Lozano, R.; Garza-Villarreal, E.A. The Mexican dataset of a repetitive transcranial magnetic stimulation clinical trial on cocaine use disorder patients: SUDMEX TMS. Sci. Data 2024, 11, 408. [Google Scholar] [CrossRef]
- Esteban, O.; Markiewicz, C.J.; Blair, R.W.; Moodie, C.A.; Isik, A.I.; Erramuzpe, A.; Kent, J.D.; Goncalves, M.; DuPre, E.; Snyder, M.; et al. fMRIPrep: A robust preprocessing pipeline for functional MRI. Nat. Methods 2019, 16, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Esteban, O.; Ciric, R.; Finc, K.; Blair, R.W.; Markiewicz, C.J.; Moodie, C.A.; Kent, J.D.; Goncalves, M.; DuPre, E.; Gomez, D.E.P.; et al. Analysis of task-based functional MRI data preprocessed with fMRIPrep. Nat. Protoc. 2020, 15, 2186–2202. [Google Scholar] [CrossRef] [PubMed]
- Mehta, K.; Salo, T.; Madison, T.J.; Adebimpe, A.; Bassett, D.S.; Bertolero, M.; Cieslak, M.; Covitz, S.; Houghton, A.; Keller, A.S.; et al. XCP-D: A robust pipeline for the post-processing of fMRI data. Imaging Neurosci. 2024, 2, 1–26. [Google Scholar] [CrossRef]
- Yan, X.; Kong, R.; Xue, A.; Yang, Q.; Orban, C.; An, L.; Holmes, A.J.; Qian, X.; Chen, J.; Zuo, X.-N.; et al. Homotopic local-global parcellation of the human cerebral cortex from resting-state functional connectivity. NeuroImage 2023, 273, 120010. [Google Scholar] [CrossRef]
- Tian, Y.; Margulies, D.S.; Breakspear, M.; Zalesky, A. Topographic organization of the human subcortex unveiled with functional connectivity gradients. Nat. Neurosci. 2020, 23, 1421–1432. [Google Scholar] [CrossRef]
- Yeh, F.-C.; Wedeen, V.J.; Tseng, W.-Y.I. Estimation of fiber orientation and spin density distribution by diffusion deconvolution. NeuroImage 2011, 55, 1054–1062. [Google Scholar] [CrossRef]
- Yeh, F.-C.; Verstynen, T.D.; Wang, Y.; Fernández-Miranda, J.C.; Tseng, W.-Y.I. Deterministic Diffusion Fiber Tracking Improved by Quantitative Anisotropy. PLoS ONE 2013, 8, e80713. [Google Scholar] [CrossRef]
- Yeh, F.-C.; Panesar, S.; Fernandes, D.; Meola, A.; Yoshino, M.; Fernandez-Miranda, J.C.; Vettel, J.M.; Verstynen, T. Population-averaged atlas of the macroscale human structural connectome and its network topology. NeuroImage 2018, 178, 57–68. [Google Scholar] [CrossRef]
- Singleton, S.P.; Luppi, A.I.; Carhart-Harris, R.L.; Cruzat, J.; Roseman, L.; Nutt, D.J.; Deco, G.; Kringelbach, M.L.; Stamatakis, E.A.; Kuceyeski, A. Receptor-informed network control theory links LSD and psilocybin to a flattening of the brain’s control energy landscape. Nat. Commun. 2022, 13, 5812. [Google Scholar] [CrossRef]
- Thomas Yeo, B.T.; Krienen, F.M.; Sepulcre, J.; Sabuncu, M.R.; Lashkari, D.; Hollinshead, M.; Roffman, J.L.; Smoller, J.W.; Zöllei, L.; Polimeni, J.R.; et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 1125–1165. [Google Scholar] [CrossRef]
- Perl, Y.S.; Escrichs, A.; Tagliazucchi, E.; Kringelbach, M.L.; Deco, G. Strength-dependent perturbation of whole-brain model working in different regimes reveals the role of fluctuations in brain dynamics. PLoS Comput. Biol. 2022, 18, e1010662. [Google Scholar] [CrossRef]
- Spiegler, A.; Hansen, E.C.A.; Bernard, C.; McIntosh, A.R.; Jirsa, V.K. Selective Activation of Resting-State Networks following Focal Stimulation in a Connectome-Based Network Model of the Human Brain. eNeuro 2016, 3, 5. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Castaldo, F.; Vohryzek, J.; Litvak, V.; Bick, C.; Lambiotte, R.; Friston, K.; Kringelbach, M.L.; Deco, G. Metastable oscillatory modes emerge from synchronization in the brain spacetime connectome. Commun. Phys. 2022, 5, 184. [Google Scholar] [CrossRef] [PubMed]
- Maruyama, G. Continuous Markov processes and stochastic equations. Rend. Circ. Mat. Palermo 1955, 4, 48–90. [Google Scholar] [CrossRef]
- Kringelbach, M.L.; Perl, Y.S.; Tagliazucchi, E.; Deco, G. Toward naturalistic neuroscience: Mechanisms underlying the flattening of brain hierarchy in movie-watching compared to rest and task. Sci. Adv. 2023, 9, eade6049. [Google Scholar] [CrossRef]
- Deco, G.; Sanz Perl, Y.; Bocaccio, H.; Tagliazucchi, E.; Kringelbach, M.L. The INSIDEOUT framework provides precise signatures of the balance of intrinsic and extrinsic dynamics in brain states. Commun. Biol. 2022, 5, 572. [Google Scholar] [CrossRef]
- G-Guzmán, E.; Perl, Y.S.; Vohryzek, J.; Escrichs, A.; Manasova, D.; Türker, B.; Tagliazucchi, E.; Kringelbach, M.; Sitt, J.D.; Deco, G. The lack of temporal brain dynamics asymmetry as a signature of impaired consciousness states. Interface Focus. 2023, 13, 20220086. [Google Scholar] [CrossRef]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. NeuroImage 2017, 160, 84–96. [Google Scholar] [CrossRef]
- Bzdok, D.; Ioannidis, J.P.A. Exploration, Inference, and Prediction in Neuroscience and Biomedicine. Trends Neurosci. 2019, 42, 251–262. [Google Scholar] [CrossRef]
- Bzdok, D.; Yeo, B.T.T. Inference in the age of big data: Future perspectives on neuroscience. NeuroImage 2017, 155, 549–564. [Google Scholar] [CrossRef] [PubMed]
- de la Fuente, L.A.; Zamberlan, F.; Bocaccio, H.; Kringelbach, M.; Deco, G.; Perl, Y.S.; Pallavicini, C.; Tagliazucchi, E. Temporal irreversibility of neural dynamics as a signature of consciousness. Cereb. Cortex 2023, 33, 1856–1865. [Google Scholar] [CrossRef] [PubMed]
- Koob, G.F.; Volkow, N.D. Neurocircuitry of Addiction. Neuropsychopharmacology 2010, 35, 217–238. [Google Scholar] [CrossRef] [PubMed]
- Menon, V. 20 years of the default mode network: A review and synthesis. Neuron 2023, 111, 2469–2487. [Google Scholar] [CrossRef]
- Sakoglu, U.; Mete, M.; Esquivel, J.; Rubia, K.; Briggs, R.; Adinoff, B. Classification of cocaine-dependent participants with dynamic functional connectivity from functional magnetic resonance imaging data. J. Neurosci. Res. 2019, 97, 790–803. [Google Scholar] [CrossRef]
- Zhang, R.; Yan, W.; Manza, P.; Shokri-Kojori, E.; Demiral, S.B.; Schwandt, M.; Vines, L.; Sotelo, D.; Tomasi, D.; Giddens, N.T.; et al. Disrupted brain state dynamics in opioid and alcohol use disorder: Attenuation by nicotine use. Neuropsychopharmacology 2024, 49, 876–884. [Google Scholar] [CrossRef]
- Mahoney III, J.J. Cognitive dysfunction in individuals with cocaine use disorder: Potential moderating factors and pharmacological treatments. Exp. Clin. Psychopharmacol. 2019, 27, 203–214. [Google Scholar] [CrossRef]
- Paludetto, L.S.; Florence, L.L.A.; Torales, J.; Ventriglio, A.; Castaldelli-Maia, J.M. Mapping the Neural Substrates of Cocaine Craving: A Systematic Review. Brain Sci. 2024, 14, 329. [Google Scholar] [CrossRef]
- Wilcox, C.E.; Abbott, C.C.; Calhoun, V.D. Alterations in resting-state functional connectivity in substance use disorders and treatment implications. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2019, 91, 79–93. [Google Scholar] [CrossRef]
- Poireau, M.; Milpied, T.; Maillard, A.; Delmaire, C.; Volle, E.; Bellivier, F.; Icick, R.; Azuar, J.; Marie-Claire, C.; Bloch, V.; et al. Biomarkers of Relapse in Cocaine Use Disorder: A Narrative Review. Brain Sci. 2022, 12, 1013. [Google Scholar] [CrossRef]
- Balodis, I.M.; Kober, H.; Worhunsky, P.D.; Stevens, M.C.; Pearlson, G.D.; Carroll, K.M.; Potenza, M.N. Neurofunctional Reward Processing Changes in Cocaine Dependence During Recovery. Neuropsychopharmacology 2016, 41, 2112–2121. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, M.R.; Balodis, I.M.; DeVito, E.E.; Lacadie, C.M.; Yeston, J.; Scheinost, D.; Constable, R.T.; Carroll, K.M.; Potenza, M.N. A preliminary investigation of Stroop-related intrinsic connectivity in cocaine dependence: Associations with treatment outcomes. Am. J. Drug Alcohol. Abus. 2013, 39, 392–402. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.; Worhunsky, P.D.; Carroll, K.M.; Rounsaville, B.J.; Stevens, M.C.; Pearlson, G.D.; Potenza, M.N. An Initial Study of Neural Responses to Monetary Incentives as Related to Treatment Outcome in Cocaine Dependence. Biol. Psychiatry 2011, 70, 553–560. [Google Scholar] [CrossRef]
- Gourley, S.L.; Zimmermann, K.S.; Allen, A.G.; Taylor, J.R. The Medial Orbitofrontal Cortex Regulates Sensitivity to Outcome Value. J. Neurosci. 2016, 36, 4600–4613. [Google Scholar] [CrossRef] [PubMed]
- Wilcox, C.E.; Teshiba, T.M.; Merideth, F.; Ling, J.; Mayer, A.R. Enhanced cue reactivity and fronto-striatal functional connectivity in cocaine use disorders. Drug Alcohol. Depend. 2011, 115, 137–144. [Google Scholar] [CrossRef]
- López-González, A.; Panda, R.; Ponce-Alvarez, A.; Zamora-López, G.; Escrichs, A.; Martial, C.; Thibaut, A.; Gosseries, O.; Kringelbach, M.L.; Annen, J.; et al. Loss of consciousness reduces the stability of brain hubs and the heterogeneity of brain dynamics. Commun. Biol. 2021, 4, 1037. [Google Scholar] [CrossRef]
- Castilla-Ortega, E.; Serrano, A.; Blanco, E.; Araos, P.; Suárez, J.; Pavón, F.J.; Rodríguez de Fonseca, F.; Santín, L.J. A place for the hippocampus in the cocaine addiction circuit: Potential roles for adult hippocampal neurogenesis. Neurosci. Biobehav. Rev. 2016, 66, 15–32. [Google Scholar] [CrossRef]
- Castilla-Ortega, E.; Ladrón de Guevara-Miranda, D.; Serrano, A.; Pavón, F.J.; Suárez, J.; Rodríguez de Fonseca, F.; Santín, L.J. The impact of cocaine on adult hippocampal neurogenesis: Potential neurobiological mechanisms and contributions to maladaptive cognition in cocaine addiction disorder. Biochem. Pharmacol. 2017, 141, 100–117. [Google Scholar] [CrossRef]
- Adinoff, B.; Gu, H.; Merrick, C.; McHugh, M.; Jeon-Slaughter, H.; Lu, H.; Yang, Y.; Stein, E.A. Basal Hippocampal Activity and Its Functional Connectivity Predicts Cocaine Relapse. Biol. Psychiatry 2015, 78, 496–504. [Google Scholar] [CrossRef]
- Ma, L.; Steinberg, J.L.; Cunningham, K.A.; Bjork, J.M.; Lane, S.D.; Schmitz, J.M.; Burroughs, T.; Narayana, P.A.; Kosten, T.R.; Bechara, A.; et al. Altered anterior cingulate cortex to hippocampus effective connectivity in response to drug cues in men with cocaine use disorder. Psychiatry Res. Neuroimaging 2018, 271, 59–66. [Google Scholar] [CrossRef]
- Lee, J.-H.; Telang, F.W.; Springer, C.S.; Volkow, N.D. Abnormal brain activation to visual stimulation in cocaine abusers. Life Sci. 2003, 73, 1953–1961. [Google Scholar] [CrossRef] [PubMed]
- Hanlon, C.A.; Dowdle, L.T.; Naselaris, T.; Canterberry, M.; Cortese, B.M. Visual cortex activation to drug cues: A meta-analysis of functional neuroimaging papers in addiction and substance abuse literature. Drug Alcohol. Depend. 2014, 143, 206–212. [Google Scholar] [CrossRef]
- Güntürkün, O.; Ströckens, F.; Ocklenburg, S. Brain Lateralization: A Comparative Perspective. Physiol. Rev. 2020, 100, 1019–1063. [Google Scholar] [CrossRef]
- Hugdahl, K. Lateralization of cognitive processes in the brain. Acta Psychol. 2000, 105, 211–235. [Google Scholar] [CrossRef]
- Gordon, H.W. Laterality of Brain Activation for Risk Factors of Addiction. Curr. Drug Abus. Rev. 2016, 9, 1–18. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, S.W.S.; Nyberg, L.; Bäckman, L. Intra-individual variability in behavior: Links to brain structure, neurotransmission and neuronal activity. Trends Neurosci. 2006, 29, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Reato, D.; Rahman, A.; Bikson, M.; Parra, L.C. Effects of weak transcranial alternating current stimulation on brain activity—A review of known mechanisms from animal studies. Front. Hum. Neurosci. 2013, 7, 687. [Google Scholar] [CrossRef]
- Wang, P.; Kong, R.; Kong, X.; Liégeois, R.; Orban, C.; Deco, G.; van den Heuvel, M.P.; Thomas Yeo, B.T. Inversion of a large-scale circuit model reveals a cortical hierarchy in the dynamic resting human brain. Sci. Adv. 2019, 5, eaat7854. [Google Scholar] [CrossRef]

| Name | Type | Origin | Version | Authors and Citations |
|---|---|---|---|---|
| SUDMEX-CUD | dataset | the National Institute of Psychiatry in Mexico City | v1.1.2 | Diego Angeles-Valdez et al. [51] |
| SUDMEX-TMS | dataset | the National Institute of Psychiatry in Mexico City | v2.1.0 | Diego Angeles-Valdez et al. [52] |
| fMRIPrep | software | Stanford University, California, United States | 24.1.1 | Oscar Esteban et al. [53,54] |
| DSI studio | software | University of Pittsburgh, Pennsylvania, United States | “Hou” version | Fang-Cheng (Frank) Yeh et al. [58,59] |
| XCP-D | software | University of Pennsylvania, Pennsylvania, United States | 0.10.0rc1 | Kahini Mehta et al. [55] |
| QSDR | algorithm | University of Pittsburgh, Pennsylvania, United States | “Hou” version | Fang-Cheng (Frank) Yeh et al. [58] |
| modified FACT | algorithm | University of Pittsburgh, Pennsylvania, United States | “Hou” version | Fang-Cheng (Frank) Yeh et al. [59] |
| LEiDA | algorithm | University of Oxford, Oxford, United Kingdom | N/A | Joana Cabral et al. [14] |
| Modeling and Perturbation framework | algorithm | Universitat Pompeu Fabra, Barcelona, Spain | N/A | Gustavo Deco et al. [20,67] |
| Euler-Maruyama Numerical Scheme | algorithm | Ochanomizu University, Japan | N/A | Gisiro Maruyama et al. [66] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Yang, Y.; Zhen, Y.; Wang, X.; Liu, L.; Zheng, H.; Tang, S. Understanding Altered Dynamics in Cocaine Use Disorder Through State Transitions Mediated by Artificial Perturbations. Brain Sci. 2025, 15, 263. https://doi.org/10.3390/brainsci15030263
Zheng Y, Yang Y, Zhen Y, Wang X, Liu L, Zheng H, Tang S. Understanding Altered Dynamics in Cocaine Use Disorder Through State Transitions Mediated by Artificial Perturbations. Brain Sciences. 2025; 15(3):263. https://doi.org/10.3390/brainsci15030263
Chicago/Turabian StyleZheng, Yi, Yaqian Yang, Yi Zhen, Xin Wang, Longzhao Liu, Hongwei Zheng, and Shaoting Tang. 2025. "Understanding Altered Dynamics in Cocaine Use Disorder Through State Transitions Mediated by Artificial Perturbations" Brain Sciences 15, no. 3: 263. https://doi.org/10.3390/brainsci15030263
APA StyleZheng, Y., Yang, Y., Zhen, Y., Wang, X., Liu, L., Zheng, H., & Tang, S. (2025). Understanding Altered Dynamics in Cocaine Use Disorder Through State Transitions Mediated by Artificial Perturbations. Brain Sciences, 15(3), 263. https://doi.org/10.3390/brainsci15030263






