Examining the Effect of Ionizing Radiations in Ion-Exchange Membranes of Interest in Biomedical Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Irradiation Treatment
2.2.2. Thickness and Area
2.2.3. Swelling Degree
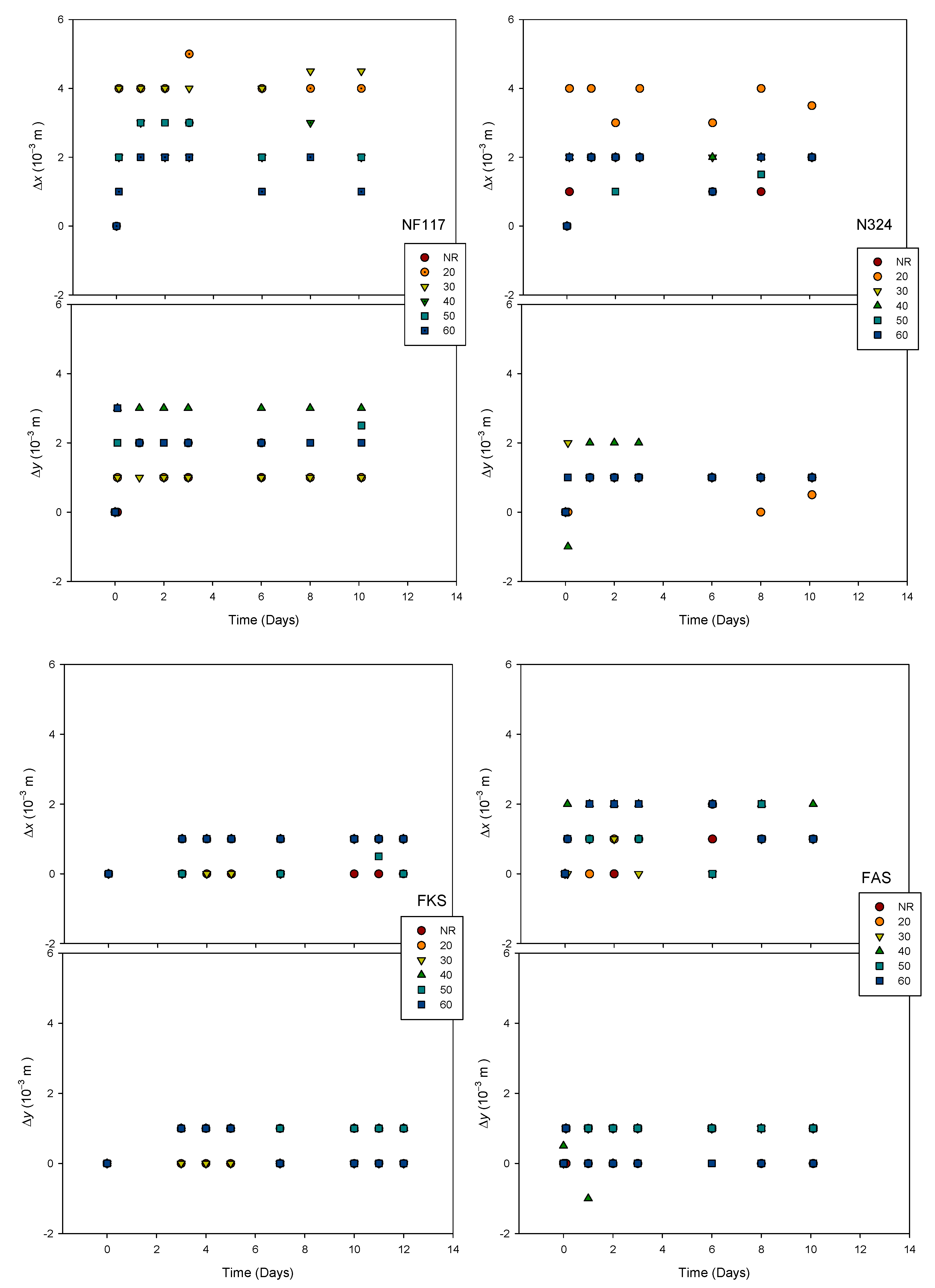
2.2.4. Dimensional Change
3. Results and Discussion
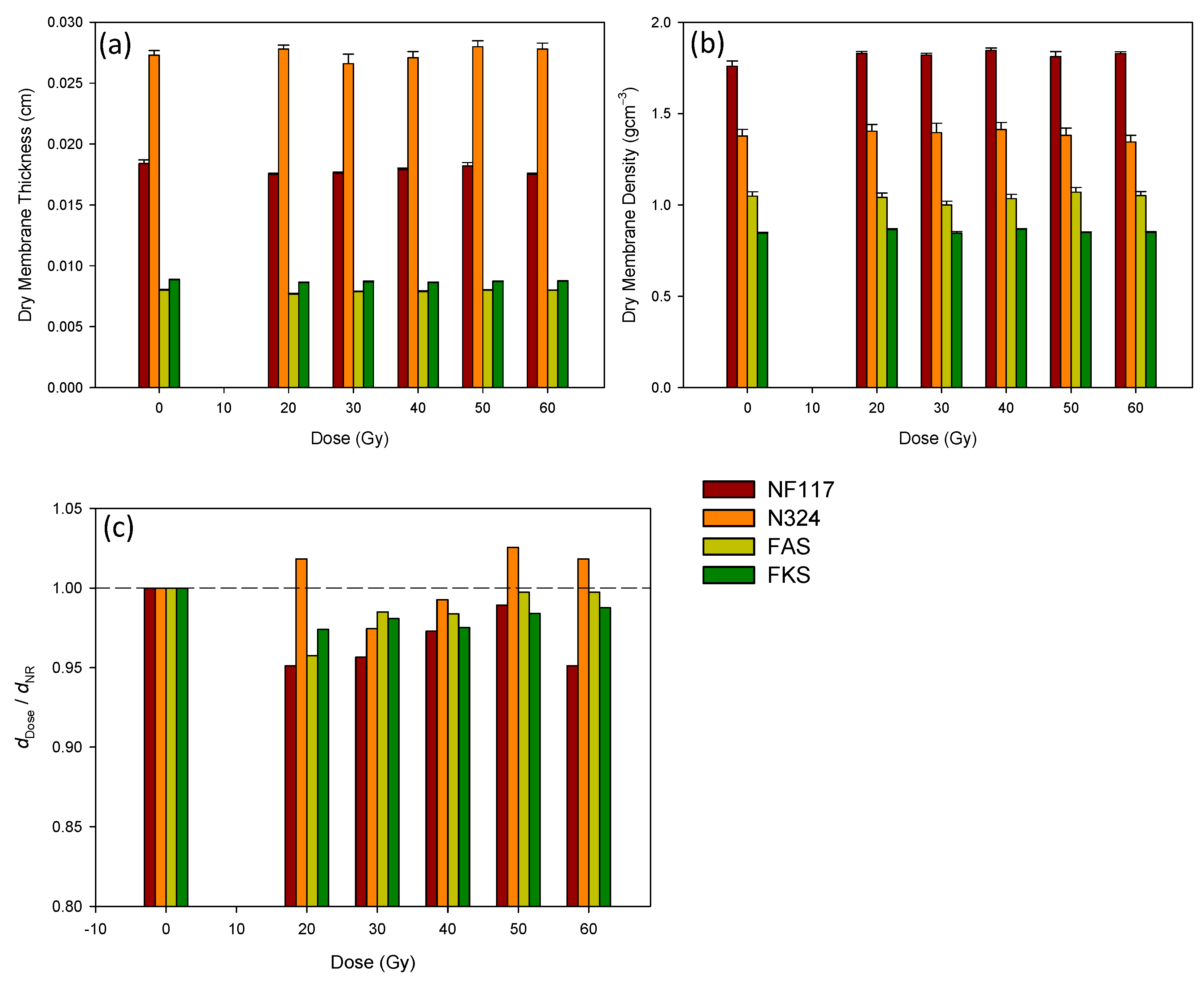
3.1. Influence of the Irradiation in the Dry Membranes
3.2. Influence of the Radiation in the Swollen Membranes
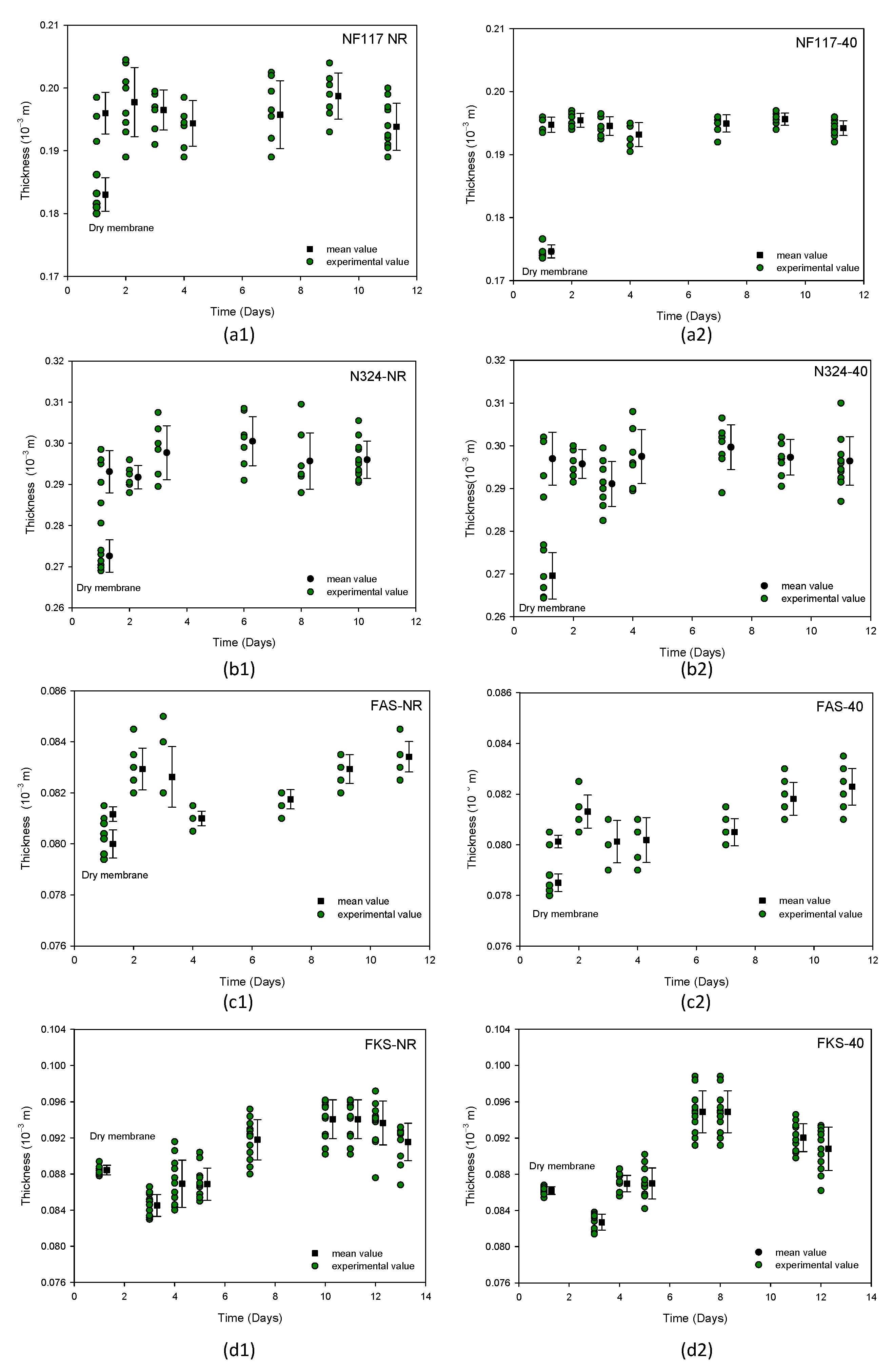
3.2.1. Membrane Dimensions
3.2.2. Swelling Behavior
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cosnier, S.; Le Golf, A.; Holzinger, M. Towards glucose biofuel cells implanted in human body for powering artificial organs: Review. Electrochem. Commun. 2014, 38, 18–23. [Google Scholar] [CrossRef]
- Rapport, B.I.; Kedzierski, J.T.; Sarpeshkar, R. A glucose fuel cell for implantable brain-machine interfaces. PLoS ONE 2012, 7, e38436. [Google Scholar]
- Liu, T. Glucose fuel cells and membranes: A brief overview and literature analysis. Sustainability 2022, 14, 8376. [Google Scholar]
- Guo, Y.; Wang, J.; Shinde, S.; Wang, X.; Li, Y.; Dai, Y.; Ren, J.; Zhang, P.; Liu, X. Simultaneous wastewater treatment and energy harvesting in microbial fuel cells: An update on the biocatalysts. RSC Adv. 2020, 10, 25874–25887. [Google Scholar] [PubMed]
- Jeon, W.Y.; Lee, J.H.; Dasbnyam, K.; Choi, Y.B.; Kim, T.H.; Lee, H.H.; Kim, H.W.; Kim, H.H. Performance of a glucose-reactive enzyme-based biofuel cell system for biomedical applications. Sci. Rep. 2019, 9, 10872. [Google Scholar] [CrossRef] [Green Version]
- Antolini, E. External abiotic glucose fuel cells. Sustain. Energy Fuels 2021, 5, 5038–5060. [Google Scholar] [CrossRef]
- Do, U.P.; Seland, F.; Johannessen, E.A. A micro fuel cell for abiotical catalysis of glucose. J. Power Sour. 2020, 478, 229032. [Google Scholar] [CrossRef]
- Maity, D.; Ray, P.G.; Buchmann, P.; Mansouri, M.; Fussenegger, M. Blood-glucose-powered metabolic fuel cell for self-sufficient bioelectronics. Adv. Mater. 2023, 35, 2300890. [Google Scholar] [CrossRef]
- Torigoe, K.; Takahashi, M.; Tsuchiya, K.; Iwabata, K.; Ichihashi, T.; Sakaguchi, K.; Sugawara, F.; Abe, M. High-Power Abiotic Direct Glucose Fuel Cell Using a Gold–Platinum Bimetallic Anode Catalyst. ACS Omega 2018, 3, 18323–18333. [Google Scholar] [CrossRef]
- Hickner, M.A.; Fujimoto, C.H.; Cornelius, C.J. Transport in sulfonated poly(phenylene)s: Proton conductivity, permeability, and the state of water. Polymer 2006, 47, 4238–4244. [Google Scholar] [CrossRef]
- Flimban, S.G.A.; Hassan, S.H.A.; Rahman, M.M.; Oh, S.-E. The effect of Nafion membrane fouling on the power generation of a microbial fuel cell. Int. J. Hydrogen Energy. 2020, 45, 13643–13651. [Google Scholar] [CrossRef]
- Freijanes, Y.; Barragán, V.M.; Muñoz, S. Chronopotentiometric study of a Nafion membrane in presence of glucose. J. Membr. Sci. 2016, 510, 79–90. [Google Scholar] [CrossRef]
- Reichmanis, E.; Frank, C.W.; O’Donnell, J.H.; Hill, D.J.T. Radiation Effect on Polymeric Materials. A brief Overview; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1993. [Google Scholar]
- Pajustea, E.; Reinholds, I.; Vaivars, G.; Antuzevic, A.; Avotin, L.; Spruģis, E.E.; Mikkoe, R.; Heikki, K.; Merif, R.M.; Kaparkalejs, R. Evaluation of radiation stability of electron beam irradiated Nafion® and sulfonated poly (ether ether ketone) membranes. Polym. Degrad. Stab. 2022, 200, 109970. [Google Scholar] [CrossRef]
- Balko, E.N.; Chaklos, J.T. Effect of ionizing radiation on perfluorosulfonic acid ion-exchange membranes. J. Appl. Polym. 1981, 26, 1519–1531. [Google Scholar]
- Wang, X.; Li, X.; Fu, X.; Chen, R.; Gao, B. Effect of ultrasound irradiation on polymeric microfiltration membranes. Desalination 2005, 175, 187–196. [Google Scholar] [CrossRef]
- Mohamed, H.F.M.; Abdel-Hady, E.E.; Abdel-Hamed, M.O.; Kamel, M.S.A. Impact of ultraviolet radiation on the performance of polymer electrolyte membrane. J. Solid State Electrochem. 2020, 24, 1217–1219. [Google Scholar] [CrossRef]
- He, D.; Susanto, H.; Ulbricht, M. Photo-irradiation for preparation, modification and stimulation of polymeric membranes. Prog. Polym. Sci. 2009, 34, 62–98. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, J.; Tang, K.Y. Study on the gravimetric measurement of the swelling behaviors of polymer films. Rev. Adv. Mater. Sci. 2013, 33, 452–458. [Google Scholar]
- Reiber, M.; Ruff, M.; Uhr, M. Ascorbate concentration in human cerebrospinal fluid (CSF) and serum. Intrathecal accumulation and CSF flow rate. Clin. Chim. Acta 1993, 217, 155–164. [Google Scholar] [CrossRef]
- Willers, H.; Dahm-Daphi, J.; Powell, S. Repair of radiation damage to DNA. Br. J. Cancer 2004, 90, 1297–1301. [Google Scholar] [CrossRef] [Green Version]
- Morris, D.R.; Sun, X. Water-sorption and transport properties of Nafion 117. J. Appl. Polym. Sci. 1993, 50, 1445–1452. [Google Scholar] [CrossRef]
- Ninham, B.W.; Bolotskova, P.N.; Gudkov, S.V.; Baranova, E.N.; Kozlov, V.A.; Shkirin, A.V.; Vu, M.T.; Bunkin, N.F. Nafion swelling in salt solutions in a finite sized cell: Curious phenomena dependent on sample preparation protocol. Polymers 2022, 14, 1511. [Google Scholar] [CrossRef] [PubMed]
- Barragán, V.M.; Pérez-Haro, M.J. Correlations between water uptake and effective fixed charge concentration at high univalent electrolyte concentrations in sulfonated polymer cation-exchange membranes with different morphology. Electrochim. Acta. 2011, 24, 8630–8637. [Google Scholar] [CrossRef]
- Helfferich, F. Ion-Exchange; Dover Publication Inc.: New York, NY, USA, 1995. [Google Scholar]
- Madhav, D.; Sha, C.; Mus, J.; Buysschaert, F.; Vandegiste, V. The effect of salty environments of the degradation behavior and mechanical properties of Nafion membranes. Energies 2023, 6, 2256. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, G.; Shen, Q.; Li, S.; Li, Z.; Liao, J.; Jiang, Z.; Wang, H.; Zhang, H.; Ye, W. Study on the transport performance degradation of Nafion membrane due to the presence of Na+ and Ca2+ using molecular dynamics simulations. J. Power Sources 2022, 542, 231740. [Google Scholar] [CrossRef]
- Katime, I.; Velada, J.L.; Novoa, R.; Díaz de Apodaca, E. Swelling kinetic of poly(acrylamide)/(poly(mono-n-alkyl itaconates)hydrogels. Polym. Int. 1996, 40, 281–286. [Google Scholar] [CrossRef]
- Sarkar, B.; Jaiswal, M.; Satapathy, K. Swelling kinetics and electrical charge transport in PEDOT:PSS thin films exposed to water. J. Phys. Condens. Matter 2018, 30, 225101. [Google Scholar] [CrossRef]
- Schott, H. Swelling kinetics of polymers. J. Macromol. Sci. 1992, 31, 1–9. [Google Scholar] [CrossRef]




| Membrane | NF117 | N324 | FKS | FAS |
|---|---|---|---|---|
| Type | Cationic | Cationic | Cationic | Anionic |
| Reinforcement | No | PTF | Polyester | Polyester |
| Thickness (10−6 m) | 183 | 152/280 | 74–87 | 72–85 |
| IEC (meq g−1) | 0.90 | 0.92 | 1.0 | 1.12 |
| Fixed group | ||||
| Provided ionic form | H+ | H+ | H+ | Br- |
| Basic weight (mg·cm−2) | 36 | 48 | 8.1–9.1 | 9.8–12.5 |
| Membrane | ||||
|---|---|---|---|---|
| Dose (Gy) | NF117 | N324 | FKS | FAS |
| 0 | 0.198 ± 0.005 | 0.296 ± 0.004 | 0.092 ± 0.003 | 0.083 ± 0.006 |
| 20 | 0.191 ± 0.002 | 0.305 ± 0.006 | 0.086 ± 0.003 | 0.079 ± 0.001 |
| 30 | 0.192 ± 0.002 | 0.291 ± 0.006 | 0.087 ± 0.003 | 0.081 ± 0.006 |
| 40 | 0.196 ± 0.001 | 0.296 ± 0.006 | 0.093 ± 0.003 | 0.082 ± 0.007 |
| 50 | 0.197 ± 0.002 | 0.294 ± 0.004 | 0.086 ± 0.002 | 0.082 ± 0.007 |
| 60 | 0.191 ± 0.002 | 0.302 ± 0.004 | 0.088 ± 0.003 | 0.082 ± 0.004 |
| Membrane | ||||
|---|---|---|---|---|
| Dose (Gy) | NF117 | N324 | FKS | FAS |
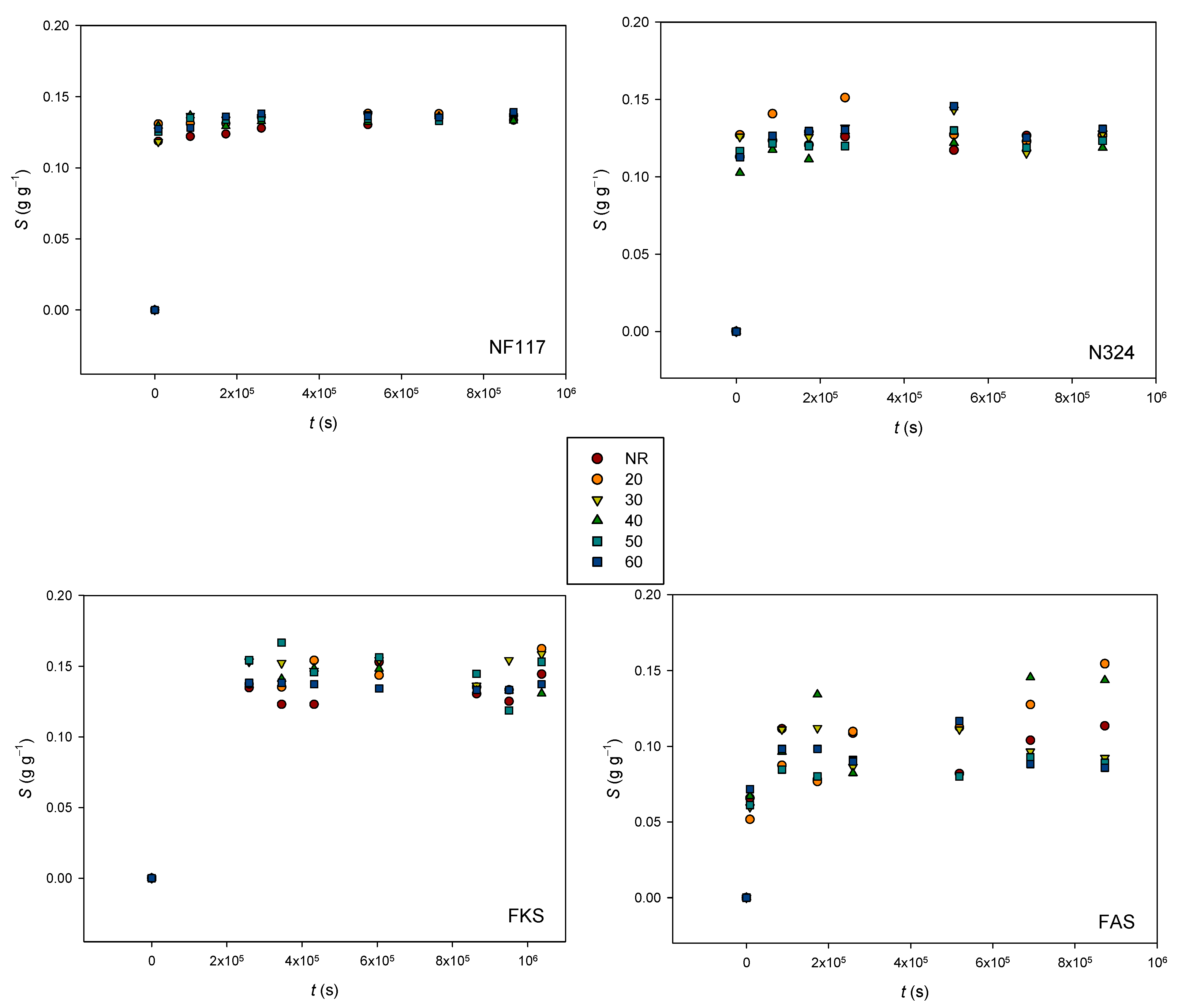
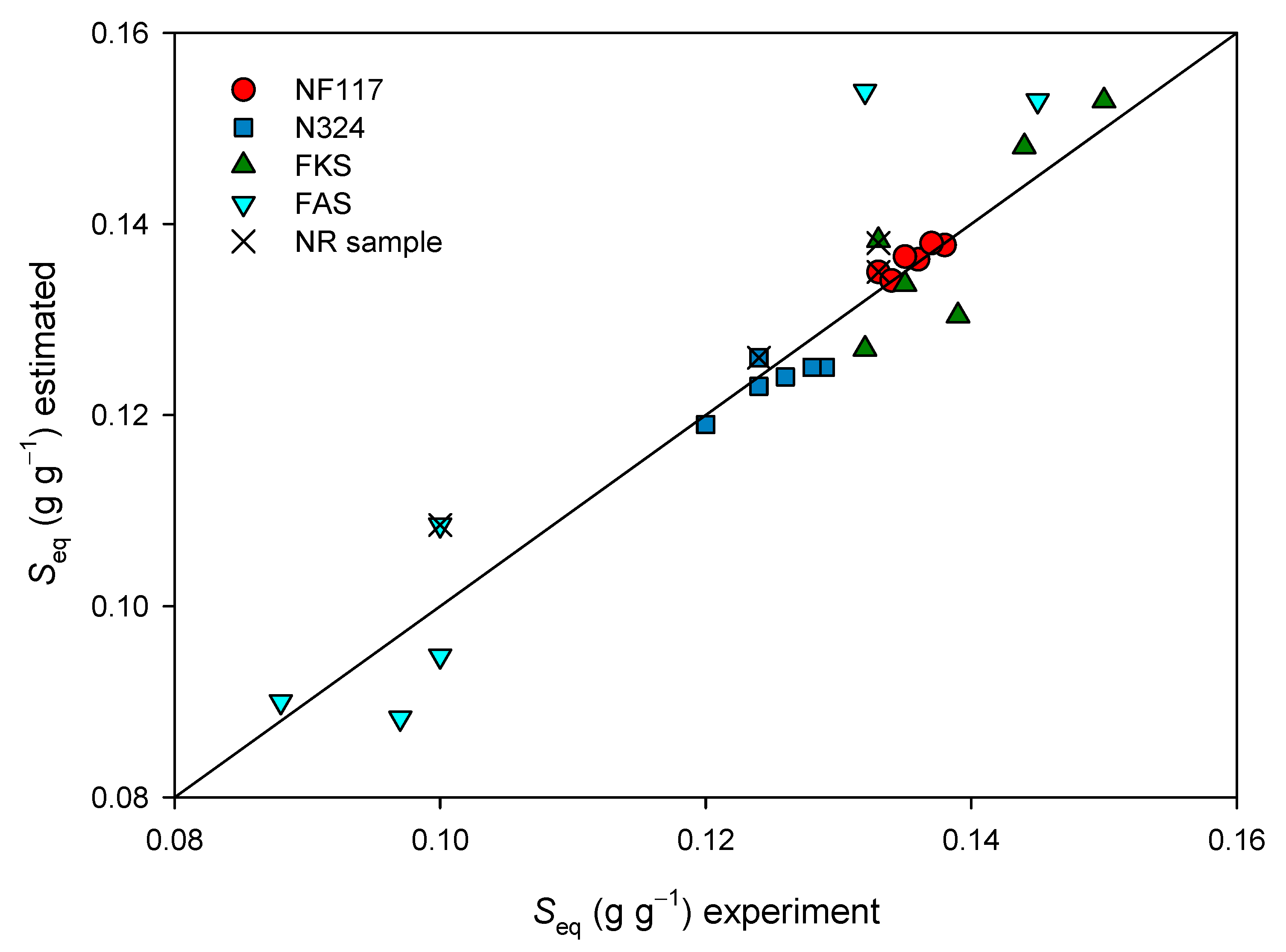
| 0 | 0.133 ± 0.003 | 0.124 ± 0.005 | 0.133 ± 0.010 | 0.100 ± 0.016 |
| 20 | 0.138 ± 0.001 | 0.126 ± 0.003 | 0.144 ± 0.016 | 0.132 ± 0.021 |
| 30 | 0.136 ± 0.001 | 0.129 ± 0.002 | 0.150 ± 0.012 | 0.100 ± 0.010 |
| 40 | 0.134 ± 0.003 | 0.120 ± 0.002 | 0.132 ± 0.012 | 0.145 ± 0.013 |
| 50 | 0.135 ± 0.003 | 0.124 ± 0.006 | 0.139 ± 0.018 | 0.088 ± 0.007 |
| 60 | 0.137 ± 0.002 | 0.128 ± 0.004 | 0.135 ± 0.023 | 0.097 ± 0.017 |
| Membrane | ||||
|---|---|---|---|---|
| Dose (Gy) | NF117 | N324 | FKS | FAS |
| 0 | −1.28 ± 0.03 | −1.11 ± 0.03 | −3.64 ± 0.15 | −9.06 ± 0.13 |
| 20 | −1.25 ± 0.03 | −1.27 ± 0.03 | −0.93 ± 0.15 | −7.59 ± 0.13 |
| 30 | −1.29 ± 0.03 | −1.25 ± 0.03 | −1.99 ± 0.15 | −8.47 ± 0.13 |
| 40 | −1.30 ± 0.03 | −1.33 ± 0.03 | −1.03 ± 0.15 | −7.94 ± 0.13 |
| 50 | −1.44 ± 0.03 | −0.92 ± 0.03 | −1.46 ± 0.15 | −8.47 ± 0.13 |
| 60 | −1.15 ± 0.03 | −1.05 ± 0.03 | −0.81 ± 0.15 | −8.33 ± 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara, Í.; Freijanes, Y.; Muñoz, S.; Ruiz, G.; Barragán, V.M. Examining the Effect of Ionizing Radiations in Ion-Exchange Membranes of Interest in Biomedical Applications. Membranes 2023, 13, 592. https://doi.org/10.3390/membranes13060592
Lara Í, Freijanes Y, Muñoz S, Ruiz G, Barragán VM. Examining the Effect of Ionizing Radiations in Ion-Exchange Membranes of Interest in Biomedical Applications. Membranes. 2023; 13(6):592. https://doi.org/10.3390/membranes13060592
Chicago/Turabian StyleLara, Íñigo, Yago Freijanes, Sagrario Muñoz, Gema Ruiz, and V. María Barragán. 2023. "Examining the Effect of Ionizing Radiations in Ion-Exchange Membranes of Interest in Biomedical Applications" Membranes 13, no. 6: 592. https://doi.org/10.3390/membranes13060592
APA StyleLara, Í., Freijanes, Y., Muñoz, S., Ruiz, G., & Barragán, V. M. (2023). Examining the Effect of Ionizing Radiations in Ion-Exchange Membranes of Interest in Biomedical Applications. Membranes, 13(6), 592. https://doi.org/10.3390/membranes13060592







