The Holistic Coronary Physiology Display: Calculation of the Flow Separation Index in Vessel-Specific Individual Flow Range during Fractional Flow Reserve Measurement Using 3D Coronary Reconstruction
Abstract
:1. Introduction
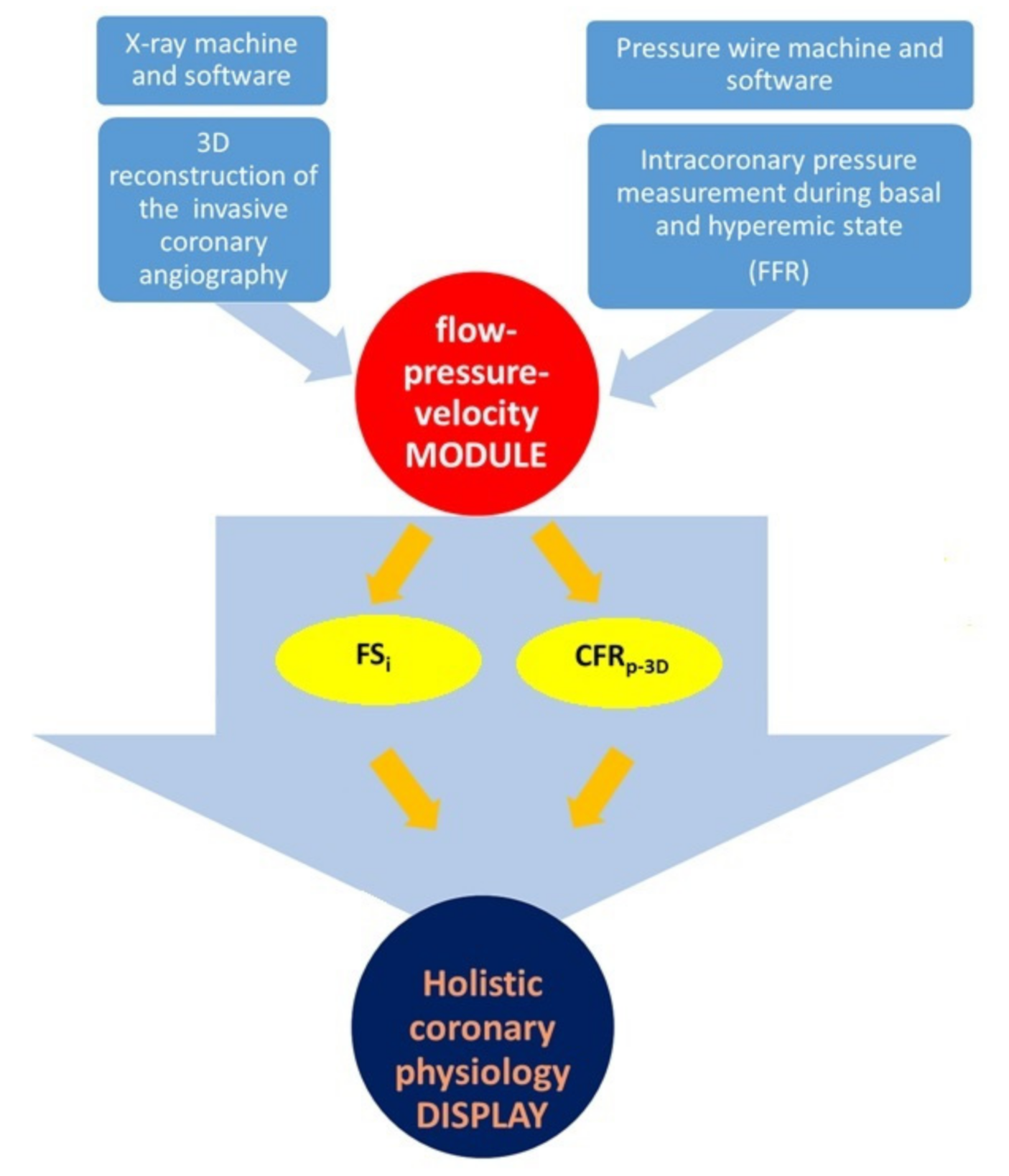
2. Materials and Methods
2.1. Coronary Angiography and Fractional Flow Reserve Measurement
2.2. Three-Dimensional Quantitative Coronary Reconstruction
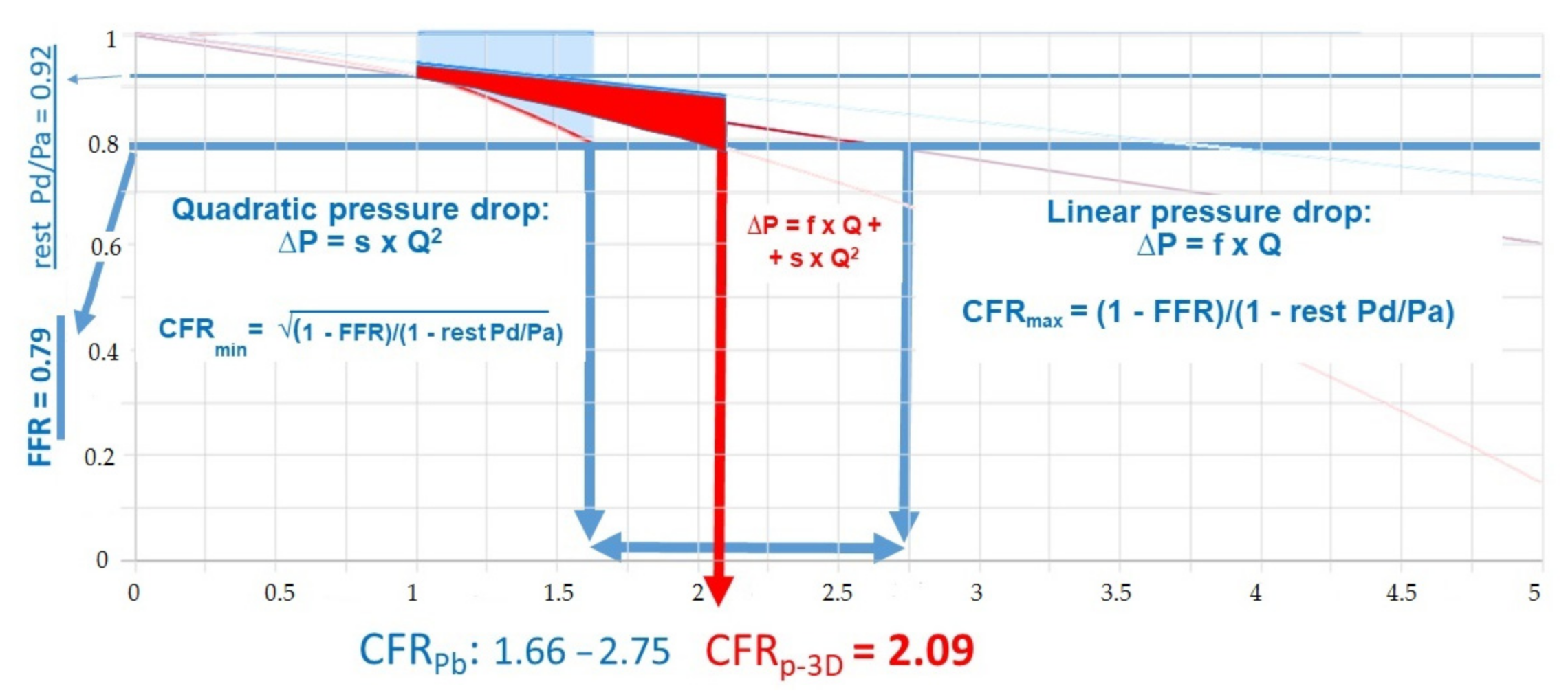
2.3. Calculation of CFRp-3D
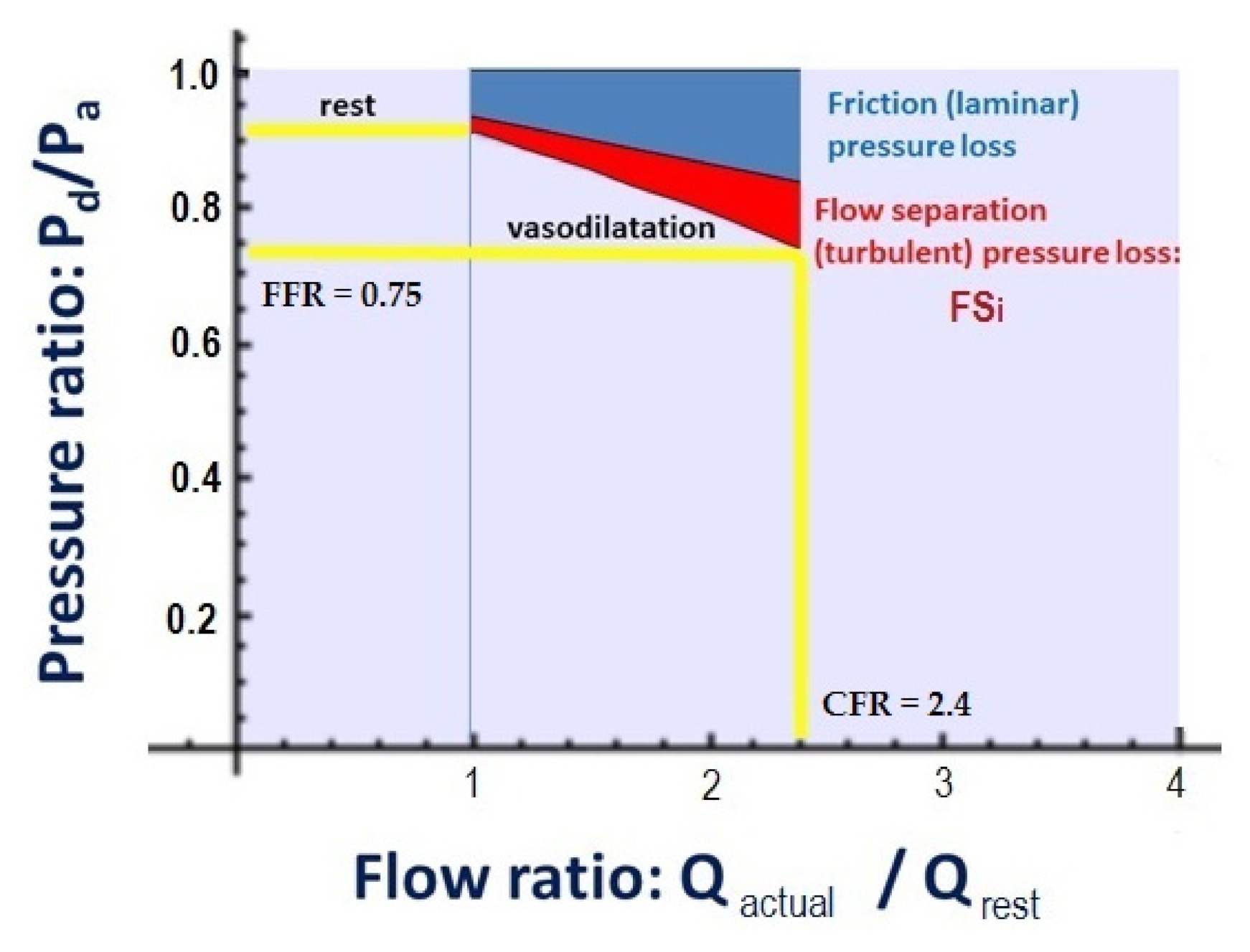
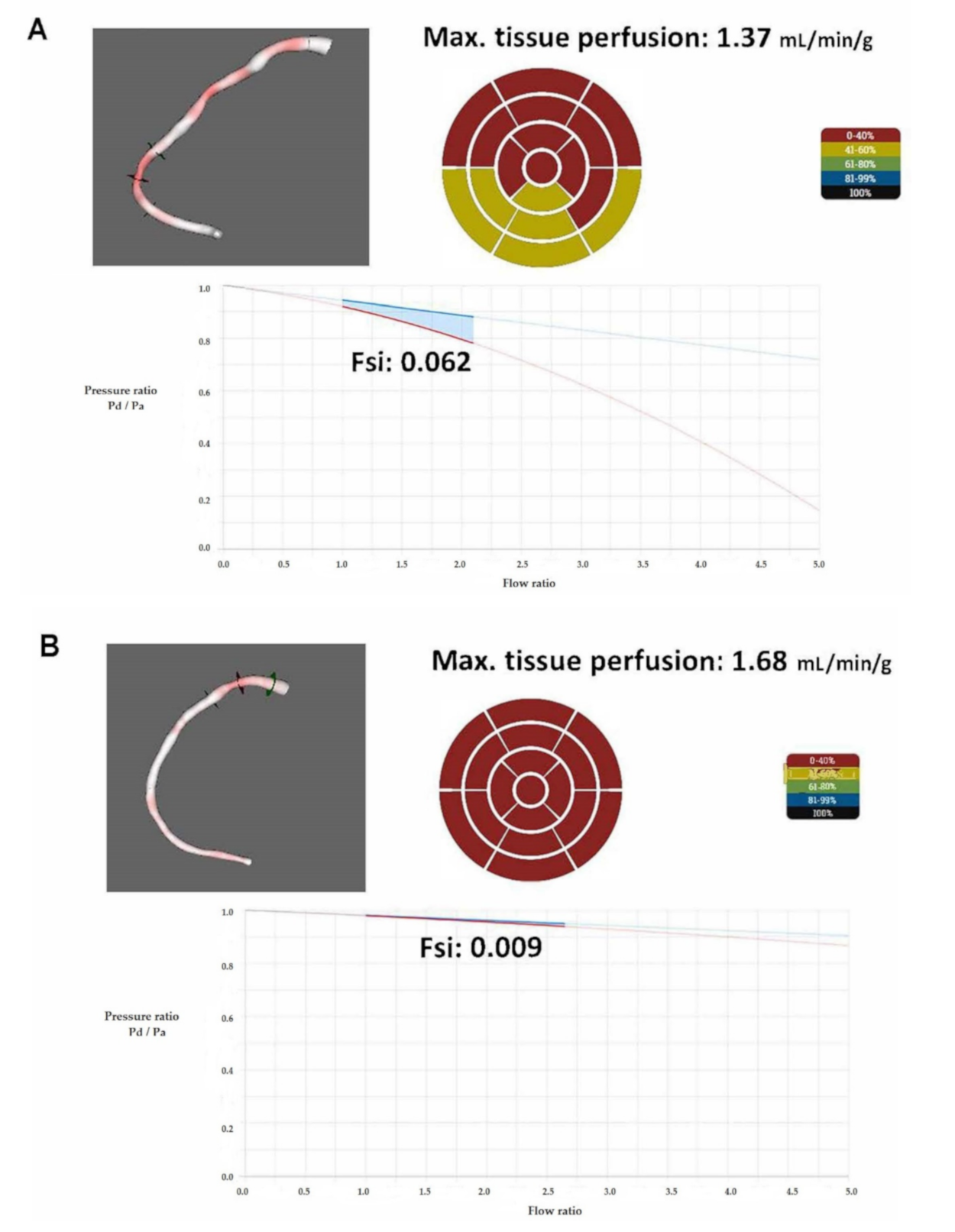
2.4. The Calculation of Flow Separation Index
2.5. Patient Population
2.6. Statistical Analysis
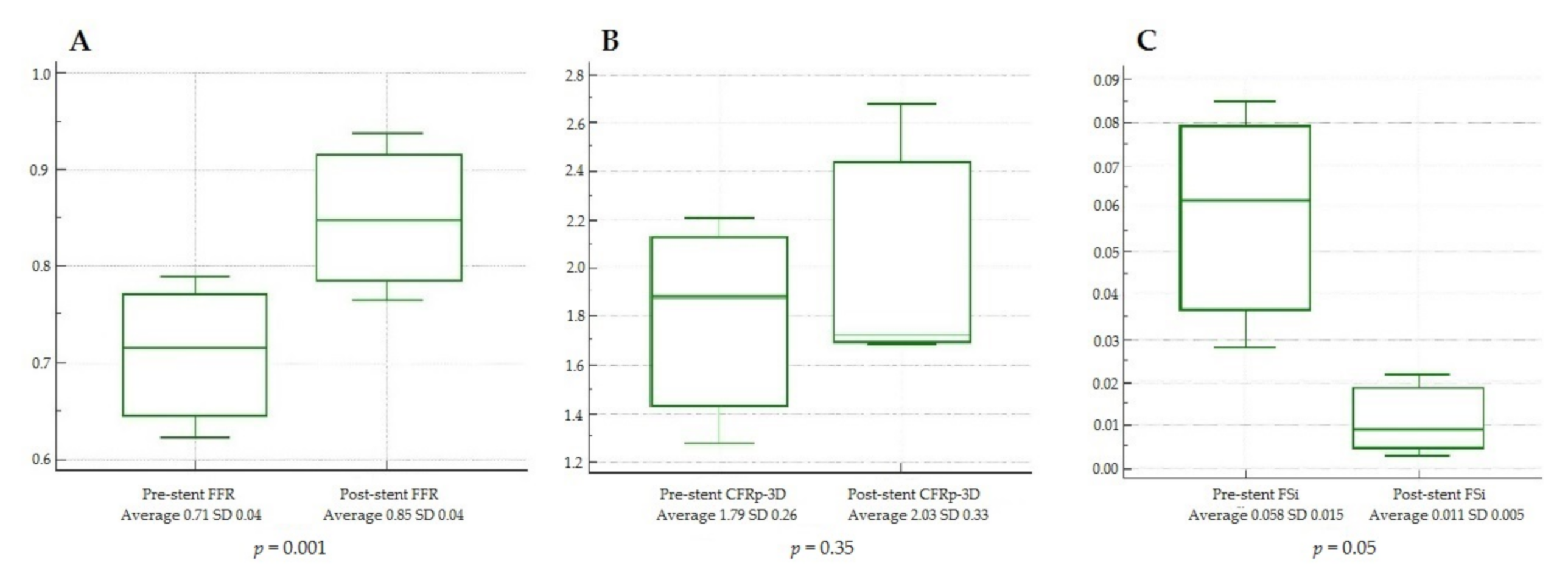
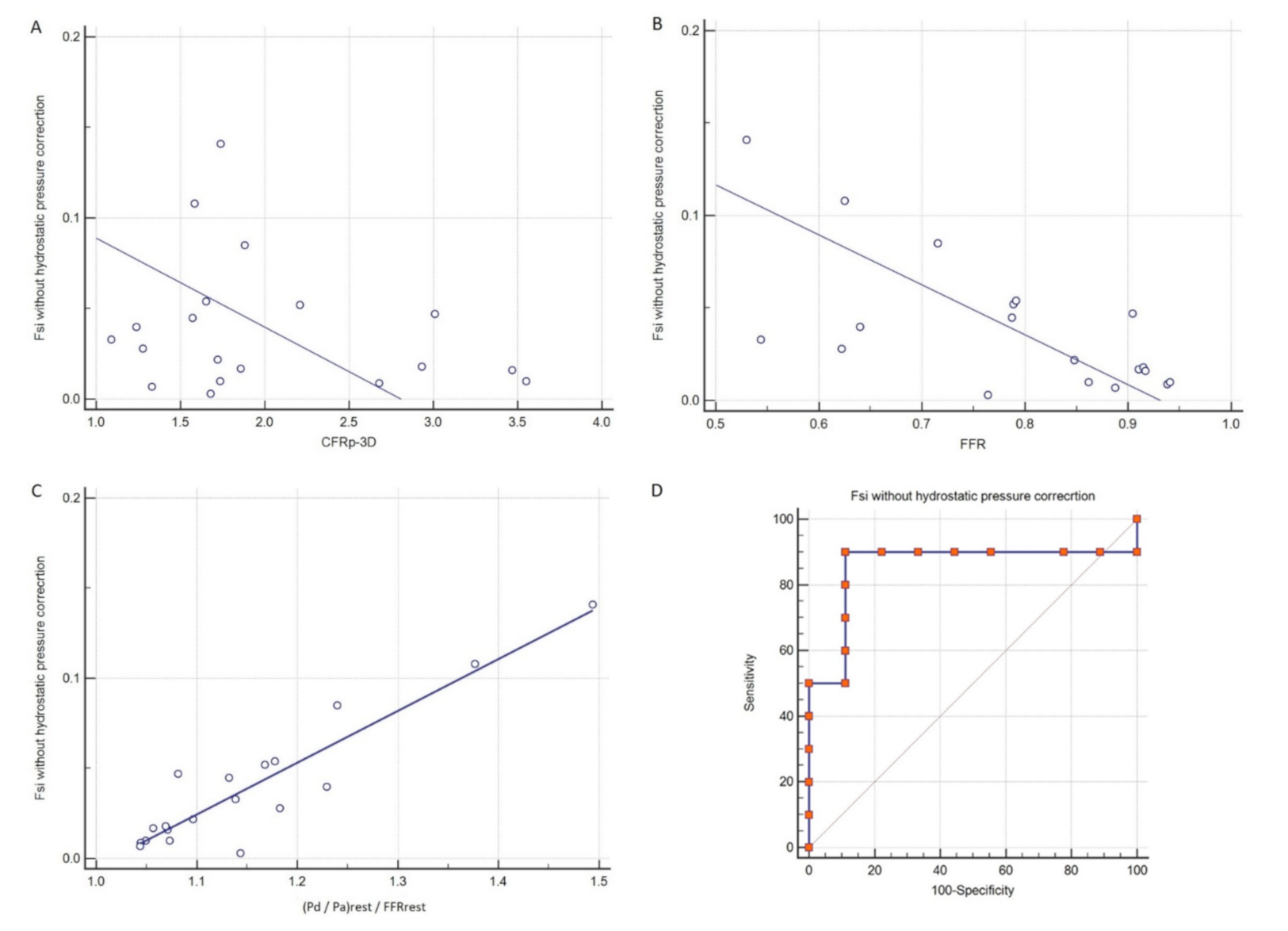
3. Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koszegi, Z.; Balkay, L.; Galuska, L.; Varga, J.; Hegedus, I.; Fulop, T.; Balogh, E.; Jenei, C.; Szabo, G.; Kolozsvari, R.; et al. Holistic polar map for integrated evaluation of cardiac imaging results. Comput. Med. Imaging Graph. 2007, 31, 577–586. [Google Scholar] [CrossRef] [PubMed]
- Knuuti, J.; Wijns, W.; Achenbach, S.; Agewall, S.; Barbato, E.; Bax, J.J.; Capodanno, D.; Cuisset, T.; Deaton, C.; Dickstein, K.; et al. 2019 ESC Guidelines for the diagnosis and management of chronic coronary syndromes. Eur. Heart J. 2020, 41, 407–477. [Google Scholar] [CrossRef] [PubMed]
- Neumann, F.-J.; Sousa-Uva, M.; Ahlsson, A.; Alfonso, F.; Banning, A.P.; Benedetto, U.; A Byrne, R.; Collet, J.-P.; Falk, V.; Head, S.J.; et al. 2018 ESC/EACTS Guidelines on myocardial revascularization. Eur. Heart J. 2018, 40, 87–165. [Google Scholar] [CrossRef] [PubMed]
- Pijls, N.H.; Van Son, J.A.; Kirkeeide, R.L.; De Bruyne, B.; Gould, K.L. Experimental basis of determining maximum coronary, myocardial, and collateral blood flow by pressure measurements for assessing functional stenosis severity before and after percutaneous transluminal coronary angioplasty. Circulation 1993, 87, 1354–1367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bruyne, B.; Fearon, W.F.; Pijls, N.H.; Barbato, E.; Tonino, P.; Piroth, Z.; Jagic, N.; Mobius-Winckler, S.; Rioufol, G.; Witt, N.; et al. Fractional flow reserve-guided PCI for stable coronary artery disease. N. Engl. J. Med. 2014, 371, 1208–1217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serruys, P.W.; Zijlstra, F.; Laarman, G.J.; Reiber, H.H.C.; Beatt, K.; Roelandt, J. A comparison of two methods to measure coronary flow reserve in the setting of coronary angioplasty: Intracoronary blood flow velocity measurements with a Doppler catheter, and digital subtraction cineangiography. Eur. Heart J. 1989, 10, 725–736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cortigiani, L.; Rigo, F.; Gherardi, S.; Bovenzi, F.; Molinaro, S.; Picano, E.; Sicari, R. Coronary Flow Reserve During Dipyridamole Stress Echocardiography Predicts Mortality. JACC Cardiovasc. Imaging 2012, 5, 1079–1085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murthy, V.L.; Naya, M.; Foster, C.R.; Hainer, J.; Gaber, M.; Di Carli, G.; Blankstein, R.; Dorbala, S.; Sitek, A.; Pencina, M.J.; et al. Improved Cardiac Risk Assessment With Noninvasive Measures of Coronary Flow Reserve. Circulation 2011, 124, 2215–2224. [Google Scholar] [CrossRef] [Green Version]
- Gan, L.-M.; Wikström, J.; Fritsche-Danielson, R. Coronary Flow Reserve from Mouse to Man—From Mechanistic Understanding to Future Interventions. J. Cardiovasc. Transl. Res. 2013, 6, 715–728. [Google Scholar] [CrossRef] [Green Version]
- Johnson, N.P.; Kirkeeide, R.L.; Gould, K.L. Is Discordance of Coronary Flow Reserve and Fractional Flow Reserve Due to Methodology or Clinically Relevant Coronary Pathophysiology? JACC Cardiovasc. Imaging 2012, 5, 193–202. [Google Scholar] [CrossRef] [Green Version]
- Gould, K.L.; Johnson, N.P.; Bateman, T.M.; Beanlands, R.S.; Bengel, F.M.; Bober, R.; Camici, P.G.; Cerqueira, M.D.; Chow, B.J.; Di Carli, M.F.; et al. Anatomic versus physiologic assessment of coronary artery disease. Role of coronary flow reserve, fractional flow reserve, and positron emission tomography imaging in revascularization decision-making. J. Am. Coll. Cardiol. 2013, 62, 1639–1653. [Google Scholar] [CrossRef] [Green Version]
- Shalman, E.; Barak, C.; Dgany, E.; Noskowitcz, H.; Einav, S.; Rosenfeld, M. Pressure-based simultaneous CFR and FFR measurements: Understanding the physiology of a stenosed vessel. Comput. Biol. Med. 2001, 31, 353–363. [Google Scholar] [CrossRef]
- Akasaka, T.; Yamamuro, A.; Kamiyama, N.; Koyama, Y.; Akiyama, M.; Watanabe, N.; Neishi, Y.; Takagi, T.; Shalman, E.; Barak, C.; et al. Assessment of coronary flowreserve by coronary pressure measurement: Comparison with flow- or Velocity-Derived coronary flow reserve. J. Am. Coll. Cardiol. 2003, 41, 1554–1560. [Google Scholar] [CrossRef] [Green Version]
- MacCarthy, P.; Berger, A.; Manoharan, G.; Bartunek, J.; Barbato, E.; Wijns, W.; Heyndrickx, G.R.; Pijls, N.H.; De Bruyne, B. Pressure-derived measurement of coronary flow reserve. J. Am. Coll. Cardiol. 2005, 45, 216–220. [Google Scholar] [CrossRef] [Green Version]
- Ahn, J.-M.; Shin, E.-S.; Koo, B.-K.; Lee, P.H.; Kang, S.-J.; Kim, Y.-H.; Zimmermann, F.M.; Johnson, N.P.; Park, D.-W.; Pijls, N.H. Fractional flow reserve and pressure-bounded coronary flow reserve to predict outcomes in coronary artery disease. Eur. Heart J. 2017, 38, 1980–1989. [Google Scholar] [CrossRef]
- Zimmermann, F.M.; Pijls, N.H.J.; De Bruyne, B.; Bech, G.J.-W.; Van Schaardenburgh, P.; Kirkeeide, R.L.; Gould, K.L.; Johnson, N.P. What can intracoronary pressure measurements tell us about flow reserve? Pressure-Bounded coronary flow reserve and example application to the randomized DEFER trial. Catheter. Cardiovasc. Interv. 2017, 90, 917–925. [Google Scholar] [CrossRef]
- Agostoni, P.; Biondi-Zoccai, G.; Van Langenhove, G.; Cornelis, K.; Vermeersch, P.; Convens, C.; Vassanelli, C.; Heuvel, P.V.D.; Branden, F.V.D.; Verheye, S. Comparison of Assessment of Native Coronary Arteries by Standard Versus Three-Dimensional Coronary Angiography. Am. J. Cardiol. 2008, 102, 272–279. [Google Scholar] [CrossRef]
- Yong, A.S.; Ng, A.C.; Brieger, D.; Lowe, H.C.; Ng, M.K.; Kritharides, L. Three-dimensional and two-dimensional quantitative coronary angiography, and their prediction of reduced fractional flow reserve. Eur. Heart J. 2010, 32, 345–353. [Google Scholar] [CrossRef] [Green Version]
- Warboys, C.M.; Amini, N.; de Luca, A.; Evans, P.C. The role of blood flow in determining the sites of atherosclerotic plaques. Med. Rep. 2011, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- Chatzizisis, Y.S.; Coskun, A.U.; Jonas, M.; Edelman, E.R.; Feldman, C.L.; Stone, P.H. Role of endothelial shear stress in the natural history of coronary atherosclerosis and vascular remodeling: Molecular, cellular, and vascular behavior. J. Am. Coll. Cardiol. 2007, 49, 2379–2393. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, V.; Pinho, D.; Lima, R.A.; Teixeira, J.C.; Teixeira, S. Blood Flow Modeling in Coronary Arteries: A Review. Fluids 2021, 6, 53. [Google Scholar] [CrossRef]
- Hoffman, J.I.E. Problems of Coronary Flow Reserve. Ann. Biomed. Eng. 2000, 28, 884–896. [Google Scholar] [CrossRef] [PubMed]
- Everaars, H.; De Waard, A.G.; Driessen, R.S.; Danad, I.; Raijmakers, P.G.; Lammertsma, A.A.; Van Rossum, A.C.; Knaapen, P.; Van Royen, N. 4172Doppler flow velocity and thermodilution to assess coronary flow reserve: Head-to head comparison with [15O]H2O PET imaging. Eur. Heart J. 2018, 39, 2044–2054. [Google Scholar] [CrossRef]
- Williams, R.P.; de Waard, G.A.; De Silva, K.; Lumley, M.; Asrress, K.; Arri, S.; Ellis, H.; Mir, A.; Clapp, B.; Chiribiri, A.; et al. Doppler Versus Thermodilution-Derived Coronary Microvascular Resistance to Predict Coronary Microvascular Dysfunction in Patients With Acute Myocardial Infarction or Stable Angina Pectoris. Am. J. Cardiol. 2018, 121, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Tar, B.; Jenei, C.; Dezsi, C.A.; Bakk, S.; Beres, Z.; Santa, J.; Svab, M.; Szentes, V.; Polgar, P.; Bujaky, C.; et al. Less invasive fractional flow reserve measurement from 3-dimensional quantitative coronary angiography and classic fluid dynamic equations. EuroIntervention 2018, 14, 942–950. [Google Scholar] [CrossRef] [PubMed]
- Papafaklis, M.I.; Muramatsu, T.; Ishibashi, Y.; Lakkas, L.S.; Nakatani, S.; Bourantas, C.V.; Ligthart, J.; Onuma, Y.; Echavarria-Pinto, M.; Tsirka, G.; et al. Fast virtual functional assessment of intermediate coronary lesions using routine angiographic data and blood flow simulation in humans: Comparison with pressure wire – fractional flow reserve. EuroIntervention 2014, 10, 574–583. [Google Scholar] [CrossRef]
- Chiu, J.-J.; Chien, S. Effects of Disturbed Flow on Vascular Endothelium: Pathophysiological Basis and Clinical Perspectives. Physiol. Rev. 2011, 91, 327–387. [Google Scholar] [CrossRef] [Green Version]
- Stone, P.H.; Saito, S.; Takahashi, S.; Makita, Y.; Nakamura, S.; Kawasaki, T.; Takahashi, A.; Katsuki, T.; Nakamura, S.; Namiki, A.; et al. Response to Letter Regarding Article, “Prediction of Progression of Coronary Artery Disease and Clinical Outcomes Using Vascular Profiling of Endothelial Shear Stress and Arterial Plaque Characteristics: The PREDICTION Study”. Circulation 2013, 127, e489–e490. [Google Scholar] [CrossRef] [Green Version]
- Gijsen, F.; Katagiri, Y.; Barlis, P.; Bourantas, C.; Collet, C.; Coskun, U.; Daemen, J.; Dijkstra, J.; Edelman, E.; Evans, P.; et al. Expert recommendations on the assessment of wall shear stress in human coronary arteries: Existing methodologies, technical considerations, and clinical applications. Eur. Hear. J. 2019, 40, 3421–3433. [Google Scholar] [CrossRef] [Green Version]
- Devereux, R.B.; Reichek, N. Echocardiographic determination of left ventricular mass in man. Anatomic validation of the method. Circulation 1977, 55, 613–618. [Google Scholar] [CrossRef] [Green Version]
- Koszegi, Z.; Maes, A.; Piessens, J.; Van De Werf, F.; Mortelmans, L. Segmental comparison between coronary angiography and positron emission tomography reveals low predictive value of epicardial flow for viability. Eur. Heart J. 1998, 19, 959–967. [Google Scholar] [CrossRef] [Green Version]
- Pedrigi, R.M.; Poulsen, C.B.; Mehta, V.V.; Ramsing Holm, N.; Pareek, N.; Post, A.L.; Kilic, I.D.; Banya, W.A.; Dall’Ara, G.; Mattesini, A.; et al. Inducing Persistent Flow Disturbances Accelerates Atherogenesis and Promotes Thin Cap Fibroatheroma Development in D374Y-PCSK9 Hypercholesterolemic Minipigs. Circulation 2015, 132, 1003–1012. [Google Scholar] [CrossRef] [Green Version]
- Bangalore, S.; Sharma, A.; Slotwiner, A.; Yatskar, L.; Harari, R.; Shah, B.; Ibrahim, H.; Friedman, G.H.; Thompson, C.; Alviar, C.L.; et al. ST-Segment Elevation in Patients with Covid-19—A Case Series. N. Engl. J. Med. 2020, 382, 2478–2480. [Google Scholar] [CrossRef]
- Nägele, M.P.; Haubner, B.; Tanner, F.C.; Ruschitzka, F.; Flammer, A.J. Endothelial dysfunction in COVID-19: Current findings and therapeutic implications. Atherosclerosis 2020, 314, 58–62. [Google Scholar] [CrossRef]
- Martini, R. The compelling arguments for the need of microvascular investigation in COVID-19 critical patients. Clin. Hemorheol. Microcirc. 2020, 75, 1–8. [Google Scholar] [CrossRef]
- Chu, M.; von Birgelen, C.; Li, Y.; Westra, J.; Yang, J.; Holm, N.R.; Reiber, J.H.; Wijns, W.; Tu, S. Quantification of disturbed coronary flow by disturbed vorticity index and relation with fractional flow reserve. Atherosclerosis 2018, 273, 136–144. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Thompson, E.W.; Lefieux, A.; Molony, D.S.; Davis, E.L.; Chand, N.; Fournier, S.; Lee, H.S.; Suh, J.; Sato, K.; et al. High Coronary Shear Stress in Patients With Coronary Artery Disease Predicts Myocardial Infarction. J. Am. Coll. Cardiol. 2018, 72, 1926–1935. [Google Scholar] [CrossRef]
- van de Hoef, T.P.; Echavarría-Pinto, M.; Van Lavieren, M.A.; Meuwissen, M.; Serruys, P.W.; Tijssen, J.G.; Pocock, S.J.; Escaned, J.; Piek, J.J. Diagnostic and Prognostic Implications of Coronary Flow Capacity: A Comprehensive Cross-Modality Physiological Concept in Ischemic Heart Disease. JACC Cardiovasc. Interv. 2015, 8, 1670–1680. [Google Scholar] [CrossRef]
- Van de Hoef, T.P.; Siebes, M.; Spaan, J.A.; Piek, J.J. Fundamentals in clinical coronary physiology: Why coronary flow is more important than coronary pressure. Eur. Heart J. 2015, 36, 3312–3319. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| General | |
| Age yrs (SD) | 59.56 (7.02) |
| Men n (%) | 14 (87.50) |
| CV comorbidities | |
| Hypertension n (%) | 13 (81.25) |
| Diabetes mellitus n (%) | 8 (50.00) |
| Dyslipidemia n (%) | 9 (56.25) |
| PAD n (%) | 2 (12.50) |
| Cardiac conditions | |
| CHD n (%) | 16 (100.00) |
| Previous stent implantation | 10 (62.50) |
| Case | Artery | Lesion Length 3D (mm) | Min. lumen Area 3D (mm2) | Diameter Stenosis (%) | Pa Rest mmHg | Pd Rest mmHg | Pa Vasodil mmHg | Pd Vasodil mmHg | FFR | CFRp-3D | FSi |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | RCA | 11.3 | 1.62 | 40 | 73 | 72 | 67 | 63 | 0.94 | 3.55 | 0.010 |
| 2 | LCx | 9.0 | 5.62 | 32 | 108 | 106 | 96 | 88 | 0.92 | 3.47 | 0.016 |
| 3 | RCA | 6.6 | 3.56 | 46 | 104 | 100 | 100 | 91 | 0.91 | 1.86 | 0.017 |
| 4 | LAD | 39.3 | 1.69 | 49 | 93 | 86 | 94 | 81 | 0.86 | 1.74 | 0.010 |
| 5 | LAD | 18.7 | 0.44 | 69 | 93 | 80 | 80 | 50 | 0.63 | 1.58 | 0.108 |
| 6 | LAD | 27.1 | 1.17 | 64 | 89 | 70 | 75 | 48 | 0.64 | 1.24 | 0.040 |
| 7 | LAD | 16.5 | 2.79 | 44 | 117 | 109 | 91 | 72 | 0.79 | 1.65 | 0.054 |
| 8 | LAD | 15.6 | 2.32 | 47 | 95 | 88 | 89 | 79 | 0.89 | 1.33 | 0.007 |
| 9 | RCA | 11.7 | 2.23 | 70 | 91 | 89 | 94 | 85 | 0.90 | 3.01 | 0.047 |
| 10 | LAD | 53.8 | 0.95 | 70 | 96 | 76 | 100 | 53 | 0.53 | 1.74 | 0.141 |
| 11 | LCx | 34.0 | 0.78 | 77 | 105 | 65 | 103 | 56 | 0.54 | 1.09 | 0.033 |
| 12 | LCx | 8.2 | 1.98 | 39 | 90 | 88 | 82 | 75 | 0.91 | 2.93 | 0.018 |
| 13 | LAD | 19.7 | 2.11 | 52 | 110 | 98 | 108 | 85 | 0.79 | 1.57 | 0.045 |
| 14A | RCA | 12.2 | 1.00 | 54 | 101 | 93 | 104 | 82 | 0.79 | 2.21 | 0.062 |
| 14B | RCA | 14.4 * | 2.38 * | 37 * | 97 | 95 | 97 | 91 | 0.94 | 2.68 | 0.009 |
| 15A | LAD | 36.1 | 1.41 | 60 | 115 | 102 | 116 | 83 | 0.72 | 1.88 | 0.085 |
| 15B | LAD | 18.1 * | 2.75 * | 42 * | 113 | 105 | 105 | 89 | 0.85 | 1.72 | 0.022 |
| 16A | LAD | 50.7 | 0.80 | 57 | 87 | 64 | 82 | 51 | 0.62 | 1.28 | 0.028 |
| 16B | LAD | 8.4 * | 4.78 * | 26 * | 79 | 69 | 72 | 55 | 0.76 | 1.68 | 0.003 |
| Mean | na. | 21.65 | 2.13 | 51.32 | 97.68 | 87.11 | 92.37 | 72.47 | 0.79 | 2.01 | 0.040 |
| SD | na. | 11.69 | 0.99 | 11.70 | 9.63 | 12.09 | 10.63 | 13.87 | 0.11 | 0.61 | 0.028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabó, G.T.; Üveges, Á.; Tar, B.; Ágoston, A.; Dorj, A.; Jenei, C.; Kolozsvári, R.; Csippa, B.; Czuriga, D.; Kőszegi, Z. The Holistic Coronary Physiology Display: Calculation of the Flow Separation Index in Vessel-Specific Individual Flow Range during Fractional Flow Reserve Measurement Using 3D Coronary Reconstruction. J. Clin. Med. 2021, 10, 1910. https://doi.org/10.3390/jcm10091910
Szabó GT, Üveges Á, Tar B, Ágoston A, Dorj A, Jenei C, Kolozsvári R, Csippa B, Czuriga D, Kőszegi Z. The Holistic Coronary Physiology Display: Calculation of the Flow Separation Index in Vessel-Specific Individual Flow Range during Fractional Flow Reserve Measurement Using 3D Coronary Reconstruction. Journal of Clinical Medicine. 2021; 10(9):1910. https://doi.org/10.3390/jcm10091910
Chicago/Turabian StyleSzabó, Gábor Tamás, Áron Üveges, Balázs Tar, András Ágoston, Azzaya Dorj, Csaba Jenei, Rudolf Kolozsvári, Benjamin Csippa, Dániel Czuriga, and Zsolt Kőszegi. 2021. "The Holistic Coronary Physiology Display: Calculation of the Flow Separation Index in Vessel-Specific Individual Flow Range during Fractional Flow Reserve Measurement Using 3D Coronary Reconstruction" Journal of Clinical Medicine 10, no. 9: 1910. https://doi.org/10.3390/jcm10091910
APA StyleSzabó, G. T., Üveges, Á., Tar, B., Ágoston, A., Dorj, A., Jenei, C., Kolozsvári, R., Csippa, B., Czuriga, D., & Kőszegi, Z. (2021). The Holistic Coronary Physiology Display: Calculation of the Flow Separation Index in Vessel-Specific Individual Flow Range during Fractional Flow Reserve Measurement Using 3D Coronary Reconstruction. Journal of Clinical Medicine, 10(9), 1910. https://doi.org/10.3390/jcm10091910






