Diagnostic and Therapeutic Issues in Glioma Using Imaging Data: The Challenge of Numerical Twinning
Abstract
:1. Introduction
2. Choosing the Parameters
3. Automatic Analysis of Tumoral Heterogeneity: The Challenge of Segmentation
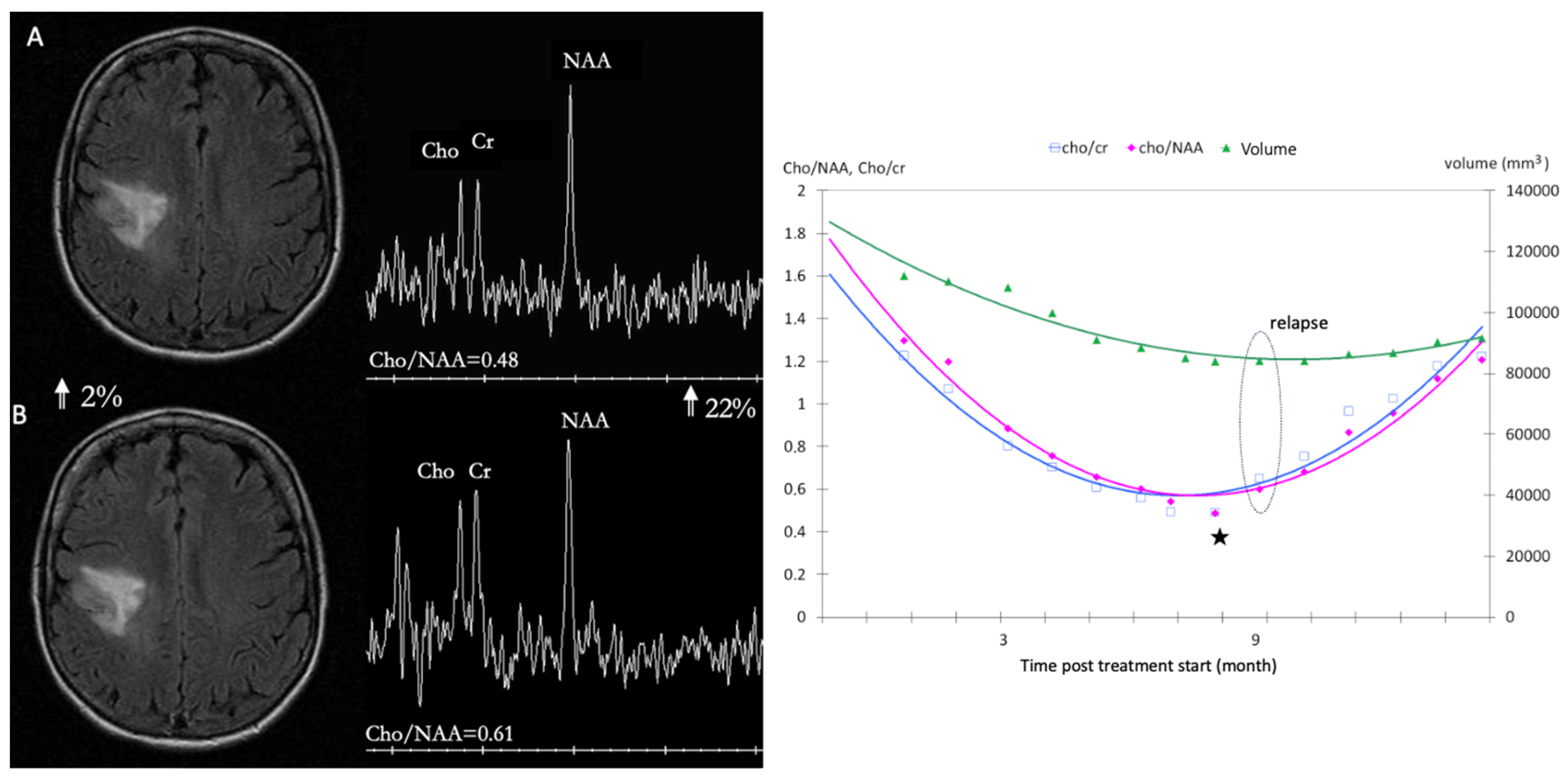
4. Oncometabolic Representation: Dynamic Representation of Tumor Behavior
5. Other Genetic-Metabolic Issues
6. Building Connectomes
6.1. Metabolic Connectome
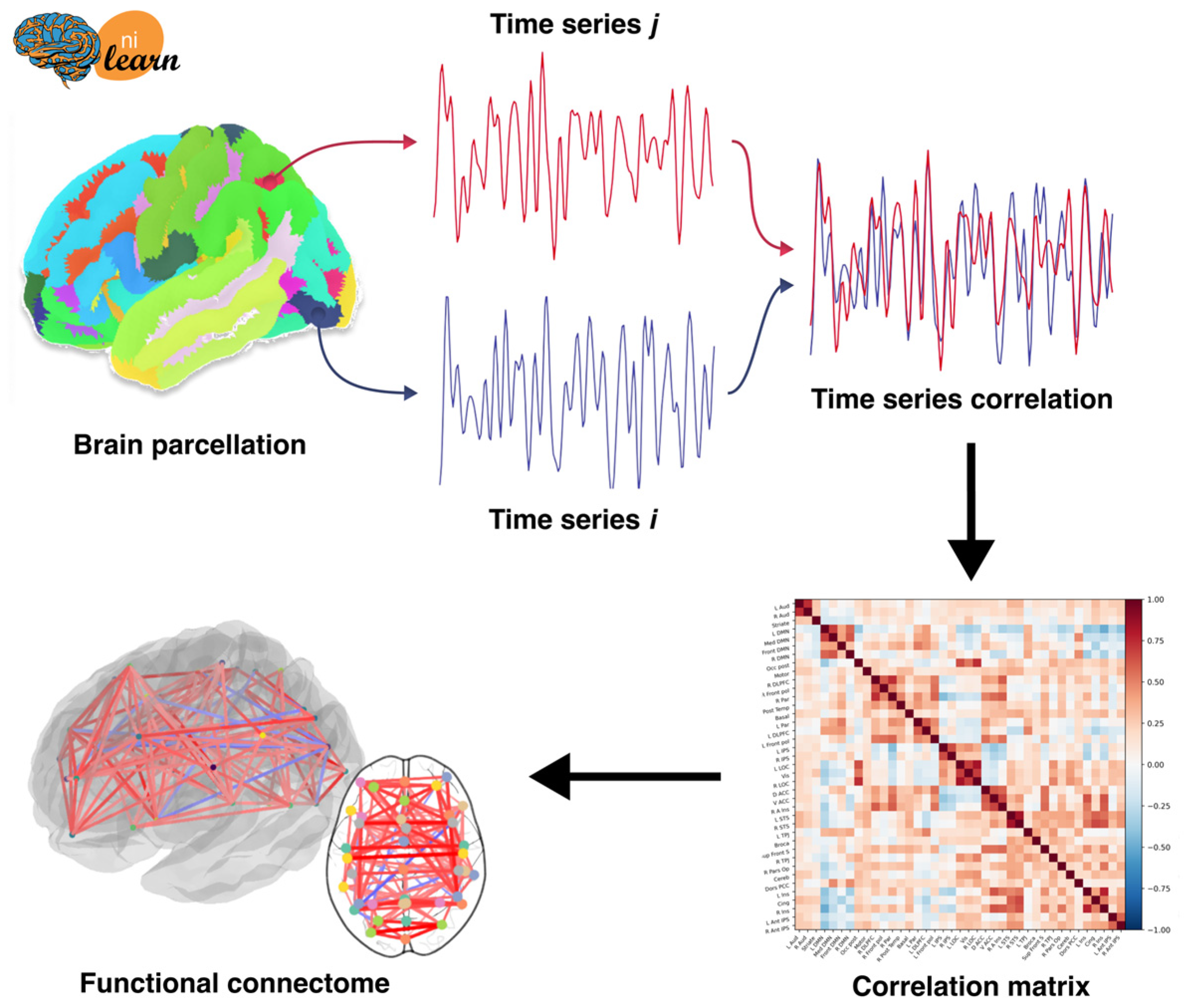
6.2. Functional Connectome
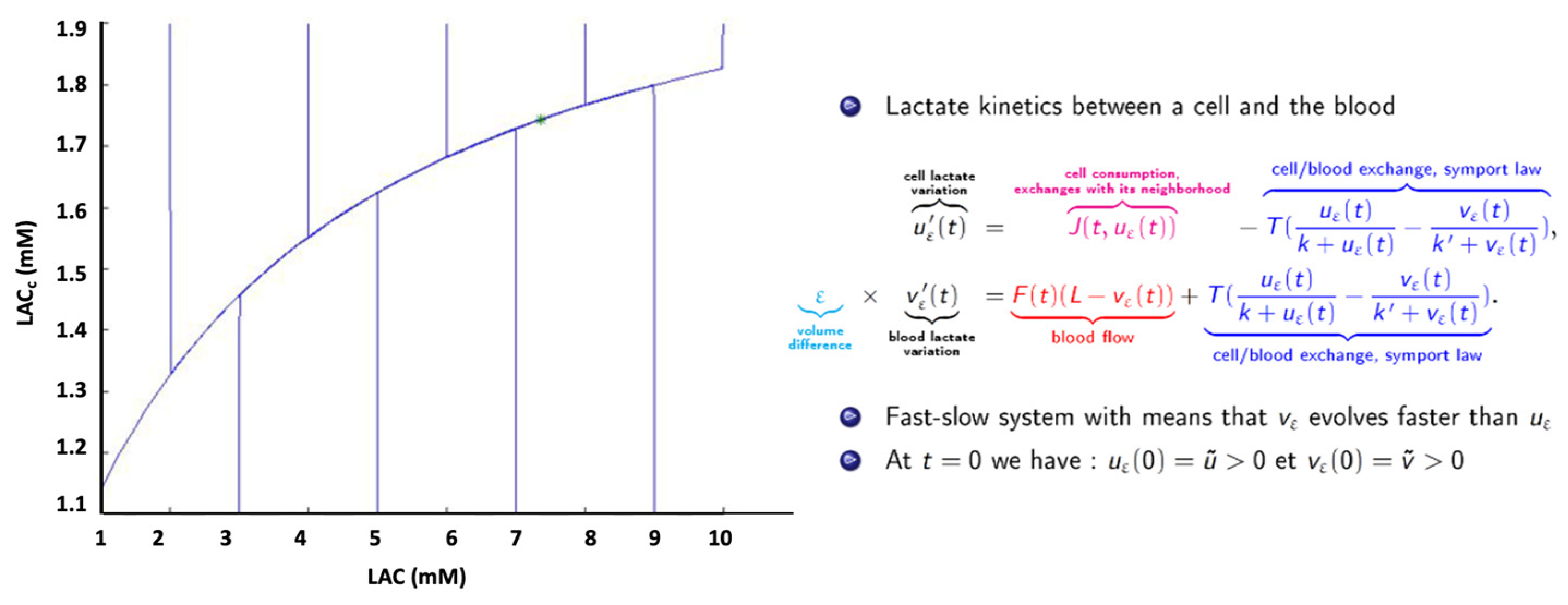
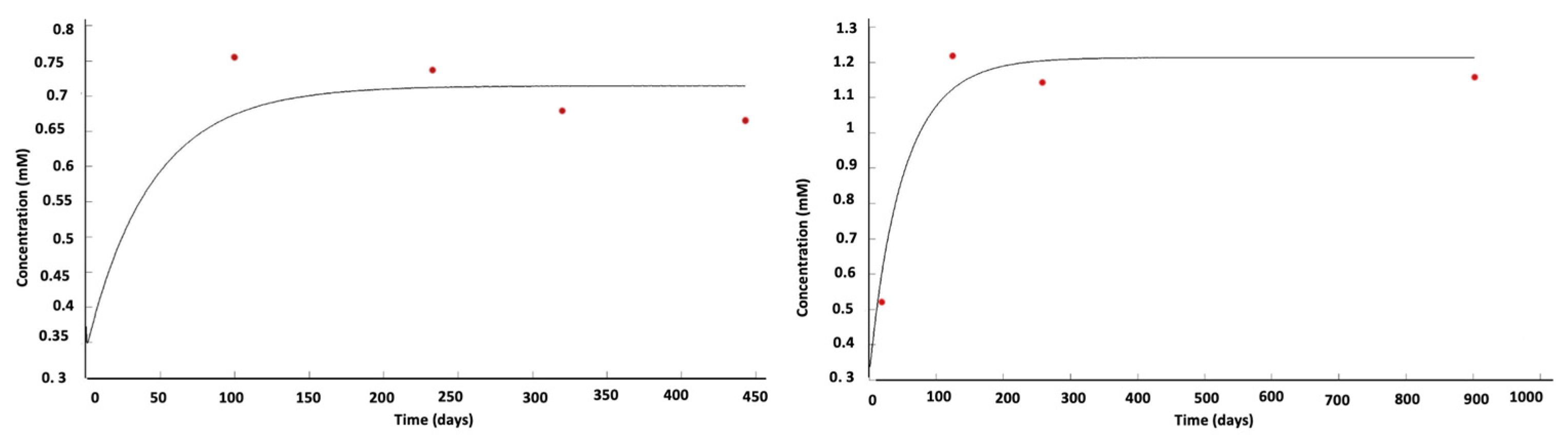
7. Therapeutic Simulation: Chemotherapy Modulation
8. Outcome Prediction
9. Digital Twin: Issues
10. Conclusions and Future Directions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Di Ieva, A.; Magnussen, J.S.; McIntosh, J.; Mulcahy, M.J.; Pardey, M.; Choi, C. Magnetic Resonance Spectroscopic Assessment of Isocitrate Dehydrogenase Status in Gliomas: The New Frontiers of Spectrobiopsy in Neurodiagnostics. World Neurosurg. 2020, 133, e421–e427. [Google Scholar] [CrossRef]
- Biswal, B.; Yetkin, F.Z.; Haughton, V.M.; Hyde, J.S. Functional Connectivity in the Motor Cortex of Resting Human Brain Using Echo-Planar MRI. Magn. Reson. Med. 1995, 34, 537–541. [Google Scholar] [CrossRef]
- Baxter, D.A.; Byrne, J.H. Simulator for Neural Networks and Action Potentials. Methods Mol. Biol. 2007, 401, 127–154. [Google Scholar] [CrossRef]
- Schilling, K.G.; Tax, C.M.W.; Rheault, F.; Landman, B.A.; Anderson, A.W.; Descoteaux, M.; Petit, L. Prevalence of White Matter Pathways Coming into a Single White Matter Voxel Orientation: The Bottleneck Issue in Tractography. Hum. Brain Mapp. 2022, 43, 1196–1213. [Google Scholar] [CrossRef]
- Hart, M.G.; Ypma, R.J.F.; Romero-Garcia, R.; Price, S.J.; Suckling, J. Graph Theory Analysis of Complex Brain Networks: New Concepts in Brain Mapping Applied to Neurosurgery. J. Neurosurg. 2016, 124, 1665–1678. [Google Scholar] [CrossRef] [PubMed]
- Fornito, A.; Zalesky, A.; Breakspear, M. Graph Analysis of the Human Connectome: Promise, Progress, and Pitfalls. NeuroImage 2013, 80, 426–444. [Google Scholar] [CrossRef]
- Smith, S.M.; Beckmann, C.F.; Andersson, J.; Auerbach, E.J.; Bijsterbosch, J.; Douaud, G.; Duff, E.; Feinberg, D.A.; Griffanti, L.; Harms, M.P.; et al. Resting-State fMRI in the Human Connectome Project. NeuroImage 2013, 80, 144–168. [Google Scholar] [CrossRef]
- Sporns, O.; Tononi, G.; Kötter, R. The Human Connectome: A Structural Description of the Human Brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef] [PubMed]
- Discovering the Human Connectome—Sporns, Olaf: 9780262017909—AbeBooks. Available online: https://www.abebooks.fr/9780262017909/Discovering-Human-Connectome-Sporns-Olaf-0262017903/plp (accessed on 3 November 2023).
- He, J.; Zhang, F.; Pan, Y.; Feng, Y.; Rushmore, J.; Torio, E.; Rathi, Y.; Makris, N.; Kikinis, R.; Golby, A.J.; et al. Reconstructing the Somatotopic Organization of the Corticospinal Tract Remains a Challenge for Modern Tractography Methods. Hum. Brain Mapp. 2023, 44, 6055–6073. [Google Scholar] [CrossRef] [PubMed]
- Conturo, T.E.; Lori, N.F.; Cull, T.S.; Akbudak, E.; Snyder, A.Z.; Shimony, J.S.; McKinstry, R.C.; Burton, H.; Raichle, M.E. Tracking Neuronal Fiber Pathways in the Living Human Brain. Proc. Natl. Acad. Sci. USA 1999, 96, 10422–10427. [Google Scholar] [CrossRef]
- Mori, S.; Crain, B.J.; Chacko, V.P.; van Zijl, P.C. Three-Dimensional Tracking of Axonal Projections in the Brain by Magnetic Resonance Imaging. Ann. Neurol. 1999, 45, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Basser, P.J.; Pajevic, S.; Pierpaoli, C.; Duda, J.; Aldroubi, A. In Vivo Fiber Tractography Using DT-MRI Data. Magn. Reson. Med. 2000, 44, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, P.; Lavrador, J.P.; Baig Mirza, A.; Pereira, N.; Keeble, H.; Borri, M.; Furlanetti, L.; Brogna, C.; Jarosz, J.; Gullan, R.; et al. Intraoperative Mapping of Pre-Central Motor Cortex and Subcortex: A Proposal for Supplemental Cortical and Novel Subcortical Maps to Penfield’s Motor Homunculus. Brain Struct. Funct. 2021, 226, 1601–1611. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.K.; Cloughesy, T.F.; Sinha, U.; Garakian, J.; Lazareff, J.; Rubino, G.; Rubino, L.; Becker, D.P.; Vinters, H.V.; Alger, J.R. Relationships between Choline Magnetic Resonance Spectroscopy, Apparent Diffusion Coefficient and Quantitative Histopathology in Human Glioma. J. Neurooncol. 2000, 50, 215–226. [Google Scholar] [CrossRef]
- Barajas, R.F.; Hodgson, J.G.; Chang, J.S.; Vandenberg, S.R.; Yeh, R.-F.; Parsa, A.T.; McDermott, M.W.; Berger, M.S.; Dillon, W.P.; Cha, S. Glioblastoma Multiforme Regional Genetic and Cellular Expression Patterns: Influence on Anatomic and Physiologic MR Imaging. Radiology 2010, 254, 564–576. [Google Scholar] [CrossRef]
- Verma, P.; Singh, B.K.; Sudhan, M.D.; Singh, R.K.; Bagul, S.D.; Chandak, A.R.; Soni, B.K.; Shelly, D.; Basu, S. 68 Ga-PSMA-11 PET/CT Imaging in Brain Gliomas and Its Correlation with Clinicopathological Prognostic Parameters. Clin. Nucl. Med. 2023, 48, e559–e563. [Google Scholar] [CrossRef]
- Guillevin, R.; Menuel, C.; Abud, L.; Costalat, R.; Capelle, L.; Hoang-Xuan, K.; Habas, C.; Chiras, J.; Vallee, J.N. Proton MR Spectroscopy in Predicting the Increase of Perfusion MR Imaging for WHO Grade II Gliomas. J. Magn. Reson. Imaging 2012, 35, 543–550. [Google Scholar] [CrossRef]
- Choi, C.; Ganji, S.K.; DeBerardinis, R.J.; Hatanpaa, K.J.; Rakheja, D.; Kovacs, Z.; Yang, X.-L.; Mashimo, T.; Raisanen, J.M.; Marin-Valencia, I.; et al. 2-Hydroxyglutarate Detection by Magnetic Resonance Spectroscopy in IDH-Mutated Patients with Gliomas. Nat. Med. 2012, 18, 624–629. [Google Scholar] [CrossRef]
- Franco, P.; Huebschle, I.; Simon-Gabriel, C.P.; Dacca, K.; Schnell, O.; Beck, J.; Mast, H.; Urbach, H.; Wuertemberger, U.; Prinz, M.; et al. Mapping of Metabolic Heterogeneity of Glioma Using MR-Spectroscopy. Cancers 2021, 13, 2417. [Google Scholar] [CrossRef]
- Warburg, O. Über den Stoffwechsel der Carcinomzelle. Naturwissenschaften 1924, 12, 1131–1137. [Google Scholar] [CrossRef]
- Sonkar, K.; Ayyappan, V.; Tressler, C.M.; Adelaja, O.; Cai, R.; Cheng, M.; Glunde, K. Focus on the Glycerophosphocholine Pathway in Choline Phospholipid Metabolism of Cancer. NMR Biomed. 2019, 32, e4112. [Google Scholar] [CrossRef] [PubMed]
- White, K.A.; Grillo-Hill, B.K.; Barber, D.L. Cancer Cell Behaviors Mediated by Dysregulated pH Dynamics at a Glance. J. Cell Sci. 2017, 130, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Bachert, P.; Bellemann, M.E. Kinetics of the in vivo31P 1H Nuclear Overhauser Effect of the Human-Calf-Muscle Phosphocreatine Resonance. J. Magn. Reson. 1992, 100, 146–156. [Google Scholar] [CrossRef]
- Louis, D.N.; Perry, A.; Reifenberger, G.; von Deimling, A.; Figarella-Branger, D.; Cavenee, W.K.; Ohgaki, H.; Wiestler, O.D.; Kleihues, P.; Ellison, D.W. The 2016 World Health Organization Classification of Tumors of the Central Nervous System: A Summary. Acta Neuropathol. 2016, 131, 803–820. [Google Scholar] [CrossRef] [PubMed]
- Lechelek, L.; Horna, S.; Zrour, R.; Naudin, M.; Guillevin, C. A Hybrid Method for 3D Reconstruction of MR Images. J. Imaging 2022, 8, 103. [Google Scholar] [CrossRef]
- Gerbaud, S.; Horna, S.; Zrour, R.; Naudin, M.; Guillevin, C.; Meseure, P. Reconstruction and Topological Cleaning of Brain MR Images. In Proceedings of the 2021 Sixth International Conference on Advances in Biomedical Engineering (ICABME), Werdanyeh, Lebanon, 7–9 October 2021; IEEE: New York, NY, USA; pp. 89–92. [Google Scholar]
- Obeid, H.A.A.; Mercier, B.; Zrour, R.; Horna, S.; Naudin, M.; Khalil, M. 3D Multimodal Visualization of Medical Data: Applied to Perfusion-Weighted MRI. In Proceedings of the 2023 Seventh International Conference on Advances in Biomedical Engineering (ICABME), Baabda, Lebanon, 12–13 October 2023; pp. 167–173. [Google Scholar]
- Coupet, M.; Urruty, T.; Leelanupab, T.; Naudin, M.; Bourdon, P.; Maloigne, C.F.; Guillevin, R. A Multi-Sequences MRI Deep Framework Study Applied to Glioma Classfication. Multimed. Tools Appl. 2022, 81, 13563–13591. [Google Scholar] [CrossRef]
- Dequidt, P.; Bourdon, P.; Ben Ahmed, O.; Tremblais, B.; Guillevin, C.; Naudin, M.; Fernandez-Maloigne, C.; Guillevin, R. Recent Advances in Glioma Grade Classification Using Machine and Deep Learning on MR Data. In Proceedings of the 2019 Fifth International Conference on Advances in Biomedical Engineering (ICABME), Tripoli, Lebanon, 17–19 October 2019; pp. 1–4. [Google Scholar]
- Perrillat-Mercerot, A.; Miranville, A.; Bourmeyster, N.; Guillevin, C.; Naudin, M.; Guillevin, R. What Mathematical Models Can or Cannot Do in Glioma Description and Understanding. Discret. Contin. Dyn. Syst.-S 2020, 13, 2165–2193. [Google Scholar] [CrossRef]
- Cho, N.S.; Sanvito, F.; Thakuria, S.; Wang, C.; Hagiwara, A.; Nagaraj, R.; Oshima, S.; Lopez Kolkovsky, A.L.; Lu, J.; Raymond, C.; et al. Multi-Nuclear Sodium, Diffusion, and Perfusion MRI in Human Gliomas. J. Neurooncol. 2023, 163, 417–427. [Google Scholar] [CrossRef]
- Shaffer, A.; Kwok, S.S.; Naik, A.; Anderson, A.T.; Lam, F.; Wszalek, T.; Arnold, P.M.; Hassaneen, W. Ultra-High-Field MRI in the Diagnosis and Management of Gliomas: A Systematic Review. Front. Neurol. 2022, 13, 857825. [Google Scholar] [CrossRef]
- Zaiss, M.; Windschuh, J.; Paech, D.; Meissner, J.-E.; Burth, S.; Schmitt, B.; Kickingereder, P.; Wiestler, B.; Wick, W.; Bendszus, M.; et al. Relaxation-Compensated CEST-MRI of the Human Brain at 7T: Unbiased Insight into NOE and Amide Signal Changes in Human Glioblastoma. NeuroImage 2015, 112, 180–188. [Google Scholar] [CrossRef]
- Blystad, I.; Warntjes, J.B.M.; Smedby, Ö.; Lundberg, P.; Larsson, E.-M.; Tisell, A. Quantitative MRI Using Relaxometry in Malignant Gliomas Detects Contrast Enhancement in Peritumoral Oedema. Sci. Rep. 2020, 10, 17986. [Google Scholar] [CrossRef] [PubMed]
- Vallée, R.; Vallée, J.-N.; Guillevin, C.; Lallouette, A.; Thomas, C.; Rittano, G.; Wager, M.; Guillevin, R.; Vallée, A. Machine Learning Decision Tree Models for Multiclass Classification of Common Malignant Brain Tumors Using Perfusion and Spectroscopy MRI Data. Front. Oncol. 2023, 13, 1089998. [Google Scholar] [CrossRef] [PubMed]
- Vallée, A.; Guillevin, C.; Wager, M.; Delwail, V.; Guillevin, R.; Vallée, J.-N. Added Value of Spectroscopy to Perfusion MRI in the Differential Diagnostic Performance of Common Malignant Brain Tumors. Am. J. Neuroradiol. 2018, 39, 1423–1431. [Google Scholar] [CrossRef] [PubMed]
- McKnight, T.R. Proton Magnetic Resonance Spectroscopic Evaluation of Brain Tumor Metabolism. Semin. Oncol. 2004, 31, 605–617. [Google Scholar] [CrossRef] [PubMed]
- Chaumeil, M.M.; Radoul, M.; Najac, C.; Eriksson, P.; Viswanath, P.; Blough, M.D.; Chesnelong, C.; Luchman, H.A.; Cairncross, J.G.; Ronen, S.M. Hyperpolarized (13)C MR Imaging Detects No Lactate Production in Mutant IDH1 Gliomas: Implications for Diagnosis and Response Monitoring. NeuroImage Clin. 2016, 12, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Chronaiou, I.; Stensjøen, A.L.; Sjøbakk, T.E.; Esmaeili, M.; Bathen, T.F. Impacts of MR Spectroscopic Imaging on Glioma Patient Management. Acta Oncol. 2014, 53, 580–589. [Google Scholar] [CrossRef] [PubMed]
- Golman, K.; Zandt, R.I.; Lerche, M.; Pehrson, R.; Ardenkjaer-Larsen, J.H. Metabolic Imaging by Hyperpolarized 13C Magnetic Resonance Imaging for In Vivo Tumor Diagnosis. Cancer Res. 2006, 66, 10855–10860. [Google Scholar] [CrossRef] [PubMed]
- Hart, M.G.; Price, S.J.; Suckling, J. Connectome Analysis for Pre-Operative Brain Mapping in Neurosurgery. Br. J. Neurosurg. 2016, 30, 506–517. [Google Scholar] [CrossRef]
- Pérez-Escuredo, J.; Van Hée, V.F.; Sboarina, M.; Falces, J.; Payen, V.L.; Pellerin, L.; Sonveaux, P. Monocarboxylate Transporters in the Brain and in Cancer. Biochim. Biophys. Acta 2016, 1863, 2481–2497. [Google Scholar] [CrossRef]
- Guillevin, R.; Menuel, C.; Duffau, H.; Kujas, M.; Capelle, L.; Aubert, A.; Taillibert, S.; Idbaih, A.; Pallud, J.; Demarco, G.; et al. Proton Magnetic Resonance Spectroscopy Predicts Proliferative Activity in Diffuse Low-Grade Gliomas. J. Neurooncol. 2008, 87, 181–187. [Google Scholar] [CrossRef]
- Nagashima, H.; Tanaka, K.; Sasayama, T.; Irino, Y.; Sato, N.; Takeuchi, Y.; Kyotani, K.; Mukasa, A.; Mizukawa, K.; Sakata, J.; et al. Diagnostic Value of Glutamate with 2-Hydroxyglutarate in Magnetic Resonance Spectroscopy for IDH1 Mutant Glioma. Neuro-Oncology 2016, 18, 1559–1568. [Google Scholar] [CrossRef]
- Guillevin, R.; Menuel, C.; Vallee, J.N.; Francoise, J.P.; Capelle, L.; Habas, C.; De Marco, G.; Chiras, J.; Costalat, R. Mathematical Modeling of Energy Metabolism and Hemodynamics of WHO Grade II Gliomas Using In Vivo MR Data. Comptes Rendus Biol. 2011, 334, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chang, K.; Bai, H.X.; Xiao, B.; Su, C.; Bi, W.L.; Zhang, P.J.; Senders, J.T.; Vallières, M.; Kavouridis, V.K.; et al. Machine Learning Reveals Multimodal MRI Patterns Predictive of Isocitrate Dehydrogenase and 1p/19q Status in Diffuse Low- and High-Grade Gliomas. J. Neurooncol. 2019, 142, 299–307. [Google Scholar] [CrossRef]
- Branzoli, F.; Liserre, R.; Deelchand, D.K.; Poliani, P.L.; Bielle, F.; Nichelli, L.; Sanson, M.; Lehéricy, S.; Marjańska, M. Neurochemical Differences between 1p/19q Codeleted and Noncodeleted IDH-Mutant Gliomas by in Vivo MR Spectroscopy. Radiology 2023, 308, e223255. [Google Scholar] [CrossRef] [PubMed]
- Diamandis, E.; Gabriel, C.P.S.; Würtemberger, U.; Guggenberger, K.; Urbach, H.; Staszewski, O.; Lassmann, S.; Schnell, O.; Grauvogel, J.; Mader, I.; et al. MR-Spectroscopic Imaging of Glial Tumors in the Spotlight of the 2016 WHO Classification. J. Neurooncol. 2018, 139, 431–440. [Google Scholar] [CrossRef] [PubMed]
- Ropella-Panagis, K.M.; Seiberlich, N.; Gulani, V. Magnetic Resonance Fingerprinting: Implications and Opportunities for PET/MR. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 3, 388–399. [Google Scholar] [CrossRef] [PubMed]
- Danilov, G.V.; Kalayeva, D.B.; Vikhrova, N.B.; Konakova, T.A.; Zagorodnova, A.I.; Popova, A.A.; Postnov, A.A.; Shugay, S.V.; Pronin, I.N. Radiomics in Determining Tumor-to-Normal Brain SUV Ratio Based on 11C-Methionine PET/CT in Glioblastoma. Sovrem. Tekhnol. Med. 2023, 15, 5–11. [Google Scholar] [CrossRef]
- Tracqui, P.; Cruywagen, G.C.; Woodward, D.E.; Bartoo, G.T.; Murray, J.D.; Alvord, E.C., Jr. A Mathematical Model of Glioma Growth: The Effect of Chemotherapy on Spatio-Temporal Growth. Cell Prolif. 1995, 28, 17–31. [Google Scholar] [CrossRef]
- Duffau, H. The Anatomo-Functional Connectivity of Language Revisited. New Insights Provided by Electrostimulation and Tractography. Neuropsychologia 2008, 46, 927–934. [Google Scholar] [CrossRef]
- Mandonnet, E.; Delattre, J.Y.; Tanguy, M.L.; Swanson, K.R.; Carpentier, A.F.; Duffau, H.; Cornu, P.; Van Effenterre, R.; Alvord, E.C., Jr.; Capelle, L. Continuous Growth of Mean Tumor Diameter in a Subset of Grade II Gliomas. Ann. Neurol. 2003, 53, 524–528. [Google Scholar] [CrossRef]
- Mandonnet, E.; Pallud, J.; Clatz, O.; Taillandier, L.; Konukoglu, E.; Duffau, H.; Capelle, L. Computational Modeling of the WHO Grade II Glioma Dynamics: Principles and Applications to Management Paradigm. Neurosurg. Rev. 2008, 31, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Li, L. On a Cahn–Hilliard–Oono Model for Image Segmentation. Asymptot. Anal. 2023, 132, 519–548. [Google Scholar] [CrossRef]
- Perrillat-Mercerot, A.; Miranville, A.; Agosti, A.; Rocca, E.; Ciarletta, P.; Guillevin, R. Partial Differential Model of Lactate Neuro-Energetics: Analytic Results and Numerical Simulations. Math. Med. Biol. 2021, 38, 178–201. [Google Scholar] [CrossRef] [PubMed]
- Perrillat-Mercerot, A.; Bourmeyster, N.; Guillevin, C.; Miranville, A.; Guillevin, R. Analysis of a Mathematical Model for the Glutamate/Glutamine Cycle in the Brain. Bull. Math. Biol. 2019, 81, 4251–4270. [Google Scholar] [CrossRef] [PubMed]
- Perrillat-Mercerot, A.; Guillevin, C.; Miranville, A.; Guillevin, R. Using Mathematics in MRI Data Management for Glioma Assesment. J. Neuroradiol. 2021, 48, 282–290. [Google Scholar] [CrossRef] [PubMed]
- Davnall, F.; Yip, C.S.P.; Ljungqvist, G.; Selmi, M.; Ng, F.; Sanghera, B.; Ganeshan, B.; Miles, K.A.; Cook, G.J.; Goh, V. Assessment of Tumor Heterogeneity: An Emerging Imaging Tool for Clinical Practice? Insights Imaging 2012, 3, 573–589. [Google Scholar] [CrossRef] [PubMed]
- Miles, K.A.; Ganeshan, B.; Hayball, M.P. CT Texture Analysis Using the Filtration-Histogram Method: What Do the Measurements Mean? Cancer Imaging 2013, 13, 400–406. [Google Scholar] [CrossRef]
- Helseth, R.; Helseth, E.; Johannesen, T.B.; Langberg, C.W.; Lote, K.; Rønning, P.; Scheie, D.; Vik, A.; Meling, T.R. Overall Survival, Prognostic Factors, and Repeated Surgery in a Consecutive Series of 516 Patients with Glioblastoma Multiforme. Acta Neurol. Scand. 2010, 122, 159–167. [Google Scholar] [CrossRef]
- Grabner, G.; Kiesel, B.; Wöhrer, A.; Millesi, M.; Wurzer, A.; Göd, S.; Mallouhi, A.; Knosp, E.; Marosi, C.; Trattnig, S.; et al. Local Image Variance of 7 Tesla SWI Is a New Technique for Preoperative Characterization of Diffusely Infiltrating Gliomas: Correlation with Tumour Grade and IDH1 Mutational Status. Eur. Radiol. 2017, 27, 1556–1567. [Google Scholar] [CrossRef]
- Jiménez, J.; López, A.M.; Cruz, J.; Esteban, F.J.; Navas, J.; Villoslada, P.; Ruiz de Miras, J. A Web Platform for the Interactive Visualization and Analysis of the 3D Fractal Dimension of MRI Data. J. Biomed. Inform. 2014, 51, 176–190. [Google Scholar] [CrossRef]
- Mani, T.; Tircsó, G.; Togao, O.; Zhao, P.; Soesbe, T.C.; Takahashi, M.; Sherry, A.D. Modulation of Water Exchange in Eu(III) DOTA-Tetraamide Complexes: Considerations for in Vivo Imaging of PARACEST Agents. Contrast Media Mol. Imaging 2009, 4, 183–191. [Google Scholar] [CrossRef]
- van Zijl, P.C.M.; Jones, C.K.; Ren, J.; Malloy, C.R.; Sherry, A.D. MRI Detection of Glycogen in Vivo by Using Chemical Exchange Saturation Transfer Imaging (glycoCEST). Proc. Natl. Acad. Sci. USA 2007, 104, 4359–4364. [Google Scholar] [CrossRef] [PubMed]
- Sagiyama, K.; Mashimo, T.; Togao, O.; Vemireddy, V.; Hatanpaa, K.J.; Maher, E.A.; Mickey, B.E.; Pan, E.; Sherry, A.D.; Bachoo, R.M.; et al. In Vivo Chemical Exchange Saturation Transfer Imaging Allows Early Detection of a Therapeutic Response in Glioblastoma. Proc. Natl. Acad. Sci. USA 2014, 111, 4542–4547. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wood, T.C.; Derks, S.H.A.E.; Pruis, I.J.; van der Voort, S.; van Zanten, S.E.M.V.; Smits, M.; Warnert, E.A.H. Reproducibility of APT-Weighted CEST-MRI at 3T in Healthy Brain and Tumor across Sessions and Scanners. Sci. Rep. 2023, 13, 18115. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Trokowski, R.; Zhang, S.; Malloy, C.R.; Sherry, A.D. Imaging the Tissue Distribution of Glucose in Livers Using a PARACEST Sensor. Magn. Reson. Med. 2008, 60, 1047–1055. [Google Scholar] [CrossRef]
- Zhou, J.; Payen, J.-F.; Wilson, D.A.; Traystman, R.J.; van Zijl, P.C.M. Using the Amide Proton Signals of Intracellular Proteins and Peptides to Detect pH Effects in MRI. Nat. Med. 2003, 9, 1085–1090. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Hsu, J.-L.; Lin, K.-J.; Liu, H.-L.; Wey, S.-P.; Hsiao, I.-T. Alzheimer’s Disease Neuroimaging Initiative Characteristic Patterns of Inter- and Intra-Hemispheric Metabolic Connectivity in Patients with Stable and Progressive Mild Cognitive Impairment and Alzheimer’s Disease. Sci. Rep. 2018, 8, 13807. [Google Scholar] [CrossRef]
- Perrillat-Mercerot, A.; Deliot, N.; Miranville, A.; Guillevin, R.; Constantin, B. Mathematical Analysis of Membrane Transporters Dynamics: A Calcium Fluxes Case Study. Acta Biotheor. 2022, 70, 14. [Google Scholar] [CrossRef]
- Schu, G.; Brum, W.S.; Rodrigues, Y.E.; de Azeredo, J.C.; Pascoal, T.A.; Benedet, A.L.; Mathotaarachchi, S.; Rosa-Neto, P.; Almeida, J.; Zimmer, E.R.; et al. Stable Brain PET Metabolic Networks Using a Multiple Sampling Scheme. bioRxiv 2021. [Google Scholar] [CrossRef]
- Perrillat-Mercerot, A.; Bourmeyster, N.; Guillevin, C.; Miranville, A.; Guillevin, R. Mathematical Modeling of Substrates Fluxes and Tumor Growth in the Brain. Acta Biotheor. 2019, 67, 149–175. [Google Scholar] [CrossRef]
- Lv, K.; Cao, X.; Wang, R.; Du, P.; Fu, J.; Geng, D.; Zhang, J. Neuroplasticity of Glioma Patients: Brain Structure and Topological Network. Front. Neurol. 2022, 13, 871613. [Google Scholar] [CrossRef]
- Chen, H.S.-M.; Kumar, V.A.; Johnson, J.M.; Chen, M.M.; Noll, K.R.; Hou, P.; Prabhu, S.S.; Schomer, D.F.; Liu, H.-L. Effect of Brain Normalization Methods on the Construction of Functional Connectomes from Resting-State Functional MRI in Patients with Gliomas. Magn. Reson. Med. 2021, 86, 487–498. [Google Scholar] [CrossRef]
- Suero Molina, E.; Tait, M.J.; Di Ieva, A. Connectomics as a Prognostic Tool of Functional Outcome in Glioma Surgery of the Supplementary Motor Area: Illustrative Case. J. Neurosurg. Case Lessons 2023, 6, CASE23286. [Google Scholar] [CrossRef] [PubMed]
- Swanson, K.R.; Bridge, C.; Murray, J.D.; Alvord, E.C. Virtual and Real Brain Tumors: Using Mathematical Modeling to Quantify Glioma Growth and Invasion. J. Neurol. Sci. 2003, 216, 1–10. [Google Scholar] [CrossRef]
- Swanson, K.R.; Rockne, R.C.; Claridge, J.; Chaplain, M.A.; Alvord, E.C., Jr.; Anderson, A.R.A. Quantifying the Role of Angiogenesis in Malignant Progression of Gliomas: In Silico Modeling Integrates Imaging and Histology. Cancer Res. 2011, 71, 7366–7375. [Google Scholar] [CrossRef] [PubMed]
- Konukoglu, E.; Clatz, O.; Menze, B.H.; Stieltjes, B.; Weber, M.-A.; Mandonnet, E.; Delingette, H.; Ayache, N. Image Guided Personalization of Reaction-Diffusion Type Tumor Growth Models Using Modified Anisotropic Eikonal Equations. IEEE Trans. Med. Imaging 2010, 29, 77–95. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sadowski, S.M.; Weisbrod, A.B.; Kebebew, E.; Summers, R.M.; Yao, J. Patient Specific Tumor Growth Prediction Using Multimodal Images. Med. Image Anal. 2014, 18, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Mandonnet, E. Biomathematical Modeling of DLGG. In Diffuse Low-Grade Gliomas in Adults; Duffau, H., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 651–664. ISBN 978-3-319-55466-2. [Google Scholar]
- Lagaert, J.-B. Modélisation de la Croissance Tumorale: Estimation de Paramètres d’un Modèle de Croissance et Introduction d’un Modèle Spécifique Aux Gliomes de Tout Grade. Ph.D. Thesis, Université Sciences et Technologies-Bordeaux I, Talence, France, 2011. [Google Scholar]
- Saut, O.; Lagaert, J.-B.; Colin, T.; Fathallah-Shaykh, H.M. A Multilayer Grow-or-Go Model for GBM: Effects of Invasive Cells and Anti-Angiogenesis on Growth. Bull. Math. Biol. 2014, 76, 2306–2333. [Google Scholar] [CrossRef] [PubMed]
- Sherer, E.; Hannemann, R.E.; Rundell, A.; Ramkrishna, D. Analysis of Resonance Chemotherapy in Leukemia Treatment via Multi-Staged Population Balance Models. J. Theor. Biol. 2006, 240, 648–661. [Google Scholar] [CrossRef]
- Stupp, R.; Dietrich, P.-Y.; Ostermann Kraljevic, S.; Pica, A.; Maillard, I.; Maeder, P.; Meuli, R.; Janzer, R.; Pizzolato, G.; Miralbell, R.; et al. Promising Survival for Patients with Newly Diagnosed Glioblastoma Multiforme Treated with Concomitant Radiation plus Temozolomide Followed by Adjuvant Temozolomide. J. Clin. Oncol. 2002, 20, 1375–1382. [Google Scholar] [CrossRef]
- Stupp, R.; Mason, W.P.; van den Bent, M.J.; Weller, M.; Fisher, B.; Taphoorn, M.J.B.; Belanger, K.; Brandes, A.A.; Marosi, C.; Bogdahn, U.; et al. Radiotherapy plus Concomitant and Adjuvant Temozolomide for Glioblastoma. N. Engl. J. Med. 2005, 352, 987–996. [Google Scholar] [CrossRef] [PubMed]
- Cherfils, L.; Gatti, S.; Miranville, A.; Guillevin, R. Analysis of a Model for Tumor Growth and Lactate Exchanges in a Glioma. Discret. Contin. Dyn. Syst.-S 2021, 14, 2729–2749. [Google Scholar] [CrossRef]
- Chang, K.; Bai, H.X.; Zhou, H.; Su, C.; Bi, W.L.; Agbodza, E.; Kavouridis, V.K.; Senders, J.T.; Boaro, A.; Beers, A.; et al. Residual Convolutional Neural Network for the Determination of IDH Status in Low- and High-Grade Gliomas from MR Imaging. Clin. Cancer Res. 2018, 24, 1073–1081. [Google Scholar] [CrossRef]
- Chang, P.; Grinband, J.; Weinberg, B.D.; Bardis, M.; Khy, M.; Cadena, G.; Su, M.-Y.; Cha, S.; Filippi, C.G.; Bota, D.; et al. Deep-Learning Convolutional Neural Networks Accurately Classify Genetic Mutations in Gliomas. Am. J. Neuroradiol. 2018, 39, 1201–1207. [Google Scholar] [CrossRef]
- Choi, Y.S.; Bae, S.; Chang, J.H.; Kang, S.-G.; Kim, S.H.; Kim, J.; Rim, T.H.; Choi, S.H.; Jain, R.; Lee, S.-K. Fully Automated Hybrid Approach to Predict the IDH Mutation Status of Gliomas via Deep Learning and Radiomics. Neuro-Oncology 2021, 23, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Chang, K.; Ramkissoon, S.; Tanguturi, S.; Bi, W.L.; Reardon, D.A.; Ligon, K.L.; Alexander, B.M.; Wen, P.Y.; Huang, R.Y. Multimodal MRI Features Predict Isocitrate Dehydrogenase Genotype in High-Grade Gliomas. Neuro-Oncology 2017, 19, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.H.; Bansal, A.G.; Young, E.B.; Batchala, P.P.; Patrie, J.T.; Lopes, M.B.; Jain, R.; Fadul, C.E.; Schiff, D. Extent of Surgical Resection in Lower-Grade Gliomas: Differential Impact Based on Molecular Subtype. Am. J. Neuroradiol. 2019, 40, 1149–1155. [Google Scholar] [CrossRef] [PubMed]
- Guillevin, R.; Menuel, C.; Taillibert, S.; Capelle, L.; Costalat, R.; Abud, L.; Habas, C.; De Marco, G.; Hoang-Xuan, K.; Chiras, J.; et al. Predicting the Outcome of Grade II Glioma Treated with Temozolomide Using Proton Magnetic Resonance Spectroscopy. Br. J. Cancer 2011, 104, 1854–1861. [Google Scholar] [CrossRef]
- Litvin, A.A.; Burkin, D.A.; Kropinov, A.A.; Paramzin, F.N. Radiomics and Digital Image Texture Analysis in Oncology (Review). Mod. Technol. Med. 2021, 13, 97–104. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Jarrett, A.M.; Lorenzo, G.; Lima, E.A.B.F.; Wu, C.; Chung, C.; Patt, D.; Yankeelov, T.E. Math, Magnets, and Medicine: Enabling Personalized Oncology. Expert Rev. Precis. Med. Drug Dev. 2021, 6, 79–81. [Google Scholar] [CrossRef]
- Enderling, H.; Alfonso, J.C.L.; Moros, E.; Caudell, J.J.; Harrison, L.B. Integrating Mathematical Modeling into the Roadmap for Personalized Adaptive Radiation Therapy. Trends Cancer 2019, 5, 467–474. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, A.; Pash, G.; Hormuth, D.A.; Lorenzo, G.; Kapteyn, M.; Wu, C.; Lima, E.A.B.F.; Yankeelov, T.E.; Willcox, K. Predictive Digital Twin for Optimizing Patient-Specific Radiotherapy Regimens under Uncertainty in High-Grade Gliomas. Front. Artif. Intell. 2023, 6, 1222612. [Google Scholar] [CrossRef] [PubMed]
- Oren, O.; Gersh, B.J.; Bhatt, D.L. Artificial Intelligence in Medical Imaging: Switching from Radiographic Pathological Data to Clinically Meaningful Endpoints. Lancet Digit. Health 2020, 2, e486–e488. [Google Scholar] [CrossRef] [PubMed]
- Traverso, A.; Wee, L.; Dekker, A.; Gillies, R. Repeatability and Reproducibility of Radiomic Features: A Systematic Review. Int. J. Radiat. Oncol. 2018, 102, 1143–1158. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillevin, R.; Naudin, M.; Fayolle, P.; Giraud, C.; Le Guillou, X.; Thomas, C.; Herpe, G.; Miranville, A.; Fernandez-Maloigne, C.; Pellerin, L.; et al. Diagnostic and Therapeutic Issues in Glioma Using Imaging Data: The Challenge of Numerical Twinning. J. Clin. Med. 2023, 12, 7706. https://doi.org/10.3390/jcm12247706
Guillevin R, Naudin M, Fayolle P, Giraud C, Le Guillou X, Thomas C, Herpe G, Miranville A, Fernandez-Maloigne C, Pellerin L, et al. Diagnostic and Therapeutic Issues in Glioma Using Imaging Data: The Challenge of Numerical Twinning. Journal of Clinical Medicine. 2023; 12(24):7706. https://doi.org/10.3390/jcm12247706
Chicago/Turabian StyleGuillevin, Rémy, Mathieu Naudin, Pierre Fayolle, Clément Giraud, Xavier Le Guillou, Clément Thomas, Guillaume Herpe, Alain Miranville, Christine Fernandez-Maloigne, Luc Pellerin, and et al. 2023. "Diagnostic and Therapeutic Issues in Glioma Using Imaging Data: The Challenge of Numerical Twinning" Journal of Clinical Medicine 12, no. 24: 7706. https://doi.org/10.3390/jcm12247706
APA StyleGuillevin, R., Naudin, M., Fayolle, P., Giraud, C., Le Guillou, X., Thomas, C., Herpe, G., Miranville, A., Fernandez-Maloigne, C., Pellerin, L., & Guillevin, C. (2023). Diagnostic and Therapeutic Issues in Glioma Using Imaging Data: The Challenge of Numerical Twinning. Journal of Clinical Medicine, 12(24), 7706. https://doi.org/10.3390/jcm12247706







