Perspectives on Optimized Transcranial Electrical Stimulation Based on Spatial Electric Field Modeling in Humans
Abstract
:1. Introduction
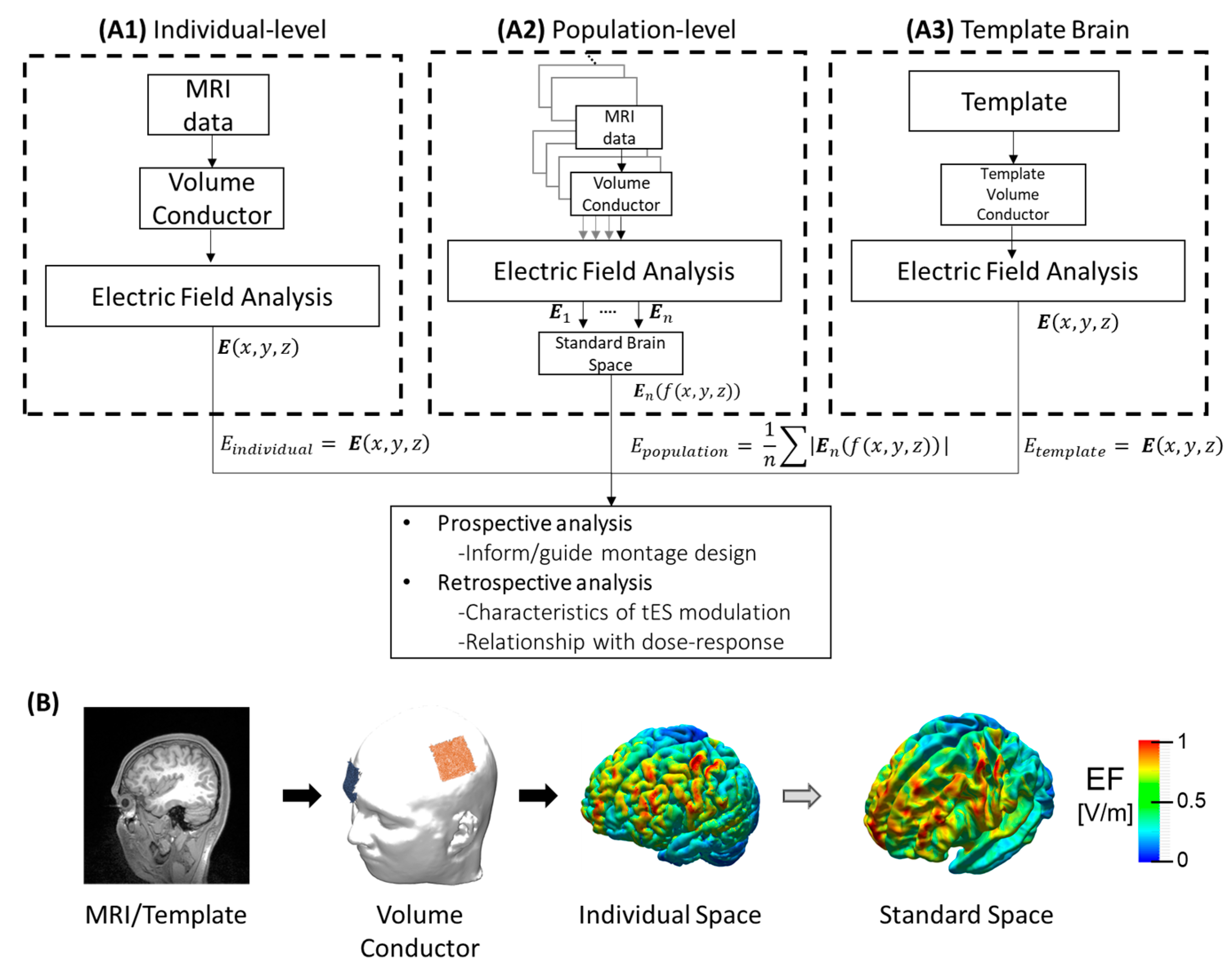
2. Outline of tES Computational Model for Electric Field Analysis
2.1. tES Parameter Space
2.2. Physics of tES
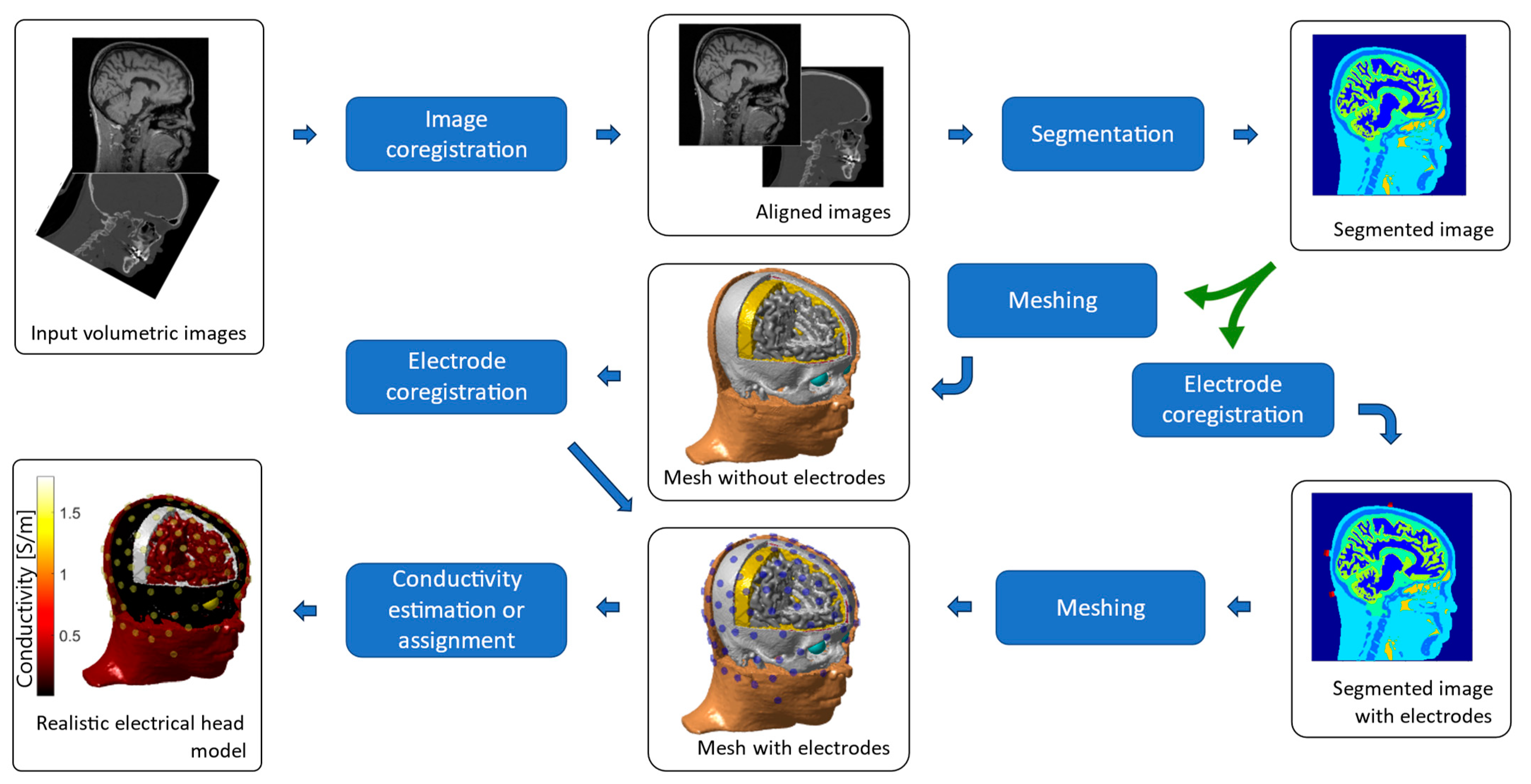
2.3. TES Forward Problem Computation
2.4. Individualized Head Model
2.5. Brain Template (Standard Space)
2.6. Electrical Conductivity
3. The Use of Computational Electric Field Modeling in tES
3.1. Individual-Level Electric Field
3.2. Population Level Electric Field
| Study | Template | No. Subjects | Target | Montage | Notes |
|---|---|---|---|---|---|
| Laakso et al. (2015) [18] | Nonlinear MNI ICBM 2009a | 24 healthy male subjects (38.63 ± 11.24) | Hand motor area | C3-Fp2 (35 cm2) | Mean electric field of 20%. |
| Laakso et al. (2016) [24]. | ・Custom averaged template (Yeo et al., 2010) ・Nonlinear MNI ICBM 2009a | 62 healthy subjects (29.2 ± 11.2 years, 12 female) | Motor and frontal areas | 16 bipolar montages (35 cm2) | Different templates do not produce significant differences for the group-level electric field in the target population. |
| Csifcsák et al. (2018) [89] | Fsaverage template using flatmaps (Pycortex) | ・19 patients with major depressive disorder (33.52 ± 13.35 years) ・19 healthy adults (28.79 ± 10.86 years). | Prefrontal cortex | 9 bipolar montages (5 × 7 or 5 × 5 cm2) and two HD (4 × 1) | MDD-associated anatomical variations are not likely to substantially influence current flow. |
| Gomez-Tames et al. (2019) [25] | ・Nonlinear MNI ICBM 2009a | 18 healthy males (43.4 ± 9.8 years) | Cerebellum (seven functional networks) | 15 bipolar montages (5 × 5 cm2 and 2 × 2 cm2) | Systematic target emerges beneath the active electrode in group-level analysis. Standard deviations of the electric field up to 55% of the mean. |
| Gomez-Tames et al. (2020) [90] | ・Nonlinear MNI ICBM 2009a | 18 healthy males (43.4 ± 9.8 years) | Seven deep brain regions | 7 bipolar montages (5 × 5 cm2) | Group-level hotspots appeared in deep brain regions (<70% of the cortical electric field). |
| Indahlastari et al. (2020) [91] | ・Customized template (UFAB-587) ・Nonlinear ICBM-152 | 587 healthy patients (51 to 98 years, 262 males) | Dorsolateral prefrontal cortex | Two bipolar montages (F3–F4, M1–SO, size of 5 × 5 cm2) | Customized template improved the accuracy of tES current prediction in an older adult population. |
| Rezaee et al. (2020) [92] | Age-group MRI brain templates and SUIT template for cerebellum | 18 age-groups of healthy adults (18 to 89 years) | Cerebellum (28 lobules) | Bipolar montage (one electrode 1 cm below and 3 cm lateral to Iz and second over the right buccinator muscle (5 × 5 cm2) | Averaged cerebellar shrinkage and increasing CSF content can lead to increased off-target stimulation. |
| Soleimani et al. (2021) [93] | Fsaverage template | 60 males with methamphetamine use disorder (35.86 ± 8.47 years) | Network (Yeo7 Schaefer-400 atlas and Brainnectomate atlas) | In the frontal site, a 4 × 1 HD ring-centered electrode over F3 | Group-level head models may be compared to a standard head model when high precision is not required. |
| Antonenko et al. (2021) [94] | Fsaverage template | ・20 young adults (20–35 years) ・20 older adults (64–79 years) | ・Middle frontal gyrus, ・Left precentral gyrus ・Left inferior parietal gyrus | Six bipolar montages of 19.6 cm2 | Normalized spatial distribution of the electric field did not differ between young and older adult populations. Higher variability observed in young compared to older adults. |
| Suzuki et al. (2022) [95] | Nonlinear MNI ICBM 2009a | 18 healthy males (43.4 ± 9.8 years) | Hand motor area | Seven bipolar montages of 3.24 cm2 | First selection of montage based on maximizing group-level electric field intensity and reducing variability. |
| Bhattacharjee et al. (2022) [96] | Talairach template | 250 healthy subjects divided in ・Three Male groups: 36.6 ± 8.4, 52.7 ± 18.6, and 74.2 ± 7.6 ・Three female groups: 34.9 ± 8.7, 53.07 ± 7.8, 74.08 ± 7.5 | ・Middle frontal gyrus, ・Left precentral gyrus | Two bipolar montages (CP5-CZ and F3-Fp2, size of 5 × 5 cm2) | Higher group-level electric currents were received by young males compared to young females at the (the opposite was observed for the old age group). |
| Mizutani-Tiebel et al. (2022) [97] | Conte69 surface template | ・25 subjects with major depressive disorder (5.5 ± 11.28 years) ・25 subjects with schizophrenia (38.1 ± 10.46) ・25 healthy subjects (36.9 ± 13.71) | Prefrontal cortex | F3–F4 (4.5 × 6.5 cm2) | There are significant differences in the group-level electric field between clinical and non-clinical populations, but no significant differences between the two populations. |
3.3. Correlations between Electric Field Calculations and Responses
| Study | tES Modality | Measurement | Physical Quantity | Relationship | Montage | Amplitude (mA) | Duration (min) | No. Participants |
| Antonenko et al. (2019) [99] | Anodal Anodal Cathodic Anodal Cathodal | GABA GABA GABA SMN * SMN | E-Field Strength Normal Component E-Field Strength Normal Component E-Field Strength | ・r = 0.53, p = 0.013 ・r = 0.47, p = 0.032 ・r = 0.45, p = 0.027 ・r = 0.53, p = 0.015 ・r = −0.49, p = 0.017 | C3 (5 × 7 cm2)– SO (10 × 10 cm2) | 1 | 15 | 24 young adults (25 years) |
| Kasten et al. (2019) [100] | tACS (α-band, 10 Hz) | EEG power increase | Electric field Strength | ・R2 = 0.76 (positive), p < 0.001 | Cz (7 × 5 cm2)–Oz (4 × 4 cm2) | 1 (peak-to-peak) | 20 | 40 young healthy adults (24.3 ± 3 years) |
| Laakso et al. (2019) [101] | Anodal tDCS | MEP | Normal Component | ・r = −0.63, p = 0.0005 | M1–SO (5 × 5 cm2) | 1 | 20 | 28 healthy young adults (27 ± 6 years) |
| Jamil et al. (2019) [102] | Anodal tDCS | Cerebral perfusion change | Electric field Strength | ・r = 0.295, p < 0.001 | M1 (35 cm2)–SO (10 × 10 cm2) | 1.5 | 90 | 29 young healthy adults (25.0 ± 4.4 years) |
| Abellaneda-Pérez et al. (2021) [103] | tDCS | Resting fMRI | Current Density | ・r = −0.401, p = 0.0023 | Multifocal montage (8 circular electrodes of 8 cm) | 4 mA maximum (2 mA limit per electrode | 25 | 31 older healthy adults (71.68 ± 2.5 years) |
| Indahlastari et al. (2021) [104] | Anodal tDCS | Functional connectivity | Current Density | ・R2 = 0.523 (positive), p < 0.05 | F3–F4 (5 × 7 cm2) | 2 | 12 | 15 older healthy adults (71.8, 61–82 years) |
| Mezger et al. (2021) [105] | tDCS | Glutamate | Electric field | - | F3–F4 (5 × 7 cm2) | 2 | 20 | 25 young adults (23.7 ± 2.0 years) |
| Zanto et al. (2021) [106] | tACS | Performance rate (NeuroRacer paradigm | Electric field | ・R2 = 0.28, p = 0.017 * ・R2 = 0.34, p = 0.012 ** ・R2 = 0.45, p = 0.003 *** * post-tACS ** 1-day follow-up *** 1-month follow-up | F3–F4 (3.14 cm2) | 2 mA peak-to-peak | 26.67 | 60 healthy older adults (60 to 80 years) |
| Nandi et al. (2022) [107] | Anodal tDCS | GABA | Electric field Strength | ・R2 = 0.46 (negative) | M1–SO (5 × 7 cm2) | 1 | 10/20 | 24 young adults (23 years) |
| Preisig et al. (2022) [108] | tACS (α-band, 40 Hz) | EEG power increase | Electric field Strength | ・r = −0.30, p = 0.13 | Two high-density montages (Cp4 and Cp6). Inner electrode radius: 1.25 cm. External electrode: inner/external radius of 3.9/5.0 cm. | 1.5 mA (peak-to-peak) | 7 | 27 young healthy adults (21.9 ± 3.1 years) |
| Yuan et al. (2023) [109] | Anodal tDCS | resting fMRI | Normal Component | ・r = 0.84, p < 0.001 | C3/C4 and FP1/FP2 (5 × 5 cm2) | 1 | 20 | 25 older stroke participants approximately (61 years) |
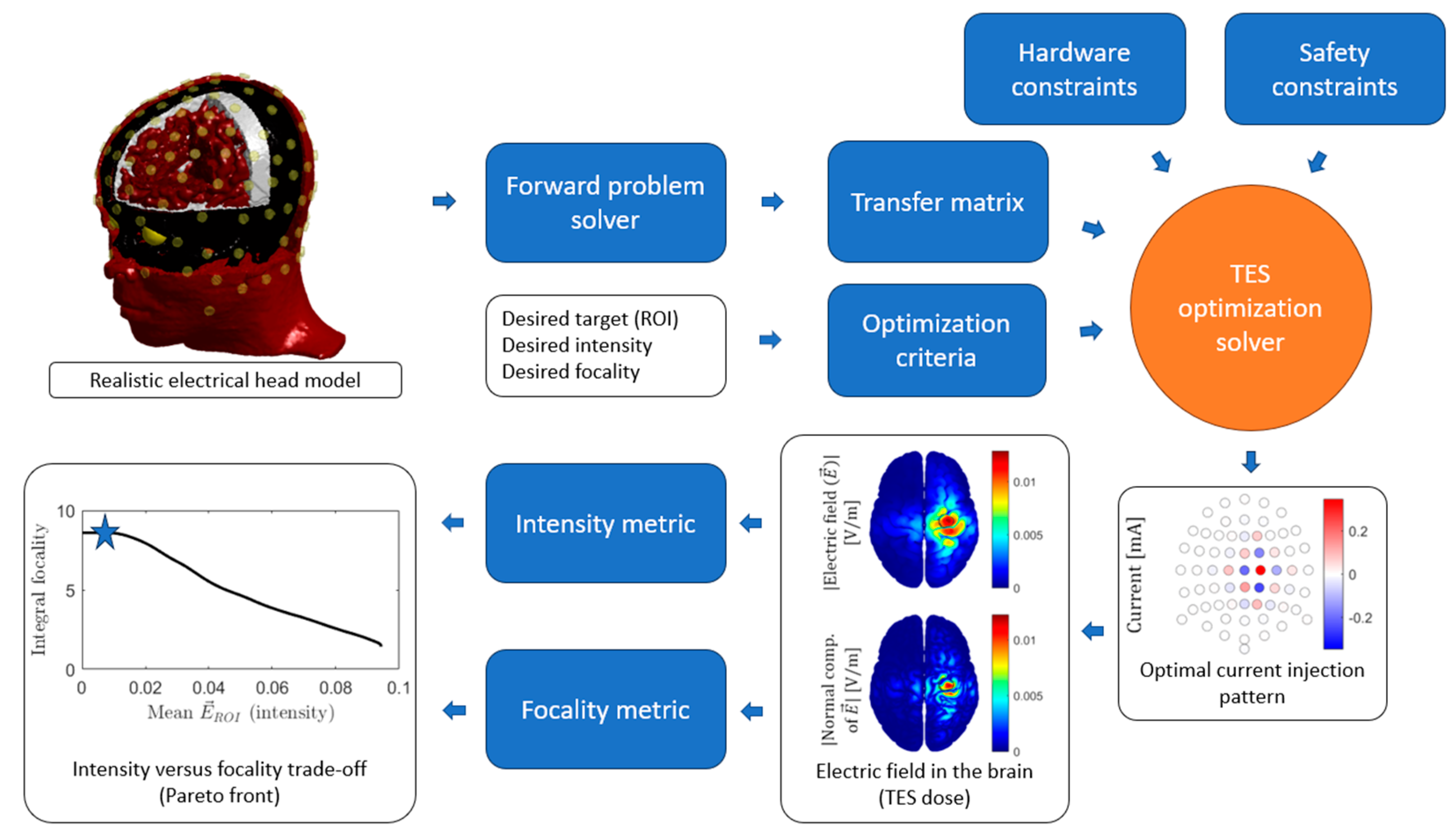
3.4. Montage Optimization
3.4.1. Methodology
3.4.2. tTIS Optimization
| Ref. | Study | Approach | Constraints | Problem Type | Algorithm/ Function | Note |
| [110] | Im et al., 2008 | Directional Maximization | Max total current | Convex | Evolutionary Strategy | |
| [28] | Dmochowski et al., 2011, Problem 1 (P1) | WLS | ・None | Convex | Closed formula | |
| Dmochowski et al., 2011, (P2) | Constrained WLS | ・Max total current ・Max per electrode current | Convex | Matlab disciplined convex programming | ||
| Dmochowski et al., 2011, (P3) | Minimize energy with the fixed field at the target (LCMV) | ・Fixed field at target | Convex | Closed formula | ||
| Dmochowski et al., 2011, (P4) | Minimize energy with the fixed field at the target (LCMV) | ・Fixed field at target ・Max total current ・Max per electrode current | Convex | Matlab disciplined convex programming | ||
| Dmochowski et al., 2011, (P5) | Directional Maximization | ・Max total current | Convex | Matlab disciplined convex programming | Equal to [110] but solved differently. | |
| [117] | Park et al., 2011 | Module Maximization | ・Max total potential | Non-convex | Nelder–Mead | |
| [118] | Sadleir et al., 2012 | Module Maximization | ・Max total current ・Max non-target intensity (focality) ・Min target/non-target ratio (focality) | Non-convex | Interior-point (Matlab fmincon) | Similar to [117] |
| [114] | Ruffini et al., 2014 | Constrained WLS | ・Max total current ・Max per electrode current ・Max number of active electrodes | Combinatorial | Genetic Algorithm | |
| [112] | Guler et al., 2016 | Directional Maximization | ・Max total current ・Max per electrode current ・Max non-target energy (focality) | Convex | CVX Matlab package [122] | Evolution of [28] (P5) (more constraints) |
| [111] | Fernández-Corazza et al., 2016 | Directional Maximization | ・Max total current ・Max per electrode current | Convex | Closed formula | Evolution of [28] (P5) (more constraints) Included in [112] (less constraints) |
| [113] | Wagner et al., 2016 | Directional Maximization | ・Max total current ・Max per electrode current ・Max non-target intensity (focality) | Convex | Alternating direction method of multipliers (ADMM) | Small difference with [112] |
| [123] | Saturnino et al., 2019 P1 | Minimize energy | ・Fixed normal component at Target | Convex | Active-set (Python) | Similar to [28] (P4) but fixing the normal component instead of the three components of the electric field. |
| Saturnino et al., 2019 P2 | Directional Maximization | ・Max total current ・Max per electrode current | Convex | Active-set (Python) | Equal to [111] | |
| Saturnino et al., 2019 P3 | Minimize energy | ・Fixed normal component at Target ・Max total current ・Max per electrode current | Convex | Active-set (Python) | Similar to [28] (P4) but fixing the normal component instead of the three components of the electric field. | |
| Saturnino et al., 2019 P4 | Minimize energy | ・Fixed normal component at Target ・Max total current ・Max per electrode current ・Max number of active electrodes | Combinatorial | Branch and bound | ||
| Saturnino et al., 2019 P5 | Directional maximization | ・Max total current ・Max per electrode current ・Min angle | Convex | Active-set (Python) | The angle restriction depends on the solution, which makes it iterative (no examples shown) | |
| Saturnino et al., 2019 P6 | Minimize energy | ・Fixed normal component at Target ・Max total current ・Max per electrode current ・Min angle | Convex | Active-set (Python) | ||
| Saturnino et al., 2019 P7 | Minimize energy | ・Fixed normal component at Target ・Max total current ・Max per electrode current ・Min angle ・Max number of active electrodes | Combinatorial | Branch and bound | ||
| Saturnino et al., 2019 P8 | Minimize energy | ・Fixed normal component at many targets ・Max total current ・Max per electrode current | Convex | Active-set (Python) | ||
| Saturnino et al., 2019 P9 | Directional maximization for many targets | ・Max normal component at the targets ・Max total current ・Max per electrode current | Convex | Active-set (Python) | ||
| Saturnino et al., 2019 P10 | Minimize energy | ・Fixed normal component at many targets ・Max total current ・Max per electrode current ・Max number of active electrodes | Combinatorial | Branch and Bound | ||
| [30] | Fernandez Corazza et al., 2020 | Directional maximization | ・Max total current ・Max per electrode current ・Max non-target energy or intensity (focality) | Convex | Matlab CVX and closed-form | Links [112] with [28] (P1), [112] with [111], and [113] with [111]. |
| [115] | Kahn et al., 2022 | Directional maximization | ・Max total current ・Max per electrode current ・l1 norm in the solution | Convex | [not stated] | |
| [116] | Galaz Prieto et al., 2022 | Weighted L1 norm | ・Max total current ・l1 norm in the solution | Convex | Matlab CVX | |
| WLS | ・Max total current ・l1 norm in the solution | Convex | Matlab CVX | |||
| WLS with Tikhonov regularization | ・Max total current ・Total energy (focality) ・l2 norm in the solution | Convex | Matlab CVX | |||
| Weighted L1 norm | ・Max total current ・l1 norm in the solution ・Max number of active electrodes | Convex | Matlab CVX | The max number of active electrodes constraint is forced (not optimal) in a second step | ||
| WLS | Same as above | Convex | Matlab CVX | Same as above | ||
| WLS with Tikhonov regularization | ・Max total current ・Total energy (focality) ・l2 norm in the solution ・Max number of active electrodes | Convex | Matlab CVX | Same as above | ||
| [121] | Wang et al., 2022 | Directional maximization | ・Total energy (focality) ・Max total current ・Max per electrode current | Convex | Matlab CVX | Equivalent to [112] |
3.4.3. Applications of These Methodologies to Simulated Experiments
3.4.4. Applications of These Methodologies to Real-Subject Experiments
3.4.5. Optimization Summary
4. Final Overview
4.1. Application of Electric Field Analysis in Clinical Practice
4.2. Electric Field Optimization
4.3. Limitations
4.4. Future Directions and Challenges
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 3.1. Individual Level Electric Field | |||||||
| Search data | TS = (“tES” OR “tDCS” OR “tACS” OR “transcranial electri* stimulation” OR “transcranial direct current stimulation” OR “Transcranial Alternating Current Stimulation”) AND TS = (“electric field” OR “current density”) AND TS = (Comput* OR Model* OR Simulation$) AND TS = (Individual$ OR Subject$ OR Human$ OR Head$) AND TS = ((Brain$ or tissue$ or cereb*) and (atrophy* or lesion$)) NOT TS = (Animal$) | ||||||
| Identified from database | 23 | Excluded (not relevant) | 7 | Relevant | 16 | Identified from other sources | 0 |
| Included in analysis | 9 | ||||||
| 3.2. Population Level Electric Field | |||||||
| Search data | TS = (“tES” OR “tDCS” OR “tACS” OR “transcranial electri* stimulation” OR “transcranial direct current stimulation” OR “Transcranial Alternating Current Stimulation”) AND TS = (“electric field” OR “current density”) AND TS = (Comput∗ OR Model∗ OR Simulation$) AND TS = (Individual$ OR Subject$ OR Human$ OR Head$) AND TS = (Group NEAR/5 level OR Group NEAR/5 Simulat* OR Standard OR Template$ OR Atlas OR Warp* OR MNI OR Talairach) NOT TS = (Animal$) | ||||||
| Identified from database | 48 | Excluded (not relevant) | 29 | Relevant | 19 | Identified from other sources | 2 |
| Included in analysis | 12 | ||||||
| 3.3. Correlations between Electric Field Calculations and Responses | |||||||
| Search data | TS = (“tES” OR “tDCS” OR “tACS” OR “transcranial electri* stimulation” OR “transcranial direct current stimulation” OR “Transcranial Alternating Current Stimulation”) AND TS = (“electric field” OR “current density”) AND TS = (Comput∗ OR Model∗ OR Simulation$) AND TS = (Individual$ OR Subject$ OR Human$ OR Head$) AND TS = (Individual* OR Personal*) NOT TS = (Animal$) | ||||||
| Identified from database | 110 | Excluded (not relevant) | 69 | Relevant | 41 | Identified from other sources | 0 |
| Included in analysis | 12 | ||||||
| 3.4. Montage Optimization | |||||||
| Search data | TS = (“tES” OR “tDCS” OR “tACS” OR “transcranial electri* stimulation” OR “transcranial direct current stimulation” OR “Transcranial Alternating Current Stimulation”) AND TS = (“electric field$” OR “current densit*” OR “current flow field$”) AND TS = (Comput∗ OR Model∗ OR Simulation$) AND TS = (Individual$ OR Subject$ OR Human$ OR Head$) AND TS = (optimi*) NOT TS = (Animal$) | ||||||
| Identified from database | 79 | Excluded (not relevant) | 44 | Relevant | 35 | Identified from other sources | 5 |
| Included in analysis | 24 | ||||||
References
- Nitsche, M.A.; Paulus, W. Excitability Changes Induced in the Human Motor Cortex by Weak Transcranial Direct Current Stimulation. J. Physiol. 2000, 527, 633–639. [Google Scholar] [CrossRef] [PubMed]
- Antal, A.; Boros, K.; Poreisz, C.; Chaieb, L.; Terney, D.; Paulus, W. Comparatively Weak After-Effects of Transcranial Alternating Current Stimulation (TACS) on Cortical Excitability in Humans. Brain Stimul. 2008, 1, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Sampaio, B.; Tortella, G.; Borrione, L.; Moffa, A.H.; Machado-Vieira, R.; Cretaz, E.; Da Silva, A.F.; Fraguas, R.; Aparício, L.V.; Klein, I.; et al. Efficacy and Safety of Transcranial Direct Current Stimulation as an Add-on Treatment for Bipolar Depression: A Randomized Clinical Trial. JAMA Psychiatry 2018, 75, 158–166. [Google Scholar] [CrossRef] [PubMed]
- Valiengo, L.D.C.L.; Goerigk, S.; Gordon, P.C.; Padberg, F.; Serpa, M.H.; Koebe, S.; Dos Santos, L.A.; Lovera, R.A.M.; De Carvalho, J.B.; Van De Bilt, M.; et al. Efficacy and Safety of Transcranial Direct Current Stimulation for Treating Negative Symptoms in Schizophrenia: A Randomized Clinical Trial. JAMA Psychiatry 2020, 77, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Loo, C.K.; Husain, M.M.; McDonald, W.M.; Aaronson, S.; O’Reardon, J.P.; Alonzo, A.; Weickert, C.S.; Martin, D.M.; McClintock, S.M.; Mohan, A.; et al. International Randomized-Controlled Trial of Transcranial Direct Current Stimulation in Depression. Brain Stimul. 2018, 11, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Cappon, D.; Jahanshahi, M.; Bisiacchi, P. Value and Efficacy of Transcranial Direct Current Stimulation in the Cognitive Rehabilitation: A Critical Review since 2000. Front. Neurosci. 2016, 10, 177344. [Google Scholar] [CrossRef] [PubMed]
- Li, L.M.; Uehara, K.; Hanakawa, T. The Contribution of Interindividual Factors to Variability of Response in Transcranial Direct Current Stimulation Studies. Front. Cell. Neurosci. 2015, 9, 181. [Google Scholar] [CrossRef]
- Rush, S.; Driscoll, D. A Current Distribution in the Brain from Surface Electrodes. Anesth. Analg. 1968, 47, 717–723. [Google Scholar] [CrossRef]
- Saypol, J.M.; Roth, B.J.; Cohen, L.G.; Hallett, M. A Theoretical Comparison of Electric and Magnetic Stimulation of the Brain. Ann. Biomed. Eng. 1991, 19, 317–328. [Google Scholar] [CrossRef]
- Ferdjallah, M.; Bostick, F.X.; Barr, R.E. Potential and Current Density Distributions of Cranial Electrotherapy Stimulation (CES) in a Four-Concentric-Spheres Model. IEEE Trans. Biomed. Eng. 1996, 43, 939–943. [Google Scholar] [CrossRef]
- Miranda, P.C.; Lomarev, M.; Hallett, M. Modeling the Current Distribution during Transcranial Direct Current Stimulation. Clin. Neurophysiol. 2006, 117, 1623–1629. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Elwassif, M.; Battaglia, F.; Bikson, M. Transcranial Current Stimulation Focality Using Disc and Ring Electrode Configurations: FEM Analysis. J. Neural Eng. 2008, 5, 163–174. [Google Scholar] [CrossRef] [PubMed]
- Sekino, M.; Ueno, S. FEM-Based Determination of Optimum Current Distribution in Transcranial Magnetic Stimulation as an Alternative to Electroconvulsive Therapy. IEEE Trans. Magn. 2004, 40, 2167–2169. [Google Scholar] [CrossRef]
- Wagner, T.; Eden, U.; Fregni, F.; Valero-Cabre, A.; Ramos-Estebanez, C.; Pronio-Stelluto, V.; Grodzinsky, A.; Zahn, M.; Pascual-Leone, A. Transcranial Magnetic Stimulation and Brain Atrophy: A Computer-Based Human Brain Model Study. Exp. Brain Res. 2008, 186, 539–550. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Bansal, V.; Diaz, J.; Patel, J.; Reato, D.; Bikson, M. Gyri-Precise Head Model of Transcranial Direct Current Stimulation: Improved Spatial Focality Using a Ring Electrode versus Conventional Rectangular Pad. Brain Stimul. 2009, 2, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Windhoff, M.; Opitz, A.; Thielscher, A. Electric Field Calculations in Brain Stimulation Based on Finite Elements: An Optimized Processing Pipeline for the Generation and Usage of Accurate Individual Head Models. Hum. Brain Mapp. 2013, 34, 923–935. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Datta, A.; Bikson, M.; Parra, L.C. Realistic Volumetric-Approach to Simulate Transcranial Electric Stimulation-ROAST-a Fully Automated Open-Source Pipeline. J. Neural Eng. 2019, 16, 56006. [Google Scholar] [CrossRef]
- Laakso, I.; Tanaka, S.; Koyama, S.; De Santis, V.; Hirata, A. Inter-Subject Variability in Electric Fields of Motor Cortical TDCS. Brain Stimul. 2015, 8, 906–913. [Google Scholar] [CrossRef] [PubMed]
- Opitz, A.; Paulus, W.; Will, S.; Antunes, A.; Thielscher, A. Determinants of the Electric Field during Transcranial Direct Current Stimulation. Neuroimage 2015, 109, 140–150. [Google Scholar] [CrossRef]
- Saturnino, G.B.; Antunes, A.; Thielscher, A. On the Importance of Electrode Parameters for Shaping Electric Field Patterns Generated by TDCS. Neuroimage 2015, 120, 25–35. [Google Scholar] [CrossRef]
- Gomez-Tames, J.; Hamasaka, A.; Hirata, A.; Laakso, I.; Lu, M.; Ueno, S. Group-Level Analysis of Induced Electric Field in Deep Brain Regions by Different TMS Coils. Phys. Med. Biol. 2020, 65, 025007. [Google Scholar] [CrossRef]
- Huang, Y.; Parra, L.C. Can Transcranial Electric Stimulation with Multiple Electrodes Reach Deep Targets? Brain Stimul. 2019, 12, 30–40. [Google Scholar] [CrossRef]
- Hunold, A.; Haueisen, J.; Nees, F.; Moliadze, V.; Antonella Ghiani, C.; Johnson Reviewed by Jose Gomez-Tames, E.; Vergallito, A.; Antonenko, D. Review of Individualized Current Flow Modeling Studies for Transcranial Electrical Stimulation. J. Neurosci. Res. 2023, 101, 405–423. [Google Scholar] [CrossRef]
- Laakso, I.; Tanaka, S.; Mikkonen, M.; Koyama, S.; Sadato, N.; Hirata, A. Electric Fields of Motor and Frontal TDCS in a Standard Brain Space: A Computer Simulation Study. Neuroimage 2016, 137, 140–151. [Google Scholar] [CrossRef]
- Gomez-Tames, J.; Asai, A.; Mikkonen, M.; Laakso, I.; Tanaka, S.; Uehara, S.; Otaka, Y.; Hirata, A. Group-Level and Functional-Region Analysis of Electric-Field Shape during Cerebellar Transcranial Direct Current Stimulation with Different Electrode Montages. J. Neural Eng. 2019, 16, 036001. [Google Scholar] [CrossRef] [PubMed]
- Rezaee, Z.; Dutta, A. Cerebellar Lobules Optimal Stimulation (CLOS): A Computational Pipeline to Optimize Cerebellar Lobule-Specific Electric Field Distribution. Front. Neurosci. 2019, 13, 266. [Google Scholar] [CrossRef]
- Yatsuda, K.; Yu, W.; Gomez-Tames, J. Population-Level Insights into Temporal Interference for Focused Deep Brain Neuromodulation. Front. Hum. Neurosci. 2024, 18, 1308549. [Google Scholar] [CrossRef]
- Dmochowski, J.P.; Datta, A.; Bikson, M.; Su, Y.; Parra, L.C. Optimized Multi-Electrode Stimulation Increases Focality and Intensity at Target. J. Neural Eng. 2011, 8, 46011. [Google Scholar] [CrossRef] [PubMed]
- Saturnino, G.B.; Siebner, H.R.; Thielscher, A.; Madsen, K.H. Accessibility of Cortical Regions to Focal TES: Dependence on Spatial Position, Safety, and Practical Constraints. Neuroimage 2019, 203, 116183. [Google Scholar] [CrossRef]
- Fernández-Corazza, M.; Turovets, S.; Muravchik, C.H. Unification of Optimal Targeting Methods in Transcranial Electrical Stimulation. Neuroimage 2020, 209, 116403. [Google Scholar] [CrossRef]
- Huang, Y.; Datta, A.; Parra, L.C. Optimization of Interferential Stimulation of the Human Brain with Electrode Arrays. J. Neural Eng. 2020, 17, 036023. [Google Scholar] [CrossRef]
- Grossman, N.; Bono, D.; Dedic, N.; Kodandaramaiah, S.B.; Rudenko, A.; Suk, H.J.; Cassara, A.M.; Neufeld, E.; Kuster, N.; Tsai, L.H.; et al. Noninvasive Deep Brain Stimulation via Temporally Interfering Electric Fields. Cell 2017, 169, 1029–1041.e16. [Google Scholar] [CrossRef] [PubMed]
- Bikson, M.; Rahman, A.; Datta, A. Computational Models of Transcranial Direct Current Stimulation. Clin. EEG Neurosci. 2012, 43, 176–183. [Google Scholar] [CrossRef]
- Miranda, P.C.; Callejón-Leblic, M.A.; Salvador, R.; Ruffini, G. Realistic Modeling of Transcranial Current Stimulation: The Electric Field in the Brain. Curr. Opin. Biomed. Eng. 2018, 8, 20–27. [Google Scholar] [CrossRef]
- Bikson, M.; Grossman, P.; Thomas, C.; Zannou, A.L.; Jiang, J.; Adnan, T.; Mourdoukoutas, A.P.; Kronberg, G.; Truong, D.; Boggio, P.; et al. Safety of Transcranial Direct Current Stimulation: Evidence Based Update 2016. Brain Stimul. 2016, 9, 641–661. [Google Scholar] [CrossRef]
- Antal, A.; Alekseichuk, I.; Bikson, M.; Brockmöller, J.; Brunoni, A.R.; Chen, R.; Cohen, L.G.; Dowthwaite, G.; Ellrich, J.; Flöel, A.; et al. Low Intensity Transcranial Electric Stimulation: Safety, Ethical, Legal Regulatory and Application Guidelines. Clin. Neurophysiol. 2017, 128, 1774–1809. [Google Scholar] [CrossRef]
- Agboada, D.; Mosayebi Samani, M.; Jamil, A.; Kuo, M.F.; Nitsche, M.A. Expanding the Parameter Space of Anodal Transcranial Direct Current Stimulation of the Primary Motor Cortex. Sci. Rep. 2019, 9, 18185. [Google Scholar] [CrossRef] [PubMed]
- Chhatbar, P.Y.; Chen, R.; Deardorff, R.; Dellenbach, B.; Kautz, S.A.; George, M.S.; Feng, W. Safety and Tolerability of Transcranial Direct Current Stimulation to Stroke Patients—A Phase I Current Escalation Study. Brain Stimul. 2017, 10, 553–559. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Tames, J.; Sugiyama, Y.; Laakso, I.; Tanaka, S.; Koyama, S.; Sadato, N.; Hirata, A. Effect of Microscopic Modeling of Skin in Electrical and Thermal Analysis of Transcranial Direct Current Stimulation. Phys. Med. Biol. 2016, 61, 8825–8838. [Google Scholar] [CrossRef]
- Luu, P.; Essaki Arumugam, E.M.; Anderson, E.; Gunn, A.; Rech, D.; Turovets, S.; Tucker, D.M. Slow-Frequency Pulsed Transcranial Electrical Stimulation for Modulation of Cortical Plasticity Based on Reciprocity Targeting with Precision Electrical Head Modeling. Front. Hum. Neurosci. 2016, 10, 377. [Google Scholar] [CrossRef]
- Plonsey, R.; Heppner, D.B. Considerations of Quasi-Stationarity in Electrophysiological Systems. Bull. Math. Biophys. 1967, 29, 657–664. [Google Scholar] [CrossRef]
- Gomez-Tames, J.; Asai, A.; Hirata, A. Multiscale Computational Model Reveals Nerve Response in a Mouse Model for Temporal Interference Brain Stimulation. Front. Neurosci. 2021, 15, 684465. [Google Scholar] [CrossRef] [PubMed]
- Caussade, T.; Paduro, E.; Courdurier, M.; Cerpa, E.; Grill, W.M.; Medina, L.E. Towards a More Accurate Quasi-Static Approximation of the Electric Potential for Neurostimulation with Kilohertz-Frequency Sources. J. Neural Eng. 2023, 20, 066035. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Pursiainen, S.; Lucka, F.; Wolters, C.H. Complete Electrode Model in EEG: Relationship and Differences to the Point Electrode Model. Phys. Med. Biol. 2012, 57, 999–1017. [Google Scholar] [CrossRef]
- Frank, E. Electric Potential Produced by Two Point Current Sources in a Homogeneous Conducting Sphere. J. Appl. Phys. 1952, 23, 1225–1228. [Google Scholar] [CrossRef]
- Calderón, A.P. On an Inverse Boundary Value Problem. In Proceedings of the Seminar on Numerical Analysis and Its Applications to Continuum Physics, Sociedade Brasileira de Matematica, Rio de Janeiro, Brazil, 24–28 March 1980; pp. 65–73. [Google Scholar]
- de Munck, J.C.; Peters, M.J. A Fast Method to Compute the Potential in the Multisphere Model. IEEE Trans. Biomed. Eng. 1993, 40, 1166–1174. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Parra, L.C.; Haufe, S. The New York Head—A Precise Standardized Volume Conductor Model for EEG Source Localization and TES Targeting. Neuroimage 2016, 140, 150–162. [Google Scholar] [CrossRef]
- Pursiainen, S.; Agsten, B.; Wagner, S.; Wolters, C.H. Advanced Boundary Electrode Modeling for TES and Parallel TES/EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 37–44. [Google Scholar] [CrossRef]
- Turovets, S.; Volkov, V.; Zherdetsky, A.; Prakonina, A.; Malony, A.D. A 3D Finite-Difference BiCG Iterative Solver with the Fourier-Jacobi Preconditioner for the Anisotropic EIT/EEG Forward Problem. Comput. Math. Methods Med. 2014, 2014, 426902. [Google Scholar] [CrossRef]
- Si, H. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 2015, 41, 2629697. [Google Scholar] [CrossRef]
- The CGAL Project. In CGAL User and Reference Manual; 4.9; CGAL Editorial Board, 2016; Available online: https://doc.cgal.org/latest/Manual/how_to_cite_cgal.html (accessed on 7 March 2024).
- Dale, A.M.; Fischl, B.; Sereno, M.I. Cortical Surface-Based Analysis. Neuroimage 1999, 9, 179–194. [Google Scholar] [CrossRef]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.J.; Woolrich, M.W.; Smith, S.M. FSL. Neuroimage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Henschel, L.; Conjeti, S.; Estrada, S.; Diers, K.; Fischl, B.; Reuter, M. Fastsurfer—A fast and accurate deep learning based neuroimaging pipeline. NeuroImage 2020, 219, 117012. [Google Scholar] [CrossRef] [PubMed]
- Rashed, E.A.; Gomez-Tames, J.; Hirata, A. End-to-End Semantic Segmentation of Personalized Deep Brain Structures for Non-Invasive Brain Stimulation. Neural Netw. 2020, 125, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Wolters, C.H.; Anwander, A.; Berti, G.; Hartmann, U. Geometry-Adapted Hexahedral Meshes Improve Accuracy of Finite-Element- Method-Based EEG Source Analysis. IEEE Trans. Biomed. Eng. 2007, 54, 890736. [Google Scholar] [CrossRef]
- Ramon, C.; Garguilo, P.; Fridgeirsson, E.A.; Haueisen, J. Changes in Scalp Potentials and Spatial Smoothing Effects of Inclusion of Dura Layer in Human Head Models for EEG Simulations. Front. Neuroeng. 2014, 7, 32. [Google Scholar] [CrossRef]
- von Ellenrieder, N.; Beltrachini, L.; Blenkmann, A.; Fernández-Corazza, M.; Kochen, S.; Muravchik, C.H. A Low-Cost and Robust Photogrammetry Method for Determining Electrode Positions. In Proceedings of the 30th International Epilepsy Congress, Montreal, Canada, 23–27 June 2013; Volume 54, p. 358. [Google Scholar]
- Lamm, C.; Windischberger, C.; Leodolter, U.; Moser, E.; Bauer, H. Co-Registration of EEG and MRI Data Using Matching of Spline Interpolated and MRI-Segmented Reconstructions of the Scalp Surface. Brain Topogr. 2001, 14, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Corazza, M.; Turovets, S.; Govyadinov, P.; Muravchik, C.H.H.; Tucker, D.; Fernandez-Corazza, M.; Turovets, S.; Govyadinov, P.; Muravchik, C.H.H.; Tucker, D. Effects of Head Model Inaccuracies on Regional Scalp and Skull Conductivity Estimation Using Real EIT Measurements. In Proceedings of the IFMBE Proceedings, Singapore, 4–7 December 2016; Simini, F., Bertemes-Filho, P., Eds.; Springer: Singapore, 2016; Volume 54, pp. 4–7. [Google Scholar]
- Fonov, V.S.; Evans, A.C.; McKinstry, R.C.; Almli, C.R. Unbiased Nonlinear Average Age-Appropriate Brain Templates from Birth to Adulthood. Neuroimage 2009, 47, S102. [Google Scholar] [CrossRef]
- Fischl, B. FreeSurfer. Neuroimage 2012, 62, 774–781. [Google Scholar] [CrossRef] [PubMed]
- Thomas Yeo, B.T.; Krienen, F.M.; Sepulcre, J.; Sabuncu, M.R.; Lashkari, D.; Hollinshead, M.; Roffman, J.L.; Smoller, J.W.; Zöllei, L.; Polimeni, J.R.; et al. The Organization of the Human Cerebral Cortex Estimated by Intrinsic Functional Connectivity. J. Neurophysiol. 2011, 106, 1125–1165. [Google Scholar] [CrossRef]
- Evans, A.C.; Marrett, S.; Neelin, P.; Collins, L.; Worsley, K.; Dai, W.; Milot, S.; Meyer, E.; Bub, D. Anatomical Mapping of Functional Activation in Stereotactic Coordinate Space. Neuroimage 1992, 1, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Collins, D.L.; Neelin, P.; Peters, T.M.; Evans, A.C. Automatic 3d Intersubject Registration of Mr Volumetric Data in Standardized Talairach Space. J. Comput. Assist. Tomogr. 1994, 18, 192–205. [Google Scholar] [CrossRef]
- Mazziotta, J.; Toga, A.; Evans, A.; Fox, P.; Lancaster, J.; Zilles, K.; Woods, R.; Paus, T.; Simpson, G.; Pike, B.; et al. A Four-Dimensional Probabilistic Atlas of the Human Brain. J. Am. Med. Inform. Assoc. 2001, 8, 401–430. [Google Scholar] [CrossRef] [PubMed]
- Desikan, R.S.; Ségonne, F.; Fischl, B.; Quinn, B.T.; Dickerson, B.C.; Blacker, D.; Buckner, R.L.; Dale, A.M.; Maguire, R.P.; Hyman, B.T.; et al. An Automated Labeling System for Subdividing the Human Cerebral Cortex on MRI Scans into Gyral Based Regions of Interest. Neuroimage 2006, 31, 968–980. [Google Scholar] [CrossRef] [PubMed]
- Fonov, V.; Evans, A.C.; Botteron, K.; Almli, C.R.; McKinstry, R.C.; Collins, D.L.; Brain Development Cooperative Group. Unbiased Average Age-Appropriate Atlases for Pediatric Studies. Neuroimage 2011, 54, 313–327. [Google Scholar] [CrossRef] [PubMed]
- Horesh, L. Some Novel Approaches in Modelling and Image Reconstruction for Multi-Frequency Electrical Impedance Tomography of the Human Brain; University College London: London, UK, 2006. [Google Scholar]
- Ramon, C.; Schimpf, P.H.; Haueisen, J. Influence of Head Models on EEG Simulations and Inverse Source Localizations. Biomed. Eng. Online 2006, 5, 10. [Google Scholar] [CrossRef] [PubMed]
- Oostendorp, T.F.; Delbeke, J.; Stegeman, D.F. The Conductivity of the Human Skull: Results of in Vivo and in Vitro Measurements. IEEE Trans. Biomed. Eng. 2000, 47, 1487–1492. [Google Scholar] [CrossRef] [PubMed]
- McCann, H.; Pisano, G.; Beltrachini, L. Variation in Reported Human Head Tissue Electrical Conductivity Values. Brain Topogr. 2019, 32, 825–858. [Google Scholar] [CrossRef] [PubMed]
- Shahid, S.S.; Bikson, M.; Salman, H.; Wen, P.; Ahfock, T. The Value and Cost of Complexity in Predictive Modelling: Role of Tissue Anisotropic Conductivity and Fibre Tracts in Neuromodulation. J. Neural Eng. 2014, 11, 036002. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Truong, D.Q.; Esmaeilpour, Z.; Huang, Y.; Badran, B.W.; Bikson, M. Enhanced TES and TDCS Computational Models by Meninges Emulation. J. Neural Eng. 2020, 17, 016027. [Google Scholar] [CrossRef]
- Datta, A.; Baker, J.M.; Bikson, M.; Fridriksson, J. Individualized Model Predicts Brain Current Flow during Transcranial Direct-Current Stimulation Treatment in Responsive Stroke Patient. Brain Stimul. 2011, 4, 169–174. [Google Scholar] [CrossRef]
- Halko, M.A.; Datta, A.; Plow, E.B.; Scaturro, J.; Bikson, M.; Merabet, L.B. Neuroplastic Changes Following Rehabilitative Training Correlate with Regional Electrical Field Induced with TDCS. Neuroimage 2011, 57, 885–891. [Google Scholar] [CrossRef]
- Wagner, T.; Fregni, F.; Fecteau, S.; Grodzinsky, A.; Zahn, M.; Pascual-Leone, A. Transcranial Direct Current Stimulation: A Computer-Based Human Model Study. Neuroimage 2007, 35, 1113–1124. [Google Scholar] [CrossRef]
- Galletta, E.E.; Cancelli, A.; Cottone, C.; Simonelli, I.; Tecchio, F.; Bikson, M.; Marangolo, P. Use of Computational Modeling to Inform TDCS Electrode Montages for the Promotion of Language Recovery in Post-Stroke Aphasia. Brain Stimul. 2015, 8, 1108–1115. [Google Scholar] [CrossRef]
- Minjoli, S.; Saturnino, G.B.; Blicher, J.U.; Stagg, C.J.; Siebner, H.R.; Antunes, A.; Thielscher, A. The Impact of Large Structural Brain Changes in Chronic Stroke Patients on the Electric Field Caused by Transcranial Brain Stimulation. Neuroimage Clin. 2017, 15, 106–117. [Google Scholar] [CrossRef] [PubMed]
- Mahdavi, S.; Towhidkhah, F. Computational Human Head Models of TDCS: Influence of Brain Atrophy on Current Density Distribution. Brain Stimul. 2018, 11, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Lam, L.C.W.; Ning, Y. Scalp-to-Cortex Distance of Left Primary Motor Cortex and Its Computational Head Model: Implications for Personalized Neuromodulation. CNS Neurosci. Ther. 2019, 25, 1270–1276. [Google Scholar] [CrossRef]
- Unal, G.; Ficek, B.; Webster, K.; Shahabuddin, S.; Truong, D.; Hampstead, B.; Bikson, M.; Tsapkini, K. Impact of Brain Atrophy on TDCS and HD-TDCS Current Flow: A Modeling Study in Three Variants of Primary Progressive Aphasia. Neurol. Sci. 2020, 41, 1781–1789. [Google Scholar] [CrossRef] [PubMed]
- Indahlastari, A.; Albizu, A.; Boutzoukas, E.M.; O’Shea, A.; Woods, A.J. White Matter Hyperintensities Affect Transcranial Electrical Stimulation in the Aging Brain. Brain Stimul. 2021, 14, 69–73. [Google Scholar] [CrossRef]
- Piastra, M.C.; Van Der Cruijsen, J.; Piai, V.; Jeukens, F.E.M.; Manoochehri, M.; Schouten, A.C.; Selles, R.W.; Oostendorp, T. ASH: An Automatic Pipeline to Generate Realistic and Individualized Chronic Stroke Volume Conduction Head Models. J. Neural Eng. 2021, 18, 044001. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, M.; Wu, D.; Zhang, J.; Zhang, S. In Vivo Measurements of Transcranial Electrical Stimulation in Lesioned Human Brain: A Case Report. Brain Sci. 2022, 12, 1455. [Google Scholar] [CrossRef] [PubMed]
- Kalloch, B.; Weise, K.; Lampe, L.; Bazin, P.L.; Villringer, A.; Hlawitschka, M.; Sehm, B. The Influence of White Matter Lesions on the Electric Field in Transcranial Electric Stimulation. Neuroimage Clin. 2022, 35, 103071. [Google Scholar] [CrossRef] [PubMed]
- Csifcsák, G.; Boayue, N.M.; Puonti, O.; Thielscher, A.; Mittner, M. Effects of Transcranial Direct Current Stimulation for Treating Depression: A Modeling Study. J. Affect. Disord. 2018, 234, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Tames, J.; Asai, A.; Hirata, A. Significant Group-Level Hotspots Found in Deep Brain Regions during TDCS: A Computational Analysis of Electric Field. Clin. Neurophysiol. 2020, 3, 755–765. [Google Scholar] [CrossRef] [PubMed]
- Indahlastari, A.; Albizu, A.; O’Shea, A.; Forbes, M.A.; Nissim, N.R.; Kraft, J.N.; Evangelista, N.D.; Hausman, H.K.; Woods, A.J. Modeling Transcranial Electrical Stimulation in the Aging Brain. Brain Stimul. 2020, 13, 664–674. [Google Scholar] [CrossRef] [PubMed]
- Rezaee, Z.; Kaura, S.; Solanki, D.; Dash, A.; Padma Srivastava, M.V.; Lahiri, U.; Dutta, A. Deep Cerebellar Transcranial Direct Current Stimulation of the Dentate Nucleus to Facilitate Standing Balance in Chronic Stroke Survivors-A Pilot Study. Brain Sci. 2020, 10, 94. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, G.; Saviz, M.; Bikson, M.; Towhidkhah, F.; Kuplicki, R.; Paulus, M.P.; Ekhtiari, H. Group and Individual Level Variations between Symmetric and Asymmetric DLPFC Montages for TDCS over Large Scale Brain Network Nodes. Sci. Rep. 2021, 11, 1271. [Google Scholar] [CrossRef] [PubMed]
- Antonenko, D.; Grittner, U.; Saturnino, G.; Nierhaus, T.; Thielscher, A.; Flöel, A. Inter-Individual and Age-Dependent Variability in Simulated Electric Fields Induced by Conventional Transcranial Electrical Stimulation. Neuroimage 2021, 224, 117413. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, M.; Tanaka, S.; Gomez-Tames, J.; Okabe, T.; Cho, K.; Iso, N.; Hirata, A. Nonequivalent After-Effects of Alternating Current Stimulation on Motor Cortex Oscillation and Inhibition: Simulation and Experimental Study. Brain Sci. 2022, 12, 195. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Kashyap, R.; Goodwill, A.M.; O’Brien, B.A.; Rapp, B.; Oishi, K.; Desmond, J.E.; Chen, S.H.A. Sex Difference in TDCS Current Mediated by Changes in Cortical Anatomy: A Study across Young, Middle and Older Adults. Brain Stimul. 2022, 15, 125–140. [Google Scholar] [CrossRef]
- Mizutani-Tiebel, Y.; Takahashi, S.; Karali, T.; Mezger, E.; Bulubas, L.; Papazova, I.; Dechantsreiter, E.; Stoecklein, S.; Papazov, B.; Thielscher, A.; et al. Differences in Electric Field Strength between Clinical and Non-Clinical Populations Induced by Prefrontal TDCS: A Cross-Diagnostic, Individual MRI-Based Modeling Study. Neuroimage Clin. 2022, 34, 103011. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Kim, D.W.; Chang, W.H.; Kim, Y.H.; Kim, K.; Im, C.H. Inconsistent Outcomes of Transcranial Direct Current Stimulation May Originate from Anatomical Differences among Individuals: Electric Field Simulation Using Individual MRI Data. Neurosci. Lett. 2014, 564, 6–10. [Google Scholar] [CrossRef] [PubMed]
- Antonenko, D.; Thielscher, A.; Saturnino, G.B.; Aydin, S.; Ittermann, B.; Grittner, U.; Flöel, A. Towards Precise Brain Stimulation: Is Electric Field Simulation Related to Neuromodulation? Brain Stimul. 2019, 194, 136–148. [Google Scholar] [CrossRef] [PubMed]
- Kasten, F.H.; Duecker, K.; Maack, M.C.; Meiser, A.; Herrmann, C.S. Integrating Electric Field Modeling and Neuroimaging to Explain Inter-Individual Variability of TACS Effects. Nat. Commun. 2019, 10, 5427. [Google Scholar] [CrossRef] [PubMed]
- Laakso, I.; Mikkonen, M.; Koyama, S.; Hirata, A.; Tanaka, S. Can Electric Fields Explain Inter-Individual Variability in Transcranial Direct Current Stimulation of the Motor Cortex? Sci. Rep. 2019, 9, 626. [Google Scholar] [CrossRef] [PubMed]
- Jamil, A.; Batsikadze, G.; Kuo, H.I.; Meesen, R.L.J.; Dechent, P.; Paulus, W.; Nitsche, M.A. Current Intensity- and Polarity-Specific Online and Aftereffects of Transcranial Direct Current Stimulation: An FMRI Study. Hum. Brain Mapp. 2020, 41, 24901. [Google Scholar] [CrossRef] [PubMed]
- Abellaneda-Pérez, K.; Vaqué-Alcázar, L.; Perellón-Alfonso, R.; Solé-Padullés, C.; Bargalló, N.; Salvador, R.; Ruffini, G.; Nitsche, M.A.; Pascual-Leone, A.; Bartrés-Faz, D. Multifocal Transcranial Direct Current Stimulation Modulates Resting-State Functional Connectivity in Older Adults Depending on the Induced Current Density. Front. Aging Neurosci. 2021, 13, 725013. [Google Scholar] [CrossRef]
- Indahlastari, A.; Albizu, A.; Kraft, J.N.; O’Shea, A.; Nissim, N.R.; Dunn, A.L.; Carballo, D.; Gordon, M.P.; Taank, S.; Kahn, A.T.; et al. Individualized TDCS Modeling Predicts Functional Connectivity Changes within the Working Memory Network in Older Adults. Brain Stimul. 2021, 14, 1205–1215. [Google Scholar] [CrossRef] [PubMed]
- Mezger, E.; Rauchmann, B.S.; Brunoni, A.R.; Bulubas, L.; Thielscher, A.; Werle, J.; Mortazavi, M.; Karali, T.; Stöcklein, S.; Ertl-Wagner, B.; et al. Effects of Bifrontal Transcranial Direct Current Stimulation on Brain Glutamate Levels and Resting State Connectivity: Multimodal MRI Data for the Cathodal Stimulation Site. Eur. Arch. Psychiatry Clin. Neurosci. 2021, 271, 111–122. [Google Scholar] [CrossRef]
- Zanto, T.P.; Jones, K.T.; Ostrand, A.E.; Hsu, W.Y.; Campusano, R.; Gazzaley, A. Individual Differences in Neuroanatomy and Neurophysiology Predict Effects of Transcranial Alternating Current Stimulation. Brain Stimul. 2021, 14, 1317–1329. [Google Scholar] [CrossRef]
- Nandi, T.; Puonti, O.; Clarke, W.T.; Nettekoven, C.; Barron, H.C.; Kolasinski, J.; Hanayik, T.; Hinson, E.L.; Berrington, A.; Bachtiar, V.; et al. TDCS Induced GABA Change Is Associated with the Simulated Electric Field in M1, an Effect Mediated by Grey Matter Volume in the MRS Voxel. Brain Stimul. 2022, 15, 1153–1162. [Google Scholar] [CrossRef] [PubMed]
- Preisig, B.C.; Hervais-Adelman, A. The Predictive Value of Individual Electric Field Modeling for Transcranial Alternating Current Stimulation Induced Brain Modulation. Front. Cell. Neurosci. 2022, 16, 818703. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.; Ti, C.H.E.; Wang, X.; Chen, C.; Lau, C.C.Y.; Chu, W.C.W.; Tong, R.K.Y. Individual Electric Field Predicts Functional Connectivity Changes after Anodal Transcranial Direct-Current Stimulation in Chronic Stroke. Neurosci. Res. 2023, 186, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Im, C.H.; Jung, H.H.; Do Choi, J.; Lee, S.Y.; Jung, K.Y. Determination of Optimal Electrode Positions for Transcranial Direct Current Stimulation (TDCS). Phys. Med. Biol. 2008, 53, N219. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Corazza, M.; Turovets, S.; Luu, P.; Anderson, E.; Tucker, D. Transcranial Electrical Neuromodulation Based on the Reciprocity Principle. Front. Psychiatry 2016, 7, 180386. [Google Scholar] [CrossRef]
- Guler, S.; Dannhauer, M.; Erem, B.; Macleod, R.; Tucker, D.; Turovets, S.; Luu, P.; Erdogmus, D.; Brooks, D.H. Optimization of Focality and Direction in Dense Electrode Array Transcranial Direct Current Stimulation (TDCS). J. Neural Eng. 2016, 13, 36020. [Google Scholar] [CrossRef] [PubMed]
- Wagner, S.; Burger, M.; Wolters, C.H. An Optimization Approach for Well-Targeted Transcranial Direct Current Stimulation. SIAM J. Appl. Math. 2016, 76, 2154–2174. [Google Scholar] [CrossRef]
- Ruffini, G.; Fox, M.D.; Ripolles, O.; Miranda, P.C.; Pascual-Leone, A. Optimization of Multifocal Transcranial Current Stimulation for Weighted Cortical Pattern Targeting from Realistic Modeling of Electric Fields. Neuroimage 2014, 89, 216–225. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Antonakakis, M.; Vogenauer, N.; Haueisen, J.; Wolters, C.H. Individually Optimized Multi-Channel TDCS for Targeting Somatosensory Cortex. Clin. Neurophysiol. 2022, 134, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Galaz Prieto, F.; Rezaei, A.; Samavaki, M.; Pursiainen, S. L1-Norm vs. L2-Norm Fitting in Optimizing Focal Multi-Channel TES Stimulation: Linear and Semidefinite Programming vs. Weighted Least Squares. Comput. Methods Programs Biomed. 2022, 226, 107084. [Google Scholar] [CrossRef]
- Park, J.-H.; Hong, S.B.; Kim, D.-W.; Suh, M.; Im, C.-H. A Novel Array-Type Transcranial Direct Current Stimulation (TDCS) System for Accurate Focusing on Targeted Brain Areas. IEEE Trans. Magn. 2011, 47, 882–885. [Google Scholar] [CrossRef]
- Sadleir, R.; Vannorsdall, T.D.; Schretlen, D.J.; Gordon, B. Target Optimization in TDCS. Front. Psychiatry 2012, 3, 90. [Google Scholar] [PubMed]
- Wang, Y.; Brand, J.; Liu, W. Stimulation Montage Achieves Balanced Focality and Intensity. Algorithms 2022, 15, 169. [Google Scholar] [CrossRef]
- Rampersad, S.; Roig-Solvas, B.; Yarossi, M.; Kulkarni, P.P.; Santarnecchi, E.; Dorval, A.D.; Brooks, D.H. Prospects for Transcranial Temporal Interference Stimulation in Humans: A Computational Study. Neuroimage 2019, 202, 116124. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Lou, K.; Liu, Z.; Wei, P.; Liu, Q. Multi-Objective Optimization via Evolutionary Algorithm (MOVEA) for High-Definition Transcranial Electrical Stimulation of the Human Brain. Neuroimage 2023, 280, 120331. [Google Scholar] [CrossRef] [PubMed]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Ver 2.2. Available online: https://cvxr.com/cvx (accessed on 1 January 2020).
- Nielsen, J.D.; Madsen, K.H.; Puonti, O.; Siebner, H.R.; Bauer, C.; Madsen, C.G.; Saturnino, G.B.; Thielscher, A. Automatic Skull Segmentation from MR Images for Realistic Volume Conductor Models of the Head: Assessment of the State-of-the-Art. Neuroimage 2018, 174, 587–598. [Google Scholar] [CrossRef]
- Dmochowski, J.P.; Datta, A.; Huang, Y.; Richardson, J.D.; Bikson, M.; Fridriksson, J.; Parra, L.C. Targeted Transcranial Direct Current Stimulation for Rehabilitation after Stroke. Neuroimage 2013, 75, 12–19. [Google Scholar] [CrossRef] [PubMed]
- van der Cruijsen, J.; Dooren, R.F.; Schouten, A.C.; Oostendorp, T.F.; Frens, M.A.; Ribbers, G.M.; van der Helm, F.C.T.; Kwakkel, G.; Selles, R.W. Addressing the Inconsistent Electric Fields of TDCS by Using Patient-Tailored Configurations in Chronic Stroke: Implications for Treatment. Neuroimage Clin. 2022, 36, 103178. [Google Scholar] [CrossRef] [PubMed]
- Radecke, J.-O.; Khan, A.; Engel, A.K.; Wolters, C.H.; Schneider, T.R. Individual Targeting Increases Control Over Inter-Individual Variability in Simulated Transcranial Electric Fields. IEEE Access 2020, 8, 182610–182624. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.; Park, J.; Im, C.H. Individually Customized Transcranial Temporal Interference Stimulation for Focused Modulation of Deep Brain Structures: A Simulation Study with Different Head Models. Sci. Rep. 2020, 10, 11730. [Google Scholar] [CrossRef]
- Holmes, M.D.; Feng, R.; Wise, M.V.; Ma, C.; Ramon, C.; Wu, J.; Luu, P.; Hou, J.; Pan, L.; Tucker, D.M. Safety of Slow-pulsed Transcranial Electrical Stimulation in Acute Spike Suppression. Ann. Clin. Transl. Neurol. 2019, 6, 2579–2585. [Google Scholar] [CrossRef] [PubMed]
- Klírová, M.; Voráčková, V.; Horáček, J.; Mohr, P.; Jonáš, J.; Dudysová, D.U.; Kostýlková, L.; Fayette, D.; Krejčová, L.; Baumann, S.; et al. Modulating Inhibitory Control Processes Using Individualized High Definition Theta Transcranial Alternating Current Stimulation (HD θ-TACS) of the Anterior Cingulate and Medial Prefrontal Cortex. Front. Syst. Neurosci. 2021, 15, 611507. [Google Scholar] [CrossRef] [PubMed]
- Sahib, A.Y.; Seyedarabi, H.; Afrouzian, R.; Farhoudi, M. A MATLAB-Based Toolbox to Simulate Transcranial Direct-Current Stimulation Using Flexible, Fast, and High Quality Tetrahedral Mesh Generation. IEEE Access 2022, 10, 76573–76585. [Google Scholar] [CrossRef]
- Kalloch, B.; Bazin, P.L.; Villringer, A.; Sehm, B.; Hlawitschka, M. A Flexible Workflow for Simulating Transcranial Electric Stimulation in Healthy and Lesioned Brains. PLoS ONE 2020, 15, e0228119. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Liu, A.A.; Lafon, B.; Friedman, D.; Dayan, M.; Wang, X.; Bikson, M.; Doyle, W.K.; Devinsky, O.; Parra, L.C. Measurements and Models of Electric Fields in the in Vivo Human Brain during Transcranial Electric Stimulation. Elife 2017, 6, e18834. [Google Scholar] [CrossRef] [PubMed]
- Göksu, C.; Hanson, L.G.; Siebner, H.R.; Ehses, P.; Scheffler, K.; Thielscher, A. Human In-Vivo Brain Magnetic Resonance Current Density Imaging (MRCDI). Neuroimage 2018, 171, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Feng, T.; Jiang, H.; Zhu, J.; Feng, W.; Chhatbar, P.Y.; Zhang, J.; Zhang, S. In Vivo Measurements of Electric Fields During Cranial Electrical Stimulation in the Human Brain. Front. Hum. Neurosci. 2022, 16, 829745. [Google Scholar] [CrossRef] [PubMed]
- Antonakakis, M.; Schrader, S.; Aydin, Ü.; Khan, A.; Gross, J.; Zervakis, M.; Rampp, S.; Wolters, C.H. Inter-Subject Variability of Skull Conductivity and Thickness in Calibrated Realistic Head Models. Neuroimage 2020, 223, 117353. [Google Scholar] [CrossRef] [PubMed]
- Fernandez Corazza, M.; Turovets, S.; Luu, P.; Price, N.; Muravchik, C.C.H.C.C.H.; Tucker, D.; Fernandez-Corazza, M.; Turovets, S.; Luu, P.; Price, N.; et al. Skull Modeling Effects in Conductivity Estimates Using Parametric Electrical Impedance Tomography. IEEE Trans. Biomed. Eng. 2018, 65, 1785–1797. [Google Scholar] [CrossRef]
- Engwer, C.; Vorwerk, J.; Ludewig, J.; Wolters, C.H. A Discontinuous Galerkin Method to Solve the EEG Forward Problem Using the Subtraction Approach. SIAM J. Sci. Comput. 2017, 39, B138–B164. [Google Scholar] [CrossRef]
- Puonti, O.; Saturnino, G.B.; Madsen, K.H.; Thielscher, A. Value and Limitations of Intracranial Recordings for Validating Electric Field Modeling for Transcranial Brain Stimulation. Neuroimage 2020, 208, 116431. [Google Scholar] [CrossRef] [PubMed]
- Ghasemian-Shirvan, E.; Mosayebi-Samani, M.; Farnad, L.; Kuo, M.F.; Meesen, R.L.J.; Nitsche, M.A. Age-Dependent Non-Linear Neuroplastic Effects of Cathodal TDCS in the Elderly Population: A Titration Study. Brain Stimul. 2022, 15, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.; Vécsei, L. From Lab to Life: Exploring Cutting-Edge Models for Neurological and Psychiatric Disorders. Biomedicines 2024, 12, 613. [Google Scholar] [CrossRef]
- Di Gregorio, F.; Battaglia, S. The Intricate Brain–Body Interaction in Psychiatric and Neurological Diseases. Adv. Clin. Exp. Med. 2024, 33, 185689. [Google Scholar] [CrossRef] [PubMed]
- Guler, S.; Dannhauer, M.; Roig-Solvas, B.; Gkogkidis, A.; Macleod, R.; Ball, T.; Ojemann, J.G.; Brooks, D.H. Computationally Optimized ECoG Stimulation with Local Safety Constraints. Neuroimage 2018, 173, 35–48. [Google Scholar] [CrossRef]
- Collavini, S.; Fernández-Corazza, M.; Oddo, S.; Princich, J.P.; Kochen, S.; Muravchik, C.H. Improvements on Spatial Coverage and Focality of Deep Brain Stimulation in Pre-Surgical Epilepsy Mapping. J. Neural Eng. 2021, 18, 046004. [Google Scholar] [CrossRef]
| Study | Lesion | Affected Tissue Conductivity (S/m) | Montage (Area cm2) | Subjects (Years) |
|---|---|---|---|---|
| Galletta et al. (2015) [80] | Stroke (frontal area) | 1.65 | Five montages: CP5/F5/CP6/F6-SO, F2–F3 (5 × 7) | One adult male (N.A) |
| Minjoli et al. (2017) [81] | Stroke | N.A | Near cortical lesion (7) | Two-stroke adults (36 and 44) One healthy control (adults) |
| Mahdavi et al. (2018) [82] | Mild cognitive impairment | N.A | Two montages: T3/F3-SO (7 × 5) | Healthy youth (24), healthy elder (78), and mild cognitively impaired elder (78) |
| Lu et al. (2019) [83] | Dementia | N.A | C3–C4 (5 × 5) | 164 cognitively normal adults (40 young age: 29.4 ± 4.0, 65 middle age: 50.2 ± 5.4, and 62 old age: 75.7 ± 8.1), and 43 dementia patients (76 ± 6.8) |
| Unal et al. (2020) [84] | Local cortical atrophy variant of primary progressive | Same as the surrounding tissue’s conductivity | -F7-right cheek (5 × 5) −4 × 1 high-definition centered over left IFG * area | Four adults (69, 59, and 71) |
| Indahlastari et al. (2021) [85] | Lesion volumes based on training data from multiple sclerosis patients | 1.65 | F3–F4 (5 × 7) | 130 adults (71, 65–85 range) |
| Piastra et al. (2021) [86] | Stroke | 0.126 to 1.654 | C3-Fp2, C4-Fp1 (Area N.A.) | 16 adults (N.A) |
| Jiang et al. (2022) [87] | Two congenital malacia foci | 0.8 | T7-Fp2, T7–T8 (3.14) | 1 young adult (21) |
| Kalloch et al. (2022) [88] | White matter (divided into four Fazekas scores) | 1 (beta distribution) | Oz-Fpz (25) | 88 old adults (70.8 ± 4 years) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Tames, J.; Fernández-Corazza, M. Perspectives on Optimized Transcranial Electrical Stimulation Based on Spatial Electric Field Modeling in Humans. J. Clin. Med. 2024, 13, 3084. https://doi.org/10.3390/jcm13113084
Gomez-Tames J, Fernández-Corazza M. Perspectives on Optimized Transcranial Electrical Stimulation Based on Spatial Electric Field Modeling in Humans. Journal of Clinical Medicine. 2024; 13(11):3084. https://doi.org/10.3390/jcm13113084
Chicago/Turabian StyleGomez-Tames, Jose, and Mariano Fernández-Corazza. 2024. "Perspectives on Optimized Transcranial Electrical Stimulation Based on Spatial Electric Field Modeling in Humans" Journal of Clinical Medicine 13, no. 11: 3084. https://doi.org/10.3390/jcm13113084
APA StyleGomez-Tames, J., & Fernández-Corazza, M. (2024). Perspectives on Optimized Transcranial Electrical Stimulation Based on Spatial Electric Field Modeling in Humans. Journal of Clinical Medicine, 13(11), 3084. https://doi.org/10.3390/jcm13113084







