Experiment of Canopy Leaf Area Density Estimation Method Based on Ultrasonic Echo Signal
Abstract
1. Introduction
2. Materials and Methods
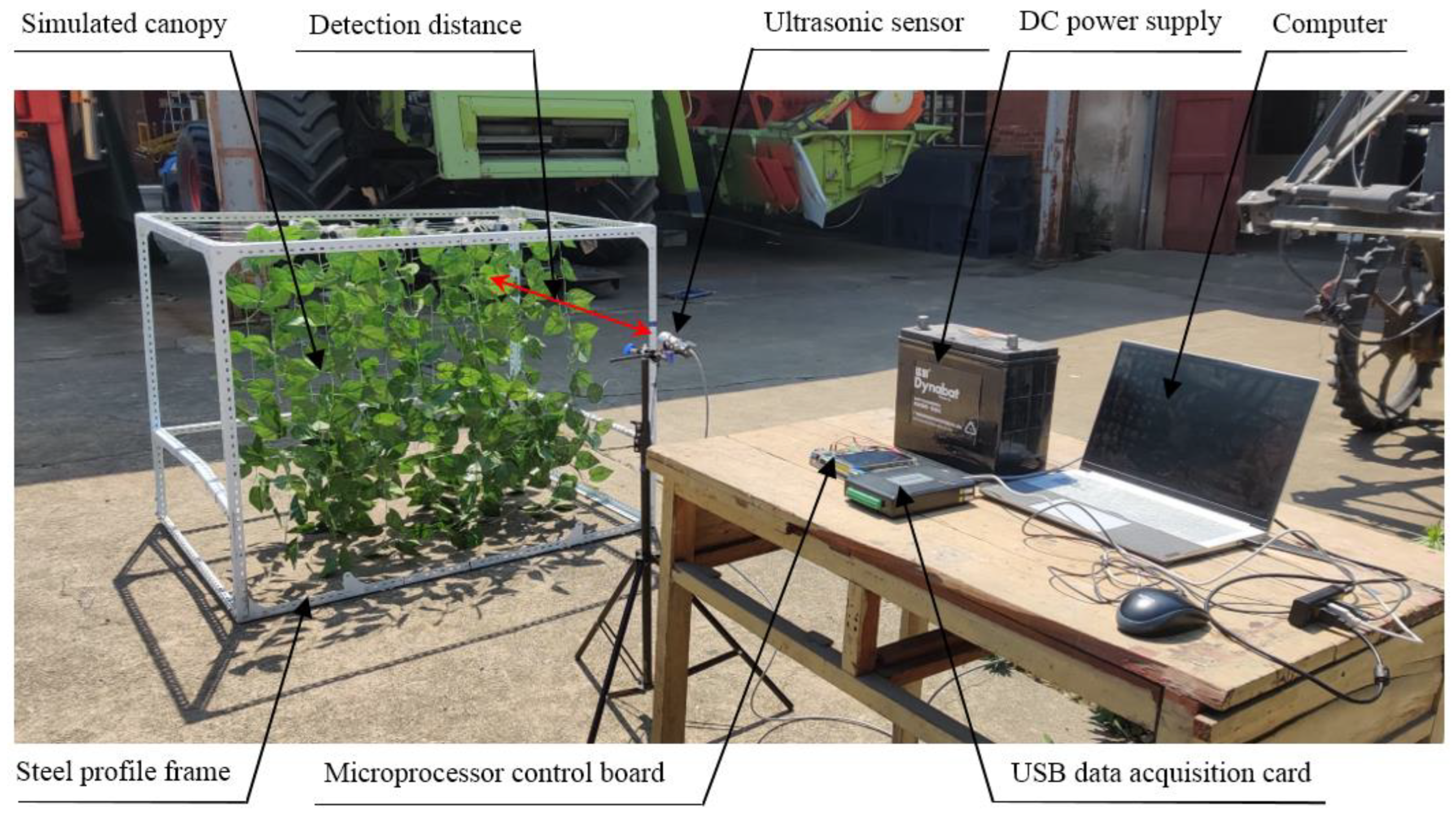
2.1. Laboratory-Simulated Canopy Experimental Setup
2.2. Canopy Leaf Area Density Estimation Equations
2.3. Experiment to Establish Canopy Leaf Area Density Model
2.3.1. Orthogonal Regression Experiment Design
2.3.2. Detection Points Arrangement
2.4. Laboratory-Simulated Canopy Verification
2.5. Outdoor Tree Canopy Verification
3. Results
3.1. Mathematical Model Analysis
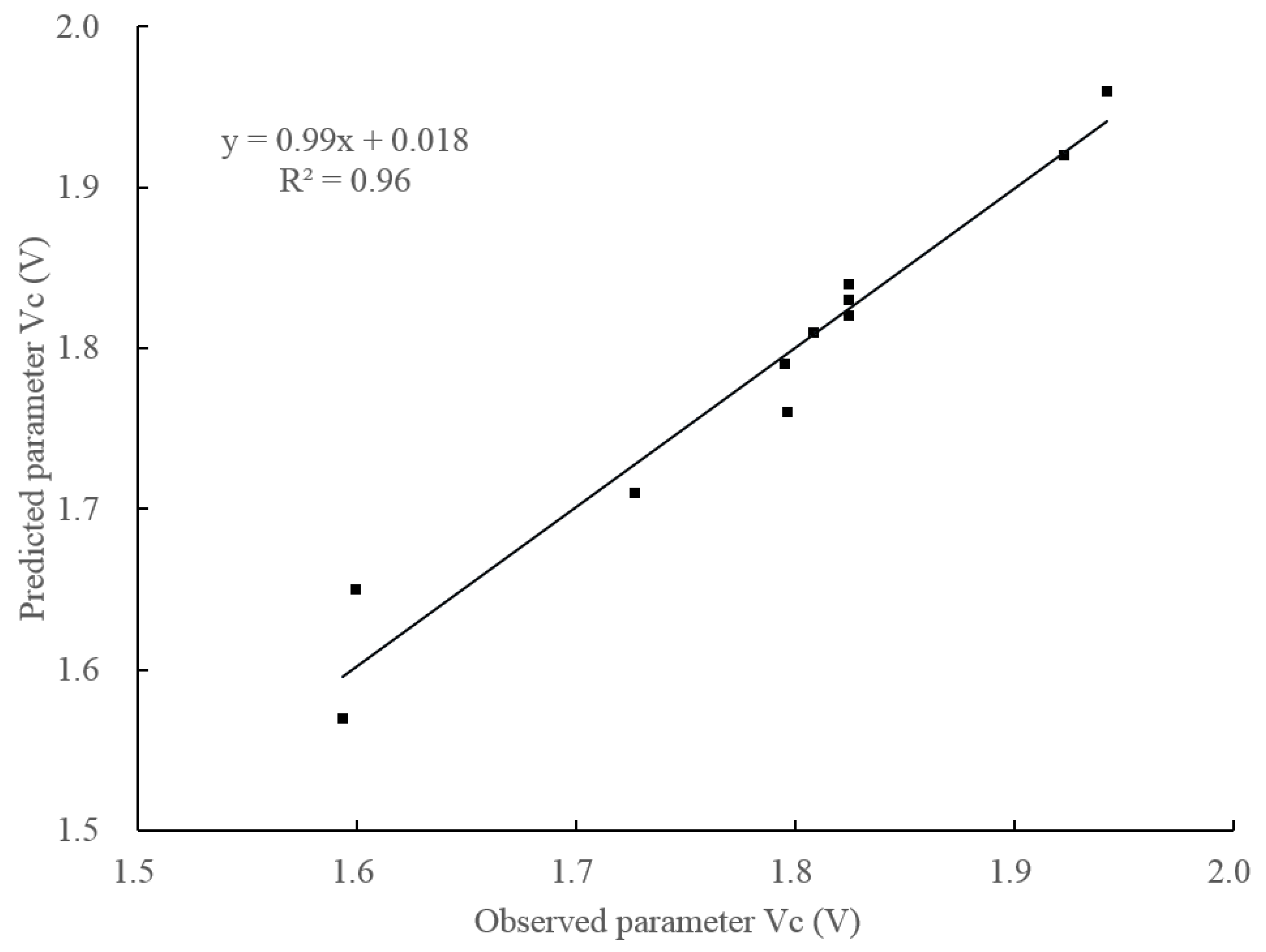
3.2. Laboratory-Simulated Canopy Verification Results
3.3. Outdoor Tree Canopy Verification Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Appah, S.; Jia, W.; Ou, M.; Wang, P.; Asante, E.A. Analysis of Potential Impaction and Phytotoxicity of Surfactant-Plant Surface Interaction in Pesticide Application. Crop Prot. 2020, 127, 104961. [Google Scholar] [CrossRef]
- Lu, X.; Garcia-Ruiz, F.; Fabregas, F.X. Pesticide dose based on canopy characteristics in apple trees: Reducing environmental risk by reducing the amount of pesticide while maintaining pest and disease control efficacy. Sci. Total Environ. 2022, 826, 154204. [Google Scholar] [CrossRef]
- Abbas, I.; Liu, J.; Faheem, M.; Noor, R.S.; Shaikh, S.A.; Solangi, K.A.; Raza, S.M. Different Sensor Based Intelligent Spraying Systems in Agriculture. Sens. Actuators Phys. 2020, 316, 112265. [Google Scholar] [CrossRef]
- Nan, Y.; Zhang, H.; Xu, Y.; Jiao, X.; Zheng, J.; Liu, D. Research progress on profiling target spray and its control technology in agriculture and forestry. World For. Res. 2018, 31, 54–58. [Google Scholar]
- Salcedo, R.; Zhu, H.; Jeon, H.; Ozkan, E.; Wei, Z.; Gil, E. Characterisation of activation pressure, flowrate and spray angle for hollow-cone nozzles controlled by pulse width modulation. Biosyst. Eng. 2022, 218, 139–152. [Google Scholar] [CrossRef]
- Jeon, H.Y.; Zhu, H. Development of a Variable-Rate Sprayer for Nursery Liner Applications. Trans. ASABE 2012, 55, 303–312. [Google Scholar] [CrossRef]
- Dou, H.; Zhang, C.; Li, L.; Hao, G.; Ding, B.; Gong, W.; Huang, P. Application of Variable Spray Technology in Agriculture. IOP Conf. Ser. Earth Environ. Sci. 2018, 186, 012007. [Google Scholar] [CrossRef]
- Mäkelä, H.; Pekkarinen, A. Estimation of Forest Stand Volumes by Landsat TM Imagery and Stand-Level Field-Inventory Data. For. Ecol. Manag. 2004, 196, 245–255. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Pereira, J.M.C.; Pereira, J.S. Estimation of Tree Canopy Cover in Evergreen Oak Woodlands Using Remote Sensing. For. Ecol. Manag. 2006, 223, 45–53. [Google Scholar] [CrossRef]
- Solanelles, F.; Escolà, A.; Planas, S.; Rosell, J.R.; Camp, F.; Gràcia, F. An Electronic Control System for Pesticide Application Proportional to the Canopy Width of Tree Crops. Biosyst. Eng. 2006, 95, 473–481. [Google Scholar] [CrossRef]
- Giles, D.K.; Klassen, P.; Niederholzer, F.J.A.; Downey, D. “Smart” Sprayer Technology Provides Environmental and Economic Benefits in California Orchards. Calif. Agric. 2011, 65, 85–89. [Google Scholar] [CrossRef]
- Rosell Polo, J.R.; Sanz, R.; Llorens, J.; Arnó, J.; Escolà, A.; Ribes-Dasi, M.; Masip, J.; Camp, F.; Gràcia, F.; Solanelles, F.; et al. A Tractor-Mounted Scanning LIDAR for the Non-Destructive Measurement of Vegetative Volume and Surface Area of Tree-Row Plantations: A Comparison with Conventional Destructive Measurements. Biosyst. Eng. 2009, 102, 128–134. [Google Scholar] [CrossRef]
- Rosell, J.R.; Llorens, J.; Sanz, R.; Arnó, J.; Ribes-Dasi, M.; Masip, J.; Escolà, A.; Camp, F.; Solanelles, F.; Gràcia, F.; et al. Obtaining the Three-Dimensional Structure of Tree Orchards from Remote 2D Terrestrial LIDAR Scanning. Agric. For. Meteorol. 2009, 149, 1505–1515. [Google Scholar] [CrossRef]
- Asaei, H.; Jafari, A.; Loghavi, M. Site-Specific Orchard Sprayer Equipped with Machine Vision for Chemical Usage Management. Comput. Electron. Agric. 2019, 162, 431–439. [Google Scholar] [CrossRef]
- Llorens, J.; Gil, E.; Llop, J.; Escolà, A. Ultrasonic and LIDAR Sensors for Electronic Canopy Characterization in Vineyards: Advances to Improve Pesticide Application Methods. Sensors 2011, 11, 2177–2194. [Google Scholar] [CrossRef]
- Jeon, H.Y.; Zhu, H.; Derksen, R.C.; Ozkan, H.E.; Krause, C.R.; Fox, R.D. Performance Evaluation of a Newly Developed Variable-Rate Sprayer for Nursery Liner Applications. Trans. ASABE 2011, 54, 1997–2007. [Google Scholar] [CrossRef]
- Tewari, V.K.; Chandel, A.K.; Nare, B.; Kumar, S. Sonar Sensing Predicated Automatic Spraying Technology for Orchards. Curr. Sci. 2018, 115, 1115–1123. [Google Scholar] [CrossRef]
- Tumbo, S.D.; Salyani, M.; Whitney, J.D.; Wheaton, T.A.; Miller, W.M. Investigation of laser and ultrasonic ranging sensors for measurements of citrus canopy volume. Appl. Eng. Agric. 2002, 18, 367–372. [Google Scholar] [CrossRef]
- Palleja, T.; Landers, A.J. Real Time Canopy Density Estimation Using Ultrasonic Envelope Signals in the Orchard and Vineyard. Comput. Electron. Agric. 2015, 115, 108–117. [Google Scholar] [CrossRef]
- Palleja, T.; Landers, A.J. Real Time Canopy Density Validation Using Ultrasonic Envelope Signals and Point Quadrat Analysis. Comput. Electron. Agric. 2017, 134, 43–50. [Google Scholar] [CrossRef]
- Gil, E.; Escolà, A.; Rosell, J.R.; Planas, S.; Val, L. Variable Rate Application of Plant Protection Products in Vineyard Using Ultrasonic Sensors. Crop Prot. 2007, 26, 1287–1297. [Google Scholar] [CrossRef]
- Li, H.; Zhai, C.; Weckler, P.; Wang, N.; Yang, S.; Zhang, B. A Canopy Density Model for Planar Orchard Target Detection Based on Ultrasonic Sensors. Sensors 2017, 17, 31. [Google Scholar] [CrossRef] [PubMed]
- Nan, Y.; Zhang, H.; Zheng, J.; Bian, L.; Li, Y.; Yang, Y.; Zhang, M.; Ge, Y. Estimating Leaf Area Density of Osmanthus Trees Using Ultrasonic Sensing. Biosyst. Eng. 2019, 186, 60–70. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, W.; Li, Y.; Ou, M. Method for Estimating Canopy Thickness Using Ultrasonic Sensor Technology. Agriculture 2021, 11, 1011. [Google Scholar] [CrossRef]



| Code | Factors | |
|---|---|---|
| −r | 0.5 | 0.54 |
| −1 | 0.55 | 0.79 |
| 0 | 0.9 | 2.95 |
| 1 | 1.25 | 5.09 |
| r | 1.3 | 5.4 |
| Number | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | 0.9 | 2.95 |
| 2 | −r | 0 | 0.5 | 2.95 |
| 3 | 0 | r | 0.9 | 5.4 |
| 4 | 1 | 1 | 1.25 | 5.09 |
| 5 | 1 | −1 | 1.25 | 0.79 |
| 6 | 0 | 0 | 0.9 | 2.95 |
| 7 | 0 | −r | 0.9 | 0.54 |
| 8 | 0 | 0 | 0.9 | 2.95 |
| 9 | r | 0 | 1.3 | 2.95 |
| 10 | −1 | −1 | 0.55 | 0.79 |
| 11 | −1 | 1 | 0.55 | 5.09 |
| 0.90 | 2.95 | 1.95 | 4.51 | 1.83 |
| 0.50 | 2.95 | 2.14 | 5.41 | 1.96 |
| 0.90 | 5.40 | 1.94 | 5.05 | 1.81 |
| 1.25 | 5.09 | 1.90 | 4.11 | 1.79 |
| 1.25 | 0.79 | 1.70 | 2.47 | 1.65 |
| 0.90 | 2.95 | 1.94 | 4.53 | 1.84 |
| 0.90 | 0.54 | 1.59 | 1.97 | 1.57 |
| 0.90 | 2.95 | 1.96 | 4.52 | 1.82 |
| 1.30 | 2.95 | 1.86 | 3.74 | 1.76 |
| 0.55 | 0.79 | 1.82 | 3.62 | 1.71 |
| 0.55 | 5.09 | 2.11 | 5.25 | 1.92 |
| p value | 0.0005 | 0.0023 | 0.0003 |
| 0.97 | 0.95 | 0.93 | |
| Lack of Fit p value | 0.0461 | 0.0005 | 0.0722 |
| Source | Sum of Squares | df | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| Model | 0.12 | 4 | 0.024 | 29.80 | 0.0010 |
| X1 | 0.026 | 1 | 0.026 | 32.24 | 0.0024 |
| X2 | 0.060 | 1 | 0.06 | 73.26 | 0.0004 |
| X1 × X2 | 1 | 1.50 | 0.2745 | ||
| 1 | 4.98 | 0.0461 | |||
| 0.032 | 1 | 0.032 | 39.33 | 0.0015 | |
| Residual | 6 | ||||
| Lack of Fit | 4 | 13.01 | 0.0722 | ||
| Pure Error | 2 | ||||
| Cor Total | 0.13 | 10 |
| Source | Sum of Squares | df | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| Model | 0.12 | 4 | 0.030 | 34.01 | 0.0003 |
| X1 | 0.026 | 1 | 0.026 | 29.77 | 0.0016 |
| X2 | 0.060 | 1 | 0.060 | 67.57 | 0.0002 |
| 1 | 4.59 | 0.0449 | |||
| 0.032 | 1 | 0.032 | 36.28 | 0.0009 | |
| Residual | 6 | ||||
| Lack of Fit | 4 | 12.85 | 0.0735 | ||
| Pure Error | 2 | ||||
| Cor Total | 0.13 | 10 |
| Detection Distance (m) | (V) | (V) | Relative Error | |
|---|---|---|---|---|
| 0.8 | 0.98 | 1.67 | 1.60 | 4.37% |
| 1.0 | 0.98 | 1.64 | 1.51 | 8.61% |
| 1.2 | 0.98 | 1.62 | 1.53 | 5.88% |
| 0.8 | 2.95 | 1.85 | 1.77 | 4.52% |
| 1.0 | 2.95 | 1.81 | 1.87 | −3.21% |
| 1.2 | 2.95 | 1.79 | 1.87 | −4.28% |
| 0.8 | 4.92 | 1.85 | 1.77 | 4.52% |
| 1.0 | 4.92 | 1.82 | 1.70 | 7.06% |
| 1.2 | 4.92 | 1.80 | 1.70 | 5.88% |
| Detection Point | Detection Distance (m) | (V) | (V) | Relative Error | |
|---|---|---|---|---|---|
| 1 | 1.05 | 2.11 | 1.75 | 1.73 | 1.36 |
| 2 | 0.88 | 2.05 | 1.77 | 1.76 | 0.73 |
| 3 | 0.90 | 2.63 | 1.81 | 1.65 | 9.32 |
| 4 | 1.06 | 3.27 | 1.82 | 1.83 | −0.79 |
| 5 | 1.04 | 1.80 | 1.72 | 2.02 | −14.71 |
| 6 | 1.02 | 5.60 | 1.78 | 1.84 | −3.27 |
| 7 | 1.11 | 4.71 | 1.81 | 1.91 | −5.25 |
| 8 | 1.11 | 5.28 | 1.79 | 1.82 | −1.91 |
| 9 | 1.10 | 5.88 | 1.75 | 1.76 | −0.56 |
| 10 | 1.11 | 5.41 | 1.78 | 1.92 | −7.03 |
| 11 | 1.02 | 4.82 | 1.82 | 1.93 | −6.04 |
| 12 | 1.04 | 5.38 | 1.79 | 1.82 | −1.46 |
| 13 | 1.08 | 4.71 | 1.82 | 1.99 | −8.56 |
| 14 | 1.07 | 4.82 | 1.81 | 1.86 | −2.36 |
| 15 | 1.11 | 5.40 | 1.78 | 1.82 | −2.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, M.; Hu, T.; Hu, M.; Yang, S.; Jia, W.; Wang, M.; Jiang, L.; Wang, X.; Dong, X. Experiment of Canopy Leaf Area Density Estimation Method Based on Ultrasonic Echo Signal. Agriculture 2022, 12, 1569. https://doi.org/10.3390/agriculture12101569
Ou M, Hu T, Hu M, Yang S, Jia W, Wang M, Jiang L, Wang X, Dong X. Experiment of Canopy Leaf Area Density Estimation Method Based on Ultrasonic Echo Signal. Agriculture. 2022; 12(10):1569. https://doi.org/10.3390/agriculture12101569
Chicago/Turabian StyleOu, Mingxiong, Tianhang Hu, Mingshuo Hu, Shuai Yang, Weidong Jia, Ming Wang, Li Jiang, Xiaowen Wang, and Xiang Dong. 2022. "Experiment of Canopy Leaf Area Density Estimation Method Based on Ultrasonic Echo Signal" Agriculture 12, no. 10: 1569. https://doi.org/10.3390/agriculture12101569
APA StyleOu, M., Hu, T., Hu, M., Yang, S., Jia, W., Wang, M., Jiang, L., Wang, X., & Dong, X. (2022). Experiment of Canopy Leaf Area Density Estimation Method Based on Ultrasonic Echo Signal. Agriculture, 12(10), 1569. https://doi.org/10.3390/agriculture12101569






