Impact of Population Aging and Renewable Energy Consumption on Agricultural Green Total Factor Productivity in Rural China: Evidence from Panel VAR Approach
Abstract
:1. Introduction
2. Literature Review
3. Method
3.1. Model Specification
3.2. Cross-Sectional Dependence Tests
3.3. Unit Root Test
3.3.1. Levin–Lin–(Chao) Test
3.3.2. Augmented Dickey–Fuller (ADF) Test
3.3.3. Phillips–Perron Test
3.3.4. Panel Cointegration Test
3.3.5. Fully Modified Ordinary Least Squares (FMOLS) and Dynamic Ordinary Least Squares (DOLS)
3.3.6. Variance Decomposition and Impulse Response Method
4. Results
4.1. Cross-Section Correlation and Unit Root Test Results
4.2. Kao’s Residual Panel Cointegration Test (ADF) Results
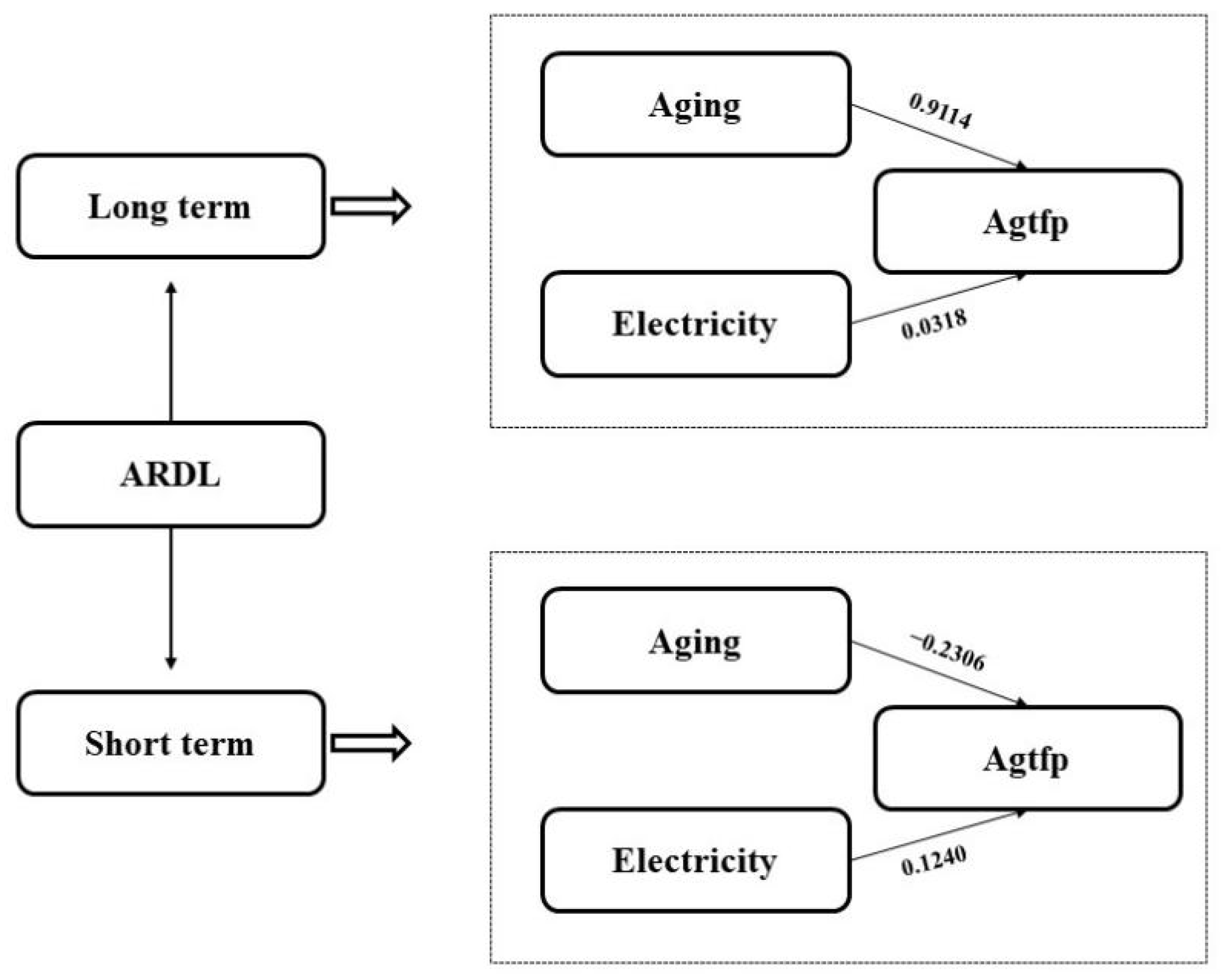
4.3. Long-Run and Short-Run Estimates
4.4. Robustness Tests
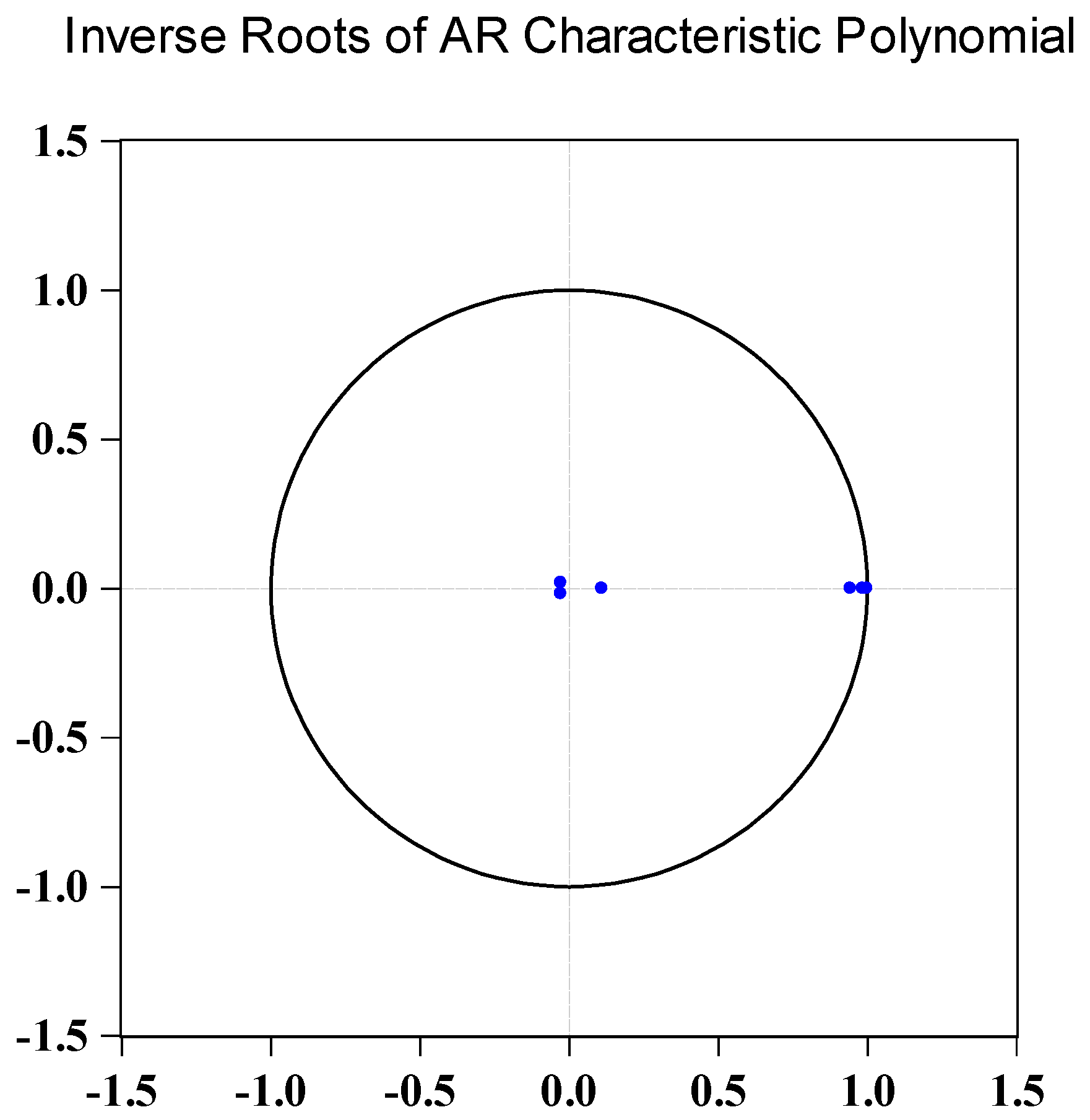
4.5. Stability of the Panel VAR Model
4.6. Variance Decomposition and Impulse Response Analysis Results
4.7. Discussion
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Period | S.E. | LNAGTFP | LNAGING | LNELECTRICITY |
|---|---|---|---|---|
| Variance Decomposition of LNAGTFP: | ||||
| 1 | 0.0906 | 100.0000 | 0.0000 | 0.0000 |
| 2 | 0.1273 | 99.7680 | 0.1693 | 0.0626 |
| 3 | 0.1533 | 99.6444 | 0.2843 | 0.0713 |
| 4 | 0.1735 | 99.5375 | 0.4016 | 0.0609 |
| 5 | 0.1900 | 99.4220 | 0.5272 | 0.0508 |
| 6 | 0.2038 | 99.2895 | 0.6626 | 0.0479 |
| 7 | 0.2156 | 99.1369 | 0.8078 | 0.0553 |
| 8 | 0.2258 | 98.9632 | 0.9623 | 0.0744 |
| 9 | 0.2348 | 98.7685 | 1.1255 | 0.1059 |
| 10 | 0.2427 | 98.5533 | 1.2965 | 0.1502 |
| 11 | 0.2497 | 98.3183 | 1.4743 | 0.2074 |
| 12 | 0.2559 | 98.0645 | 1.6580 | 0.2774 |
| 13 | 0.2616 | 97.7932 | 1.8466 | 0.3602 |
| 14 | 0.2667 | 97.5053 | 2.0392 | 0.4555 |
| 15 | 0.2713 | 97.2022 | 2.2348 | 0.5629 |
| Variance Decomposition of LNAGING: | ||||
| 1 | 0.0672 | 0.7778 | 99.2222 | 0.0000 |
| 2 | 0.0919 | 0.4920 | 99.0290 | 0.4790 |
| 3 | 0.1108 | 0.3589 | 98.9191 | 0.7220 |
| 4 | 0.1263 | 0.2809 | 98.8292 | 0.8900 |
| 5 | 0.1397 | 0.2299 | 98.7446 | 1.0255 |
| 6 | 0.1516 | 0.1959 | 98.6591 | 1.1450 |
| 7 | 0.1622 | 0.1737 | 98.5705 | 1.2558 |
| 8 | 0.1719 | 0.1608 | 98.4779 | 1.3613 |
| 9 | 0.1808 | 0.1552 | 98.3810 | 1.4637 |
| 10 | 0.1890 | 0.1558 | 98.2800 | 1.5641 |
| 11 | 0.1966 | 0.1616 | 98.1752 | 1.6632 |
| 12 | 0.2037 | 0.1718 | 98.0668 | 1.7614 |
| 13 | 0.2104 | 0.1858 | 97.9552 | 1.8590 |
| 14 | 0.2168 | 0.2029 | 97.8408 | 1.9562 |
| 15 | 0.2227 | 0.2229 | 97.7240 | 2.0531 |
| Variance Decomposition of LNELECTRICITY: | ||||
| 1 | 0.1862 | 0.4799 | 0.0299 | 99.4902 |
| 2 | 0.2708 | 0.2537 | 0.0381 | 99.7081 |
| 3 | 0.3348 | 0.1834 | 0.0265 | 99.7901 |
| 4 | 0.3882 | 0.1532 | 0.0206 | 99.8262 |
| 5 | 0.4349 | 0.1389 | 0.0234 | 99.8378 |
| 6 | 0.4768 | 0.1324 | 0.0352 | 99.8324 |
| 7 | 0.5151 | 0.1304 | 0.0561 | 99.8135 |
| 8 | 0.5507 | 0.1311 | 0.0857 | 99.7833 |
| 9 | 0.5840 | 0.1334 | 0.1237 | 99.7429 |
| 10 | 0.6154 | 0.1368 | 0.1698 | 99.6934 |
| 11 | 0.6452 | 0.1409 | 0.2235 | 99.6356 |
| 12 | 0.6736 | 0.1454 | 0.2845 | 99.5701 |
| 13 | 0.7008 | 0.1501 | 0.3525 | 99.4974 |
| 14 | 0.7269 | 0.1549 | 0.4270 | 99.4181 |
| 15 | 0.7522 | 0.1596 | 0.5077 | 99.3327 |
References
- Clancy, M.; Fuglie, K.O.; Heisey, P.U.S. Agricultural R&D in an Era of Falling Public Funding; Amber Waves; USDA-Economic Research Service: Washington, DC, USA, 2016. [Google Scholar]
- Fang, L.; Hu, R.; Mao, H.; Chen, S.J. How crop insurance influences agricultural green total factor productivity: Evidence from Chinese farmers. J. Clean. Prod. 2021, 321, 128977. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Denny, M.; Fuss, M. Estimation and decomposition of productivity change when production is not efficient: A panel data approach. Econom. Rev. 2000, 19, 312–320. [Google Scholar] [CrossRef]
- Wang, H.; Cui, H.; Zhao, Q. Effect of green technology innovation on green total factor productivity in China: Evidence from spatial Durbin model analysis. J. Clean. Prod. 2021, 288, 125624. [Google Scholar] [CrossRef]
- Wang, S.J.; Huang, J.K.; Wang, X.B. Francis Tuan. Are China’s regional agricultural productivities converging: How and why? Food Policy 2019, 86, 101727. [Google Scholar] [CrossRef]
- Ota, T.; Kakinaka, M.; Kotani, K. Demographic effects on residential electricity and city gas consumption in the aging society of Japan. Energy Policy 2018, 115, 503–513. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.C. Changing energy intensity of economies in the world and its decomposition. Energy Econ. 2013, 40, 637–644. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, Z. Industrial electricity consumption, human capital investment and economic growth in Chinese cities. Econ. Model. 2018, 69, 205–219. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hosan, S.; Karmaker, S.C.; Chapman, A.J.; Saha, B.B. The effect of remittance on energy consumption: Panel cointegration and dynamic causality analysis for South Asian countries. Energy 2020, 220, 119684. [Google Scholar] [CrossRef]
- Deichmann, U.; Reuter, A.; Vollmer, S.; Zhang, F. The relationship between energy intensity and economic growth: New evidence from a multi-country multi-sectorial dataset. World Dev. 2019, 124, 104664. [Google Scholar] [CrossRef]
- Hall, R.E.; Jones, C.I. Why do some countries produce so much more output per worker than others? Q. J. Econom. 1999, 114, 83–116. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, C. What drives the fluctuations of “green” productivity in China’s agricultural sector? A weighted Russell directional distance approach. Resour. Conserv. Recycl. 2019, 147, 201–213. [Google Scholar] [CrossRef]
- Lin, B.; Chen, Z. Does factor market distortion inhibit the green total factor productivity in China? J. Clean. Prod. 2018, 197, 25–33. [Google Scholar] [CrossRef]
- Dokić, D.; Gavran, M.; Gregić, M.; Gantner, V. The impact of trade balance of agri-food products on the state’s ability to withstand the crisis. HighTech Innov. J. 2020, 1, 107–111. [Google Scholar] [CrossRef]
- Jin, S.; Ma, H.; Huang, J.; Hu, R.; Rozelle, S. Productivity, efficiency and technical change: Measuring the performance of China’s transforming agriculture. J. Prod. Anal. 2010, 33, 191–207. [Google Scholar] [CrossRef]
- Adnan, N.; Nordin, S.M.; Ali, M. A solution for the sunset industry: Adoption of green fertilizer technology amongst Malaysian paddy farmers. Land Use Policy 2018, 79, 575–584. [Google Scholar] [CrossRef]
- Ang, J.B.; Madsen, J.B.; Islam, M.R. The effects of human capital composition on technological convergence. J. Macroecon. 2011, 33, 465–476. [Google Scholar] [CrossRef]
- Cole, S. Age and Scientific Performance. Am. J. Sociol. 1979, 84, 958–977. [Google Scholar] [CrossRef]
- Levin, S.G.; Stephan, P.E. Research Productivity over the Life Cycle: Evidence for Academic Scientists. Am. Econ. Assoc. 1991, 81, 114–132. [Google Scholar]
- Benhabib, J.; Spiegel, M.M. Chapter 13 Human Capital and Technology Diffusion; Aghion, P., Steven, N., Eds.; Durlauf, Handbook of Economic Growth; Elsevier: Amsterdam, The Netherlands, 2005; Volume 1, pp. 935–966. [Google Scholar] [CrossRef]
- Nelson, R.R.; Phelps, E.S. Investment in Humans, Technological Diffusion and Economic Growth; Cowles Foundation Discussion Papers 189; Cowles Foundation for Research in Economics, Yale University: New Haven, CT, USA, 1965. [Google Scholar]
- Romer, P.M. Endogenous Technological Change. J. Political Econ. 1990, 98, 71–102. [Google Scholar] [CrossRef] [Green Version]
- Choi, K.-H.; Shin, S. Population aging, economic growth, and the social transmission of human capital: An analysis with an overlapping generations model. Econ. Model. 2015, 50, 138–147. [Google Scholar] [CrossRef]
- Bairoliya, N.; Miller, R. Demographic transition, human capital and economic growth in China. J. Econ. Dyn. Control 2021, 127, 104117. [Google Scholar] [CrossRef] [PubMed]
- Khor, N.; Pang, L.; Liu, C.; Chang, F.; Mo, D.; Loyalka, P.; Rozelle, S. China’s Looming Human Capital Crisis:Upper Secondary Educational Attainment Rates and the Middle-income Trap. China Q. 2016, 228, 905–926. [Google Scholar] [CrossRef]
- Fougère, M.; Mérette, M. Population ageing and economic growth in seven OECD countries. Econ. Model. 1999, 16, 411–427. [Google Scholar] [CrossRef]
- Fougère, M.; Harvey, S.; Mercenier, J.; Mérette, M. Population ageing, time allocation and human capital: A general equilibrium analysis for Canada. Econ. Model. 2009, 26, 30–39. [Google Scholar] [CrossRef]
- Čiutienė, R.; Railaitė, R. A Development of Human Capital in the Context of an Aging Population. Procedia Soc. Behav. Sci. 2015, 213, 753–757. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, J.; Lee, R. Rising longevity, education, savings, and growth. J. Dev. Econ. 2003, 70, 83–101. [Google Scholar] [CrossRef]
- Gradstein, M.; Kaganovich, M. Aging Population and Education Finance. J. Public Econ. 2003, 88, 2469–2485. [Google Scholar] [CrossRef]
- Ozcan, B.; Danish; Temiz, M. An empirical investigation between renewable energy consumption, globalization and human capital: A dynamic auto-regressive distributive lag simulation. Renew. Energy 2022, 193, 195–203. [Google Scholar] [CrossRef]
- Alvarado, R.; Deng, Q.; Tillaguango, B.; Méndez, P.; Bravo, D.; Chamba, J.; Alvarado-Lopez, M.; Ahmad, M. Do economic development and human capital decrease non-renewable energy consumption? Evidence for OECD countries. Energy 2021, 215, 119147. [Google Scholar] [CrossRef]
- Yao, Y.; Ivanovski, K.; Inekwe, J.; Smyth, R. Human capital and energy consumption: Evidence from OECD countries. Energy Econ. 2019, 84, 104534. [Google Scholar] [CrossRef]
- Bano, S.; Liu, L.; Khan, A. Dynamic influence of aging, industrial innovations, and ICT on tourism development and renewable energy consumption in BRICS economies. Renew. Energy 2022, 192, 431–442. [Google Scholar] [CrossRef]
- Zhang, Z.; Hao, Y.; Lu, Z.N.; Deng, Y. How does demographic structure affect environmental quality? Empirical evidence from China. Resour. Conserv. Recycl. 2018, 133, 242–249. [Google Scholar] [CrossRef]
- Willis, K.; Scarpa, R.; Gilroy, R.; Hamza, N. Renewable energy adoption in an ageing population: Heterogeneity in preferences for micro-generation technology adoption. Energy Policy 2011, 39, 6021–6029. [Google Scholar] [CrossRef]
- Tarazkar, M.H.; Dehbidi, N.K.; Ozturk, I.; Al-Mulali, U. The impact of age structure on carbon emission in the Middle East: The panel autoregressive distributed lag approach. Environ. Sci. Pollut. Res. 2021, 28, 33722–33734. [Google Scholar] [CrossRef]
- Sims, C.A. Comparison of interwar and postwar business cycle. Am. Econ. Rev. 1980, 1980, 250–257. [Google Scholar]
- Holtz-Eakin, D.; Newey, W.; Rosen, H.S. Estimating Vector Autoregressions with Panel Data. Econometrica. 1988, 56, 1371–1395. [Google Scholar] [CrossRef]
- Levin, A.; Lin, C.F.; Chu, C.S.J. Unit Root Tests in Panel Data: Asymptotic and Finite-Sample Properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Hadri, K. Testing for stationarity in heterogeneous panel data. Econom. J. 2001, 3, 148–161. [Google Scholar] [CrossRef]
- O’Connell, P.G.J. The overvaluation of purchasing power parity. J. Int. Econ. 1998, 44, 1–19. [Google Scholar] [CrossRef]
- Pesaran, M.H. General Diagnostic Tests for Cross Section Dependence in Panels. Camb. Work. Pap. Econ. 2004, 69, 1240. [Google Scholar] [CrossRef]
- Choi, I. Unit root tests for panel data. J. Int. Money Financ. 2001, 20, 249–272. [Google Scholar] [CrossRef]
- Phillips, P.C.B. Time Series Regression with a Unit Root. Econometrica 1987, 55, 277. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a Unit Root in Time Series Regression. Biometrika 1988, 75, 335. [Google Scholar] [CrossRef]
- Kao, C. Spurious regression and residual-based tests for cointegration in panel data. J. Econom. 1999, 90, 1–44. [Google Scholar] [CrossRef]
- Stock, J.H. Asymptotic Properties of Least Squares Estimators of Cointegrating Vectors. Econometrica 1987, 55, 1035. [Google Scholar] [CrossRef]
- Banerjee, A.; Dolado, J.J.; Hendry, D.; Smith, G. Exploring equilibrium relationships in econometrics through static models: Some Monte-Carlo evidence. Oxf. Bull. Econ. Stat. 1986, 48, 253–277. [Google Scholar] [CrossRef] [Green Version]
- Phillips, P.C.B.; Hansen, B.E. Statistical Inference in Instrumental Variables Regression with I(1) Processes. Rev. Econ. Stud. 1990, 57, 99. [Google Scholar] [CrossRef]
- Banerjee, A. Panel Data Unit Roots and Cointegration: An Overview. Oxf. Bull. Econ. Stat. 1999, 61, 607–629. [Google Scholar] [CrossRef]
- Dreger, C.; Reimers, H.E. Health Care Expenditures in OECD Countries: A Panel Unit Root and Cointegration Analysis; Social Science Electronic Publishing: Rochester, NY, USA, 2005. [Google Scholar] [CrossRef]
- Lanne, M.; Nyberg, H. Generalized forecast error variance decomposition for linear and nonlinear multivariate models. Oxf. Bull. Econ. Stat. 2016, 78, 595–603. [Google Scholar] [CrossRef] [Green Version]
- Dong, K.; Dong, X.; Jiang, Q. How does renewable energy consumption lower global CO2 emissions? Evidence from countries with different income levels. World Econ. 2019, 43, 1665–1689. [Google Scholar] [CrossRef]
- Vandenbussche, J.; Aghion, P.; Meghir, C. Growth, distance to frontier and composition of human capital. J. Econ. Growth 2006, 11, 97–127. [Google Scholar] [CrossRef]
- Minihan, E.S.; Wu, Z. Economic structure and strategies for greenhouse gas mitigation. Energy Econ. 2012, 34, 350–357. [Google Scholar] [CrossRef]
- Shimada, K.; Tanaka, Y.; Gomi, K.; Matsuoka, Y. Developing a long-term local society design methodology towards a low-carbon economy: An application to Shiga Prefecture in Japan. Energy Policy 2007, 35, 4688–4703. [Google Scholar] [CrossRef]
- Gittleman, M.; Raa, T.T.; Wolff, E.N. The vintage effect in TFP-growth: An analysis of the age structure of capital. Struct. Chang. Econ. Dyn. 2006, 17, 306–328. [Google Scholar] [CrossRef] [Green Version]
- Pais-Magalhães, V.; Moutinho, V.; Robaina, M. Is an ageing population impacting energy use in the European Union? Drivers, lifestyles, and consumption patterns of elderly households. Energy Res. Soc. Sci. 2022, 85, 102443. [Google Scholar] [CrossRef]
- Aslam, M.; Ahmad, E. Impact of ageing and generational effects on household energy consumption behavior: Evidence from Pakistan. Energies 2018, 11, 2003. [Google Scholar] [CrossRef] [Green Version]
- Estiri, H.; Zagheni, E. Age matters: Ageing and household energy demand in the United States. Energy Res. Soc. Sci. 2019, 55, 62–70. [Google Scholar] [CrossRef]
- Gao, F. Evolution trend and internal mechanism of regional total factor productivity in Chinese agriculture. J. Quant. Tech. Econ. 2015, 32, 3–19. [Google Scholar]
- Liu, Z. Analysis on the dynamic and influencing factors of agricultural total factor productivity in China. Chin. J. Agric. Resour. Reg. Plan. 2018, 39, 104–111. [Google Scholar]
- Ge, P.F.; Wang, S.J.; Huang, X.L. Measurement for China’s agricultural green TFP. China Popul. Resour. Environ. 2018, 28, 66–74. [Google Scholar]
- Naseem, A.; Spielman, D.J.; Omamo, S.W. Private-sector investment in R&D: A review of policy options to promote its growth in developing-country agriculture. Agribusiness 2010, 26, 143–173. [Google Scholar]
- Liu, F.; Lv, N. The threshold effect test of human capital on the growth of agricultural green total factor productivity: Evidence from China. Int. J. Electr. Eng. Educ. 2021. [Google Scholar] [CrossRef]
- Tang, C.F.; Tan, E.C. Exploring the nexus of electricity consumption, economic growth, energy prices and technology innovation in Malaysia. Appl. Energy 2013, 104, 297–305. [Google Scholar] [CrossRef]
- Irandoust, M. The renewable energy-growth nexus with carbon emissions and technological innovation: Evidence from the Nordic countries. Ecol. Indic. 2016, 69, 118–125. [Google Scholar] [CrossRef]
- Garau, G.; Lecca, P.; Mandras, G. The impact of population ageing on energy use: Evidence from Italy. Econ. Model. 2013, 35, 970–980. [Google Scholar] [CrossRef]
- Engbom, N. Firm and Worker Dynamics in an Aging Labor Market; Federal Reserve Bank of Minneapolis: Minneapolis, MN, USA, 2019. [Google Scholar]
- Park, C.-Y.; Shin, K.; Kikkawa, A. Demographic change, technological advance, and growth: A cross-country analysis. Econ. Model. 2022, 108, 105742. [Google Scholar] [CrossRef]



| Test | Statistic | Prob. |
|---|---|---|
| Breusch–Pagan LM | 2331.903 | 0.0000 |
| Pesaran scaled LM | 64.31103 | 0.0000 |
| Pesaran CD | 22.04594 | 0.0000 |
| Variables | Level | First-Order Difference | ||
|---|---|---|---|---|
| Intercept | Intercept and Trend | Intercept | Intercept and Trend | |
| LLC test | ||||
| lnagtfp | 0.9987 | 0.0002 | 0.0000 | 0.0000 |
| lnaging | 0.9687 | 0.0845 | 0.0000 | 0.0000 |
| lnelectricity | 0.0000 | 0.5146 | 0.0000 | 0.0000 |
| Im, Pesaran and Shin test | ||||
| lnagtfp | 1.0000 | 0.1861 | 0.0000 | 0.0000 |
| lnaging | 1.0000 | 0.2029 | 0.0000 | 0.0000 |
| lnelectricity | 0.0066 | 0.9589 | 0.0000 | 0.0000 |
| ADF-Fisher Chi-square test | ||||
| lnagtfp | 0.8787 | 0.0004 | 0.0000 | 0.0000 |
| lnaging | 0.9988 | 0.1046 | 0.0000 | 0.0000 |
| lnelectricity | 0.0000 | 0.2113 | 0.0000 | 0.0000 |
| PP-Fisher Chi-square test | ||||
| lnagtfp | 0.9711 | 0.0033 | 0.0000 | 0.0000 |
| lnaging | 1.0000 | 0.4615 | 0.0000 | 0.0000 |
| lnelectricity | 0.0000 | 0.5060 | 0.0000 | 0.0000 |
| Null Hypothesis | t-Statistics | Probability | |
|---|---|---|---|
| ADF | No co-integration | −2.662113 | 0.0039 |
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| Long-Run Equation | ||||
| LNAGING | 0.9114 | 0.1006 | 9.0641 | 0.0000 |
| LNELECTRICITY | 0.0318 | 0.0226 | 1.4098 | 0.1594 |
| Short-Run Equation | ||||
| COINTEQ01 | −0.2286 | 0.0293 | −7.7910 | 0.0000 |
| D(LNAGING) | −0.2306 | 0.0502 | −4.5929 | 0.0000 |
| D(LNELECTRICITY) | 0.1240 | 0.0728 | 1.7044 | 0.0890 |
| C | 0.3738 | 0.0493 | 7.5811 | 0.0000 |
| Variables | Coefficient | S.E. | t-Statistic | Prob. |
|---|---|---|---|---|
| FMOLS | ||||
| LNAGING | 0.4530 | 0.0788 | 5.7497 | 0.0000 |
| LNELECTRICITY | 0.0900 | 0.0229 | 3.9279 | 0.0001 |
| DOLS | ||||
| LNAGING | 0.3384 | 0.1170 | 2.8918 | 0.0042 |
| LNELECTRICITY | 0.0684 | 0.0304 | 2.2499 | 0.0254 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhou, X.; Tang, M.; Guo, L. Impact of Population Aging and Renewable Energy Consumption on Agricultural Green Total Factor Productivity in Rural China: Evidence from Panel VAR Approach. Agriculture 2022, 12, 715. https://doi.org/10.3390/agriculture12050715
Li H, Zhou X, Tang M, Guo L. Impact of Population Aging and Renewable Energy Consumption on Agricultural Green Total Factor Productivity in Rural China: Evidence from Panel VAR Approach. Agriculture. 2022; 12(5):715. https://doi.org/10.3390/agriculture12050715
Chicago/Turabian StyleLi, Houjian, Xiaolei Zhou, Mengqian Tang, and Lili Guo. 2022. "Impact of Population Aging and Renewable Energy Consumption on Agricultural Green Total Factor Productivity in Rural China: Evidence from Panel VAR Approach" Agriculture 12, no. 5: 715. https://doi.org/10.3390/agriculture12050715
APA StyleLi, H., Zhou, X., Tang, M., & Guo, L. (2022). Impact of Population Aging and Renewable Energy Consumption on Agricultural Green Total Factor Productivity in Rural China: Evidence from Panel VAR Approach. Agriculture, 12(5), 715. https://doi.org/10.3390/agriculture12050715






