Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus
Abstract
:1. Introduction
2. Materials and Methods
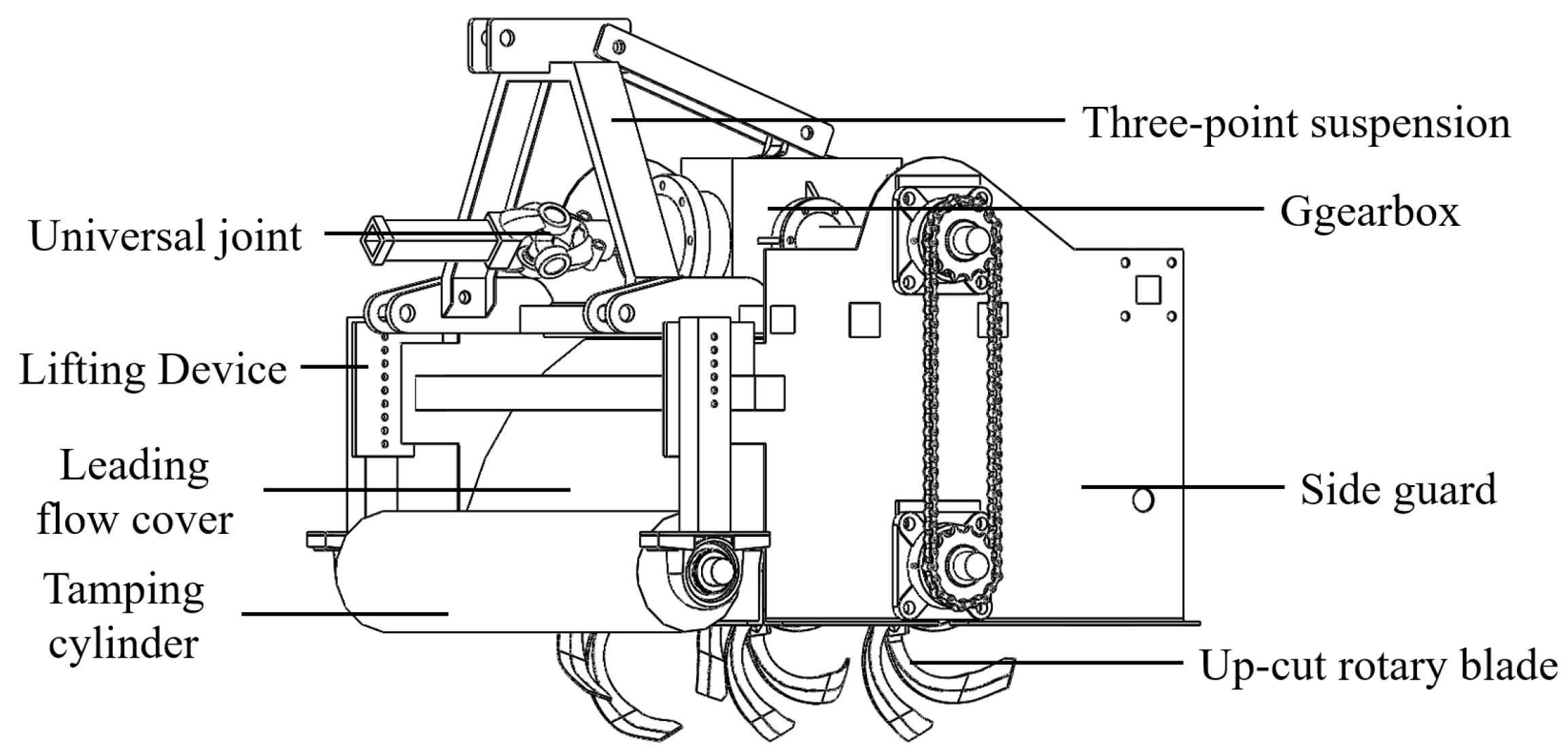
2.1. General Structure and Working Principle
2.1.1. General Structure and Parameters
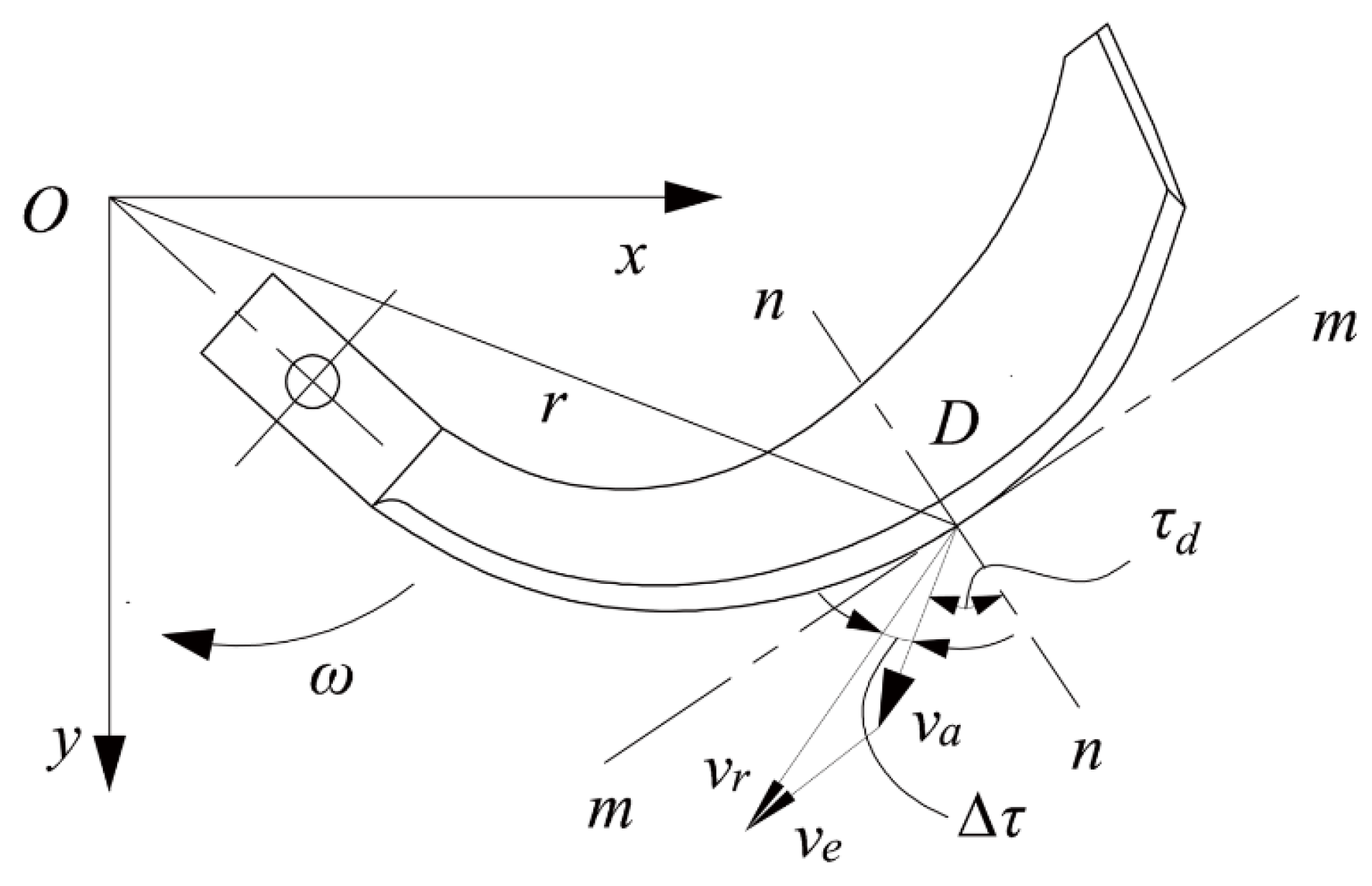
2.1.2. Working Principle
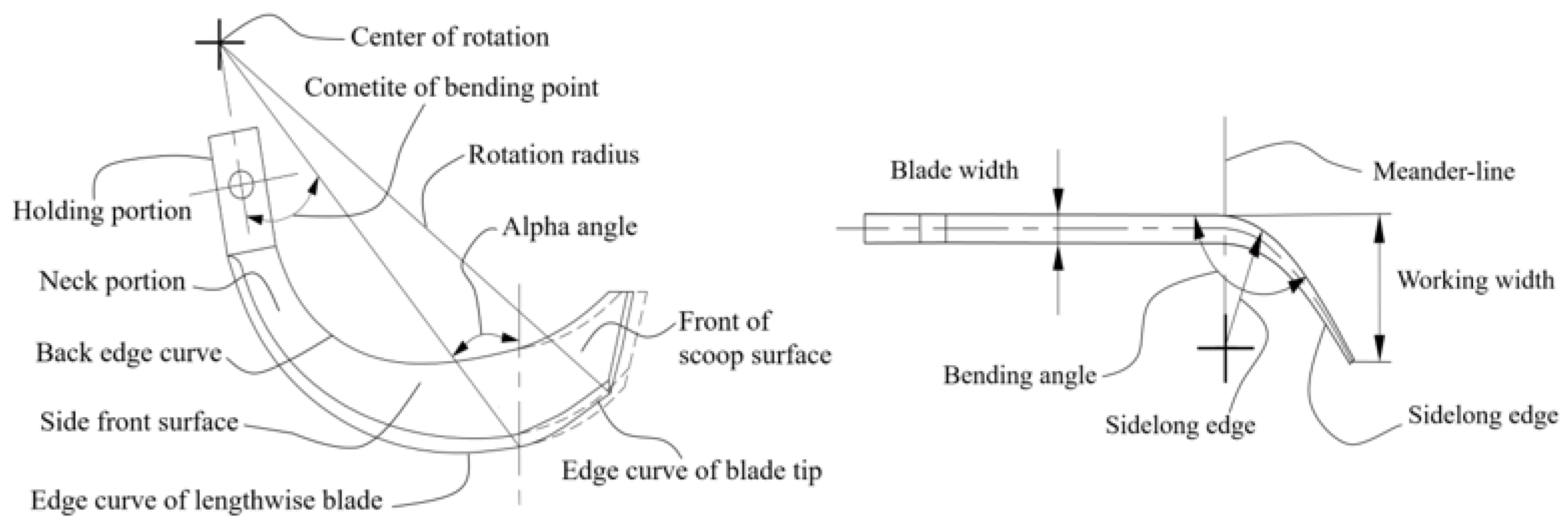
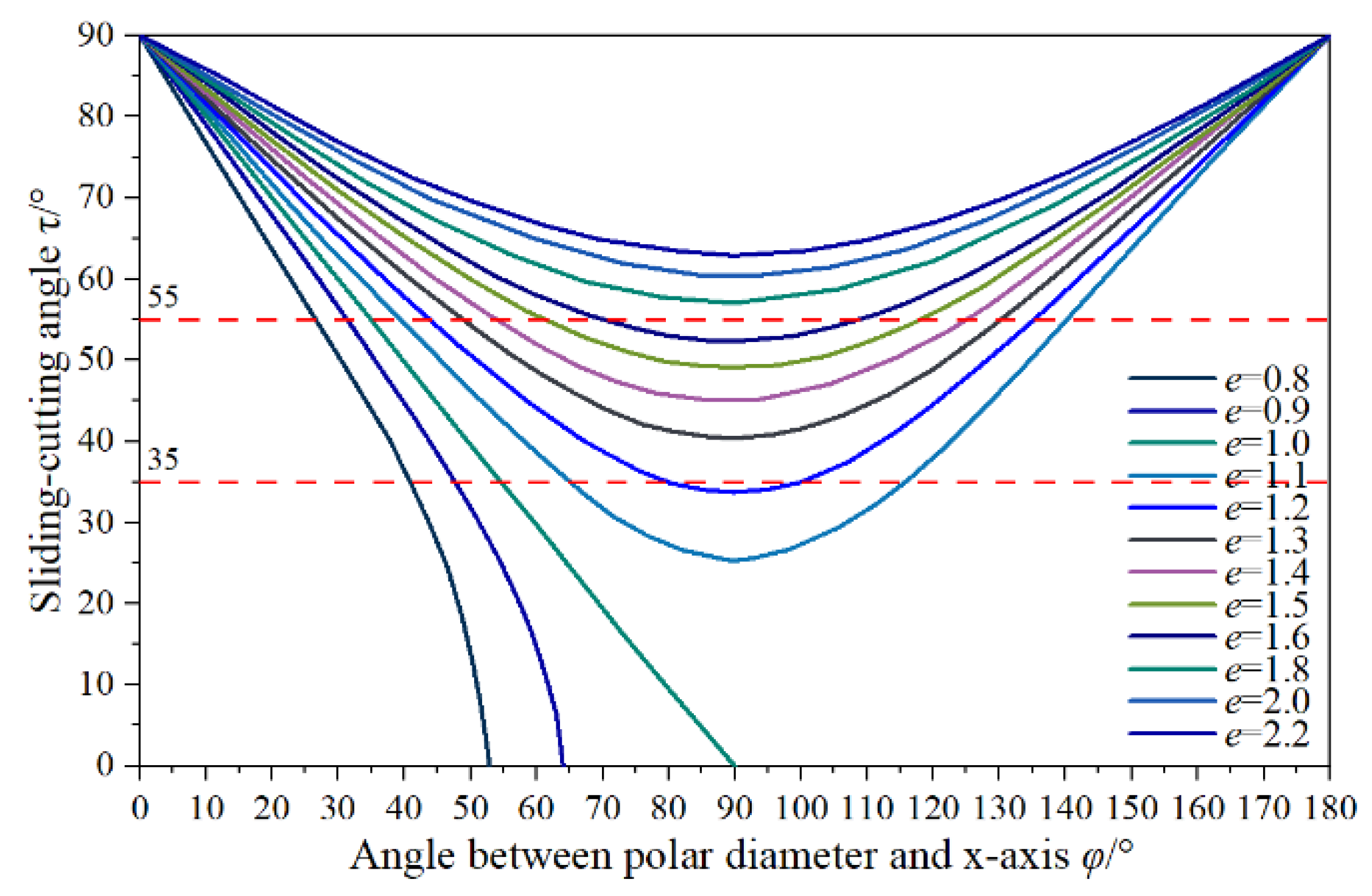
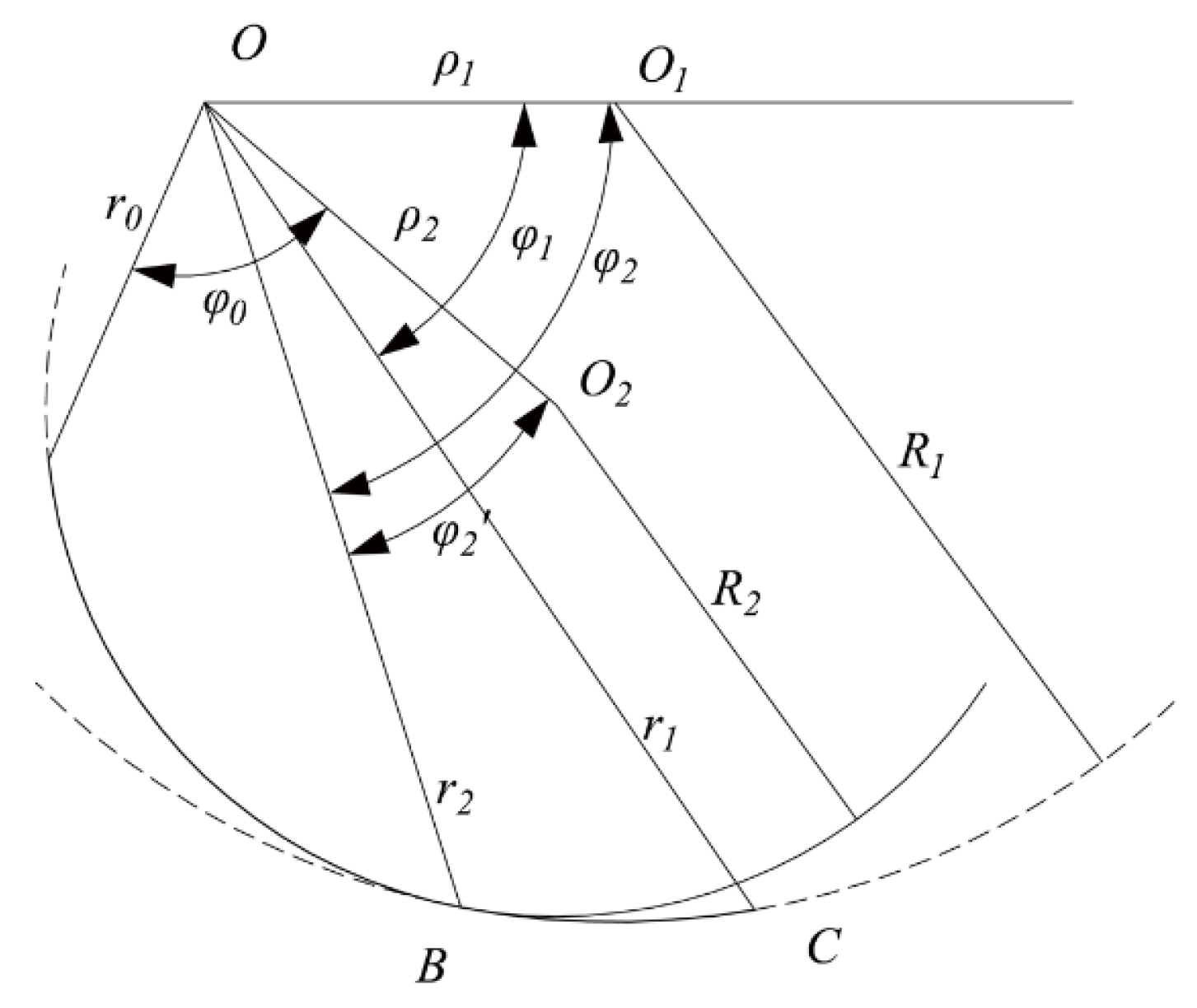
2.2. Design of Rotary Blade Edge Curve
2.3. Discrete Element Simulation
2.3.1. Rotary Blade Model
2.3.2. Soil Model
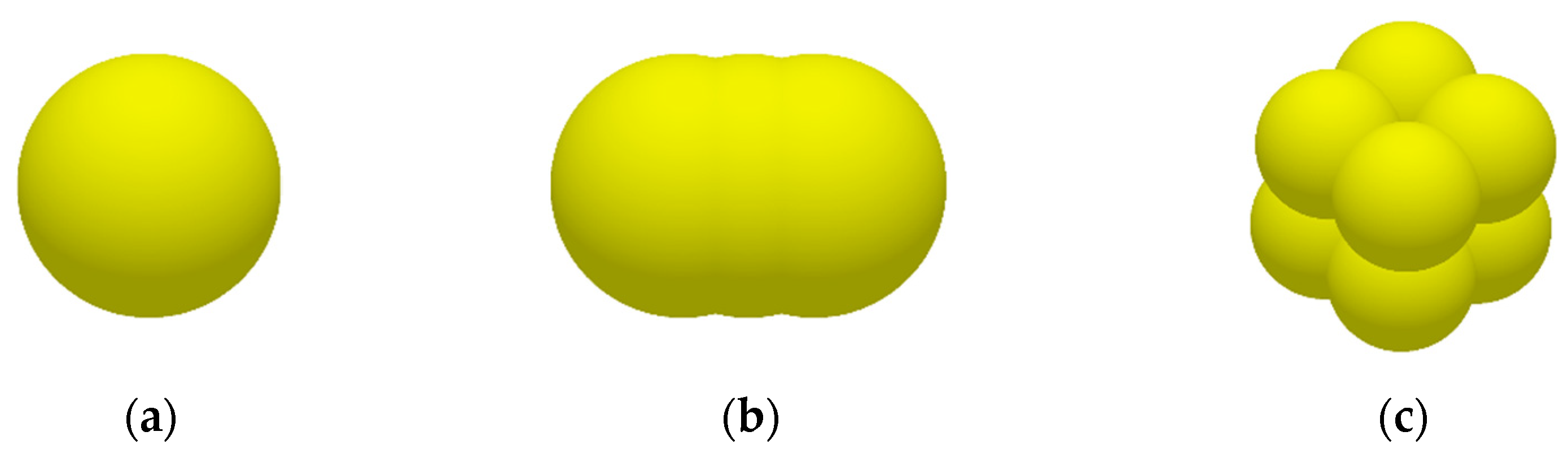
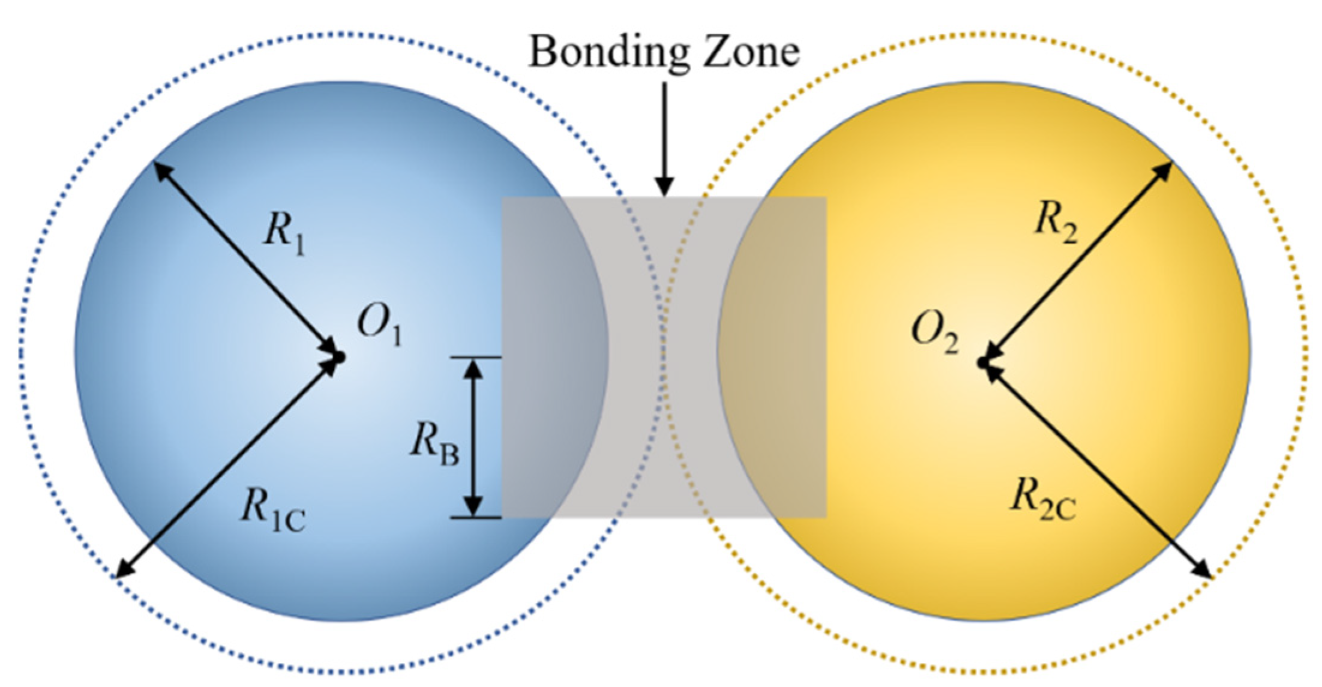
2.3.3. Cyperus esculentus Plant Model
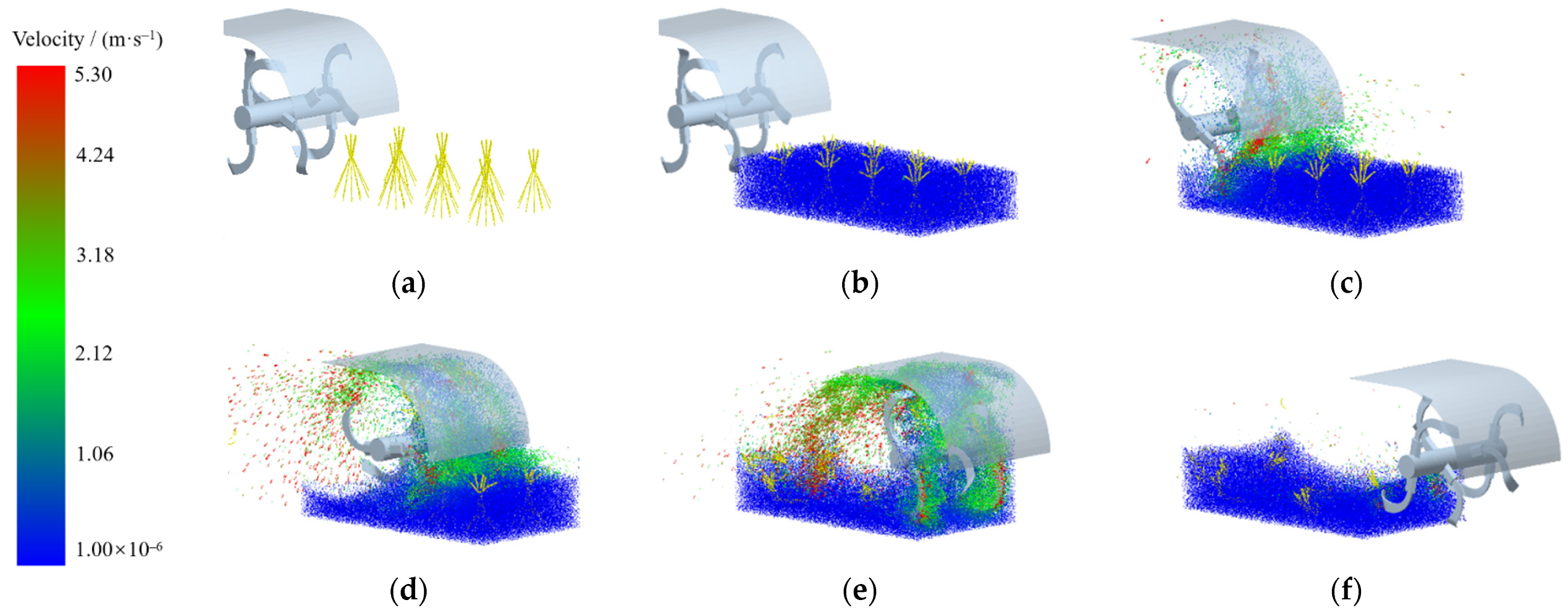
2.3.4. Discrete Element Simulation of Soil–Plant–Rotary Blade
2.4. Evaluation Index of Rotary Tillage Quality
2.4.1. Power Consumption
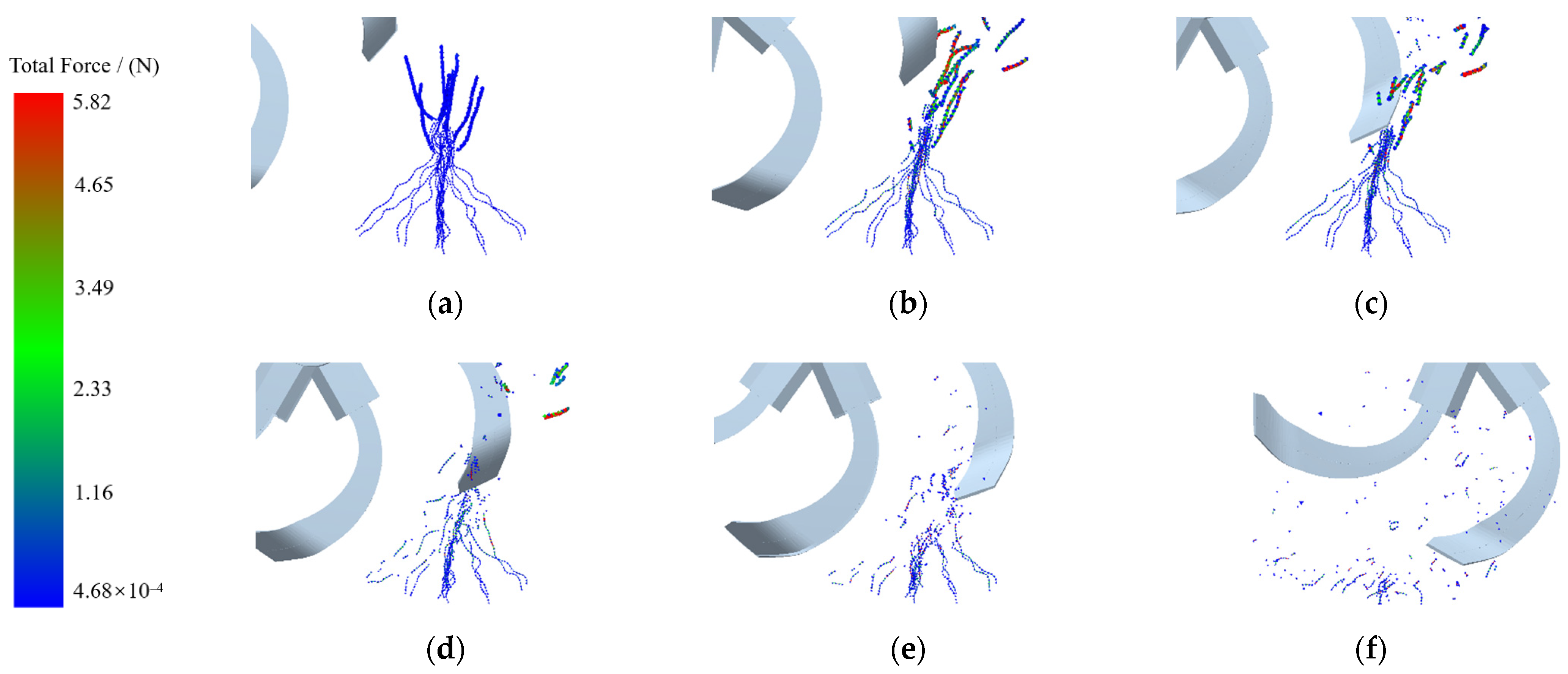
2.4.2. Plant-Crushing Performance
2.5. Field Experiment
2.5.1. Test Conditions
2.5.2. Index and Factor of Test
3. Results and Analysis
3.1. Evaluation Index of Rotary Tillage Quality
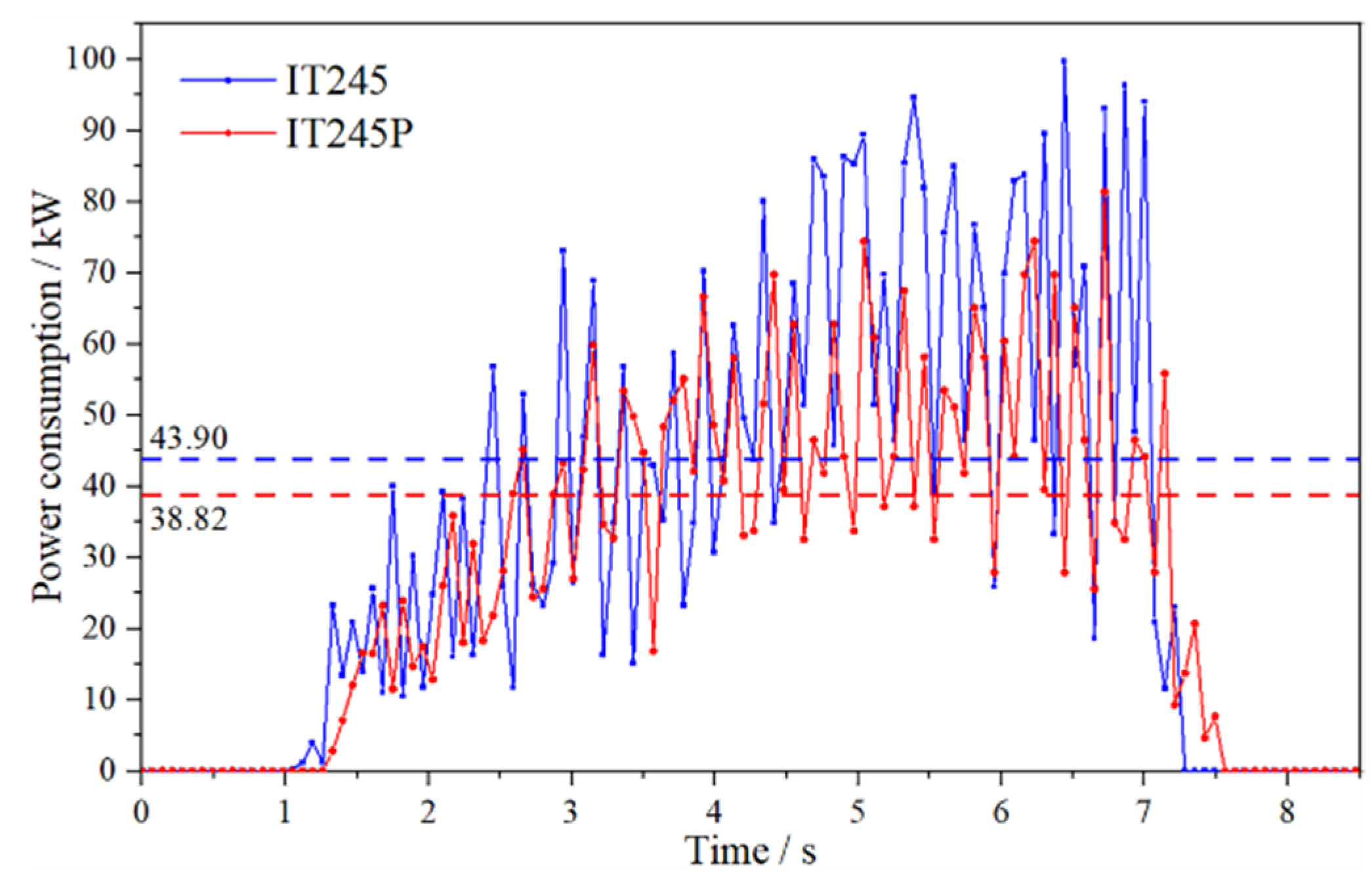
3.1.1. Analysis of Power Consumption
3.1.2. Analysis of Plant-Crushing Performance
3.2. Field Experiment
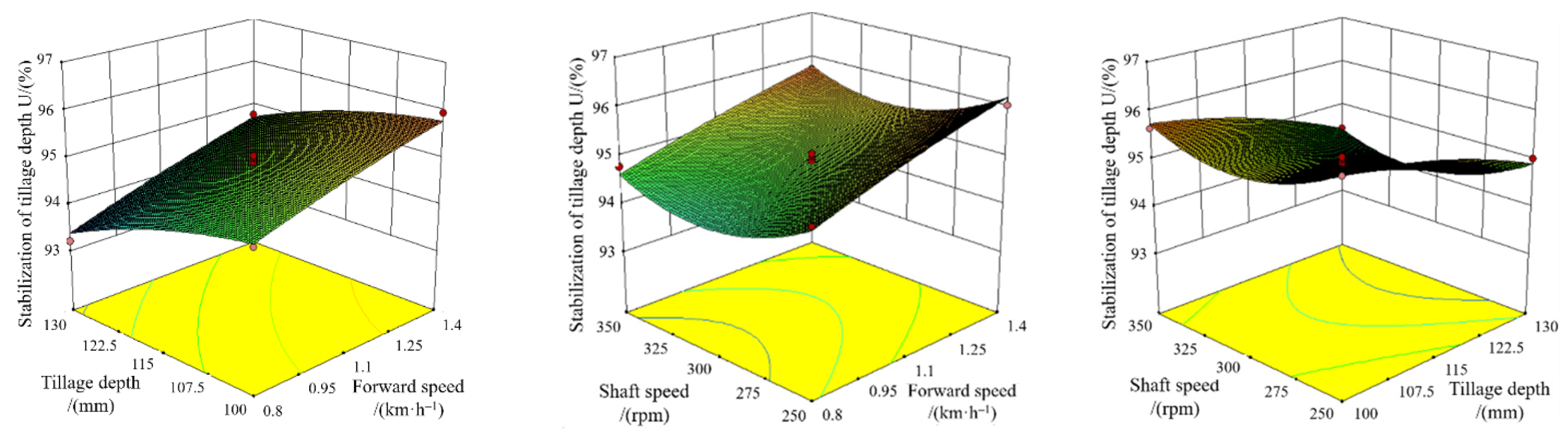
3.2.1. Tillage Depth Stability of Cyperus esculentus Harvesting
3.2.2. Power Consumption of Cyperus esculentus Harvesting
4. Conclusions
- (1)
- In this study, two eccentric arcs with different sliding–cutting performances were used to design a rotary blade edge curve according to the requirements of Cyperus esculentus harvesting. By taking equidistant points of the lengthwise blade edge curve, it was calculated that the dynamic sliding–cutting angle was proportional to the pole radius. The dynamic sliding–cutting angle at the tool holder increased rapidly from 35.15° to 46.15°, which reduced plant entanglement and shortened the length of the secondary working area. The dynamic sliding–cutting angle at the tool tip increased slowly from 46.15° to 54.30°, forming a longer primary working area and good plant-crushing performance.
- (2)
- Based on the discrete element method, a sandy loam soil model and a flexible model of the Cyperus esculentus plant were established. The power consumption and plant-crushing performance of the IT245 and IT245P rotary blades were compared by simulation tests. The results showed that the average power consumption of the IT245P rotary blade was reduced by 13.10% and the crushing rate of Cyperus esculentus plants was increased by 11.75%.
- (3)
- The forward speed, tillage depth, and shaft speed were selected as the test factors, and the tillage depth stability and power consumption were selected as the evaluation indexes for the field test. The best combination of operating parameters of the reverse rotary tiller was 1.08 m/s for the forward speed, 107.11 mm for the tillage depth, and 258.05 r/min for the shaft speed. Under this optimal parameter combination, the stability of the tillage depth was 94.63% and the power consumption was 42.35 kW. This study showed that the rotary blade with a double-eccentric circular-edge curve could better complete the plant-crushing and power consumption reduction operations and meet the requirements for the harvesting of Cyperus esculentus.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, S.B.; Cui, G.F.; Wang, C.L. A new high-yield oil crop Cyperus esculentus. Xinjiang Agric. Sci. Technol. 2001, 4, 40. [Google Scholar]
- Guo, T.T.; Wan, C.J.; Huang, F.H.; Wei, C.L.; Hu, Z.H. Research Progress on main nutritional components and physiological functions of Cyperus esculentus. Chin. J. Oil Crop Sci. 2021, 43, 1174–1180. [Google Scholar]
- Tal, A.; Rubin, B. Cyperus esculentus L.—A new weed in Israe. Phytoparasitica 2005, 33, 245–246. [Google Scholar] [CrossRef]
- Zhang, S.A.; Li, P.Z.; Wei, Z.M.; Cheng, Y.; Liu, J.Y.; Yang, Y.M.; Wang, Y.Y.; Mu, Z.S. Cyperus (Cyperus esculentus L.): A Review of Its Compositions, Medical Efficacy, Antibacterial Activity and Allelopathic Potentials. Plants 2022, 11, 1127. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.H.; Mu, Z.J.; Zhao, J.L.; Bao, J.W.; Zhao, X.Q.; Wang, J.G.; Lu, Z.Y. Construction of evaluation index system for the windbreak and sand-fixing technology model of Cyperus esculentus guided by ecology, life and production integration concepts in windy and sandy areas in northern China. J. North. Agric. 2021, 49, 127–134. [Google Scholar]
- Yang, Z.L. Characteristics and research progress of Cyperus esculentus. North. Hortic. 2017, 17, 192–201. [Google Scholar]
- Ren, W.; Guo, D.Q.; Xing, G.J.; Yang, C.M.; Zhang, Y.Y.; Yang, J.; Niu, L.; Zhong, X.F.; Zhao, Q.Q.; Cui, Y.; et al. Complete Chloroplast Genome Sequence and Comparative and Phylogenetic Analyses of the Cultivated Cyperus esculentus. Diversity 2021, 13, 405. [Google Scholar] [CrossRef]
- Umerie, S.C.; Uka, A.S. Brew wort from Cyperus esculentus tubers. Bioresour. Technol. 1998, 66, 83–85. [Google Scholar] [CrossRef]
- Wang, Z.C.; Li, S.S.; Liang, X.; Xu, L.J.; Zou, X.J. Development status and prospect of Cyperus esculentus industry in China. Sci. Technol. Indus. 2022, 22, 62–67. [Google Scholar]
- Zhu, H.B.; Qian, C.; Bai, L.Z.; Zhao, H.R.; Ma, S.W.; Zhang, X.; Li, H. Design and test of positive and negative rotating power corn stubble anti blocking device. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–11. [Google Scholar]
- Zhang, C.L.; Xia, J.F.; Zhang, J.M.; Zhou, H.; Zhu, Y.H.; Wang, J.W. Design and test of cutter roller of six head spiral straw returning tillage machine. Trans. Chin. Soc. Agric. Mach. 2019, 50, 25–34. [Google Scholar]
- Wang, J.Y.; Zhao, S.H.; Gao, L.L.; Yuan, Y.Y.; Yang, Y.Q. Design and test of passive disc stubble cutter with self-adjusting blade angle for corn ridge farming. Trans. Chin. Soc. Agric. Mach. 2021, 52, 59–67. [Google Scholar]
- Pirchio, M.; Fontanelli, M.; Labanca, F.; Sportelli, M.; Frasconi, C. Energetic Aspects of Turfgrass Mowing: Comparison of Different Rotary Mowing Systems. Agriculture 2019, 9, 178. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.J.; Wang, J.W. Analysis of the sliding cutting angle and installation angle of machete for returning the whole rice straw to the field and burying grass. J. Agric. Mech. Res. 2007, 11, 58–60, 63. [Google Scholar]
- Zhao, T.J. Study on Optimal Design of Working Parameters of Rice Straw Returning Machine. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2007. [Google Scholar]
- Modak, S.P.; Dogra, B.; Dogra, R.; Kumar, D. Design of rotary weeder blade. AMA-Agr. Mech Asia Af. 2016, 47, 32–40. [Google Scholar]
- Habibi, A.J.; Surendra, S. Optimization and evaluation of rotary tiller blades: Computer solution of mathematical relations. Soil Tillage. Res. 2009, 106, 1–7. [Google Scholar]
- Wang, Q. Design and Experimental Research of Rice Whole Stalk Deep Buried Returning Device. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2016. [Google Scholar]
- He, J.; Zhen, K.; Li, H.W.; Wang, Q.J.; Chen, W.Z.; Zhang, X.C.; Wang, X.L.; Zhang, Z.Q.; You, B.X.; Zhao, H.B. Drag Reducing Rotary Tiller with Long and Short Rotary Blades. China Patent CN204948642U, 13 January 2016. [Google Scholar]
- Lu, Z.C. Design and Experimental Research on Test Device for Cutting Corn Stubble with Discstubble Cutter. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, 2016. [Google Scholar]
- Selvi, K.C. A new blade design of rotary tiller and static analysis using computer-aided tool. Inma-Agric. Eng. 2017, 53, 29–34. [Google Scholar]
- Huang, W.Y.; Ren, D.Z.; Gong, Y.J.; Bai, X.W.; Shao, H.; Liu, C.W. Simulation and Experiment of Coupled Corn Straw Hides and Ranges Separation Based on Abaqus. Trans. Chin. Soc. Agric. Mach. 2021, 52, 124–133. [Google Scholar]
- Lee, K.S.; Park, S.H.; Park, W.Y.; Lee, C.S. Strip tillage characteristics of rotary tiller blades for use in a dryland direct rice seeder. Soil Tillage. Res. 2003, 71, 25–32. [Google Scholar] [CrossRef]
- Satit, K.; Was, M.S.; Panadda, N. Wear resistance of thermally sprayed rotary tiller blades. Wear 2007, 263, 604–608. [Google Scholar]
- Guo, Q. Experimental Study on Cutting Mechanism and Performance of Cane Straw. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2016. [Google Scholar]
- Guo, X.; Zhang, X.L.; Xu, Y.F.; Li, P.P.; Chen, C. Mechanism and Simulation Research on efficient cutting of tomato vine straw. J. Agric. Mech. Res. 2017, 39, 17–24. [Google Scholar]
- Tanya, N.; Sirisak, C. Development of blades for rotary tiller for use in Thai soils. J. Food. Agric. Environ. 2010, 8, 1336–1344. [Google Scholar]
- Ding, W.M.; Wang, Y.H.; Peng, S.Z. Analysis and calculation of sliding cutting angle of reverse rotary tillage knife. Trans. Chin. Soc. Agric. Mach. 2001, 6, 26–29+21. [Google Scholar]
- Wilmer, P.G.; Hugo, G.; Alejandro, T. Abrasive wear of rotary plow blades in a sandy loams soil. Dyna-Colombia. 2010, 77, 105–114. [Google Scholar]
- Zhou, H.; Zhang, W.L.; Yang, Q.J.; Li, D.D.; Xia, J.F. Design and test of sliding cutting self-excited vibration drag reduction subsoiling device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 71–78. [Google Scholar]
- Zhang, Y.; Liu, J.; Yuan, W.; Zhang, R.; Xi, X. Multiple Leveling for Paddy Field Preparation with Double Axis Rotary Tillage Accelerates Rice Growth and Economic Benefits. Agriculture 2021, 11, 1223. [Google Scholar] [CrossRef]
- Zhen, K.; Liu, G.Y.; Xia, J.F.; Chen, J.; Xu, L.; Liu, B.; Zhang, J.M.; Du, J.; Li, D.; Liu, Z.Y.; et al. Subsoiling Rotary Tillage Combined Tillage Machine for Reducing Viscosity and Resistance. China Patent CN213245577U, 25 May 2021. [Google Scholar]
- Liu, J.Z.; Chen, H.Y.; Jin, Y.X. Straw Returning Multiple Operation Machine. China Patent CN202354047U, 1 August 2012. [Google Scholar]
- Zhao, H.; Huang, Y.; Liu, Z.; Liu, W.; Zheng, Z. Applications of Discrete Element Method in the Research of Agricultural Machinery: A Review. Agriculture 2021, 11, 425. [Google Scholar] [CrossRef]
- He, X.N.; Zhang, X.J.; Zhao, Z.; Shang, S.Q.; Wang, D.W.; Yuan, X.W. Design and test of resistance reducing excavation device for Cyperus esculentus based on discrete element method. Trans. Chin. Soc. Agric. Mach. 2021, 52, 124–133. [Google Scholar]
- Zhao, T.J.; Wang, J.W.; Ge, Y.Y.; Zhang, M.Q.; Li, S.W.; Chen, Z.X. Improved design of cutter head of rice straw returning machine. In Proceedings of the Academic Annual Meeting of China Agricultural Engineering Society, Baoding, China, 20–22 October 2007. [Google Scholar]
- Ji, K.Z.; Li, Y.M.; Liang, Z.W.; Liu, Y.B.; Cheng, J.H. Device and Method Suitable for Matching and Adjusting Reel Speed and Forward Speed of Multi-Crop Harvesting. Agriculture 2022, 12, 213. [Google Scholar] [CrossRef]
- Zhou, M.K.; Xia, J.F.; Zhang, S.; Hu, M.J.; Liu, Z.Y.; Liu, G.Y.; Luo, C.M. Development of a Depth Control System Based on Variable-Gain Single-Neuron PID for Rotary Burying of Stubbles. Agriculture 2022, 12, 30. [Google Scholar] [CrossRef]
- Mostafa, B.; Mojtaba, N.B.; Davoud, G.; Mustafa, U.; Thomas, K. Simulation of plate sinkage in soil using discrete element modelling: Calibration of model parameters and experimental validation. Soil Tillage. Res. 2020, 203, 1047–1060. [Google Scholar]
- Subhash, C.T.; Morrissey, J.P.; Jin, S.; Chen, J.F.; Jin, Y.O. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model. Gemmina 2014, 16, 383–400. [Google Scholar]
- Hu, M.J.; Xia, J.; Zhou, Y.; Luo, C.; Zhou, M.; Liu, Z. Measurement and calibration of the discrete element parameters of coated delinted cotton seeds. Agriculture 2020, 12, 286. [Google Scholar] [CrossRef]
- Jan, D.P.; Gemmina, D.E.; Daniel, V.F.R.; Adam, B.; Wim, M.C. Calibration of DEM material parameters to simulate stress-strain behavior of unsaturated soils during uniaxial compression. Soil Tillage. Res. 2019, 194, 104303–104312. [Google Scholar]
- Magalhães, P.S.G.; Bianchini, A.; Braunbeck, O.A. Simulated and Experimental Analyses of a Toothed Rolling Coulter for Cutting Crop Residues. Biosyst. Eng. 2007, 96, 193–200. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, J.F.; Liu, X.Y.; Xi, L.Q.; Liao, J.A. Simulation and Test of “Separated Burying Device” of Green Manure Returning Machine Based on the EDEM Software. Agriculture 2022, 12, 569. [Google Scholar] [CrossRef]
- Xu, G.M.; Xie, Y.X.; Matin, M.A.; He, R.Y.; Ding, Q.S. Effect of Straw Length, Stubble Height and Rotary Speed on Residue Incorporation by Rotary Tillage in Intensive Rice–Wheat Rotation System. Agriculture 2022, 12, 222. [Google Scholar] [CrossRef]
- Chinese Academy of Agricultural Mechanization Sciences. Agricultural Machinery Design Manual; China Agricultural Science and Technology Press: Beijing, China, 2007; p. 854. [Google Scholar]
- Han, L.J.; Yuan, W.; Yu, J.J.; Jin, J.J. Xie, D.S. Simulation and Experiment of Spiral Soil Separation Mechanism of Compound Planter Based on Discrete Element Method (DEM). Agriculture 2022, 12, 511. [Google Scholar] [CrossRef]
- Shi, G.K.; Ding, L.P.; Zhang, Z.Y.; Ding, H.Z.; Kan, Z. Calibration and Tests for the Discrete Element Simulation Parameters of Fallen Jujube Fruit. Agriculture 2022, 12, 38. [Google Scholar] [CrossRef]
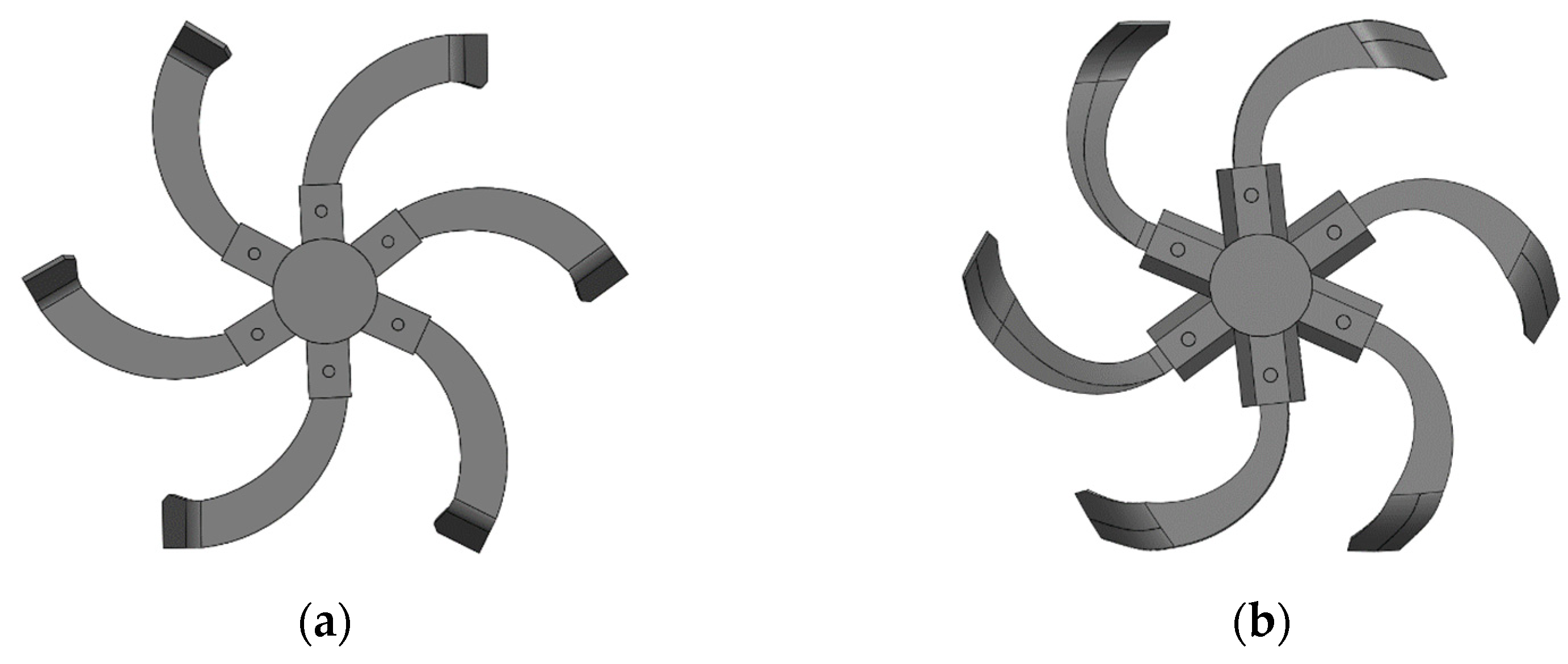








| Parameters | Values |
|---|---|
| Matching power/(kW) | 80 |
| Dimension (L × W × H)/(mm) | 1480 × 950 × 880 |
| Operation efficiency/(km·h−1) | 0~1.5 |
| Working width/(mm) | 1200 |
| Shaft speed/(r·min−1) | 0~400 |
| Tillage depth/(mm) | 0~150 |
| Eccentric Circular Arc | NO. | Polar Radius r/mm | Polar Angle/(°) | Static Cutting Angle φ/(°) | Static Sliding–Cutting Angle τs/(°) | Dynamic Sliding–Cutting Angle τd/(°) | Difference between τs and τd Δτ/(°) |
|---|---|---|---|---|---|---|---|
| AB | 1 | 125.00 | 63.26 | 48.07 | 41.93 | 35.15 | 6.78 |
| 2 | 137.34 | 58.16 | 45.05 | 44.95 | 38.77 | 6.18 | |
| 3 | 149.48 | 53.03 | 41.73 | 48.27 | 42.59 | 5.68 | |
| 4 | 160.00 | 48.42 | 38.54 | 51.46 | 46.15 | 5.31 | |
| BC | 1 | 174.39 | 80.22 | 38.01 | 51.99 | 47.11 | 4.87 |
| 2 | 196.35 | 71.28 | 36.29 | 53.71 | 49.38 | 4.33 | |
| 3 | 214.73 | 64.04 | 34.18 | 55.82 | 51.86 | 3.96 | |
| 4 | 230.00 | 58.01 | 32.37 | 58.00 | 54.30 | 3.70 |
| Contact Model | Static Friction Coefficient | Rolling Friction Coefficient | Restitution Coefficient |
|---|---|---|---|
| Soil–Soil | 0.55 | 0.15 | 0.43 |
| Plant–Plant | 0.34 | 0.08 | 0.35 |
| Soil–Plant | 0.48 | 0.05 | 0.32 |
| Soil–65Mn | 0.52 | 0.12 | 0.20 |
| Plant–65Mn | 0.33 | 0.10 | 0.30 |
| Test Site | Soil Type | Soil Moisture Content/(%) | Soil Density /(kg m−3) | Soil Firmness/(kPa) | Row Spacing/(mm) | Plant Spacing/(mm) | Stubble Height/(mm) | Yield Per Mu/(kg) |
|---|---|---|---|---|---|---|---|---|
| Minquan County | Sandy Loam | 15.36 ± 1.56 | 2650 ± 50 | 425 ± 50 | 200 ± 15 | 150 ± 10 | 90 ± 7 | 1265 ± 50 |
| Test Factor | Symbol | Test Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| Forward speed/(km·h−1) | A | 0.8 | 1.1 | 1.4 |
| Tillage depth/(mm) | B | 100 | 115 | 130 |
| Shaft speed/(r·min−1) | C | 250 | 300 | 350 |
| No. | Test Factor | Evaluation Index | |||
|---|---|---|---|---|---|
| Forward Speed | Tillage Depth | Shaft Speed | Tillage Depth Stability U/% | Power Consumption W/(kW) | |
| 1 | 0 | −1 | −1 | 95.99 | 42.51 |
| 2 | −1 | 0 | −1 | 95.01 | 42.03 |
| 3 | −1 | −1 | 0 | 94.63 | 42.20 |
| 4 | 1 | 1 | 0 | 94.78 | 45.90 |
| 5 | −1 | 1 | 0 | 93.21 | 44.35 |
| 6 | 0 | 0 | 0 | 94.94 | 43.43 |
| 7 | 0 | −1 | 1 | 95.64 | 43.67 |
| 8 | 1 | −1 | 0 | 95.96 | 43.84 |
| 9 | 0 | 0 | 0 | 94.74 | 43.41 |
| 10 | 0 | 1 | 1 | 94.47 | 46.59 |
| 11 | 0 | 0 | 0 | 94.89 | 43.17 |
| 12 | 0 | 0 | 0 | 95.05 | 43.01 |
| 13 | 1 | 0 | −1 | 96.04 | 41.84 |
| 14 | 0 | 1 | −1 | 95.02 | 44.87 |
| 15 | 0 | 0 | 0 | 94.82 | 43.82 |
| 16 | −1 | 0 | 1 | 94.79 | 42.90 |
| 17 | 1 | 0 | 1 | 95.74 | 44.63 |
| Source | Sum of Squares | Freedom | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 7.54 | 9 | 0.84 | 28.49 | <0.01 ** |
| A | 2.81 | 1 | 2.81 | 95.53 | <0.01 ** |
| B | 0.25 | 1 | 0.25 | 8.57 | 0.0221 * |
| C | 2.98 | 1 | 2.98 | 101.26 | <0.01 ** |
| AB | 0.010 | 1 | 0.010 | 0.34 | 0.5780 |
| AC | 0.014 | 1 | 0.014 | 0.49 | 0.5066 |
| BC | 1.6 × 10−3 | 1 | 1.6 × 10−3 | 0.054 | 0.8222 |
| A2 | 0.13 | 1 | 0.13 | 4.59 | 0.0694 |
| B2 | 1.37 | 1 | 1.37 | 46.70 | <0.01 ** |
| C2 | 0.017 | 1 | 0.017 | 0.59 | 0.4687 |
| Residual | 0.21 | 7 | 0.029 | —— | —— |
| Lack of Fit | 0.15 | 3 | 0.050 | 3.61 | 0.1233 |
| Pure Error | 0.055 | 4 | 0.014 | —— | —— |
| Source | Sum of Squares | Freedom | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 26.38 | 9 | 2.93 | 21.91 | <0.01 ** |
| A | 2.80 | 1 | 2.80 | 20.90 | <0.01 ** |
| B | 11.26 | 1 | 11.26 | 84.12 | <0.01 ** |
| C | 5.35 | 1 | 5.35 | 39.95 | <0.01 ** |
| AB | 2.0 × 10−3 | 1 | 2.0 × 10−3 | 0.015 | 0.9056 |
| AC | 0.92 | 1 | 0.92 | 6.89 | 0.0342 * |
| BC | 0.078 | 1 | 0.078 | 0.59 | 0.4690 |
| A2 | 0.77 | 1 | 0.77 | 5.76 | 0.0475 * |
| B2 | 5.40 | 1 | 5.40 | 40.34 | <0.01 ** |
| C2 | 0.034 | 1 | 0.034 | 0.26 | 0.6282 |
| Residual | 0.94 | 7 | 0.13 | —— | —— |
| Lack of Fit | 0.56 | 3 | 0.19 | 1.98 | 0.2596 |
| Pure Error | 0.38 | 4 | 0.094 | —— | —— |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; He, X.; Shang, S.; Zhao, Z.; Wang, H.; Tan, Y.; Li, C.; Wang, D. Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus. Agriculture 2022, 12, 862. https://doi.org/10.3390/agriculture12060862
Zhu H, He X, Shang S, Zhao Z, Wang H, Tan Y, Li C, Wang D. Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus. Agriculture. 2022; 12(6):862. https://doi.org/10.3390/agriculture12060862
Chicago/Turabian StyleZhu, Hao, Xiaoning He, Shuqi Shang, Zhuang Zhao, Haiqing Wang, Ying Tan, Chengpeng Li, and Dongwei Wang. 2022. "Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus" Agriculture 12, no. 6: 862. https://doi.org/10.3390/agriculture12060862
APA StyleZhu, H., He, X., Shang, S., Zhao, Z., Wang, H., Tan, Y., Li, C., & Wang, D. (2022). Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus. Agriculture, 12(6), 862. https://doi.org/10.3390/agriculture12060862






