Test and Analysis on Friction Characteristics of Major Cotton Stalk Cultivars in Xinjiang
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Materials and Instruments
2.2. Test Methods
2.3. Test Design
3. Results and Discussion
3.1. ANOVA of Friction Characteristics
3.1.1. ANOVA of Static Sliding Friction Coefficient
3.1.2. ANOVA of Stable Static Rolling Angle
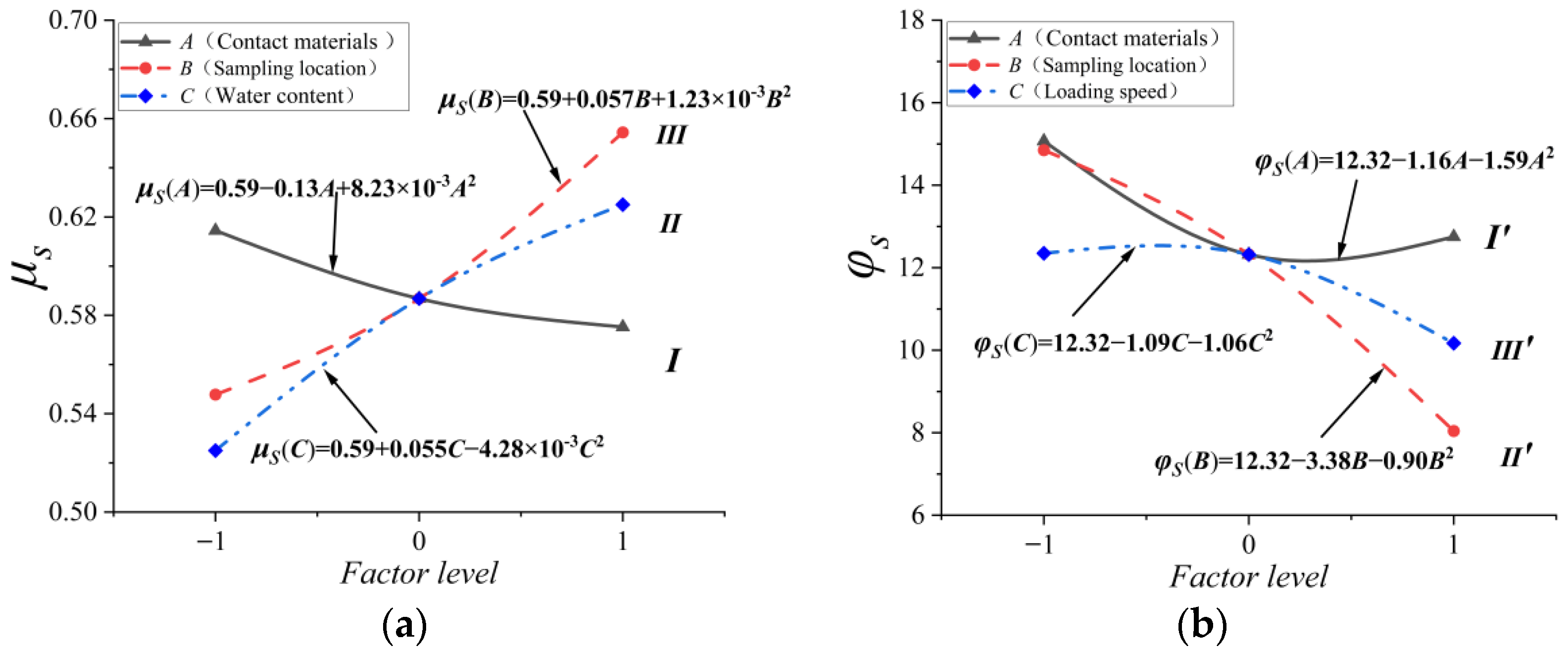
3.2. Single-Factor Effect Analysis
3.2.1. Influence of Single-Factor on Static Sliding Friction Coefficient
3.2.2. Influence of Single-Factor on Static Rolling Angle
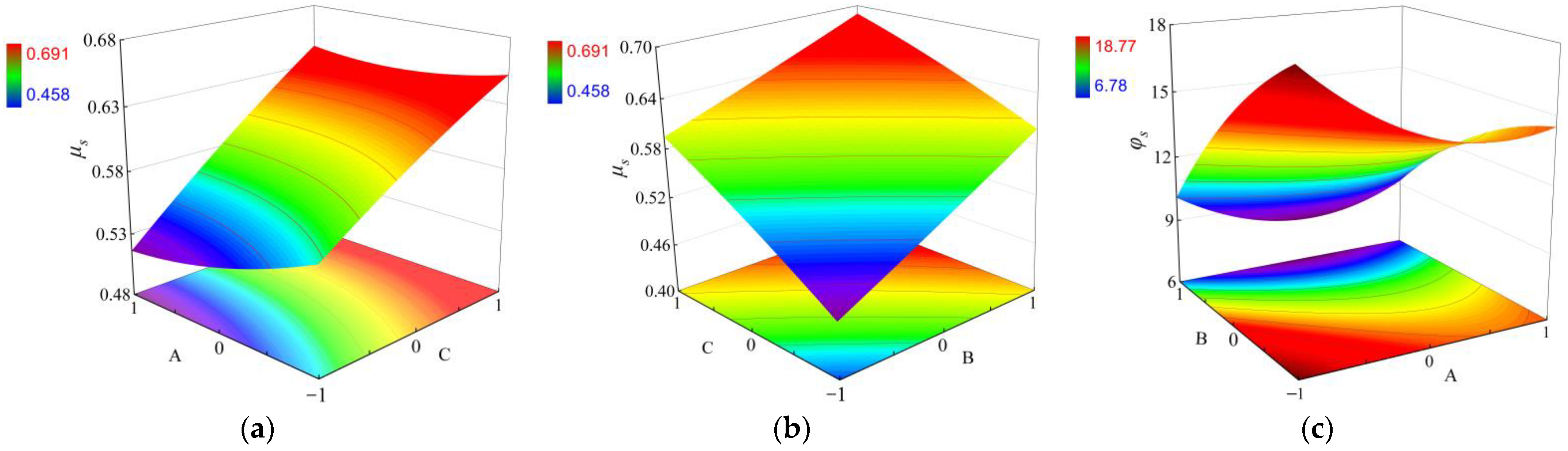
3.3. Interaction Effect Analysis
3.3.1. Influence of Interaction Terms on Static Sliding Friction Coefficient
3.3.2. Influence of Interaction Terms on Static Rolling Angle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, R.; Chen, X.; Zhang, B.; Meng, H.; Jiang, P.; Peng, X.; Kan, Z.; Li, W. Problems and countermeasures of recycling methods and resource reuse of residual film in cotton fields of Xinjiang. Trans. Chin. Soc. of Agric. Eng. 2019, 35, 1–13. [Google Scholar]
- Hu, C.; Wang, X.; Chen, X.; Tang, X.; Zhao, Y.; Yan, C. Current situation and control strategies of residual film pollution in Xinjiang. Trans. Chin. Soc. Agric. Eng. 2019, 35, 223–234. [Google Scholar]
- Chen, X.; Zhao, Y. Development of double-film mulch precision planter for cotton seeding. Trans. Chin. Soc. Agric. Eng. 2010, 26, 106–112. [Google Scholar]
- Dai, J.; Luo, Z.; Li, W.; Tang, W.; Zhang, D.; Lu, H.; Li, Z.; Xin, C.; Kong, X.; Eneji, A.E.; et al. A simplified pruning method for profitable cotton production in the Yellow River valley of China. Field Crops Res. 2014, 164, 22–29. [Google Scholar] [CrossRef]
- Wang, X.; Hu, C.; Lu, B.; Jiang, J.; Hou, S. Wind tunnel test on damages of plastic film under the wind-sand effect in south Xinjiang of China. Int. Agric. Eng. J. 2017, 26, 16–23. [Google Scholar]
- Liu, E.; He, W.; Yan, C. ‘White revolution’ to ‘white pollution’-agricultural plastic film mulch in China. Environ. Res. Lett. 2014, 9, 091001. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Wang, Z.; Zheng, X.; Zhang, J.; Li, W. Effects of biodegradation film mulching on soil temperature, moisture and yield of cotton under drip irrigation in typical oasis area. Trans. Chin. Soc. Agric. Eng. 2017, 33, 135–143. [Google Scholar]
- Zhang, Z.; Li, J.; Wang, X.; Zhao, Y.; Xue, S.; Su, Z. Parameters Optimization and Test of an Arc-Shaped Nail-Tooth Roller-Type Recovery Machine for Sowing Layer Residual Film. Agriculture 2022, 12, 660. [Google Scholar] [CrossRef]
- Liang, R.; Chen, X.; Zhang, B.; Peng, X.; Kan, Z. Tests and analyses on mechanical characteristics of dwarf-dense-early major cotton variety stalks. Int. Agrophys. 2020, 34, 333–342. [Google Scholar] [CrossRef]
- Puchalski, C.; Brusewitz, G.H. Coefficient of friction of watermelon. Trans. ASAE 1996, 39, 589–594. [Google Scholar] [CrossRef]
- Quist, J.; Evertsson, C.M. Cone crusher modelling and simulation using DEM. Miner. Eng. 2016, 85, 92–105. [Google Scholar] [CrossRef]
- Shinners, K.J.; Koegel, R.G.; Lehman, L.L. Friction Coeeficient Of Alfalfa. Trans. ASAE 1991, 34, 33–37. [Google Scholar] [CrossRef]
- Parde, S.R.; Johal, A.; Jayas, D.S.; White, N.D.G. Physical properties of buckwheat cultivars. Can. Biosyst. Eng. 2003, 45, 3.19–3.22. [Google Scholar]
- Mani, S.; Tabil, L.G.; Sokhansanj, S.; Roberge, M. Mechanical properties of corn stover grind. Trans. ASAE 2004, 47, 1983–1990. [Google Scholar] [CrossRef]
- Afzalinia, S.; Roberge, M. Physical and mechanical properties of selected forage materials. Can. Biosyst. Eng. 2007, 49, 2.23–2.27. [Google Scholar]
- Chevanan, N.; Womac, A.R.; Bitra, V.S.P.; Yoder, D.C.; Sokhansanj, S. Flowability parameters for chopped switchgrass, wheat straw and corn stover. Powder Technol. 2009, 193, 79–86. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z.; Xu, L. Tribological Characteristics of Adhesive Materials on Cleaning Sieve of Rape Combine Harvester. Trans. Chin. Soc. Agric. Mach. 2010, 41, 54–57. [Google Scholar]
- Kalkan, F.; Kara, M. Handling, frictional and technological properties of wheat as affected by moisture content and cultivar. Powder Technol. 2011, 213, 116–122. [Google Scholar] [CrossRef]
- Fang, X.; Chen, H.; Huag, Z.; Xia, L. Sliding Friction Characteristic of Different Moisture Content of Soybean Stalk with Different Materials. Soybean Sci. 2012, 31, 838–841. [Google Scholar]
- Huo, L.; Meng, H.; Tian, Y.; Zhao, L.; Hou, S. Experimental study on physical property of smashed crop straw. Trans. Chin. Soc. Agric. Eng. 2012, 28, 189–195. [Google Scholar]
- Zhang, Q.; Ding, W.; Deng, L.; Li, Y.; Zhao, Y. Experimental study on friction characteristics of gorgon nuts (Euryale ferox) in mechanical shelling. Trans. Chin. Soc. Agric. Eng. 2013, 29, 56–63. [Google Scholar]
- Lu, C.; Zhao, C.; Meng, Z.; Wang, X.; Wu, G.; Gao, N. Straw friction characteristic based on rotary cutting anti-blocking device with slide plate pressing straw. Trans. Chin. Soc. Agric. Eng. 2016, 32, 83–89. [Google Scholar]
- Wang, D.F.; Jiang, Z.G.; Li, B.; Wang, G.; Jiang, Y. Experiment on sliding friction characteristics between rice straw and baler steel-roll. Trans. Chin. Soc. Agric. Eng. 2017, 33, 44–51. [Google Scholar]
- Kaliniewicz, Z.; Żuk, Z.; Krzysiak, Z. Influence of steel plate roughness on the frictional properties of cereal kernels. Sustainability 2018, 10, 1003. [Google Scholar] [CrossRef] [Green Version]
- Wen, B.Q.; Li, Y.; Kan, Z.; Li, J.B.; Li, L.; Ge, J.; Ding, L.; Wang, K.; Zou, S.; Li, W. Experimental research on the bending characteristics of glycyrrhiza glabra stems. Trans. ASABE 2020, 63, 1499. [Google Scholar] [CrossRef]
- Bucklin, R.A.; Thompson, S.A.; Ross, I.J.; Biggs, R.H. Apparent coefficient of friction of wheat on bin wall material. Trans. ASAE 1989, 32, 1769–1773. [Google Scholar] [CrossRef]
- Kweon, G.; Grift, T.E.; Miclet, D. Dynamic friction coefficient measurement of granular fertiliser particles. Biosyst. Eng. 2006, 97, 145–152. [Google Scholar] [CrossRef]
- Molenda, M.; Horabik, J.; Ross, I.J.; Montross, M.D. Friction of wheat: Grain–on–grain and on corrugated steel. Trans. ASAE 2002, 45, 415–420. [Google Scholar] [CrossRef]
- Locurto, G.J.; Bucklin, R.A.; Thompson, S.A.; Abdel-Hadi, A.I.; Walton, O.R. Soybean coefficients of friction for aluminum, glass, and acrylic surfaces. Appl. Eng. Agric. 2014, 30, 285–289. [Google Scholar]
- Hirai, Y.; Inoue, E.; Mori, K.; Hashiguchi, K. Investigation of mechanical interaction between a combine harvester reel and crop stalks. Biosyst. Eng. 2002, 83, 307–317. [Google Scholar] [CrossRef]
- Liang, R.; Chen, X.; Zhang, B.; Li, J.; Meng, H.; Peng, X.; Jiang, P.; Zhou, P.; Kan, Z. Analysis of shear-compressive stress characteristics of Dwarf-Dense-Early cotton variety stalks in Xinjiang. Int. Agric. Eng. J. 2020, 29, 380–391. [Google Scholar]
- Zhou, Z.E. Agricultural Materials Science; Agricultural Press: Beijing, China, 1994; Volume 1. [Google Scholar]
- Aydın, I.; Arslan, S. Mechanical properties of cotton shoots for topping. Ind. Crop. Prod. 2018, 112, 396–401. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Y.; Xu, L. Theoretical analysis of micro-vibration between a high moisture content rape stalk and a non-smooth surface of a reciprocating metal cleaning screen matrix. Biosyst. Eng. 2015, 129, 258–267. [Google Scholar] [CrossRef]

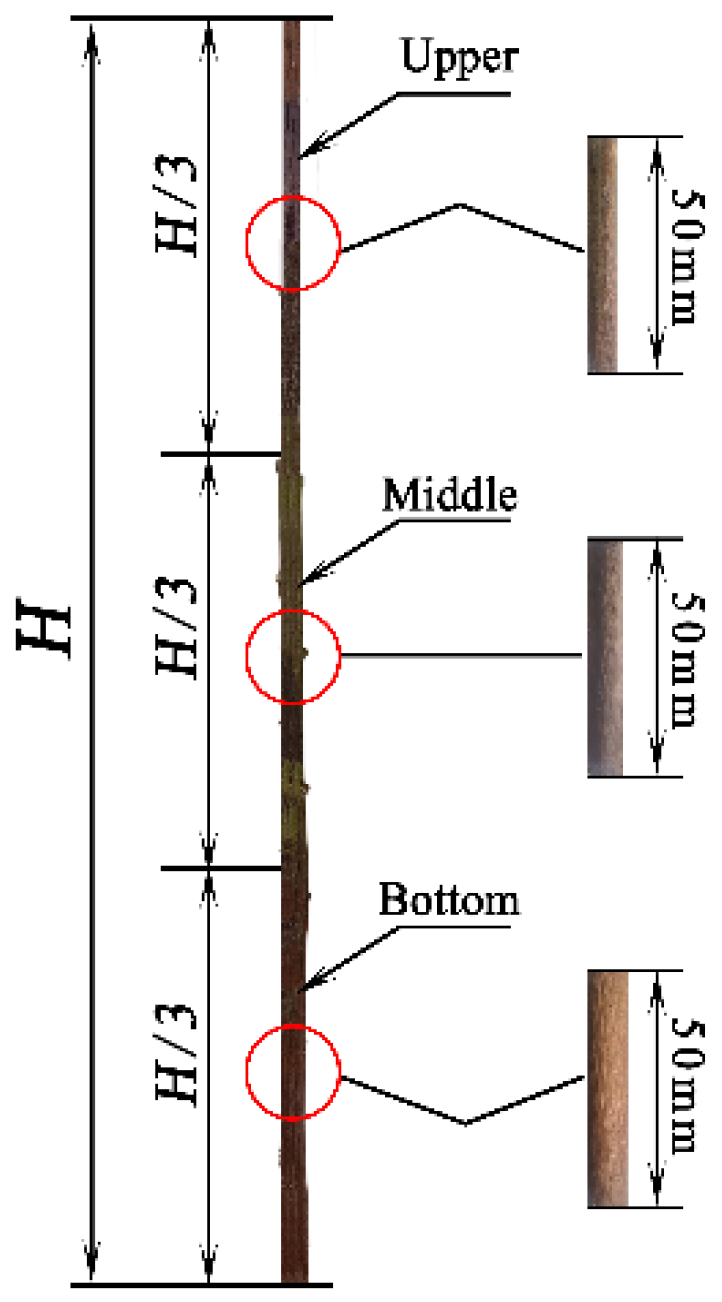
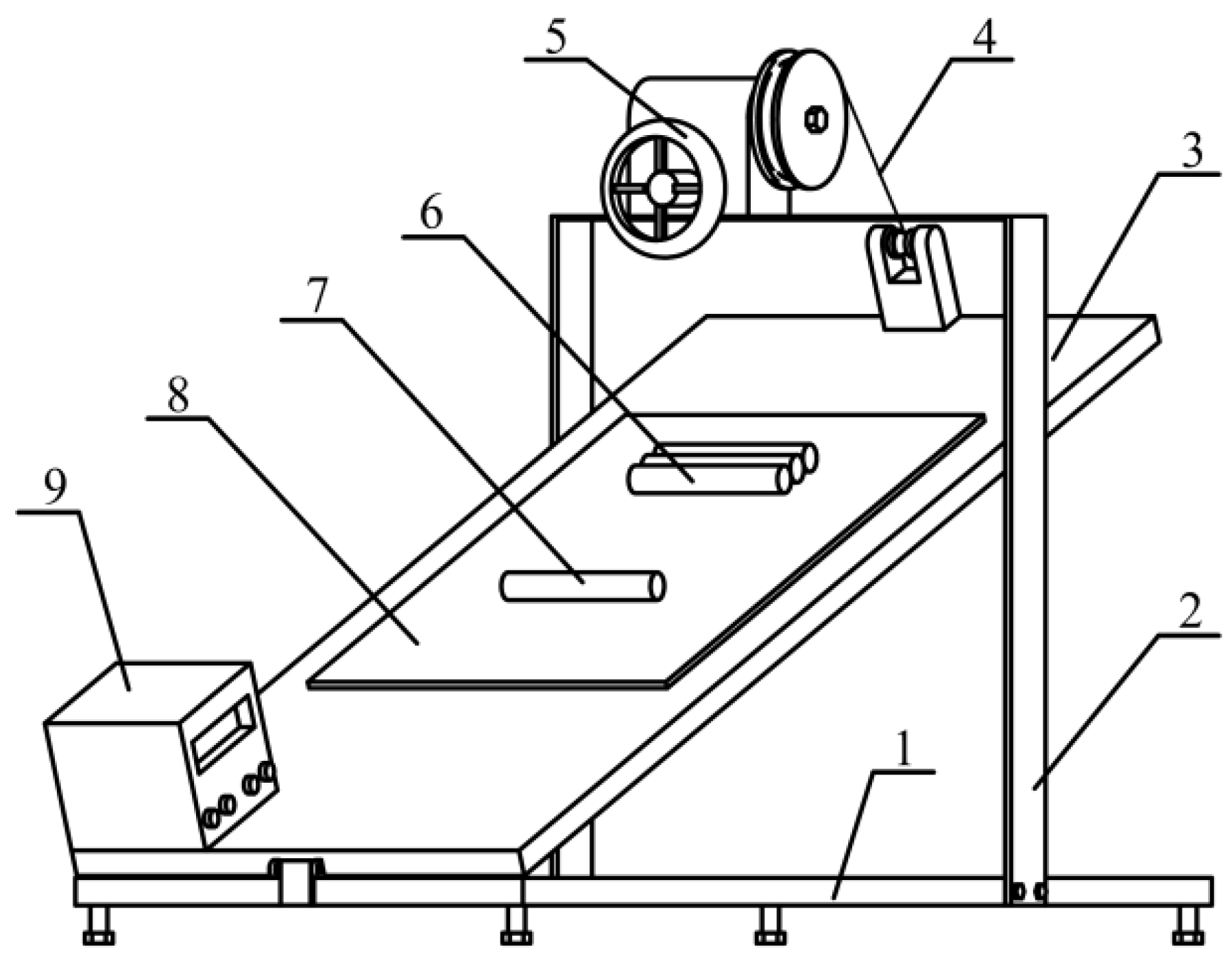
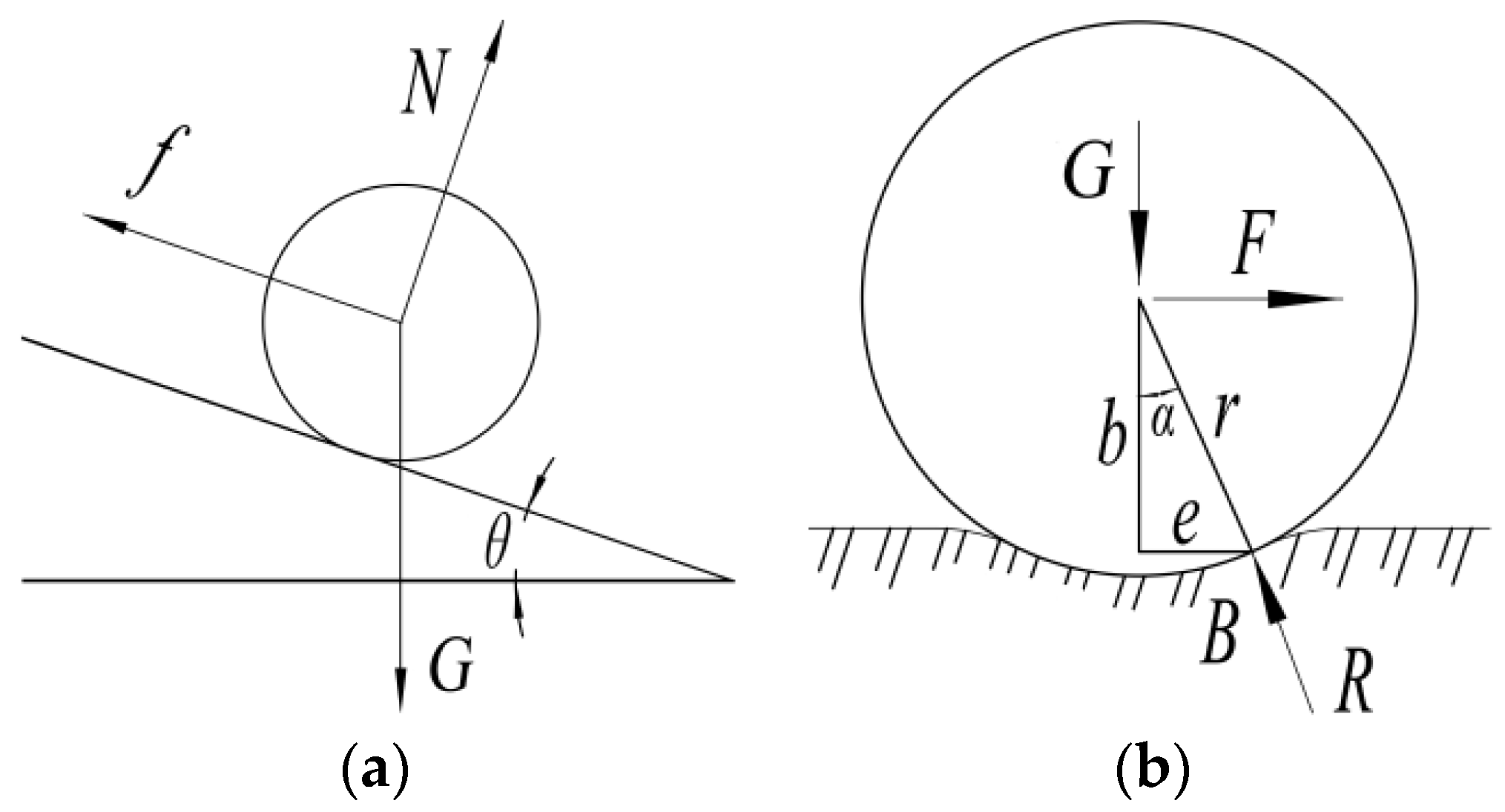
| Level | Contact Materials A | Sampling Location B | Moisture Content (%) C |
|---|---|---|---|
| −1 | Cotton stalk | upper | 10 |
| 0 | Plastic film | middle | 30 |
| +1 | Stainless steel | lower | 50 |
| Test No. | A | B | C | μs | φs (°) |
|---|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 0.557 ± 0.035 | 18.77 ± 2.50 |
| 2 | 1 | −1 | 0 | 0.530 ± 0.041 | 14.93 ± 2.96 |
| 3 | −1 | 1 | 0 | 0.659 ± 0.036 | 9.66 ± 1.80 |
| 4 | 1 | 1 | 0 | 0.639 ± 0.037 | 8.66 ± 1.76 |
| 5 | −1 | 0 | −1 | 0.558 ± 0.048 | 15.08 ± 2.04 |
| 6 | 1 | 0 | −1 | 0.511 ± 0.036 | 12.87 ± 3.59 |
| 7 | −1 | 0 | 1 | 0.651 ± 0.043 | 12.82 ± 2.08 |
| 8 | 1 | 0 | 1 | 0.643 ± 0.026 | 10.61 ± 2.62 |
| 9 | 0 | −1 | −1 | 0.458 ± 0.033 | 14.69 ± 2.78 |
| 10 | 0 | 1 | −1 | 0.600 ± 0.039 | 8.11 ± 1.44 |
| 11 | 0 | −1 | 1 | 0.586 ± 0.026 | 11.83 ± 2.95 |
| 12 | 0 | 1 | 1 | 0.691 ± 0.025 | 6.78 ± 1.02 |
| 13 | 0 | 0 | 0 | 0.593 ± 0.025 | 12.90 ± 2.38 |
| 14 | 0 | 0 | 0 | 0.579 ± 0.025 | 12.05 ± 1.44 |
| 15 | 0 | 0 | 0 | 0.588 ± 0.01 | 11.97 ± 1.34 |
| 16 | 0 | 0 | 0 | 0.593 ± 0.01 | 12.61 ± 1.44 |
| 17 | 0 | 0 | 0 | 0.581 ± 0.011 | 12.05 ± 1.55 |
| Source | df | μs | φs | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S·S | M·S | F Value | p-Value | S·S | M·S | F Value | p-Value | ||
| Model | 9 | 0.053 | 5.92 × 10−3 | 119.26 | <1 × 10−4 ** | 131.91 | 14.66 | 41.33 | <1 × 10−4 ** |
| A | 1 | 1.3 × 10−3 | 1.3 × 10−3 | 26.21 | 1.4 × 10−4 ** | 10.72 | 10.72 | 30.23 | 9 × 10−4 ** |
| B | 1 | 0.026 | 0.026 | 528.49 | <1 × 10−4 ** | 91.19 | 91.19 | 257.17 | <1 × 10−4 ** |
| C | 1 | 0.025 | 0.025 | 496.67 | <1 × 10−4 ** | 9.48 | 9.48 | 26.74 | 1.3 × 10−4 ** |
| AB | 1 | 1.2 × 10−5 | 59.29 | 0.25 | 0.635 | 2.02 | 2.02 | 5.69 | 0.049 * |
| AC | 1 | 3.8 × 10−4 | 3.8 × 10−4 | 7.66 | 0.028 * | 0 | 0 | 0 | 1.00 NS |
| BC | 1 | 3.42 × 10−4 | 3.42 × 10−4 | 6.90 | 0.034 * | 0.59 | 0.59 | 1.65 | 0.24 NS |
| A2 | 1 | 2.85 × 10−4 | 2.85 × 10−4 | 5.74 | 0.048 * | 10.65 | 10.65 | 30.05 | 9 × 10−4 ** |
| B2 | 1 | 6.32 × 10−6 | 6.32 × 10−6 | 0.13 | 0.732 | 3.42 | 3.42 | 9.66 | 1.71 × 10−4 * |
| C2 | 1 | 7.7 × 10−5 | 7.7 × 10−5 | 1.55 | 0.253 | 4.75 | 4.75 | 13.39 | 8.11 × 10−4 ** |
| Residual | 7 | 3.47 × 10−4 | 4.96 × 10−5 | 2.48 | 0.35 | ||||
| Lack of Fit | 3 | 1.75 × 10−4 | 5.81 × 10−5 | 1.35 | 0.378 | 2.48 | 0.60 | 3.47 | 0.130 |
| Pure Error | 4 | 1.73 × 10−4 | 4.32 × 10−5 | 0.69 | 0.17 | ||||
| Cor Total | 16 | 0.054 | 134.39 | ||||||
| R2 = 0.99, R 2adj = 0.99, CV = 1.20% | R2 = 0.98, R 2adj = 0.96, CV = 4.90% | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Liang, R.; Li, J.; Li, Y.; Meng, H.; Kan, Z. Test and Analysis on Friction Characteristics of Major Cotton Stalk Cultivars in Xinjiang. Agriculture 2022, 12, 906. https://doi.org/10.3390/agriculture12070906
Zhang B, Liang R, Li J, Li Y, Meng H, Kan Z. Test and Analysis on Friction Characteristics of Major Cotton Stalk Cultivars in Xinjiang. Agriculture. 2022; 12(7):906. https://doi.org/10.3390/agriculture12070906
Chicago/Turabian StyleZhang, Bingcheng, Rongqing Liang, Jiali Li, Yaping Li, Hewei Meng, and Za Kan. 2022. "Test and Analysis on Friction Characteristics of Major Cotton Stalk Cultivars in Xinjiang" Agriculture 12, no. 7: 906. https://doi.org/10.3390/agriculture12070906
APA StyleZhang, B., Liang, R., Li, J., Li, Y., Meng, H., & Kan, Z. (2022). Test and Analysis on Friction Characteristics of Major Cotton Stalk Cultivars in Xinjiang. Agriculture, 12(7), 906. https://doi.org/10.3390/agriculture12070906






