Analysis and Simulation of Wheel-Track High Clearance Chassis of Rape Windrower
Abstract
:1. Introduction
2. Performance and Simulation Analysis of Chassis
2.1. Structure and Working Principle of a Wheel-Track High Clearance Chassis for Rape Windrower
2.2. Analysis of Driving Resistance
2.2.1. Analysis of Wheel and Track Load
2.2.2. Analysis of Driving Resistance
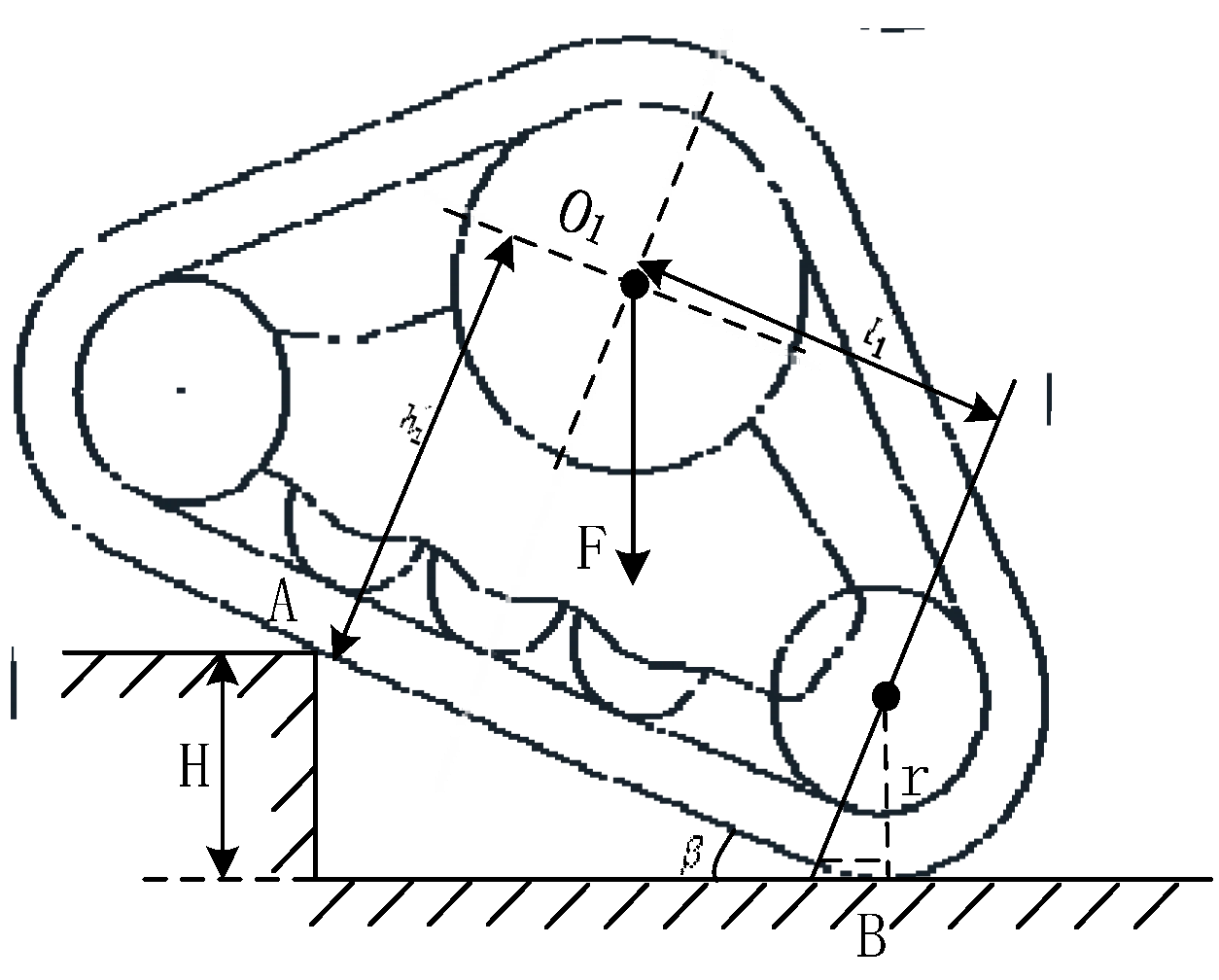
2.3. Performance Analysis of Uphill and Downhill
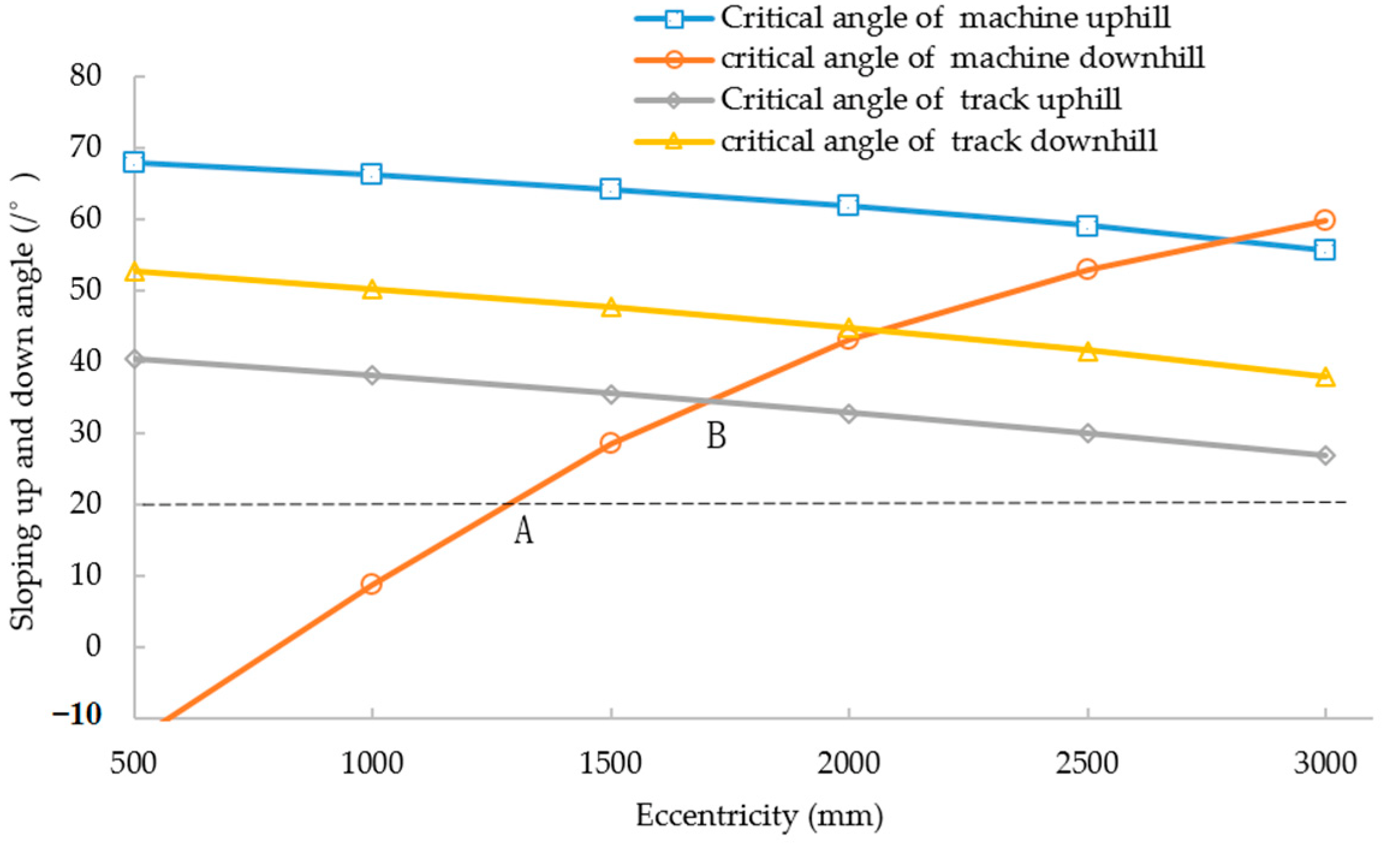
2.3.1. The Whole Machine Stability Analysis of Uphill and Downhill
2.3.2. The Track Stability Analysis of Uphill and Downhill
2.4. Performance Analysis of Ridge Crossing
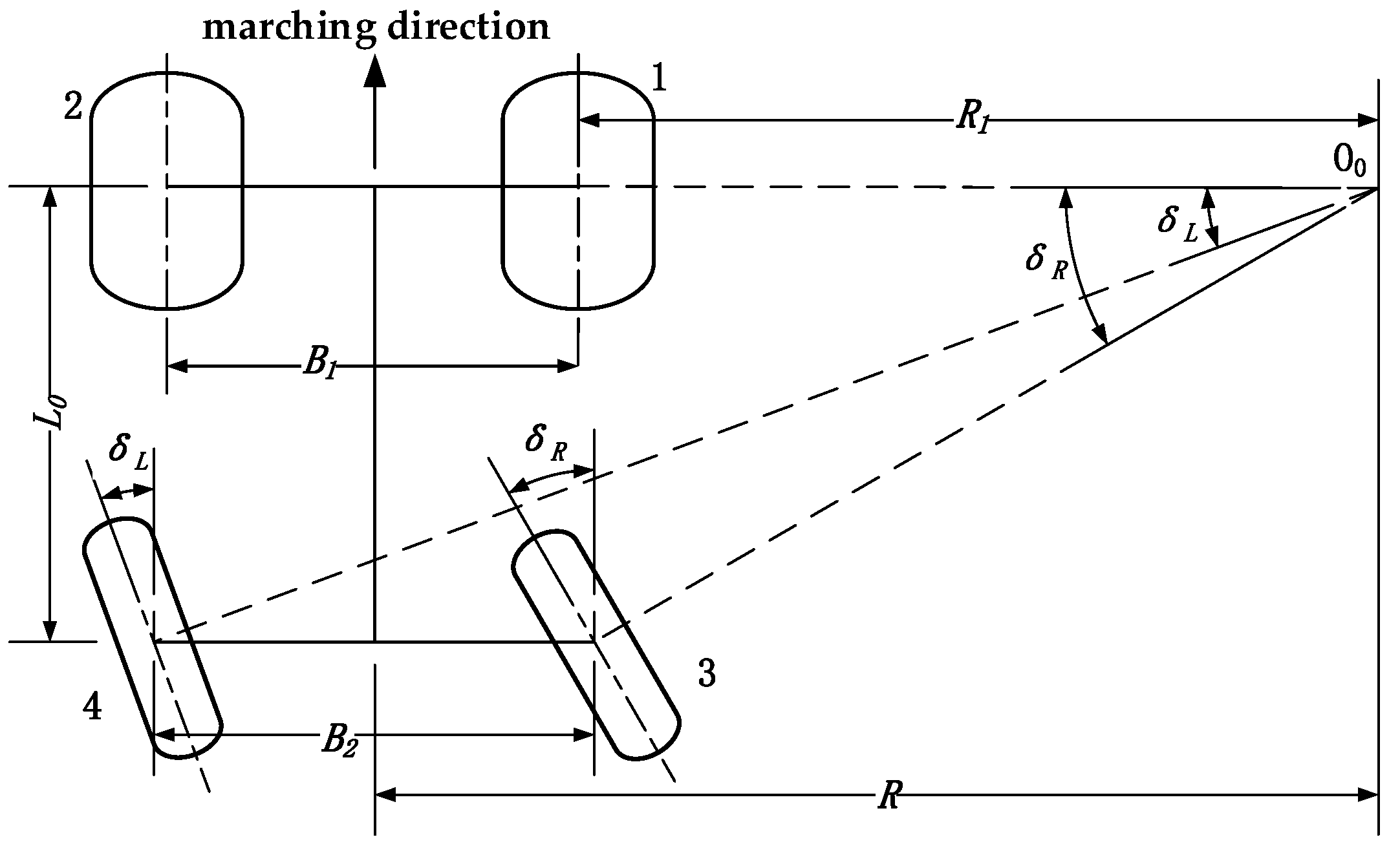
2.5. Analysis of Turning Performance
2.6. Kinematics Simulation and Analysis
2.6.1. Creation of Simulation Model
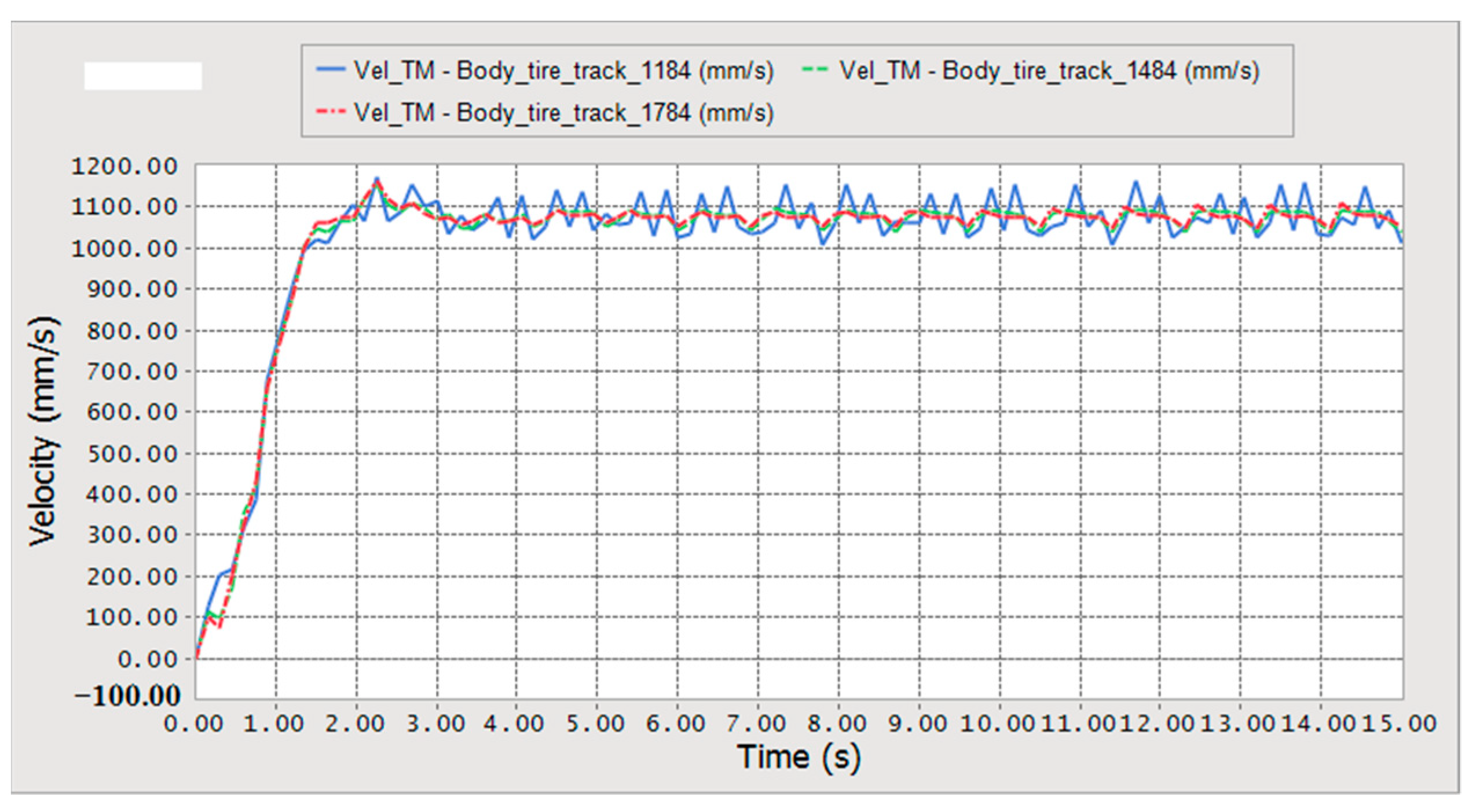
2.6.2. Simulation Analysis of Walking on Flat Ground
2.6.3. Simulation of Uphill and Downhill
3. Test Results and Discussion
3.1. Walking Performance
3.2. Climbing Test
3.3. Turning Radius Test
4. Conclusions
- (1)
- The mechanism and working principle of the wheel-track high clearance chassis of rape windrower were introduced, and the models of mathematical relations between the walking performance, stability performance and the eccentricity of the chassis frame were built.
- (2)
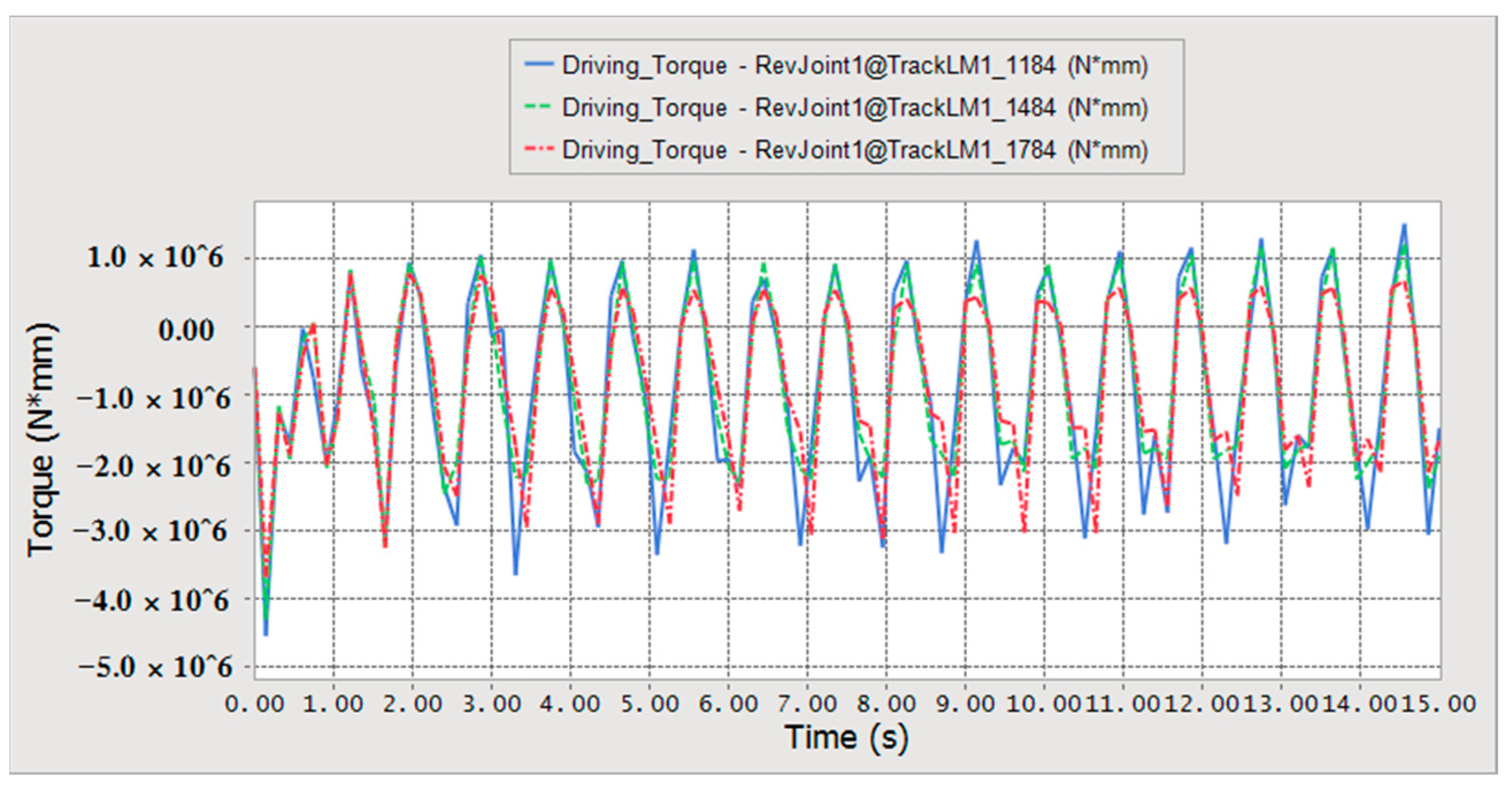
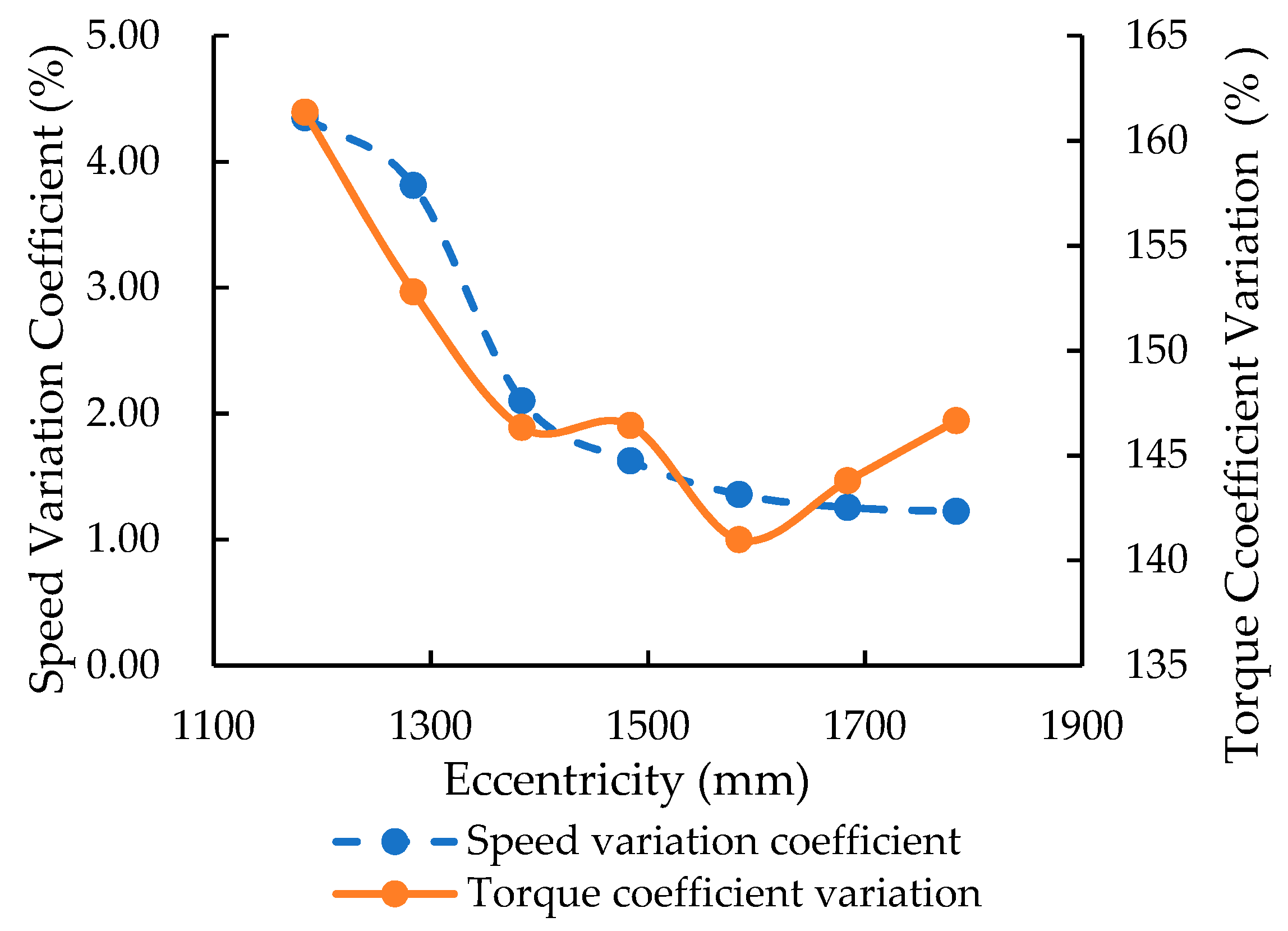
- Three-dimensional model and dynamic simulations of a wheel-track high clearance rape windrower were conducted using Pro/E and RecurDyn software. When the machine was driven at the same speed, the walking speed changed little with the increase of eccentricity, and the coefficient variation of speed decreased gradually. The average driving torque and the coefficient variation decreased first and then increased. Minimum driving torque and the coefficient variation were obtained when the eccentricities were 1484 mm and 1584 mm. The chassis frame eccentricity was defined as 1500 mm, according to the theoretical calculation and simulation analysis. The maximum angle of uphill and downhill was 28° and the maximum height of the crossing ridge was 266.15 mm.
- (3)
- The performance experiments of wheel-track high clearance rape windrower in flat hard ground and rice stubble field were carried out. The test showed that the speed running on flat hard road was 0~20.22 km/h and the minimum turning radius was 5.965 m; the working speed in rice stubble field was 0~9.12 km/h and the minimum turning radius was 6.498 m. The machine could steadily climb the slope of 20°.
- (4)
- A new kind of wheel-track high clearance chassis was developed, which could hang on the swath header over than 3.5 m wide. All parameters of the chassis met the design requirements, and the work efficiency increased over 100% compared with the existing two-tracked rape windrower. This provided another kind of equipment for rapeseed harvesting in the Yangtze River Basin.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, Z.; Wu, M.; Yang, W. Research status and development measures of rape segment harvester in China. Agric. Eng. 2015, 5, 1–4. [Google Scholar]
- Li, P. Experimental Study and Working Mechanism of Key Parts for Rape Windrower for 4SY 1.8. Ph.D. Thesis, Huazhong agricultural university, Wuhan, China, 2014. [Google Scholar]
- Jin, C.; Yang, T.; Liu, G. Design and Test of Posture Controlled Chassis for Caterpillar Combine. Trans. Chin. Soc. Agric. Mach. 2020, 51, 393–402. [Google Scholar]
- Hu, K.; Zhang, W.; Li, K. Multi-body dynamics modeling and experiment of triangular tracked chassis with high ground clearance. Trans. Chin. Soc. Agric. Mach. 2021, 52, 386–394. [Google Scholar]
- Zhou, J.; Cheng, X.; Li, H. Research and development on the wheel electric rape harvester. J. Agric. Mech. Res. 2012, 34, 80–85. [Google Scholar]
- Zhu, Y.; Fei, Y.; Xu, H. Analysis for obstacle negotiation of a wheel-track-leg hybrid mobile robot machine design and research. Mach. Des. Res. 2017, 33, 28–32. [Google Scholar]
- Shuai, L.; Su, H.; Zhen, L. Study on steering movement of track-wheel mobile robot. J. Harbin Eng. Univ. 2017, 38, 1630–1634. [Google Scholar]
- Zhang, S.; Yao, J.; Xu, Y. Design and analysis of moving mechanism of shape reconfigurable mobile robot. Trans. Chin. Soc. Agric. Mach. 2019, 50, 418–426. [Google Scholar]
- Guo, T. Power consumption of tracked and wheeled small mobile robots on deformable terrains–model and experimental validation. Mech. Mach. Theory 2019, 133, 347–364. [Google Scholar] [CrossRef]
- Jun, L.; Andrew, A.G. Development of a terrain adaptive tracked vehicle and its derivative-dual mode vehicle. In Proceedings of the 1st WRC Symposium on Advanced Robotics and Automation, Beijing, China, 16 August 2018. [Google Scholar]
- Zang, L.; Yang, S.; Wu, C. Design and kinematics analysis of coordinated variable wheel-track walking mechanism. Int. J. Adv. Robot. Syst. 2020, 17, 1–12. [Google Scholar] [CrossRef]
- Bai, Y. Design and Test on Delta Tracks Chassis of Chopper Sugarcane Harvester. Master’s Thesis, South China Agricultural University, Guangzhou, China, 2014. [Google Scholar]
- Cai, G. The Design and Mechanical Analysis of Oil Camellia Fruit Picking Machine’s Rubber Track System Chassis. Ph.D. Thesis, Central South University of Forestry and Technology, Changsha, China, 2014. [Google Scholar]
- Wang, F. Study on Slope Passability of the Orchard Power Chassis in Hilly Area. Master’s Thesis, Southwest University, Chongqing, China, 2020. [Google Scholar]
- Zeng, S.; Liu, J.; Luo, X. Design and experiment of wheel-track compound power chassis for high clearance sprayer in paddy field. J. South China Agric. Univ. 2019, 40, 14–22. [Google Scholar]
- Hao, Z.; Yang, X.; Liu, L. Design and experiment of multifunctional dynamic chassis for orchard. Trans. Chin. Soc. Agric. Mach. 2018, 49, 66–73+92. [Google Scholar]
- Pan, G.; Yang, F.; Sun, J. Analysis and test of obstacle negotiation performance of small hillside crawler tractor during climbing process. Trans. Chin. Soc. Agric. Mach. 2020, 51, 374–383. [Google Scholar]
- Feng, Y. Tank and Armored Vehicle Design; Chemical Industry Press: Beijing, China, 2015; pp. 31–72. [Google Scholar]
- Ge, J.; Zhang, D.; Wang, X.; Cao, C.; Fang, L.; Duan, L. Tractive performances of single grouser shoe affected by different soils with varied moisture contents. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Chen, B. Engineering Machinery Chassis Theory; China Communications Press: Beijing, China, 2001; pp. 15–70. [Google Scholar]
- Deng, Z.; Ding, L.; Gao, H. Influence of soil properties on lunar rover’s wheel-oil interaction mechanics. J. Harbin Inst. Technol. 2010, 42, 1724–1729. [Google Scholar]
- Zhao, J.; Wang, F.; Yu, B. Research on All-terrain profiling crawler power chassis. Trans. Chin. Soc. Agric. Mach. 2014, 45, 20–24. [Google Scholar]
- Zhu, Y.; Sang, Y.; Hu, M. Design and tability analysis of sprayer with adjustable height gap. J. Agric. Mech. Res. 2020, 42, 68–73. [Google Scholar]
- Xu, C.; Chen, Y.; Li, R. Design and research on Highland gap self-propelled lance spray. J. Chin. Agric. Mech. 2016, 37, 51–54. [Google Scholar]
- Wang, H.; Wang, Q.; Rui, Q. Analyzing and testing verification the performance about high-speed tracked vehicles in steering process. J. Mech. Eng. 2014, 50, 162–172. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, J.; Peng, B. Recurdyn Multibody Systems Optimization Simulation Technology; Tsinghua University Press: Beijing, China, 2010; pp. 62–101. [Google Scholar]
- Liu, Y.; Zhang, T.; Xie, N. Multi-body dynamic modeling and verification of small agricultural crawler chassis. Trans. Chin. Soc. Agric. Eng. 2019, 3, 39–46. [Google Scholar]
- Chen, J.; Huang, R.; Mo, R. Analysis and simulation of obstacle crossing performance of tracked chassis of small hedge trimmer based on RecurDyn. J. Chin. Agric. Mech. 2020, 41, 89–98. [Google Scholar]
- Ma, P.; Liu, Y.; Shi, C. Dynamics analysis and simulation of variant wheel-track wheel based on RecurDyn. J. Mil. Transp. Univ. 2017, 19, 35–39. [Google Scholar]
- Jiang, Q.; Ni, W.; Zhang, X.; Chen, P.; Yang, Y. Evaluation of tractor driving comfort according to the steering angle and speed using a virtual prototype. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 50–61. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Sun, Z. Improvement and verification of pressure-sinkage model in homogeneous soil. Trans. Chin. Soc. Agric. Eng. 2016, 32, 60–66. [Google Scholar]
- Yao, Y. Research on the trafficability of low-seed tracked vehicle based on track-soil coupling system. Ph.D. Thesis, Jilin University, Changchun, China, 2016. [Google Scholar]
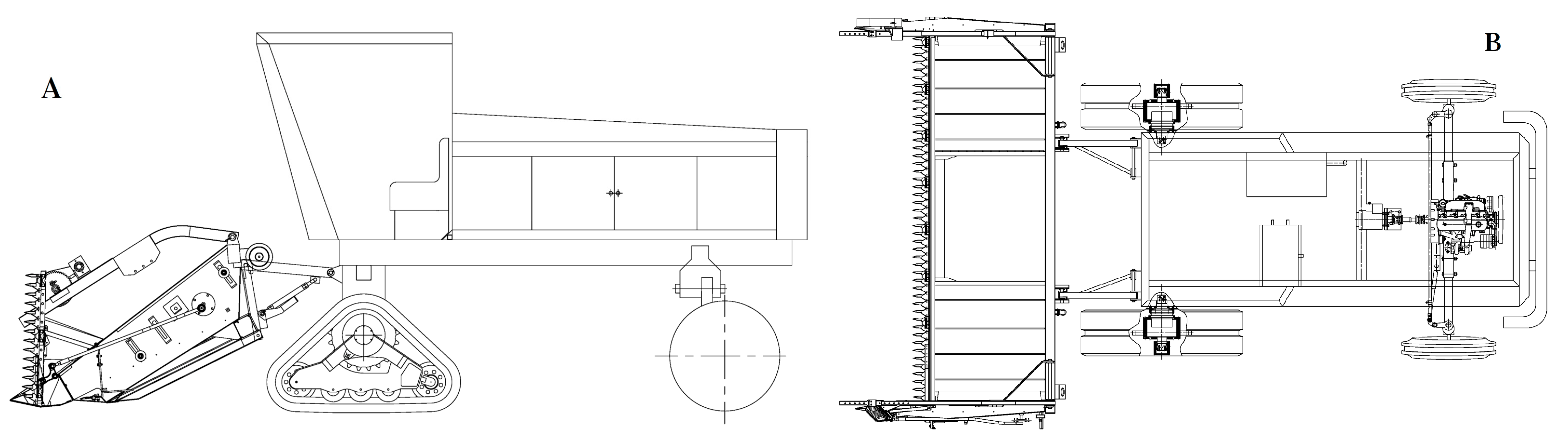


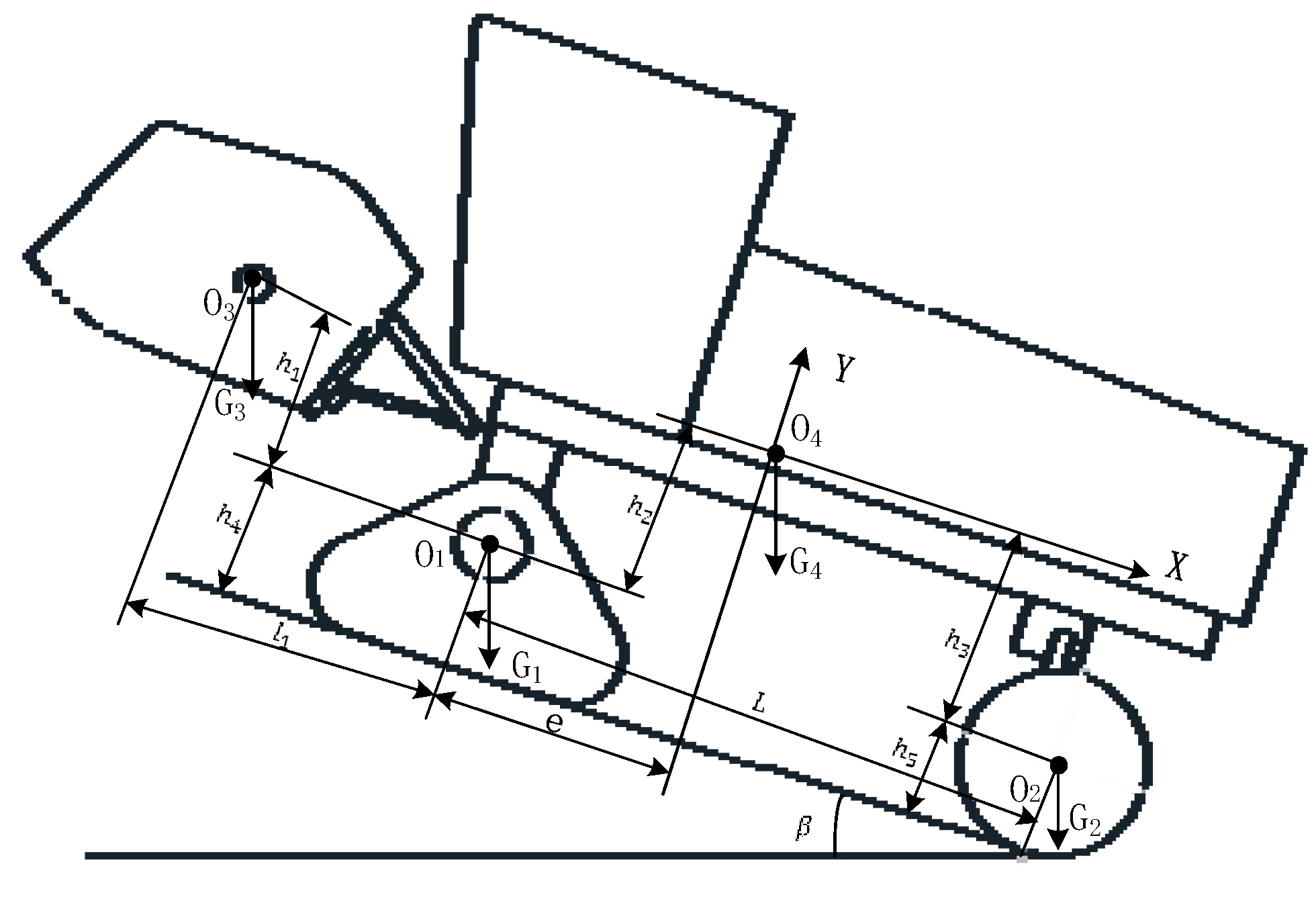
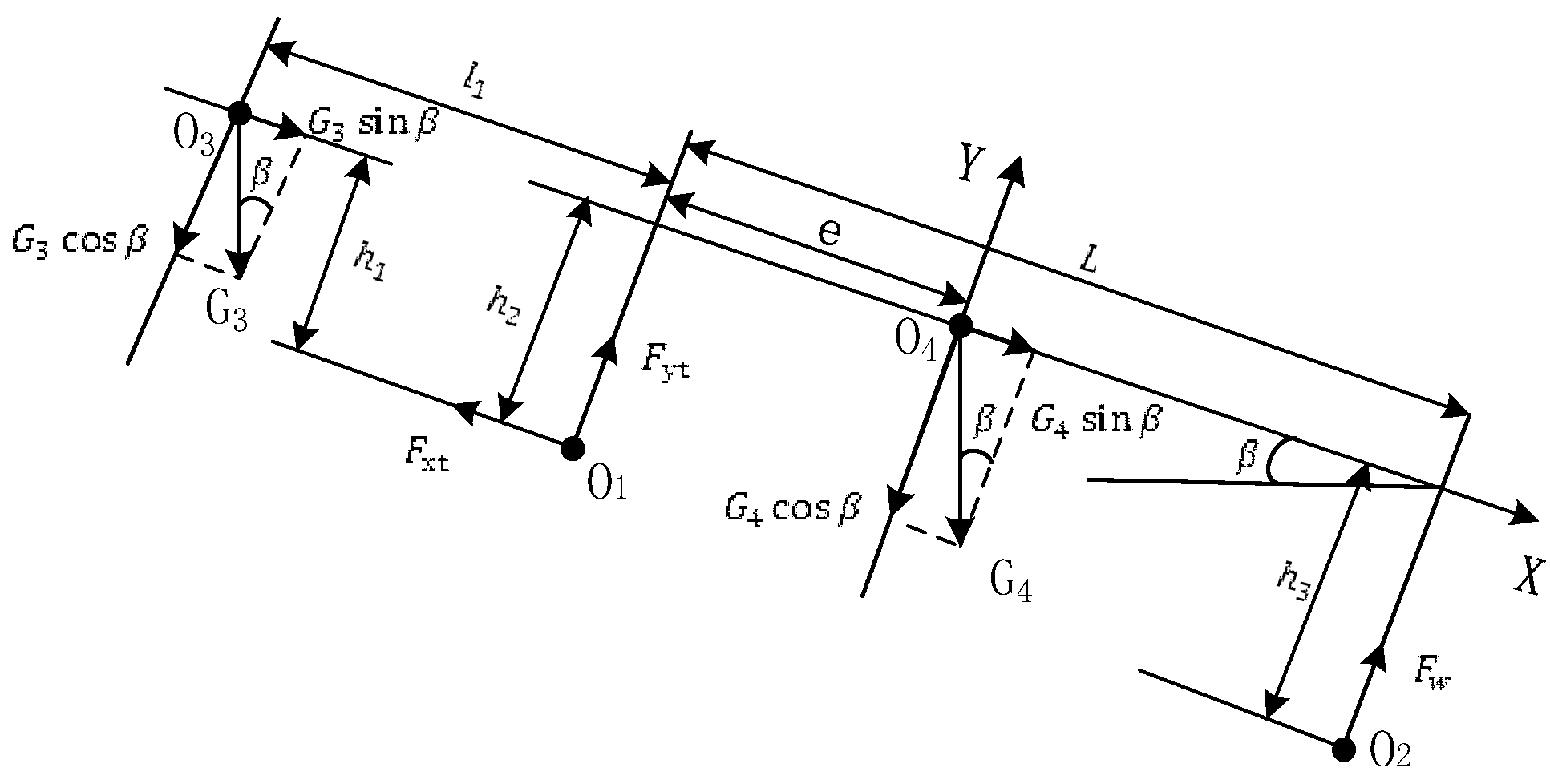

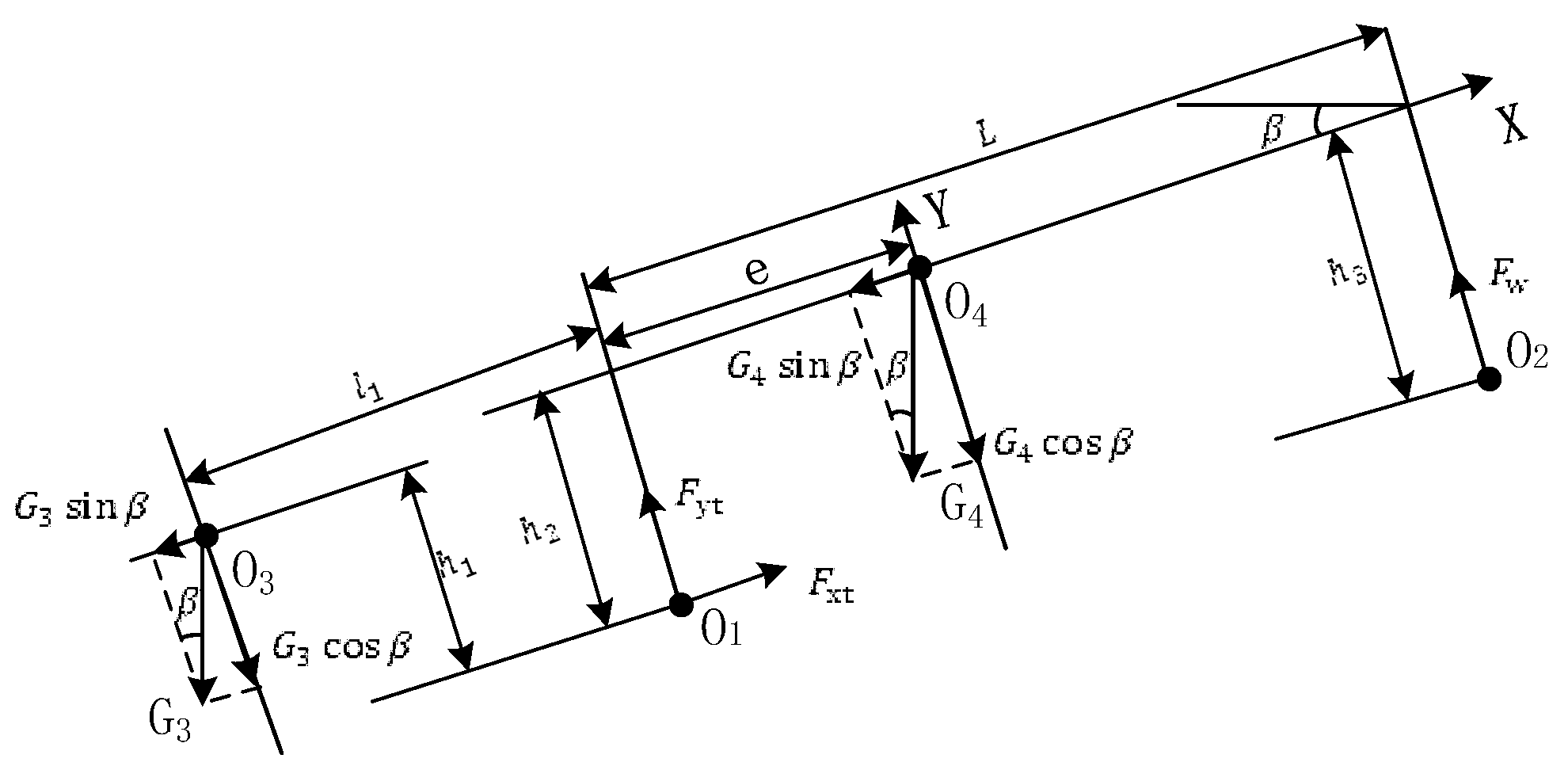







| Parameters/Units | Numerical Value (Manner) |
|---|---|
| Power/kW | 68 |
| Driving mode | Two-track drive |
| Steering mode | Rear-wheel steering |
| Walking mechanism | Wheel-track combination |
| Minimum ground clearance/mm | 970 |
| Front track gauge/mm | 2090 |
| Rear wheel gauge/mm | 2646 |
| Wheelbase | 2950 |
| Uphill and downhill angle/° | 20 |
| Walking speed/km/h | ≥20 |
| Serial Number | 1/mm | 2/mm | 3/mm | Average Value/mm | |
|---|---|---|---|---|---|
| Flat and hard road | Left-turn | 4950 | 4880 | 4890 | 4906.7 |
| Right-turn | 4960 | 4900 | 4900 | 4920 | |
| Rice stubble field | Left-turn | 5450 | 5440 | 5440 | 5443.3 |
| Right-turn | 5460 | 5450 | 5450 | 5453.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, M.; Zhang, M.; Wang, G.; Liang, S.; Wu, C.; He, R. Analysis and Simulation of Wheel-Track High Clearance Chassis of Rape Windrower. Agriculture 2022, 12, 1150. https://doi.org/10.3390/agriculture12081150
Jin M, Zhang M, Wang G, Liang S, Wu C, He R. Analysis and Simulation of Wheel-Track High Clearance Chassis of Rape Windrower. Agriculture. 2022; 12(8):1150. https://doi.org/10.3390/agriculture12081150
Chicago/Turabian StyleJin, Mei, Min Zhang, Gang Wang, Suning Liang, Chongyou Wu, and Ruiyin He. 2022. "Analysis and Simulation of Wheel-Track High Clearance Chassis of Rape Windrower" Agriculture 12, no. 8: 1150. https://doi.org/10.3390/agriculture12081150
APA StyleJin, M., Zhang, M., Wang, G., Liang, S., Wu, C., & He, R. (2022). Analysis and Simulation of Wheel-Track High Clearance Chassis of Rape Windrower. Agriculture, 12(8), 1150. https://doi.org/10.3390/agriculture12081150






