SpikoPoniC: A Low-Cost Spiking Neuromorphic Computer for Smart Aquaponics
Abstract
:1. Introduction
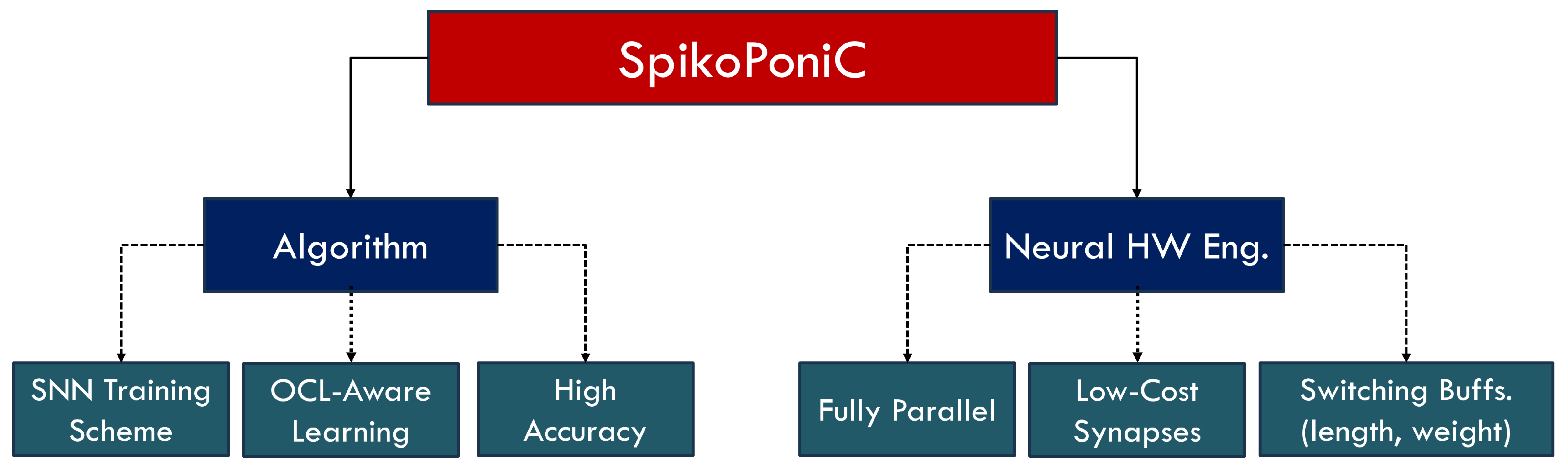
- Main Contributions
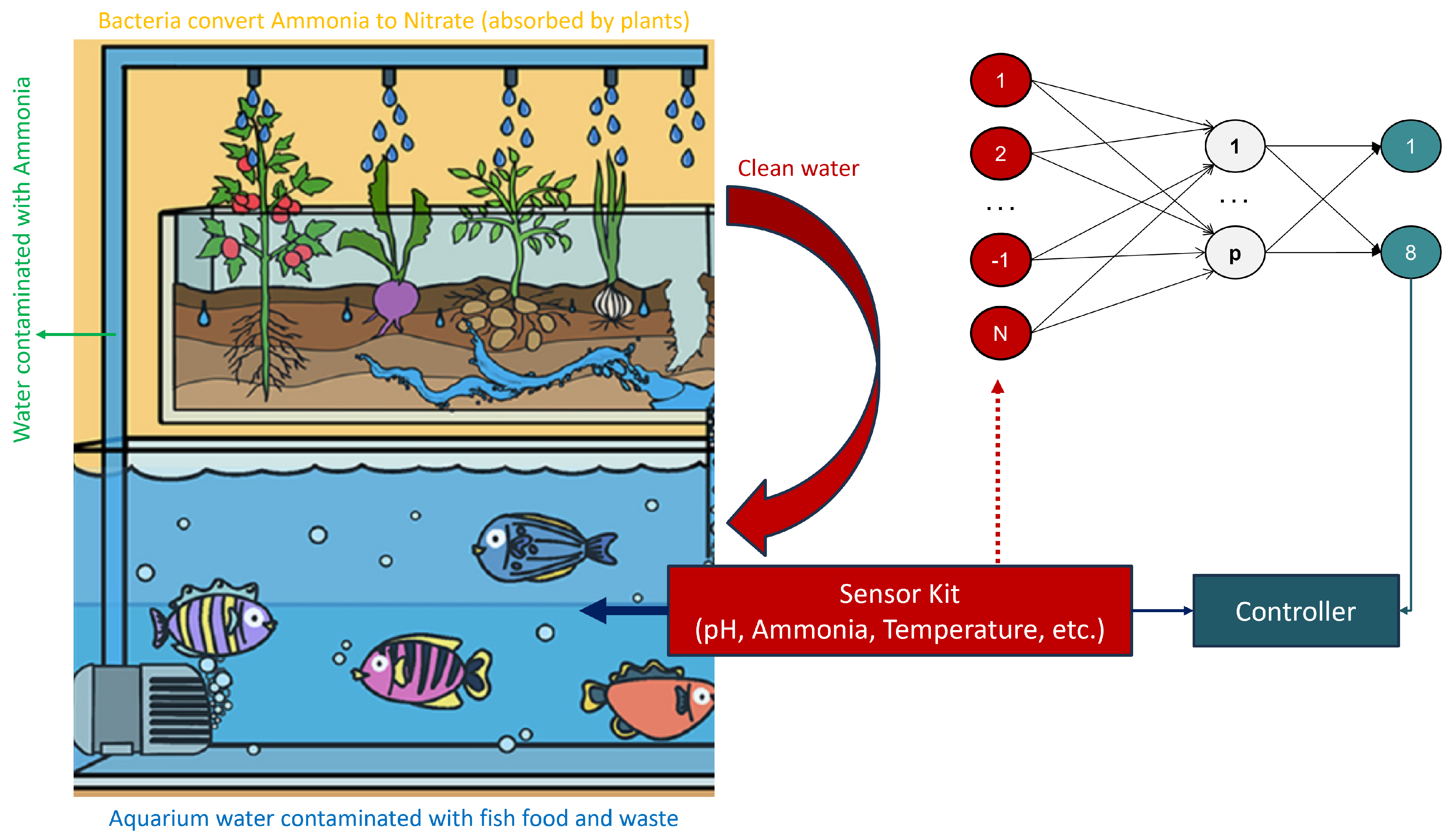
- To provide a complete methodology to develop an aquaponic monitoring system that uses spiking neural networks to predict fish size. The system is capable of predicting both the length and weight of a fish, unlike other systems that can predict either length or weight, not both. In the proposed system, this is done using two switching buffers: one for predicting the weight, and the other one for predicting length.
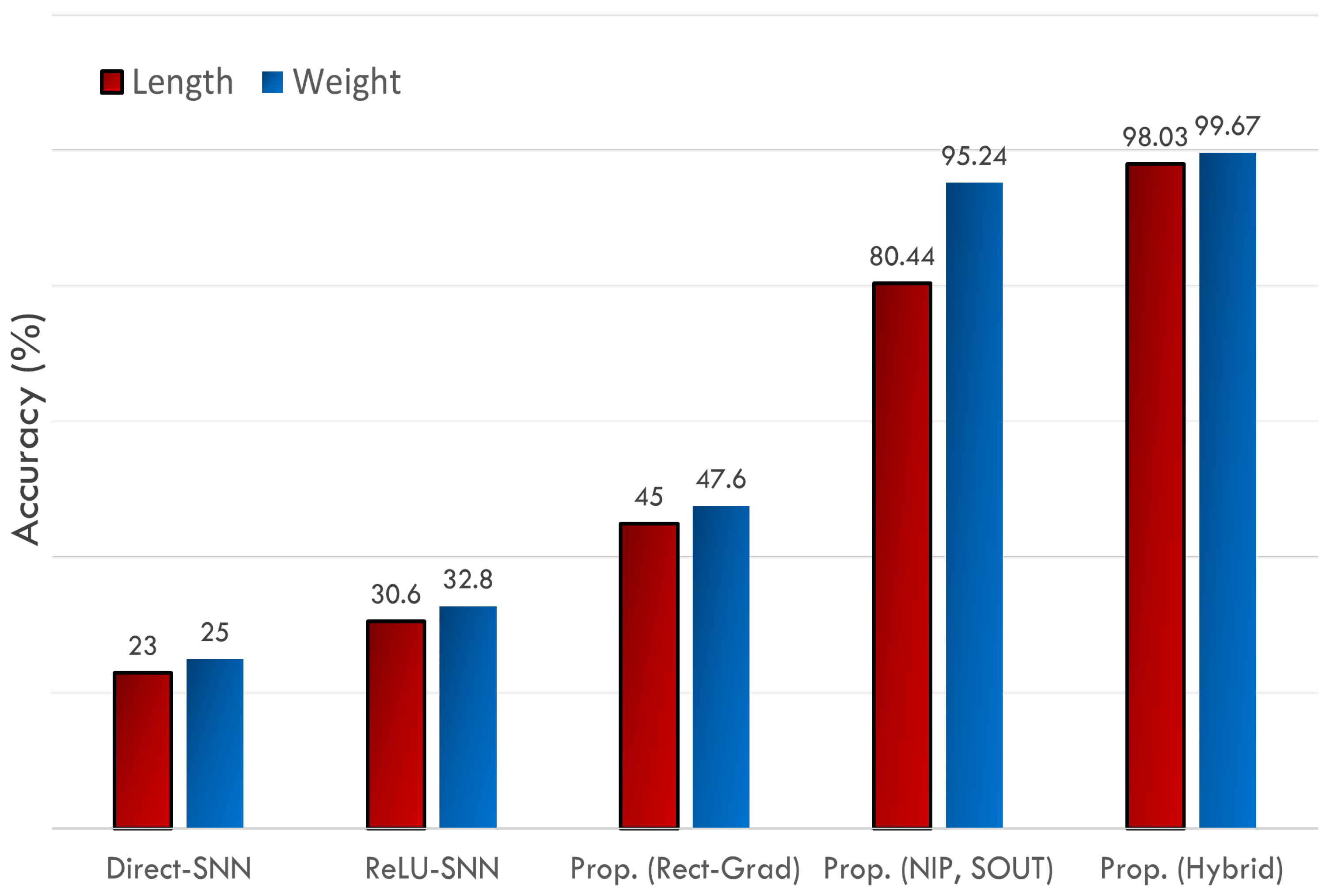
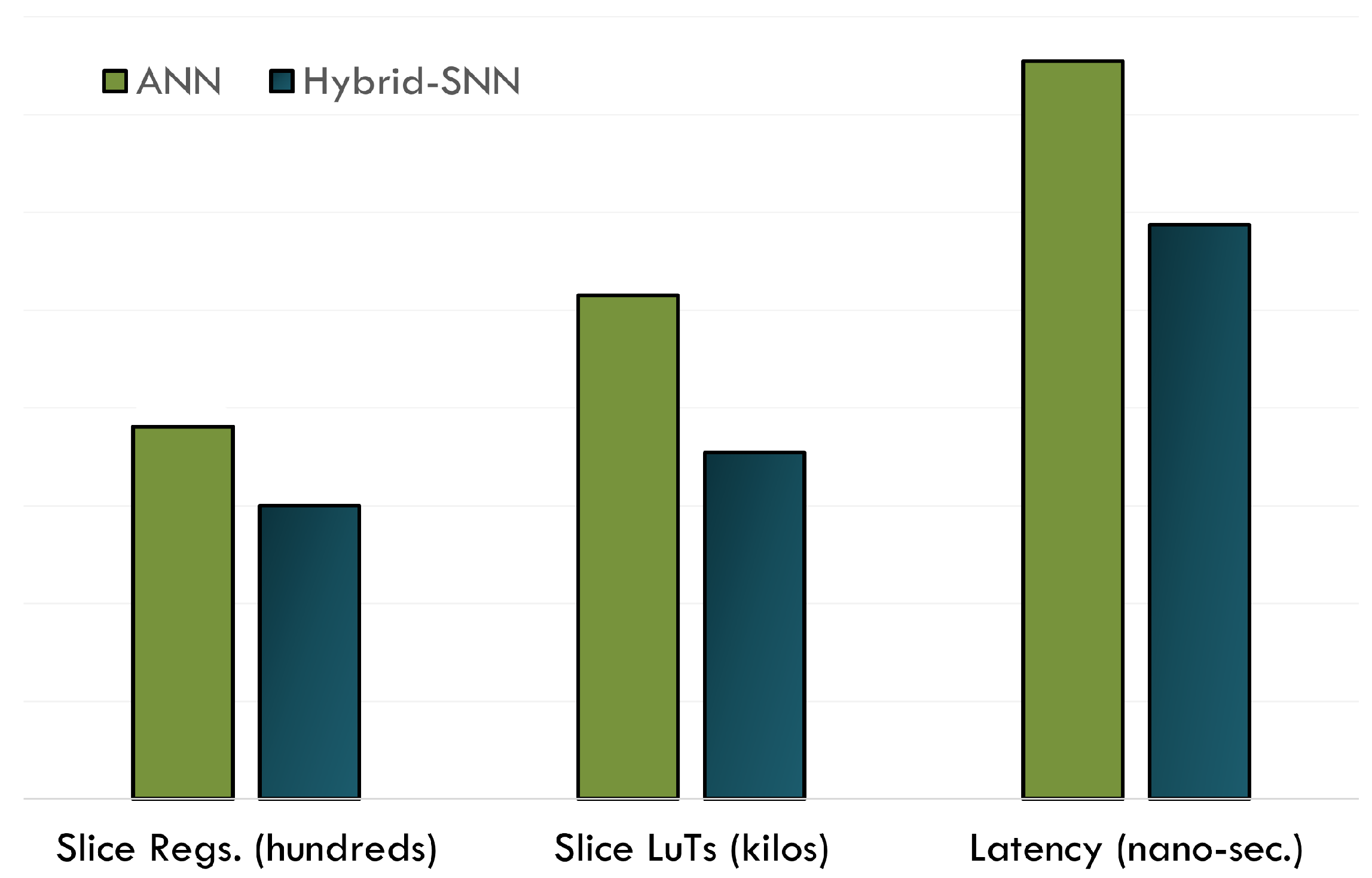
- A proposal of a novel hybrid training scheme that uses both ANN and SNN layers to achieve a blend of high accuracy and hardware efficiency. The system uses direct training for SNNs and standard backpropagation for ANN layers. The proposed implementation is much more hardware-efficient not only than a typical, fully ANN implementation but other SNN implementations too, without any loss of accuracy. The system can estimate the range of length with more than 98.03% accuracy, and the range of weight with 99.67% accuracy.
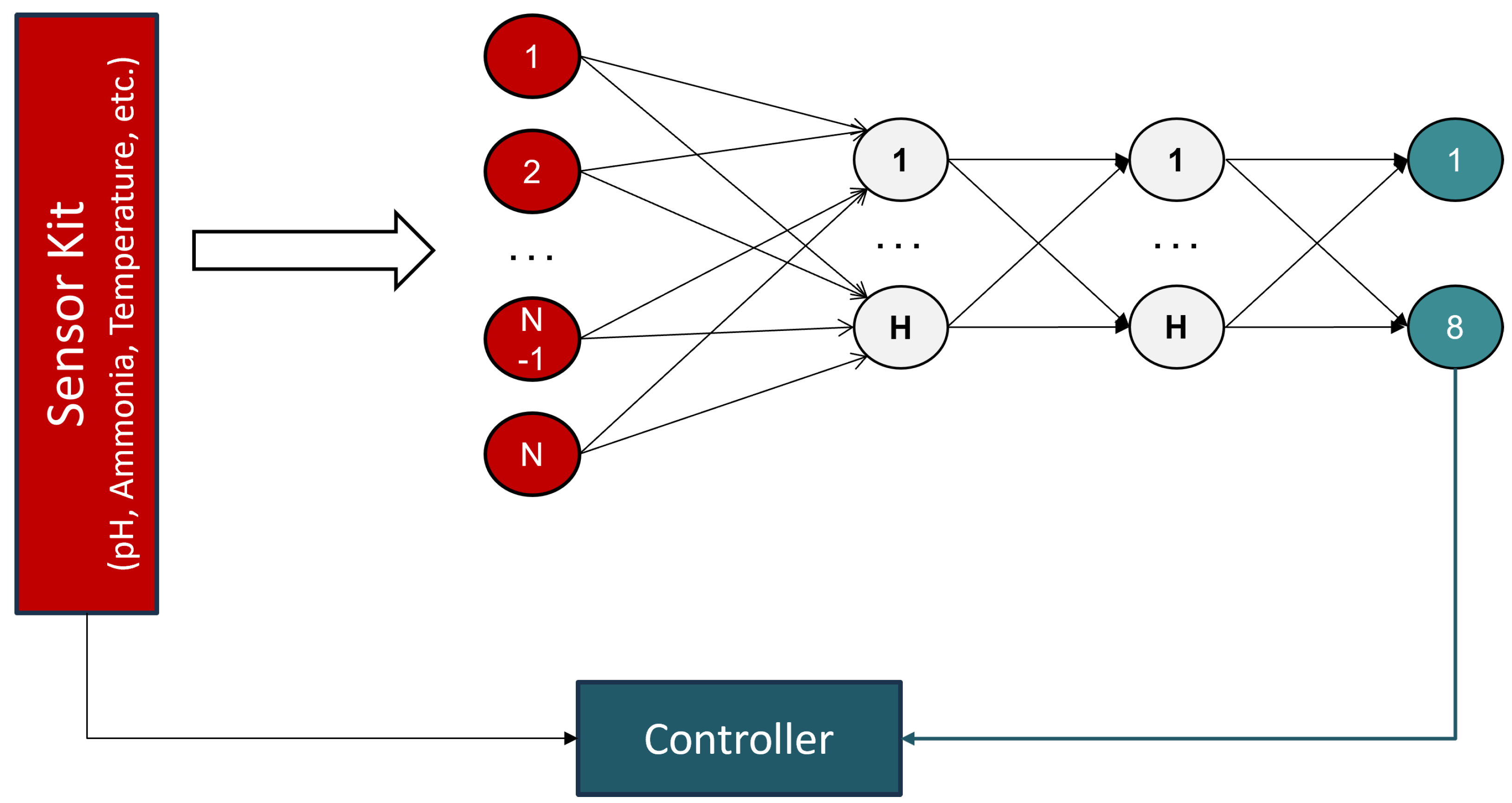
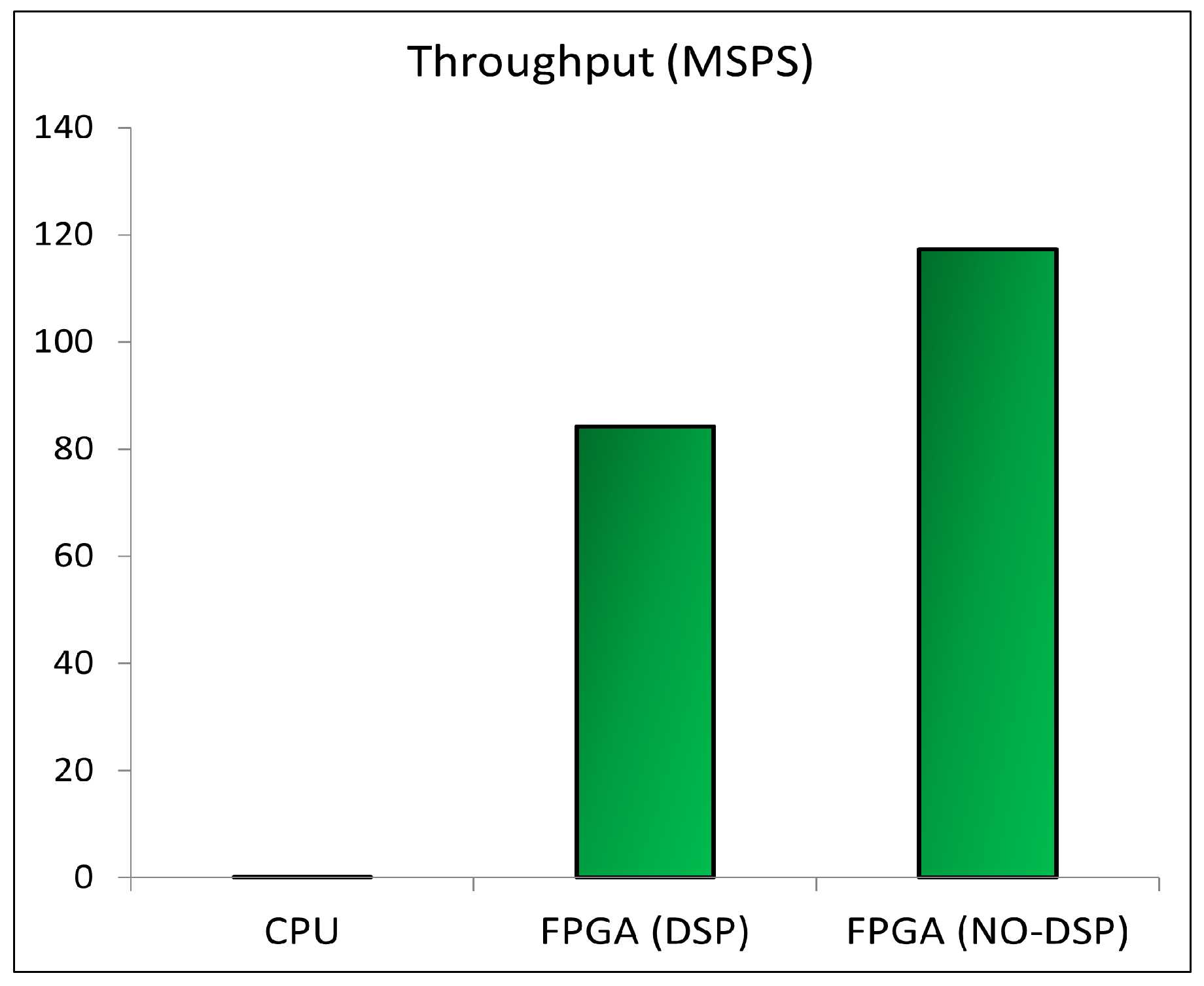
- An SNN-based neuromorphic system implemented on a field programmable gate array (FPGA) for real-time aquaponic monitoring. It is an edge computer capable of predicting fish size (length and weight) on the basis of input parameters. The proposed edge computer can predict 8 different fish size categories based on the given data. The system can operate in the ‘fully parallel’ mode and can estimate 84.23 million samples in a second. The throughput is about 3369 times higher than a typical CPU-based software system, making it suitable for large-scale commercial use. While other systems use only a few hundred samples for testing purposes, the proposed system has been trained/tested on 175,000 samples, which proves that the obtained results are more reliable than others’.
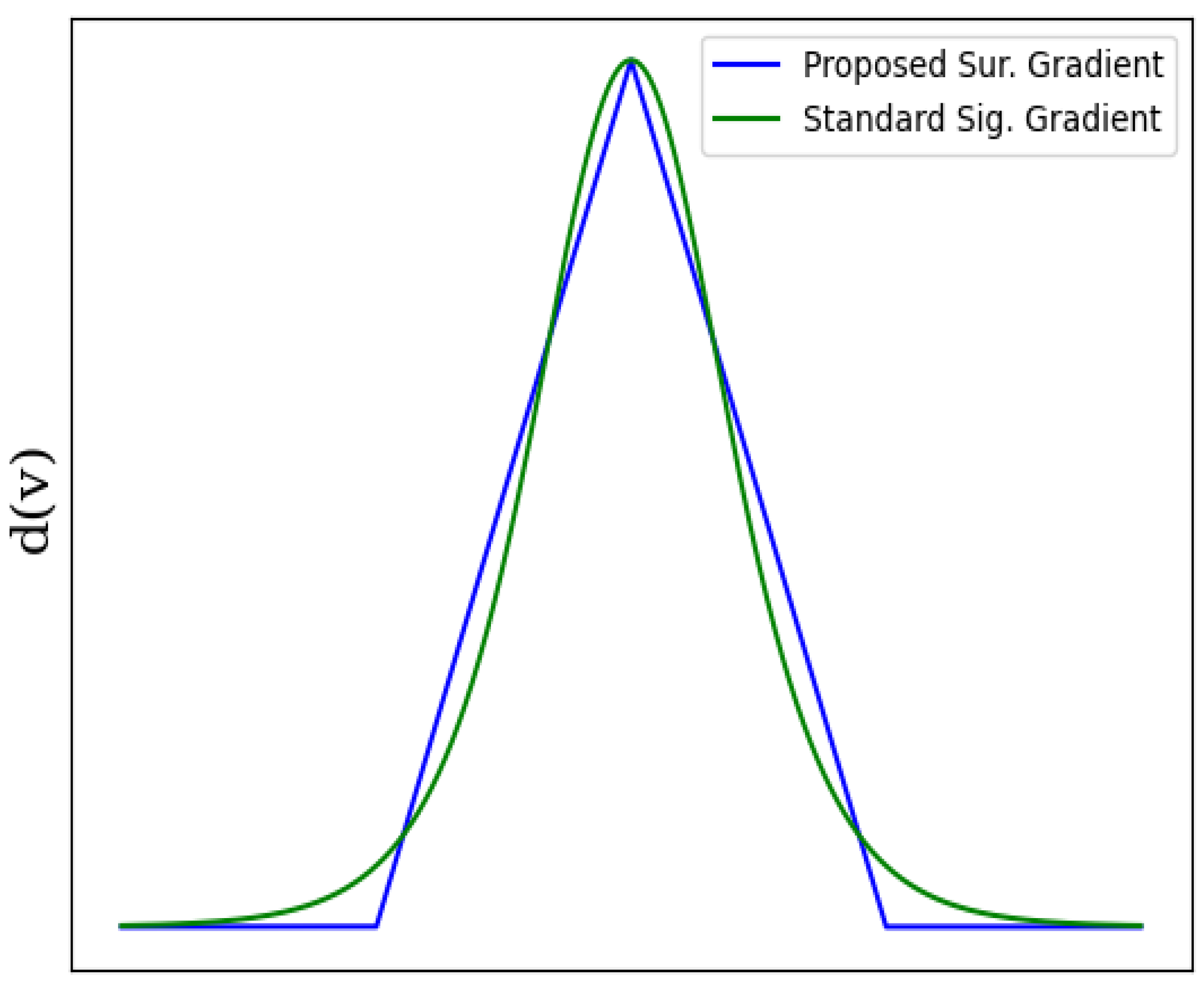
- The proposal of a hardware-efficient surrogate gradient that is as efficient as sigmoid but has higher flexibility. The mean-squared error between the sigmoidal derivative and the proposed derivative is 0.013%. The learning technique is suitable for developing on-chip learning (OCL) systems since the proposed surrogate gradient requires far fewer hardware resources than most gradients proposed in the literature while being extremely accurate.
- Related Work and Problem Definition
1.1. Smart Aquaponics: Algorithms and Monitoring Systems
- Firstly, no SAS-specific SNN system is available in the literature. All the smart aquaponic systems presented in the literature use artificial neural networks for parameter prediction and other tasks.
- Secondly, most SNN systems presented in the literature yield very low accuracy, even for digit classification tasks. Only a few SNN schemes achieve high accuracy. This is because spikes are non-differentiable in nature and direct backpropagation is quite tricky to apply [15]. The non-differentiable nature of spikes is shown in Figure 5. Therefore, most researchers typically use an unsupervised algorithm spike-timing-dependent plasticity (STDP) for SNN training.
- SNNs, unlike ANNs, require multiple time steps to process an input. This is why SNNs, sometimes, can consume a lot of time and hardware energy.
1.2. Neuromorphic Accelerators (NMAs)
Problem Definition
2. Materials and Methods
- Forward NN Pass
- Backward NN Pass
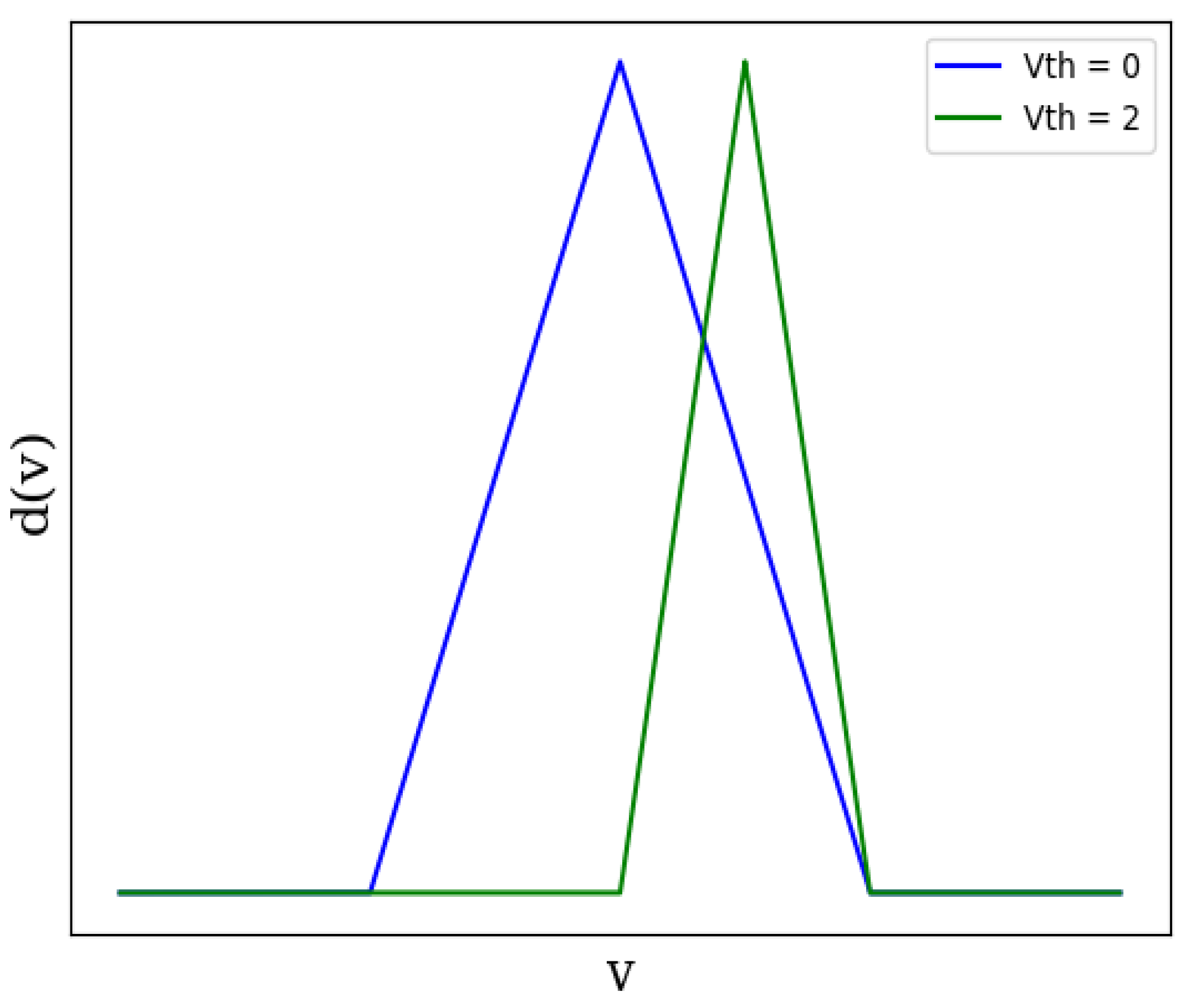
- Proposed Surrogate Gradient
- Experimental and Mathematical Proofs
- Experimental Proof: The proposed Spikoponic derivative is used for backpropagation to train a network that classifies fish on the basis of their weight and length. Extensive experiments have been carried out using the proposed Spikoponic derivative. The details of the dataset are given in Section 3.1; the parameter values are given in Table 2. The results are given in Section 3.2. As shown in results, the proposed derivative works perfectly and can train an SNN for fish size estimation.
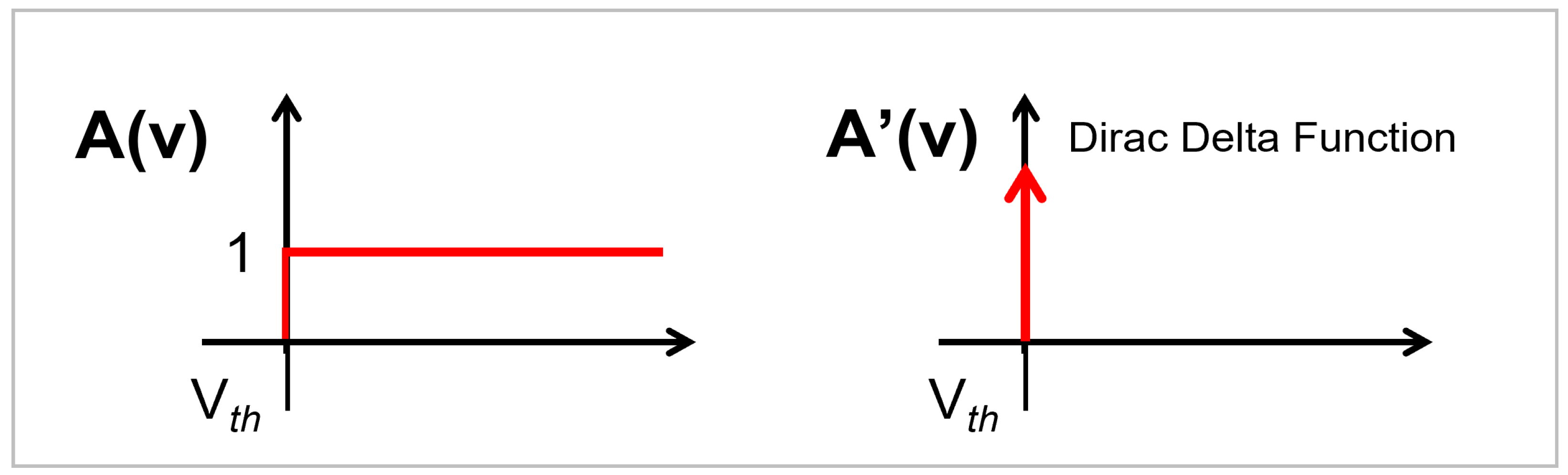
- Mathematical Proof: In order to perform backpropagation, the activation function must have a finite derivative [9,15,47]. The proposed spikoponic derivative, given in Equation (8), is finite. The derivative holds valid values since it is not always equal to zero or infinity.Moreover, if the parameter a (in the Spikoponic derivative function) is equal to ∞, the derivative converges to the dirac delta function, shown in Figure 5. This behavior clearly shows that the Spikoponic derivative is a valid function for the backward pass if step function is used in the forward pass. The mathematical expression for this behavior is given in Equation (9).The weights and DTCs are updated according to gradient descent rules, where network layers are iteratively updated based on an error function. Though all these processes are integrated into modern Python packages and we do not have to code everything in detail, we give a brief overview just to enhance readers’ understanding. The two basic parameter update rules are given in (10) and (11).In the above equations, W represents ‘weight vector’ and C represents the DTC vector at layer l. Here, represents the learning rate, the parameter that determines the speed at which the network updates weights in a training iteration. The term describes the changes in loss function with respect to weights at layer l. Both these terms are calculated using the chain rule, as in [9,15,17].Since there are multiple layers in the proposed network, it would be unnecessary to derive mathematical expressions for all the layers. Therefore, we derive expressions only for one layer as a reference, just to give an idea of how the system works. Expressions for other layers can be derived using the same principle.We mathematically establish the dependence of loss functions on Layer 2 synaptic strengths in Equation (12), and on Layer 2 DTC () in Equation (13). To make the analysis understandable, the mean squared error (MSE) function has been used for reference. In the following equations, is the obtained output value at Layer 3, and y is the label voltage. The Spikoponic derivative function is already given in Equation (8). In order to keep mathematics simple, we do not incorporate terms associated with the optimization methhods such as ADAM [48] in the presented mathematical expressions. Equations (12) and (13) do not incorporate the temporal dependence of the network parameters and have been derived for one time step, which is one of the main goals of this work. To ignore temporal dependence, we make equal to zero.
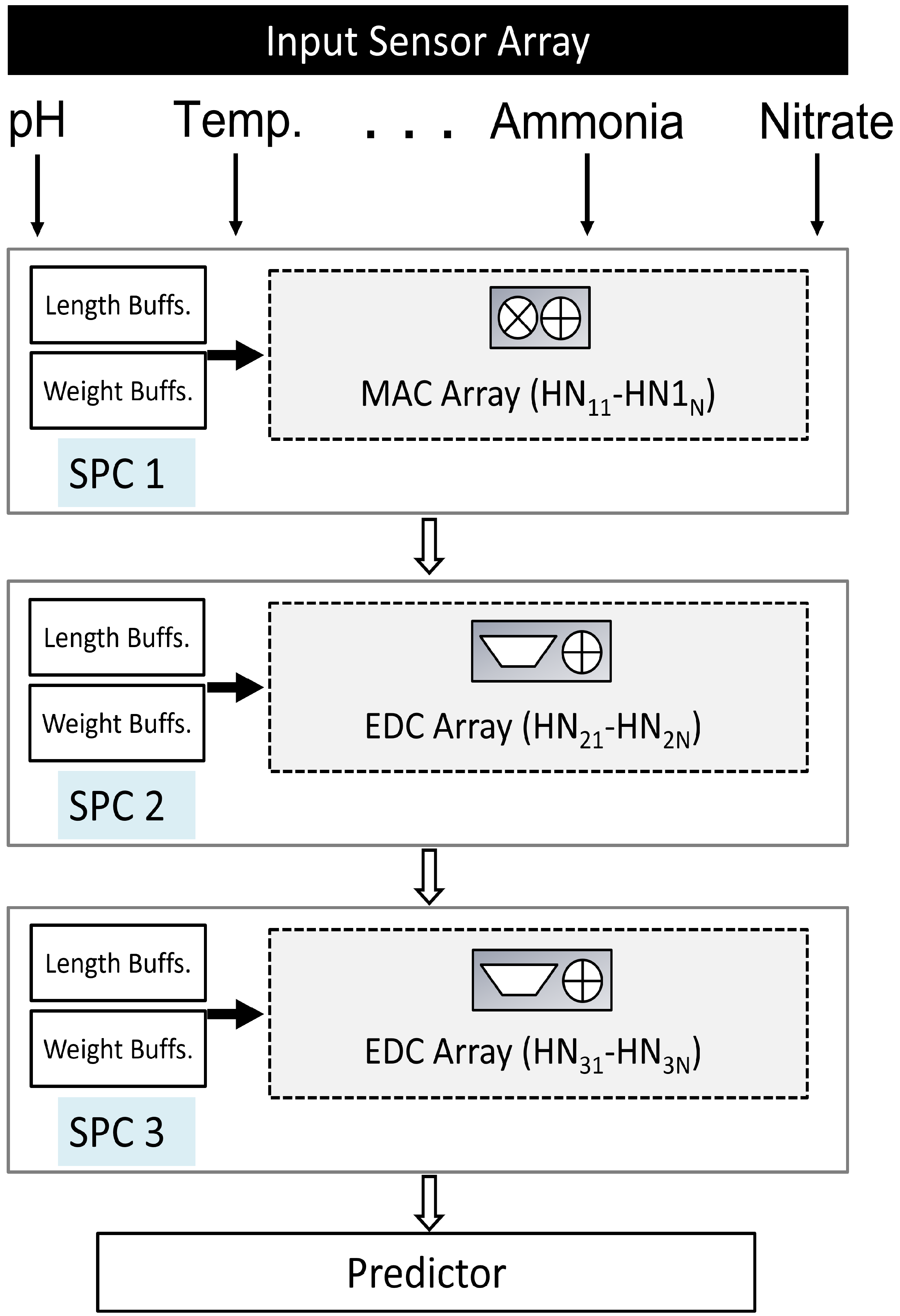
- Proposed SpikoPoniC Hardware Engine
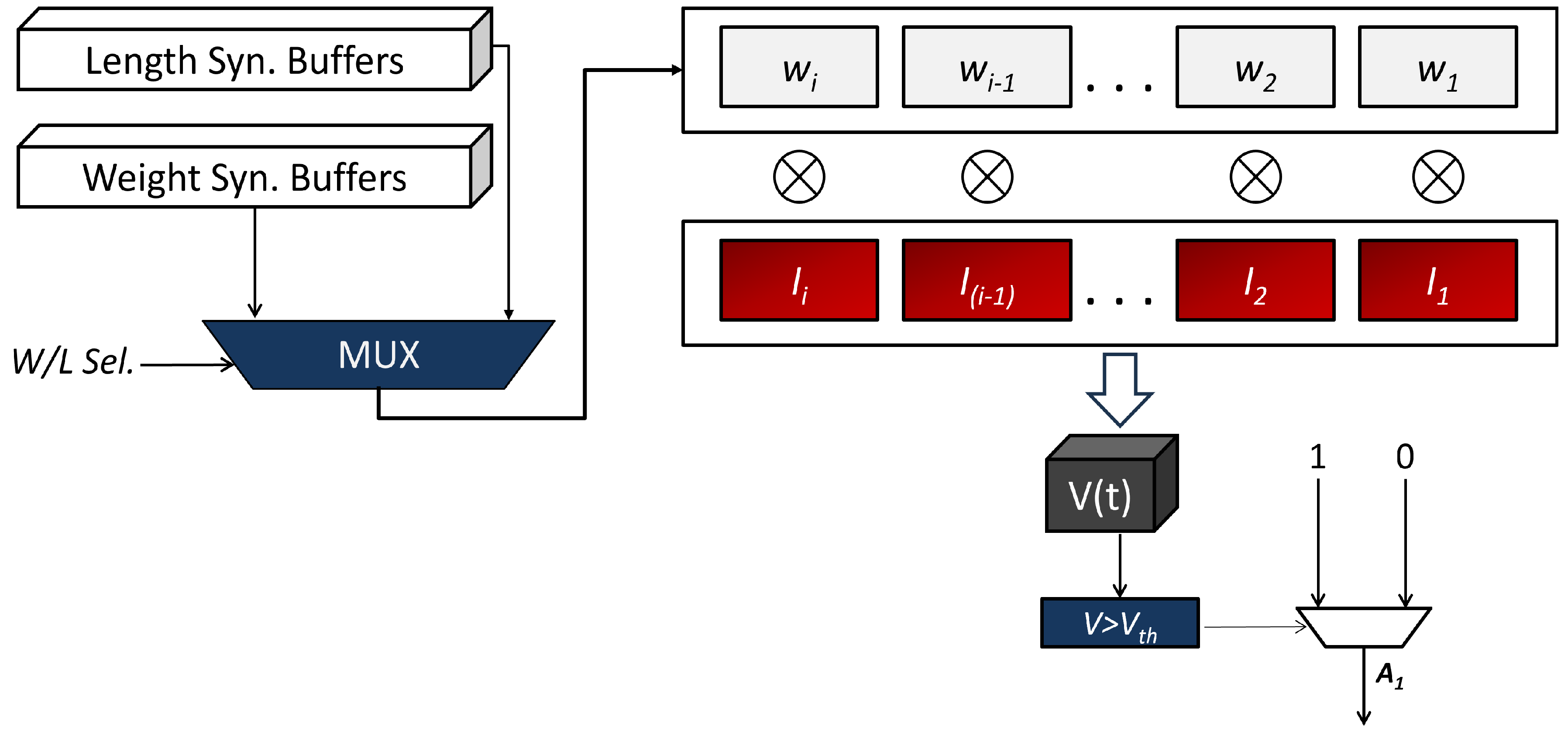
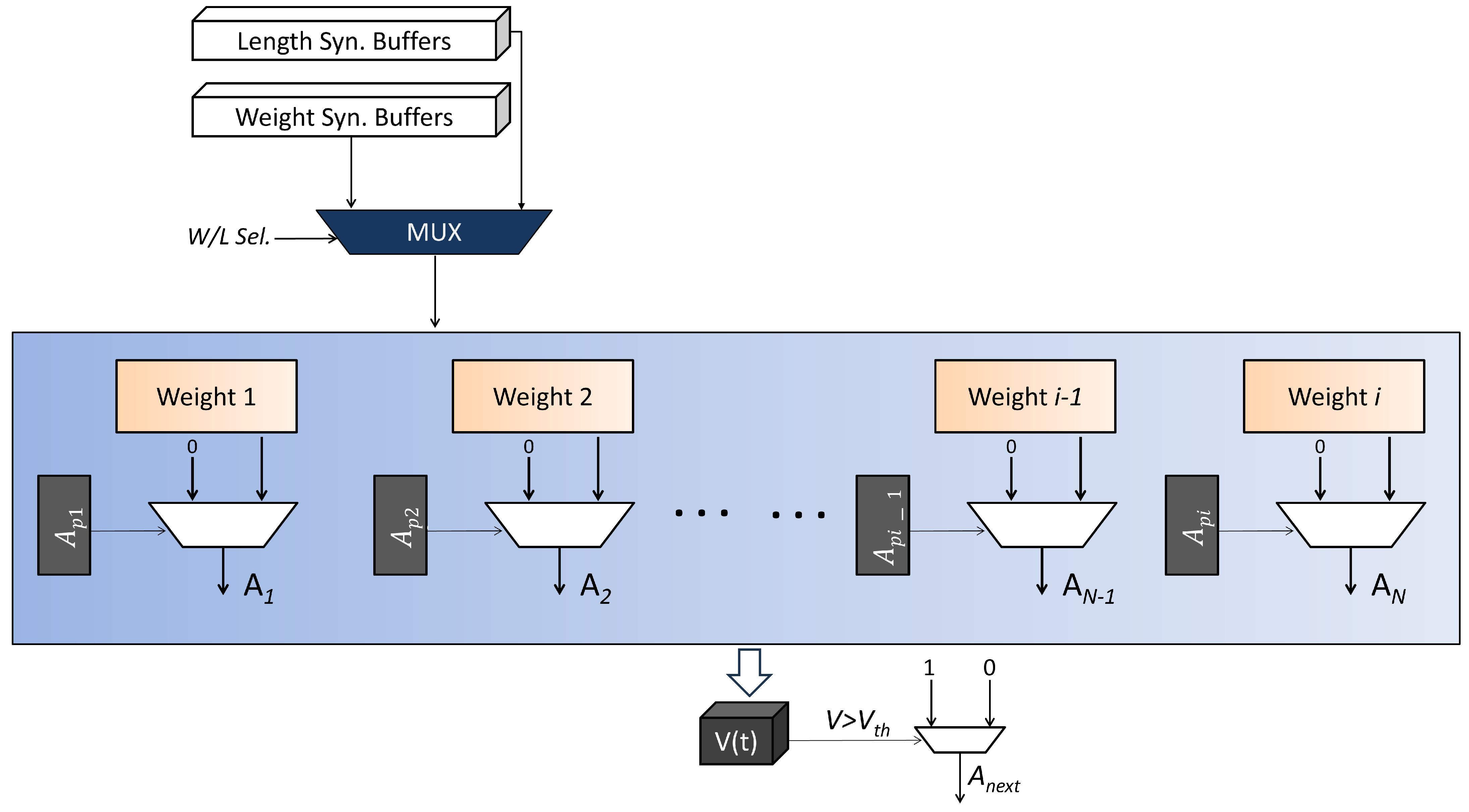
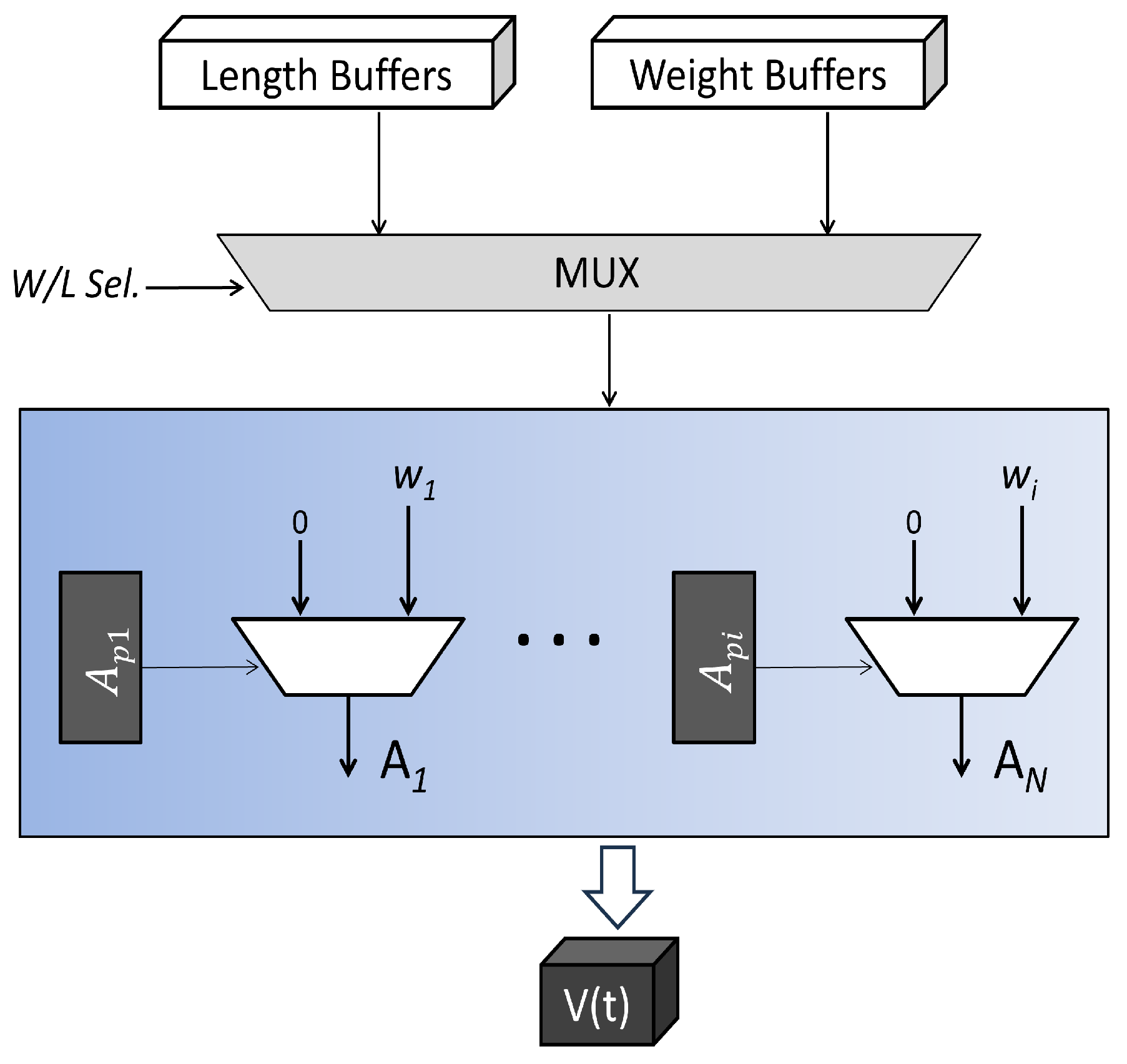
2.1. Switching Buffers
2.2. Event-Driven Spiking Computers (EDCs)—Hidden Layer 1
2.3. EDCs—Hidden Layer 2
2.4. Output-Layer EDCs
3. Results and Discussion
3.1. Benchmarks and Test Conditions
3.2. Algorithmic Efficiency Evaluation and Comparisons
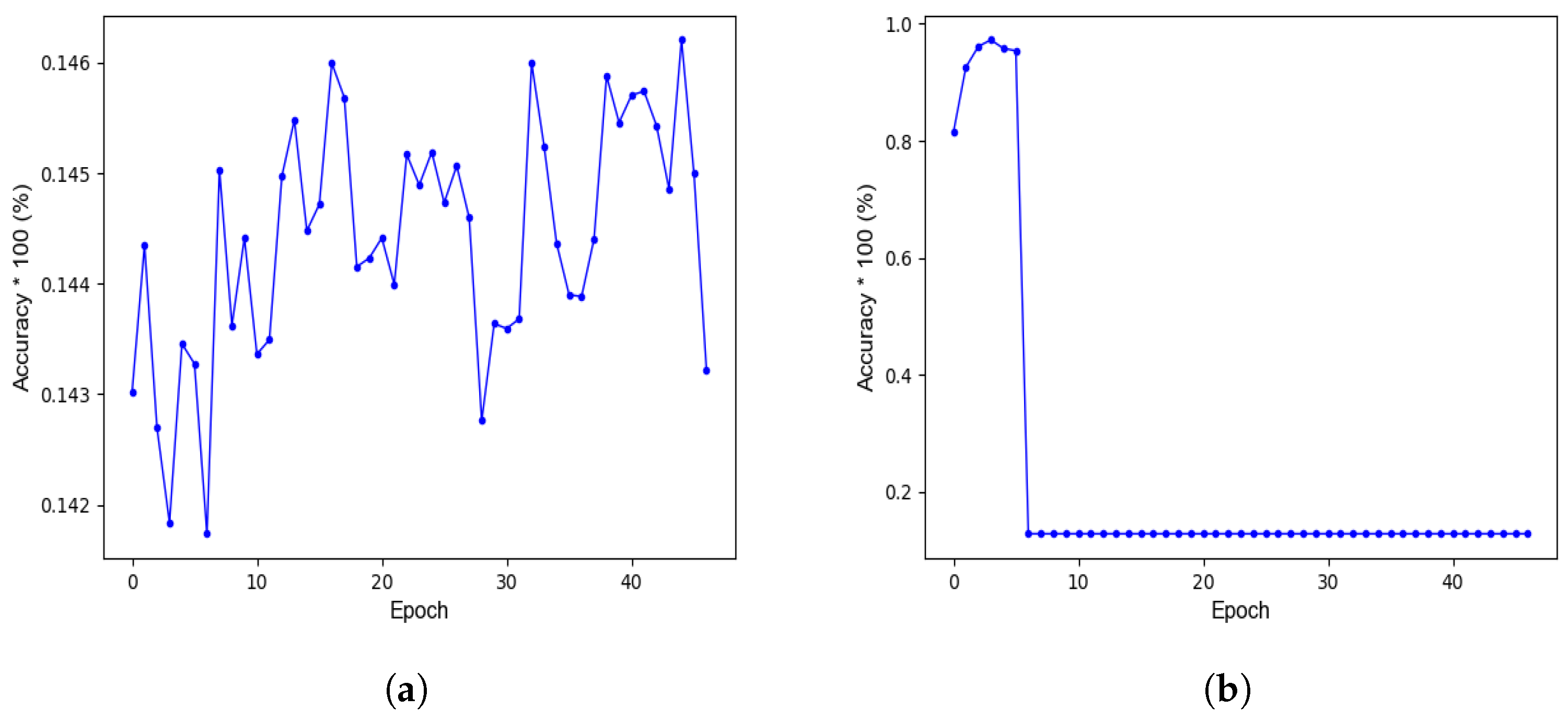
- All the layers use spikes in the forward pass and surrogate gradient (sigmoidal gradient [15]) in the backward pass. The network achieves very low accuracy since there is only one time step for which we have to train the network.
- ReLU-SNN Conversion (ReLU-SNN) [19].The network is trained using ReLU function, and the trained network is then converted into an SNN. No weight-threshold normalization is applied since the purpose is to devise an algorithm that is hardware-efficient if on-chip learning is required. Normalization processes can never be efficient for on-chip learning [9]. For better accuracy, the inputs are not converted into spikes since this results in a loss of accuracy [19].
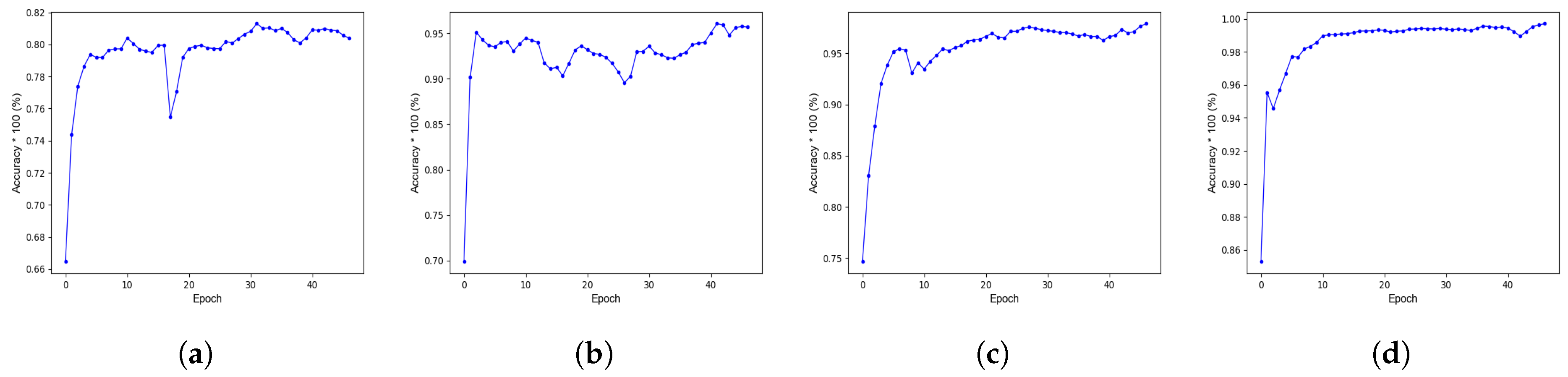
- Rectangular Straight-Through Estimator (Rect-STE) [17].The network uses spikes in the forward pass, and the rectangular-shaped surrogate gradient in the backward pass, as in [17]. For achieving high accuracy, full-resolution inputs are used and no conversion to spikes takes place.
- Proposed Algorithm (Normalized Inputs, Spiking Outputs).The proposed algorithm, as mentioned in Section 2, is applied with full-resolution inputs but spiking outputs.
- Proposed Algorithm (Normalized Inputs, Full-Resolution Outputs).The proposed algorithm, as described in Section 2, is applied with full-resolution inputs and outputs (logits).
3.3. Hardware Efficiency Evaluation and Comparisons
| System | Application | Topology | Accur. | Regs. | LuTs | DSPs | Platform | TP | PTPS |
|---|---|---|---|---|---|---|---|---|---|
| () | (s) | ||||||||
| [33] | Epilepsy Det. | 5-12-3 | 95.14% | 114 | 12,960 | 116 | Cyclone IV | 50 | 0.02 |
| [34] | Cancer Det. | 30-5-2 | 98.23% | 983 | 2654 | 234 | Virtex 6 | 63.5 | 0.0157 |
| [22] | Digit Class. | 64-20-10 | 94.28% | 4677 | 30,654 | 0 | Virtex 6 | 93.2 | 0.0107 |
| [35] | Bin. Class. | 25-5-1 | 89% | 1023 | 11,339 | - | Virtex 6 | 1.89 | >0.53 |
| [57] | None | 5-5-2 | - | 1898 | 3124 | 154 | Virtex 5 | - | - |
| [56] | None | - | - | 790 | 1195 | 14 | Spartan 3 | 10 | 0.1 |
| Prop. | Aquaponics | 8-16-16-8 | 98.85% | 1091 | 3749 | 128 | Virtex 6 | 84.23 | 0.012 |
| Prop. | Aquaponics | 8-16-16-8 | 98.85% | 4259 | 18,283 | 0 | Virtex 6 | 117.33 | 0.008 |
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| ASIC | Application-specific integrated circuit |
| DL | Deep learning |
| FPGA | Field programmable gate array |
| GPC | General-purpose computer |
| SAS | Smart aquaponic system |
| SNN | Spiking neural network |
References
- Calone, R.; Orsini, F. Aquaponics: A Promising Tool for Environmentally Friendly Farming. Front. Young Minds 2022, 10, 707801. [Google Scholar] [CrossRef]
- Taha, M.F.; ElMasry, G.; Gouda, M.; Zhou, L.; Liang, N.; Abdalla, A.; Rousseau, D.; Qiu, Z. Recent Advances of Smart Systems and Internet of Things (IoT) for Aquaponics Automation: A Comprehensive Overview. Chemosensors 2022, 10, 303. [Google Scholar] [CrossRef]
- Dhal, S.B.; Jungbluth, K.; Lin, R.; Sabahi, S.P.; Bagavathiannan, M.; Braga-Neto, U.; Kalafatis, S. A machine-learning-based IoT system for optimizing nutrient supply in commercial aquaponic operations. Sensors 2022, 22, 3510. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Jalal, A.; Salman, A.; Mian, A.; Shortis, M.; Shafait, F. Fish detection and species classification in underwater environments using deep learning with temporal information. Ecol. Inform. 2020, 57, 101088. [Google Scholar] [CrossRef]
- Hasan, N.; Ibrahim, S.; Aqilah Azlan, A. Fish diseases detection using convolutional neural network (CNN). Int. J. Nonlinear Anal. Appl. 2022, 13, 1977–1984. [Google Scholar]
- Ubina, N.; Cheng, S.C.; Chang, C.C.; Chen, H.Y. Evaluating fish feeding intensity in aquaculture with convolutional neural networks. Aquac. Eng. 2021, 94, 102178. [Google Scholar] [CrossRef]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef]
- Siddique, A.; Vai, M.I.; Pun, S.H. A low cost neuromorphic learning engine based on a high performance supervised SNN learning algorithm. Sci. Rep. 2023, 13, 6280. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.; Na, B.; Yoon, S. Spiking-YOLO: Spiking neural network for energy-efficient object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11270–11277. [Google Scholar]
- Maass, W.; Papadimitriou, C.H.; Vempala, S.; Legenstein, R. Brain computation: A computer science perspective. Comput. Softw. Sci. 2019, 10000, 184–199. [Google Scholar]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Han, J.; Li, Z.; Zheng, W.; Zhang, Y. Hardware implementation of spiking neural networks on FPGA. Tsinghua Sci. Technol. 2020, 25, 479–486. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Qiao, G.; Hu, S.; Chen, T.; Rong, L.; Ning, N.; Yu, Q.; Liu, Y. STBNN: Hardware-friendly spatio-temporal binary neural network with high pattern recognition accuracy. Neurocomputing 2020, 409, 351–360. [Google Scholar] [CrossRef]
- Yin, S.; Venkataramanaiah, S.K.; Chen, G.K.; Krishnamurthy, R.; Cao, Y.; Chakrabarti, C.; Seo, J. Algorithm and hardware design of discrete-time spiking neural networks based on back propagation with binary activations. In Proceedings of the 2017 IEEE Biomedical Circuits and Systems Conference (BioCAS), Torino, Italy, 19–21 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Diehl, P.U.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef]
- Azghadi, M.R.; Lammie, C.; Eshraghian, J.K.; Payvand, M.; Donati, E.; Linares-Barranco, B.; Indiveri, G. Hardware implementation of deep network accelerators towards healthcare and biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1138–1159. [Google Scholar] [CrossRef]
- Ortega-Zamorano, F.; Jerez, J.M.; Urda Muñoz, D.; Luque-Baena, R.M.; Franco, L. Efficient Implementation of the Backpropagation Algorithm in FPGAs and Microcontrollers. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1840–1850. [Google Scholar] [CrossRef]
- Siddique, A.; Iqbal, M.A.; Aleem, M.; Islam, M.A. A 218 GOPS neural network accelerator based on a novel cost-efficient surrogate gradient scheme for pattern classification. Microprocess. Microsyst. 2023, 99, 104831. [Google Scholar] [CrossRef]
- Junior, A.d.S.O.; Sant’Ana, D.A.; Pache, M.C.B.; Garcia, V.; de Moares Weber, V.A.; Astolfi, G.; de Lima Weber, F.; Menezes, G.V.; Menezes, G.K.; Albuquerque, P.L.F.; et al. Fingerlings mass estimation: A comparison between deep and shallow learning algorithms. Smart Agric. Technol. 2021, 1, 100020. [Google Scholar] [CrossRef]
- Ren, Q.; Zhang, L.; Wei, Y.; Li, D. A method for predicting dissolved oxygen in aquaculture water in an aquaponics system. Comput. Electron. Agric. 2018, 151, 384–391. [Google Scholar] [CrossRef]
- Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [PubMed]
- Saunders, D.J.; Siegelmann, H.T.; Kozma, R. STDP learning of image patches with convolutional spiking neural networks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–7. [Google Scholar]
- Vicente-Sola, A.; Manna, D.L.; Kirkland, P.; Di Caterina, G.; Bihl, T. Keys to accurate feature extraction using residual spiking neural networks. Neuromorphic Comput. Eng. 2022, 2, 044001. [Google Scholar] [CrossRef]
- Deng, S.; Gu, S. Optimal conversion of conventional artificial neural networks to spiking neural networks. arXiv 2021, arXiv:2103.00476. [Google Scholar]
- Fang, W.; Yu, Z.; Chen, Y.; Huang, T.; Masquelier, T.; Tian, Y. Deep residual learning in spiking neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 21056–21069. [Google Scholar]
- Zhang, W.; Li, P. Temporal spike sequence learning via backpropagation for deep spiking neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 12022–12033. [Google Scholar]
- Tavanaei, A.; Maida, A. BP-STDP: Approximating backpropagation using spike timing dependent plasticity. Neurocomputing 2019, 330, 39–47. [Google Scholar] [CrossRef]
- Tavanaei, A.; Kirby, Z.; Maida, A.S. Training spiking convnets by stdp and gradient descent. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Sarić, R.; Jokić, D.; Beganović, N.; Pokvić, L.G.; Badnjević, A. FPGA-based real-time epileptic seizure classification using Artificial Neural Network. Biomed. Signal Process. Control 2020, 62, 102106. [Google Scholar] [CrossRef]
- Siddique, A.; Iqbal, M.A.; Aleem, M.; Lin, J.C.W. A high-performance, hardware-based deep learning system for disease diagnosis. PeerJ Comput. Sci. 2022, 8, e1034. [Google Scholar] [CrossRef]
- Farsa, E.Z.; Ahmadi, A.; Maleki, M.A.; Gholami, M.; Rad, H.N. A low-cost high-speed neuromorphic hardware based on spiking neural network. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1582–1586. [Google Scholar] [CrossRef]
- Sun, C.; Sun, H.; Xu, J.; Han, J.; Wang, X.; Wang, X.; Chen, Q.; Fu, Y.; Li, L. An Energy Efficient STDP-Based SNN Architecture With On-Chip Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 5147–5158. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Mao, R.; Xiao, J.; Chang, L.; Zhou, J. A Fast and Energy-Efficient SNN Processor With Adaptive Clock/Event-Driven Computation Scheme and Online Learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1543–1552. [Google Scholar] [CrossRef]
- Siddique, A.; Vai, M.I.; Pun, S.H. A low-cost, high-throughput neuromorphic computer for online SNN learning. Clust. Comput. 2023, 1–18. [Google Scholar] [CrossRef]
- Zhang, G.; Li, B.; Wu, J.; Wang, R.; Lan, Y.; Sun, L.; Lei, S.; Li, H.; Chen, Y. A low-cost and high-speed hardware implementation of spiking neural network. Neurocomputing 2020, 382, 106–115. [Google Scholar] [CrossRef]
- Heidarpur, M.; Ahmadi, A.; Ahmadi, M.; Azghadi, M.R. CORDIC-SNN: On-FPGA STDP learning with izhikevich neurons. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2651–2661. [Google Scholar] [CrossRef]
- Lammie, C.; Hamilton, T.; Azghadi, M.R. Unsupervised character recognition with a simplified FPGA neuromorphic system. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Ma, D.; Shen, J.; Gu, Z.; Zhang, M.; Zhu, X.; Xu, X.; Xu, Q.; Shen, Y.; Pan, G. Darwin: A neuromorphic hardware co-processor based on spiking neural networks. J. Syst. Archit. 2017, 77, 43–51. [Google Scholar] [CrossRef]
- Neil, D.; Liu, S.C. Minitaur, an event-driven FPGA-based spiking network accelerator. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 2621–2628. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Lee, C.; Roy, K. Towards Understanding the Effect of Leak in Spiking Neural Networks. arXiv 2020, arXiv:2006.08761. [Google Scholar] [CrossRef]
- Zhang, M.; Vassiliadis, S.; Delgado-Frias, J.G. Sigmoid generators for neural computing using piecewise approximations. IEEE Trans. Comput. 1996, 45, 1045–1049. [Google Scholar] [CrossRef]
- Wuraola, A.; Patel, N.; Nguang, S.K. Efficient activation functions for embedded inference engines. Neurocomputing 2021, 442, 73–88. [Google Scholar] [CrossRef]
- Esser, S.K.; Appuswamy, R.; Merolla, P.; Arthur, J.V.; Modha, D.S. Backpropagation for energy-efficient neuromorphic computing. Adv. Neural Inf. Process. Syst. 2015, 28, 1117–1125. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Xilinx. Virtex-6 Family Overview. Available online: https://www.digikey.com/htmldatasheets/production/738648/0/0/1/virtex-6-fpga-family%20overview.html (accessed on 9 October 2023).
- Collins Udanor. Sensor Based Aquaponics Fish Pond Datasets. Available online: https://www.kaggle.com/datasets/ogbuokiriblessing/sensor-based-aquaponics-fish-pond-datasets?resource=download (accessed on 5 May 2023).
- Zheng, A. Evaluating Machine Learning Models: A Beginner’s Guide to Key Concepts and Pitfalls. 2015. Available online: https://www.oreilly.com/content/evaluating-machine-learning-models/ (accessed on 9 October 2023).
- Taha, M.F.; Abdalla, A.; ElMasry, G.; Gouda, M.; Zhou, L.; Zhao, N.; Liang, N.; Niu, Z.; Hassanein, A.; Al-Rejaie, S.; et al. Using deep convolutional neural network for image-based diagnosis of nutrient deficiencies in plants grown in aquaponics. Chemosensors 2022, 10, 45. [Google Scholar] [CrossRef]
- Monkman, G.G.; Hyder, K.; Kaiser, M.J.; Vidal, F.P. Using machine vision to estimate fish length from images using regional convolutional neural networks. Methods Ecol. Evol. 2019, 10, 2045–2056. [Google Scholar] [CrossRef]
- Yadav, A.; Thakur, U.; Saxena, R.; Pal, V.; Bhateja, V.; Lin, J.C.W. AFD-Net: Apple Foliar Disease multi classification using deep learning on plant pathology dataset. Plant Soil 2022, 477, 595–611. [Google Scholar] [CrossRef]
- Álvarez-Ellacuría, A.; Palmer, M.; Catalán, I.A.; Lisani, J.L. Image-based, unsupervised estimation of fish size from commercial landings using deep learning. ICES J. Mar. Sci. 2020, 77, 1330–1339. [Google Scholar] [CrossRef]
- Shymkovych, V.; Telenyk, S.; Kravets, P. Hardware implementation of radial-basis neural networks with Gaussian activation functions on FPGA. Neural Comput. Appl. 2021, 33, 9467–9479. [Google Scholar] [CrossRef]
- Tiwari, V.; Khare, N. Hardware implementation of neural network with Sigmoidal activation functions using CORDIC. Microprocess. Microsyst. 2015, 39, 373–381. [Google Scholar] [CrossRef]

| Parameters | #Adds. | #Mults. | #Div. | #Exp. | #Cmp. | Flexibility | Sig-MSE | |
|---|---|---|---|---|---|---|---|---|
| Rectangular | 0 | 0 | 0 | 0 | 1 | None | High (cond.) | |
| Sigmoid’ | 2 | 1 | 1 | 1 | 0 | None | 0 | |
| Gaussian | 0 | 2 | 0 | 1 | 0 | None | N.A. | |
| LogSQNL’ [46] | 2 | 0 | 0 | 0 | 1 | None | 0.41% | |
| Zhang Sigmoid’ | 2 | 0 | 0 | 0 | 1 | None | 0.013% | |
| Proposed | General | 3 | 0 | 0 | 0 | 1 | Absolute | ≤0.013% |
| Parameter | Value |
|---|---|
| #TimeSteps | 1 |
| Learning Rate () | Default (0.001) |
| Batch Size | Default (32) |
| Optimizer | Adam |
| Loss Function | Cross Entropy |
| Leak () | 0 |
| Output Coding | One Hot |
| Test Samples | 20% |
| #Epochs | 47 |
| Accuracy | Application | |
|---|---|---|
| [6] | 94.44% | Fish disease detection |
| [23] | 67.08% | Fingerling weight estimation |
| [7] | 95% | Feeding intensity estimation |
| [52] | 96.50% | Plant detection |
| [53] | 97.80% | Fish length estimation |
| [54] | 92.60% | Plant detection |
| [54] | 98.70% | Plant detection |
| [55] | 87% | Fish size estimation |
| Prop. | 99.67% | Fish weight estimation |
| Prop. | 98.03% | Fish length estimation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddique, A.; Sun, J.; Hou, K.J.; Vai, M.I.; Pun, S.H.; Iqbal, M.A. SpikoPoniC: A Low-Cost Spiking Neuromorphic Computer for Smart Aquaponics. Agriculture 2023, 13, 2057. https://doi.org/10.3390/agriculture13112057
Siddique A, Sun J, Hou KJ, Vai MI, Pun SH, Iqbal MA. SpikoPoniC: A Low-Cost Spiking Neuromorphic Computer for Smart Aquaponics. Agriculture. 2023; 13(11):2057. https://doi.org/10.3390/agriculture13112057
Chicago/Turabian StyleSiddique, Ali, Jingqi Sun, Kung Jui Hou, Mang I. Vai, Sio Hang Pun, and Muhammad Azhar Iqbal. 2023. "SpikoPoniC: A Low-Cost Spiking Neuromorphic Computer for Smart Aquaponics" Agriculture 13, no. 11: 2057. https://doi.org/10.3390/agriculture13112057
APA StyleSiddique, A., Sun, J., Hou, K. J., Vai, M. I., Pun, S. H., & Iqbal, M. A. (2023). SpikoPoniC: A Low-Cost Spiking Neuromorphic Computer for Smart Aquaponics. Agriculture, 13(11), 2057. https://doi.org/10.3390/agriculture13112057









