Path Tracking Control of a Tractor on a Sloping Road with Steering Compensation
Abstract
:1. Introduction
1.1. Path Tracking Control for a Tractor
1.2. Path Tracking Control of Tractors on Sloping Roads
1.3. Main Contributions of This Paper
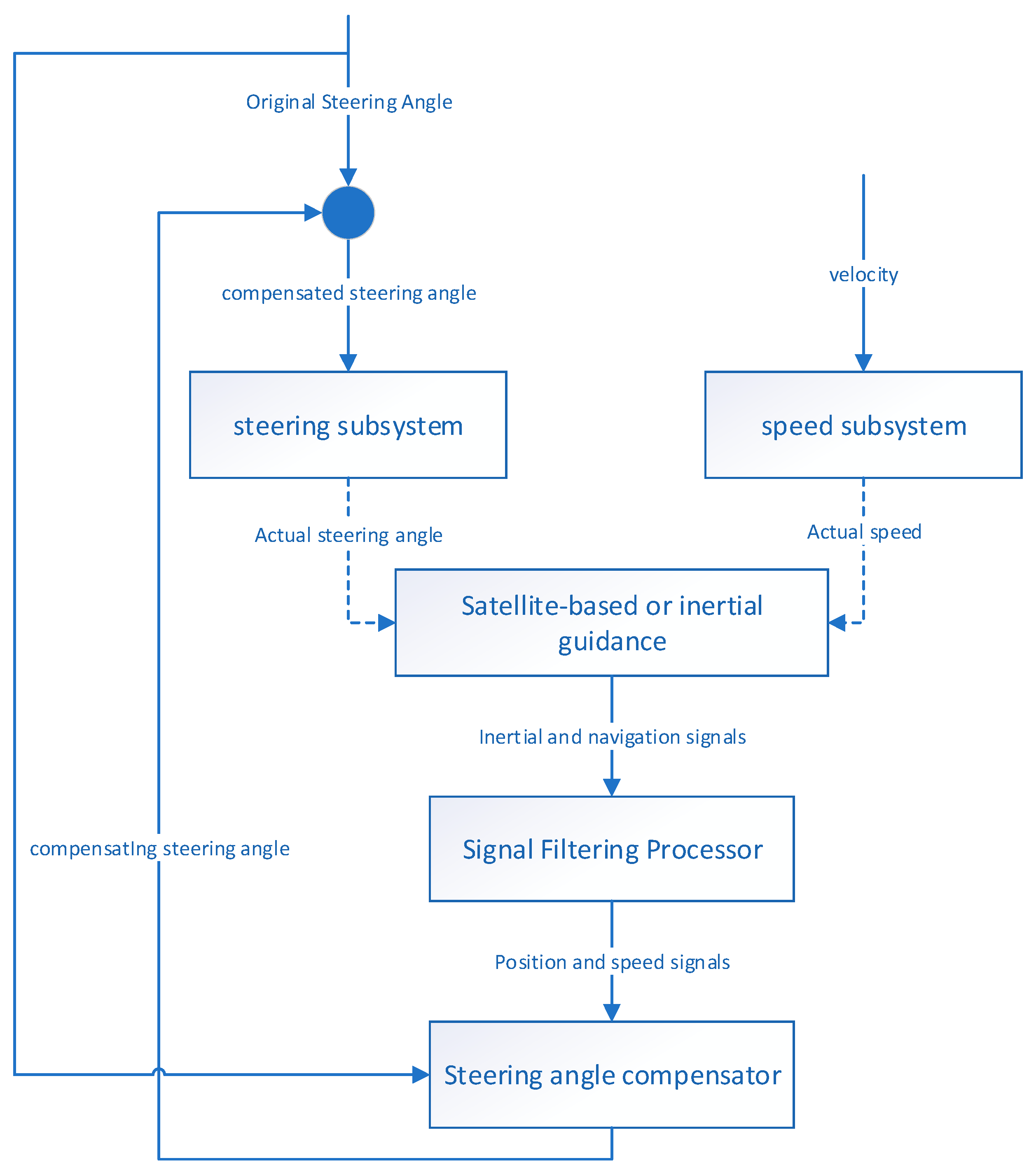
2. Design of Steering Angle Compensators
2.1. Force Analysis of a Tractor Traveling on Slopes
2.2. Automatic Correction Method for Compensation Coefficients
2.3. Steering Angle Compensation Algorithm
| Algorithm 1. Flowchart of the compensation algorithm |
| Input: proportion, integral, differential coefficient , and period . Initialized with . |
| Step 1: When , this step is skipped; otherwise, the kinematic model is used to calculate the “desired point” . Step 2: Position , original steering angle , and roll angle of the tractor are measured and obtained. Step 3: When , let the angle between the actual traveling route and the “desired route” be ; otherwise, based on position of the tractor, and the “desired point” , is calculated by Equation (5). Step 4: Based on and , the compensation coefficient is calculated by Equation (7). Step 5: Based on the roll angle and the compensation coefficient , the compensated steering angle is obtained. Step 6: The compensated steering angle is obtained and applied to the system based on summing the compensating angle with the original steering angle . Let . |
| Output: sum of the compensating angle and the original steering angle . |
2.4. Symbols Covered in This Section and Their Meanings
3. Model Predictive Control for Path Tracking of a Tractor
4. Model Predictive Controller with Steering Angle Compensator
| Algorithm 2. Flowchart of the MPC algorithm with a compensator. |
| Input: proportional, integral, and differential coefficients , real position, heading angle, speed and steering angle of the tractor roll angle reference position, heading angle, speed and steering angle series of the tractor , control and predictive horizon , weighting matrices and coefficient for objective function , upper and lower bounds for control increments and control variables as well as control period . Initialized with . |
| Step 1: Solve the optimization problem (18) to obtain the velocity control increments and the steering angle increments . And . Step 2: When , this step is skipped; otherwise, based on the previous position of the tractor as well as the velocity and steering angle outputted from MPC at the previous period , the kinematic model (4) is used to calculate the “desired point”. Step 3: When , set the angle between the actual traveling route and the “desired route” to zero, ; otherwise, let , and is calculated based on the vehicle position , , and the “desired point” using Equation (5). Step 4: Based on , and , the compensation coefficient is calculated by Equation (7) and . Step 5: Based on the roll angle and the compensation coefficient , the compensating steering angle is calculated using . Step 6: The compensating steering angle and the original steering angle are summed to obtain the compensated steering angle, which is the output and acts on the system with velocity . Let . |
| Output: compensated steering angle and velocity . |
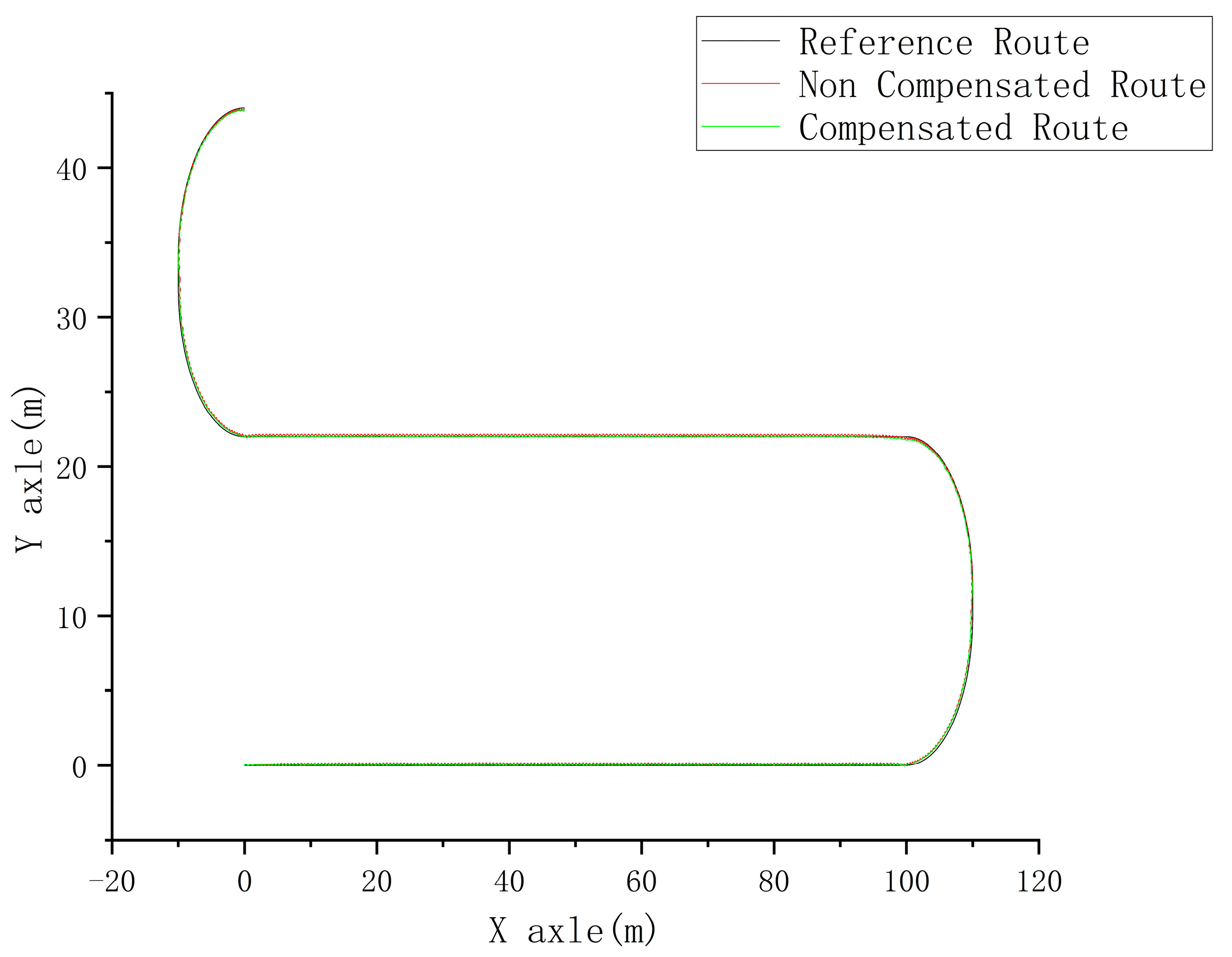
5. Simulation Results
5.1. Simulation Results of a Tractor Traveling in a Straight Line at Different Speeds
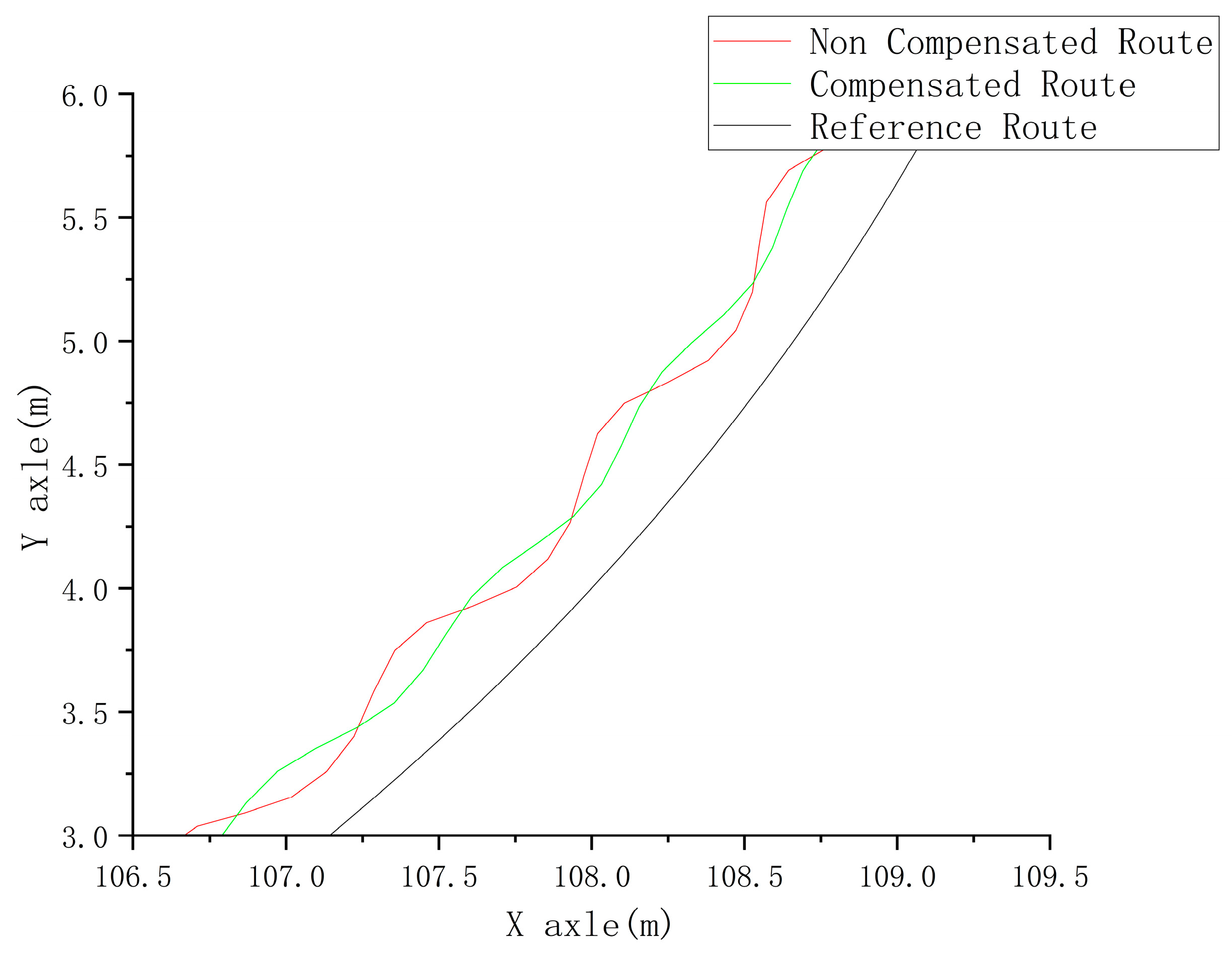
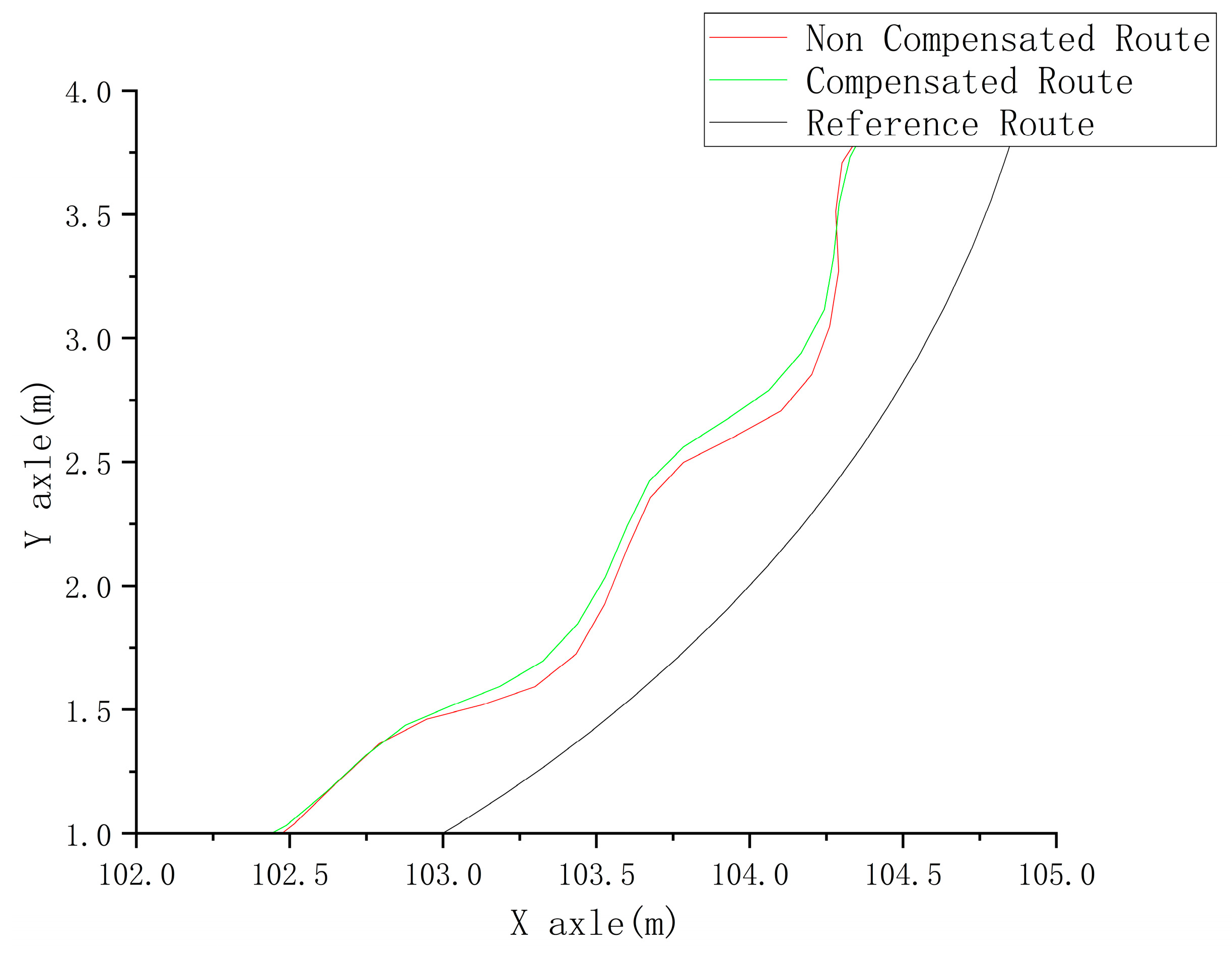
5.2. Simulation Results of a Tractor Traveling under Different Turning Radii
5.3. Simulation Results of a Tractor Traveling under Different Slope Gradients
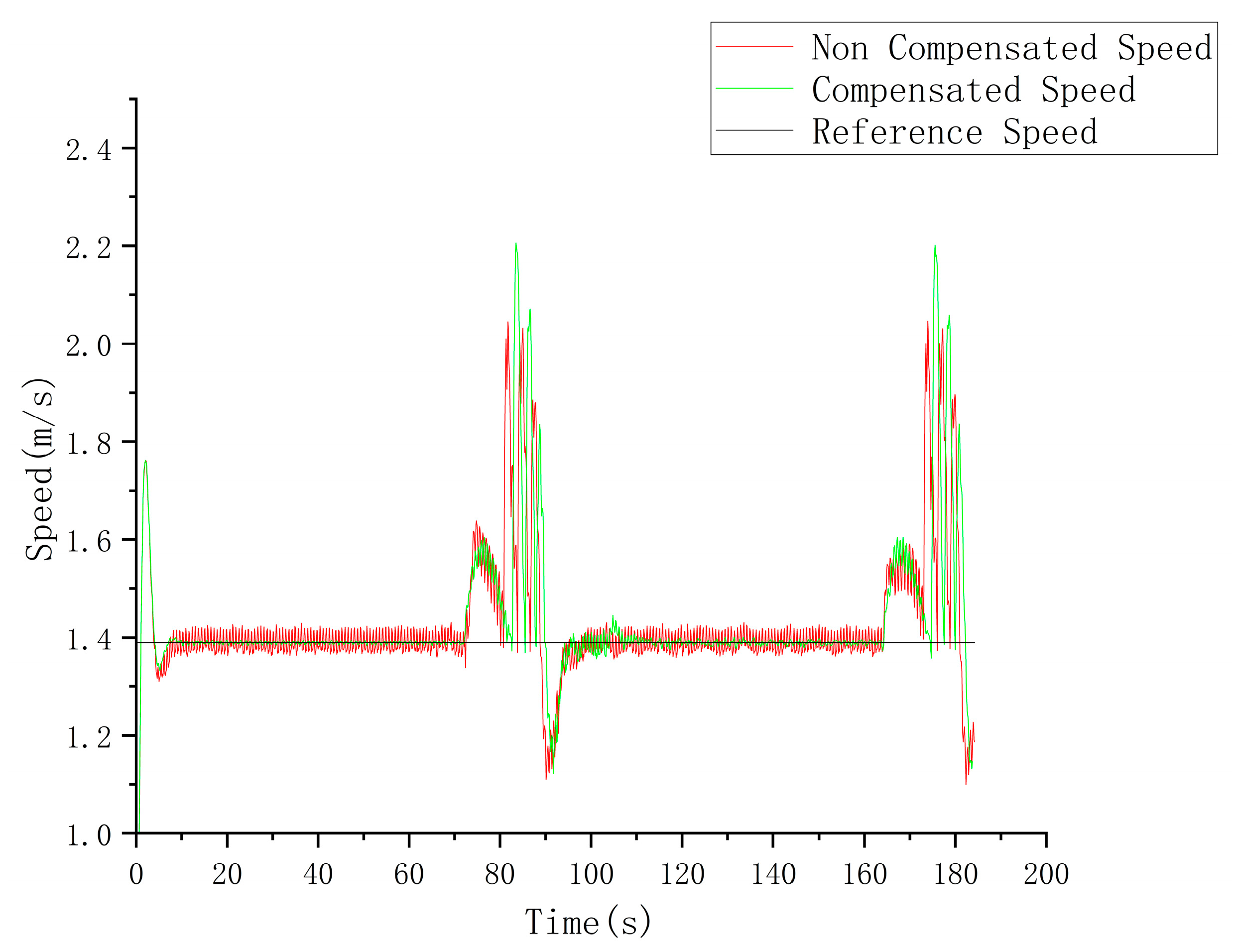
5.4. Effect of Compensator Incorporation on Speed and Steering Angle
6. Summary and Outlook
6.1. Summary
6.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Wang, G.; Luo, X.; Zhang, Z.; Gao, Y.; He, J.; Yue, B. Path tracking control method of agricultural machine navigation based on aiming pursuit model. Trans. Chin. Soc. Agric. Eng. 2019, 35, 11–19. [Google Scholar]
- Han, X.Z.; Kim, H.-J.; Moon, H.-C.; Kang, Y.-S.; Kim, J.-H.; Kim, Y.-J. Development of path generation algorithms for Korean auto-guidance tillage tractor. In Proceedings of the American Society of Agricultural and Biological Engineers Annual International Meeting, Dallas, TX, USA, 29 July–1 August 2012; pp. 4723–4732. [Google Scholar]
- Han, J.-H.; Park, C.-H.; Kwon, J.H.; Lee, J.; Kim, T.S.; Jang, Y.Y. Performance Evaluation of Autonomous Driving Control Algorithm for a Crawler-Type Agricultural Vehicle Based on Low-Cost Multi-Sensor Fusion Positioning. Appl. Sci. 2020, 10, 4667. [Google Scholar] [CrossRef]
- Han, X.Z.; Kim, H.J.; Kim, J.Y.; Yi, S.Y.; Moon, H.C.; Kim, J.H.; Kim, Y.J. Path-tracking simulation and field tests for an auto-guidance tillage tractor for a paddy field. Comput. Electron. Agric. 2015, 112, 161–171. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Guo, L.; Tong, J.; He, Y. Improved Pure Pursuit Algorithm for Rice Transplanter Path Tracking. Trans. Chin. Soc. Agric. Mach. 2018, 49, 21–26. [Google Scholar]
- Yao, L.; Pitla Santosh, K.; Yang, Z.; Xia, P.; Zhao, C. Path tracking of mobile platform in agricultural facilities based on ultra wideband wireless positioning. Trans. Chin. Soc. Agric. Eng. 2019, 35, 17–24. [Google Scholar]
- Zhang, W.; Ai, C.-S.; Zhang, Y.-Z.; Li, W.-X. Intelligent path tracking control for plant protection robot based on fuzzy PD. In Proceedings of the 2nd International Conference on Advanced Robotics and Mechatronics (ICARM), Hefei, China, 27–31August 2017; pp. 88–93. [Google Scholar]
- Taka, R.; Barawid, O.; Ish, K.; Noguch, N. Development of Crawler-Type Robot Tractor based on GPS and IMU. IFAC Proc. Vol. 2010, 43, 151–156. [Google Scholar] [CrossRef]
- Arvanitis, K.G.; Pasgianos, G.D.; Kalogeropoulos, G. Controller design for automatic guidance of agricultural vehicles at high field speeds. In Proceedings of the 15th Mediterranean Conference on Control and Automation, Athens, Greece, 27–29 June 2007; p. 1403. [Google Scholar]
- English, A.; Ross, P.; Ball, D.; Upcroft, B.; Corke, P. Learning Crop Models for Vision-Based Guidance of Agricultural Robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1158–1163. [Google Scholar]
- Hu, J.; Li, T. Cascaded navigation control for agricultural vehicles tracking straight paths. Int. J. Agric. Biol. Eng. 2014, 7, 36–44. [Google Scholar]
- Zhang, M.; Lu, X.; Tao, J.; Yin, W.; Feng, X. Design and Experiment of Automatic Guidance Control System in Agricultural Vehicle. Trans. Chin. Soc. Agric. Mach. 2016, 47, 42–47. [Google Scholar]
- Liu, Z.; Chen, Y.; Xi, Y.; Liu, G.; Zhang, M.; Liu, J. Machine Vision Based Path Tracking for Agricultural Vehicles. J. Agric. Mach. 2009, 40, 18–22. [Google Scholar]
- Ding, Y.; Zhan, P.; Zhou, Y.; Yang, J.; Zhang, W.; Zhu, K. Design and experiment of motion controller for information collection platform in field with Beidou positioning. Trans. Chin. Soc. Agric. Eng. 2017, 33, 178–185. [Google Scholar]
- Jeon, C.W.; Kim, H.-J.; Han, X.Z.; Kim, J.-H. Fuzzy logic-based steering controller for an autonomous head—Feed combine harvester. In Proceedings of the 2017 ASABE Annual International Meeting, Spokane, WA, USA, 16–19 July 2017. [Google Scholar]
- Meng, Q.; Qiu, R.; He, J.; Zhang, M.; Ma, X.; Liu, G. Development of agricultural implement system based on machine vision and fuzzy control. Comput. Electron. Agric. 2015, 112, 128–138. [Google Scholar] [CrossRef]
- Wang, F.J.; Hang, B. Path Tracking Control For a Four Wheel Differentially Steered Vision Robot. In Proceedings of the 11th International Conference on Electrical Machines and Systems, Huazhong Univ Sci & Technol, Wuhan, China, 17–20 October 2008; pp. 1608–1611. [Google Scholar]
- Wei, L.; Zhang, X.; Jia, Q.; Liu, Y. Automatic Navigation System Research for PZ60 Rice Planter. In Proceedings of the 8th IFIP WG 5.14 International Conference (CCTA), Beijing, China, 16–19 September 2014; pp. 653–661. [Google Scholar]
- Xie, Y.; Yin, J.; Yu, C.; He, K.; Hu, X.; Li, R. Obstacle Avoidance Navigation Algorithm and Analog Experiment for Wheeled AGV Running along Vineyard Ridge Road. Trans. Chin. Soc. Agric. Mach. 2018, 49, 13–22. [Google Scholar]
- Zhang, T.; Li, H.; Chen, D.; Huang, P.; Zhuang, X. Agricultural Vehicle Path Tracking Navigation System Based on Information Fusion of Multi-source Sensor. Trans. Chin. Soc. Agric. Mach. 2015, 46, 37–42. [Google Scholar]
- Zhou, J.; Cao, M.g.; Zhang, M.; Li, S. Remote Monitoring and Automatic Navigation System for Agricultural Vehicles Based on WLAN. In Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–17 October 2008; IEEE: Piscataway, NJ, USA; p. 2991. [Google Scholar]
- Zhou, J.; Wang, X.; Wang, X.; Liu, G.; Li, S. Autonomous Navigation System based on GPS for Agricultural Vehicles. In Proceedings of the International Forum on Mechanical and Material Engineering (IFMME 2013), Guangzhou, China, 13–14 June 2013; p. 1404. [Google Scholar]
- Zhou, J.; Zhang, M.; Cao, M.g.; Li, S.; Liu, B. Automatic navigation system for electric power vehicles with EPS. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference (VPPC), Piscataway, NJ, USA, 3–5 September 2008. [Google Scholar]
- Liu, Z.; Zhang, W.; Lu, Z.; Zheng, W.; Mu, G.; Cheng, X. Design on Trajectory Tracking Controller of Agricultural Vehicles under Disturbances. Trans. Chin. Soc. Agric. Mach. 2018, 49, 378–386. [Google Scholar]
- Mitsuhashi, T.; Chida, Y.; Tanemura, M. Autonomous Travel of Lettuce Harvester using Model Predictive Control. In Proceedings of the 6th International-Federation-of-Automatic-Control (IFAC) Conference on Sensing, Control and Automation Technologies for Agriculture (AGRICONTROL), Sydney, Australia, 4–6 December 2019; pp. 155–160. [Google Scholar]
- Peilin, X.; Yuan, W.; Guodong, Y.; Shuaipeng, L.; Yunyi, S. Path Tracking of Orchard Tractor Based on Linear Time-varying Model Predictive Control. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Piscataway, NJ, USA, 3–5 June 2019. [Google Scholar]
- Xu, G.; Chen, M.; He, X.; Pang, H.; Miao, H.; Cui, P.; Wang, W.; Diao, P. Path following control of tractor with an electro-hydraulic coupling steering system: Layered multi-loop robust control architecture. Biosyst. Eng. 2021, 209, 282–299. [Google Scholar] [CrossRef]
- Yao, Z.; Liu, G.; Zhang, D.; Shen, Y.; Wang, Z. Path Tracking Control for Four-Wheel-Independent-Driven Agricultural High Clearance Sprayer with New Front-Rear-Dual-Steering-Axle. In Proceedings of the 2020 Chinese Automation Congress, Shanghai, China, 6–8 November 2020. [Google Scholar]
- Yiheng, L.; Guodong, Y.; Qingfeng, L.; Li, W. Cross-line-Turn Path Tracking of Intelligent Agricultural Vehicle Based on MPC in Standard Orchard. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Piscataway, NJ, USA, 9–11 June 2018. [Google Scholar]
- Sun, J.; Liu, Z.; Yang, F.; Sun, Q.; Liu, Q.; Luo, P. A Review of Research on Agricultural Equipment and Key Technologies for Slope Operations in Hilly Mountainous Areas. J. Agric. Mach. 2023, 54, 1–18. [Google Scholar]
- Kraus, T.; Ferreau, H.J.; Kayacan, E.; Ramon, H.; De Baerdemaeker, J.; Diehl, M.; Saeys, W. Moving horizon estimation and nonlinear model predictive control for autonomous agricultural vehicles. Comput. Electron. Agric. 2013, 98, 25–33. [Google Scholar] [CrossRef]
- Backman, J.; Oksanen, T.; Visala, A. Nonlinear model predictive trajectory control in tractor-trailer system for parallel guidance in agricultural field operations. IFAC Proc. Vol. 2010, 43, 133–138. [Google Scholar] [CrossRef]
- Hill, A.; Laneurit, J.; Lenain, R.; Lucet, E. Online gain setting method for path tracking using CMA-ES: Application to off-road mobile robot control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Electr Network, 24 October–24 January 2020; IEEE: Piscataway, NJ, USA; pp. 7697–7702. [Google Scholar]
- Gong, J.; Xu, Y.J.W. Trajectory tracking control for a given trajectory. In Model Predictive Control for Driverless Vehicles; Beijing Institute of Technology Press: Beijing, China, 2014; pp. 74–81. [Google Scholar]
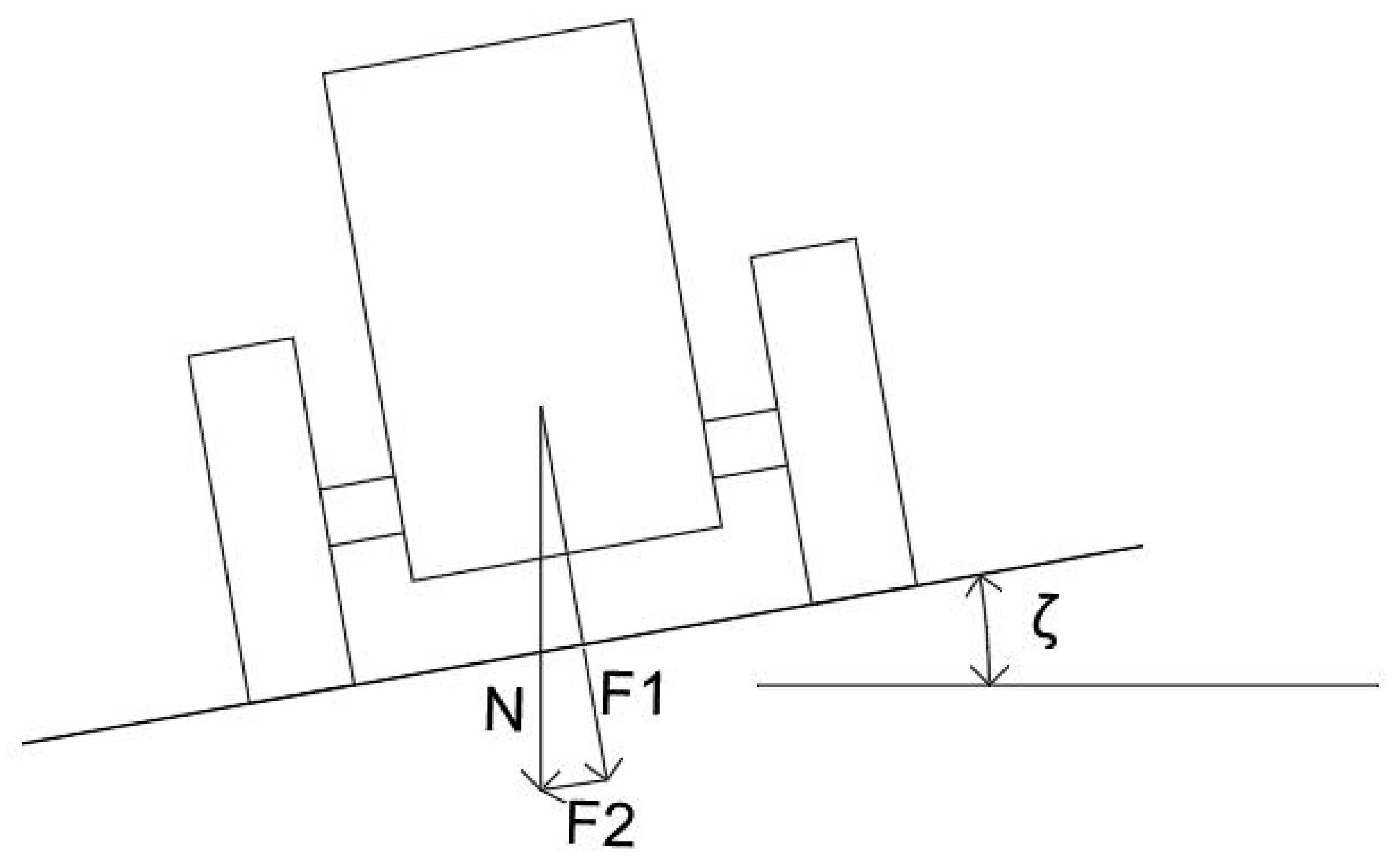
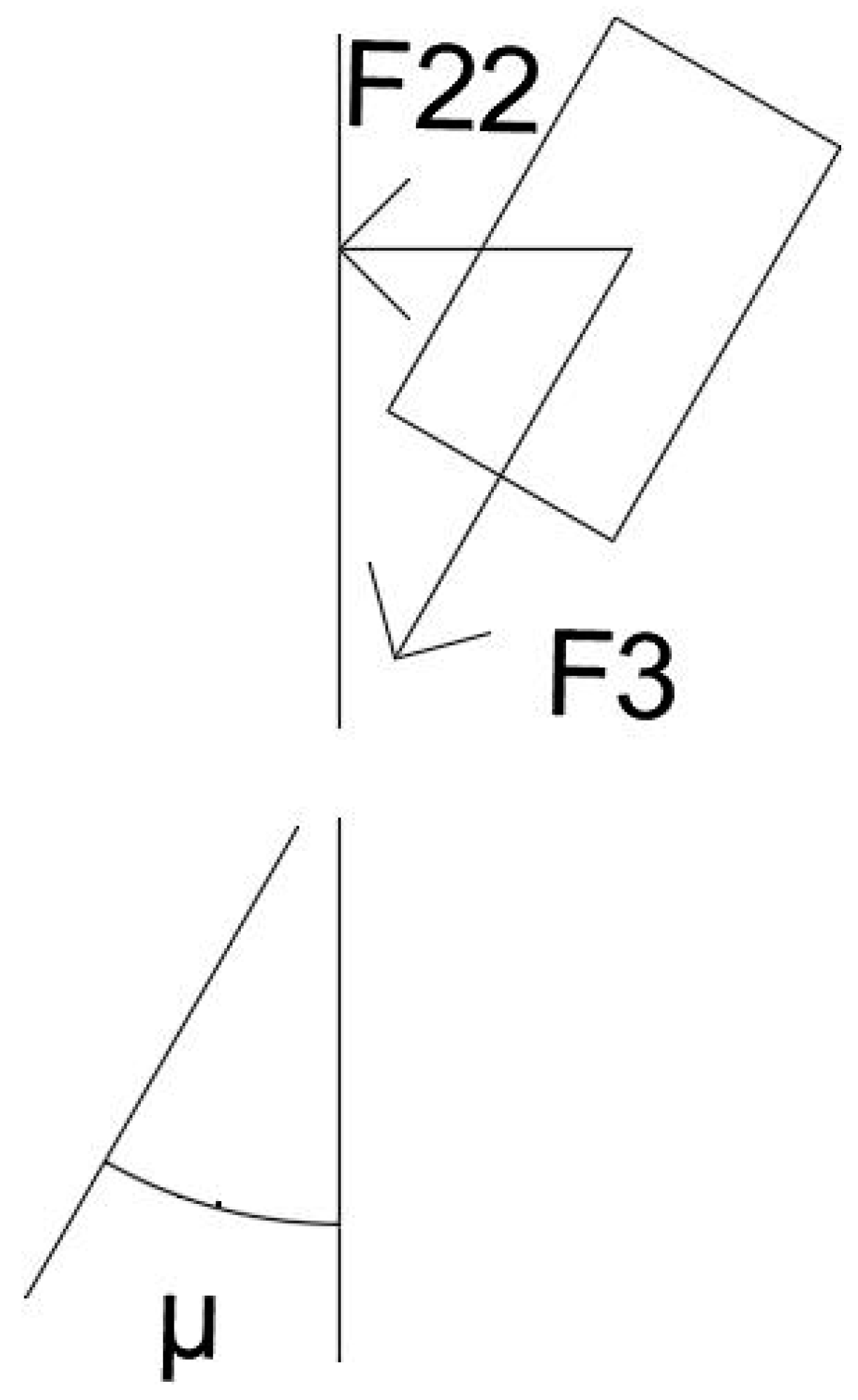











| Gravitational Force on the Tractor | Force on the Tractor Perpendicular to the Ground | Force on the Tractor Parallel to the Ground |
| Steering angle of a tire | Catch force of a tire | Component force of F3 perpendicular to the direction of travel of the tractor before steering |
| Angle made by the slope to the horizontal | K = N/F3 | Location of the tractor |
| ζ | ||
| Actual traveling path | A discrete time variable | Period |
| Velocity | Steering angle | “Desired path” |
| Control increment | Proportion coefficient | Integration coefficient |
| Differentiation coefficient | Difference between the target value and the actual output of a system | |
| Height of the Front Wheel Center | Height of the Rear Wheel Center | Length of the Wheelbase |
| 550 mm | 750 mm | 1050 mm |
| Longitudinal distance between the wheel centers | Sprung mass | Roll inertia |
| 2050 mm | 3000 kg | 377.1 |
| Pitch inertia | Yaw inertia | |
| 1765 | 1765 |
| Predictive Horizon | Control Horizon | Control Period T |
| 10 | 10 | 0.1 s |
| Weight of the speed increment | Weight of the steering angle increment | Weight of the route |
| 0.1 | Changes with experiments | 1 |
| The weight of the heading angle | The lower bound of the constraint of the speed increment | The upper bound of the constraint of the speed increment |
| 0.01 | −0.05 m/s | 0.05 m/s |
| The lower bound of the constraint of speed | The upper bound of the constraint of speed | The lower bound of the constraint of the steering angle increment |
| 0 m/s | 3 m/s | −0.1 rad |
| The upper bound of the constraint of the steering angle increment | The lower bound of the constraint of the steering angle | The upper bound of the constraint of the steering angle |
| 0.1 rad | −0.5 rad | 0.5 rad |
| Proportion Coefficient | Integration Coefficient | Differentiation Coefficient |
|---|---|---|
| Changes with experiments | Changes with experiments | 0.02 |
| 3 km/h | 5 km/h | 7 km/h | 10 km/h | |
|---|---|---|---|---|
| Weight of the steering angle increment | 0.5 | 1.1 | 1.3 | 1 |
| Proportion coefficient | 0.1 | 0.1 | 0.1 | 0.1 |
| Integration coefficient | 0.001 | 0.001 | 0.001 | 0.002 |
| 3 km/h | 5 km/h | 7 km/h | 10 km/h | |
|---|---|---|---|---|
| Average distance (with compensator) | 0.00092 m | 0.008144 m | −0.00492 m | 0.003037 m |
| Average absolute value of the distance(with compensator) | 0.025 m | 0.017 m | 0.027 m | 0.053 m |
| Average distance (without compensator) | 0.050191 m | 0.054592 m | 0.048394 m | 0.074208 m |
| Average absolute value of the distance(without compensator) | 0.052 m | 0.047 m | 0.042 m | 0.053 m |
| 10 m | 7 m | 5 m | |
|---|---|---|---|
| Weight of the steering angle increment | 1.1 | 1.1 | 0.6 |
| Proportion coefficient | 0.1 | 0.1 | 0.4 |
| Integration coefficient | 0.001 | 0.001 | 0.001 |
| 10 m | 7 m | 5 m | |
|---|---|---|---|
| Average distance (with compensator) | 0.221492 m | 0.197354 m | 0.353256 m |
| Average absolute value of the distance(with compensator) | 0.041 m | 0.041 m | 0.059 m |
| Average distance (without compensator) | 0.211663 m | 0.282611 m | 0.322454 m |
| Average absolute value of the distance(without compensator) | 0.062 m | 0.059 m | 0.060 m |
| 0.11 (6.28°) | 0.22 (12.42°) | 0.33 (18.27°) | |
|---|---|---|---|
| Weight of the steering angle increment | 0.5 | 0.5 | 0.4 |
| Proportion coefficient | 0.1 | 0.1 | 0.1 |
| Integration coefficient | 0.0005 | 0.001 | 0.001 |
| 0.11 (6.28°) | 0.22 (12.42°) | 0.33 (18.27°) | |
|---|---|---|---|
| Average distance (with compensator) | −0.00465 m | 0.000982 m | 0.003815 m |
| Average absolute value of the distance(with compensator) | 0.028 m | 0.025 m | 0.018 m |
| Average distance (without compensator) | 0.034339 m | 0.050191 m | 0.074009 m |
| Average absolute value of the distance(without compensator) | 0.066 m | 0.053 m | 0.041 m |
| Weight of Steering Angle Increment | Proportion Coefficient | Integration Coefficient |
|---|---|---|
| 1.1 | 0.1 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.; Fu, Q.; Tang, R.; Du, J.; Xu, L. Path Tracking Control of a Tractor on a Sloping Road with Steering Compensation. Agriculture 2023, 13, 2160. https://doi.org/10.3390/agriculture13112160
Ou J, Fu Q, Tang R, Du J, Xu L. Path Tracking Control of a Tractor on a Sloping Road with Steering Compensation. Agriculture. 2023; 13(11):2160. https://doi.org/10.3390/agriculture13112160
Chicago/Turabian StyleOu, Jieyong, Qiang Fu, Rui Tang, Jianwei Du, and Lihong Xu. 2023. "Path Tracking Control of a Tractor on a Sloping Road with Steering Compensation" Agriculture 13, no. 11: 2160. https://doi.org/10.3390/agriculture13112160
APA StyleOu, J., Fu, Q., Tang, R., Du, J., & Xu, L. (2023). Path Tracking Control of a Tractor on a Sloping Road with Steering Compensation. Agriculture, 13(11), 2160. https://doi.org/10.3390/agriculture13112160






