Research on Polygon Pest-Infected Leaf Region Detection Based on YOLOv8
Abstract
:1. Introduction
- We have constructed a PolyCorn dataset of corn pest-infected regions annotated with polygons, providing a dataset for detecting polygon pest-infected regions domain.
- We have proposed a novel polygon-based object detection model that effectively balances detection accuracy and speed. This model outperforms other baseline models in detecting corn pest-infected regions.
2. Related Work
2.1. Two-Stage Detectors
2.2. Single-Stage Detectors
2.3. Polygon Object Detectors
2.4. Image Classification and Instance Segmentation Detectors
2.5. Our Work
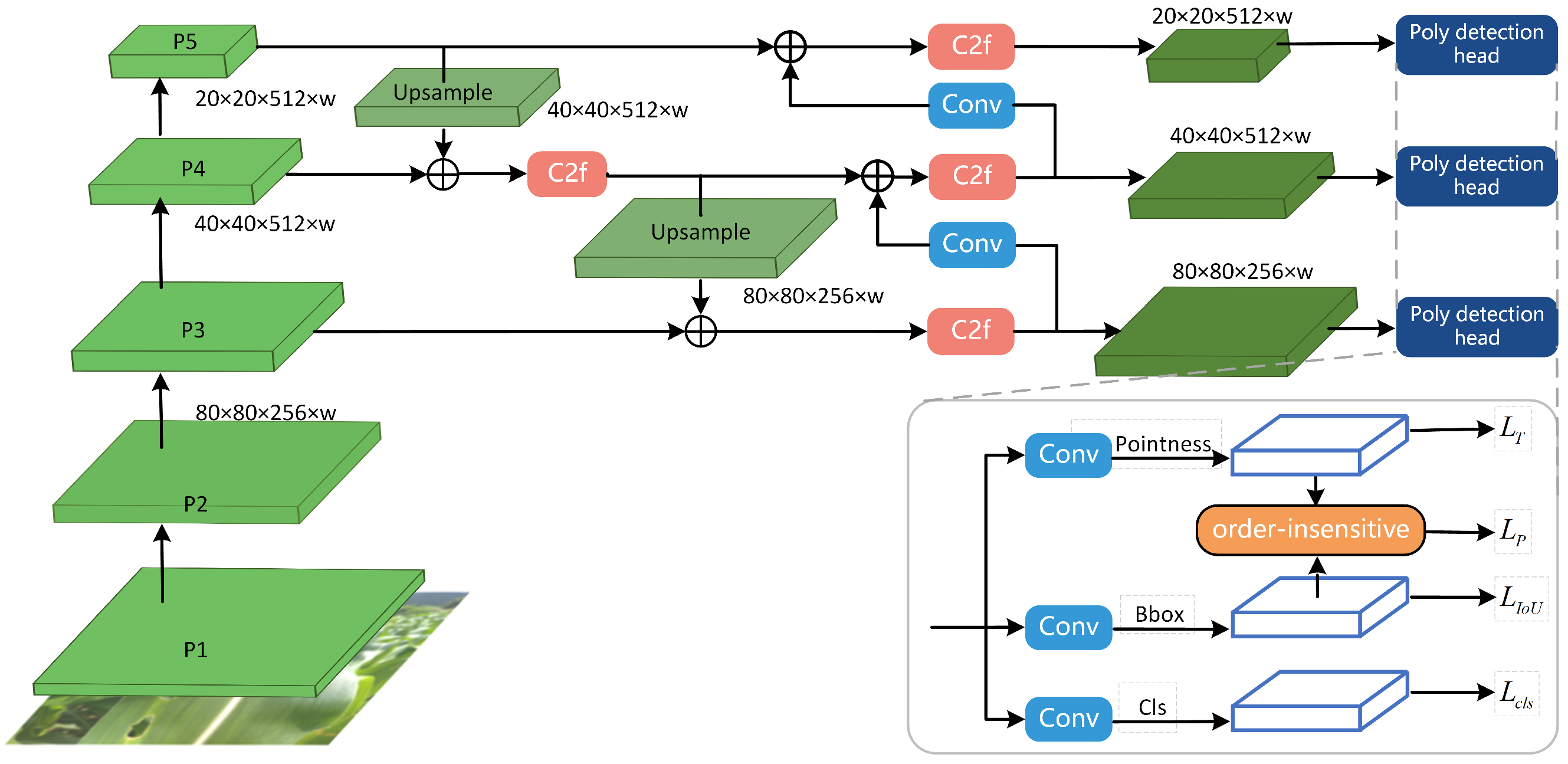
3. Model
3.1. Data Loading
3.2. Backbone Network
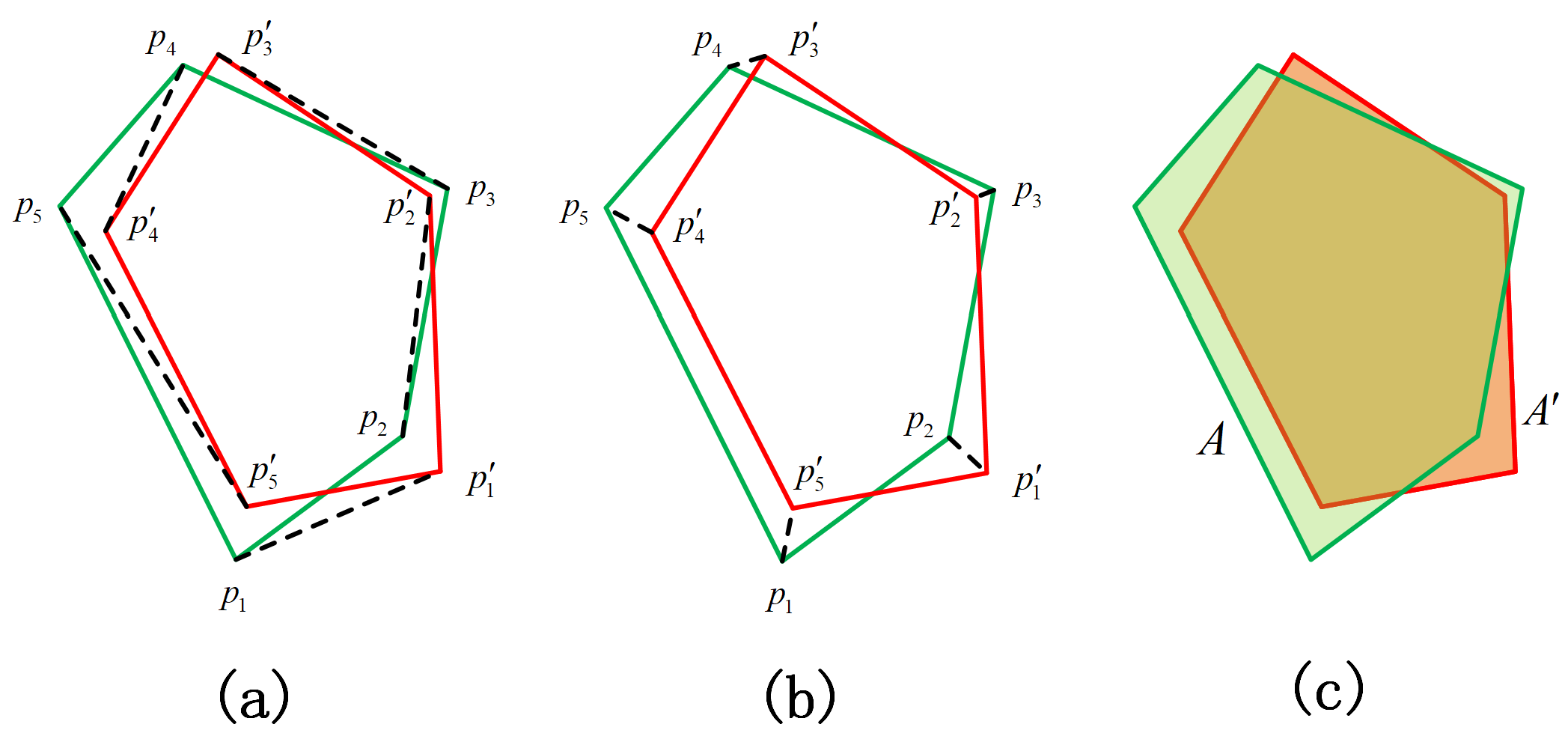
3.3. Improved Polygon Detection Head
| Algorithm 1 Order-insensitive algorithm |
|
4. Experiments
4.1. Data Processing
4.2. Evaluation Metrics
4.3. Parameter Settings
4.4. Baseline Models
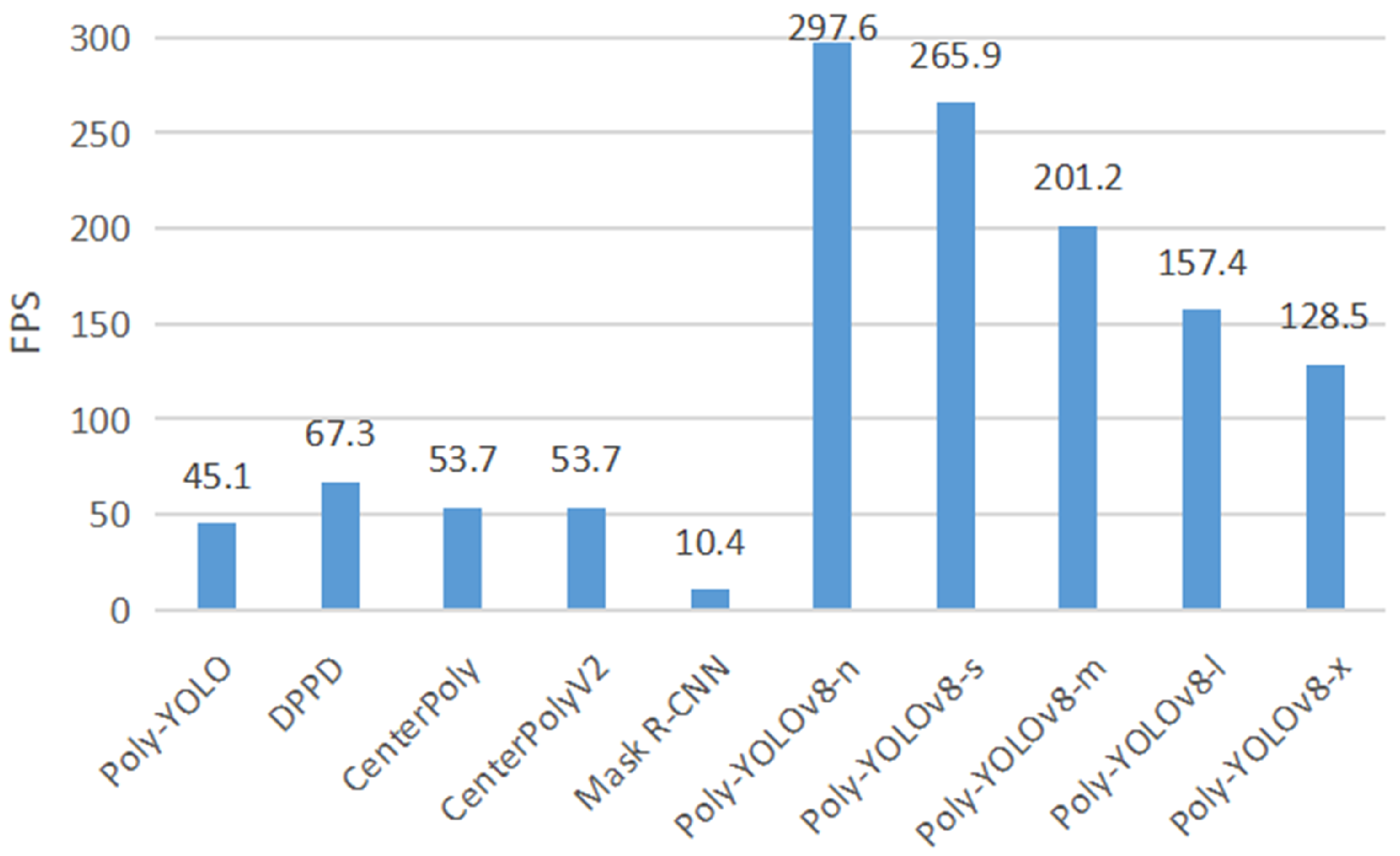
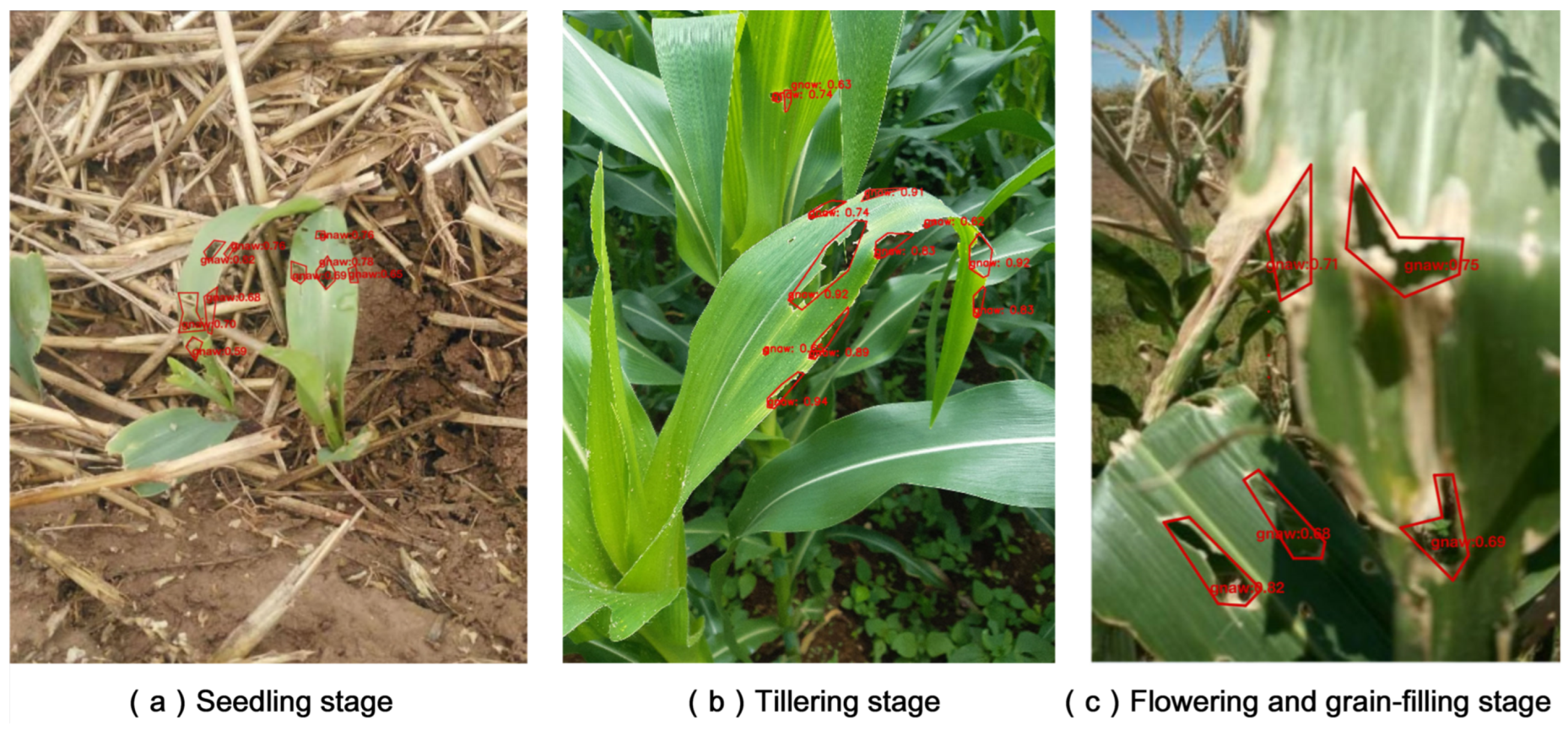
4.5. Comparative Experiment Analysis
- As seen in Table 3, the detection performance of the model gradually increased from Poly-YOLO to Poly-YOLOv8-x. Compared with Mask R-CNN, the various metrics of Poly-YOLOv8-x were improved by 5.54%, 2.67%, 1.57%, and 3.93%, respectively, reflecting that the Poly-YOLOv8-x model is more powerful in detecting pest-infected regions. It suggested that the Poly-YOLOv8-x can better extract the shape features of those regions than the baseline models.
- Compared with traditional polygon object detection models (Poly-YOLO, DPPD, CenterPoly, CenterPolyV2), Poly-YOLOv8-x had an advantage in accuracy, which suggested that the new polygon detection head was effective in predicting pest-infected regions. Compared to CenterPoly and CenterPolyV2, the improved loss calculation method enhanced the model’s ability to learn the shape features of pest-infected regions rather than only fitting the order coordinates of region vertices. Overall, the evaluation metrics of the Poly-YOLOv8-x were higher than the baseline models. The improved Poly-YOLOv8-x had more robust polygon object detection abilities, achieving higher and more stable detection performance in complex scenarios.
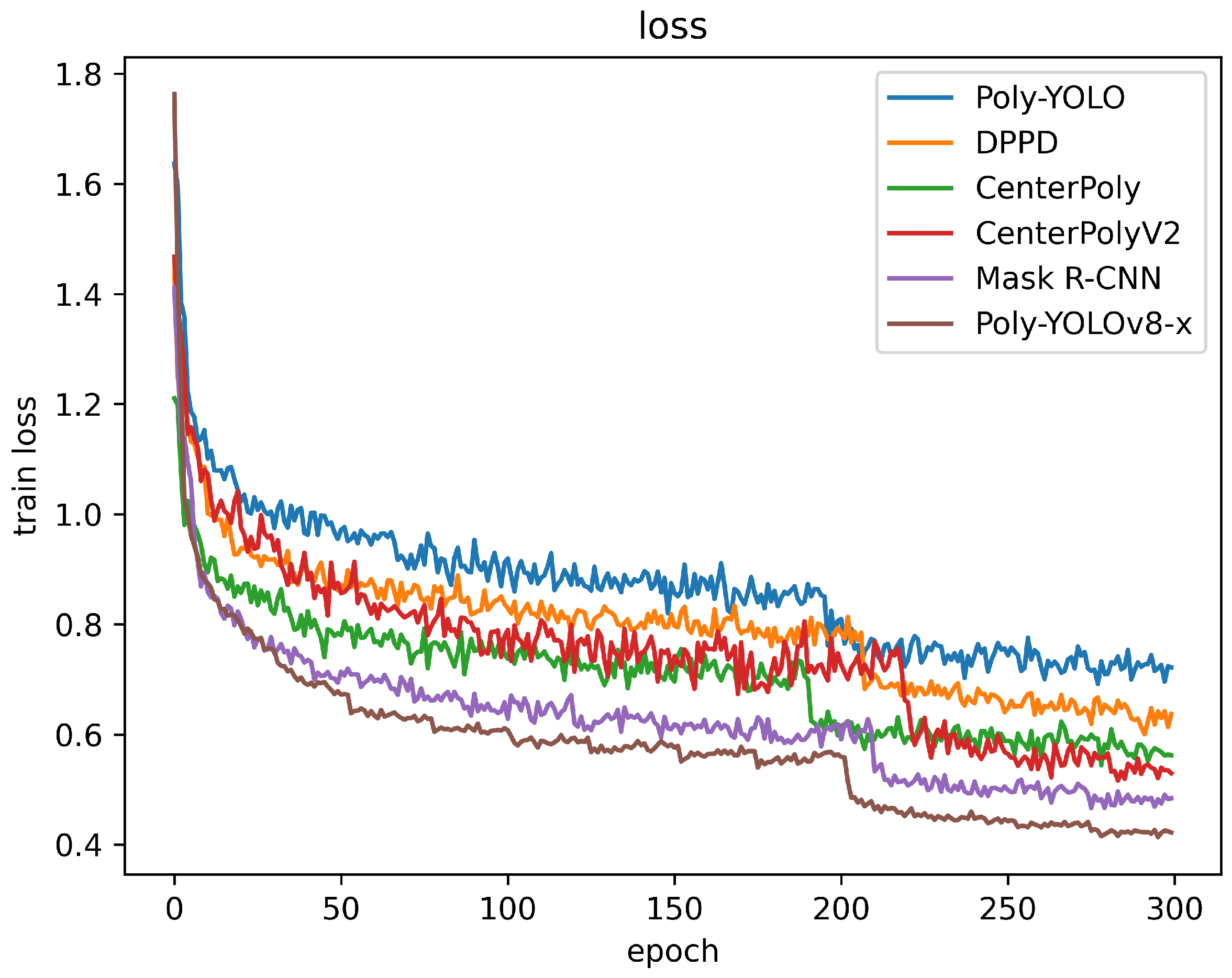
- As can be seen from Figure 5, the improved Poly-YOLOv8-x fluctuates less when converging. This indicated that our model had better robustness and faster convergence. Simultaneously, our improved loss calculation method effectively focuses on the shape features of pest-infected regions. In summary, compared with baseline models, the Poly-YOLOv8-x had better detection performance on the corn leaves.
4.6. Ablation Experiment
4.7. Overall Experimental Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zaidi, S.S.A.; Ansari, M.S.; Aslam, A.; Kanwal, N.; Asghar, M.; Lee, B. A survey of modern deep learning based object detection models. Digit. Signal Process. 2022, 126, 103514. [Google Scholar] [CrossRef]
- Daneshwari, A.N.; Basavaraju, D.R. Corn leaf image classification based on machine learning techniques for accurate leaf disease detection. Int. J. Electr. Comput. Eng. 2022, 12, 2509. [Google Scholar]
- Gu, W.; Bai, S.; Kong, L. A review on 2D instance segmentation based on deep neural networks. Image Vis. Comput. 2022, 120, 104401. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Diwan, T.; Anirudh, G.; Tembhurne, J.V. Object detection using YOLO: Challenges, architectural successors, datasets and applications. Multimed. Tools Appl. 2023, 82, 9243–9275. [Google Scholar] [CrossRef] [PubMed]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Jiao, L.; Xie, C.; Chen, P.; Du, J.; Li, R.; Zhang, J. Adaptive feature fusion pyramid network for multi-classes agricultural pest detection. Comput. Electron. Agric. 2022, 195, 106827. [Google Scholar] [CrossRef]
- Rahman, C.R.; Arko, P.S.; Ali, M.E.; Khan, M.A.I.; Apon, S.H.; Nowrin, F.; Wasif, A. Identification and recognition of rice diseases and pests using convolutional neural networks. Biosyst. Eng. 2020, 194, 112–120. [Google Scholar] [CrossRef]
- Selvaraj, M.G.; Vergara, A.; Ruiz, H.; Safari, N.; Elayabalan, S.; Ocimati, W.; Blomme, G. AI-powered banana diseases and pest detection. Plant Methods 2019, 15, 1–11. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, F.; Sun, M.; Qu, J.; Xue, J. Identification of tomato disease types and detection of infected areas based on deep convolutional neural networks and object detection techniques. Comput. Intell. Neurosci. 2019, 2019, 9142753. [Google Scholar] [CrossRef]
- Xie, X.; Ma, Y.; Liu, B.; He, J.; Li, S.; Wang, H. A deep-learning-based real-time detector for grape leaf diseases using improved convolutional neural networks. Front. Plant Sci. 2020, 11, 751. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Liu, J.; Wang, X. Tomato diseases and pests detection based on improved Yolo V3 convolutional neural network. Front. Plant Sci. 2020, 11, 898. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X. Early recognition of tomato gray leaf spot disease based on MobileNetv2-YOLOv3 model. Plant Methods 2020, 16, 1–16. [Google Scholar] [CrossRef]
- Ganesan, G.; Chinnappan, J. Hybridization of ResNet with YOLO classifier for automated paddy leaf disease recognition: An optimized model. J. Field Robot. 2022, 39, 1085–1109. [Google Scholar] [CrossRef]
- Leng, S.; Musha, Y.; Yang, Y.; Feng, G. CEMLB-YOLO: Efficient Detection Model of Maize Leaf Blight in Complex Field Environments. Appl. Sci. 2023, 13, 9285. [Google Scholar] [CrossRef]
- Li, J.; Qiao, Y.; Liu, S.; Zhang, J.; Yang, Z.; Wang, M. An improved YOLOv5-based vegetable disease detection method. Comput. Electron. Agric. 2022, 202, 107345. [Google Scholar] [CrossRef]
- Qi, J.; Liu, X.; Liu, K.; Xu, F.; Guo, H.; Tian, X.; Li, M.; Bao, Z.; Li, Y. An improved YOLOv5 model based on visual attention mechanism: Application to recognition of tomato virus disease. Comput. Electron. Agric. 2022, 194, 106780. [Google Scholar] [CrossRef]
- Khan, F.; Zafar, N.; Tahir, M.N.; Aqib, M.; Waheed, H.; Haroon, Z. A mobile-based system for maize plant leaf disease detection and classification using deep learning. Front. Plant Sci. 2023, 14, 1079366. [Google Scholar] [CrossRef]
- Hurtik, P.; Molek, V.; Hula, J.; Vajgl, M.; Vlasanek, P.; Nejezchleba, T. Poly-YOLO: Higher speed, more precise detection and instance segmentation for YOLOv3. Neural Comput. Appl. 2022, 34, 8275–8290. [Google Scholar] [CrossRef]
- Perreault, H.; Bilodeau, G.A.; Saunier, N.; Héritier, M. Centerpoly: Real-time instance segmentation using bounding polygons. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2982–2991. [Google Scholar]
- Jodogne-Del Litto, K.; Bilodeau, G.A. Real-time instance segmentation with polygons using an Intersection-over-Union loss. arXiv 2023, arXiv:2305.05490. [Google Scholar]
- Zheng, Y.; Andrienko, O.; Zhao, Y.; Park, M.; Pham, T. DPPD: Deformable Polar Polygon Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 78–87. [Google Scholar]
- Padilla, D.A.; Pajes, R.A.I.; De Guzman, J.T. Detection of corn leaf diseases using convolutional neural network with openmp implementation. In Proceedings of the 2020 IEEE 12th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Manila, Philippines, 3–7 December 2020; pp. 1–6. [Google Scholar]
- Singh, U.P.; Chouhan, S.S.; Jain, S.; Jain, S. Multilayer convolution neural network for the classification of mango leaves infected by anthracnose disease. IEEE Access 2019, 7, 43721–43729. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, J.; Li, Z.; Qi, F. Grape disease image classification based on lightweight convolution neural networks and channelwise attention. Comput. Electron. Agric. 2020, 178, 105735. [Google Scholar] [CrossRef]
- Stewart, E.L.; Wiesner-Hanks, T.; Kaczmar, N.; DeChant, C.; Wu, H.; Lipson, H.; Nelson, R.J.; Gore, M.A. Quantitative phenotyping of northern leaf blight in UAV images using deep learning. Remote Sens. 2019, 11, 2209. [Google Scholar] [CrossRef]
- Lin, K.; Gong, L.; Huang, Y.; Liu, C.; Pan, J. Deep learning-based segmentation and quantification of cucumber powdery mildew using convolutional neural network. Front. Plant Sci. 2019, 10, 155. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, Y.; Dang, L.M.; Moon, H. An efficient attention module for instance segmentation network in pest monitoring. Comput. Electron. Agric. 2022, 195, 106853. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Liu, J.; Wang, L.; Zhang, J.; Fan, X. The detection method of potato foliage diseases in complex background based on instance segmentation and semantic segmentation. Front. Plant Sci. 2022, 13, 899754. [Google Scholar] [CrossRef]
- Da Silva Vieira, G.; Rocha, B.M.; Fonseca, A.U.; de Sousa, N.M.; Ferreira, J.C.; Cabacinha, C.D.; Soares, F. Automatic detection of insect predation through the segmentation of damaged leaves. Smart Agric. Technol. 2022, 2, 100056. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part V 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Varma, G.; Subramanian, A.; Namboodiri, A.; Chandraker, M.; Jawahar, C. IDD: A dataset for exploring problems of autonomous navigation in unconstrained environments. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; pp. 1743–1751. [Google Scholar]




| Parameters | Setup |
|---|---|
| Epochs | 300 |
| Batch Size | 16 |
| Image Size | |
| Optimizer | SGD |
| Momentum | 0.937 |
| Weight Decay | |
| Initial Learning Rate | |
| Final Learning Rate | |
| Save Period | 10 |
| Image Scale | 0.5 |
| Image Flip Left-Right | 0.5 |
| Mosaic | 1.0 |
| Image Translation | 0.1 |
| NMS IoU | 0.7 |
| w |
| Ref. | Models | Datasets |
| [9] | Mask R-CNN | COCO [35] |
| [23] | Poly-YOLO | Simulator, Cityscapes [36], and IDD [37] |
| [26] | DPPD | Cityscapes and Crosswalk |
| [24] | CenterPoly | Cityscapes, KITTI, and IDD |
| [25] | CenterPolyV2 | Cityscapes and IDD |
| Ref. | Contributions | Remarks |
| [9] | Using mask mechanism | Slow training and detection |
| [23] | Using YOLOv3 for detection | Poor performance and slow detection |
| [26] | Using the deformable polygon detection | Detection with a fixed number of vertices |
| [24] | Using central polygon method | Relies on a pre-defined center key point |
| [25] | Using the improved regression loss | Overfitting the coordinate order loss |
| Model | P | R | ||
|---|---|---|---|---|
| Poly-YOLO | 60.64% | 52.36% | 54.46% | 31.85% |
| DPPD | 64.23% | 56.54% | 60.38% | 38.46% |
| CenterPoly | 66.67% | 58.61% | 62.35% | 40.58% |
| CenterPolyV2 | 67.57% | 59.36% | 63.82% | 42.64% |
| Mask R-CNN | 69.34% | 62.16% | 65.69% | 44.21% |
| Poly-YOLOv8-x | 74.88% | 64.83% | 67.26% | 48.14% |
| Model | Parameters | ||
|---|---|---|---|
| Poly-YOLOv8-n | 60.74% | 37.90% | 3.25 M |
| Poly-YOLOv8-s | 64.36% | 42.15% | 11.78 M |
| Poly-YOLOv8-m | 66.02% | 45.76% | 27.22 M |
| Poly-YOLOv8-l | 66.75% | 46.43% | 45.91 M |
| Poly-YOLOv8-x | 67.26% | 48.14% | 71.72 M |
| Model | Order-Insensitive Loss | ||
|---|---|---|---|
| Poly-YOLOv8-n | ✘ | 59.96% | 36.04% |
| Poly-YOLOv8-s | ✘ | 63.89% | 40.48% |
| Poly-YOLOv8-m | ✘ | 65.61% | 43.91% |
| Poly-YOLOv8-l | ✘ | 65.93% | 44.42% |
| Poly-YOLOv8-x | ✘ | 66.48% | 46.24% |
| Poly-YOLOv8-n | ✔ | 60.74% | 37.90% |
| Poly-YOLOv8-s | ✔ | 64.36% | 42.15% |
| Poly-YOLOv8-m | ✔ | 66.02% | 45.76% |
| Poly-YOLOv8-l | ✔ | 66.75% | 46.43% |
| Poly-YOLOv8-x | ✔ | 67.26% | 48.14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Hao, F.; Ma, D. Research on Polygon Pest-Infected Leaf Region Detection Based on YOLOv8. Agriculture 2023, 13, 2253. https://doi.org/10.3390/agriculture13122253
Zhu R, Hao F, Ma D. Research on Polygon Pest-Infected Leaf Region Detection Based on YOLOv8. Agriculture. 2023; 13(12):2253. https://doi.org/10.3390/agriculture13122253
Chicago/Turabian StyleZhu, Ruixue, Fengqi Hao, and Dexin Ma. 2023. "Research on Polygon Pest-Infected Leaf Region Detection Based on YOLOv8" Agriculture 13, no. 12: 2253. https://doi.org/10.3390/agriculture13122253
APA StyleZhu, R., Hao, F., & Ma, D. (2023). Research on Polygon Pest-Infected Leaf Region Detection Based on YOLOv8. Agriculture, 13(12), 2253. https://doi.org/10.3390/agriculture13122253






