A New Method for Estimating Irrigation Water Use via Soil Moisture
Abstract
1. Introduction
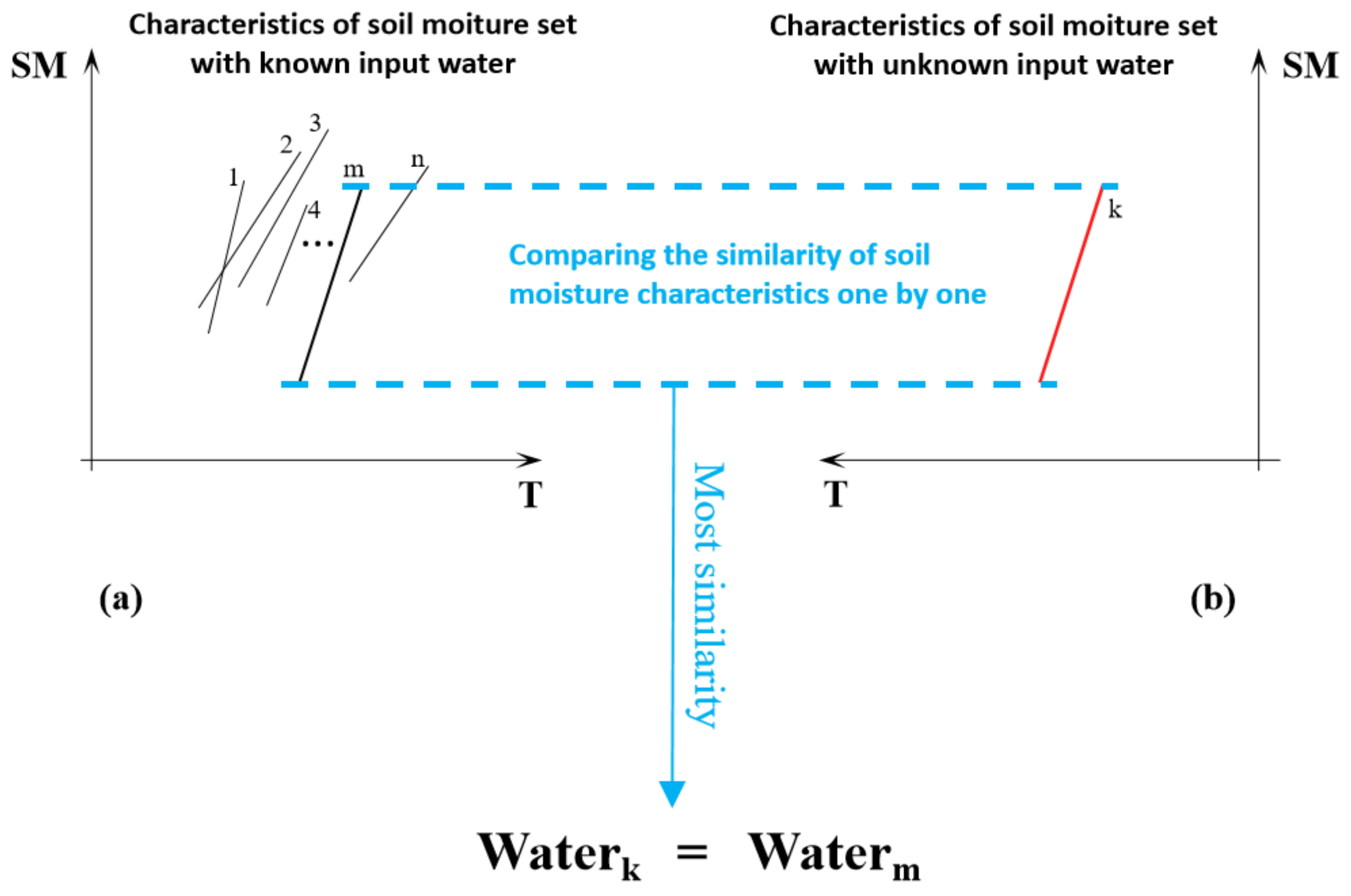
2. Basic Idea
3. Study Area and Data Sets
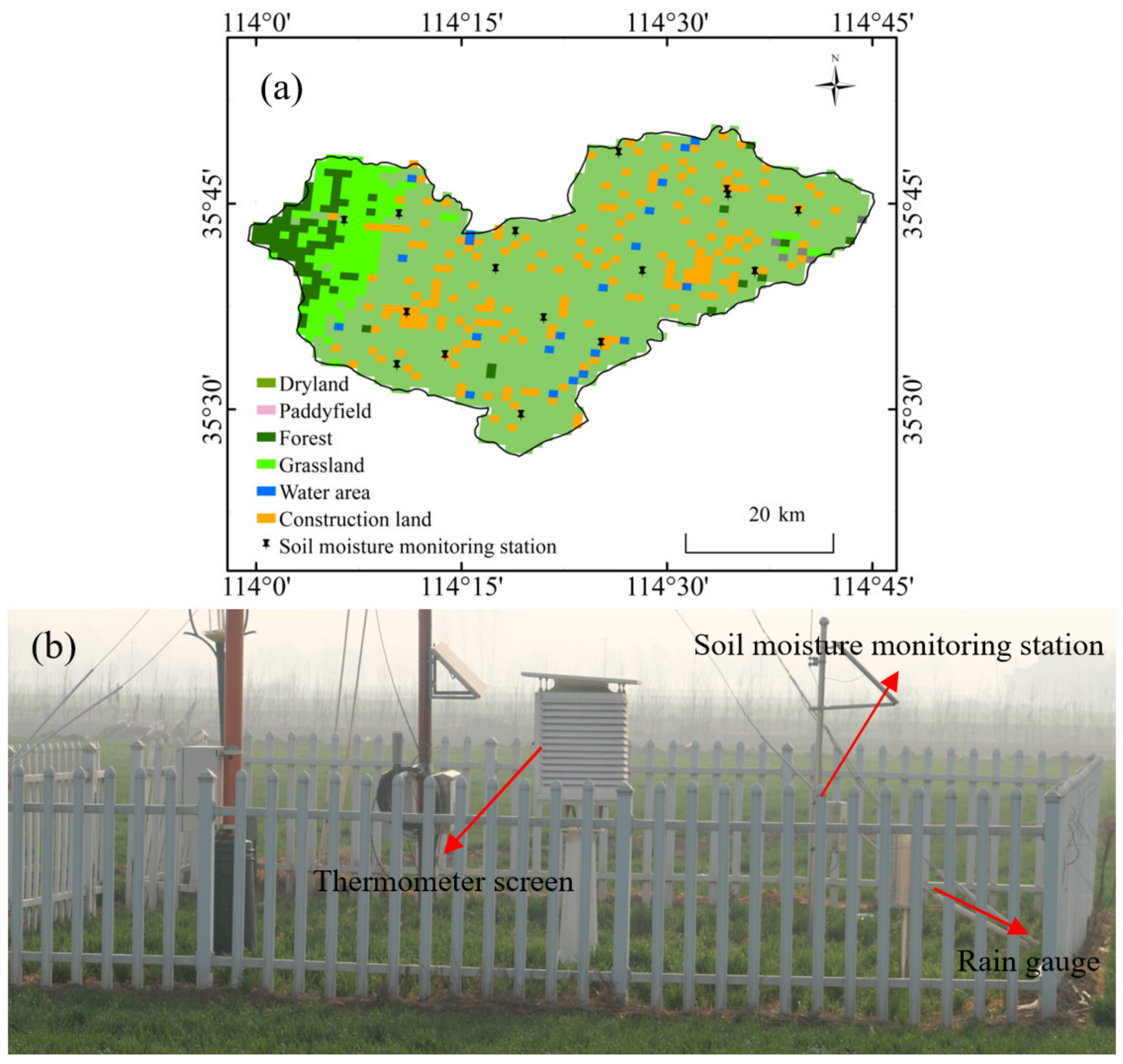
3.1. Study Area
3.2. Data Set
- (1)
- In situ soil moisture and precipitation data
- (2)
- Records of irrigation water use
- (3)
- Auxiliary data set
4. Methods
4.1. Calculation of Soil Moisture Similarity
4.1.1. Construction of the Samples of Soil Water Characteristics
4.1.2. Calculation of the Similarity of Soil Moisture Characteristics
4.2. Contrast Models
4.2.1. Linear Model
4.2.2. Logarithmic Model
4.2.3. Soil Water Balance Model
5. Results
5.1. Parameters of the Proposed Model
5.2. Parameters of the Contrast Models
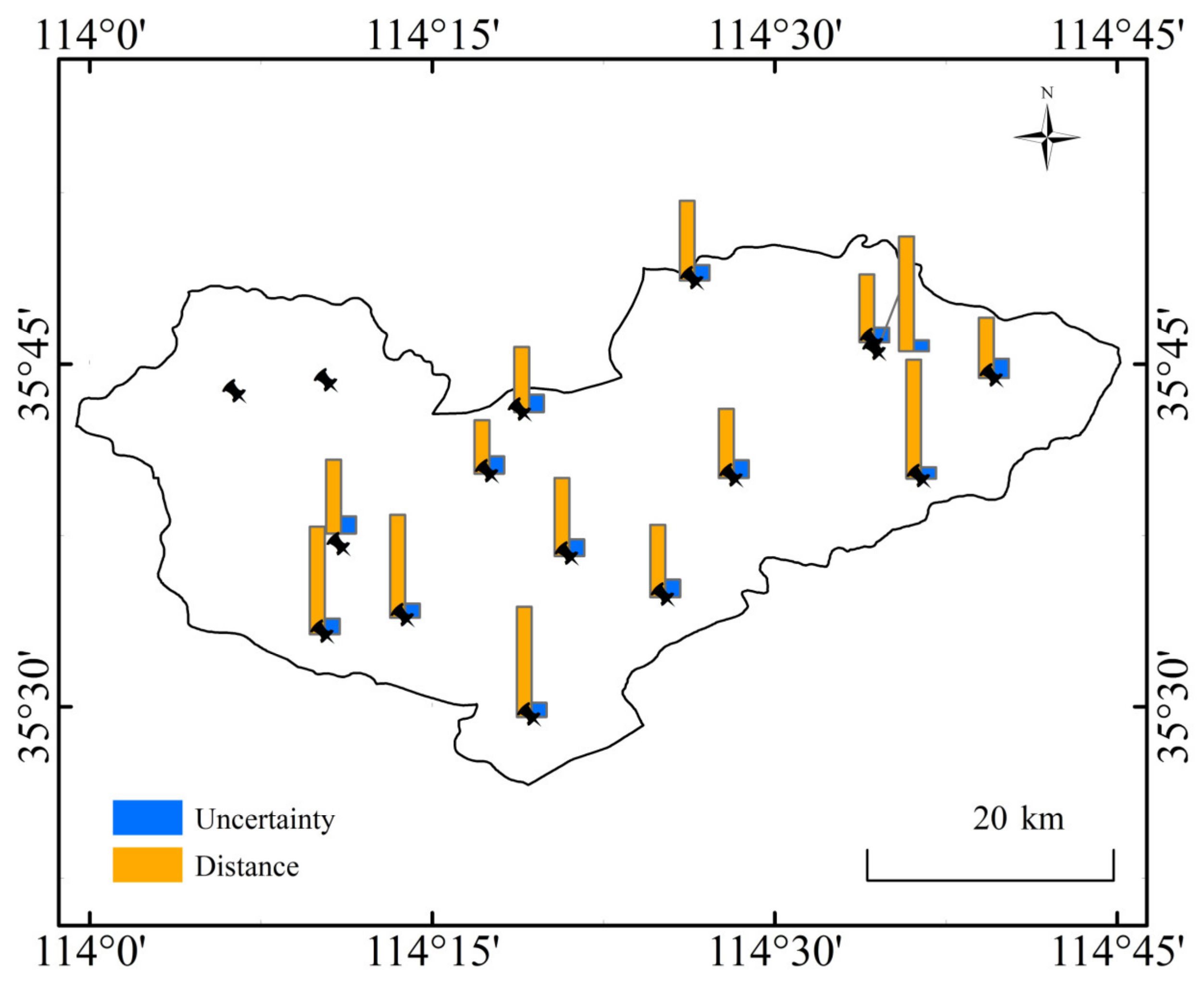
5.3. Validation of the Simulation Results
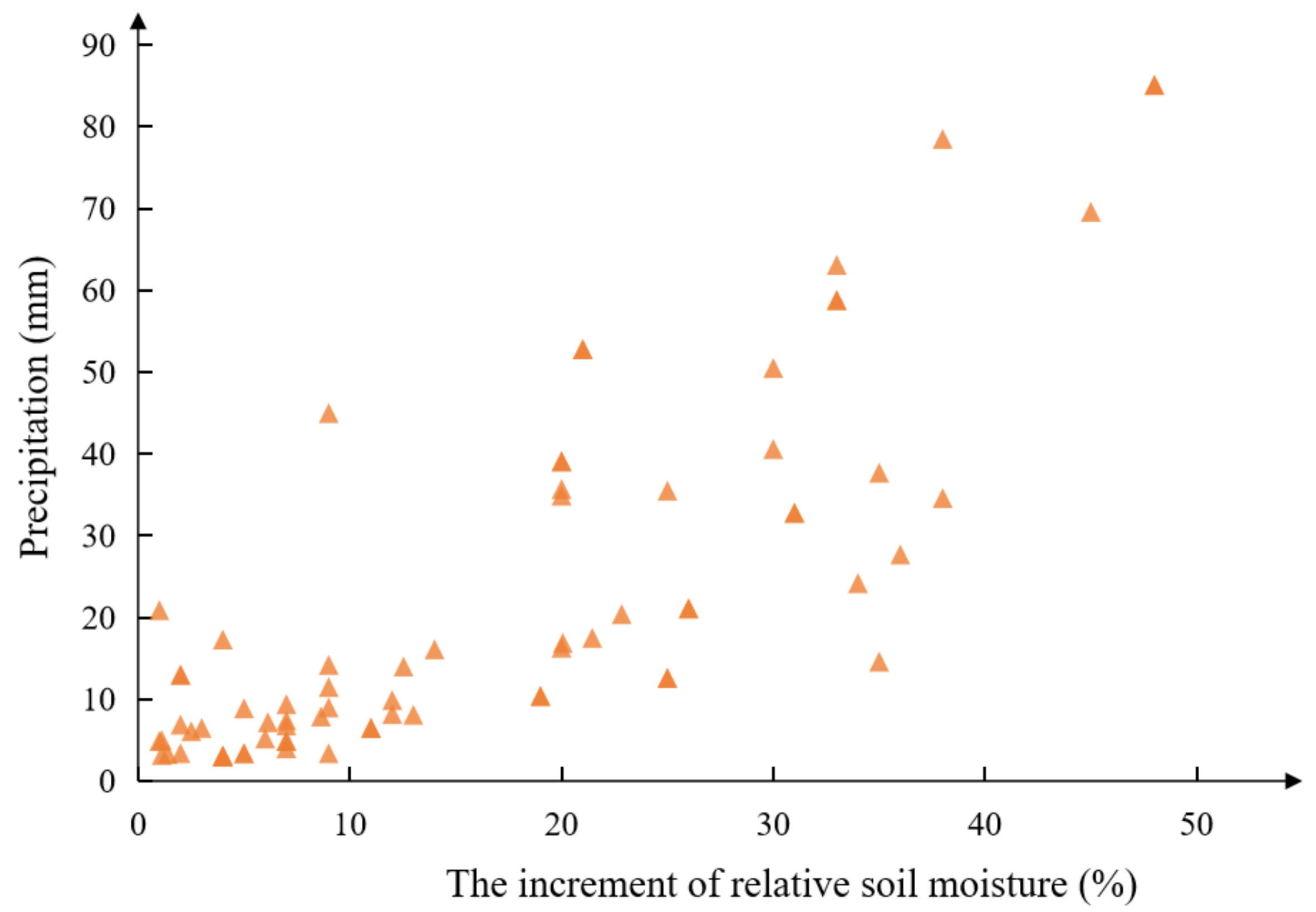
6. Discussion
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leng, G.; Huang, M.; Tang, Q.; Sacks, W.J.; Lei, H.; Leung, L.R. Modeling the effects of irrigation on land surface fluxes and states over the conterminous United States: Sensitivity to input data and model parameters. J. Geophys. Res. Atmos. 2013, 118, 9789–9803. [Google Scholar] [CrossRef]
- Toureiro, C.; Serralheiro, R.; Shahidian, S.; Sousa, A. Irrigation management with remote sensing: Evaluating irrigation requirement for maize under Mediterranean climate condition. Agric. Water Manag. 2017, 184, 211–220. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.-M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Douglas, E.; Beltrán-Przekurat, A.; Niyogi, D.; Pielke, R.; Vörösmarty, C. The impact of agricultural intensification and irrigation on land–atmosphere interactions and Indian monsoon precipitation—A mesoscale modeling perspective. Glob. Planet. Chang. 2009, 67, 117–128. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Tang, Q.; Leung, L.R. A modeling study of irrigation effects on global surface water and groundwater resources under a changing climate. J. Adv. Model. Earth Syst. 2015, 7, 1285–1304. [Google Scholar] [CrossRef]
- Douglas, E.M.; Niyogi, D.; Frolking, S.; Yeluripati, J.B.; Pielke, R.A.; Niyogi, N.; Vörösmarty, C.J.; Mohanty, U.C. Changes in moisture and energy fluxes due to agricultural land use and irrigation in the Indian Monsoon Belt. Geophys. Res. Lett. 2006, 33, 5. [Google Scholar] [CrossRef]
- Ozdogan, M.; Gutman, G. A new methodology to map irrigated areas using multi-temporal MODIS and ancillary data: An application example in the continental US. Remote Sens. Environ. 2008, 112, 3520–3537. [Google Scholar] [CrossRef]
- Ferguson, I.M.; Maxwell, R.M. Human impacts on terrestrial hydrology: Climate change versus pumping and irrigation. Environ. Res. Lett. 2012, 7, 3061–3078. [Google Scholar] [CrossRef]
- Cheviron, B.; Vervoort, R.; Albasha, R.; Dairon, R.; Le Priol, C.; Mailhol, J.-C. A framework to use crop models for multi-objective constrained optimization of irrigation strategies. Environ. Model. Softw. 2016, 86, 145–157. [Google Scholar] [CrossRef]
- Lobell, D.B.; Bonfils, C. The Effect of Irrigation on Regional Temperatures: A Spatial and Temporal Analysis of Trends in California, 1934–2002. J. Clim. 2008, 21, 2063–2071. [Google Scholar] [CrossRef]
- Lobell, D.; Bala, G.; Mirin, A.; Phillips, T.; Maxwell, R.; Rotman, D. Regional Differences in the Influence of Irrigation on Climate. J. Clim. 2009, 22, 2248–2255. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. North China Plain threatened by deadly heatwaves due to climate change and irrigation. Nat. Commun. 2018, 9, 9. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models—Part 2: Representation of water supply and allocation and opportunities for improved modeling. Hydrol. Earth Syst. Sci. 2015, 19, 63–90. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models—Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef]
- Tang, Q.; Oki, T.; Kanae, S.; Hu, H. The Influence of Precipitation Variability and Partial Irrigation within Grid Cells on a Hydrological Simulation. J. Hydrometeorol. 2007, 8, 499–512. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S. Influence of modern land cover on the climate of the United States. Clim. Dyn. 2009, 33, 945–958. [Google Scholar] [CrossRef]
- Haddeland, I.; Skaugen, T.; Lettenmaier, D.P. Anthropogenic impacts on continental surface water fluxes. Geophys. Res. Lett. 2006, 33, L08406. [Google Scholar] [CrossRef]
- Bonfils, C.; Lobell, D. Empirical evidence for a recent slowdown in irrigation-induced cooling. Proc. Natl. Acad. Sci. USA 2007, 104, 13582–13587. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.; Velpuri, M.; Gumma, M.; Gangalakunta, O.R.P.; Turral, H.; Cai, X.; et al. Global irrigated area map (GIAM), derived from remote sensing, for the end of the last millennium. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Puma, M.J.; Cook, B.I. Effects of irrigation on global climate during the 20th century. J. Geophys. Res-Atmos. 2010, 115, D16120. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, 34. [Google Scholar] [CrossRef]
- Teuling, A.J.; Lehner, I.; Kirchner, J.W.; Seneviratne, S.I. Catchments as simple dynamical systems: Experience from a Swiss prealpine catchment. Water Resour. Res. 2010, 46, 15. [Google Scholar] [CrossRef]
- He, Z.; Zhao, W.; Liu, H.; Chang, X. The response of soil moisture to rainfall event size in subalpine grassland and meadows in a semi-arid mountain range: A case study in northwestern China’s Qilian Mountains. J. Hydrol. 2012, 420, 183–190. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Krier, R.; Matgen, P.; Goergen, K.; Pfister, L.; Hoffmann, L.; Kirchner, J.; Uhlenbrook, S.; Savenije, H.H.G. Inferring catchment precipitation by doing hydrology backward: A test in 24 small and mesoscale catchments in Luxembourg. Water Resour. Res. 2012, 48, W10525. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.H. Response of Soil Moisture to Precipitation Pulse by Stable Isotope in Desert Area of the Hexi Corrodo. J. Desert Res. 2016, 36, 1637–1645. (In Chinese) [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Ciabatta, L.; Moramarco, T.; Penna, D.; Zuecco, G.; Pianezzola, L.; Borga, M.; Matgen, P.; Martínez-Fernández, J. Rainfall estimation from in situ soil moisture observations at several sites in Europe: An evaluation of the SM2RAIN algorithm. J. Hydrol. Hydromech. 2015, 63, 201–209. [Google Scholar] [CrossRef]
- Brocca, L.; Tarpanelli, A.; Filippucci, P.; Dorigo, W.; Zaussinger, F.; Gruber, A.; Fernández-Prieto, D. How much water is used for irrigation? A new approach exploiting coarse resolution satellite soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 752–766. [Google Scholar] [CrossRef]
- Jalilvand, E.; Tajrishy, M.; Ghazi Zadeh Hashemi, S.A.; Brocca, L. Quantification of irrigation water using remote sensing of soil moisture in a semi-arid region. Remote Sens. Environ. 2019, 231, 111226. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, A.-X. Extraction of Irrigation Signals by Using SMAP Soil Moisture Data. Remote Sens. 2021, 13, 2142. [Google Scholar] [CrossRef]
- Zhu, A.X.; Lv, G.N.; Zhou, C.H. Geographic Similarity: Third Law of Geography. J. Geoinf. Sci. 2020, 22, 673–679. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Zeng, J.; Yang, J.; Zha, Y.; Yao, Y.; Cao, G. Estimation of actual irrigation amount and its impact on groundwater depletion: A case study in the Hebei Plain, China. J. Hydrol. 2016, 543, 433–449. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Luo, L.; Pokhrel, Y.; Deb, K.; Huang, J.; Ran, Y. Detecting irrigation extent, frequency, and timing in a heterogeneous arid agricultural region using MODIS time series, Landsat imagery, and ancillary data. Remote Sens. Environ. 2017, 204, 197–211. [Google Scholar] [CrossRef]
- Li, X.; Jiang, W.; Duan, D. Spatio-temporal analysis of irrigation water use coefficients in China. J. Environ. Manag. 2020, 262, 110242. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Kumar, S.V. Irrigation Signals Detected from SMAP Soil Moisture Retrievals. Geophys. Res. Lett. 2017, 44, 11860–11867. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, Z.; Zhang, C.; Wang, H.; Jiang, Y. Detecting Winter Wheat Irrigation Signals Using SMAP Gridded Soil Moisture Data. Remote Sens. 2019, 11, 2390. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Gabellani, S.; Puca, S.; Wagner, W. Rainfall-runoff modelling by using SM2RAIN-derived and state-of-the-art satellite rainfall products over Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 163–173. [Google Scholar] [CrossRef]
- Zaussinger, F.; Dorigo, W.; Gruber, A.; Tarpanelli, A.; Filippucci, P.; Brocca, L. Estimating irrigation water use over the contiguous United States by combining satellite and reanalysis soil moisture data. Hydrol. Earth Syst. Sci. 2019, 23, 897–923. [Google Scholar] [CrossRef]
- Zohaib, M.; Choi, M. Satellite-based global-scale irrigation water use and its contemporary trends. Sci. Total. Environ. 2020, 714, 136719. [Google Scholar] [CrossRef]
- Crow, W.T.; van den Berg, M.J.; Huffman, G.J.; Pellarin, T. Correcting rainfall using satellite-based surface soil moisture retrievals: The Soil Moisture Analysis Rainfall Tool (SMART). Water Resour. Res. 2011, 47, 15. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozovi, N.J.W.R.R. Satellite-based Monitoring of Irrigation Water Use: Assessing Measurement Errors and Their Implications for Agricultural Water Management Policy. Water. Resour. Res. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]

| SN | Station_ID | Longitude | Latitude | Land Use/Cover Land Use |
|---|---|---|---|---|
| 1 | 53974 | 114.183 | 35.616 | Irrigated farmland |
| 2 | O2063 | 114.23 | 35.565 | Irrigated farmland |
| 3 | O2647 | 114.171 | 35.553 | Irrigated farmland |
| 4 | O2913 | 114.174 | 35.736 | Irrigated farmland |
| 5 | O2922 | 114.107 | 35.728 | Irrigated farmland |
| 6 | 53990 | 114.315 | 35.715 | Irrigated farmland |
| 7 | 53992 | 114.574 | 35.759 | Rain-fed farmland |
| 8 | O2067 | 114.572 | 35.766 | Irrigated farmland |
| 9 | O2068 | 114.322 | 35.492 | Irrigated farmland |
| 10 | O2069 | 114.47 | 35.667 | Irrigated farmland |
| 11 | O2073 | 114.291 | 35.67 | Irrigated farmland |
| 12 | O2850 | 114.42 | 35.58 | Irrigated farmland |
| 13 | O2907 | 114.606 | 35.666 | Irrigated farmland |
| 14 | O2908 | 114.66 | 35.74 | Irrigated farmland |
| 15 | O2909 | 114.441 | 35.811 | Irrigated farmland |
| 16 | O2910 | 114.35 | 35.61 | Irrigated farmland |
| Sites | Parameters | |
|---|---|---|
| d | U b | |
| 53974 | 2.260 | 0.769 |
| O2063 | 3.228 | 0.578 |
| O2647 | 3.042 | 0.604 −0.3205 |
| 53990 | 2.555 −0.0524 | 0.686 |
| 53992 | 4.01 | 5.424 |
| O2067 | 1.691 | 0.771 |
| O2068 | 3.613 | 0.668 |
| O2069 | 3.062 | 0.727 |
| O2073 | 2.200 16.3980 | 0.719 2.8298 |
| O2850 | 4.325 12.7480 | 0.510 |
| O2907 | 3.888 10.4300 | 0.668 |
| O2908 | 2.474 5.7828 | 0.782 −4.0405 |
| O2909 | 3.270 | 0.632 −9.2438 |
| O2910 | 3.808 | 0.599 −24.231 |
| Sites | Parameters | |||
|---|---|---|---|---|
| Linear Model | Logarithmic Model | |||
| a | b | a | b | |
| 53974 | 0.3794 | 2.3807 | 8.3197 | −12.085 |
| O2063 | 0.8556 | 8.9150 | 11.8280 | −3.3142 |
| O2647 | 1.6673 | 6.2382 | 13.4010 | −0.3205 |
| 53990 | 1.3278 | −0.0524 | 13.239 | −9.5774 |
| 53992 | 0.6733 | 16.369 | 11.426 | 2.0776 |
| O2067 | 1.3081 | 4.0355 | 18.754 | −22.242 |
| O2068 | 0.5826 | 10.528 | 8.2337 | 2.5125 |
| O2069 | 0.7007 | 15.202 | 7.1063 | 10.5300 |
| O2073 | 0.4479 | 16.3980 | 8.6754 | 2.8298 |
| O2850 | 0.8849 | 12.7480 | 10.3710 | 3.5289 |
| O2907 | 1.3137 | 10.4300 | 12.1970 | 3.2405 |
| O2908 | 1.2849 | 5.7828 | 13.8980 | −4.0405 |
| O2909 | 0.3137 | 16.9470 | 11.0590 | −9.2438 |
| O2910 | 0.6502 | 14.2030 | 17.782 | −24.231 |
| Sites | Parameters | ||
|---|---|---|---|
| Z | a | b | |
| 53974 | 28.8 | 3.6 | 2.5 |
| O2063 | 57.9 | 8.2 | 8.2 |
| O2647 | 99.9 | 31.1 | 2.0 |
| 53990 | 99.9 | 13.2 | 7.7 |
| 53992 | 47.7 | 46.7 | 3.4 |
| O2067 | 99.7 | 50.9 | 3.5 |
| O2068 | 48.6 | 19.8 | 1.0 |
| O2069 | 35.9 | 31.2 | 1.0 |
| O2073 | 38.4 | 49.0 | 4.0 |
| O2850 | 70.3 | 21.6 | 1.0 |
| O2907 | 99.9 | 29.7 | 1.0 |
| O2908 | 88.3 | 50.9 | 2.4 |
| O2909 | 12.1 | 36.7 | 1.7 |
| O2910 | 47.3 | 50.9 | 5.5 |
| Sites | Similarity Model | Linear Model | Logarithmic Model | Soil Water Balance Model | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R/A | RMSE | R/A | RMSE | R/A | RMSE | R/A | |
| 53974 | 3.926 | 0.213 | 13.587 | 0.688 | 11.215 | 0.568 | 9.882 | 0.500 |
| O2063 | 7.597 | 0.237 | 6.507 | 0.300 | 8.784 | 0.405 | 9.407 | 0.433 |
| O2647 | 6.909 | 0.191 | 7.227 | 0.320 | 10.360 | 0.459 | 7.470 | 0.331 |
| 53990 | 7.524 | 0.238 | 10,547 | 0.512 | 10,302 | 0.500 | 8.619 | 0.418 |
| 53992 | 4.178 | 0.142 | 22.129 | 1.018 | 21.644 | 0.996 | 23.124 | 1.064 |
| O2067 | 6.263 | 0.196 | 8.016 | 0.464 | 11.920 | 0.691 | 5.655 | 0.328 |
| O2068 | 3.978 | 0.137 | 14.227 | 0.698 | 13.171 | 0.647 | 13.189 | 0.622 |
| O2069 | 5.884 | 0.254 | 14.401 | 0.855 | 12.673 | 0.752 | 10.243 | 0.608 |
| O2073 | 9.214 | 0.355 | 16.756 | 0.647 | 15.707 | 0.607 | 23.331 | 0.901 |
| O2850 | 7.016 | 0.148 | 22.664 | 1.128 | 17.412 | 0.866 | 20.540 | 1.022 |
| O2907 | 7.744 | 0.190 | 21.125 | 0.631 | 22.005 | 0.657 | 21.302 | 0.636 |
| O2908 | 7.342 | 0.180 | 23.519 | 0.903 | 24.012 | 0.921 | 23.026 | 0.884 |
| O2909 | 8.235 | 0.352 | 21.860 | 0.644 | 21.631 | 0.638 | 16.735 | 0.494 |
| O2910 | 4.103 | 0.134 | 22.359 | 0.584 | 20.933 | 0.547 | 19.460 | 0.508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Gu, Z.; Tian, G.; Zhang, J. A New Method for Estimating Irrigation Water Use via Soil Moisture. Agriculture 2023, 13, 757. https://doi.org/10.3390/agriculture13040757
Zhu L, Gu Z, Tian G, Zhang J. A New Method for Estimating Irrigation Water Use via Soil Moisture. Agriculture. 2023; 13(4):757. https://doi.org/10.3390/agriculture13040757
Chicago/Turabian StyleZhu, Liming, Zhangze Gu, Guizhi Tian, and Jiahao Zhang. 2023. "A New Method for Estimating Irrigation Water Use via Soil Moisture" Agriculture 13, no. 4: 757. https://doi.org/10.3390/agriculture13040757
APA StyleZhu, L., Gu, Z., Tian, G., & Zhang, J. (2023). A New Method for Estimating Irrigation Water Use via Soil Moisture. Agriculture, 13(4), 757. https://doi.org/10.3390/agriculture13040757







