Research on the Flexible Heating Model of an Air-Source Heat Pump System in Nursery Pig Houses
Abstract
:1. Introduction
2. Materials and Methods
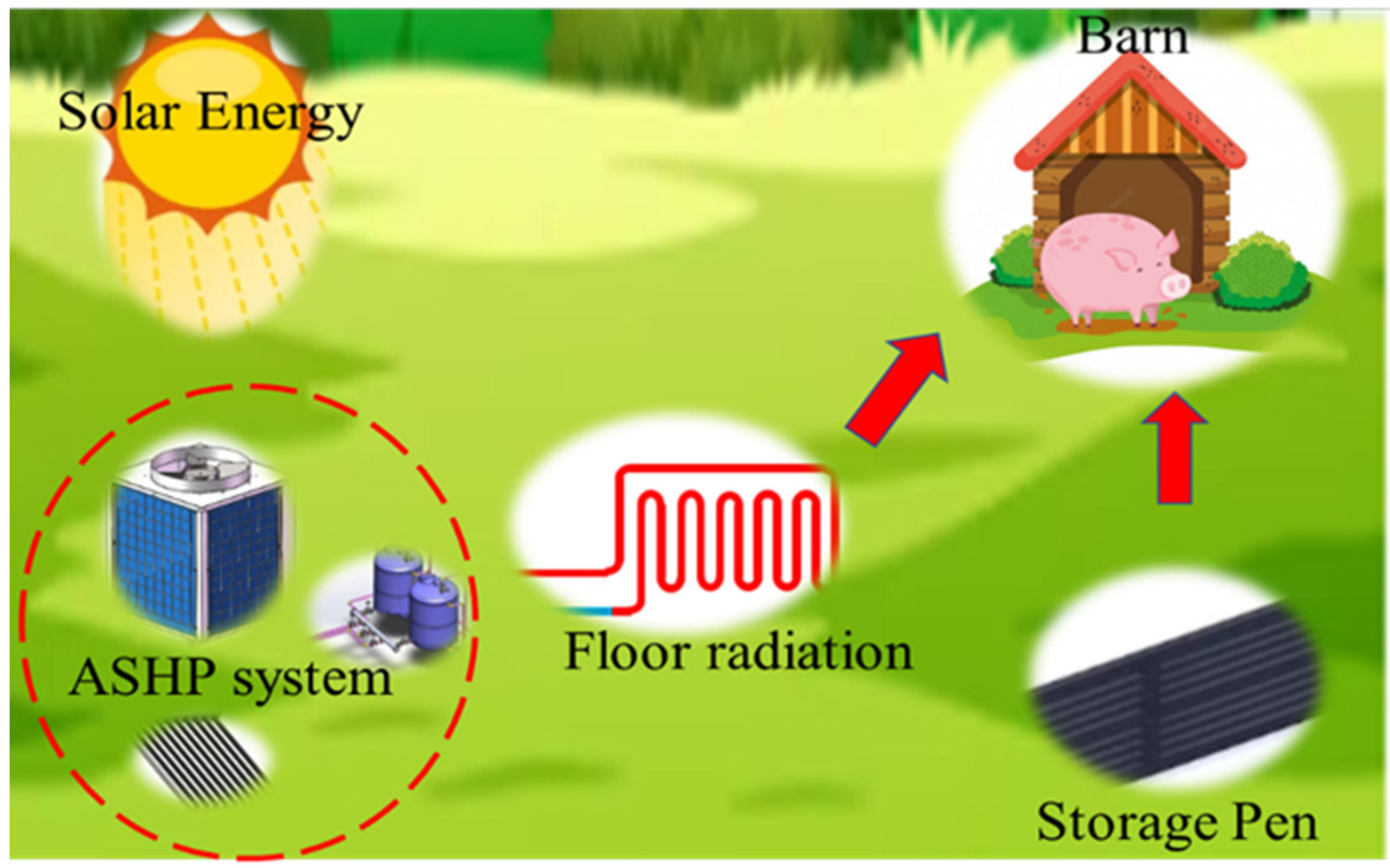
2.1. Geometric Model
2.2. ASHP System
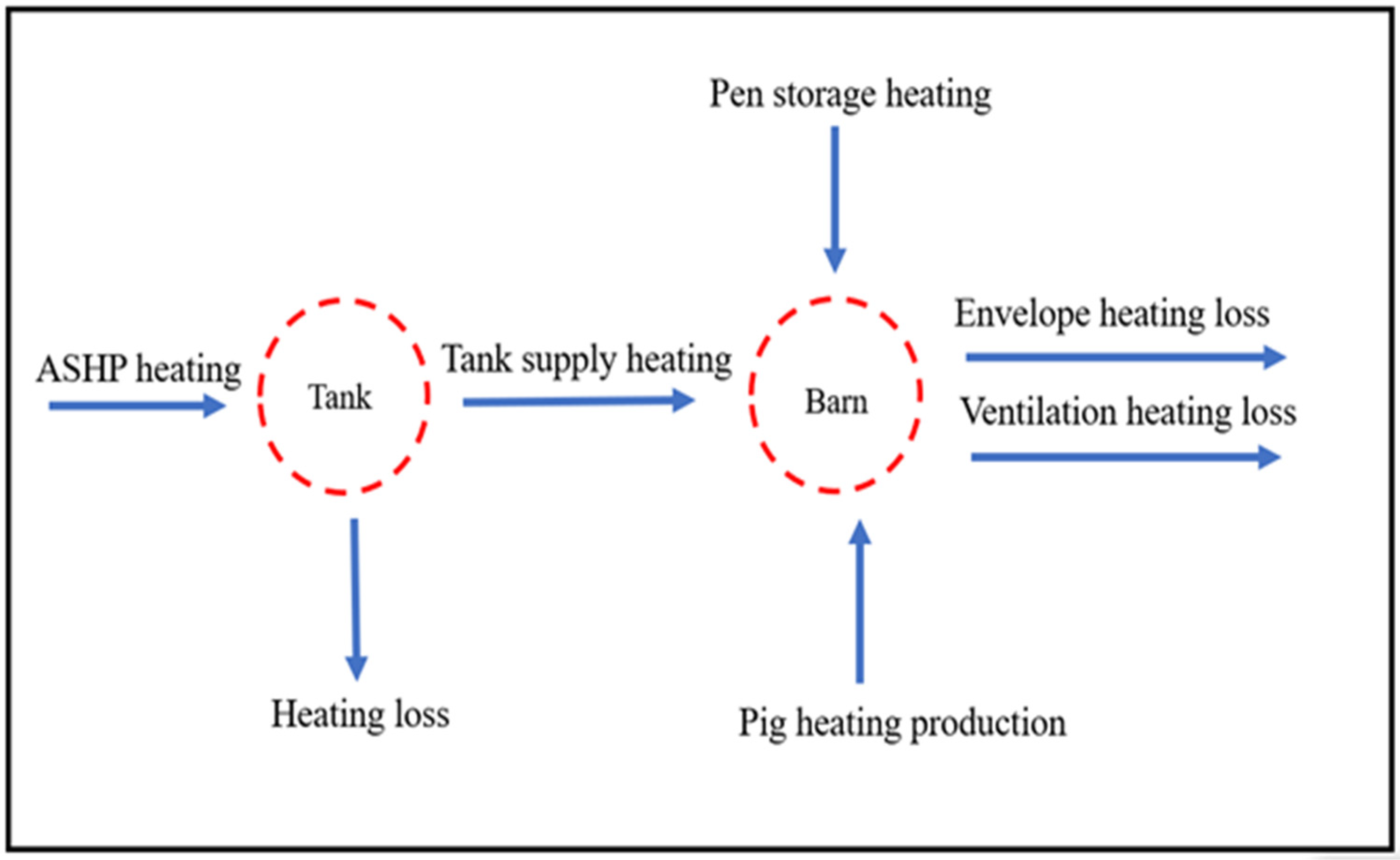
2.3. Mathematical Models
2.4. Boundary Conditions
2.5. ASHP System Measuring Points
3. Results and Discussion
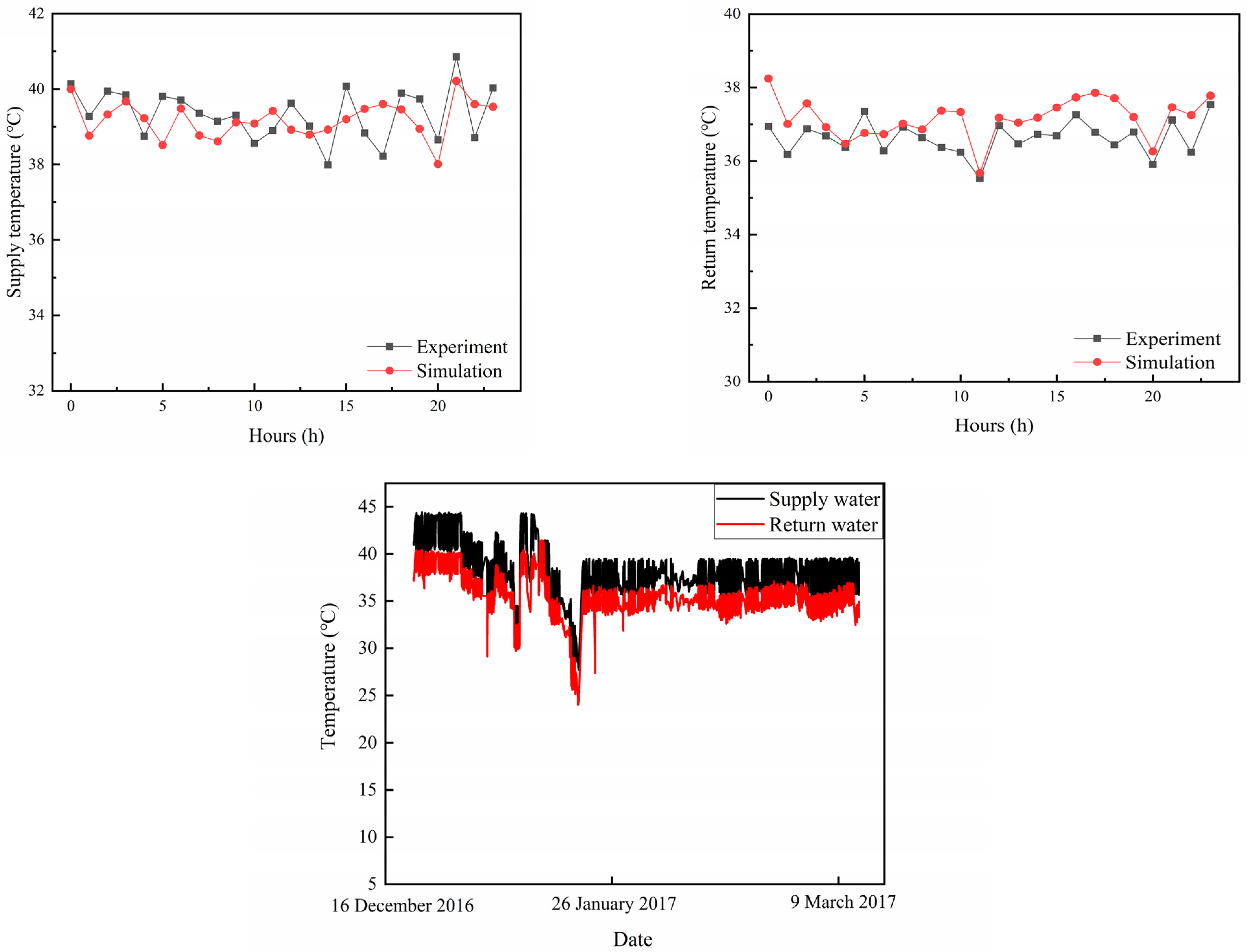
3.1. Model Validation
3.2. Analysis of Heat Storage and Release of the Pen
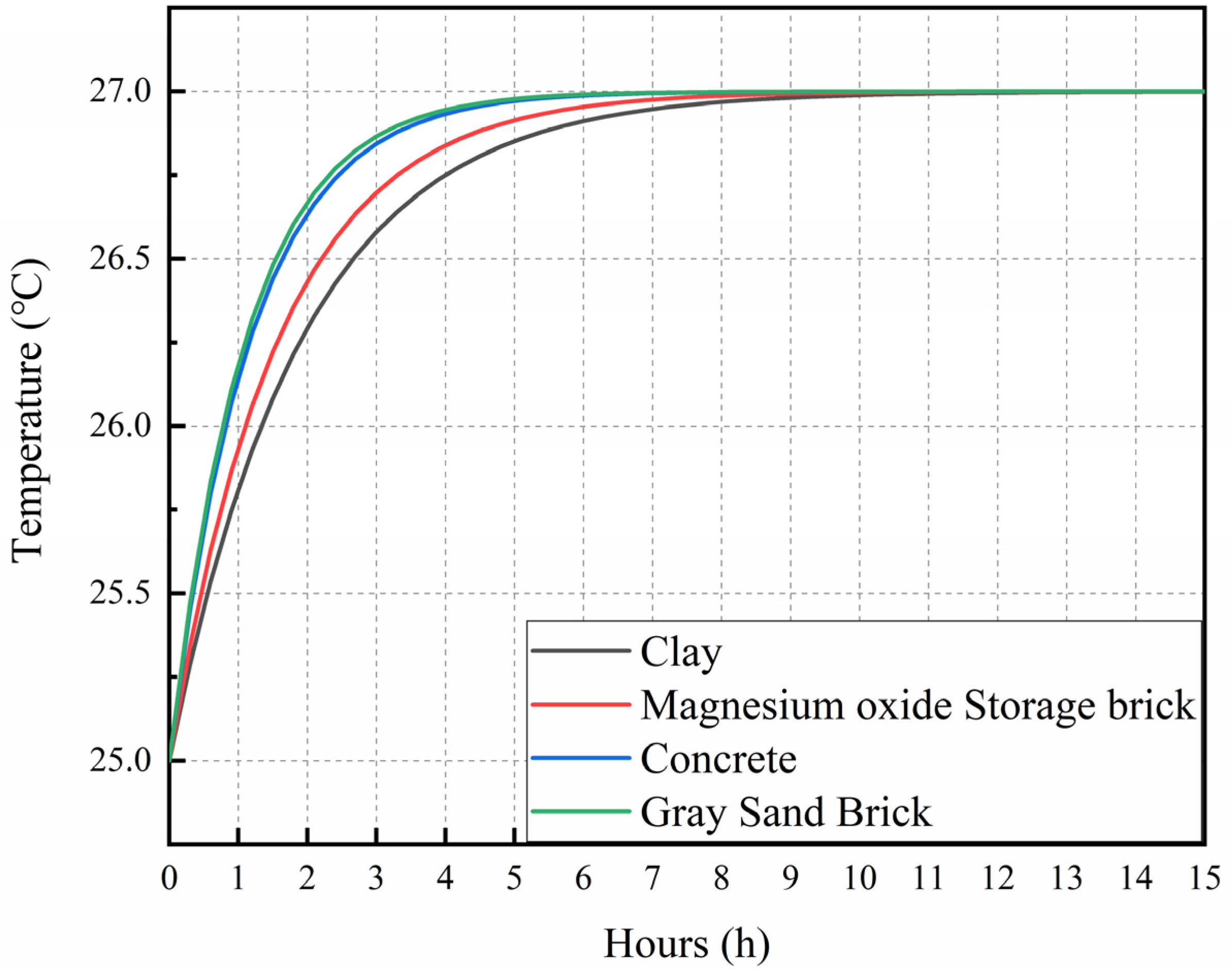
3.2.1. Analysis of Heat Storage
3.2.2. Analysis of Heat Release
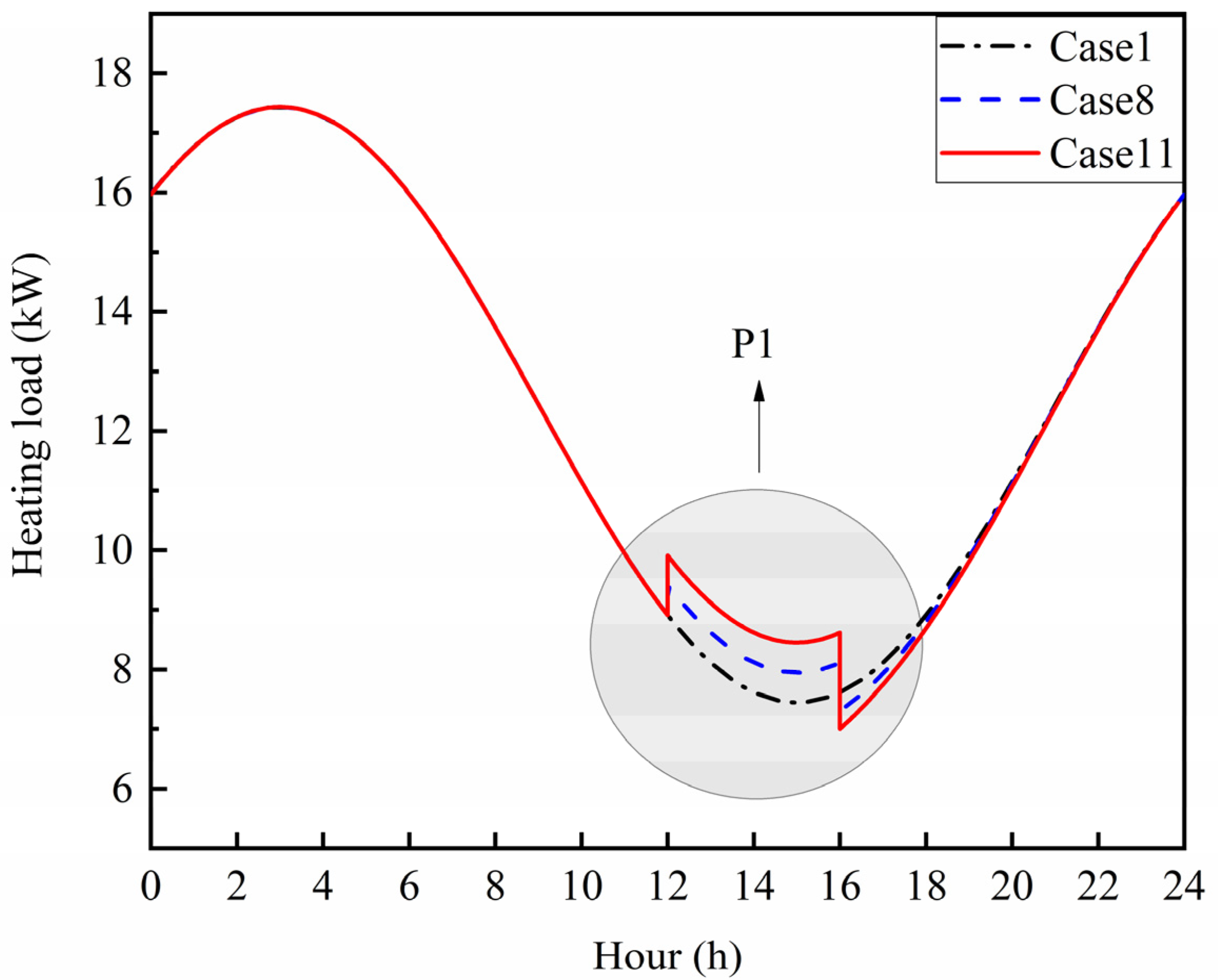
3.3. The Analysis of F-ASHP Heat Load
4. Conclusions
- (1)
- The F-ASHP model for a nursery pig house can accurately predict the heat load demand with a relative error of 5.1%. This model can be used to evaluate the feasibility of F-ASHP in different regions with abundant solar energy.
- (2)
- The energy storage pen effectively stores heat during solar peak times and releases it during solar intermittency, achieving hour-scale energy transfer. Compared with the ASHP system, the magnesium oxide energy storage pen reduced the heat load demand in the pig house by 10.1%, resulting in a highly flexible barn heat load demand.
- (3)
- Among the four energy storage pens, the magnesium oxide storage brick demonstrated the best performance, with a total accumulated heat storage of 3319.20 kJ.
5. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Ab | Area of barn, m2 |
| Ap | Area of pen, m2 |
| Cpa | Air of specific heat capacity, J/kg·K |
| Cp | Water of specific heat capacity, J/kg·K; |
| Csp | Energy storage pen of specific heat capacity, J/kg·K |
| FR | Heat transfer factor |
| G | Quality flow rate, kg/s |
| K | Heat transfer coefficient of energy storage pen, W/m2·K |
| Ki | Heat transfer coefficient of enclosure, W/m2·K |
| m | Quality of nursery pig, kg |
| Ms | Quality of energy storage pen, kg |
| MTANK | Quality of water tank, kg |
| QASHP | Heat of the ASHP, W |
| QLoss | Heat loss of the tank, W |
| Qpig | Pig heat production, W |
| Qs | Solar energy, W |
| Qsource | Energy storage pen of heat, W |
| Qventilation | Heat loss of Ventilation, W |
| S | Solar radiation intensity, W/m2 |
| Ta | Ambient temperature, °C |
| Ta,p | Average ambient temperature, °C |
| Ta,min | Min ambient temperature °C |
| Tbarn | Supply air temperature, °C |
| Tf,i | Heat collector inlet temperature, °C |
| Tf,o | Heat collector outlet temperature, °C |
| Tin | Return temperature of the tank, °C |
| Tout | Supply temperature of the tank, °C |
| Ts | Average temperature of energy storage pens, °C 2 |
| UL | Heating loss, W/m2·°C |
| V | Ventilation rate of nursery pig, m3/h. |
| Air density, kg m−3 | |
| Abbreviations | |
| ASHP | Air-source heat pump |
| F-ASHP | Flexible air-source heat pump system |
| COP | Coefficient of performance |
| PAV | Pen-attached ventilation |
References
- Goel, A.; Ganesh, L.S.; Kaur, A. Sustainability integration in the management of construction projects: A morphological analysis of over two decades’ research literature. J. Clean. Prod. 2019, 236, 117676. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, X.; Cui, C.; Skitmore, M. BIM-based approach for the integrated assessment of life cycle carbon emission intensity and life cycle costs. Build. Environ. 2022, 226, 109691. [Google Scholar] [CrossRef]
- Yang, X.; Hu, M.; Wu, J.; Zhao, B. Building-information-modeling enabled life cycle assessment, a case study on carbon footprint accounting for a residential building in China. J. Clean. Prod. 2018, 183, 729–743. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Zhao, Z.; Ren, J.; Chen, X. Research on carbon emission reduction effect of China’s regional digital trade under the “double carbon” target—Combination of the regulatory role of industrial agglomeration and carbon emissions trading mechanism. J. Clean. Prod. 2023, 405, 137049. [Google Scholar] [CrossRef]
- Bao, J.; Xie, Q. Artificial intelligence in animal farming: A systematic literature review. J. Clean. Prod. 2022, 331, 129956. [Google Scholar] [CrossRef]
- Yeo, U.-H.; Lee, I.-B.; Kim, R.-W.; Lee, S.-Y.; Kim, J.-G. Computational fluid dynamics evaluation of pig house ventilation systems for improving the internal rearing environment. Biosyst. Eng. 2019, 186, 259–278. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, J.; Liu, H.; Bao, J.; Xie, Q.; Teng, X. A wireless intelligent thermal control and management system for piglet in large-scale pig farms. Inf. Process. Agric. 2021, 8, 341–349. [Google Scholar] [CrossRef]
- Gautam, K.R.; Rong, L.; Zhang, G.; Bjerg, B.S. Temperature distribution in a finisher pig building with hybrid ventilation. Biosyst. Eng. 2020, 200, 123–137. [Google Scholar] [CrossRef]
- Vasdal, G.; Møgedal, I.; Bøe, K.E.; Kirkden, R.; Andersen, I.L. Piglet preference for infrared temperature and flooring. Appl. Anim. Behav. Sci. 2010, 122, 92–97. [Google Scholar] [CrossRef]
- Requejo, J.M.; Garrido-Izard, M.; Correa, E.C.; Villarroel, M.; Diezma, B. Pig ear skin temperature and feed efficiency: Using the phase space to estimate thermoregulatory effort. Biosyst. Eng. 2018, 174, 80–88. [Google Scholar] [CrossRef]
- Wang, H.; Yi, L.; Wu, Z.; Liu, J.; Wang, M. Feasibility of the air source heat pump system for heating wine houses in Beijing. Trans. CSAE 2021, 37, 236–242. [Google Scholar]
- Wang, M.; Yi, L.; Liu, J.; Yang, L.; Chen, Z.; Wu, Z. Study on heating effect of air source heat pump for floor heating of nursery pig house in Beijing. Trans. CSAE 2019, 35, 203–210. [Google Scholar]
- Tu, Q.; Zhang, L.; Li, L.; Deng, C.; Wang, B.; Gu, B.; Dai, Z. Comparison of Application Effects of Capillary Radiation Heat Pump and Electric Heating Wire in Greenhouse Seedling Cultivation. Agriculture 2022, 12, 1401. [Google Scholar] [CrossRef]
- Ma, J.; Kim, D.; Braun, J.E.; Horton, W.T. Development and validation of a dynamic modeling framework for air-source heat pumps under cycling of frosting and reverse-cycle defrosting. Energy 2023, 272, 127030. [Google Scholar] [CrossRef]
- Bansal, P.; Mohabir, A.; Miller, W. A novel method to determine air leakage in heat pump clothes dryers. Energy 2016, 96, 1–7. [Google Scholar] [CrossRef]
- Song, B.; Bai, L.; Yang, L. Analysis of the long-term effects of solar radiation on the indoor thermal comfort in office buildings. Energy 2022, 247, 123499. [Google Scholar] [CrossRef]
- Kim, T.; Choi, B.-I.; Han, Y.-S.; Do, K.H. A comparative investigation of solar-assisted heat pumps with solar thermal collectors for a hot water supply system. Energy Convers. Manag. 2018, 172, 472–484. [Google Scholar] [CrossRef]
- Besagni, G.; Croci, L.; Nesa, R.; Molinaroli, L. Field study of a novel solar-assisted dual-source multifunctional heat pump. Renew. Energy 2019, 132, 1185–1215. [Google Scholar] [CrossRef]
- Sezen, K.; Tuncer, A.D.; Akyuz, A.O.; Gungor, A. Effects of ambient conditions on solar assisted heat pump systems: A review. Sci. Total Environ. 2021, 778, 146362. [Google Scholar] [CrossRef]
- Choi, Y.; Takase, K.; Mae, M. System performance of a residential building using the air-based solar heating system. Solar Energy 2018, 171, 47–63. [Google Scholar] [CrossRef]
- Chung, M.H.; Park, J.C. Development of PCM cool roof system to control urban heat island considering temperate climatic conditions. Energy Build. 2016, 116, 341–348. [Google Scholar] [CrossRef]
- Ye, X.; Kang, Y.; Yang, X.; Zhong, K. Temperature distribution and energy consumption in impinging jet and mixing ventilation heating rooms with intermittent cold outside air invasion. Energy Build. 2018, 158, 1510–1522. [Google Scholar] [CrossRef]
- El Haj Assad, M.; Nazari, M.A.; Ehyaei, M.A.; Rosen, M.A. Chapter 11—Heat pumps and absorption chillers. In Design and Performance Optimization of Renewable Energy Systems; Assad, M.E.H., Rosen, M.A., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 163–180. [Google Scholar]
- Wang, R.; Feng, W.; Xue, H.; Gerber, D.; Li, Y.; Hao, B.; Wang, Y. Simulation and power quality analysis of a Loose-Coupled bipolar DC microgrid in an office building. Appl. Energy 2021, 303, 117606. [Google Scholar] [CrossRef]
- Zhu, M.; Pan, Y.; Wu, Z.; Xie, J.; Huang, Z.; Kosonen, R. An occupant-centric air-conditioning system for occupant thermal preference recognition control in personal micro-environment. Build. Environ. 2021, 196, 107749. [Google Scholar] [CrossRef]
- Wang, X.; Cao, M.; Hu, F.; Yi, Q.; Amon, T.; Janke, D.; Xie, T.; Zhang, G.; Wang, K. Effect of Fans’ Placement on the Indoor Thermal Environment of Typical Tunnel-Ventilated Multi-Floor Pig Buildings Using Numerical Simulation. Agriculture 2022, 12, 891. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Wu, Z.; Feng, G.; Shen, Z.; Wang, M. Airflow characteristics of attachment ventilation in a nursery pig house under heating mode. Biosyst. Eng. 2022, 224, 346–360. [Google Scholar] [CrossRef]




| Structure | Direction | Area (m2) | Heat Transfer Coefficient (W/m2·K) |
|---|---|---|---|
| Door | West | 1.59 | 4.7 |
| Window | East | 1.26 | 1.92 |
| South | 39.02 | 4.7 | |
| West | 0.87 | 4.7 | |
| North | 11.2 | 4.7 | |
| Wall | East | 36.52 | 0.35 |
| South | 83.79 | 0.35 | |
| West | 35.32 | 0.35 | |
| North | 11.62 | 0.35 | |
| Floor | / | 396.52 | 0.22 |
| Roof | / | 380.52 | 0.47 |
| Materials | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | Heat Exchange Area (m2) | Quality (kg) |
|---|---|---|---|---|
| Concrete brick | 2300 | 920 | 1.92 | 132.48 |
| Gray sand brick | 1900 | 1050 | 1.92 | 109.44 |
| Clay brick | 1842 | 1850 | 1.92 | 106.10 |
| Magnesium oxide Storage brick | 2500 | 1140 | 1.92 | 144.00 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Water tank volume | 1000 L | Number of pigs | 448 |
| Water specific heat capacity | 4.2 kJ/kg·°C | Ventilation rate | 5.8 m3/h |
| Air specific heat capacity | 1.005 kJ/kg·k | Collector area | 6 m2 |
| Air density | 1.29 kg/m3 | Energy utilization rate | 0.8 |
| Water density | 1000 kg/m3 | Heat transfer factor | 0.9 |
| Nursery pig weight | 13.6 kg | Barn set temperature | 25 |
| Average daily solar radiation | 9.85 MJ/d | Average outdoor temperature | −7.9 |
| Lowest temperature | −18.3 °C | Flow rate | 110 L/h |
| Case | Tank Setting Temperature (°C) | Pen Material | Solar Energy | P1 Setting Temperature (°C) |
|---|---|---|---|---|
| 1 | 40 | Hollow plastic | / | 26 |
| 2 | 27 | |||
| 3 | 28 | |||
| 4 | Clay brick | Working | 26 | |
| 5 | 27 | |||
| 6 | 28 | |||
| 7 | Gray sand brick | Working | 26 | |
| 8 | 27 | |||
| 9 | 28 | |||
| 10 | Magnesium oxide Storage brick | Working | 26 | |
| 11 | 27 | |||
| 12 | 28 | |||
| 13 | Concrete brick | Working | 26 | |
| 14 | 27 | |||
| 15 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, J.; Wu, Z.; Liu, J.; Yi, L.; Li, Y.; Li, S.; Wang, M. Research on the Flexible Heating Model of an Air-Source Heat Pump System in Nursery Pig Houses. Agriculture 2023, 13, 1059. https://doi.org/10.3390/agriculture13051059
Wang H, Liu J, Wu Z, Liu J, Yi L, Li Y, Li S, Wang M. Research on the Flexible Heating Model of an Air-Source Heat Pump System in Nursery Pig Houses. Agriculture. 2023; 13(5):1059. https://doi.org/10.3390/agriculture13051059
Chicago/Turabian StyleWang, Hua, Jijun Liu, Zhonghong Wu, Jia Liu, Lu Yi, Yixue Li, Siqi Li, and Meizhi Wang. 2023. "Research on the Flexible Heating Model of an Air-Source Heat Pump System in Nursery Pig Houses" Agriculture 13, no. 5: 1059. https://doi.org/10.3390/agriculture13051059
APA StyleWang, H., Liu, J., Wu, Z., Liu, J., Yi, L., Li, Y., Li, S., & Wang, M. (2023). Research on the Flexible Heating Model of an Air-Source Heat Pump System in Nursery Pig Houses. Agriculture, 13(5), 1059. https://doi.org/10.3390/agriculture13051059








