Next Article in Journal
Establishing a Prediction Model for Tea Leaf Moisture Content Using the Free-Space Method’s Measured Scattering Coefficient
Previous Article in Journal
Growth, Physiology, and Productivity of Bouteloua gracilis and Cenchrus ciliaris Using Moisture Retainers under Different Planting Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 13
Issue 6
10.3390/agriculture13061135
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading

by
Vaidas Bivainis
,
Eglė Jotautienė
,
Kristina Lekavičienė
*,
Ramūnas Mieldažys
and
Gražvydas Juodišius
Department of Agricultural Engineering and Safety, Faculty of Engineering, Agriculture Academy, Vytautas Magnus University, Studentu Str. 15A, LT-53362 Akademija, Kaunas District, Lithuania
*
Author to whom correspondence should be addressed.
Agriculture 2023, 13(6), 1135; https://doi.org/10.3390/agriculture13061135
Submission received: 2 May 2023 / Revised: 24 May 2023 / Accepted: 26 May 2023 / Published: 28 May 2023
Browse Figures
Review Reports Versions Notes

Abstract

:
Due to the continuous creation of organic granular fertilizers of the new composition, there is a lack of knowledge about their properties and the influence of the norm on spreading efficiency. To increase the efficiency of the use of granular organic fertilizers, their spreading aims are to properly choose the most rational spreading parameters and fertilizer norms, considering the characteristics of the fertilizer. To determine this quickly and with lower costs, various theoretical models and computer programs are used to study the dynamics of fertilizer spreading. The purpose of this work was to perform theoretical and experimental comparative studies of the influence of the characteristics and dosage norms of granular fertilizers of poultry manure on the spreading efficiency. During the research, the physical properties of granular poultry manure fertilizers were determined, which have an impact on the quality of spreading. Experimental studies of fertilizer spreading were carried out using two centrifugal spreaders with the same parameters (Amazone ZA-M-1001 (spreading dosage norm, 200 kg ha−1 and 400 kg ha−1; driving speed, 10 km h−1) and ZA-M-1201 (spreading dosage norm, 600 kg ha−1, 800 kg ha−1, and 1000 kg ha−1; driving speed, 5 km h−1)). Before the fertilizer was spread, measurements were made of the flow rate of the spreadable fertilizer through one bunker shutter. Fertilizer application simulations were performed using the discrete element simulation program EDEM. Research has shown that spreading the studied granular fertilizers at the dosage norm of 600 and 800 kg ha−1 allows for the future expansion of the limits of spreading research using a spreading simulation. The most important directions of research would be the research of the spreader vanes’ shape, length, and rational settings positions, using the standard commonly used centrifugal spreader, after making small modifications of the spreader, to achieve that the spreader could spread larger norms of fertilizer or drive faster during spreading.

1. Introduction

The growing demand for organic agricultural products is encouraging the use of environmentally friendly natural materials to fertilize the soil. Organic farms can only use organic fertilizers, and their demand is growing. The negative impact of agricultural production on the environment can be reduced by applying organic farming, particularly by increasing the use of organic fertilizers [1].
Organic fertilizers, especially animal manure, contain more organic matter than chemical fertilizers and can therefore be considered a source of nutrients, especially nitrogen, phosphorus, and potassium. One such organic fertilizer is poultry manure, which contains macro- and micronutrients (manganese, iron, copper, and boron). It also contains more nitrogen than other animal fertilizers [2,3]. However, improper disposal of poultry manure on the soil surface is often reported to lead to serious environmental problems, such as the eutrophication of water bodies [4]. In addition, the application of poultry manure has been found to increase the degree of phosphorus enrichment in the soil [5]. Heavy metals can also be found in poultry manure [6]. The application of poultry manure at standard rates and for short periods does not lead to significant heavy metal contamination, but the re-application of poultry manure on agricultural soils can lead to the accumulation of heavy metals in the soil and in plants [7]. Therefore, considering the risk of environmental pollution, the use of poultry manure for the production of granular fertilizers is a viable option from both an environmental and an economic point of view [8]. Granular organic fertilizers are easier to transport, store, and spread [9,10].
When applying granular organic fertilizers, the most important thing is to spread them as evenly as possible over the soil surface [9,11]. Centrifugal spreaders are most suitable for spreading such fertilizers because of their relatively low cost, ease of maintenance, and large working width (18–50 m) [9,12]. These spreaders have a bunker with two outlets at the bottom and two discs, one rotating clockwise and the other counterclockwise [12]. Under- or overdosing of fertilizer leads to yield loss. Researchers have therefore focused on variable-rate fertilization to reduce crop inputs and thus increase profits [13]. The dynamics of fertilizer particle spreading are influenced by fixed and variable technical specifications of the spreader (rotational speed and position of the rotating discs, position of the disc blades, size of the discharge opening, the location where each particle falls on the rotating disc, the exhaust flow of the fertilizer, the travel speed, and the working width of the machine) and the physicomechanical properties of the fertilizer (coefficient of friction, shape, size, size distribution, moisture content, and density) [14,15,16,17]. According to Gavrilovic et al. [18], it is necessary to pay attention to the physical and mechanical properties of the fertilizer, as they affect the uniformity and the overall quality of the fertilization.
Researchers analyzing the simulation of poultry manure granular fertilizers found that, for a cylindrical granule spreading dosage of 200 g s−1, the distribution of particles with a diameter of 4 mm is more even than that of the ones of 6 mm in diameter. At a granule spreading dosage norm of 400 g s−1, the distribution of 6 mm diameter particles is more uniform than for 4 mm ones [15]. Experimental studies have shown that cattle manure granules are spread more evenly over the soil surface than meat and bone meal granules. This was due to the shorter length (9.50 ± 0.38 mm), larger diameter (6.0 ± 0.1 mm), lower density (1255.9 ± 67.01 kg m−3), and higher mass (0.30 ± 0.03 g) of cattle manure granules compared to meat and bone meal granules [17].
The spreading of organic granular fertilizers raises the objective of selecting the most rational spreading parameters and fertilizer rates, considering the fertilizer properties. To increase the efficiency of fertilizer application and to do so quickly and at a lower cost, various theoretical models and computer programs are used to study the dynamics of fertilizer spreading [19]. Modeling of the spreader operation allows the study of a wide range of parameters affecting particle movement [20]. Numerical experiments show that fertilizer spreading is quite accurate [19]. The agreement between modeling and experimental results suggests that the spreading of organic granular fertilizers can be modeled quite accurately by the discrete element method [21,22]. As new formulations of granular organic fertilizers are continuously being developed, there is a lack of knowledge about the influence of the properties and rates of these fertilizers, especially those with a cylindrical shape, on the spreading efficiency in comparative theoretical and experimental studies.
Therefore, to increase the efficiency of fertilizer use, this work aims to carry out theoretical and experimental comparative studies on the properties and dosage norm effects of poultry manure granular fertilizers on spreading efficiency.

2. Materials and Methods

2.1. Properties of Granular Fertilizers

Experimental studies were carried out using granulated NPK 4-3-2.5 fertilizer made from poultry manure. The composition declared by the fertilizer manufacturer [23] and the experimentally determined physical properties of the granules, which affected spreading quality, are presented in Table 1.
The diameter and length of the granules were measured for 130 randomly sampled granules. These parameters were measured using a digital caliper Mitutoyo 500-196-30 with an accuracy of 0.01 mm. The histogram of the distribution of granule lengths was constructed from the granule lengths. The granule bulk density was determined by pouring the granules into a cylindrical container with a diameter of 76.10 mm and a height of 220.44 mm (capacity of 1.00 l) and weighing the mass of the granules by using a laboratory balance Kern PCB 1000-2 with a division of 0.01 g. The density of the granule material was determined by calculating the total volume (using measured granule diameter and length) of about 50 randomly taken granules and weighing their mass.
The static and dynamic coefficient of friction between the fertilizer granules and the stainless-steel surface (the fertilizer spreader discs, vanes, and bunker shutter hole were made of stainless steel) was determined using the Thwing-Alberts friction peel tester model 225-1 (Midwest FlexSystems Inc, Flint, MI, USA). A ring with an internal diameter of 103 mm and a height of 16 mm, filled with granules and placed on a stainless-steel surface, was used for this study. A general view of the ring with granules on a stainless-steel surface is shown in Figure 1. The mass of the granules was 141.82 g, and the ring had a tensile speed of 300 mm min−1. The test lasted for 10 s; during the first two seconds of the test, the static coefficient of friction between the granules and the stainless-steel surface was determined, and during the remaining time, the dynamic coefficient was determined.
The static drained and repose angles of the granules were determined using an experimental test bench, an overview of which is given in Figure 2. The top box of this bench, which was filled with approximately 8 kg of granules for the tests, was 495 mm long, 250 mm deep, and 240 mm high. The height of this box with the granule outlet was 400 mm from the base.
All granule samples were stored for about 24 h in an environment of about 20 °C and relative humidity of about 50% before testing.

2.2. Verification of Granular Properties and Spreading Modeling Using Discrete Element Method

The modeling of the granule spreading was carried out using the discrete element DEM modeling software EDEM. The properties of the granules required for the modeling (which were not experimentally analyzed) were the Young’s modulus and Poisson‘s ratio, which were chosen after an analysis of similar studies [24,25,26,27]. Assuming that the Young’s modulus and Poisson‘s ratio have the smallest effect on the results of the granule dispersion simulation, these properties were not verified in the simulation.
The remaining properties of the granules required for their spreading modeling, such as the interaction coefficient between the granules, the interaction coefficient between the granules and the surface of the stainless steel, the static coefficient of friction between the granules, and the dynamic friction coefficient between the granules, were selected from the analysis of the literature by similar authors [26,27,28,29,30] Due to the structure and roughness of the granule surface, it was assumed that the values of the intergranular static and dynamic friction coefficients should be higher than the values of the coefficients between the granule and the surface of the stainless steel when selecting the parameters of the granule for the modeling. The static and dynamic coefficients of friction between the granules and the steel surface were determined experimentally. If these properties of the granules had the greatest effect on the results of the spreading simulation, these values were verified in the simulation.
The aforementioned properties of the granules were verified by numerical simulation studies of the granule bulk density and static drained and repose angles, as well as by comparing them with the experimental results. The intervals of values of the granule properties used for the verification are shown in Table 2 above. Five values from each interval of parameters were used for the verification. The coefficient of Restitution (Particle–Particle) was verified using the following coefficient values: 0.35; 0.40; 0.45; 0.50, and 0.50. The best agreement between the laboratory and simulation results for the bulk density and the drained and repose angles was obtained with a coefficient value of 0.45. Verification of the properties of the remaining accepted granules was carried out in a similar way.
The models used for the DEM modeling of the bulk density vessel, drained and repose angles, and the spreader were created using SolidWorks 2022-2023 EDU 3D computer modeling software.

2.3. Experimental Spread of Fertilizer under Field Conditions

Experimental studies on fertilizer spreading were carried out using two centrifugal spreaders with the same parameters: Amazone ZA-M-1001 (Amazonen-Werke, Hasbergen, Germany) and ZA-M-1201 (Amazonen-Werke, Hasbergen, Germany). The main parameters of these spreaders and the spreading parameters are presented in Table 3.
The remaining technical data of the operated spreaders (hopper capacity and configuration, the distance between spreading disks centers, the height of the disks from the ground, etc.) were also the same.
Prior to fertilizer spreading, measurements were made of the spreader‘s fertilizer mass flow through one bunker shutter. For this purpose, one disc of the spreader was removed and replaced by a special fertilizer-collecting container. The spreader was then driven for a certain distance at the required spreading dosage norm and at speeds of 5 and 10 km h−1. The mass flow of the fertilizer was estimated from the mass of the granules crumbled in the container. This measurement of the fertilizer mass flow rate was carried out several times with the spreader until the obtained value of the flow rate was close to the theoretical value. For example, at a fertilizer spreading dosage norm of 600 kg ha−1 and with the tractor and spreader movement at a speed of 5 km h−1, the theoretical value of the fertilizer flow rate through one bunker shutter is 0.83 kg s−1. In addition to the experimental studies on the determination of the fertilizer flow rate, modeling studies were carried out on the flow rate of fertilizer crumbling through a single bunker spreading shutter. The duration of the simulation study was 3 s, and the average flow rate was calculated after approximately 1.5 s of the study.
Experimental fertilizer spreading studies were carried out on two different fields with a similar surface flatness and angle of inclination. The spreading studies were carried out in October 2022 on the first field with lower dosage norms and in November 2022 on the second field with higher dosage norms. Depending on the crops fertilized with this poultry-manure-based fertilizer and the condition of the soil, the recommended fertilizer dosage norms can range from 500 to 3000 kg ha−1. For example, for many vegetables, the recommended norm is 750 to 1000 kg ha−1, and for cereals, it is 500 to 750 kg ha−1 [23,31]. Due to the relatively high spreading dosage norm of organic fertilizers, the larger volume of organic fertilizer granules, and their lower density (compared to mineral fertilizers), it is difficult to spread them evenly over the entire travel width by using standard double-disc fertilizer spreaders (which are normally designed for mineral fertilizer spreading). The first spreader, the Amazone ZA-M-1001 spreader, spread lower norms of granulated fertilizer at a speed of 10 km h−1, and the second one, the Amazone ZA-M-1201 spreader, spread higher norms of fertilizer at a speed of only 5 km h−1. Both spreaders used identical spreading discs and vanes and had the same position settings of the spreader vanes.
The tractor with the two spreaders tested had a throwing width of 20 m and a total theoretical fertilizer spread width of about 40 m. The amount of fertilizer spread and its uniformity were determined using special collection boxes that were 500 mm long, 400 mm wide, and 100 mm high. The distance between the centers of these boxes was 2 m, and a total of 11 of these boxes were used. The boxes were arranged in a single line, with the central box in the center of the tractor and spreader. The layout diagram of the boxes is shown in Figure 3. The amount of fertilizer accumulated in the boxes was weighed using a Kern PCB 1000-2 (Kern, Murnau, Germany) weighing scale with a unit value of 0.01 g.
At the time of the fertilizer application, the air temperature was about 4.0–7.0 °C, the wind speed was less than 2 m s−1, and the relative humidity was about 85.0%.
All experimental studies were repeated at least 5 times. Confidence intervals for all experimental results presented in the paper were calculated at a 95.0% confidence level.

3. Results and Discussion

3.1. Properties of Granular Fertilizers

The histogram (Figure 4) and the plot chart (Figure 5) of the length distribution of 130 randomly sampled granules are presented.
The distribution of the granule length used in the granules-spreading study was quite symmetrical, with Skewness = −0.03. The values of the average and median were close to each other. The histogram of granule length tended to be flat (platykurtic), with a Kurtosis of −0.72. Visually, the resulting distribution of granule lengths was close to the Normal distribution. For the granule-modeling studies, single-sphere, two-sphere, and four-sphere granule models were used with a diameter of 5.49 mm and an average length of the histogram range. The images of the granule models, their shape, length, and percentage of the total volume are presented in Table 4. It is claimed that organic granular fertilizers are spread more uniformly when they have a shorter length (9.50 ± 0.38 mm) and a larger diameter (6.0 ± 0.1 mm). The uniformity of flour fertilizer (lime) is lower compared to the uniformity of incorporation of organic fertilizer granules of cattle manure [17]. The uniformity of liquid fertilizer application is affected by the type of nozzle, the arrangement of the collector, and the concentration of the fertilizer solution [32].
The frictional force–displacement relationship for granules placed in a ring 16 mm high and 103 mm in diameter is shown in Figure 6. As can be seen from this dependence, the dynamic friction coefficient tended to decrease as a result of the change in the position of the tensioned granules within the ring and the change in their position relative to the plate. Here, the static coefficient of friction between the granules and the stainless-steel surface was evaluated during the first two seconds of the study, while the dynamic coefficient of friction between the granules and the stainless-steel surface was determined for the remaining 8 s of the study. The software of the friction coefficient determination automatically calculated the static friction coefficient from the first 2 s of friction force results and automatically calculated the dynamic friction coefficient from the average of the remaining 8 s of friction force results (Figure 7).
It can be seen that the values of the static and dynamic friction coefficients of the granules are symmetrically distributed, with a significant dispersion in the values obtained.

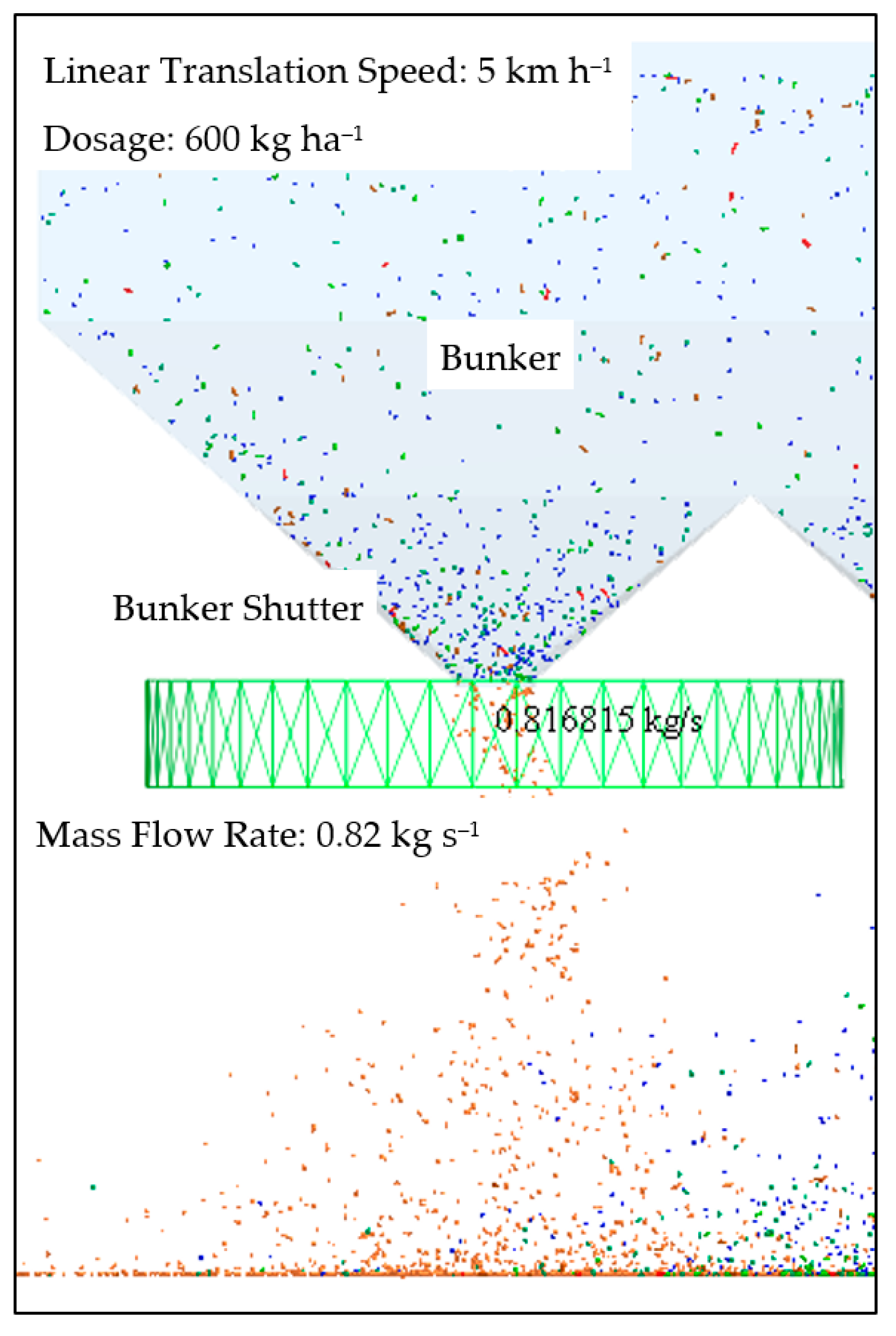
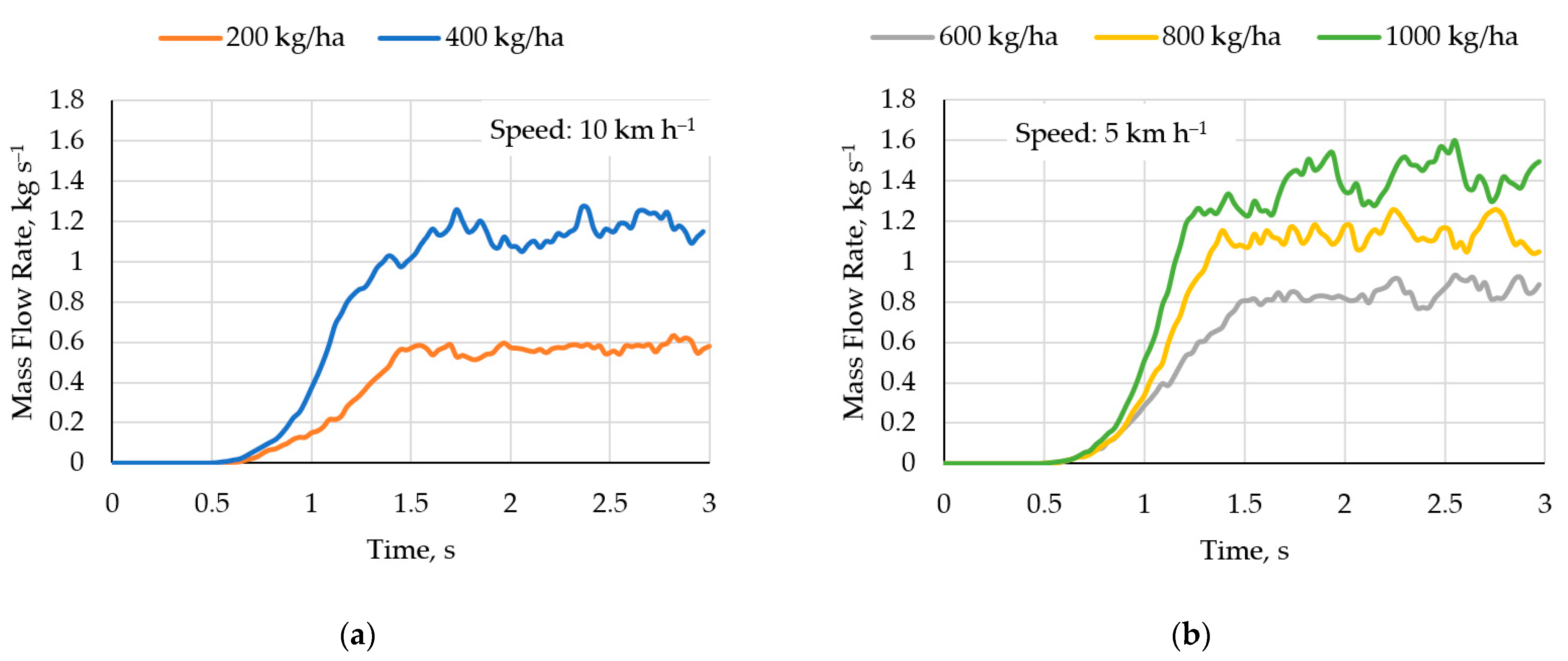
3.2. Verification of Granular Fertilizer Properties and Their Falling through the Bunker Shutter

In [25,28], the following properties of granules have the greatest effect on the accuracy of the results of granule-dispersion-modeling studies: granule size, granule size distribution, granule bulk density, and granule solid density. Granules of greater mass and volume, but less density, are distributed with more uniformity [17,32]. A smaller average particle size results in a higher mass discharge flow rate from the hopper [33]. Firstly, the selected granule properties were verified in the granule mass and bulk-density-modeling studies and are presented in Table 2. The results of the discrete element modeling of the granule “filling” of the cylindrical vessel are presented in Figure 8. It also shows an image of the experimentally filled container of about 1.00 l and the experimentally determined granule mass and bulk density, together with the calculated confidence intervals.
As can be seen from the results, the mass of the granules poured into the cylindrical container of about 1.00 l was 0.73 kg in the simulation, which was 2.7% more than the experimental result. For the bulk density of the granules in this container, the value obtained in the simulation was 726.89 kg m−3, which was 2.3% higher than the experimental value.
The next study on the modeling of the drained and repose angles of the granular structure continued the calibration studies of the selected granular material properties. The results of these investigations are presented in Figure 9. The drained and repose angles of the granules obtained from the simulation were measured using the software tools, and only the values are shown in this figure. The values of the drained and repose angles obtained from the experiments are shown next to the simulation results, together with the confidence interval. The simulation showed that the natural repose angle of the granules was about 2.4%, and the drained angle was about 4.5% higher than the experimental values for these angles. Moreover, when the visual simulation results were compared with the experimental results, the shape of the drained granule pile and the distribution of the drained granules on the ground were very similar to the experimental images, one of which is shown in Figure 2. The visual assessment also showed a good agreement between the experimental and simulated images of the granule repose angles.
A further modeling study of the fertilizer falling through one bunker shutter hole verified not only the properties of the selected granules but also the interaction of the granules with the bunker and bunker shutter models. Figure 10 shows the results of the granule flow simulation at a tractor with a spreader speed of 5 km h−1 and a spreading dosage norm of 600 kg ha−1 of organic granular fertilizer. The flow simulation studies resulted in the flow-versus-time relationships presented in Figure 11. It can be seen that the flow rate reached the required value after approximately 1.5 s; therefore, the average flow rate was calculated from approximately 1.5 s of the study. It was found that the results did not change further as the fertilizer flow simulation studies continued from approximately 3 s onwards, so the results up to the third test are presented here. These simulated granule mass flow values are presented in Table 5, which also presents the experimental field data from the experimental field studies of the single bunker shutter flow measurements of the fertilizer spreader. The calculated values of the theoretical fertilizer flow rate per bunker shutter are also given in this table.
As we can see from the above theoretical, experimental, and simulation results of the fertilizer flow, a good agreement between simulation and experimental results was obtained. The largest difference between the experimental and simulation studies was 5.10% when the spreading dosage norm of 600 kg ha−1 was used; the reasons for this discrepancy were not determined. A 9.87% difference in results was also obtained when the highest fertilizer spreading dosage norm was used. The fundamental reason for this discrepancy was that this spreading dosage norm for the used spreader is close to its maximum possible spreading dosage norm, which was very clearly shown by the fact that the experimental fertilizer spreading dosage norm after five tests was about 7.91% less than the required theoretical spreading dosage norm. Arguably, due to granule shape, size, and density; bunker shutter valve configuration; and other unidentified factors, in this case, a higher fertilizer flow was not achieved.
Summarizing all the results of the experimental verification of fertilizer properties and the results of modeling using the discrete element method, it was accepted that the granule models, granule material properties, fertilizer bunker, fertilizer bunker shutter models, and the material properties of these models were suitable. All of this was used further to simulate the spreading of these granules, using a model of a double-disc centrifugal fertilizer spreader.

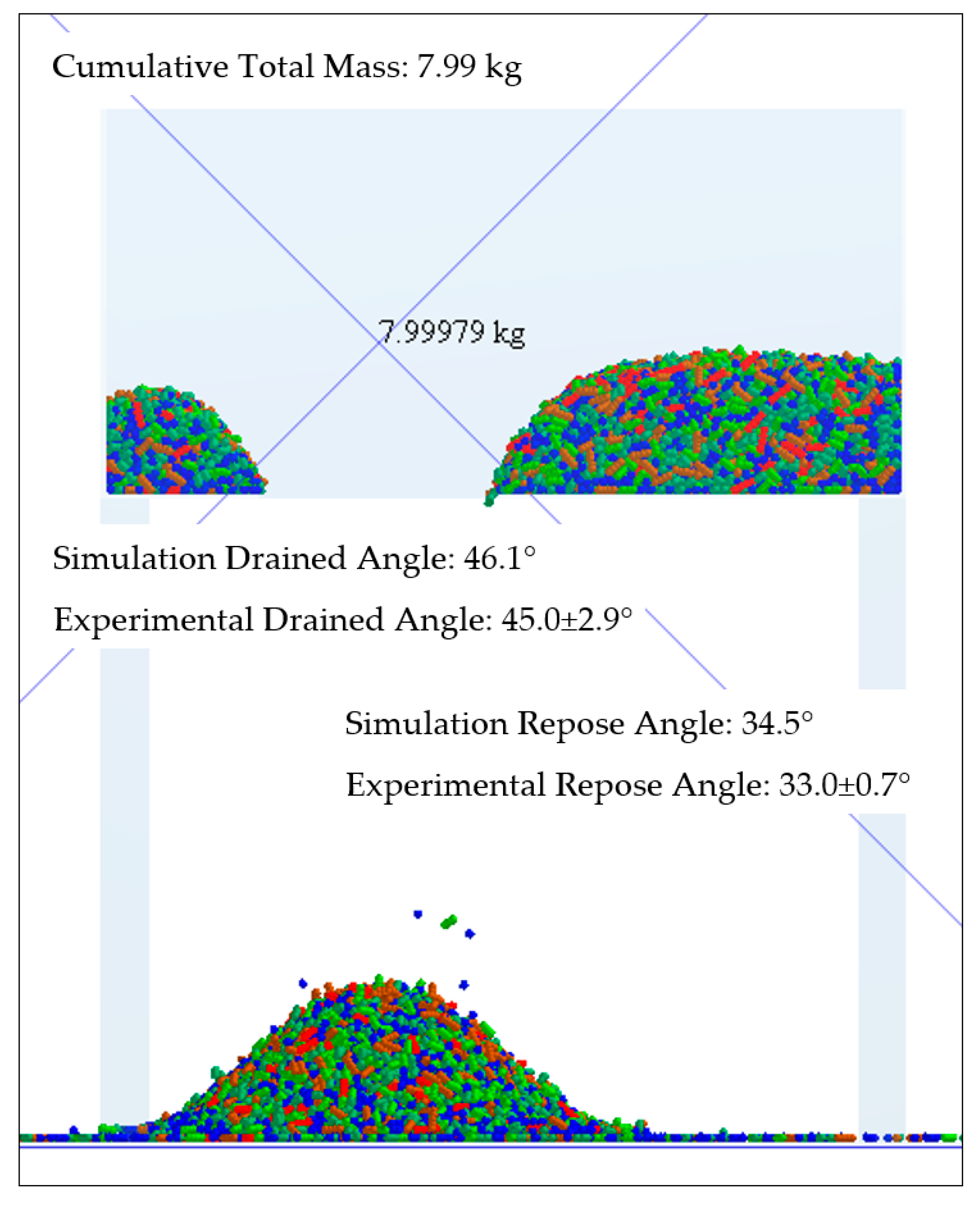
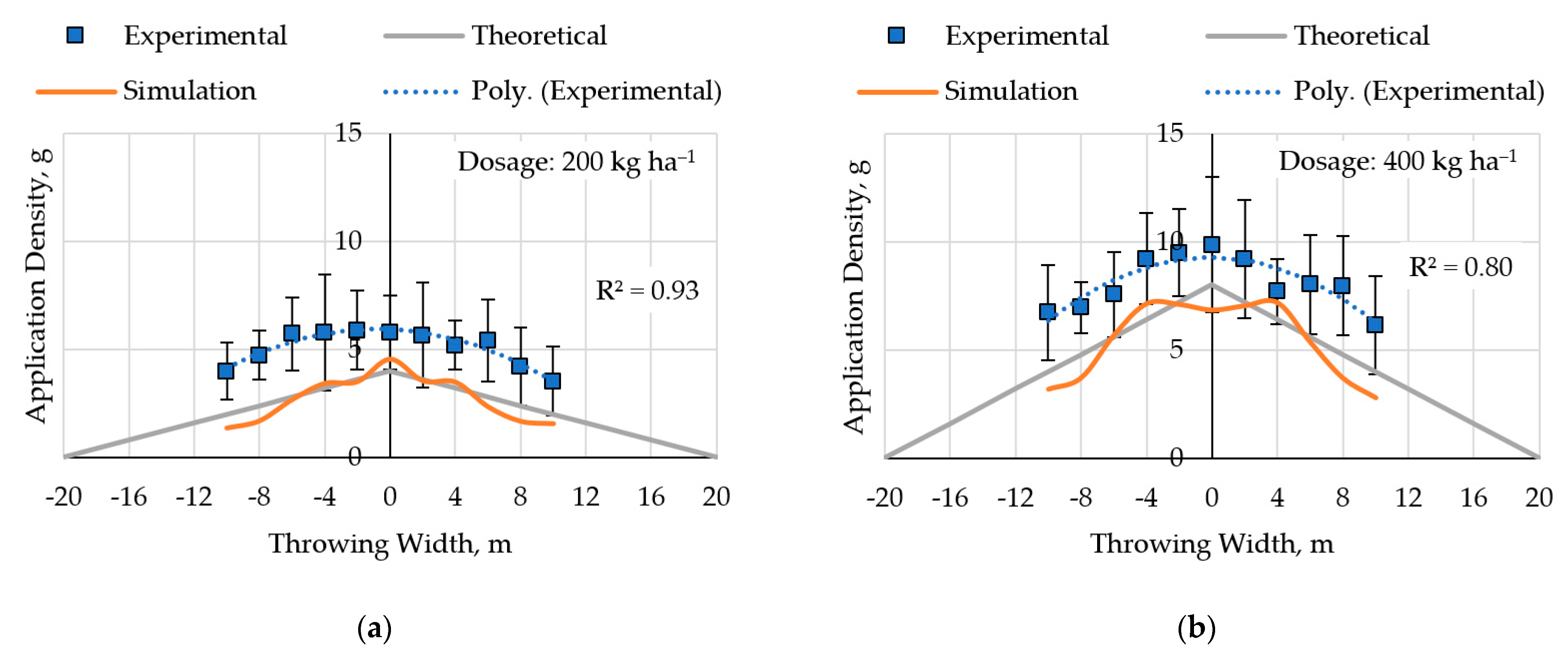
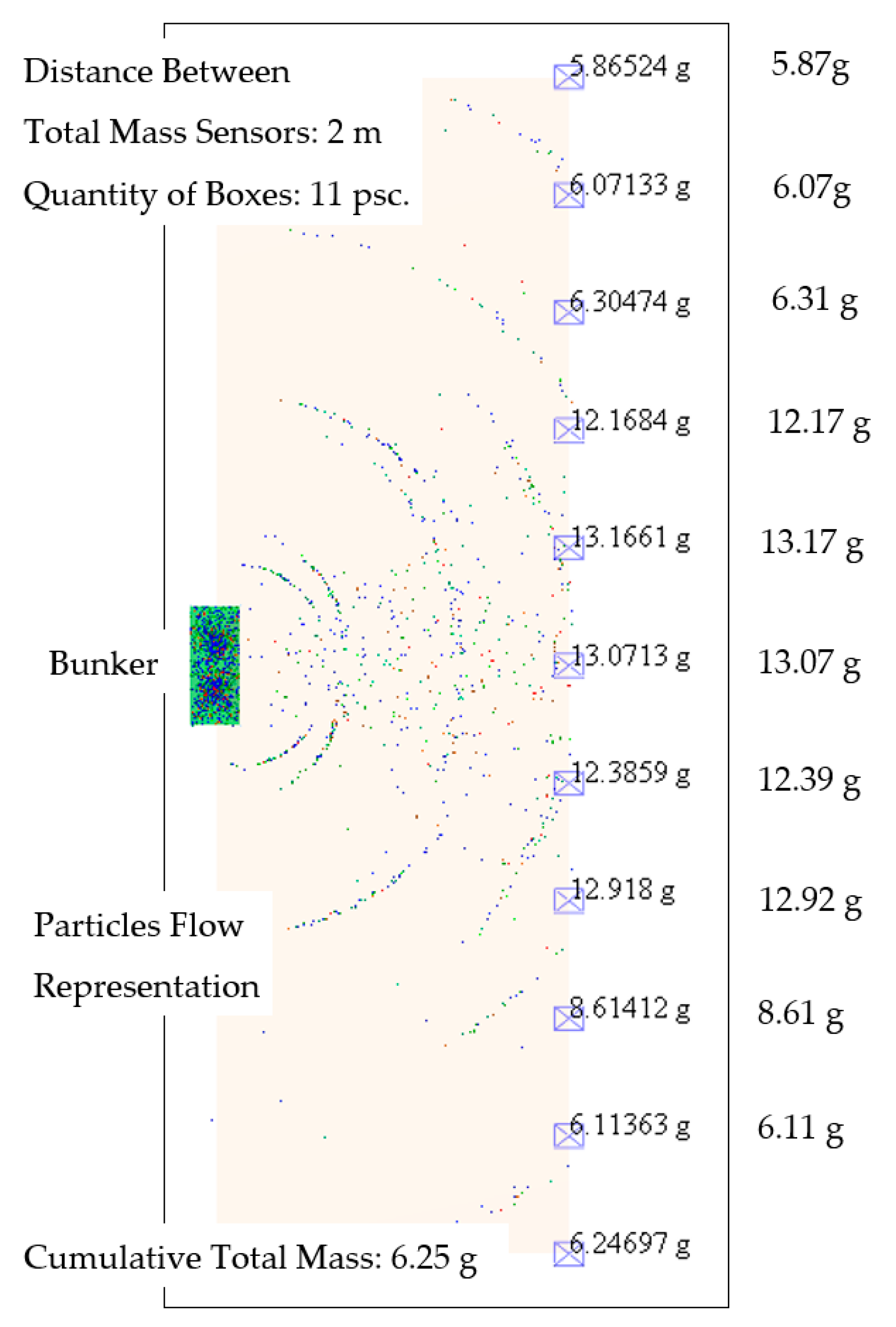
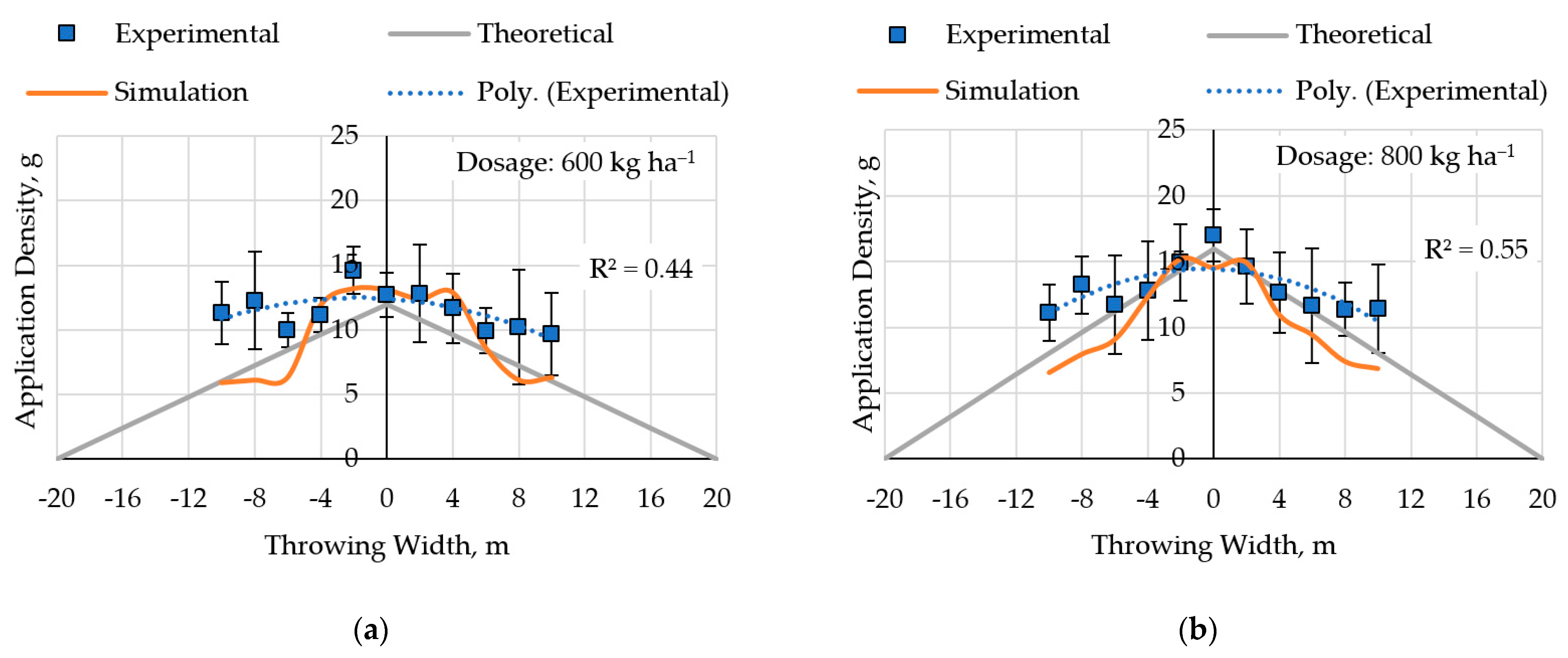
3.3. Experiment under Field Conditions and Simulation Spread of Fertilizer

Figure 12 below shows the results of spreading fertilizer at the dosage norm of 200 and 400 kg ha−1 by a centrifugal spreader. The driving speed of the tractor with the spreader was 10 km h−1, the throwing width was 20 m, and the driving of fertilizer spreading was performed in one direction. Both charts show the averages of the amount of fertilizer accumulated in the collection boxes and their confidence interval. The theoretical line of fertilizer distribution across the throwing width shows the amount of fertilizer that should be spread. For example, at a spreading dosage norm of 200 kg ha−1, a central box 400 mm long and 500 mm wide should contain 4 g of fertilizer, and then that amount of fertilizer decreases linearly over the entire throwing width. Driving in the opposite direction, or the so-called “rope” principle, theoretically covers the entire field evenly with the specified amount of fertilizer. These lines of theoretical spreading are given in all the graphs of spreading results; only, in each case, the amount of fertilizer presented depended on the norm of their spreading.
According to the above-described spreading modeling methodology, Figure 12 shows the results of spreading across the spreader’s throwing width at the fertilizer spreading dosage norm of 200 and 400 kg ha−1. The image of the double-disc spreader model used during the spreading simulation with part of the spread fertilizer is presented in Figure 13. This model consisted of a bunker with two discharge shutters, two rotating fertilizer spreading discs, and fertilizer spreading vanes. The results of fertilizer spreading across the throwing width were obtained in the discrete element simulation program by using granule mass collection sensors, which, in their size and placement in the spreading field, were identical to the spread fertilizer collection boxes used in the experiment. An image of the layout of the collection boxes used during these simulations and the amount of accumulated fertilizer in each of them are presented in Figure 14. Here, we offer a top view; the fertilizer bunker is on the left, and the fertilizer spread flow is shown between the bunker and the boxes. In this figure, simulation results were presented when the spreading dosage norm was 600 kg ha−1 and the spreading model linear movement speed was 5 km h−1. The results of the simulation of the remaining spreading dosage norms are presented only in the diagrams next to the results of experimental studies and the theoretical fertilizer spreading lines.
As we can see from the results presented in Figure 12a, the nature of the dependence of the spread distribution over the width of the field obtained during the experiment was quite close to the theoretical curve—the amount of fertilizer spread in the center was the highest, and it gradually decreased in the boxes farther away from the center. This happens due to the balance between the force of gravity and air resistance [34]. Such a tendency was also found in other scientific studies [17]. When evaluating the obtained quadratic polynomial rise with the peak of the theoretical curve, we noted that approximately 32.77% higher experimental values of fertilizer content were obtained compared to the theoretical ones. The values of the amount of fertilizer in the boxes obtained during the simulation were very close to the theoretical results. Similar results were obtained at the fertilizer dosage norm of 400 kg ha−1. The values of the experimental results were about 13.61% higher than the theoretical results. The results obtained during the simulation are close to the theoretical results; only when evaluating the nature of the curve of the simulation results, a smaller amount of spread fertilizer was obtained in the central box. It is assumed that this could have happened due to the mismatch of the parameters of the fertilizer spreader vanes in the simulation of the spreading of these fertilizers. The rather significant discrepancy between the experimental results presented in both diagrams, when small dosage norms of granular organic fertilizers were spread, and the theoretical ones could also be affected by the not quite correct position of the spreading vanes and possibly their improper length. As for the settings of the spreading discs of the machine (spreading vanes angle and angular velocity), they are difficult to determine because they depend on many factors, especially the physical and chemical properties [35]. During the experimental calibration of the fertilizer flow rate, the flow rate was found to be adequate. Additional field and dispersal-modeling studies are needed to verify these assumptions in the future.
Figure 15 shows the results of the studies at 600 and 800 kg ha−1 spreading dosage norms and a 5 km h−1 spreading speed. We see very similar trends that were presented in Figure 12. Using higher fertilization norms, the values of the fertilizer amount obtained during the experiment were very close to the theoretical amounts. According to the nature of the curves and the obtained values, the results obtained during the scattering simulation were close to the theoretical and experimental results. It can be said that, for these granules, using spreading dosage norms of 600 and 800 kg ha−1, the simulation model used, and the simulation parameters used are sufficiently accurate and allow us to expand the limits of application. The most important directions of research would be the studies of the shape, length, and position angles of rotation of rational spreading vanes and other parameters, with the aim of using a standard spreader that is used quite often, after making minor (hopefully) modifications to the equipment, so that the equipment could spread larger norms of fertilizer or drive faster during spreading. It was found that, to spread the fertilizer dosage norms of 600, 800, and 1000 kg ha−1, it is necessary to drive at a relatively low speed. Other scientific studies have found that, to achieve a more uniform distribution of cylindrical granules, it is important to increase the granule size by increasing the granule spreading flow [15], because the aerodynamic properties are greatly influenced by the size and mass of granulated fertilizers [34].
From the results of the granulated organic fertilizer spreading, using a fertilizer dosage norm of 1000 kg ha−1 and the spreader moving at a speed of 5 km h−1 (Figure 16), we can see that slightly different experimental results were obtained here compared to the results presented in Figure 12 and Figure 15. Here, it was found that the values of granule mass obtained during the experiment were lower than the theoretical values. The main reason for this discrepancy is that, during the experimental calibration of the fertilizer flow, the spreader achieved a lower-than-required flow of fertilizer dispersal through the bunker shutter. Nevertheless, we can see that this scattering was performed correctly, and the results that were obtained are reliable.

4. Conclusions

The values of the static and dynamic friction coefficients of the granules used in the simulation studies are symmetrically distributed, with a significant dispersion of values. The mass of the granules in the cylindrical container was found to be 2.7% higher than the experimental mass, and the bulk density of the granules was found to be 2.3% higher. The simulation gives a natural granule repose angle of about 2.4% and a drained angle of about 4.5% higher than in the experiment. The distribution of the crumbled granules on the ground surface obtained from the simulation was very similar to the visual images observed in the experiment. There was also an overlap in the repose angles of granules.
When comparing simulation fertilizer flow studies with experimental ones, it was found that the biggest differences of 5.10% and 9.87% were obtained when the spreading dosage norm of granular poultry manure fertilizer was 600 kg ha−1 and 1000 kg ha−1, respectively. When applying a fertilizer spreading dosage norm of 1000 kg ha−1, the essential reason for the discrepancy is that this spreading dosage norm for the used spreader is close to its maximum possible spreading dosage norm; this can be said because the experimental fertilizer spreading flow is about 7.91% lower than the required theoretical spreading dosage norm. It can be said that due to the shape, size, and density of the granules and the configuration of the bunker shutter valve, a higher fertilizer flow was not achieved.
Research has shown that when spreading granular poultry manure fertilizers at norms of 600, 800, and 1000 kg ha−1, it is necessary to drive at a relatively low speed, about 5 km h−1. It can be said that the studied granular fertilizers spreading at the dosage norm of 600 and 800 kg ha−1 allow us to expand the limits of spreading research in the future by using spreading simulation. The most important directions of research would be the research of the shape, length, and rotation angles of the rational spreader vanes, using the standard commonly used centrifugal spreader, after making small modifications of the spreader, to achieve that the spreader could spread larger norms of fertilizer or drive faster during spreading.

Author Contributions

Conceptualization, V.B., E.J. and K.L.; methodology, V.B., E.J., K.L., R.M. and G.J.; software, V.B. and R.M.; validation, V.B., E.J., K.L., R.M. and G.J.; formal analysis, V.B., E.J., K.L., R.M. and G.J.; investigation, V.B., E.J., K.L., R.M. and G.J.; resources, V.B., E.J., K.L., R.M. and G.J.; data curation, V.B., E.J., K.L., R.M. and G.J.; writing—original draft preparation, V.B., E.J., K.L., R.M. and G.J.; writing—review and editing, V.B., E.J. and K.L.; visualization, V.B., E.J., K.L., R.M. and G.J.; supervision, V.B., E.J., and K.L.; project administration, V.B., E.J. and K.L.; funding acquisition, V.B., E.J., K.L., R.M. and G.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank the Department of Agricultural Engineering and Safety of the Agriculture Academy of Vytautas Magnus University for the test development and support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rutkoviene, V.; Cesoniene, L.; Steponavicius, D. Nitrogen Losses from Organic and Mineral Fertilizers in Model Soil System. Cereal Res. Commun. 2007, 35, 313–316. [Google Scholar] [CrossRef]
  2. Raee, R.; Akbarpour, V.; Bahmanyar, M.A. Morphological Attributes and Phytochemical Compounds of Satureja hortensis L. in Response to Poultry Pellet and Zinc Sulphate Applications. J. Hortic. Sci. 2023, 36, 763–776. [Google Scholar] [CrossRef]
  3. Kaiser, D.E.; Mallarino, A.P.; Sawyer, J.E. Utilization of Poultry Manure Phosphorus for Corn Production. Soil Sci. Soc. Am. J. 2010, 74, 2211–2222. [Google Scholar] [CrossRef]
  4. Schroeder, P.D.; Radcliffe, D.E.; Cabrera, M.L. Rainfall Timing and Poultry Litter Application Rate Effects on Phosphorus Loss in Surface Runoff. J. Environ. Qual. 2004, 33, 2201–2209. [Google Scholar] [CrossRef]
  5. Abdala, D.B.; Ghosh, A.K.; da Silva, I.R.; de Novais, R.F.; Alvarez Venegas, V.H. Phosphorus Saturation of a Tropical Soil and Related P Leaching Caused by Poultry Litter Addition. Agric. Ecosyst. Environ. 2012, 162, 15–23. [Google Scholar] [CrossRef]
  6. Alloway, B.J. Sources of Heavy Metals and Metalloids in Soils. In Heavy Metals in Soils; Alloway, B., Ed.; Environmental Pollution; Springer: Dordrecht, The Netherlands, 2013; Volume 22, pp. 11–50. [Google Scholar] [CrossRef]
  7. Xiaobing, W.A.N.G.; Wuxing, L.I.U.; Zhengao, L.I.; Ying, T.E.N.G.; Christie, P.; Yongming, L.U.O. Effects of Long-Term Fertilizer Applications on Peanut Yield and Quality and Plant and Soil Heavy Metal Accumulation. Pedosphere 2020, 30, 555–562. [Google Scholar] [CrossRef]
  8. Jalali, M.; Hurseresht, Z. Assessment of Mobile and Potential Mobile Trace Elements Extractability in Calcareous Soils Using Different Extracting Agents. Front. Environ. Sci. Eng. 2020, 14, 7. [Google Scholar] [CrossRef]
  9. Jotautiene, E.; Bivainis, V.; Mieldazys, R.; Gaudutis, A.; Jasinskas, A. Experimental and Numerical Research of Granular Manure Fertilizer Application by Centrifugal Fertilizer Spreading. In Proceedings of the 21st International Scientific Conference “Engineering for Rural Development”, Jelgava, Latvia, 25–27 May 2022. [Google Scholar]
  10. Jasinskas, A.; Pekarskas, J.; Kucinskas, V.; Aboltins, A. Investigation of Natural Magnesium Mineral Fertilizer Granulation and Determination of Granule Qualitative Indicators. In Proceedings of the 15th Internal Scientific Conference “Engineering for Rural Development”, Jelgava, Latvia, 25–27 May 2016. [Google Scholar]
  11. Asgedom, H.; Tenuta, M.; Flaten, D.N.; Gao, X.; Kebreab, E. Nitrous Oxide Emissions from a Clay Soil Receiving Granular Urea Formulations and Dairy Manure. Agron. J. 2014, 106, 732–744. [Google Scholar] [CrossRef]
  12. Sulky Product List. Available online: http://www.sulky-burel.com/products (accessed on 6 April 2022).
  13. Søgaard, H.T.; Kierkegaard, P. Yield Reduction Resulting from Uneven Fertilizer Distribution. Trans. ASAE 1994, 37, 1749–1752. [Google Scholar] [CrossRef]
  14. Pocius, A.; Jotautiene, E.; Pekarskas, J.; Mieldazys, R.; Jasinskas, A. Research of Particle Geometrical Parameters and Aerodynamic Features of Granular Organic Compost Fertilizers. In Proceedings of the 13th International Scientific Conference “Engineering for Rural Development”, Jelgava, Latvia, 20–29 May 2014. [Google Scholar]
  15. Zinkevičienė, R.; Jotautienė, E.; Juostas, A.; Comparetti, A.; Vaiciukevičius, E. Simulation of Granular Organic Fertilizer Application by Centrifugal Spreader. Agronomy 2021, 11, 247. [Google Scholar] [CrossRef]
  16. Van Liedekerke, P.; Piron, E.; Vangeyte, J.; Villette, S.; Ramon, H.; Tijskens, E. Recent Results of Experimentation and DEM Modeling of Centrifugal Fertilizer Spreading. Granul. Matter 2008, 10, 247–255. [Google Scholar] [CrossRef]
  17. Zinkevičienė, R.; Jotautienė, E.; Jasinskas, A.; Kriaučiūnienė, Z.; Lekavičienė, K.; Naujokienė, V.; Šarauskis, E. Determination of Properties of Loose and Granulated Organic Fertilizers and Qualitative Assessment of Fertilizer Spreading. Sustainability 2022, 14, 4355. [Google Scholar] [CrossRef]
  18. Gavrilović, M.; Dimitrijević, A.; Radojičin, M.; Mileusnić, Z.; Miodragović, R. Effects of the Application System on the Physical and Mechanical Properties of Mineral Fertilizers. J. Process. Energy Agric. 2018, 22, 180–183. [Google Scholar] [CrossRef]
  19. Koko, J.; Virin, T. Optimization of a Fertilizer Spreading Process. Math. Comput. Simul. 2009, 79, 3099–3109. [Google Scholar] [CrossRef]
  20. Olieslagers, R.; Ramon, H.; De Baerdemaeker, J. Calculation of Fertilizer Distribution Patterns from a Spinning Disc Spreader by Means of a Simulation Model. J. Agric. Eng. Res. 1996, 63, 137–152. [Google Scholar] [CrossRef]
  21. Bivainis, V.; Jotautiene, E.; Zinkeviciene, R. Assessment of Granulated Manure Fertilizer Centrifugal Spreading Field Simulation. In Proceedings of the 20th International Conference “Engineering for Rural Development”, Jelgava, Latvia, 26–28 May 2021. [Google Scholar]
  22. Van Liedekerke, P.; Tijskens, E.; Dintwa, E.; Rioual, F.; Vangeyte, J.; Ramon, H. DEM Simulations of the Particle Flow on a Centrifugal Fertilizer Spreader. Powder Technol. 2009, 190, 348–360. [Google Scholar] [CrossRef]
  23. Organic Fertilizer ORGEVIT 4-3-2.5 Datasheet. Available online: https://memon.nl/products/orgevit-4-3-2-5/ (accessed on 10 March 2023).
  24. Ding, S.; Bai, L.; Yao, Y.; Yue, B.; Fu, Z.; Zheng, Z.; Huang, Y. Discrete Element Modelling (DEM) of Fertilizer Dual-Banding with Adjustable Rates. Comput. Electron. Agric. 2018, 152, 32–39. [Google Scholar] [CrossRef]
  25. Gallego, E.; Fuentes, J.M.; Ruiz, Á.; Hernández-Rodrigo, G.; Aguado, P.; Ayuga, F. Determination of Mechanical Properties for Wood Pellets Used in DEM Simulations. Int. Agrophys. 2020, 34, 485–494. [Google Scholar] [CrossRef]
  26. Yinyan, S.; Man, C.; Xiaochan, W.; Odhiambo, M.O.; Weimin, D. Numerical Simulation of Spreading Performance and Distribution Pattern of Centrifugal Variable-Rate Fertilizer Applicator Based on DEM Software. Comput. Electron. Agric. 2018, 144, 249–259. [Google Scholar] [CrossRef]
  27. Yang, L.; Chen, L.; Zhang, J.; Liu, H.; Sun, Z.; Sun, H.; Zheng, L. Fertilizer Sowing Simulation of a Variable-Rate Fertilizer Applicator Based on EDEM. In Proceedings of the 6th International “IFAC Conference on Bio-Robotics”, Beijing, China, 13–15 July 2018. [Google Scholar]
  28. Coetzee, C.J.; Lombard, S.G. Discrete Element Method Modelling of a Centrifugal Fertiliser Spreader. Biosyst. Eng. 2011, 109, 308–325. [Google Scholar] [CrossRef]
  29. Van Liedekerke, P.; Tijskens, E.; Ramon, H. Discrete Element Simulations of the Influence of Fertiliser Physical Properties on the Spread Pattern from Spinning Disc Spreaders. Biosyst. Eng. 2009, 102, 392–405. [Google Scholar] [CrossRef]
  30. Liping, Z.; Weiqiang, Z.; Lixin, Z.; Yulong, L. Design of a Sieve Bucket Spreading Mechanism Based on EDEM. J. Eng. Sci. Technol. Rev. 2019, 12, 84–90. [Google Scholar]
  31. Organic Fertilizer BENESOL 4-3-3 Datasheet. Available online: https://benefert.com/products/solid-organic-fertilizers/organic-fertilizer-benesol-4-3-3/ (accessed on 15 February 2023).
  32. Tang, P.; Li, H.; Issaka, Z.; Chen, C. Effect of manifold layout and fertilizer solution concentration on fertilization and flushing times and uniformity of drip irrigation systems. Agric. Water Manag. 2018, 200, 71–79. [Google Scholar] [CrossRef]
  33. Reumers, J.; Tijskens, E.; Ramon, H. Experimental characterisation of the tangential and cylindrical fertiliser distribution pattern from a spinning disc: A parameter study. Biosyst. Eng. 2003, 86, 327–337. [Google Scholar] [CrossRef]
  34. El-Emam, M.A.; Zhou, L.; Shi, W.D.; Sobhi, M. Determination of Some Engineering Properties of Jojoba Granular Matter [Simmondsia Chinensis]. Granul. Matter 2023, 25, 24. [Google Scholar] [CrossRef]
  35. Przywara, A.; Santoro, F.; Kraszkiewicz, A.; Pecyna, A.; Pascuzzi, S. Experimental study of disc fertilizer spreader performance. Agriculture 2020, 10, 467. [Google Scholar] [CrossRef]
Agriculture 13 01135 g001 550
Figure 1. The view of granulated-pellets-particle–equipment-material static and dynamic coefficients of friction determination device.
Figure 1. The view of granulated-pellets-particle–equipment-material static and dynamic coefficients of friction determination device.
Agriculture 13 01135 g001
Agriculture 13 01135 g002 550
Figure 2. The view of granulated pellets drained and repose-angle-determination device.
Figure 2. The view of granulated pellets drained and repose-angle-determination device.
Agriculture 13 01135 g002
Agriculture 13 01135 g003 550
Figure 3. Layout diagram of the fertilizer collecting boxes.
Figure 3. Layout diagram of the fertilizer collecting boxes.
Agriculture 13 01135 g003
Agriculture 13 01135 g004 550
Figure 4. Granule length distribution histogram.
Figure 4. Granule length distribution histogram.
Agriculture 13 01135 g004
Agriculture 13 01135 g005 550
Figure 5. Fertilizer granule length distribution box plot chart.
Figure 5. Fertilizer granule length distribution box plot chart.
Agriculture 13 01135 g005
Agriculture 13 01135 g006 550
Figure 6. Granule-particle–equipment-material frictional force–ring displacement dependency.
Figure 6. Granule-particle–equipment-material frictional force–ring displacement dependency.
Agriculture 13 01135 g006
Agriculture 13 01135 g007 550
Figure 7. Box plots charts of granule-particle–equipment-material static and kinetic coefficients of friction.
Figure 7. Box plots charts of granule-particle–equipment-material static and kinetic coefficients of friction.
Agriculture 13 01135 g007
Agriculture 13 01135 g008 550
Figure 8. Results of the modeling and experimental calibration of the granule mass and bulk density: (a) results of the modeling of the granule mass, (b) results of the modeling of the bulk density of the granules, and (c) a general view of the granule-filled vessel and the experimental results of the granule mass in the vessel and bulk density of the granules.
Figure 8. Results of the modeling and experimental calibration of the granule mass and bulk density: (a) results of the modeling of the granule mass, (b) results of the modeling of the bulk density of the granules, and (c) a general view of the granule-filled vessel and the experimental results of the granule mass in the vessel and bulk density of the granules.
Agriculture 13 01135 g008
Agriculture 13 01135 g009 550
Figure 9. Results of modeling and experimental studies of granule static repose and static drained angles.
Figure 9. Results of modeling and experimental studies of granule static repose and static drained angles.
Agriculture 13 01135 g009
Agriculture 13 01135 g010 550
Figure 10. Simulation results of the granule flow through one bunker shutter at a fertilizer spreading dosage norm of 600 kg ha−1 and a bunker model travel speed of 5 km h−1.
Figure 10. Simulation results of the granule flow through one bunker shutter at a fertilizer spreading dosage norm of 600 kg ha−1 and a bunker model travel speed of 5 km h−1.
Agriculture 13 01135 g010
Agriculture 13 01135 g011 550
Figure 11. Time-dependent flow rate simulations of fertilizer crumbling through a single bunker shutter: (a) mass flow rate at spreading dosage norms of 200 and 400 kg ha−1 and with the spreader model moving at a speed of 10 km h−1; and (b) mass flow rate at spreading dosage norms of 600, 800, and 1000 kg ha−1 and with the spreader model moving at a speed of 5 km h−1.
Figure 11. Time-dependent flow rate simulations of fertilizer crumbling through a single bunker shutter: (a) mass flow rate at spreading dosage norms of 200 and 400 kg ha−1 and with the spreader model moving at a speed of 10 km h−1; and (b) mass flow rate at spreading dosage norms of 600, 800, and 1000 kg ha−1 and with the spreader model moving at a speed of 5 km h−1.
Agriculture 13 01135 g011
Agriculture 13 01135 g012 550
Figure 12. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when driving speed is 10 km h−1, working width is 20 m, and throwing width is 40 m (a) Fertilizer spreading dosage norm of 200 kg ha−1 and (b) fertilizer spreading dosage norm of 400 kg ha−1.
Figure 12. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when driving speed is 10 km h−1, working width is 20 m, and throwing width is 40 m (a) Fertilizer spreading dosage norm of 200 kg ha−1 and (b) fertilizer spreading dosage norm of 400 kg ha−1.
Agriculture 13 01135 g012
Agriculture 13 01135 g013 550
Figure 13. Image of a double-disc centrifugal fertilizer spreader model and part of the spread granules and the ground base on which the granules were spread.
Figure 13. Image of a double-disc centrifugal fertilizer spreader model and part of the spread granules and the ground base on which the granules were spread.
Agriculture 13 01135 g013
Agriculture 13 01135 g014 550
Figure 14. Image of the bunker, distribution of fertilizer spreading, and sensor-boxes recording the accumulated mass of the spread fertilizer; the mass of accumulated granular organic fertilizers is presented next to them.
Figure 14. Image of the bunker, distribution of fertilizer spreading, and sensor-boxes recording the accumulated mass of the spread fertilizer; the mass of accumulated granular organic fertilizers is presented next to them.
Agriculture 13 01135 g014
Agriculture 13 01135 g015 550
Figure 15. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when driving speed is 5 km h−1, working width is 20 m, and throwing width is 40 m. (a) Fertilizer spreading dosage norm of 600 kg ha−1 and (b) fertilizer spreading dosage norm of 800 kg ha−1.
Figure 15. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when driving speed is 5 km h−1, working width is 20 m, and throwing width is 40 m. (a) Fertilizer spreading dosage norm of 600 kg ha−1 and (b) fertilizer spreading dosage norm of 800 kg ha−1.
Agriculture 13 01135 g015
Agriculture 13 01135 g016 550
Figure 16. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when the fertilizer spreading dosage norm is 1000 kg ha−1; driving speed is 5 km h−1; working width is 20 m; throwing width is 40 m.
Figure 16. Experimental, theoretical, and modeled distribution of fertilizer mass across the spreader’s throwing width when the fertilizer spreading dosage norm is 1000 kg ha−1; driving speed is 5 km h−1; working width is 20 m; throwing width is 40 m.
Agriculture 13 01135 g016
Table
Table 1. Composition of granular organic fertilizer, nutrition values, and granules’ material data.
Table 1. Composition of granular organic fertilizer, nutrition values, and granules’ material data.
IndicatorsValues
Nitrogen (N) total, %4.0
Nitrogen (N) organic, %3.6
Ammonia (NH4), %0.4
Water-soluble phosphorus pentoxide (P2O5), %3.0
Water-soluble potassium oxide (K2O), %2.5
Calcium oxide (CaO), %9.0
Magnesium oxide (MgO), %1.0
Sulphur (SO3), %1.5
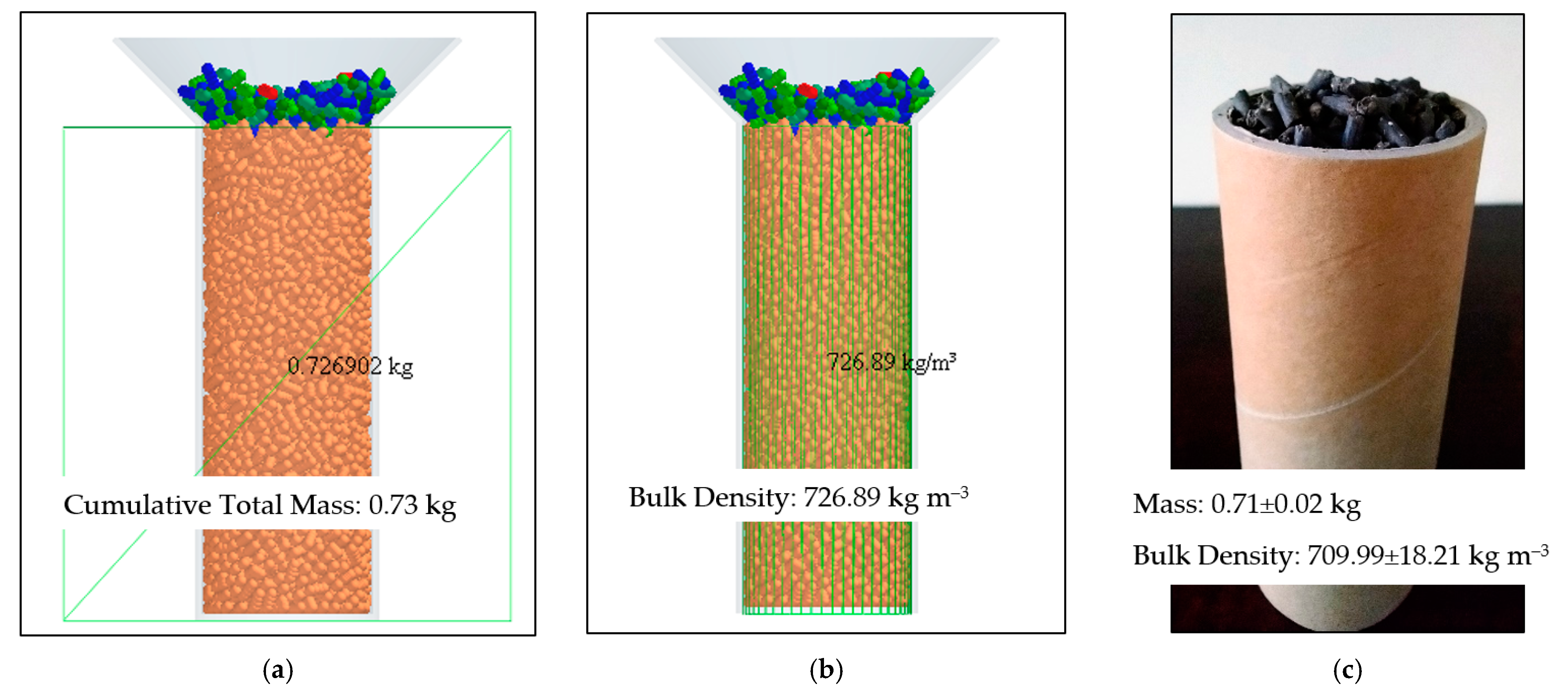
Granule diameter, mm5.49 ± 0.12 *
Granule length, mm9.60 ± 0.74 *
Granule bulk density, kg m−3709.99 ± 21 *
Granule solid density, kg m−31297.21 ± 36 *
* Confidence level (95%).
Table
Table 2. Granulated fertilizer properties for spreading DEM modeling.
Table 2. Granulated fertilizer properties for spreading DEM modeling.
IndicatorsValuesValues Variation Range in Verification
Young’s Modulus, MPa75-
Poisson’s Ratio0.25-
Coefficient of Restitution (Particle–Equipment Material)0.450.35 ÷ 0.55
Coefficient of Restitution (Particle–Particle)0.600.50 ÷ 0.70
Coefficient of Static Friction (Particle–Particle)0.500.40 ÷ 0.60
Coefficient of Kinetic Friction (Particle–Particle)0.250.15 ÷ 0.35
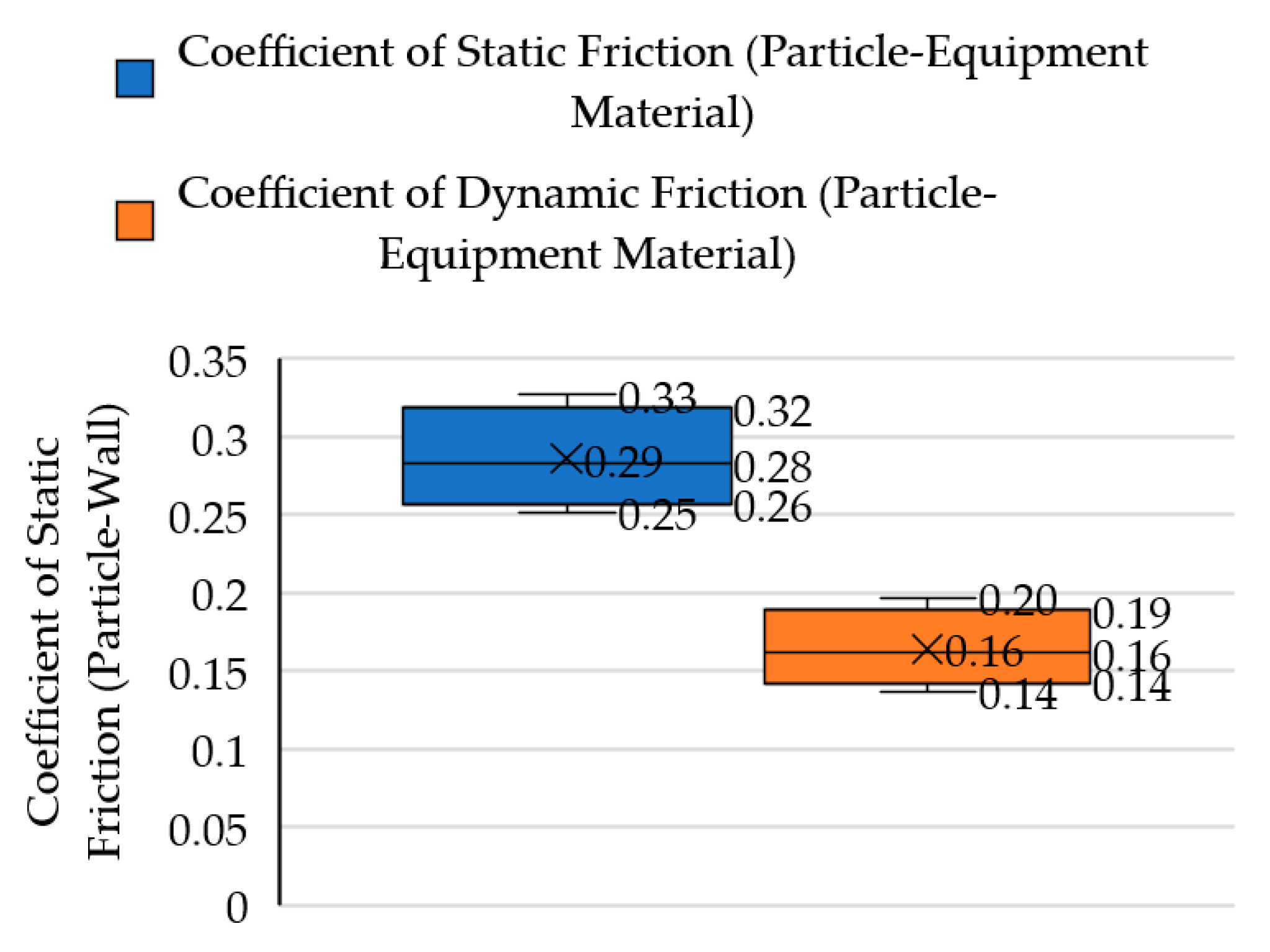
Coefficient of Static Friction (Particle–Equipment Material)0.29 ± 0.03 *-
Coefficient of Kinetic Friction (Particle–Equipment Material)0.16 ± 0.02 *-
* Confidence level (95%); these properties were experimentally determined.
Table
Table 3. Main parameters of the studies of fertilizer spreading.
Table 3. Main parameters of the studies of fertilizer spreading.
IndicatorsTechnical Parameters
Spreader modelAmazone ZA-M-1001Amazone ZA-M-1201
Spreading dosage norm, kg ha−1200 and 400600, 800 and 1000
Speed, km h−1105
Spreading disk OM 18–24 diameter, mm455455
Length of the vanes, mm260 (short); 360 (long)260 (short); 360 (long)
Vane setting positions15 (short); 43 (long)15 (short); 43 (long)
Disk speed, min−1720720
Working width, m2020
Throwing width, m4040
Table
Table 4. Images of granule models, length, and their percentage.
Table 4. Images of granule models, length, and their percentage.
Agriculture 13 01135 i001Agriculture 13 01135 i002Agriculture 13 01135 i003Agriculture 13 01135 i004Agriculture 13 01135 i005Agriculture 13 01135 i006
ShapeSingle SphereDual SphereStraight Four Sphere
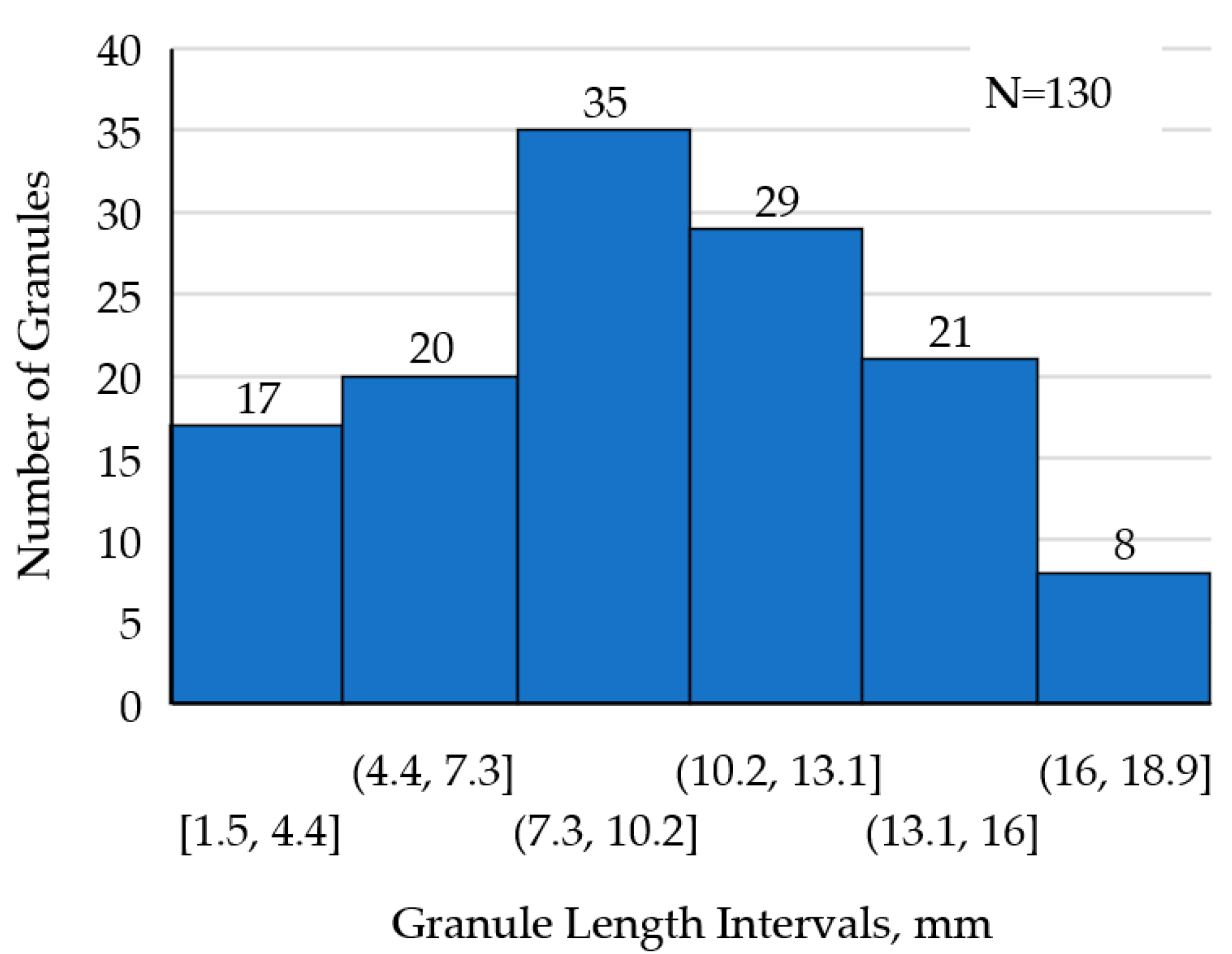
Length, mm2.955.858.7511.6514.5517.45
Proportion, %13152722166
Table
Table 5. Results of modeling and field studies of fertilizer crumbling through the bunker shutter.
Table 5. Results of modeling and field studies of fertilizer crumbling through the bunker shutter.
Spreading Dosage Norm, kg ha−1Theoretical Fertilizer Mass Flow of One Bunker Shutter, kg s−1Fertilizer Mass Flow Obtained during the Calibration of One Bunker Shutter, kg s−1Fertilizer Flow Obtained during the Simulation, kg s−1Simulation Results vs. Experimental Results, %Speed, km h−1Spreader Model
2000.560.57 ± 0.10 *0.57−0.5410Amazone ZA-M-1001
4001.111.18 ± 0.17 *1.16−1.90
6000.830.80 ± 0.12 *0.84+5.105Amazone ZA-M-1201
8001.111.17 ± 0.11 *1.13−2.98
10001.391.28 ± 0.24 *1.42+9.87
* Confidence Level (95%).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bivainis, V.; Jotautienė, E.; Lekavičienė, K.; Mieldažys, R.; Juodišius, G. Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading. Agriculture 2023, 13, 1135. https://doi.org/10.3390/agriculture13061135

AMA Style

Bivainis V, Jotautienė E, Lekavičienė K, Mieldažys R, Juodišius G. Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading. Agriculture. 2023; 13(6):1135. https://doi.org/10.3390/agriculture13061135

Chicago/Turabian Style

Bivainis, Vaidas, Eglė Jotautienė, Kristina Lekavičienė, Ramūnas Mieldažys, and Gražvydas Juodišius. 2023. "Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading" Agriculture 13, no. 6: 1135. https://doi.org/10.3390/agriculture13061135

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop