Mechanism Analysis of the Influence of Structural Parameters on the Hydraulic Performance of the Novel Y-Shaped Emitter
Abstract
:1. Introduction
2. Materials and Methods
2.1. Emitter Design and Size Parameters
2.2. Control Equations
2.3. Mesh and Boundary Conditions
2.4. Validation of the Calculated Results
3. Calculation Results and Analysis
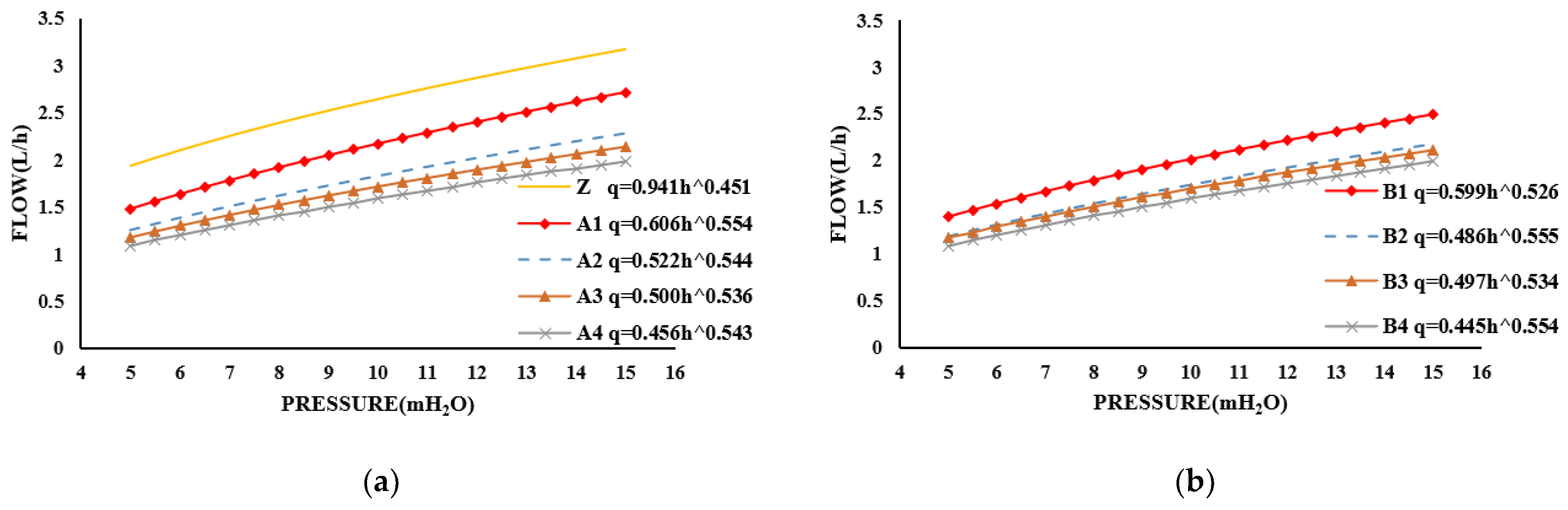
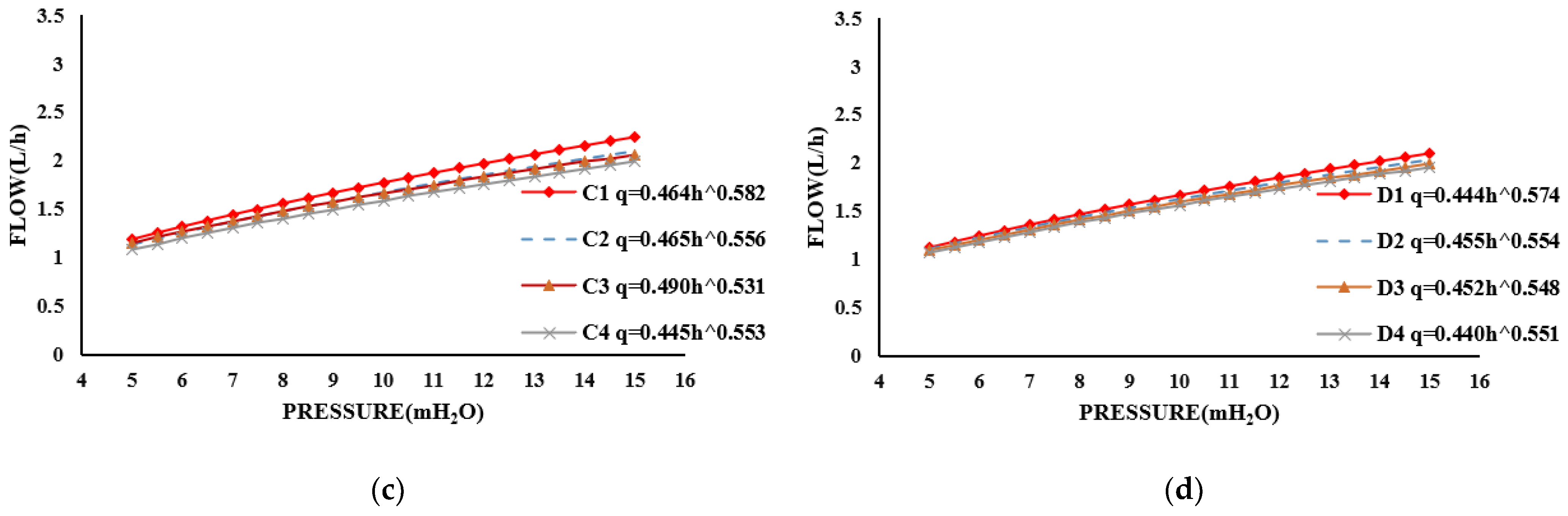
3.1. Effect of Waist-Arc Angle and Crown-To-Chord Ratio on Hydraulic Performance
3.1.1. Analysis of the Influence of the Waist-Arc Angle on Hydraulic Performance
3.1.2. Analysis of the Influence of Crown-To-Chord Ratio on Hydraulic Performance
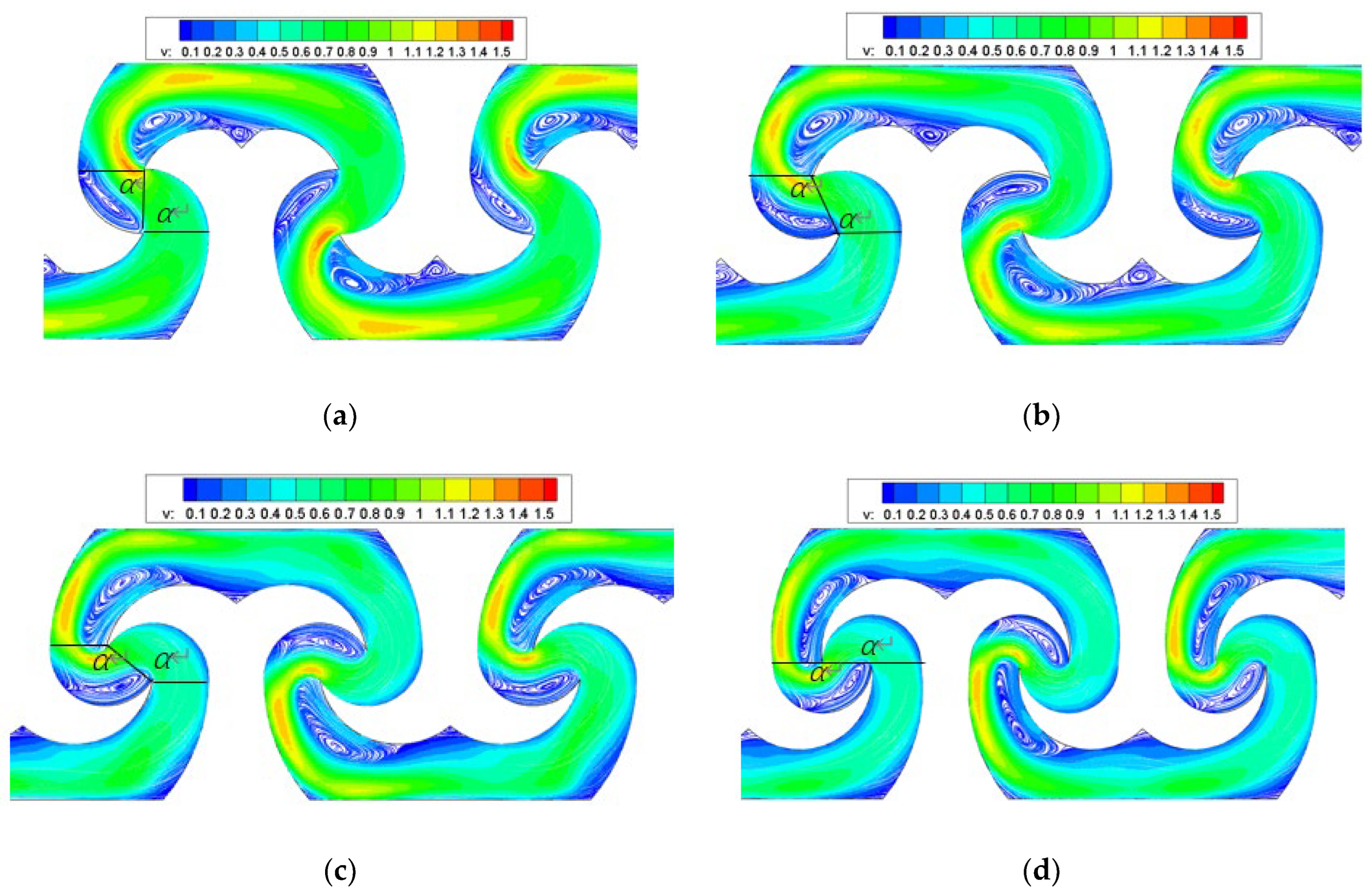
3.2. Effect of Waist-Arc Angle and Crown-To-Chord Ratio on Flow Field
3.2.1. Analysis of the Effect of the Waist-Arc Angle on the Flow Field
3.2.2. Analysis of the Effect of the Crown-To-Chord Ratio on the Flow Field
3.3. Optimization of Both Hydraulic and Anti-Clogging Performance
4. Conclusions
- If the crown-to-chord ratio was kept unchanged, the larger the waist-arc angle was, the greater the pressure drop ratio before and after the water flow through the low-speed vortex area became, and the smaller the design flow of the Y-shaped emitter; this led to improved hydraulic performance.
- As the crown-to-chord ratio of the Y-shaped emitter decreased, the influence of the waist-arc angle on the design flow and hydraulic performance diminished.
- If the waist-arc angle remained unchanged, reducing the crown-to-chord ratio could increase the vortex strength inside the channel, thereby reducing the design flow of the emitter and improving the hydraulic performance.
- As the waist-arc angle of the Y-shaped emitter increased, the influence of the crown-to-chord ratio on the design flow and hydraulic performance diminished; when the Y-shaped emitter waist-arc angle increased to 180°, the crown-to-chord ratio had little to no effect on the design flow or hydraulic performance.
- When considering both good hydraulic performance and anti-clogging performance, by enlarging the channel width by 25% (A4(2) emitter) or shortening the channel length by 44.3% (A4(4) emitter), the Y-shaped emitter, with a waist-arc angle of 180°, had a similar hydraulic performance to a commonly-used triangular-channel emitter with the same cross-sectional size and channel length.
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geng, S.; Liu, D.; Xia, P. Research on China’s water use efficiency of China based on a comparative analysis. Water. Resour. Devel. Res. 2022, 22, 77–82, (In Chinese with English Abstract). [Google Scholar]
- Chen, B.; Chen, F. Discussion on Water-saving Irrigation Technology of Farmland Water Conservancy. J. Agric. Cat. 2023, 13, 176–178, (In Chinese with English Abstract). [Google Scholar]
- Shiri, J.; Karimi, B.; Karimi, N.; Kazemi, M.H.; Karimi, S. Simulating wetting front dimensions of drip irrigation systems: Multi criteria assessment of soft computing models—Sciencedirect. J. Hydrol. 2020, 585, 124792. [Google Scholar] [CrossRef]
- Lamm, F.R.; Colaizzi, P.D.; Sorensen, R.B.; Bordovsky, J.P.; Dougherty, M.; Balkcom, K.; Zaccaria, D.; Bali, K.M.; Rudnick, D.R.; Peters, R.T. A 2020 Vision of Subsurface Drip Irrigation in the U.S. Trans. ASABE 2021, 64, 1319–1343. [Google Scholar] [CrossRef]
- Nogueira, V.H.B.; Diotto, A.V.; Thebaldi, M.S.; Colombo, A.; Silva, Y.F.; de Lima, E.M.; Resende, G.F.L. Variation in the Flow Rate of Drip Emitters in a Subsurface Irrigation System for Different Soil Types. Agric. Water Manag. 2021, 243, 106485. [Google Scholar] [CrossRef]
- Zhang, L.; Li, S. Numerical experimental investigation of douche hydraulic performance on drop irrigation of tooth-type labyrinth channel. Water. Resour. Power. 2017, 35, 103–106, (In Chinese with English Abstract). [Google Scholar]
- Wei, Q.S.; Shi, Y.S.; Dong, W.C.; Lu, G.; Huang, S.H. Study on hydraulic performance of drip emitters by computational fluid dynamics. Agric. Water. Manag. 2006, 84, 130–136. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L.; Wu, P.; Cai, Y.; Zhao, X.; Yao, C. Hydraulic performance and parameter optimisation of a microporous ceramic emitter using computational fluid dynamics, artificial neural network and multi-objective genetic algorithm. Biosyst. Eng. 2020, 189, 11–23. [Google Scholar] [CrossRef]
- Baghel, Y.; Kumar, J.; Patel, V. CFD Analysis of the Flow Characteristics of In-Line Drip Emitter with Different Labyrinth Channels. J. Inst. Eng. India Ser. A. 2021, 102, 111–119. [Google Scholar] [CrossRef]
- Zanca, R.B.; Silva, F.D.; SantAnna, D.O.; Silva, A.T.; Nova, H.F.; Santos, I.F.; Reis, J.A. Modeling and hydraulic performance evaluation of a dripper device coupled to a branched water distribution network. Rev. Ambiente Agua 2019, 14, e2340. [Google Scholar] [CrossRef]
- Mattar, M.A.; Alamoud, A.I. Gene expression programming approach for modeling the hydraulic performance of labyrinth-channel emitters. Comput. Electron. Agric. 2017, 142, 450–460. [Google Scholar] [CrossRef]
- Saccone, D.; Marchis, M. Optimization of the Design of Labyrinth Emitter for Agriculture Irrigation Using Computational Fluid Dynamic Analysis. AIP Conf. Proc. 2018, 2040, 140013. [Google Scholar]
- Zhang, C.; Niu, Y.; Liu, X. Numerical simulation of influence of tooth angle on hyaraulic characteristics of labyrinth emitter. J. Drain. Irrig. 2022, 40, 751–756, (In Chinese with English Abstract). [Google Scholar]
- Celik, H.K.; Karayel, D.; Caglayan, N.; Rennie, A.E.; Akinci, I. Rapid prototyping and flow simulation applications in design of agricultural irrigation equipment: Case study for a sample in-line drip emitter: The paper is to study CFD and RP application samples on the design issues associated with agricultural irrigation equipment. Virtual Phys. Prototyp. 2011, 6, 47–56. [Google Scholar]
- Du, P.; Li, Z.; Wang, C.; Ma, J. Analysis of the influence of the channel layout and size on the hydraulic performance of emitters. Agric. Water. Manag. 2022, 12, 541. [Google Scholar] [CrossRef]
- Patil, S.S.; Nimbalkar, P.T.; Joshi, A. Hydraulic Study, Design & Analysis of Different Geometries of Drip Irrigation Emitter Labyrinth. IJEAT 2013, 2, 455–462. [Google Scholar]
- Wang, C.; LI, Z.; Ma, J. Influence of emitter structure on its hydraulic performance based on the vortex. Agric. Water. Manag. 2021, 11, 508. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Wang, W.; Xue, S. Effect of optimization forms of flow path on emitter hydraulic and anti-clogging performance in drip irrigation system. Irrig. Sci. 2018, 36, 37–47. [Google Scholar] [CrossRef]
- Wu, F.; Dong, X.; Wu, Y.; Ma, D.; Feng, X. Hydraulic properties of the flow in a gradual shrinking and sudden enlarging channel. J. N. China Univ. Water Res. Electric Power. 2017, 38, 7, (In Chinese with English Abstract). [Google Scholar]
- Guo, L.; Bai, D.; Wang, X.; He, J.; Zhou, W.; Cheng, P. Numerical simulation and verification of hydraulic performance and energy dissipation mechanism of two-ways mixed flow emitter. Trans. CSAE 2017, 33, 100–107, (In Chinese with English Abstract). [Google Scholar]
- Xing, S.; Wang, Z.; Zhang, J.; Liu, N.; Zhou, B. Simulation and verification of hydraulic performance and energy dissipation mechanism of perforated drip irrigation emitters. Water 2021, 13, 171. [Google Scholar] [CrossRef]
- Zhu, Y.; Cao, W.; Liu, J. Study on structural design and hydraulic characteristic of a new type segmented rod emitter. Water. Sav. Irrig. 2020, 49, 5, (In Chinese with English Abstract). [Google Scholar]
- Li, Y.; Feng, X.; Liu, Y.; Han, X.; Liu, H.; Sun, Y.; Li, H.; Xie, Y. Research on hydraulic properties and energy dissipation mechanism of the novel water-retaining labyrinth channel emitters. Agronomy 2022, 12, 1708. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Xu, T.; Kang, M.; Song, X. Computational Experiments on Frictional Head Loss in Labyrinth Channel. J. Tai’ Yuan Univ. Technol. 2019, 50, 125–129. [Google Scholar]
- Camp, C.R. Subsurface drip irrigation: A review. Trans. ASAE 1998, 41, 1353–1367. [Google Scholar] [CrossRef]
- Kang, M. Influence of Double Internal Tooth Parameters on Hydraulic Performance of Labyrinth Irrigation Device. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2018. [Google Scholar]
- Zhai, Y.; Wu, W.; Wang, Z.; Hu, Y.; Xu, H. Analysis of the effect of pressure on hydraulic and anti-clogging performance of the channel unit of the irrigator based on ansys fluent software. Water Sav. Irrig. 2022, 59, 47–53, (In Chinese with English Abstract). [Google Scholar]
- Xu, T.; Zhang, L. Influence and analysis of structure design and optimization on the performance of a pit drip irrigation emitter*. Irrig. Drain. 2020, 69, 633–645. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Arnold, J.G.; Bingner, R.L.; Bingner, R.L.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy In Watershed Simulations. Trans. ASABE. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zhichang, Z. Hydraulics; China Water & Power Press: Beijing, China, 2016; Volume 7, pp. 272–277. [Google Scholar]
- Wen, S.; Niu, W.; Wu, M.; Zhang, W.; Li, X.; Yang, X. Dynamic Characteristics of Different Emitters Clogging in Drip Irrigation with Muddy Water. Trans. CSAM 2020, 51, 287–294, (In Chinese with English Abstract). [Google Scholar]



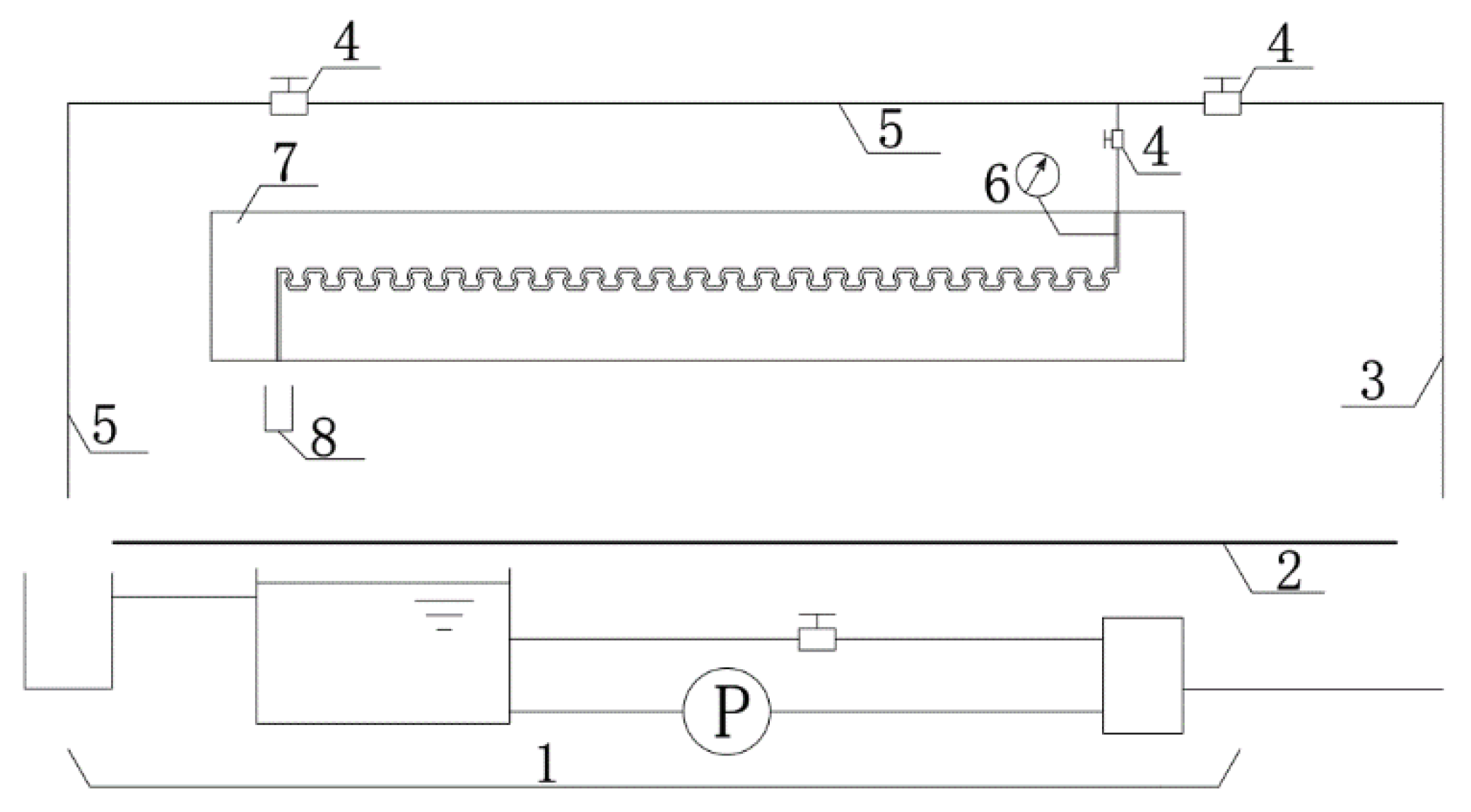


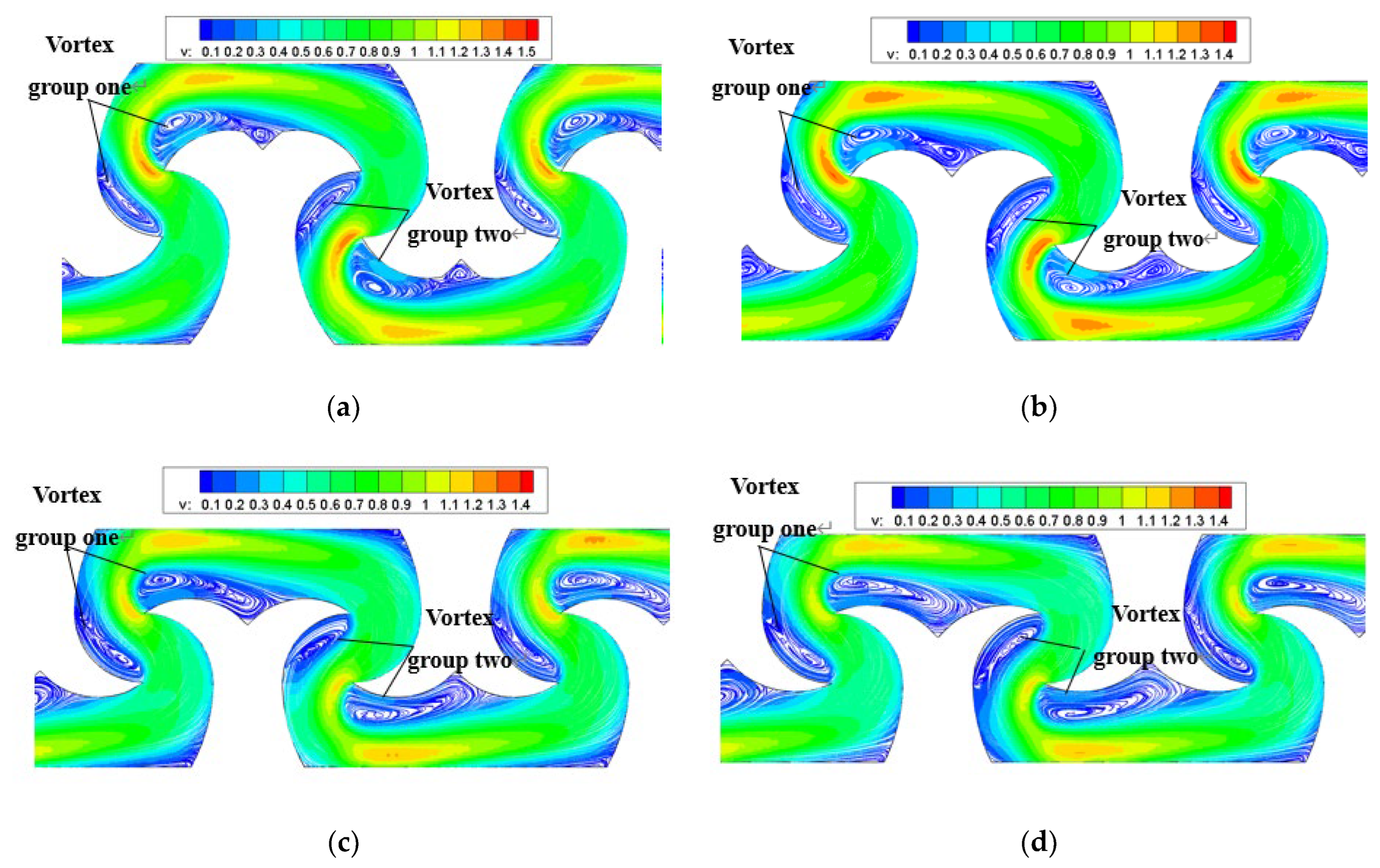
| Number | Crown Height (a) (mm) | Chord Length (b) (mm) | Crown-To-Chord Ratio (a:b) | Waist-Arc Angle (α) | Number of Units | Channel Length (mm) | Concave-Angle Width (e) (mm) | Concave-Angle Depth (n) (mm) |
|---|---|---|---|---|---|---|---|---|
| A1 | 0.6 | 3.0 | 6:30 | 90° | 50 | 299.0 | 0.5 | 0.3 |
| A2 | 120° | 43 | 300.3 | 0.8 | 0.4 | |||
| A3 | 150° | 39 | 300.7 | 1.4 | 0.3 | |||
| A4 | 180° | 38 | 303.1 | 1.8 | 0.4 | |||
| B1 | 0.4 | 3.0 | 4:30 | 90° | 50 | 299.0 | 1.2 | 0.3 |
| B2 | 120° | 43 | 300.3 | 1.3 | 0.4 | |||
| B3 | 150° | 39 | 300.7 | 1.5 | 0.4 | |||
| B4 | 180° | 38 | 303.1 | 1.6 | 0.4 | |||
| C1 | 0.2 | 3.0 | 2:30 | 90° | 50 | 299.0 | 1.4 | 0.3 |
| C2 | 120° | 43 | 300.3 | 1.6 | 0.4 | |||
| C3 | 150° | 39 | 300.7 | 1.8 | 0.5 | |||
| C4 | 180° | 38 | 303.1 | 2.2 | 0.5 | |||
| D1 | 0.1 | 3.0 | 1:30 | 90° | 50 | 299.0 | 1.4 | 0.4 |
| D2 | 120° | 43 | 300.3 | 2.0 | 0.3 | |||
| D3 | 150° | 39 | 300.7 | 2.2 | 0.3 | |||
| D4 | 180° | 38 | 303.1 | 2.0 | 0.5 |
| Method | Pressure h (mH2O) | |||||||
|---|---|---|---|---|---|---|---|---|
| 4.98 | 6.20 | 7.63 | 9.06 | 10.49 | 11.91 | 13.34 | 14.77 | |
| Numerical simulation(L/h) | 3.78 | 4.30 | 4.84 | 5.35 | 5.77 | 6.19 | 6.59 | 6.93 |
| Model test (L/h) | 3.80 | 4.32 | 4.86 | 5.37 | 5.85 | 6.28 | 6.71 | 7.11 |
| Relative error (%) | 0.53 | 0.46 | 0.41 | 0.37 | 1.37 | 1.43 | 1.79 | 2.53 |
| Number | Crown-To-Chord Ratio | Waist-Arc Angle | Design Flow q (L/h) | Slope of the Curve k | Design Flow Variation (%) | Slope of Curve Variation (%) | Formula of Parameters Variation |
|---|---|---|---|---|---|---|---|
| Z | —— | —— | 2.65 | 0.1192 | —— | —— | —— |
| A1 | 6:30 | 90° | 2.17 | 0.1202 | −18.1 | +0.84 | (WA1-WZ)/WZ |
| A2 | 120° | 1.82 | 0.0994 | −16.1 | −17.3 | (WA2-WA1)/WA1 | |
| A3 | 150° | 1.72 | 0.0921 | −20.7 | −23.4 | (WA3-WA1)/WA1 | |
| A4 | 180° | 1.59 | 0.0864 | −26.7 | −28.1 | (WA4-WA1)/WA1 | |
| B1 | 4:30 | 90° | 2.01 | 0.1058 | —— | —— | —— |
| B2 | 120° | 1.74 | 0.0968 | −13.4 | −8.50 | (WB2-WB1)/WB1 | |
| B3 | 150° | 1.70 | 0.0919 | −15.4 | −13.1 | (WB3-WB1)/WB1 | |
| B4 | 180° | 1.59 | 0.0883 | −20.9 | −16.5 | (WB4-WB1)/WB1 | |
| C1 | 2:30 | 90° | 1.77 | 0.1031 | —— | —— | —— |
| C2 | 120° | 1.67 | 0.0930 | −5.65 | −9.80 | (WC2-WC1)/WC1 | |
| C3 | 150° | 1.66 | 0.0904 | −6.21 | −12.3 | (WC3-WC1)/WC1 | |
| C4 | 180° | 1.59 | 0.0879 | −10.2 | −14.7 | (WC4-WC1)/WC1 | |
| D1 | 1:30 | 90° | 1.66 | 0.0956 | —— | —— | —— |
| D2 | 120° | 1.63 | 0.0873 | −1.81 | −8.68 | (WD2-WD1)/WD1 | |
| D3 | 150° | 1.59 | 0.0871 | −4.22 | −8.89 | (WD3-WD1)/WD1 | |
| D4 | 180° | 1.56 | 0.0862 | −6.02 | −9.83 | (WD4-WD1)/WD1 |
| Number | Waist-Arc Angle | Crown-To-Chord Ratio | Design Flow q (L/h) | Slope of the Curve k | Design Flow Variation (%) | Slope of Curve Variation (%) | Formula of Parameters Variation |
|---|---|---|---|---|---|---|---|
| A1 | 90° | 6:30 | 2.17 | 0.1202 | —— | —— | —— |
| B1 | 4:30 | 2.01 | 0.1058 | −7.37 | −12.0 | (WB1-WA1)/WA1 | |
| C1 | 2:30 | 1.77 | 0.1030 | −18.4 | −14.3 | (WC1-WA1)/WA1 | |
| D1 | 1:30 | 1.66 | 0.0956 | −23.5 | −20.5 | (WD1-WA1)/WA1 | |
| A2 | 120° | 6:30 | 1.82 | 0.0994 | —— | —— | —— |
| B2 | 4:30 | 1.74 | 0.0968 | −4.40 | −2.62 | (WB2-WA2)/WA2 | |
| C2 | 2:30 | 1.67 | 0.0930 | −8.24 | −6.43 | (WC2-WA2)/WA2 | |
| D2 | 1:30 | 1.63 | 0.0873 | −10.4 | −12.2 | (WD2-WA2)/WA2 | |
| A3 | 150° | 6:30 | 1.72 | 0.0921 | —— | —— | —— |
| B3 | 4:30 | 1.70 | 0.0919 | −1.16 | −0.22 | (WB3-WA3)/WA3 | |
| C3 | 2:30 | 1.66 | 0.0904 | −3.49 | −1.84 | (WC3-WA3)/WA3 | |
| D3 | 1:30 | 1.59 | 0.0871 | −7.56 | −5.43 | (WD3-WA3)/WA3 | |
| A4 | 180° | 6:30 | 1.59 | 0.0864 | —— | —— | —— |
| B4 | 4:30 | 1.59 | 0.0883 | 0 | +2.20 | (WB4-WA4)/WA4 | |
| C4 | 2:30 | 1.59 | 0.0879 | 0 | +1.73 | (WC4-WA4)/WA4 | |
| D4 | 1:30 | 1.56 | 0.0862 | −1.89 | −0.23 | (WD4-WA4)/WA4 |
| Number | Crown-To-Chord Ratio | Waist-Arc Angle | Waist Arc One | Waist Arc Two | ||||
|---|---|---|---|---|---|---|---|---|
| Pre-Vortex Pressure (Pa) | Post-Vortex Pressure (Pa) | Pressure Drop Ratio (%) | Pre-Vortex Pressure (Pa) | Post-Vortex Pressure (Pa) | Pressure Drop Ratio (%) | |||
| A1 | 6:30 | 90° | 8700 | 8100 | 6.89 | 8100 | 7500 | 7.41 |
| A2 | 120° | 10,200 | 9400 | 7.84 | 9400 | 8600 | 8.51 | |
| A3 | 150° | 11,500 | 10,500 | 8.69 | 10,500 | 9500 | 9.52 | |
| A4 | 180° | 12,400 | 11,200 | 9.67 | 11,200 | 10,000 | 10.7 | |
| Number | Crown-To-Chord Ratio | Vortex Group | Total Area of Vortex (mm2) | Total Vortex Strength |
|---|---|---|---|---|
| A1 | 6:30 | One | 1.2443 | 0.436 |
| Two | 1.1387 | 0.421 | ||
| B1 | 4:30 | One | 1.4085 | 0.511 |
| Two | 1.4376 | 0.519 | ||
| C1 | 2:30 | One | 1.6031 | 0.632 |
| Two | 1.5268 | 0.611 | ||
| D1 | 1:30 | One | 1.6955 | 0.714 |
| Two | 1.6767 | 0.698 |
| Number | Waist-Arc Angle | Channel Depth (mm) | Concave-Angle Width (mm) | Concave-Angle Depth (mm) | Channel Width (mm) | Number of Units | Channel Length (mm) |
|---|---|---|---|---|---|---|---|
| A4(1) | 180° | 1.0 | 1.8 | 0.4 | 1.30 | 31 | 302.9 |
| A4(2) | 180° | 1.0 | 1.8 | 0.4 | 1.25 | 32 | 303.1 |
| A43) | 180° | 1.0 | 1.8 | 0.4 | 1.20 | 33 | 302.7 |
| A4(4) | 180° | 1.0 | 1.8 | 0.4 | 1.00 | 21 | 167.1 |
| A4(5) | 180° | 1.0 | 1.8 | 0.4 | 1.00 | 26 | 207.1 |
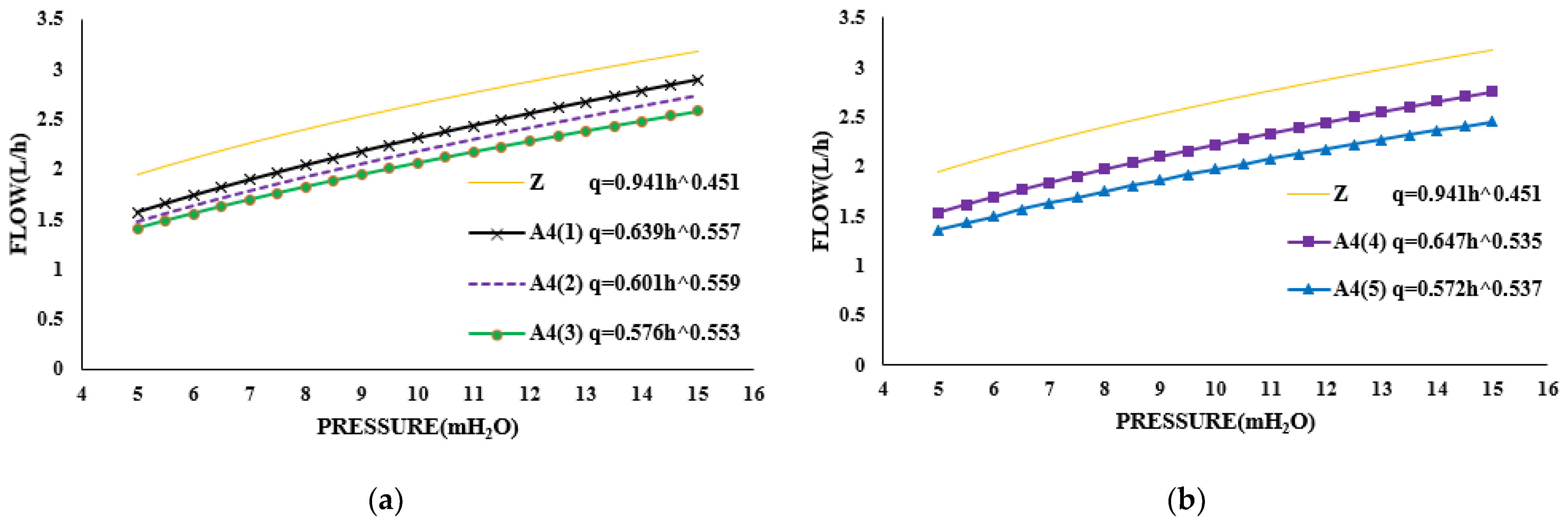
| Number | Channel Width (mm) | Channel Length (mm) | Design Flow (L/h) | Slope of the Curve | Design Flow Variation (%) | Slope of Curve Variation (%) | Channel Width Variation (%) | Channel Length Variation (%) |
|---|---|---|---|---|---|---|---|---|
| Z | 1.00 | 300.2 | 2.65 | 0.1192 | —— | —— | —— | —— |
| A4(1) | 1.30 | 302.9 | 2.30 | 0.1283 | −13.2 | +7.63 | +30.0 | −0.89 |
| A4(2) | 1.25 | 303.1 | 2.18 | 0.1217 | −17.7 | +2.09 | +25.0 | −0.96 |
| A4(3) | 1.20 | 302.7 | 2.06 | 0.1138 | −22.3 | −4.53 | +20.0 | −0.83 |
| A4(4) | 1.00 | 167.1 | 2.22 | 0.1186 | −16.2 | −0.50 | 0 | −44.3 |
| A4(5) | 1.00 | 207.1 | 1.97 | 0.1058 | −25.7 | −11.2 | 0 | −31.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Li, Z.; Du, P.; Ma, J.; Li, S. Mechanism Analysis of the Influence of Structural Parameters on the Hydraulic Performance of the Novel Y-Shaped Emitter. Agriculture 2023, 13, 1160. https://doi.org/10.3390/agriculture13061160
Li C, Li Z, Du P, Ma J, Li S. Mechanism Analysis of the Influence of Structural Parameters on the Hydraulic Performance of the Novel Y-Shaped Emitter. Agriculture. 2023; 13(6):1160. https://doi.org/10.3390/agriculture13061160
Chicago/Turabian StyleLi, Chaoxi, Zhiqin Li, Peisen Du, Juanjuan Ma, and Simin Li. 2023. "Mechanism Analysis of the Influence of Structural Parameters on the Hydraulic Performance of the Novel Y-Shaped Emitter" Agriculture 13, no. 6: 1160. https://doi.org/10.3390/agriculture13061160
APA StyleLi, C., Li, Z., Du, P., Ma, J., & Li, S. (2023). Mechanism Analysis of the Influence of Structural Parameters on the Hydraulic Performance of the Novel Y-Shaped Emitter. Agriculture, 13(6), 1160. https://doi.org/10.3390/agriculture13061160






