Vibration Characteristic Analysis and Structural Optimization of the Frame of a Triplex Row-Baling Cotton Picker
Abstract
:1. Introduction
2. Analysis of Vibration Excitation Sources
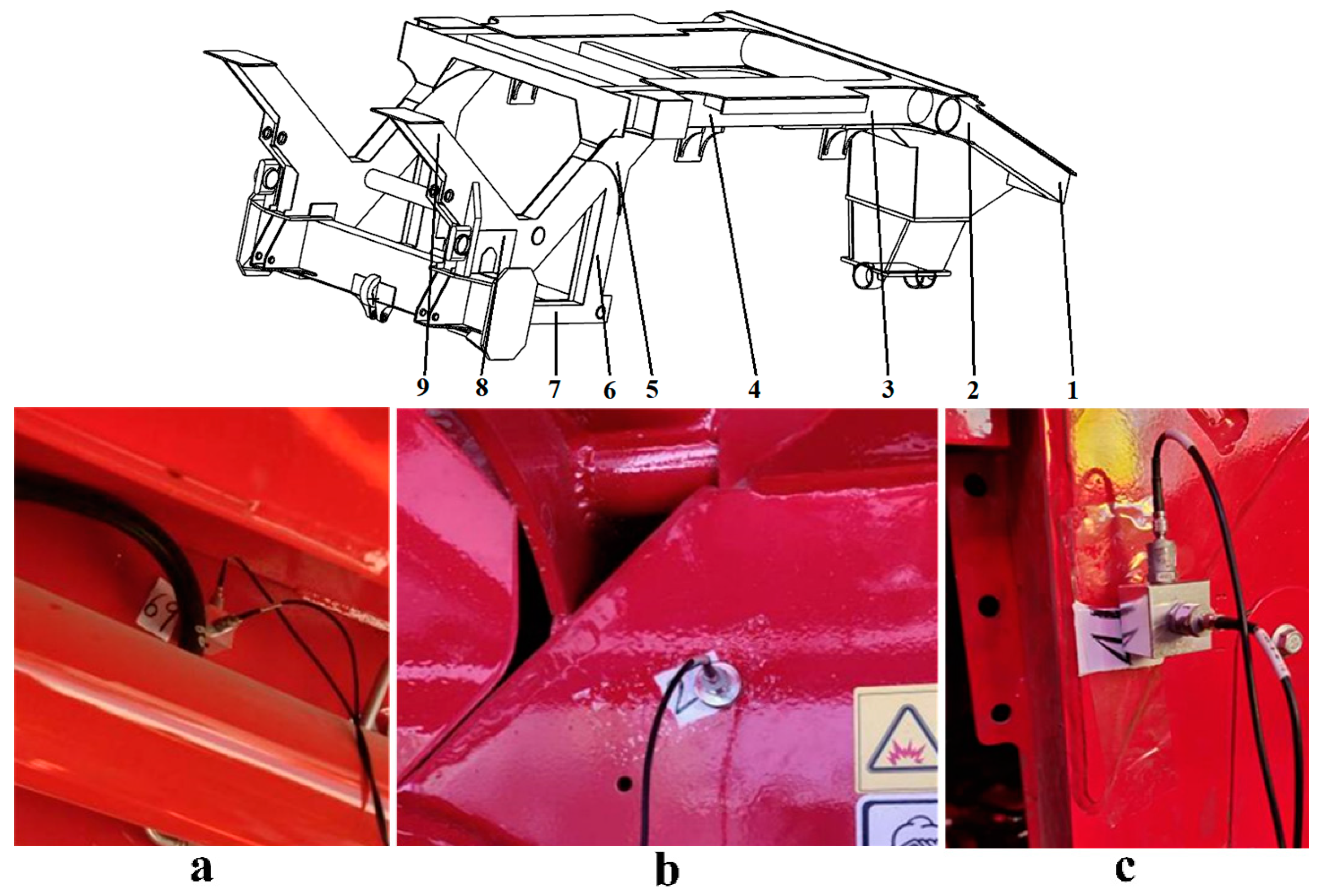
3. Investigation on Vibration Characteristics and Vibration Coupling of the Frame
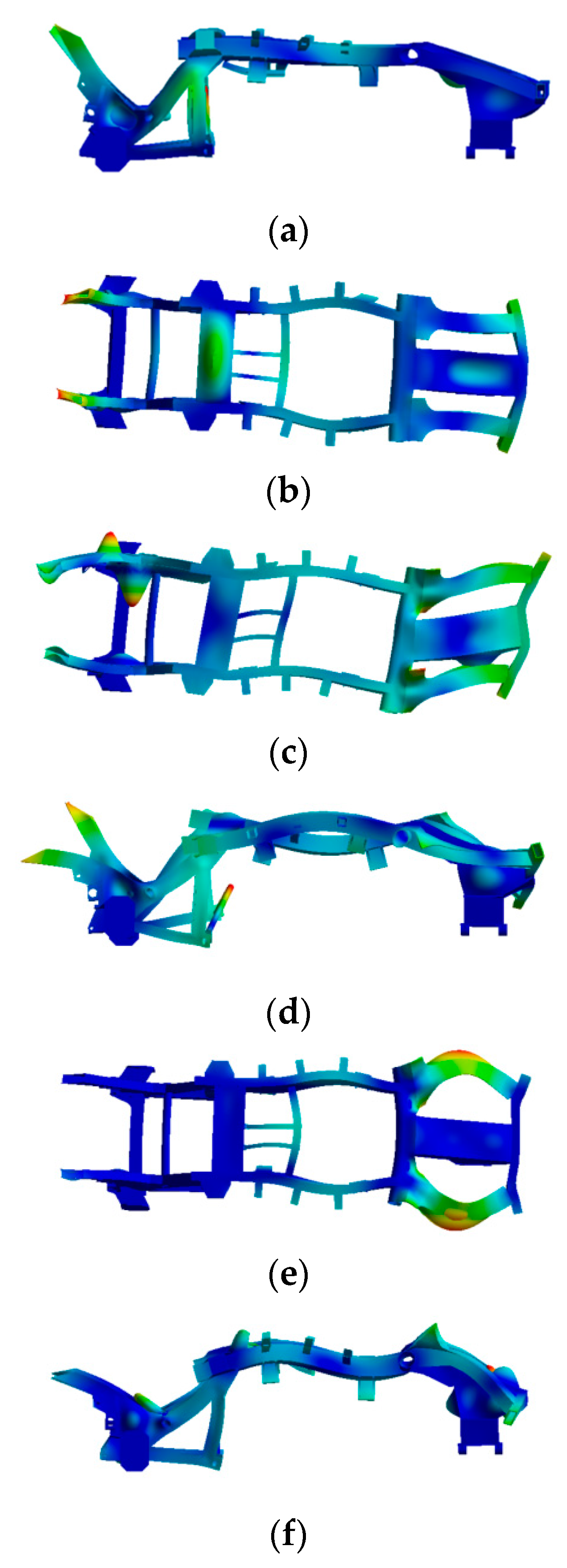
4. Modal Analysis
4.1. Finite Element Modal Analysis
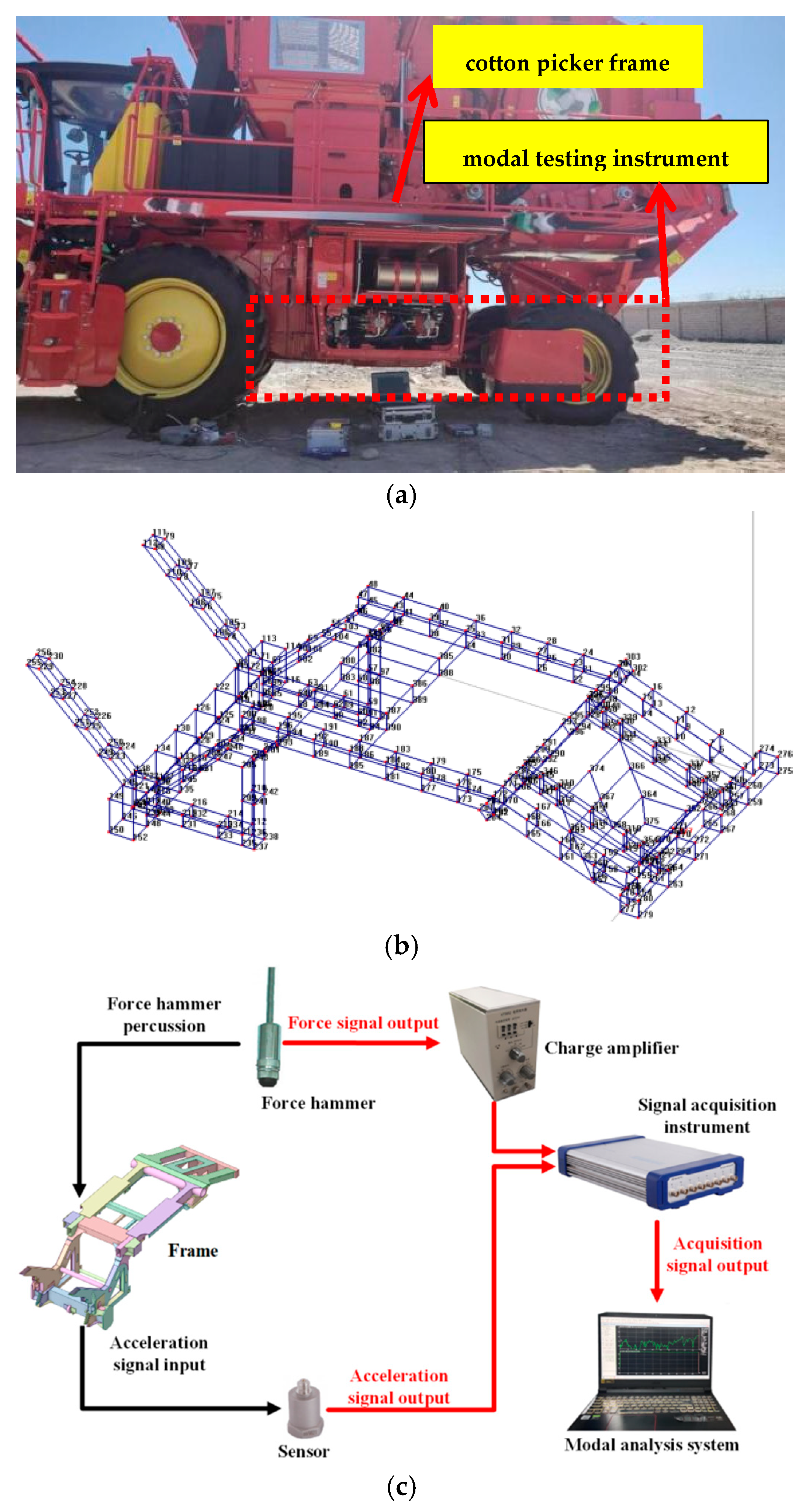
4.2. Experimental Modal Analysis
5. Optimization
- (1)
- The sensitivity analysis was performed on 20 design variables, and the variables with high sensitivity were selected.
- (2)
- Weldments with high sensitivity were designed for sampling to fit the response surface. By combining the MOGA (multi-objective genetic algorithm), the optimization and solution were completed.
- (3)
- According to the optimization results, an optimal scheme was determined using the entropy weight method and linear-weighting method.
5.1. Sensitivity Analysis
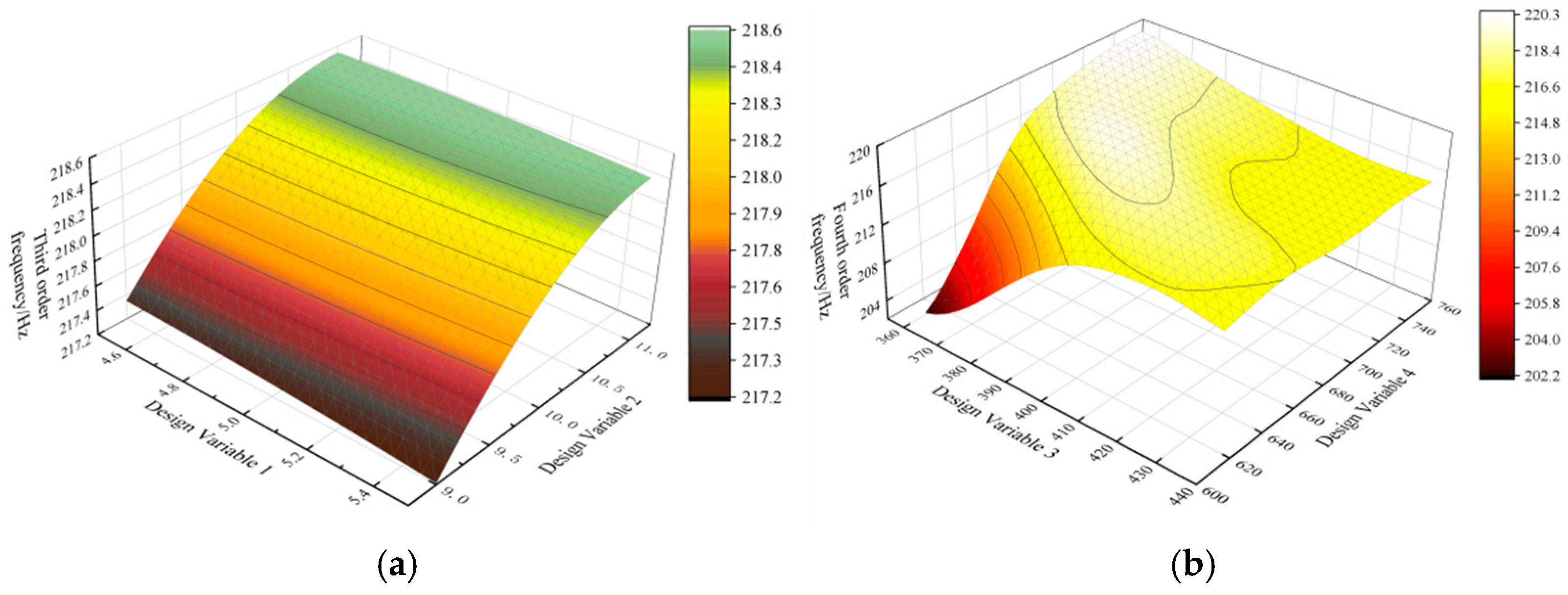
5.2. Response-Surface Fitting
5.3. Optimization Scheme and Evaluation
5.4. Test Results
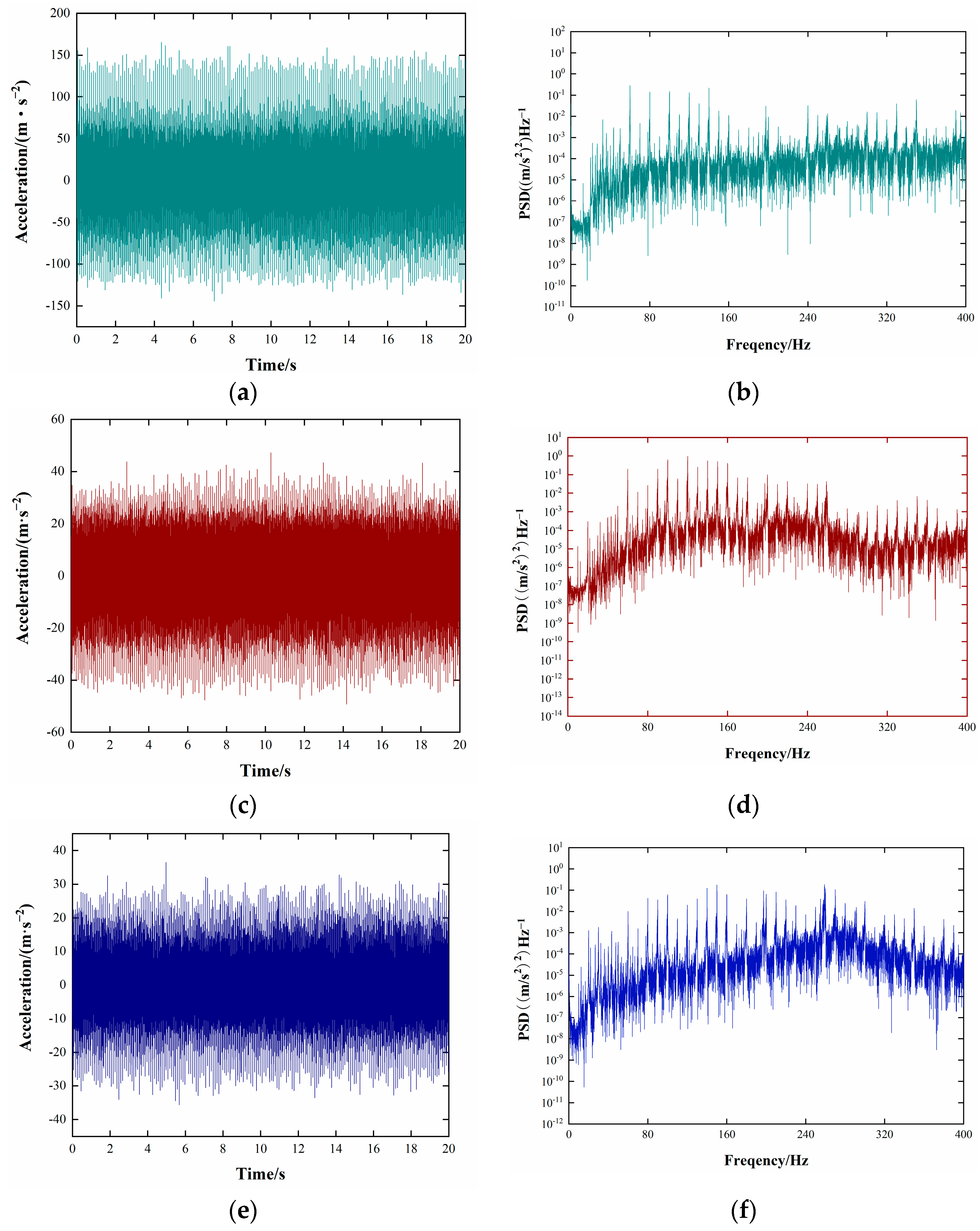
6. Random Vibration Fatigue Analysis Based on Power Spectral Density
7. Conclusions
- (1)
- Vibration tests were conducted on the engine, fan, picking head, and nine measuring points on the frame under multiple working conditions. The test results showed that the number of coupled frequencies increased with an increase in the rotary speed. Therefore, the effects of coupled excitation and vibration sources on the frame were the same.
- (2)
- The root mean square acceleration was calculated based on the data of the nine measuring points. The results showed that the engine had the greatest impact on the frame vibration, followed by the fan and picking head. The severity of the frame vibration was similar under working conditions 1 and 2, but the frame showed the most intense vibration under working condition 3. The vibration direction of the whole frame was mainly concentrated in the X-direction, followed by the Y-direction, and finally the Z-direction.
- (3)
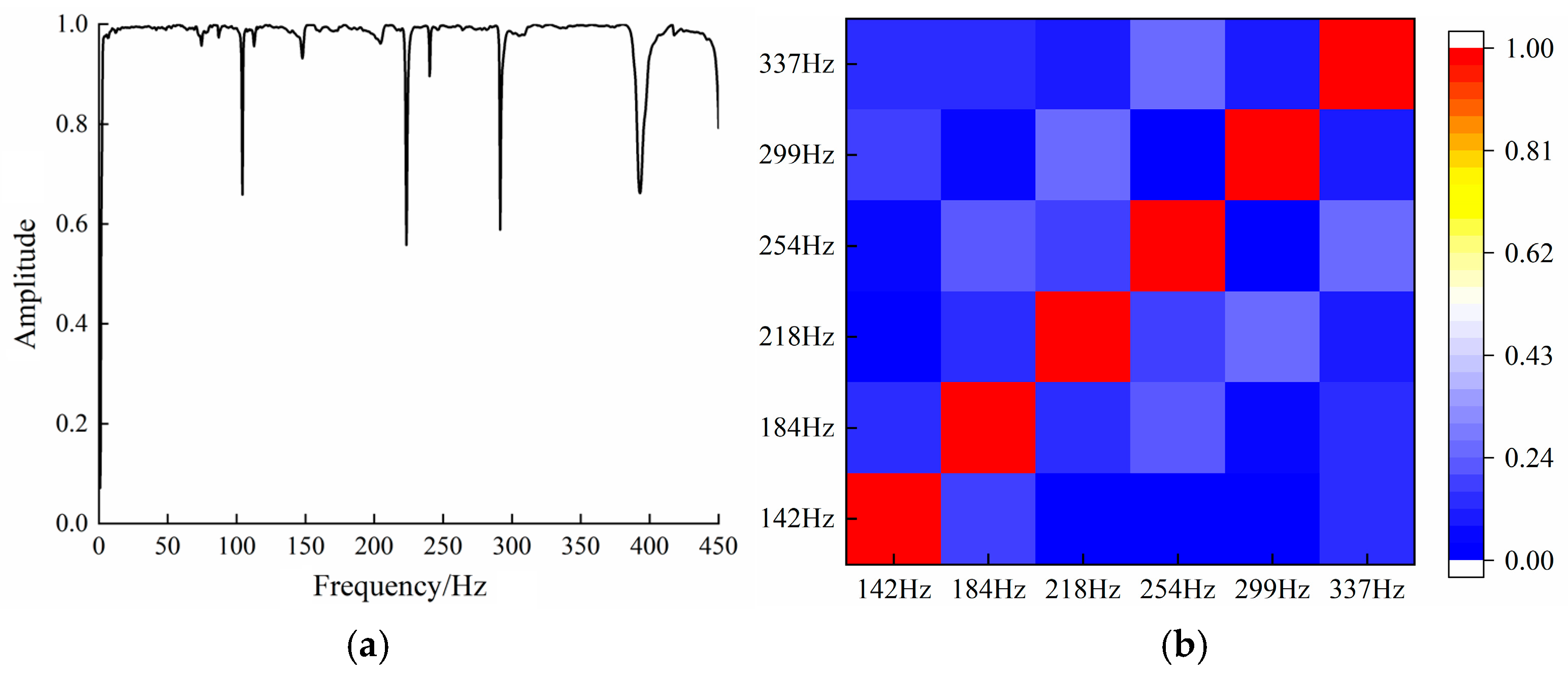
- An analysis of the finite element mode and test mode of the frame was carried out to solve the first six orders of modal frequency and mode shape. The data error was less than 4%, and the mode shape for each order showed a similar trend. This indicated that the finite element model had high accuracy, and the boundary conditions were set based on the actual conditions.
- (4)
- The results of the vibration tests and modal frequency analysis indicated significant differences between the excitation frequency and six modal frequencies. On the other hand, the excitation frequency and coupled frequency exhibited minimal differences. The coupled frequencies of 235 Hz, 260 Hz, and 330 Hz were close to the third-order, fourth-order, and six-order modal frequencies. This resulted in the generation of frame resonance. The sensitivity analysis was conducted using three coupled frequencies as the optimization objectives and the wall thickness of the frame as the design variable. Eight variables with high sensitivity were sampled, and the results were fitted. The results of the response surface were optimized using MOGA to obtain four optimization schemes. Based on the estimation of the entropy weight method and the linear weighting method, scheme 4 emerged as the optimal design.
- (5)
- The vibration acceleration signals of measuring point 4 were collected in the frame under three conditions. The power spectral density function was computed, and the lifespan was determined based on Miner’s law. The lifespan of the frame greatly improved after adding a supporting bar and increasing the local thickness at the weak points. The minimum lifespan of the frame was 7517 hours.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, X.; Chen, K.K.; Ji, J.T.; Zhao, K.X.; Du, X.W.; Ma, H. Intelligent vibration detection and control system of agricultural machinery engine. Measurement 2019, 145, 503–510. [Google Scholar] [CrossRef]
- Wang, Q.S.; Zhou, J.S.; Gong, D.; Wang, T.F.; Chen, J.X.; You, T.W.; Zhang, Z.F. The Influence of the Motor Traction Vibration on Fatigue Life of the Bogie Frame of the Metro Vehicle. Shock Vib. 2020, 2020, 7385861. [Google Scholar] [CrossRef]
- An, Q.; Li, F.; Fu, M.H. Influences of Traction Motor Vibration on Bogie Frame Fatigue Strength. J. Southwest Jiaotong Univ. 2010, 23, 209–212. [Google Scholar]
- Tang, Z.; Zhang, B.; Wang, M.L.; Zhang, H.T. Damping behaviour of a prestressed composite beam designed for the thresher of a combine harvester. Biosyst. Eng. 2021, 204, 130–146. [Google Scholar] [CrossRef]
- Reza, E.; Mohsen, E.; Saeed, Z. Vibration modeling and modification of cutting platform in a harvest combine by means of operational modal analysis (OMA). Measurement 2013, 46, 3959–3967. [Google Scholar]
- Chandravanshi, M.L.; Mukhopadhyay, A.K. Modal Analysis of a Vertically Tapered Frame. Int. J. Struct. Stab. Dyn. 2017, 17, 1771001. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C.; Xu, Y.; Wang, J.; Zhou, W.; Wang, Q.; Tang, H. Resonance Analysis and Vibration Reduction Optimization of Agricultural Machinery Frame—Taking Vegetable Precision Seeder as an Example. Processes 2021, 9, 1979. [Google Scholar] [CrossRef]
- Zhang, H.T.; Tang, Z.; Li, Y.; Liu, X.; Ren, H. Lightweight Threshing Rack under Multisource Excitation Based on Modal Optimization Method. Adv. Mater. Sci. Eng. 2020, 2020, 2029501. [Google Scholar] [CrossRef]
- Chen, S.R.; Zhou, Y.P.; Tang, Z.; Lu, S.N. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Gao, D.Y.; Yao, W.X.; Wu, T. Failure analysis on the axial-connected bolts of the thin-walled cylinder under random vibration loading. Eng. Fail. Anal. 2019, 105, 756–765. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Chen, Y.Y. Random Vibration Fatigue Life Analysis of Airborne Electrical Control Box. Appl. Sci. 2022, 12, 7335. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.X.; Li, N.P.; Yang, B.; Lei, Y.G. Remaining useful life prediction with partial sensor malfunctions using deep adversarial networks. IEEE-CAA J. Autom. Sin. 2023, 10, 121–134. [Google Scholar] [CrossRef]
- Wang, J.W.; Bai, H.C.; Sun, X.B.; Wang, J.L.; Tang, H.; Zhou, W.Q. Design and Dynamic Analysis of Spray Device for Paddy Field Sprayer. Trans. Chin. Soc. Agric. Mach. 2019, 50, 69–79. [Google Scholar]
- Lou, S.L. Analysis and Experimental Study on Vibration Characteristics of 3WQF80-10 Oil-Powered Unmanned Helicopter Rack; Chinese Academy of Agricultural Sciences: Beijing, China, 2018. [Google Scholar]
- Liu, X.G.; Wu, Z.Y.; Lu, J.; Xu, J.L. Investigation of the effect of rotation speed on the torsional vibration of transmission system. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, JAMDSM0079. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.P.; Xu, L.Z.; Li, Y.M. Vibration measure and analysis of crawler-type rice and wheat combine harvester in field harvesting condition. Trans. Chin. Soc. Agric. Eng. 2017, 33, 48–55. [Google Scholar]
- Shen, S.; Ying, H.Q.; Lei, S.H. Modal Test for Yellow River Bridge Exciting with Hammer. J. Vib. Eng. 2000, 13, 492–495, (in Chinese with English abstract). [Google Scholar]
- Ayoub, M.; Fernández, D.R.A.; Ahmed, H.; Miguel, I.; Fakher, C.; Fernando, V.; Mohamed, H. Comparison of experimental and operational modal analysis on a back to back planetary gear. Mech. Mach. Theory 2018, 124, 226–247. [Google Scholar]
- Douglas, C. Montgomery, Design and Analysis of Experiments, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wu, G.D.; Duan, K.F.; Zuo, J.; Zhao, X.B.; Tang, D.Z. Integrated Sustainability Assessment of Public Rental Housing Community Based on a Hybrid Method of AHP-Entropy Weight and Cloud Model. Sustainability 2017, 9, 603. [Google Scholar]
- Shen, Y.Y.; Chen, D.X.; Zhang, M.Z.; Zuo, T. Fuzzy Comprehensive Safety Evaluation of Pipeline Disaster in China-Russia Crude Oil Permafrost Region Based on Improved Analytic Hierarchy Process-Entropy Weight Method. Adv. Mater. Sci. Eng. 2022, 2022, 3157793. [Google Scholar] [CrossRef]
- Yuan, X.Y.; Fan, Y.G.; Zhou, C.J.; Wang, X.D.; Zhang, G.H. Research on Twin Extreme Learning Fault Diagnosis Method Based on Multi-Scale Weighted Permutation Entropy. Entropy 2022, 24, 1181. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, W.Z.; Chen, X.L.; Xu, L.Y.; Cao, Y.T. Vibration Performance Analysis and Multi-Objective Optimization Design of a Tractor Scissor Seat Suspension System. Agriculture 2023, 13, 48. [Google Scholar] [CrossRef]
- Zhong, X.; Xia, T.; Mei, Q. A Parameter-Adaptive VME Method Based on Particle Swarm Optimization for Bearing Fault Diagnosis. Exp. Technol. 2023, 47, 435–448. [Google Scholar] [CrossRef]
- Liu, F.; Wang, H.; Li, W.; Zhang, F.; Zhang, L.; Jiang, M.; Sui, Q. Fault diagnosis of rolling bearing combining improved AWSGMD-CP and ACO-ELM model. Measurement 2023, 209, 112531. [Google Scholar] [CrossRef]
- Wang, X.L.; Zheng, J.D.; Ni, Q.; Pan, H.Y.; Zhang, J. Traversal index enhanced-gram (TIEgram): A novel optimal demodulation frequency band selection method for rolling bearing fault diagnosis under non-stationary operating conditions. Mech. Syst. Signal Process. 2022, 172, 109017. [Google Scholar] [CrossRef]
- Jing, T.; Huang, D.H.; Mi, Z.; Yao, L.; Liu, X.L. An Intelligent Recognition Method of a Short-Gap Arc in Aviation Cables Based on Feature Weight Enhancement. IEEE Sens. J. 2023, 23, 3825–3836. [Google Scholar] [CrossRef]
- Wang, X.; She, B.; Shi, Z.S.; Sun, S.Y.; Qin, F.Q. Condition Monitoring of Mechanical Components Based on MEMED-NLOPE under Multiscale Features. Math. Probl. Eng. 2022, 2022, 3145402. [Google Scholar] [CrossRef]
- Laha, S.K.; Swarnakar, B.; Kansabanik, S.; Ray, S. A novel signal denoising method using stationary wavelet transform and particle swarm optimization with application to rolling element bearing fault diagnosis. Mater. Today-Proc. 2022, 66, 3935–3943. [Google Scholar] [CrossRef]
- Song, R.W.; Bai, X.L.; Zhang, R.; Jia, Y.; Pan, L.H.; Dong, Z.S. Bearing Fault Diagnosis Method Based on Multidomain Heterogeneous Information Entropy Fusion and Model Self-Optimisation. Shock Vib. 2022, 2022, 7214822. [Google Scholar] [CrossRef]
- Zhong, X.Y.; Xia, T.Y.; Zhao, Y.K.; Zhao, X. A frequency-weighted energy operator and swarm decomposition for bearing fault diagnosis. J. Intell. Fuzzy Syst. 2022, 42, 4027–4039. [Google Scholar] [CrossRef]
- Hou, B.C.; Wang, D.; Kong, J.Z.; Liu, J.; Peng, Z.K.; Tsui, K.L. Understanding importance of positive and negative signs of optimized weights used in the sum of weighted normalized Fourier spectrum/envelope spectrum for machine condition monitoring. Mech. Syst. Signal Process. 2022, 174, 109094. [Google Scholar] [CrossRef]
- Wang, C.L.; Gao, A.; Xuan, J.P. Optimal Demodulation Band Extraction Method for Bearing Faults Diagnosis Based on Weighted Geometric Cyclic Relative Entropy. Machines 2023, 11, 39. [Google Scholar] [CrossRef]
- Kong, F.N.; Song, C.; Zhuo, Y.W. Vibration Fault Analysis of Hydropower Units Based on Extreme Learning Machine Optimized by Improved Sparrow Search Algorithm. J. Vib. Eng. Technol. 2022, 11, 1609–1622. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.Q.; Zhou, F.X.; Ma, Y.J.; Yan, B.K. Weak Fault Feature Extraction Method Based on Improved Stochastic Resonance. Sensors 2022, 22, 6644. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Chen, Z.H.; Yang, L.Y.; Liang, Y.C. Principal component analysis (PCA) based sparrow search algorithm (SSA) for optimal learning vector quantized (LVQ) neural network for mechanical fault diagnosis of high voltage circuit breakers. Energy Rep. 2023, 9, 954–962. [Google Scholar] [CrossRef]
- Yang, J.Z.; Zhou, C.J.; Li, X.F.; Pan, A.; Yang, T. A Fault Feature Extraction Method Based on Improved VMD Multi-Scale Dispersion Entropy and TVD-CYCBD. Entropy 2023, 25, 277. [Google Scholar] [CrossRef] [PubMed]
- Gai, Q.K.; Gao, Y.B.; Huang, L.; Shen, X.Y.; Li, Y.B. Microseismic response difference and failure analysis of roof and floor strata under dynamic load impact. Eng. Fail. Anal. 2022, 143, 106874. [Google Scholar] [CrossRef]
- Guo, R.X.; Gong, B. Research on remaining useful life of rolling bearings using EWT-DI-ALSTM. Meas. Sci. Technol. 2022, 33, 095104. [Google Scholar] [CrossRef]
- Wang, G.B.; Zhao, S.B.; Zhong, Z.X.; Zeng, D. Research on Shaft Current Damage Identification of Variable Condition Motor Bearings Based on Multiscale Feature Label Propagation and Manifold Metric Transfer. Lubricants 2023, 11, 69. [Google Scholar] [CrossRef]
- Aykan, M.; Çelik, M. Vibration fatigue analysis and multi axial effect in testing of aerospace structures. Mech. Syst. Signal Process. 2009, 23, 897–907. [Google Scholar] [CrossRef]
- Steinberg, D.S. Vibration Analysis for Electronic Equipment; Wiley: New York, NY, USA, 1988. [Google Scholar]
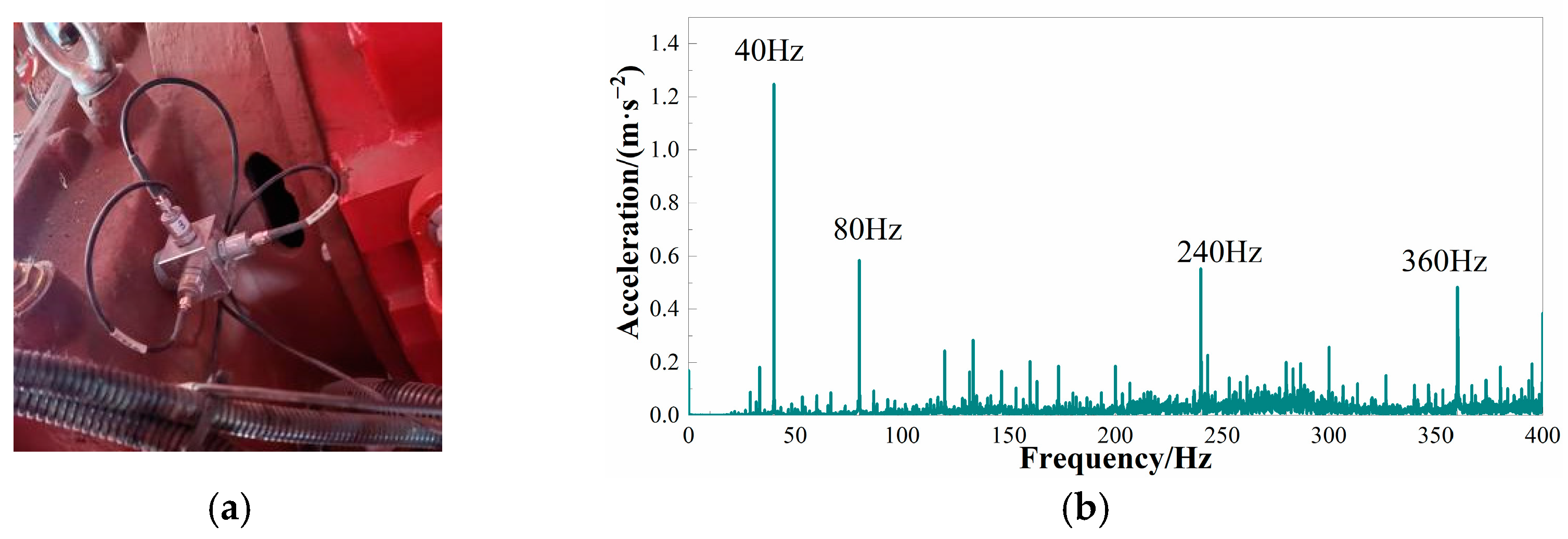
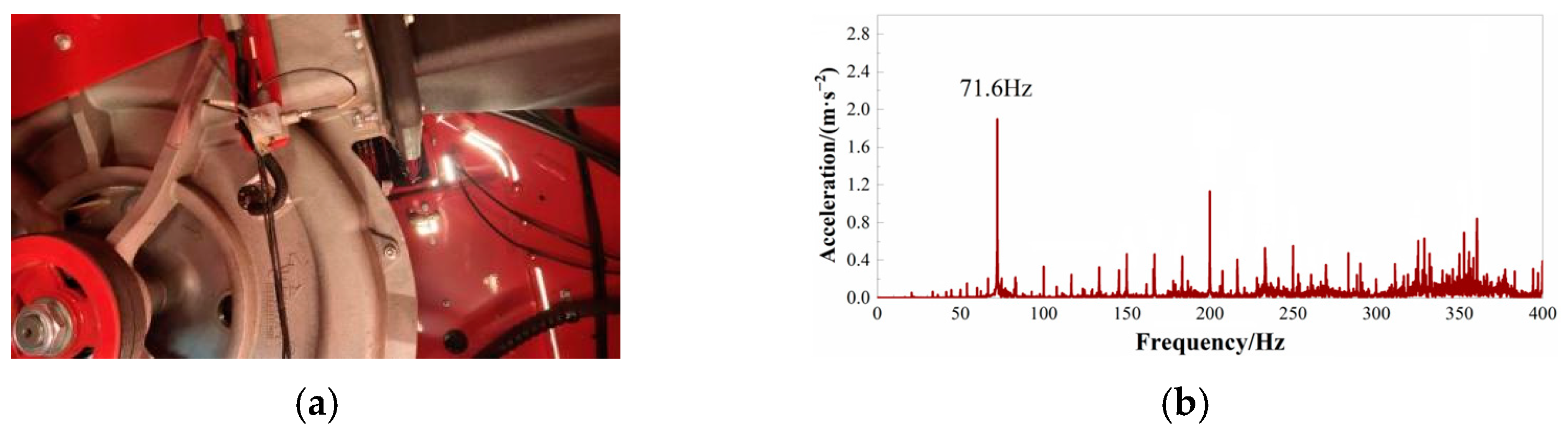
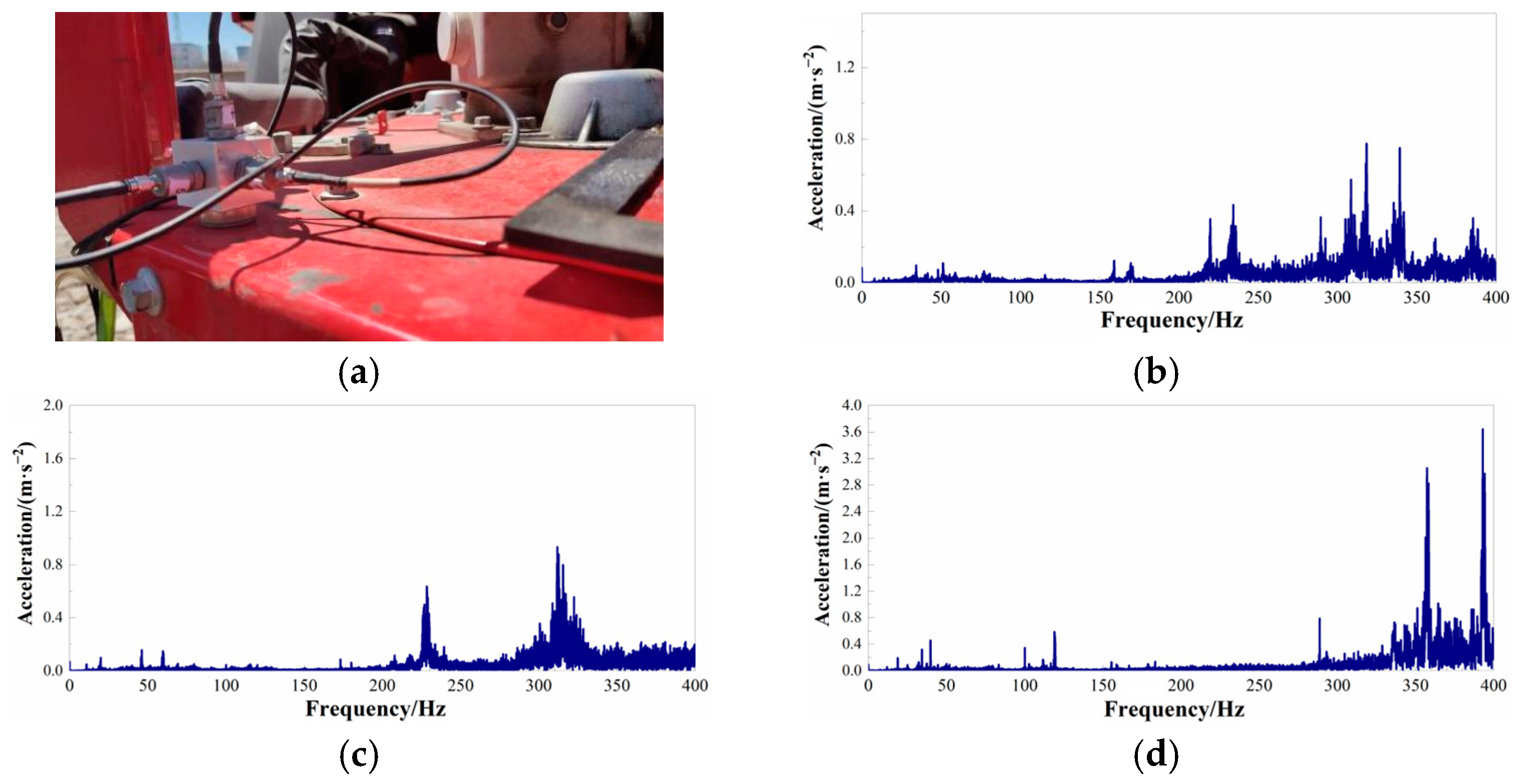



| Main Excitation Source | Gear | Rotating Speed/(r/min) | Vibration Frequency/Hz |
|---|---|---|---|
| engine | 1 | 800 | 40, 80 |
| 2 | 1200 | 60, 120 | |
| 3 | 2000 | 100, 200 | |
| Fan | 1 | 1700 | 28 |
| 2 | 2600 | 43 | |
| 3 | 4300 | 71 | |
| picking head | 1, 2 | 220~250 300~350 | |
| 3 | 350~400 |
| Measuring Points | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | |
| 1 | 4.1 | 1.3 | 5.4 | 5.7 | 1.7 | 6.8 | 17.6 | 3.4 | 10.4 |
| 2 | 5.6 | 3.0 | 2.3 | 7.6 | 4.5 | 3.1 | 22.6 | 13.5 | 9.1 |
| 3 | 4.1 | 2.2 | 5.9 | 7.2 | 3.0 | 9.3 | 11.6 | 7.2 | 16 |
| 4 | 3.6 | 3.5 | 3.4 | 5.1 | 6.2 | 5.1 | 15.1 | 16 | 9.6 |
| 5 | 4.0 | 3.2 | 3.2 | 4.9 | 5.1 | 4.9 | 9.2 | 13 | 11.6 |
| 6 | 3.4 | 4.5 | 1.4 | 4.5 | 7.1 | 2.3 | 8 | 8.1 | 6.4 |
| 7 | 3.10 | 1.5 | 1.8 | 4.1 | 1.4 | 1.8 | 8 | 2.6 | 3.4 |
| 8 | 3.4 | 1.1 | 1.4 | 4.1 | 1 | 1.7 | 9.4 | 3.7 | 3.3 |
| 9 | 3 | 1.7 | 1.2 | 4 | 1.7 | 1.4 | 8.9 | 4.9 | 3.2 |
| Measuring Points | Peak Sequences | Condition 1 | Condition 2 | Condition 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | ||
| 1 | 1 | 80 | 80 | 80 | 360 | 260 | 360 | 200 | 200 | 200 |
| 2 | 40 | 240 | 240 | 60 | 360 | 260 | 235 | 300 | 300 | |
| 2 | 1 | 240 | 80 | 240 | 60 | 120 | 260 | 235 | 200 | 200 |
| 2 | 80 | 40 | 40 | 120 | 60 | 60 | 200 | 100 | 100 | |
| 3 | 1 | 80 | 240 | 40 | 60 | 260 | 260 | 235 | 200 | 200 |
| 2 | 40 | 40 | 80 | 120 | 120 | 160 | 150 | 100 | 100 | |
| 4 | 1 | 80 | 80 | 80 | 160 | 160 | 160 | 150 | 200 | 165 |
| 2 | 40 | 40 | 40 | 120 | 120 | 260 | 200 | 100 | 100 | |
| 5 | 1 | 80 | 80 | 80 | 260 | 120 | 260 | 235 | 165 | 200 |
| 2 | 260 | 260 | 40 | 60 | 260 | 160 | 200 | 100 | 165 | |
| 6 | 1 | 80 | 80 | 40 | 100 | 120 | 120 | 200 | 200 | 200 |
| 2 | 130 | 120 | 80 | 260 | 60 | 260 | 100 | 100 | 165 | |
| 7 | 1 | 80 | 80 | 80 | 260 | 260 | 260 | 330 | 100 | 330 |
| 2 | 120 | 120 | 40 | 120 | 120 | 120 | 100 | 165 | 235 | |
| 8 | 1 | 240 | 80 | 240 | 260 | 120 | 260 | 235 | 100 | 100 |
| 2 | 80 | 240 | 40 | 120 | 60 | 100 | 200 | 200 | 200 | |
| 9 | 1 | 80 | 80 | 80 | 260 | 260 | 120 | 300 | 235 | 100 |
| 2 | 240 | 40 | 240 | 320 | 120 | 60 | 235 | 330 | 235 | |
| Density (ρ/kg·m-3) | 7850 |
|---|---|
| Young’s modulus (pa) | 2.06 × 1011 |
| Poisson’s ratio (μ) | 0.3 |
| Tensile strength σb (MPa) | 490–675 |
| Yield strength σs (MPa) | 345 |
| Elongation (δ/%) | 22 |
| FEA Modal Results | Test Modal Results | Error/% | Mode | ||
|---|---|---|---|---|---|
| Order | Frequency/ Hz | Order | Frequency/Hz | ||
| 1 | 142 | 1 | 139 | 2.1 | Homonymous bending of the frame bends along the Z-axis |
| 2 | 184 | 2 | 190 | 3.1 | Reversed bending and torsion of the frame along the X-axis |
| 3 | 218 | 3 | 221 | 1.3 | Homonymous bending and torsion of the frame along the X-axis |
| 4 | 254 | 4 | 259 | 1.9 | Reversed bending and torsion of the frame along the Z-axis |
| 5 | 299 | 5 | 291 | 2.6 | Reversed bending of the frame along the X-axis |
| 6 | 337 | 6 | 333 | 1.1 | Homonymous bending of the frame bends along the Z-axis |
| Original Size/mm | Optimum Proposal | |||||
|---|---|---|---|---|---|---|
| Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | |||
| Design Variable | 1 | 5 | 4.5 | 5.2 | 4.5 | 5.5 |
| 2 | 10 | 9 | 9 | 10.5 | 9 | |
| 3 | 400 | 440 | 440 | 360 | 380 | |
| 4 | 680 | 735 | 750 | 620 | 650 | |
| 5 | 10 | 9 | 9 | 9.5 | 9.5 | |
| 6 | 10 | 9 | 9.5 | 10 | 11 | |
| 7 | 130 | 142 | 142 | 121 | 142 | |
| 8 | 10 | 11 | 10 | 10 | 11 | |
| Optimization Objectives | Third-order frequency/Hz | 218 | 216 | 212 | 219 | 218 |
| Fourth-order frequency/Hz | 254 | 250 | 250 | 253 | 252 | |
| Sixth-order frequency/Hz | 337 | 330 | 333 | 350 | 340 | |
| Original Scheme | Optimized Scheme | |
|---|---|---|
| Quality | 1805 kg | 1890 kg |
| 1 mode frequency/Hz | 142 | 142 |
| 2 Mode frequency/Hz | 184 | 179 |
| 3 Mode frequency/Hz | 218 | 218 |
| 4 Mode frequency/Hz | 254 | 252 |
| 5 Mode frequency/Hz | 299 | 287 |
| 6 Mode frequency/Hz | 337 | 340 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Wang, G.; Lin, H.; Bi, X.; Li, Z.; Zhao, P.; Pei, T.; Tan, F. Vibration Characteristic Analysis and Structural Optimization of the Frame of a Triplex Row-Baling Cotton Picker. Agriculture 2023, 13, 1440. https://doi.org/10.3390/agriculture13071440
Dong J, Wang G, Lin H, Bi X, Li Z, Zhao P, Pei T, Tan F. Vibration Characteristic Analysis and Structural Optimization of the Frame of a Triplex Row-Baling Cotton Picker. Agriculture. 2023; 13(7):1440. https://doi.org/10.3390/agriculture13071440
Chicago/Turabian StyleDong, Jianhao, Guangheng Wang, Hui Lin, Xinsheng Bi, Zhantao Li, Pengda Zhao, Tingwen Pei, and Fei Tan. 2023. "Vibration Characteristic Analysis and Structural Optimization of the Frame of a Triplex Row-Baling Cotton Picker" Agriculture 13, no. 7: 1440. https://doi.org/10.3390/agriculture13071440
APA StyleDong, J., Wang, G., Lin, H., Bi, X., Li, Z., Zhao, P., Pei, T., & Tan, F. (2023). Vibration Characteristic Analysis and Structural Optimization of the Frame of a Triplex Row-Baling Cotton Picker. Agriculture, 13(7), 1440. https://doi.org/10.3390/agriculture13071440






