Advancing Early Fault Diagnosis for Multi-Domain Agricultural Machinery Rolling Bearings through Data Enhancement
Abstract
:1. Introduction
2. Basic Principles
2.1. Basic Principles of SMOTE
- (1)
- Distance Calculation:
- (2)
- Sampling Rate Determination:
- (3)
- New Sample Generation:
2.2. Relative Wavelet Packet Energy
2.3. Evaluation Indicators
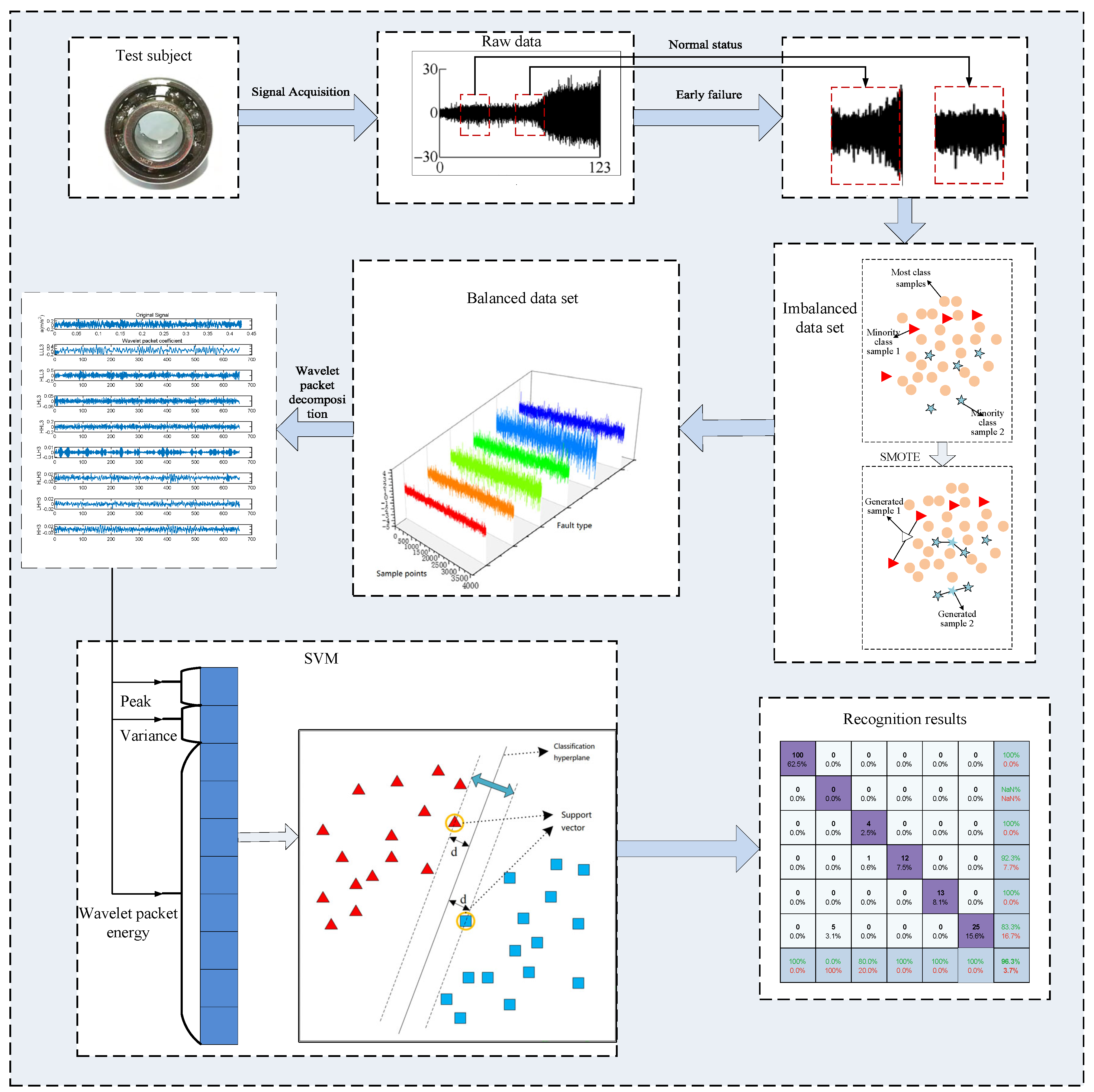
3. Advanced Early Fault Diagnosis Method for Agricultural Machinery Rolling Bearings
4. Experimental Platform and Experimental Analysis
4.1. Experimental Platform
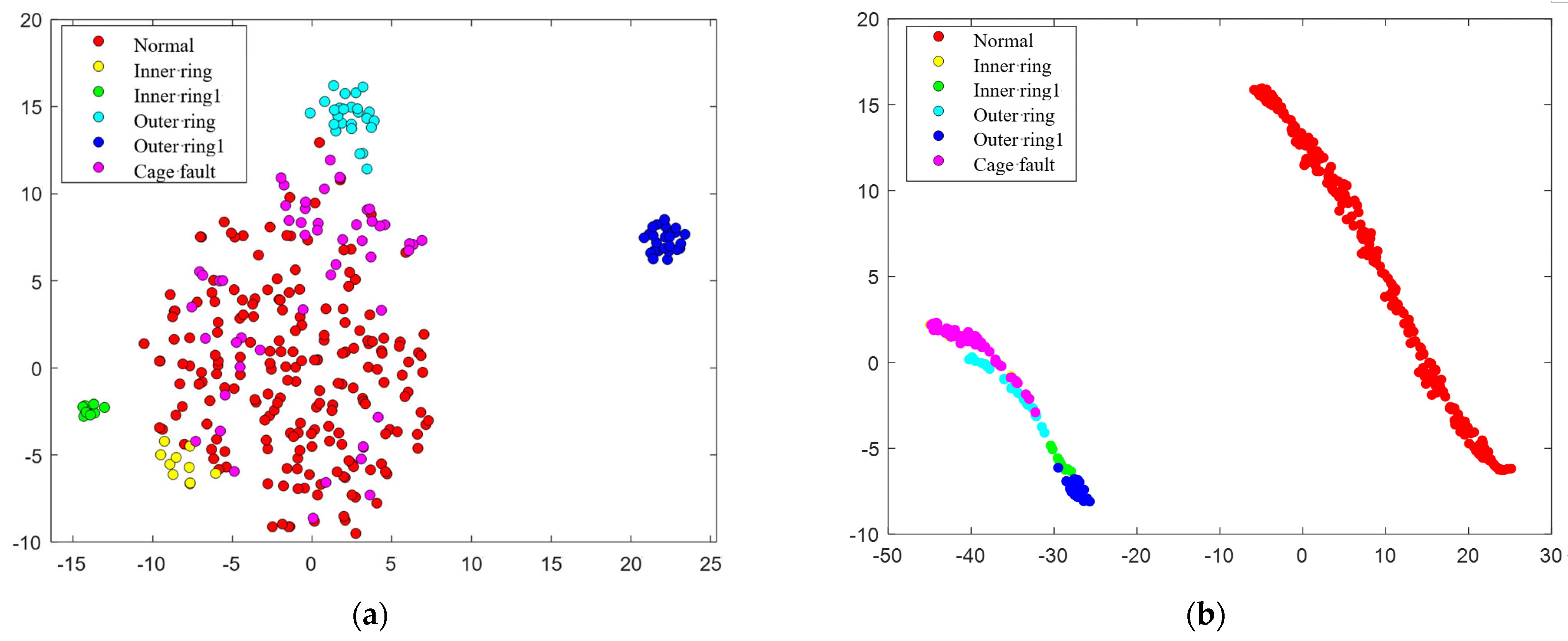
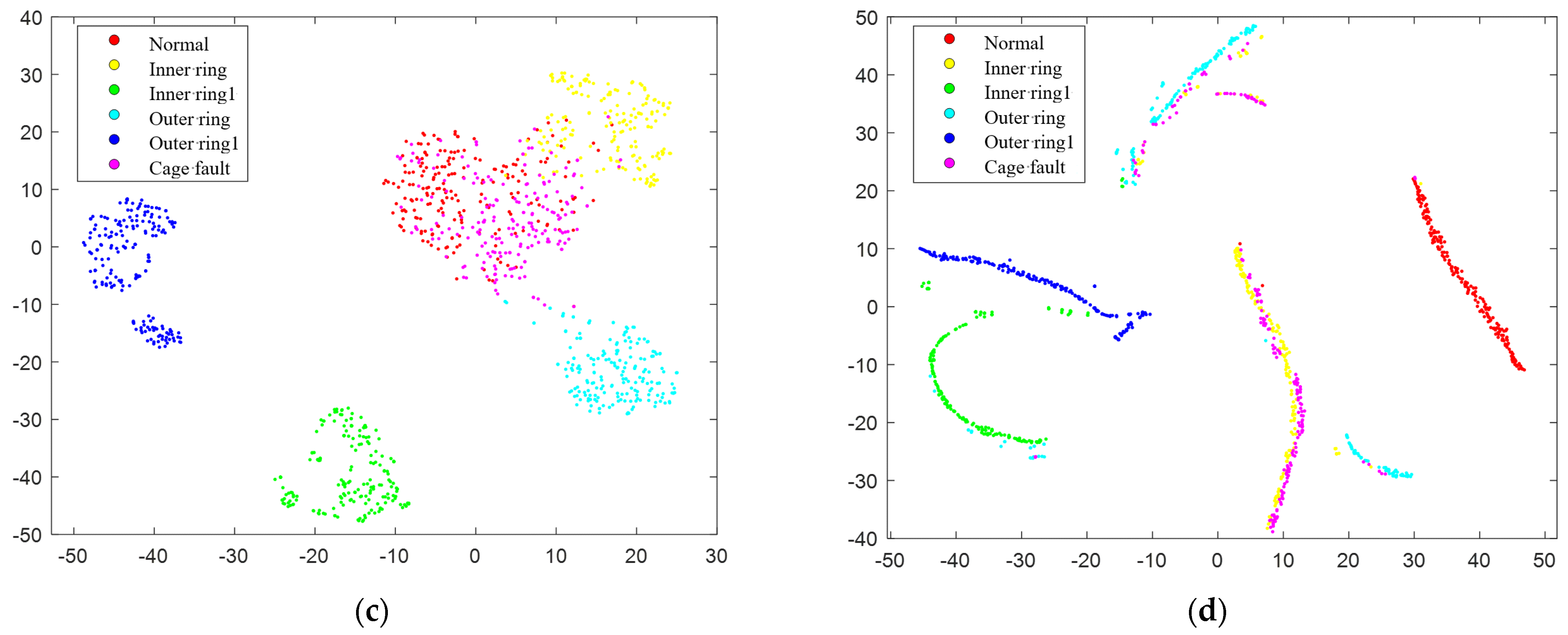
4.2. Refinement of Experimental Data Processing and Visualization Analysis
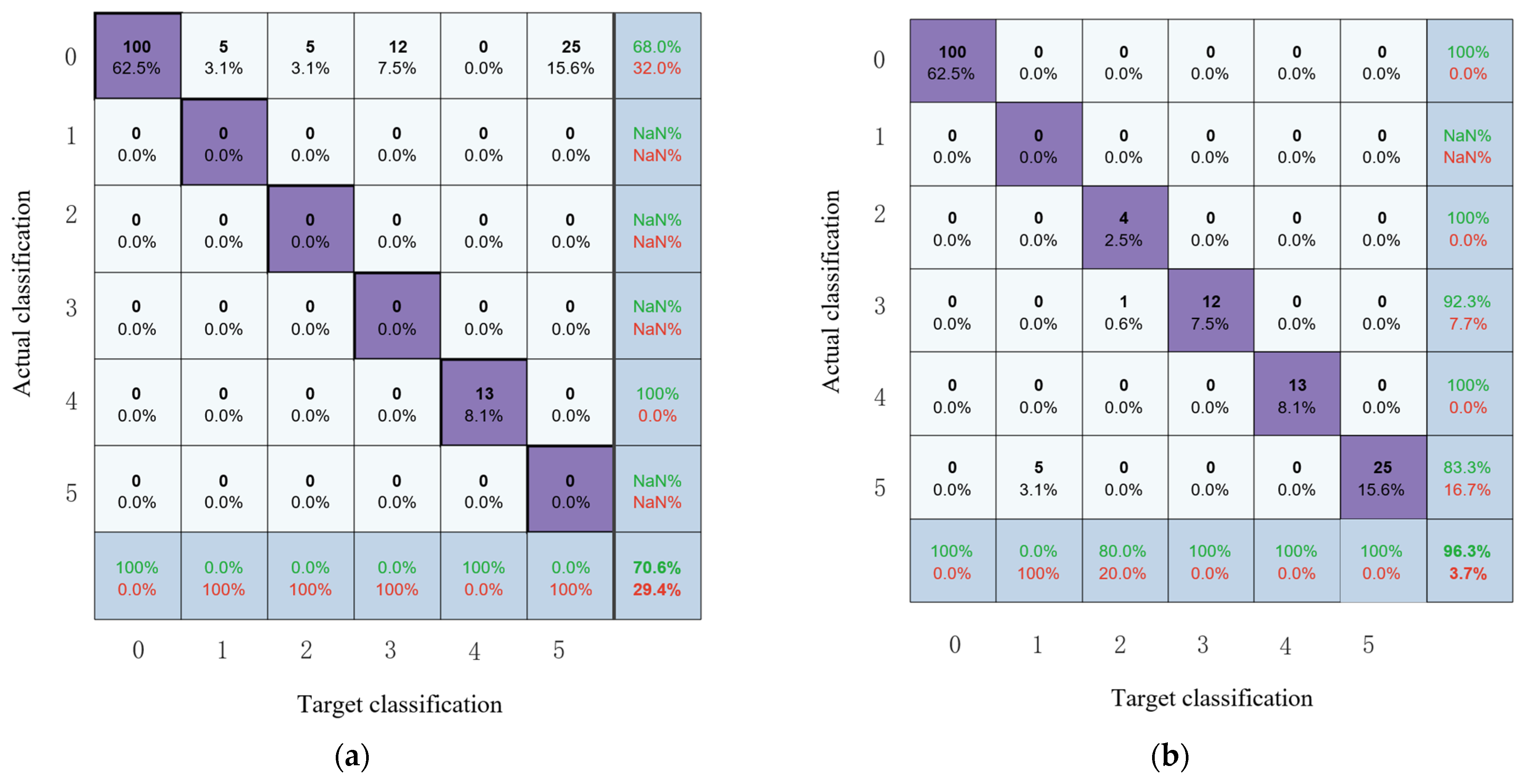
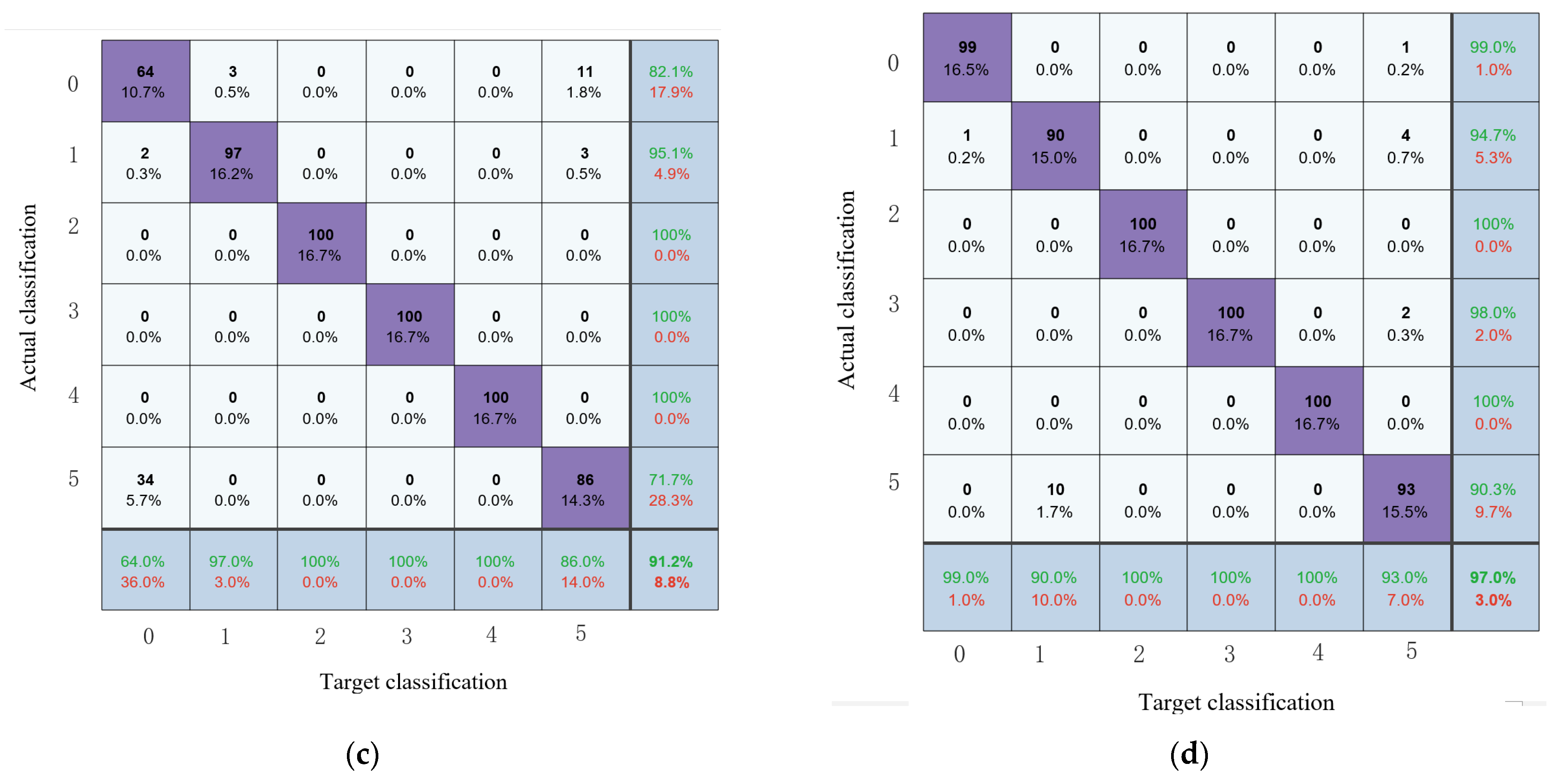
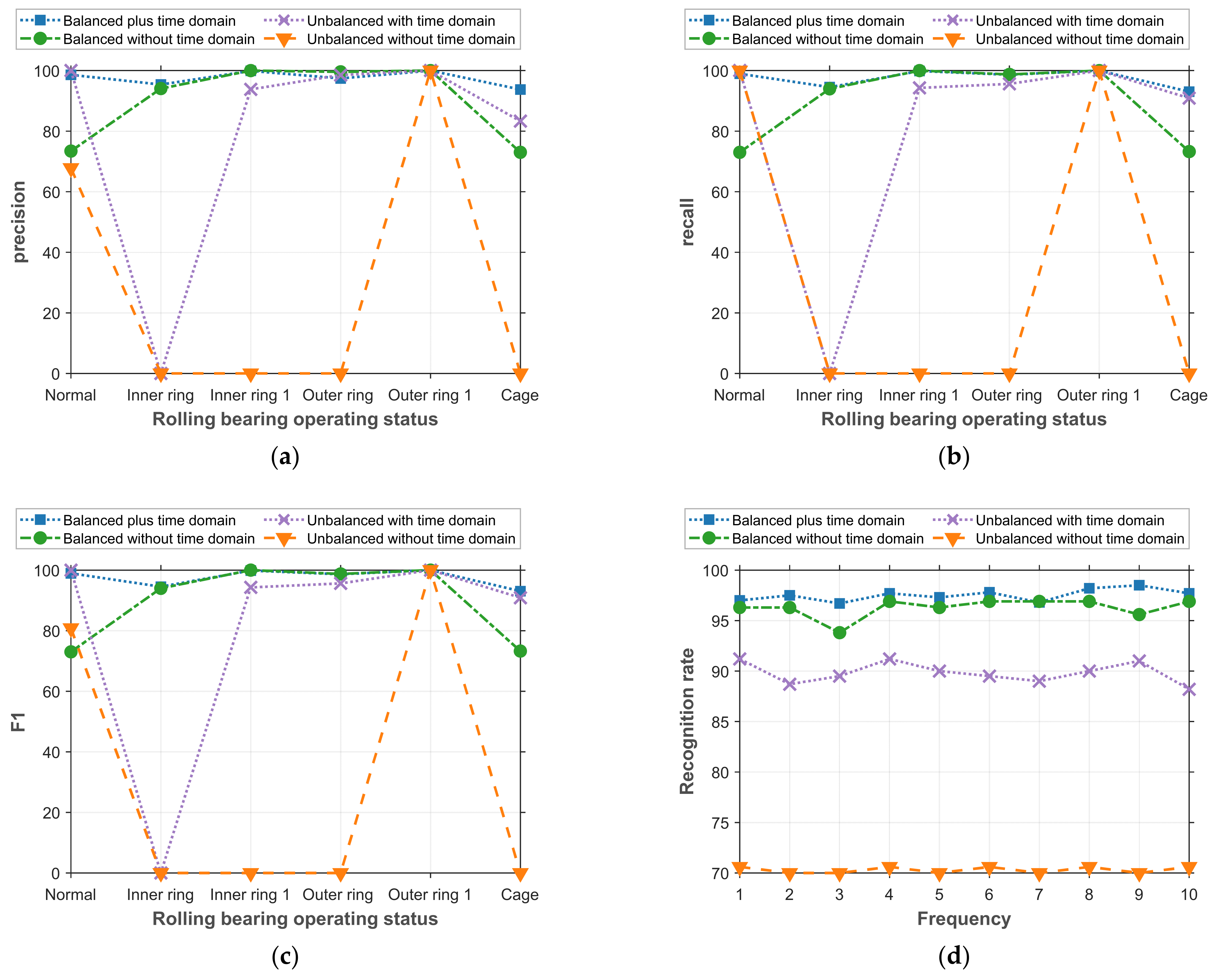
4.3. Analysis of Results
4.4. Discussion
4.4.1. Comparison of Different Models
4.4.2. Comparison with Other Studies on Similar Topics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Li, T.; Wang, G.; Zhang, Y. Adjustment of Meat Consumption Structure under the Dual Goals of Food Security and Carbon Reduction in China. Agriculture 2023, 13, 2242. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Pan, X.; Dou, H.; Zhao, X.; Gao, Y.; Yang, S.; Zhai, C. Design and Experiment of a Breakpoint Continuous Spraying System for Automatic-Guidance Boom Sprayers. Agriculture 2023, 13, 2203. [Google Scholar] [CrossRef]
- Fargnoli, M.; Lombardi, M. Safety Vision of Agricultural Tractors: An Engineering Perspective Based on Recent Studies (2009–2019). Safety 2020, 6, 1. [Google Scholar] [CrossRef]
- Fargnoli, M.; Vita, L.; Gattamelata, D.; Laurendi, V.; Tronci, M. A reverse engineering approach to enhance machinery design for safety. In Proceedings of the DS 70: DESIGN 2012, the 12th International Design Conference, Dubrovnik, Croatia, 12 August 2012; pp. 627–636. [Google Scholar]
- Woo, S.; O’Neal, D.L.; Hassen, Y.M.; Mebrahtu, G. Enhancing the Fatigue Design of Mechanical Systems Such as Refrigerator to Reserve Food in Agroindustry for the Circular Economy. Sustainability 2023, 15, 7010. [Google Scholar] [CrossRef]
- Cecchini, M.; Piccioni, F.; Ferri, S.; Coltrinari, G.; Bianchini, L.; Colantoni, A. Preliminary Investigation on Systems for the Preventive Diagnosis of Faults on Agricultural Operating Machines. Sensors 2021, 21, 1547. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ding, K.; Wang, H. Rolling bearing early weak fault intelligent diagnosis based on VMD and CNN. Modul. Mach. Tool Autom. Manuf. Tech. 2020, 11, 15–19. [Google Scholar]
- Li, J.; Li, X.; Li, Y.; Zhang, Y.; Yang, X.; Xu, P. A New Method of Tractor Engine State Identification Based on Vibration Characteristics. Processes 2023, 11, 303. [Google Scholar] [CrossRef]
- Xue, Z.; Fu, J.; Fu, Q.; Li, X.; Chen, Z. Modeling and Optimizing the Performance of Green Forage Maize Harvester Header Using a Combined Response Surface Methodology—Artificial Neural Network Approach. Agriculture 2023, 13, 1890. [Google Scholar] [CrossRef]
- Choe, H.O.; Lee, M.-H. Artificial Intelligence-Based Fault Diagnosis and Prediction for Smart Farm Information and Communication Technology Equipment. Agriculture 2023, 13, 2124. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Dai, D.; Tang, C.; Mao, X.; Chen, D.; Zhang, Y.; Wang, S. Knowledge Discovery and Diagnosis Using Temporal-Association-Rule-Mining-Based Approach for Threshing Cylinder Blockage. Agriculture 2023, 13, 1299. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Wang, G.; Hussain, G.; Zhao, S.; Zhang, H.; Xiao, M. Research on Fault Diagnosis of HMCVT Shift Hydraulic System Based on Optimized BPNN and CNN. Agriculture 2023, 13, 461. [Google Scholar] [CrossRef]
- Hao, S.; Tang, Z.; Guo, S.; Ding, Z.; Su, Z. Model and Method of Fault Signal Diagnosis for Blockage and Slippage of Rice Threshing Drum. Agriculture 2022, 12, 1968. [Google Scholar] [CrossRef]
- Fan, Y.; Cui, X.; Han, H. Chiller fault diagnosis with the technology of imbalanced data. J. Eng. Thermophys. 2019, 40, 1219–1228. [Google Scholar]
- Kaur, H.; Pannu, H.S.; Malhi, A.K. A systematic review on imbalanced data challenges in machine learning: Applications and solutions. ACM Comput. Surv. 2019, 52, 1–36. [Google Scholar] [CrossRef]
- Li, Y.; Chai, Y.; Hu, Y.; Yin, H. Review of imbalance data classification methods. Control Decis. 2019, 34, 673–688. [Google Scholar]
- Vaishal, G. An overview of classification algorithms for imbalanced datasets. Emerg. Technol. Adv. Eng. 2012, 2, 42–47. [Google Scholar]
- Meng, Z.; Guan, Y.; Pan, Z.; Sun, D.; Fan, F.; Cao, L. Fault diagnosis of rolling bearing based on secondary data enhancement and deep convolutional network. J. Mech. Eng. 2021, 57, 106–115. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Qi, S.; Hu, R.; Wang, W.; Wu, M.; Zhang, Y. Transformer fault diagnosis method based on SMOTE balanced data set and BP neural network. Shangdong Electr. Power 2022, 49, 15–22. [Google Scholar]
- Huang, H.; Wei, J.; Ren, Z.; Wu, J. Rolling bearing fault diagnosis based on imbalanced sample characteristics oversampling algorithm and SVM. J. Vibr. Shock 2020, 39, 65–74+132. [Google Scholar]
- Liu, Y.; Xu, Z.; He, J.; Wang, Q.; Gao, S. Data augmentation method for power transformer fault diagnosis based on conditional Wasserstein fenerative adversarial network. Power Syst. Technol. 2020, 44, 1505–1513. [Google Scholar]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Zixu, C.; Zhenjie, Z.; Guoliang, L. Novel early fault detection and diagnosis for rolling element bearings in graph spectrum domain. J. Vibr. Shock 2022, 41, 51–59. [Google Scholar]
- Ma, Z.; Zhang, Z.; Zhang, Z.; Song, Z.; Liu, Y.; Li, Y.; Xu, L. Durable Testing and Analysis of a Cleaning Sieve Based on Vibration and Strain Signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Jiang, W.; Shan, Y.; Xue, X.; Ma, J.; Chen, Z.; Zhang, N. Fault Diagnosis for Rolling Bearing of Combine Harvester Based on Composite-Scale-Variable Dispersion Entropy and Self-Optimization Variational Mode Decomposition Algorithm. Entropy 2023, 25, 1111. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, S.; Jotautienė, E. Vibration Analysis of a Roller Bearing Condition Used in a Tangential Threshing Drum of a Combine Harvester for the Smooth and Continuous Performance of Agricultural Crop Harvesting. Agriculture 2022, 12, 1969. [Google Scholar] [CrossRef]
- Yang, G.; Cheng, Y.; Xi, C.; Liu, L.; Gan, X. Combine Harvester Bearing Fault-Diagnosis Method Based on SDAE-RCmvMSE. Entropy 2022, 24, 1139. [Google Scholar] [CrossRef]





| Fault Type | Inner Race | Inner Race1 | Out Race | Out Race1 | Cage Fault |
|---|---|---|---|---|---|
| Number of sample groups | 10 | 10 | 25 | 25 | 50 |
| Q | 1:20 | 1:20 | 1:8 | 1:8 | 1:4 |
| Data Set | Fault Type | Basic Rating Life | Actual Life |
|---|---|---|---|
| Bearing2_1 | Inner race | 6.786~11.726 h | 8 h 11 min |
| Bearing2_2 | Out race | 2 h 41 min | |
| Bearing2_3 | Cage | 8 h 53 min | |
| Bearing3_3 | Inner race1 | 8.468~14.632 h | 6 h 11 min |
| Bearing3_5 | Out race1 | 1 h 54 min |
| Methods | Accuracy Rate |
|---|---|
| MPE + BP | 73.3% |
| CEEMD + MPE + POS + BP | 80.0% |
| MPE + POS + BP | 90.0% |
| CEEMD + CNN | 98.3% |
| SMOTE + CNN | 98.6% |
| SMOTE + SVM | 97.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; Li, G.; Liu, H.; Sun, E.; Wang, Y. Advancing Early Fault Diagnosis for Multi-Domain Agricultural Machinery Rolling Bearings through Data Enhancement. Agriculture 2024, 14, 112. https://doi.org/10.3390/agriculture14010112
Xie F, Li G, Liu H, Sun E, Wang Y. Advancing Early Fault Diagnosis for Multi-Domain Agricultural Machinery Rolling Bearings through Data Enhancement. Agriculture. 2024; 14(1):112. https://doi.org/10.3390/agriculture14010112
Chicago/Turabian StyleXie, Fengyun, Gang Li, Hui Liu, Enguang Sun, and Yang Wang. 2024. "Advancing Early Fault Diagnosis for Multi-Domain Agricultural Machinery Rolling Bearings through Data Enhancement" Agriculture 14, no. 1: 112. https://doi.org/10.3390/agriculture14010112





