Configuration Optimization of Temperature–Humidity Sensors Based on Weighted Hilbert–Schmidt Independence Criterion in Chinese Solar Greenhouses
Abstract
:1. Introduction
2. Materials and Methods
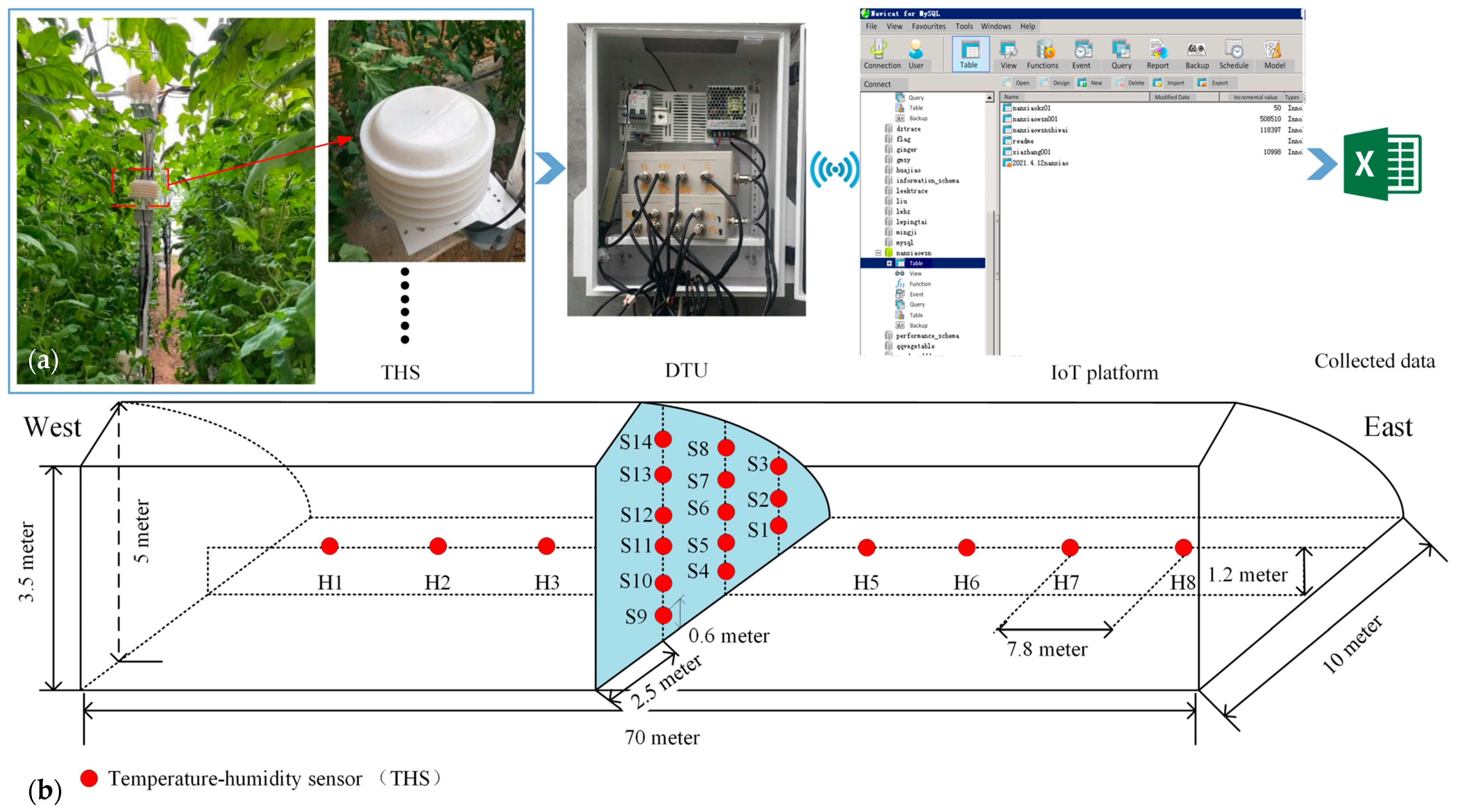
2.1. Introduction of the Test CSG
2.2. Temperature and Humidity Data Collection in the CSG
2.3. Optimization Strategy for THS Configuration
2.3.1. Monitoring Independence of the THSs
2.3.2. Selection Priority of the THSs
- (1)
- Definition of basic parameters: The set of all THSs is defined as , containing THSs; the set of sorted THSs is defined as , and the set of unsorted THSs is defined as .
- (2)
- Selection of the first THS: The first THS should be able to represent the overall trend of temperature and humidity, i.e., convey the maximum information of the CSG microclimate. Therefore, the THS with the highest IIC value should be selected. As shown in Equations (17) and (18), the first element in the set is sorted as .
- (3)
- Selection of the ith () THS: After selecting the first one, the spatial distribution information of temperature and humidity should be mainly considered in the selection of the following ones. Then, the THS in with the smallest IIC value in terms of is selected, which can maximize the information abundance of temperature and humidity spatial distribution, as shown in Equation (19). And the expressions of the set and are updated as shown in Equations (20) and (21).
- (4)
- If , repeat step (3) and sort the THSs from the set to one by one.
- (5)
- If , it means that priority sorting for all THSs has been completed, and then , .
2.3.3. Determination of the Required THS Quantity
- (1)
- Monitoring accuracy
- (2)
- Information abundance based on information entropy
- (3)
- Construction of monitoring solution
3. Results
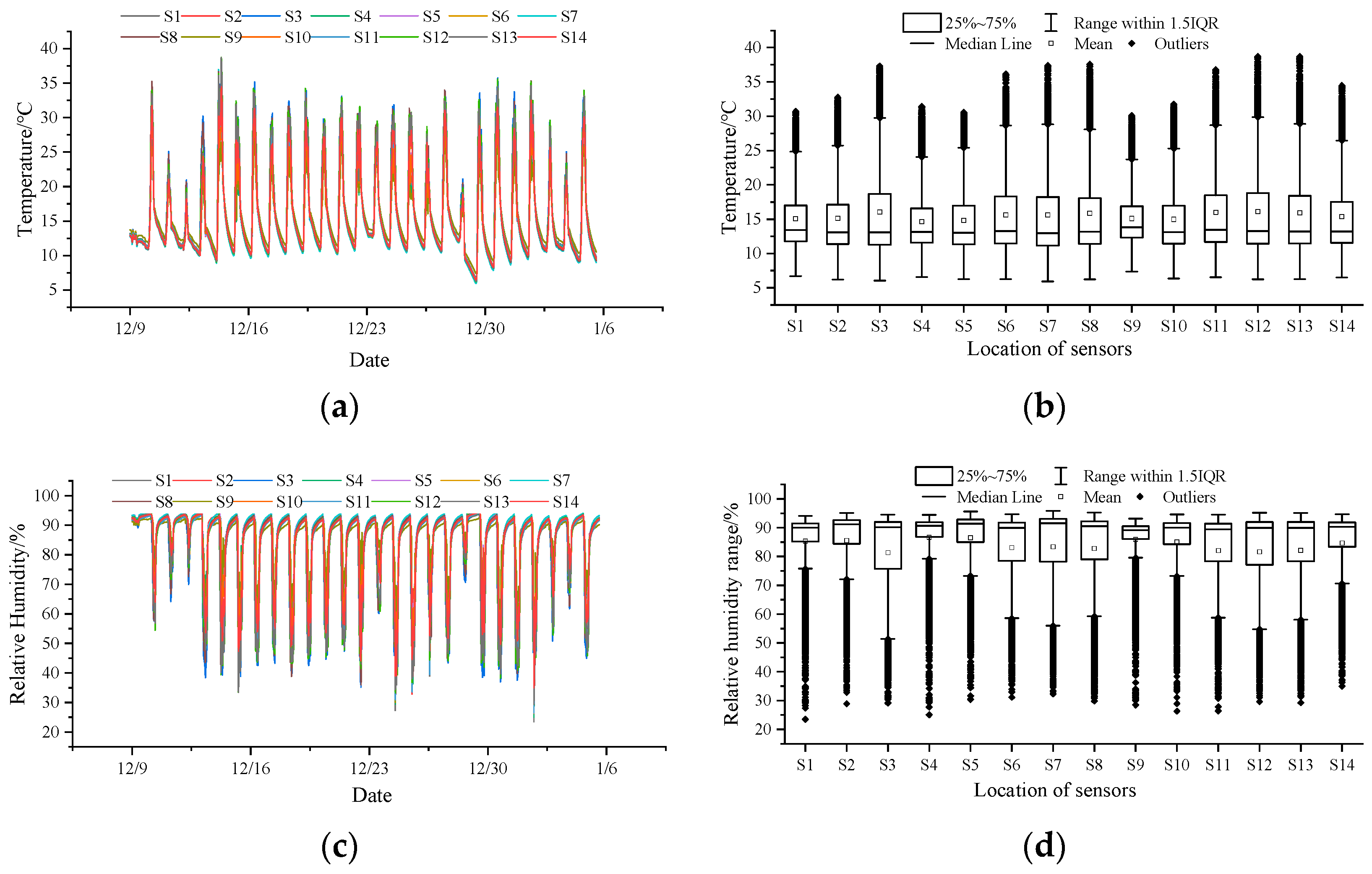
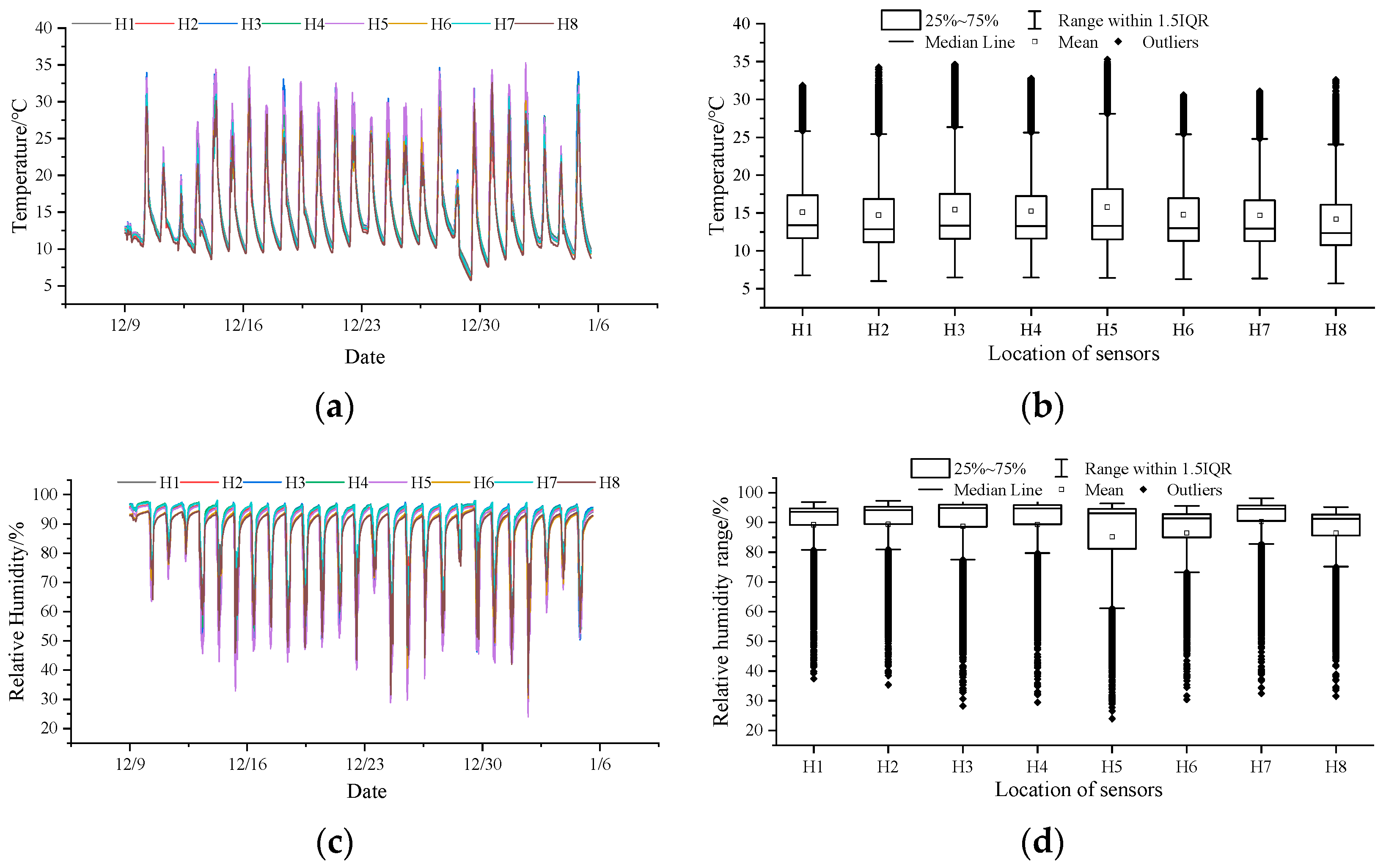
3.1. Temperature and Humidity Heterogeneity in the CSG
3.1.1. Temperature and Humidity Heterogeneity in the North–South Vertical Direction
3.1.2. Temperature and Humidity Heterogeneity in the East–West Horizontal Direction
3.2. Optimization Results of THS Configuration
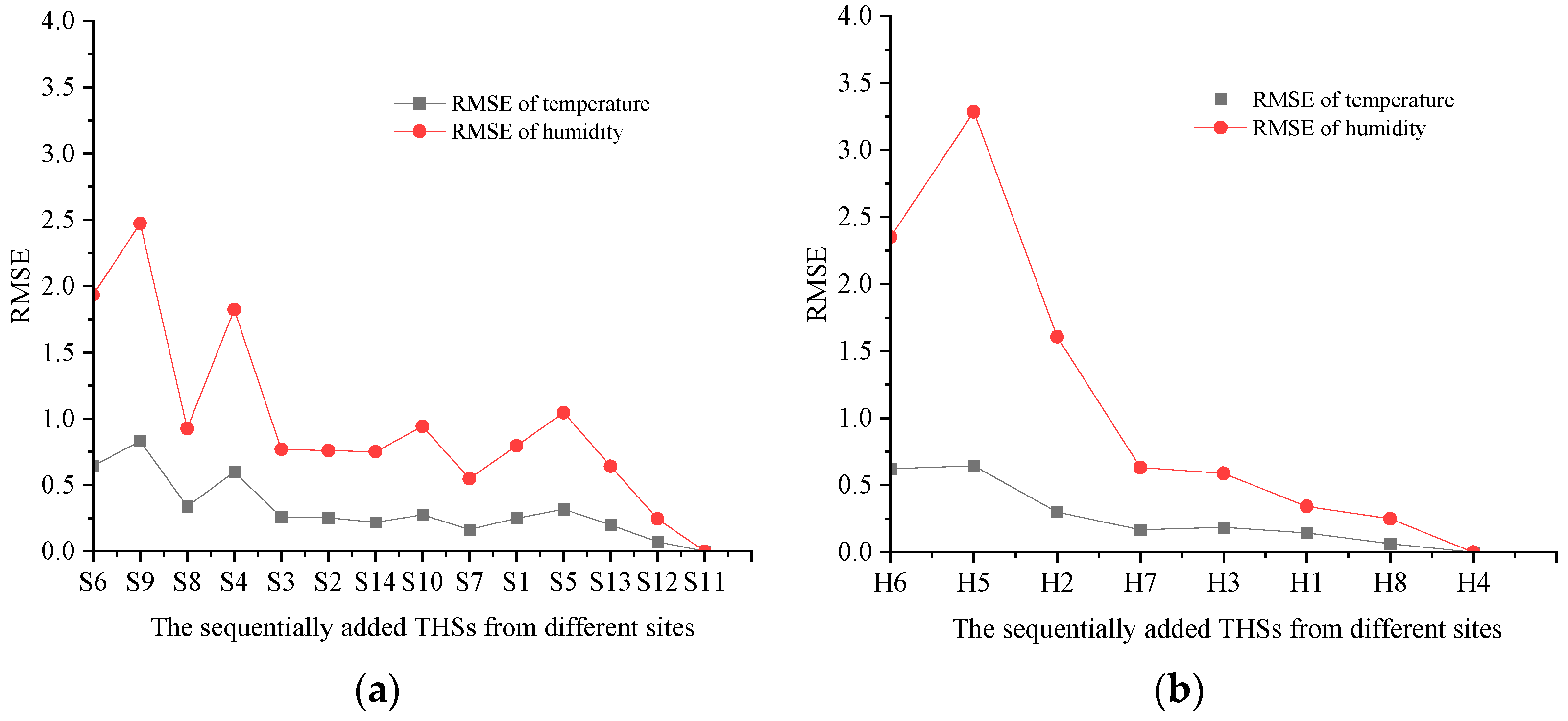
3.2.1. Priority Ranking for the THSs
3.2.2. Determination of THS Quantity Required
- (1)
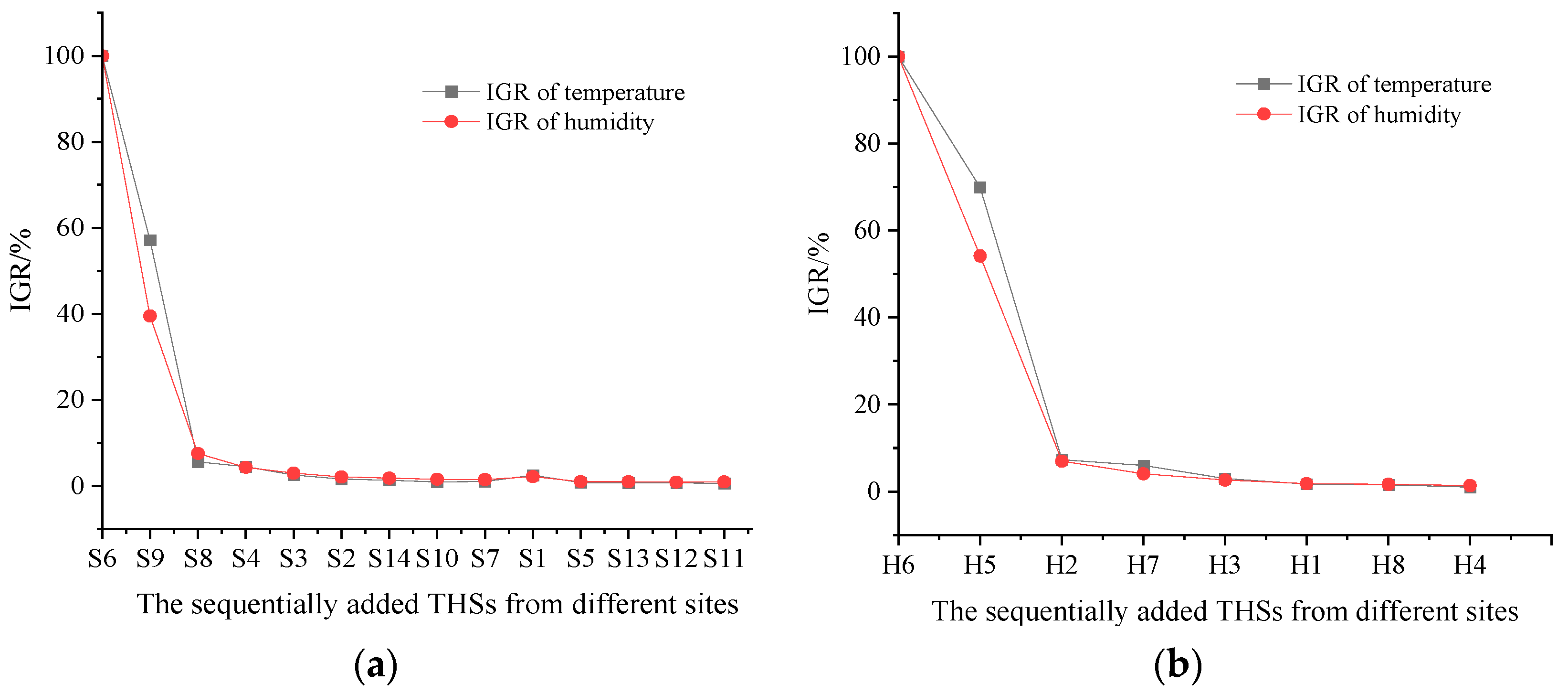
- Low monitoring requirement scenario under low cost budget: For illustration, the RMSE thresholds for temperature and relative humidity are set to 1 °C and 10%, respectively, and the IGR threshold is set to 10%. As in Figure 5a, the RMSE of temperature and relative humidity are 0.64 °C and 1.9%, respectively, with the first ranked THS S6 in the vertical direction, which meets the temperature- and humidity-monitoring requirement. However, THS S6 cannot meet the IGR requirement by itself, so the second ranked THS S9 is also needed to improve the information abundance. From Figure 6a, the temperature IGR and relative humidity IGR of the next THS are 5.5% and 7.5%, respectively, both of which meet the IGR threshold of 10%. Therefore, in this scenario, two THSs, S6 and S9, are selected in the vertical direction to meet the dual requirements of monitoring accuracy and information abundance, i.e., .
- (2)
- Scenario with high monitoring requirement under high cost budget: When the monitoring requirements of temperature and humidity are high, the cost budget should be correspondingly improved. Then, the RMSE thresholds of temperature and relative humidity are set at 0.5 °C and 5%, respectively, and the IGR threshold is set at 7%. In this scenario, as in Figure 5a, when the THS number is increased to three in the vertical direction, the RMSEs of temperature and relative humidity are 0.34 °C and 0.92%, respectively, which both meet the RMSE thresholds. Meanwhile, the temperature IGR and the relative humidity IGR of the next THS are 4.4% and 4.3%, respectively, both below the threshold value of 7%. In summary, to meet the strict requirements of monitoring accuracy and information abundance, the top three THSs in the vertical direction should be selected, i.e., .
3.2.3. Optimal Configuration of the THSs Required
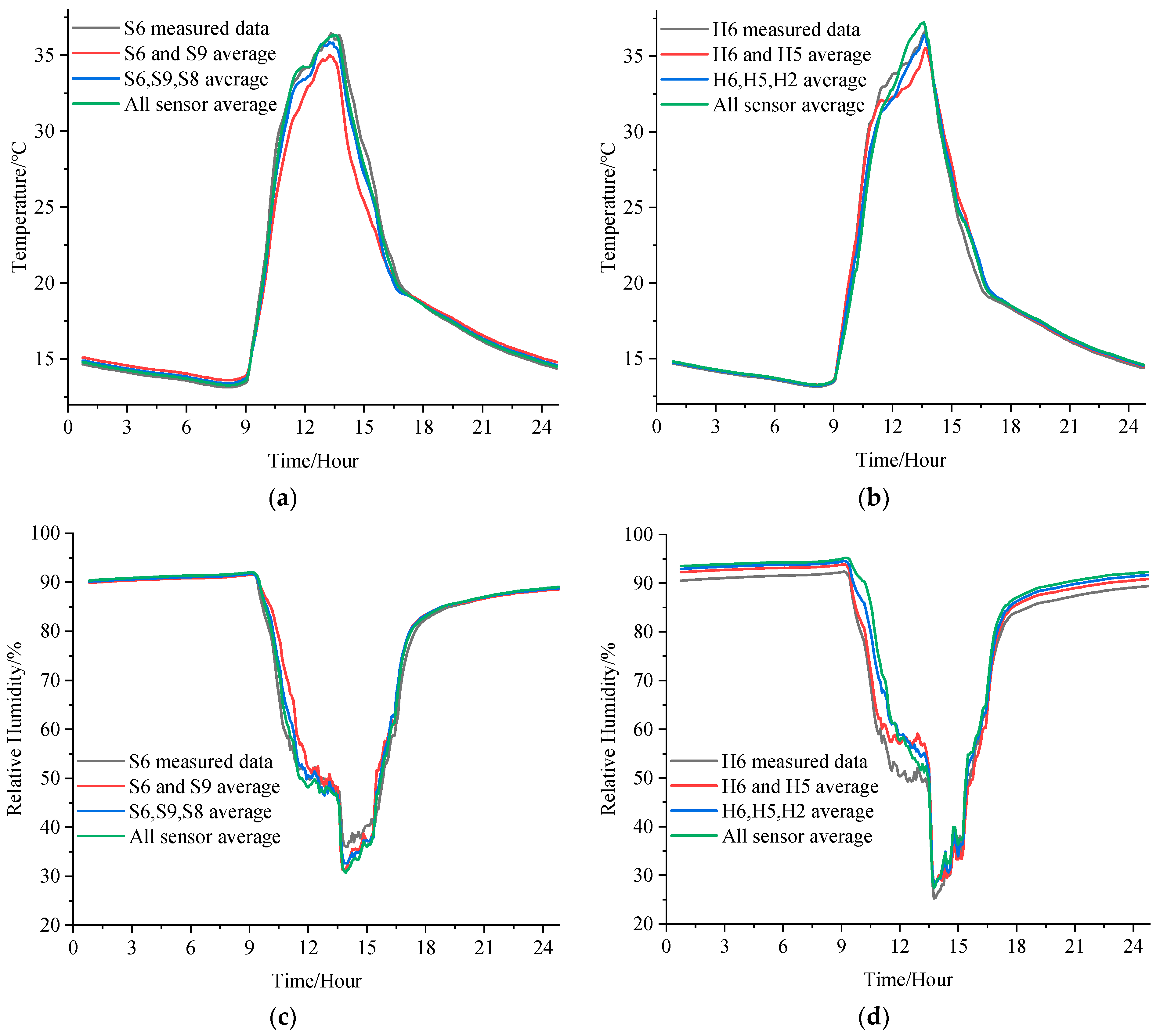
3.2.4. Validation of the Optimal Configuration Strategy
- (1)
- Characterization performance
- (2)
- Comparative advantage
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Wu, X.; Xia, T.; Fan, Z.; Shi, W.; Li, Y.; Li, T. New Insights of Designing Thermal Insulation and Heat Storage of Chinese Solar Greenhouse in High Latitudes and Cold Regions. Energy 2022, 242, 122953. [Google Scholar] [CrossRef]
- Vanthoor, B.H.E. A Model-Based Greenhouse Design Method; Wageningen University: Wageningen, The Netherlands, 2011. [Google Scholar]
- Zou, W.; Zhang, B.; Yao, F.; He, C. Verification and forecasting of temperature and humidity in solar greenhouse based on improved extreme learning machine algorithm. Trans. Chin. Soc. Agric. 2015, 31, 194–200. [Google Scholar]
- Ferentinos, K.P.; Katsoulas, N.; Tzounis, A.; Bartzanas, T.; Kittas, C. Wireless Sensor Networks for Greenhouse Climate and Plant Condition Assessment. Biosyst. Eng. 2017, 153, 70–81. [Google Scholar] [CrossRef]
- Jiang, G.; Hu, Y.; Liu, Y.; Zou, Z. Analysis on insulation performance of sunken solar greenhouse based on CFD. Trans. Chin. Soc. Agric. Eng. 2011, 27, 275–281, (In Chinese with English abstract). [Google Scholar]
- Li, Z.; Wang, T.; Gong, Z.; Li, N. Forewarning technology and application for monitoring low temperature disaster in solar greenhouses based on internet of things. Trans. Chin. Soc. Agric. Eng. 2013, 29, 229–236, (In Chinese with English abstract). [Google Scholar]
- Zong, Z. Study on Monitoring System of Greenhouse Group and the Spatial and Temporal Distribution of the Environmental Parameters; Inner Mongolia Agricultural University: Hohhot, China, 2018; (In Chinese with English abstract). [Google Scholar]
- Wang, T.; Dai, X.; Liu, Y. Learning with Hilbert–Schmidt Independence Criterion: A Review and New Perspectives. Knowl.-Based Syst. 2021, 234, 107567. [Google Scholar] [CrossRef]
- Mancuso, M.; Bustaffa, F. A Wireless Sensors Network for Monitoring Environmental Variables in a Tomato Greenhouse. In Proceedings of the 2006 IEEE International Workshop on Factory Communication Systems, Torino, Italy, 27–30 June 2006; pp. 107–110. [Google Scholar]
- Lu, X.; Ding, Y.; Hao, K. Adaptive Design Optimization of Wireless Sensor Networks Using Artificial Immune Algorithms. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 788–792. [Google Scholar]
- Feng, L.; Li, H.; Zhi, Y. Greenhouse CFD Simulation for Searching the Sensors Optimal Placements. In Proceedings of the 2013 Second International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Fairfax, VA, USA, 12–16 August 2013; pp. 504–507. [Google Scholar]
- Cheng, X.; Li, D.; Shao, L.; Ren, Z. A Virtual Sensor Simulation System of a Flower Greenhouse Coupled with a New Temperature Microclimate Model Using Three-Dimensional CFD. Comput. Electron. Agric. 2021, 181, 105934. [Google Scholar] [CrossRef]
- Ali, A.; Hassanein, H.S. Optimal Placement of Camera Wireless Sensors in Greenhouses. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Sharma, H.; Vaidya, U.; Ganapathysubramanian, B. A Transfer Operator Methodology for Optimal Sensor Placement Accounting for Uncertainty. Build. Environ. 2019, 155, 334–349. [Google Scholar] [CrossRef]
- Dur, T.H.; Arcucci, R.; Mottet, L.; Solana, M.M.; Pain, C.; Guo, Y.-K. Weak Constraint Gaussian Processes for Optimal Sensor Placement. J. Comput. Sci. 2020, 42, 101110. [Google Scholar] [CrossRef]
- Löhner, R.; Camelli, F. Optimal Placement of Sensors for Contaminant Detection Based on Detailed 3D CFD Simulations. Eng. Comput. 2005, 22, 260–273. [Google Scholar] [CrossRef]
- Arnesano, M.; Revel, G.M.; Seri, F. A Tool for the Optimal Sensor Placement to Optimize Temperature Monitoring in Large Sports Spaces. Autom. Constr. 2016, 68, 223–234. [Google Scholar] [CrossRef]
- Suryanarayana, G.; Arroyo, J.; Helsen, L.; Lago, J. A Data Driven Method for Optimal Sensor Placement in Multi-Zone Buildings. Energy Build. 2021, 243, 110956. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Kwok, H.H.L.; Li, A.T.Y.; Tong, J.C.K.; Lau, A.K.H. BIM-Supported Sensor Placement Optimization Based on Genetic Algorithm for Multi-Zone Thermal Comfort and IAQ Monitoring. Build. Environ. 2022, 216, 108997. [Google Scholar] [CrossRef]
- Lee, S.; Lee, I.; Yeo, U.; Kim, R.; Kim, J. Optimal Sensor Placement for Monitoring and Controlling Greenhouse Internal Environments. Biosyst. Eng. 2019, 188, 190–206. [Google Scholar] [CrossRef]
- Gretton, A.; Bousquet, O.; Smola, A.; Schölkopf, B. Measuring Statistical Dependence with Hilbert-Schmidt Norms. In Algorithmic Learning Theory; Jain, S., Simon, H.U., Tomita, E., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3734, pp. 63–77. ISBN 978-3-540-29242-5. [Google Scholar]
- Feng, L.; Di, T.; Zhang, Y. HSIC-Based Kernel Independent Component Analysis for Fault Monitoring. Chemom. Intell. Lab. Syst. 2018, 178, 47–55. [Google Scholar] [CrossRef]
- Rustamov, R.M.; Klosowski, J.T. Kernel Mean Embedding Based Hypothesis Tests for Comparing Spatial Point Patterns. Spat. Stat. 2020, 38, 100459. [Google Scholar] [CrossRef]
- Vitetta, G.M.; Taylor, D.P.; Colavolpe, G.; Pancaldi, F.; Martin, P.A. Elements of Information Theory; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; ISBN 978-1-118-57661-8. [Google Scholar]
- Pei, X.-Y.; Yi, T.-H.; Qu, C.-X.; Li, H.-N. Conditional Information Entropy Based Sensor Placement Method Considering Separated Model Error and Measurement Noise. J. Sound Vib. 2019, 449, 389–404. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Z.; Tsai, P.-W.; Xu, L. Entropy-Driven Data Aggregation Method for Energy-Efficient Wireless Sensor Networks. Inf. Fusion 2020, 56, 103–113. [Google Scholar] [CrossRef]
- Wang, X.; Ma, J.; Wang, S. Parallel Energy-Efficient Coverage Optimization with Maximum Entropy Clustering in Wireless Sensor Networks. J. Parallel Distrib. Comput. 2009, 69, 838–847. [Google Scholar] [CrossRef]

| THS Rank | THS Location | IIC | THS Rank | THS Location | IIC |
|---|---|---|---|---|---|
| 1 | S6 | 570 | 8 | S10 | 537 |
| 2 | S9 | 449 | 9 | S7 | 541 |
| 3 | S8 | 512 | 10 | S1 | 539 |
| 4 | S4 | 505 | 11 | S5 | 549 |
| 5 | S3 | 518 | 12 | S13 | 550 |
| 6 | S2 | 523 | 13 | S12 | 560 |
| 7 | S14 | 530 | 14 | S11 | 566 |
| THS Rank | THS Location | IIC | THS Rank | THS Location | IIC |
|---|---|---|---|---|---|
| 1 | H6 | 550 | 5 | H3 | 525 |
| 2 | H5 | 523 | 6 | H1 | 527 |
| 3 | H2 | 506 | 7 | H8 | 533 |
| 4 | H7 | 526 | 8 | H4 | 535 |
| Monitoring Orientation | Low Cost Budget | High Monitoring Requirement |
|---|---|---|
| The vertical direction | S6, S9 | S6, S9, S8 |
| The horizontal direction | H6, H5 | H6, H5, H2 |
| THS Configuration | Temperature RMSE (°C) | Relative Humidity RMSE (%) | Temperature IGR (%) | Relative Humidity IGR (%) |
|---|---|---|---|---|
| S6, S9 # | 0.60 | 1.32 | 6.70 | 10.0 |
| H6, H5 # | 0.50 | 2.30 | 9.47 | 9.1 |
| S6, S9, S8 # | 0.23 | 0.58 | 4.80 | 8.7 |
| H6, H5, H2 # | 0.33 | 1.10 | 6.90 | 6.0 |
| S6, S2 * | 0.62 | 1.8 | 13.5 | 21.5 |
| S5, S2 * | 0.51 | 1.9 | 14.3 | 21.1 |
| H1, H2 * | 0.46 | 1.35 | 12.8 | 20.2 |
| H7, H3 * | 0.47 | 1.64 | 11.3 | 20.8 |
| S6 S2 S14 * | 0.30 | 1.2 | 8.3 | 14.6 |
| S5 S2 S11 * | 0.43 | 1.48 | 8.7 | 15.0 |
| H1 H2 H4 * | 0.3 | 0.86 | 8.7 | 14.2 |
| H7 H3 H8 * | 0.33 | 0.85 | 7.2 | 13.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Liu, P.; Liu, X.; Liu, L.; Yu, Y. Configuration Optimization of Temperature–Humidity Sensors Based on Weighted Hilbert–Schmidt Independence Criterion in Chinese Solar Greenhouses. Agriculture 2024, 14, 311. https://doi.org/10.3390/agriculture14020311
Song C, Liu P, Liu X, Liu L, Yu Y. Configuration Optimization of Temperature–Humidity Sensors Based on Weighted Hilbert–Schmidt Independence Criterion in Chinese Solar Greenhouses. Agriculture. 2024; 14(2):311. https://doi.org/10.3390/agriculture14020311
Chicago/Turabian StyleSong, Chengbao, Pingzeng Liu, Xinghua Liu, Lining Liu, and Yuting Yu. 2024. "Configuration Optimization of Temperature–Humidity Sensors Based on Weighted Hilbert–Schmidt Independence Criterion in Chinese Solar Greenhouses" Agriculture 14, no. 2: 311. https://doi.org/10.3390/agriculture14020311






