Modeling Stability of Alfalfa Yield and Main Quality Traits
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material, Environment, and Experimental Design
2.2. Experimental Measurements
- (a)
- Plant height: the measurement in centimeters between the top of the stem and the soil.
- (b)
- The number of nodes, expressed as the total number of main stem nodes.
2.3. Data Elaboration
2.4. Biplot Models
2.5. Exploratory Data Analysis
3. Results
3.1. Variation in the Stability Indices
3.2. Heritability Estimations
3.3. Trait Correlations
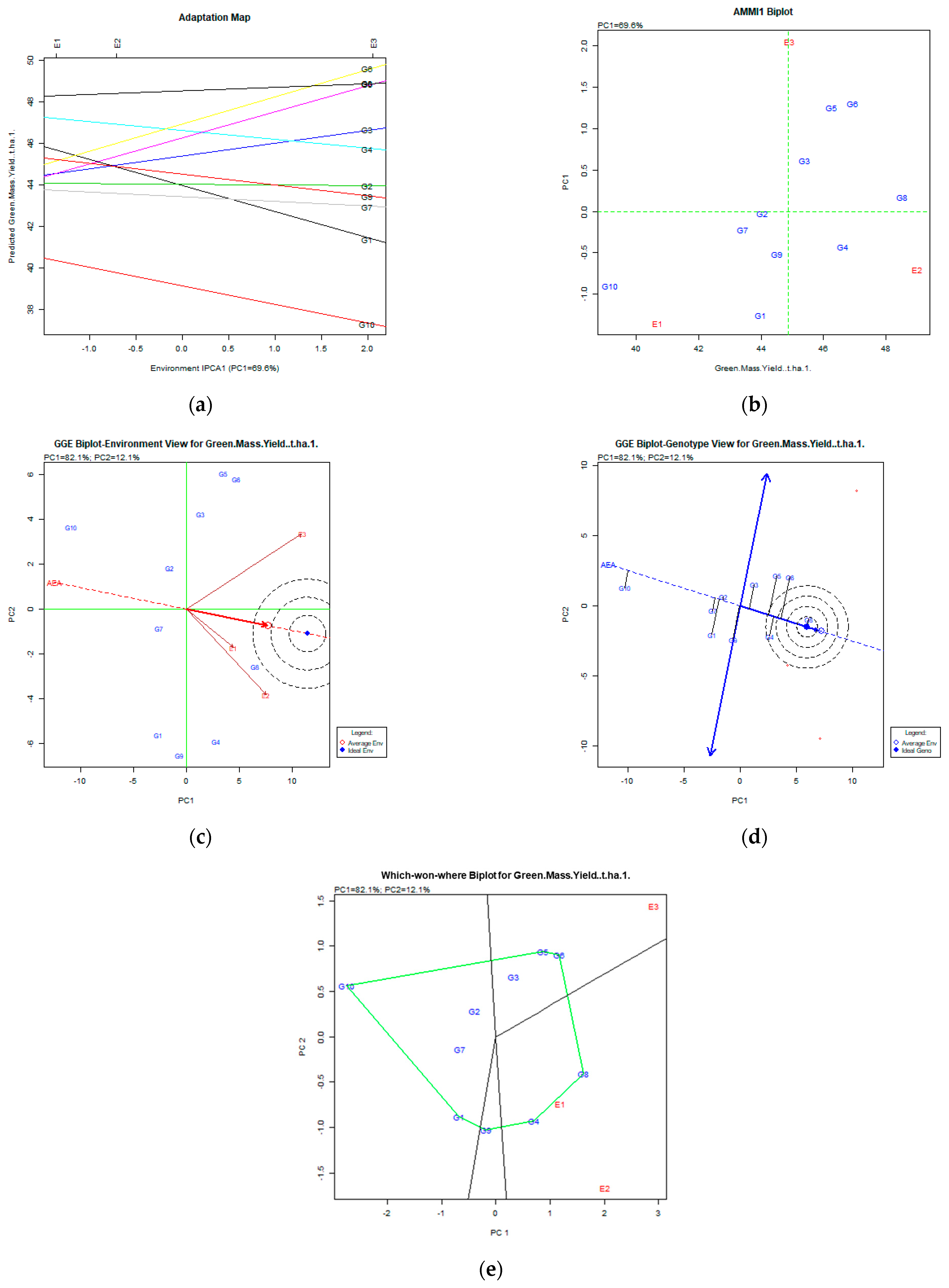
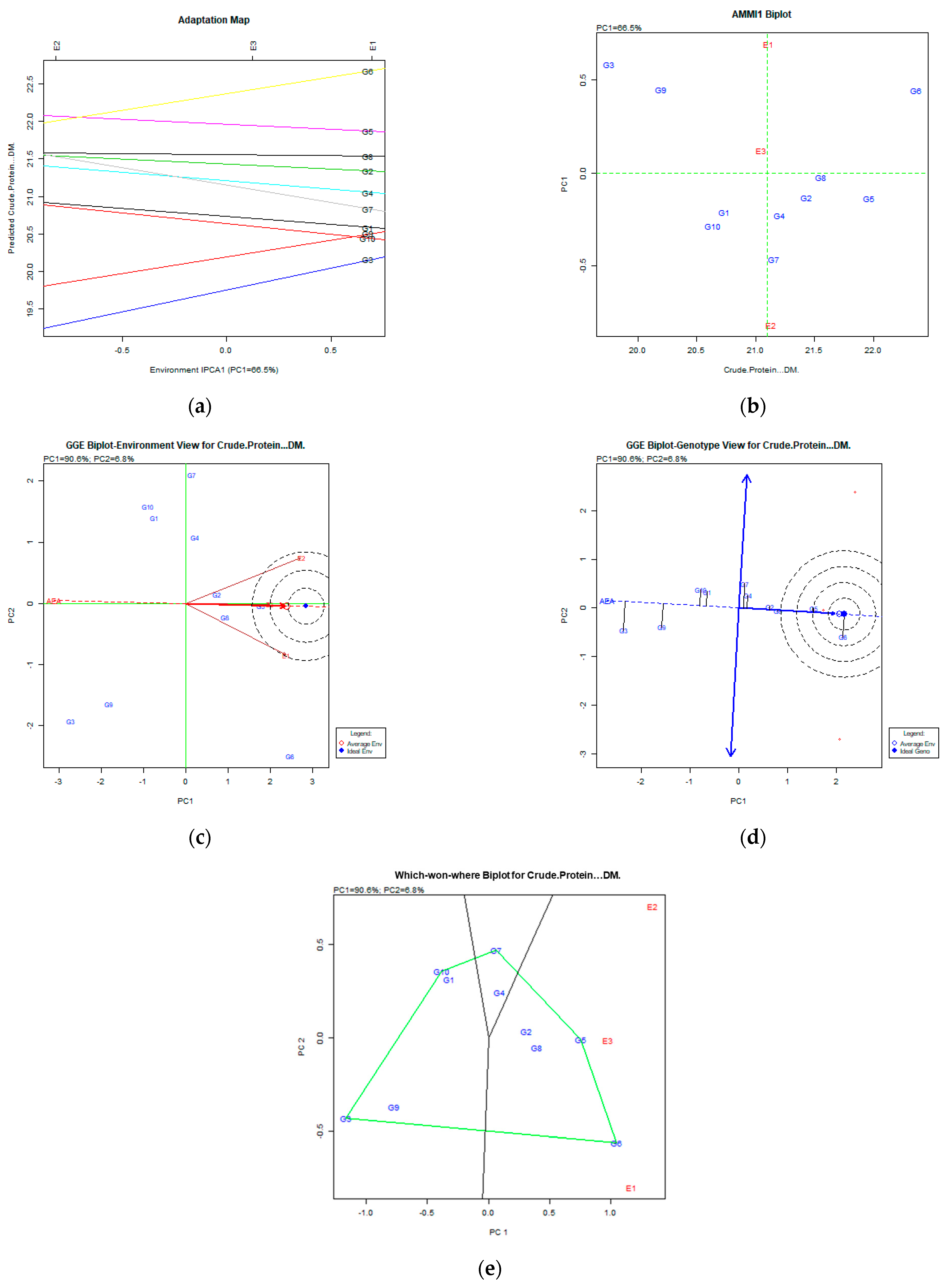
3.4. AMMI and GGE Biplots
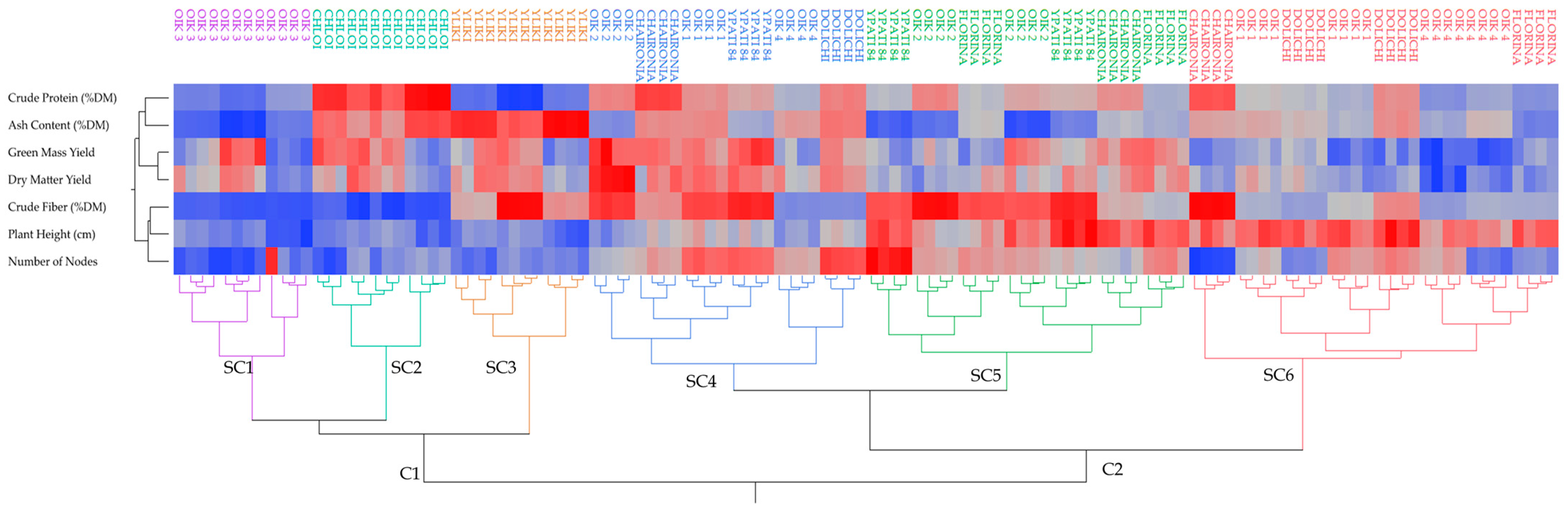
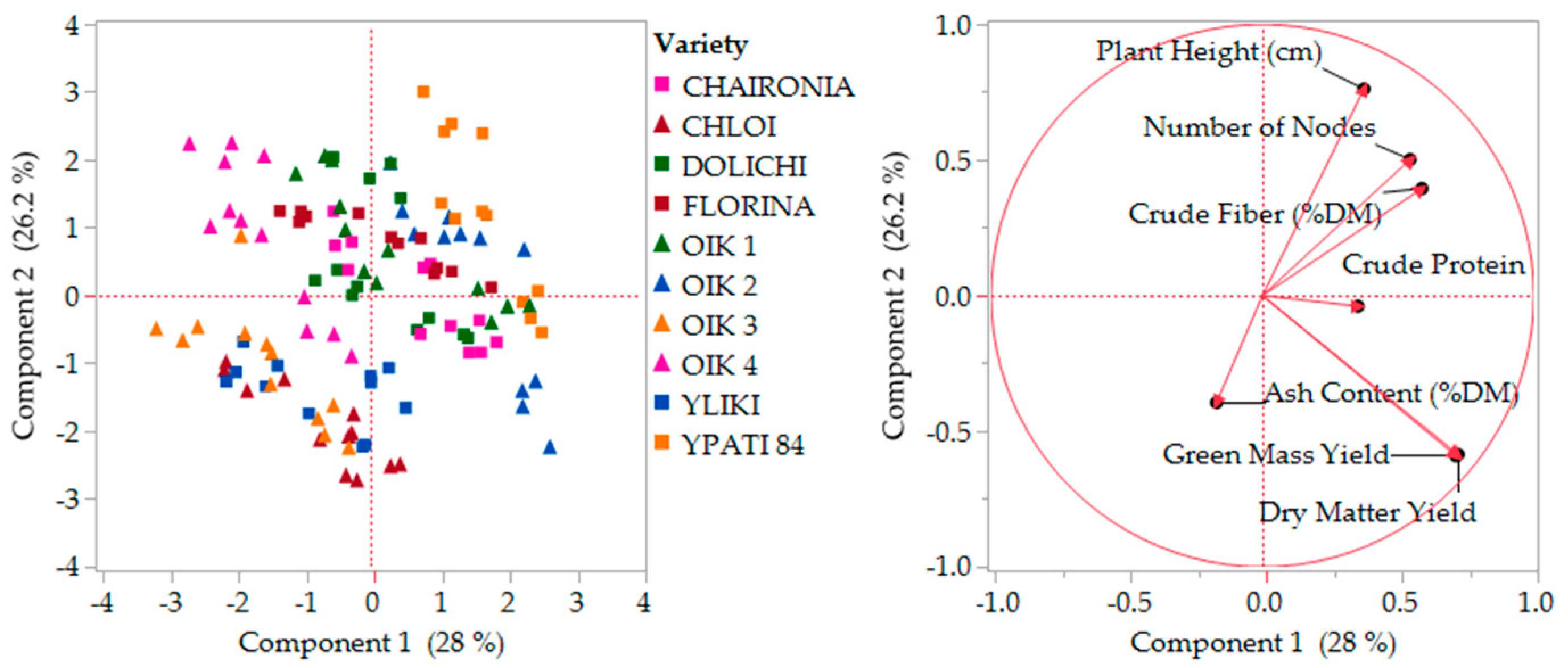
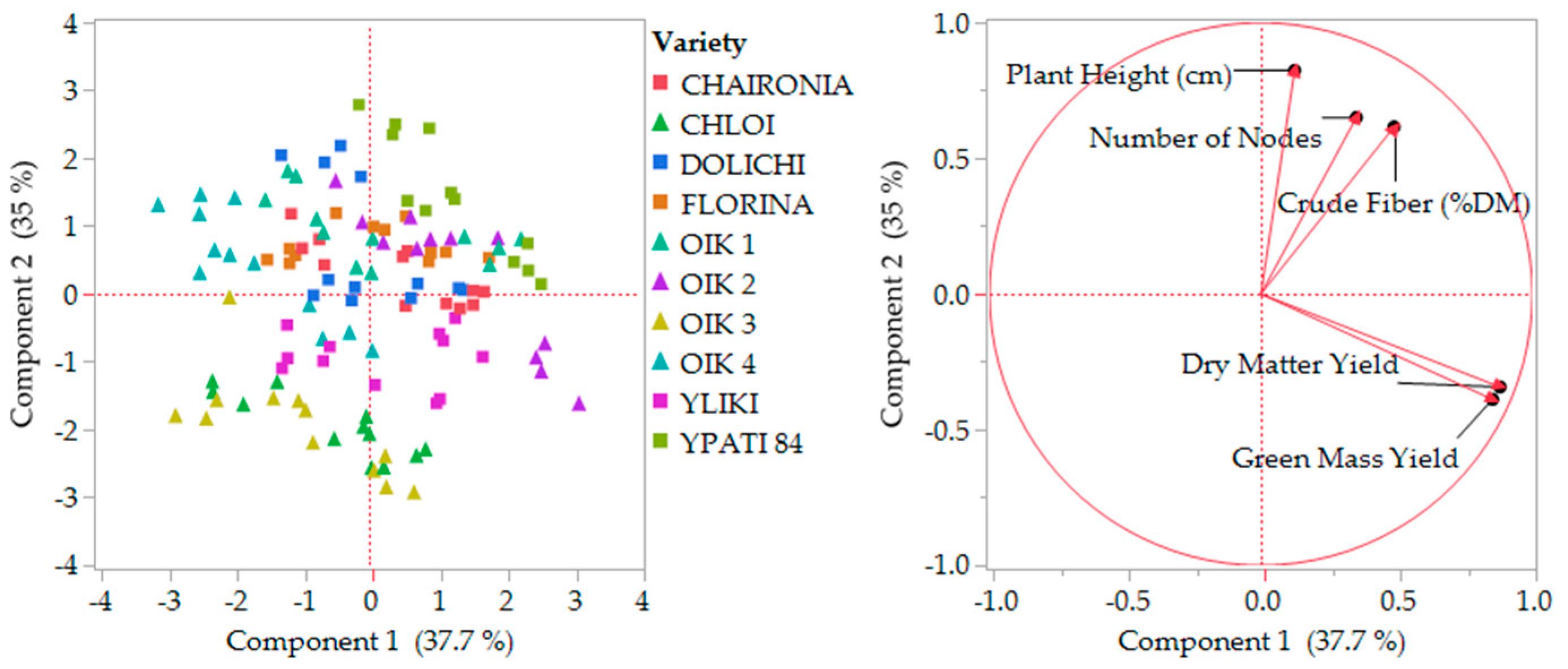
3.5. Exploratory Data Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richard, C. Utilising Lucernes potential for dairy farming. In Proceedings of the 18th International Farm Managment Congress, Methven, Canterbury, New Zealand, 20–25 March 2011; pp. 227–235. [Google Scholar]
- Rojas-Garcia, A.; Torres-Salado, N.; Joaquin-Cancino, S.; Hernandez-Garay, A.; Maldonado-Peralta, M.; Sanchez-Santillan, P. Yield Components of Alfalfa (Medicago sativa L.) Varieties. Agrociencia 2017, 51, 697–708. [Google Scholar]
- Atumo, T.T.; Kauffman, R.; Talore, D.G.; Abera, M.; Tesfaye, T.; Tunkala, B.Z.; Zeleke, M.; Kalsa, G.K. Adaptability, forage yield and nutritional quality of alfalfa (Medicago sativa) genotypes. Sustain. Environ. 2021, 7, 1895475. [Google Scholar] [CrossRef]
- Alzahrani, O.R.; Alshehri, M.A.; Alasmari, A.; Ibrahim, S.D.; Oyouni, A.A.; Siddiqui, Z.H. Evaluation of genetic diversity among Saudi Arabian and Egyptian cultivars of alfalfa (Medicago sativa L.) using ISSR and SCoT markers. J. Taibah Univ. Sci. 2023, 17, 2194187. [Google Scholar] [CrossRef]
- Liatukienė, A.; Norkevičienė, E.; Danytė, V.; Liatukas, Ž. Diversity of Agro-Biological Traits and Development of Diseases in Alfalfa Cultivars during the Contrasting Vegetation Seasons. Sustainability 2023, 15, 1445. [Google Scholar] [CrossRef]
- Yüksel, O.; Albayrak, S.; Türk, M.; Sevimay, C.S. Dry matter yields and some quality features of alfalfa (Medicago sativa L.) cultivars under two different locations of Turkey. J. Ant. Appl. Sci. 2016, 20, 155–160. [Google Scholar] [CrossRef]
- Geren, H.; Kir, B.; Demiroglu, G.; Kavut, Y.T. Effects of different soil textures on the yield and chemical composition of alfalfa (Medicago sativa L.) cultivars under Mediterranean climate conditions. Asian J. Chem. 2009, 21, 5517. [Google Scholar]
- Sommer, A.; Vodnansky, M.; Petrikovic, P.; Pozgaj, R. Influence of Lucerne and meadow hay quality on the digestibility of nutrients in the roe deer. Czech J. Anim. Sci. 2005, 50, 74–80. [Google Scholar] [CrossRef]
- Horvat, D.; Viljevac Vuletić, M.; Andrić, L.; Baličević, R.; Kovačević Babić, M.; Tucak, M. Characterization of Forage Quality, Phenolic Profiles, and Antioxidant Activity in Alfalfa (Medicago sativa L.). Plants 2022, 11, 2735. [Google Scholar] [CrossRef] [PubMed]
- Fahad, S.; Bajwa, A.A.; Nazir, U.; Anjum, S.A.; Farooq, A.; Zohaib, A.; Sadia, S.; Nasim, W.; Adkins, S.; Saud, S. Crop production under drought and heat stress: Plant responses and management options. Front. Plant Sci. 2017, 8, 1147. [Google Scholar] [CrossRef] [PubMed]
- Kebede, G.; Assefa, G.; Feyissa, F.; Mengistu, A.; Tekletsadik, T.; Minta, M.; Tesfaye, M. Biomass yield potential and herbage quality of alfalfa (Medicago sativa L.) genotypes in the central highland of Ethiopia. Int. J. Res. Stud. Agric. Sci. 2017, 3, 14–26. [Google Scholar]
- Odeseye, A.O.; Amusa, N.A.; Ijagbone, I.F.; Aladele, S.E.; Ogunkanmi, L.A. Genotype by Environment Interactions of Twenty Accessions of Cowpea [Vigna unguiculata (L.) Walp.] across Two Locations in Nigeria. Ann. Agrar. Sci. 2018, 16, 481–489. [Google Scholar] [CrossRef]
- Wayu, S.; Atsbha, T. Evaluation of dry matter yield, yield components and nutritive value of selected alfalfa (Medicago sativa L.) cultivars grown under Lowland Raya Valley, Northern Ethiopia. Afr. J. Agrc. Res. 2019, 14, 705–711. [Google Scholar]
- Avci, M.A.; Ozkose, A.; Tamkoc, A. Determination of yield and quality characteristics of alfalfa (Medicago sativa L.) varieties grown in different locations. J. Anim. Vet. Adv. 2013, 12, 487–490. [Google Scholar]
- Sayed, M.R.I.; Alshallash, K.S.; Safhi, F.A.; Alatawi, A.; Alshamrani, S.M.; Dessoky, E.S.; Althobaiti, A.T.; Althaqafi, M.M.; Gharib, H.S.; Shafie, W.W.M.; et al. Genetic Diversity, Analysis of Some Agro-Morphological and Quality Traits and Utilization of Plant Resources of Alfalfa. Genes 2022, 13, 1521. [Google Scholar] [CrossRef]
- Fasoulas, A.C. A moving block evaluation technique for improving the efficiency of pedigree selection. Euphytica 1987, 36, 473–478. [Google Scholar] [CrossRef]
- Kontsiotou, H.; Zotis, S. Variation of characteristics in 21 Greek ecotypes of alfalfa (Medicago sativa L.). In Proceedings of the 5th National Hellenic Conference in Genetics and Plant Breeding, Volos, Greece, 18–20 October 1994; pp. 220–228. [Google Scholar]
- Tavoletti, S.; Capitani, E.; Pierangeli, S. Evaluation of alfalfa populations collected in the Marche region. In Lucerne and Medics for the XXI Century, Proceedings of the XIII Eucarpia Medicago spp. Group Meeting, Perugia, Italy, 13–16 September 1999; Universita di Perugia: Perugia, Italy, 2000; pp. 228–230. [Google Scholar]
- Popovic, S.; Cupic, T.; Grljusic, S.; Tucak, M. Use of variability and path analysis in determining yield and quality of alfalfa. In Breeding and Seed Production for Conventional and Organic Agriculture, Proceedings of the XXVI Meeting of the EUCARPIA Fodder Crops and Amenity Grasses Section, XVI Meeting of the European Association for Research on Plant Breeding (EUCARPIA) Medicago spp. Group joint Meeting, Perugia, Italy, 2–7 September 2006; Universita degli Studi di Perugia—Facolta di Agraria: Perugia, Italy, 2007; pp. 95–99. [Google Scholar]
- Seiam, M.A.; El-Nahrawy, M.A. Selection of some alfalfa populatios for forage yield and quality using modified mass selection. Egypt. J. Plant Breed. 2020, 24, 617–630. [Google Scholar]
- Ünal, S.; Mutlu, Z.; Efe, B. Agromorphological, yield and quality characteristics of two populations of alfalfa developed by mass selection. Cienc. Rural. Santa Maria 2023, 53, e20220036. [Google Scholar] [CrossRef]
- Acharya, J.P.; Lopez, Y.; Gouveia, B.T.; de Bem Oliveira, I.; Resende, M.F.R., Jr.; Muñoz, P.R.; Rios, E.F. Breeding Alfalfa (Medicago sativa L.) Adapted to Subtropical Agroecosystems. Agronomy 2020, 10, 742. [Google Scholar] [CrossRef]
- Eren, B.; Keskin, B.; Demirel, F.; Demirel, S.; Türkoğlu, A.; Yilmaz, A.; Haliloğlu, K. Assessment of genetic diversity and population structure in local alfalfa genotypes using iPBS molecular markers. Genet. Resour. Crop Evol. 2023, 70, 617–628. [Google Scholar] [CrossRef]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Ipsilandis, C.G. A Stability Analysis Using AMMI and GGE Biplot Approach on Forage Yield Assessment of Common Vetch in Both Conventional and Low-Input Cultivation Systems. Agriculture 2021, 11, 567. [Google Scholar] [CrossRef]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Ipsilandis, C.G. Estimations on Trait Stability of Maize Genotypes. Agriculture 2021, 11, 952. [Google Scholar] [CrossRef]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Ipsilandis, C.G. Stability, the Last Frontier: Forage Yield Dynamics of Peas under Two Cultivation Systems. Plants 2022, 11, 892. [Google Scholar] [CrossRef] [PubMed]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Kantas, D.; Ipsilandis, C.G. Genotype-by-Environment Interaction Analysis for Quantity and Quality Traits in Faba Beans Using AMMI, GGE Models, and Stability Indices. Plants 2023, 12, 3769. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Tinker, N.A. Biplot analysis of multienvironment trial data: Principles and applications. Can. J. Plant Sci. 2006, 86, 623–645. [Google Scholar] [CrossRef]
- Seiam, M.A.; Mohamed, E.S. Forage Yield, Quality Characters and Genetic Variability of some Promising Egyptian Clover Populations. Egyptian. J. Plant Breed. 2020, 24, 839–858. [Google Scholar]
- Baxevanos, D.; Loka, D.; Tsialtas, T. Evaluation of Alfalfa Cultivars Under Rainfed Mediterranean Conditions. J. Agric. Sci. 2021, 159, 281–292. [Google Scholar] [CrossRef]
- Hakl, J.; Mofidian, S.M.A.; Kozova, Z.; Jaromir, S. Estimation of lucerne yield stability for enabling effective cultivar selection under rainfed conditions. Grass Forage Sci. 2019, 74, 687–695. [Google Scholar] [CrossRef]
- Ceccarelli, S. Positive interpretation of genotype by environment interactions in relation to sustainability and biodiversity. In Plant Adaptation and Crop Improvement; Cooper, M., Hammer, G.L., Eds.; CAB International: Wallingford, UK, 1996; pp. 467–486. [Google Scholar]
- Flores, F.; Moreno, M.T.; Cubero, J.I. A comparison of univariate and multivariate methods to analyze G × E interaction. Field Crops Res. 1998, 56, 271–286. [Google Scholar] [CrossRef]
- Elias, A.A.; Robbins, K.R.; Doerge, R.W.; Tuinstra, M.R. Half a century of studying genotype x environment interactions in plant breeding experiments. Crop Sci. 2016, 56, 2090–2105. [Google Scholar] [CrossRef]
- Zobel, R.W.; Wright, M.J.; Gauch, H.G. Statistical analysis of a yield trial. Agron. J. 1988, 80, 388–393. [Google Scholar] [CrossRef]
- Yan, W.; Hunt, L.A.; Sheng, Q.; Szlavnics, Z. Cultivar evaluation and mega-environment investigation based on the GGE biplot. Crop Sci. 2000, 40, 597–605. [Google Scholar] [CrossRef]
- Haile, G.A.; Kebede, G.Y. Identification of Stable Faba Bean (Vicia faba L.) Genotypes for Seed Yield in Ethiopia Using GGE Model. J. Plant Sci. 2021, 9, 163–169. [Google Scholar]
- Fasoula, V.A. Prognostic Breeding: A new paradigm for crop improvement. Plant Breed. Rev. 2013, 37, 297–347. [Google Scholar]
- Steel, R.G.D.; Torrie, H.; Dickey, D.A. Principles and Procedures of Statistics. A Biometrical Approach, 3rd ed.; McGraw-Hill: New York, NY, USA, 1997; p. 666. [Google Scholar]
- Enriquez-Hidalgo, D.; Cruz, T.; Teixeira, D.L.; Steinfort, U. Phenological Stages of Mediterranean Forage Legumes, Based on the BBCH Scale. Ann. Appl. Biol. 2020, 176, 357–368. [Google Scholar] [CrossRef]
- Association of Official Analytical Chemists (AOAC). Official Methods of Analysis of the Association of Official Analytical Chemists, 21st ed.; Oxford University Press: Washington, DC, USA, 2019. [Google Scholar]
- Association of Official Analytical Chemists (AOAC). Official Methods of Analysis, 18th ed.; Association of Official Analytical Chemists (AOAC): Gaithersburg, MD, USA, 2005. [Google Scholar]
- Fasoula, V.A. A novel equation paves the way for an everlasting revolution with cultivars characterized by high and stable crop yield and quality. In Proceedings of the 11th National Hellenic Conference in Genetics and Plant Breeding, Orestiada, Greece, 31 October–2 November 2006; pp. 7–14. [Google Scholar]
- Greveniotis, V.; Fasoula, V.A. Application of prognostic breeding in maize. Crop Pasture Sci. 2016, 67, 605–620. [Google Scholar] [CrossRef]
- Greveniotis, V.; Sioki, E.; Ipsilandis, C.G. Estimations of fiber trait stability and type of inheritance in cotton. Czech J. Genet. Plant Breed. 2018, 54, 190–192. [Google Scholar] [CrossRef]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Kantas, D.; Ipsilandis, C.G. A Comparative Study on Stability of Seed Characteristics in Vetch and Pea Cultivations. Agriculture 2023, 13, 1092. [Google Scholar] [CrossRef]
- Greveniotis, V.; Bouloumpasi, E.; Zotis, S.; Korkovelos, A.; Kantas, D.; Ipsilandis, C.G. Stability Dynamics of Main Qualitative Traits in Maize Cultivations across Diverse Environments regarding Soil Characteristics and Climate. Agriculture 2023, 13, 1033. [Google Scholar] [CrossRef]
- McIntosh, M.S. Analysis of Combined Experiments. Agron. J. 1983, 75, 153–155. [Google Scholar] [CrossRef]
- Johnson, H.W.; Robinson, H.E.; Comstock, R.E. Estimate of genetic and environmental variability in soybean. Agron. J. 1955, 47, 314–318. [Google Scholar] [CrossRef]
- Hanson, G.; Robinson, H.F.; Comstock, R.E. Biometrical studies on yield in segregating population of Korean Lespedeza. Agron. J. 1956, 48, 268–274. [Google Scholar] [CrossRef]
- Singh, R.K.; Chaudhary, B.D. Biometrical Methods in Quantitative Genetic Analysis; Kalyani Publishers: New Delhi, India, 1977; p. 304. [Google Scholar]
- Gauch, H., Jr. Statistical Analysis of Regional Yield Trials: AMMI Analysis of Factorial Designs; Elsevier Science Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Khan, M.M.H.; Rafii, M.Y.; Ramlee, S.I.; Jusoh, M.; Al Mamun, M. AMMI and GGE biplot analysis for yield performance and stability assessment of selected Bambara groundnut (Vigna subterranea L. Verdc.) genotypes under the multi-environmental trials (METs). Sci. Rep. 2021, 11, 22791. [Google Scholar] [CrossRef] [PubMed]
- Koundinya, A.V.V.; Ajeesh, B.R.; Hegde, V.; Sheela, M.N.; Mohan, C.; Asha, K.I. Genetic parameters, stability and selection of cassava genotypes between rainy and water stress conditions using AMMI, WAAS, BLUP and MTSI. Sci. Hortic. 2021, 281, 109949. [Google Scholar]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Andrade, M.H.M.L.; Patiño-Torres, A.J.; Cavallin, I.C.; Guedes, M.L.; Carvalho, R.P.; Gonçalves, F.M.A.; Marçal, T.D.S.; Pinto, C.A.B.P. Stability of potato clones resistant to potato virus y under subtropical conditions. Crop Breed. Appl. Biotechnol. 2021, 21, e32872118. [Google Scholar] [CrossRef]
- Bouloumpasi, E.; Skendi, A.; Soufleros, E.H. Survey on Yeast Assimilable Nitrogen Status of Musts from Native and International Grape Varieties: Effect of Variety and Climate. Fermentation 2023, 9, 773. [Google Scholar] [CrossRef]
- Metochis, C.; Orphanos, P.I. Alfalfa yield and water use when forced into dormancy by withholding water during the summer. Agron. J. 1981, 73, 1048–1050. [Google Scholar] [CrossRef]
- Tucak, M.; Popovic, S.; Bolaric, S.; Kozumplik, V. Agronomic evaluation of alfalfa genotypes under ecological conditions of eastern croatia. In proceedings of the VII. Alps-Adria Scientific Workshop, 28 April–2 May 2008, Stara Lesna, Slovakia. Part I. Cereal Res. Commun. 2008, 36, 651–654. [Google Scholar]
- Fasoulas, A.C. The Honeycomb Methodology of Plant Breeding; Department of Genetics and Plant Breeding, Aristotle University of Thessaloniki: Thessaloniki, Greece, 1988; p. 168. [Google Scholar]
- Afsharmanesh, G. Study of some morphological traits and selection of drought- resistant alfalfa cultivars (Medicago sativa L.) in Jiroft. Iran. Plant Ecophysiol. 2009, 3, 109–118. [Google Scholar]
- Tucak, M.; Popović, S.; Čupić, T.; Grljušić, S.; Bolarić, S.; Kozumplik, V. Genetic diversity of alfalfa (Medicago spp.) estimated by molecular markers and morphological characters. Period. Biol. 2008, 110, 243–249. [Google Scholar]
- Takawale, P.S.; Jade, S.S.; Bahulikar, R.A.; Desale, J.S. Diversity in Lucerne (Medicago sativa L.) germplasm for morphology, yield and molecular markers and their correlations. Indian. J. Genet. 2019, 79, 453–459. [Google Scholar] [CrossRef]
- Temesgen, T.; Keneni, G.; Sefera, T.; Jarso, M. Yield stability and relationships among stability parameters in faba bean (Vicia faba L.) genotypes. Crop J. 2015, 3, 258–268. [Google Scholar] [CrossRef]
- Gurmu, F.; Lire, E.; Asfaw, A.; Alemayehu, F.; Rezene, Y.; Ambachew, D. GGE-biplot analysis of grain yield of faba bean genotypes in southern Ethiopia. Electron. J. Plant Breed. 2012, 3, 898–907. [Google Scholar]



| Source of Variation | Plant Height (cm) | Number of Nodes | Green Mass Yield (t ha−1) | Dry Matter Yield (t ha−1) | Crude Protein (%DM) | Crude Fiber (%DM) | Ash Content (%DM) |
|---|---|---|---|---|---|---|---|
| m.s | m.s. | m.s. | m.s. | m.s. | m.s. | m.s. | |
| Year (Y) | 22.584 ** | 2.935 ** | 693.313 ** | 27.378 ** | 0.075 ** | 0.090 ** | 0.074 ** |
| Genotype (G) | 49.930 ** | 3.223 ** | 79.110 ** | 1.919 ** | 7.520 ** | 15.010 ** | 1.983 ** |
| Year × Genotype (Y × G) | 6.884 ** | 1.056 ** | 13.738 ** | 0.324 * | 0.454 ** | 1.433 ** | 0.142 ** |
| Error | 0.401 | 0.047 | 2.849 | 0.143 | 0.001 | 0.001 | 0.001 |
| Genotypes | Plant Height (cm) | Number of Nodes | Green Mass Yield (t ha−1) | Dry Matter Yield (t ha−1) | Crude Protein (%DM) | Crude Fiber (%DM) | Ash Content (%DM) |
|---|---|---|---|---|---|---|---|
| Florina | 4691 | 734 | 154 | 233 | 5562 | 1812 | 4491 |
| Dolichi | 2187 | 331 | 166 | 270 | 4693 | 1836 | 6213 |
| Yliki | 3550 | 6791 | 133 | 329 | 2749 | 1983 | 5567 |
| Ypati 84 | 1591 | 425 | 111 | 334 | 14,184 | 24,296 | 3314 |
| Chaironia | 2976 | 424 | 105 | 250 | 5250 | 2009 | 6166 |
| Chloi | 4418 | 1784 | 106 | 208 | 6393 | 10,000 | 4856 |
| Population 1 | 3800 | 1069 | 106 | 206 | 4468 | 1963 | 4756 |
| Population 2 | 1535 | 3970 | 161 | 101 | 20,209 | 13,695 | 4854 |
| Population 3 | 2757 | 312 | 63 | 176 | 5002 | 50,025 | 5373 |
| Population 4 | 1843 | 675 | 209 | 102 | 9448 | 11,233 | 5172 |
| Traits | Min. | Max. | Mean | sd | GCV (%) | PCV (%) | H2 (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| Plant Height (cm) | 62.93 | 72.34 | 68.36 | 2.345 | 3.587 | 4.161 | 2.770 | 2.984 | 86.21 |
| Number of Nodes | 11.77 | 14.70 | 12.92 | 0.699 | 0.181 | 0.269 | 3.288 | 4.010 | 67.24 |
| Green Mass Yield (t ha−1) | 35.63 | 55.67 | 44.88 | 4.676 | 5.448 | 6.592 | 5.201 | 5.721 | 82.63 |
| Dry Matter Yield (t ha−1) | 8.85 | 13.35 | 11.26 | 0.873 | 0.133 | 0.160 | 3.239 | 3.552 | 83.11 |
| Crude Protein (%DM) | 19.21 | 22.73 | 21.10 | 0.800 | 0.589 | 0.627 | 3.637 | 3.752 | 93.96 |
| Crude Fiber (%DM) | 26.02 | 29.86 | 28.19 | 1.164 | 1.131 | 1.251 | 3.773 | 3.967 | 90.45 |
| Ash Content (%DM) | 10.37 | 12.04 | 11.14 | 0.416 | 0.153 | 0.165 | 3.516 | 3.649 | 92.84 |
| Plant Height (cm) | Number of Nodes | Green Mass Yield (t ha−1) | Dry Matter Yield (t ha−1) | Crude Protein (%DM) | Crude Fiber (%DM) | |
|---|---|---|---|---|---|---|
| Number of Nodes | 0.391 ** | |||||
| Green Mass Yield (t ha−1) | −0.143 | 0.046 | ||||
| Dry Matter Yield (t ha−1) | −0.130 | 0.066 | 0.795 ** | |||
| Crude Protein (%DM) | 0.118 | 0.203 * | 0.181 * | 0.107 | ||
| Crude Fiber (%DM) | 0.427 ** | 0.335 ** | 0.113 | 0.189 * | −0.001 | |
| Ash Content (%DM) | −0.294 ** | −0.161 | −0.054 | 0.063 | 0.137 | −0.035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greveniotis, V.; Bouloumpasi, E.; Skendi, A.; Korkovelos, A.; Kantas, D.; Zotis, S.; Ipsilandis, C.G. Modeling Stability of Alfalfa Yield and Main Quality Traits. Agriculture 2024, 14, 542. https://doi.org/10.3390/agriculture14040542
Greveniotis V, Bouloumpasi E, Skendi A, Korkovelos A, Kantas D, Zotis S, Ipsilandis CG. Modeling Stability of Alfalfa Yield and Main Quality Traits. Agriculture. 2024; 14(4):542. https://doi.org/10.3390/agriculture14040542
Chicago/Turabian StyleGreveniotis, Vasileios, Elisavet Bouloumpasi, Adriana Skendi, Athanasios Korkovelos, Dimitrios Kantas, Stylianos Zotis, and Constantinos G. Ipsilandis. 2024. "Modeling Stability of Alfalfa Yield and Main Quality Traits" Agriculture 14, no. 4: 542. https://doi.org/10.3390/agriculture14040542
APA StyleGreveniotis, V., Bouloumpasi, E., Skendi, A., Korkovelos, A., Kantas, D., Zotis, S., & Ipsilandis, C. G. (2024). Modeling Stability of Alfalfa Yield and Main Quality Traits. Agriculture, 14(4), 542. https://doi.org/10.3390/agriculture14040542






