Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Establishment of Finite Element Model for the Frame and Static Analysis
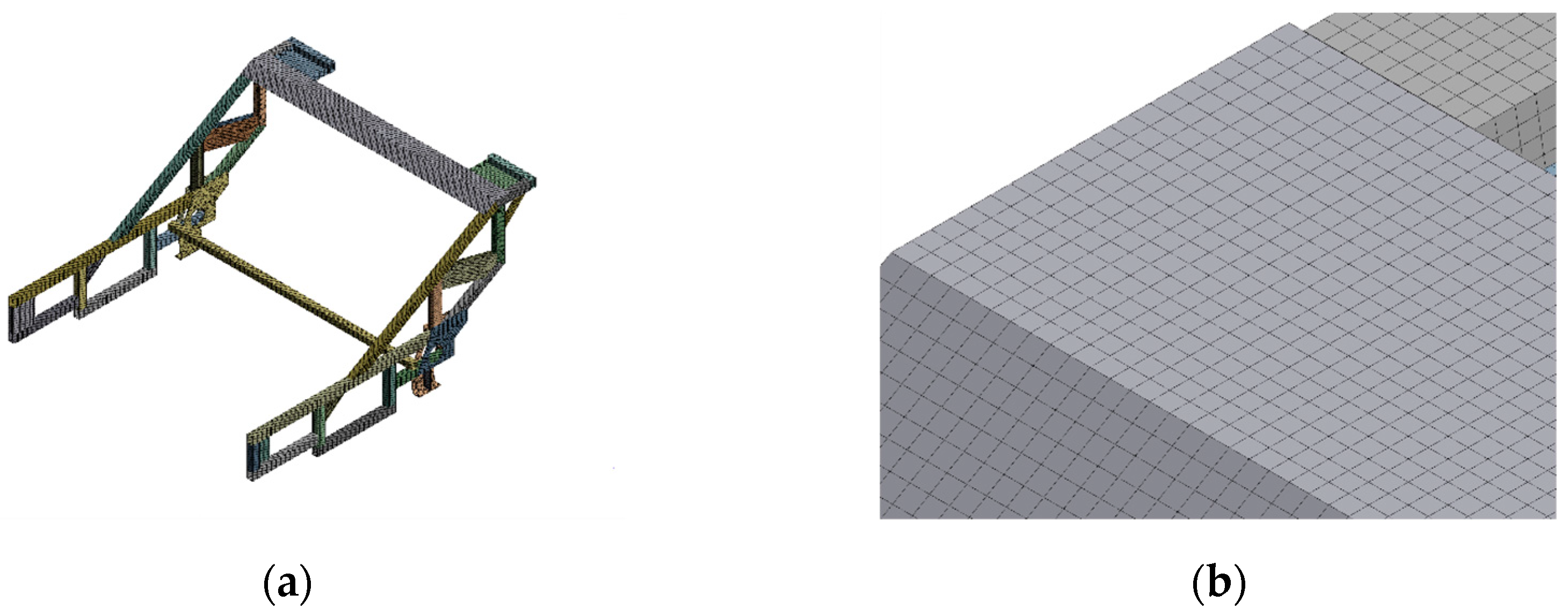
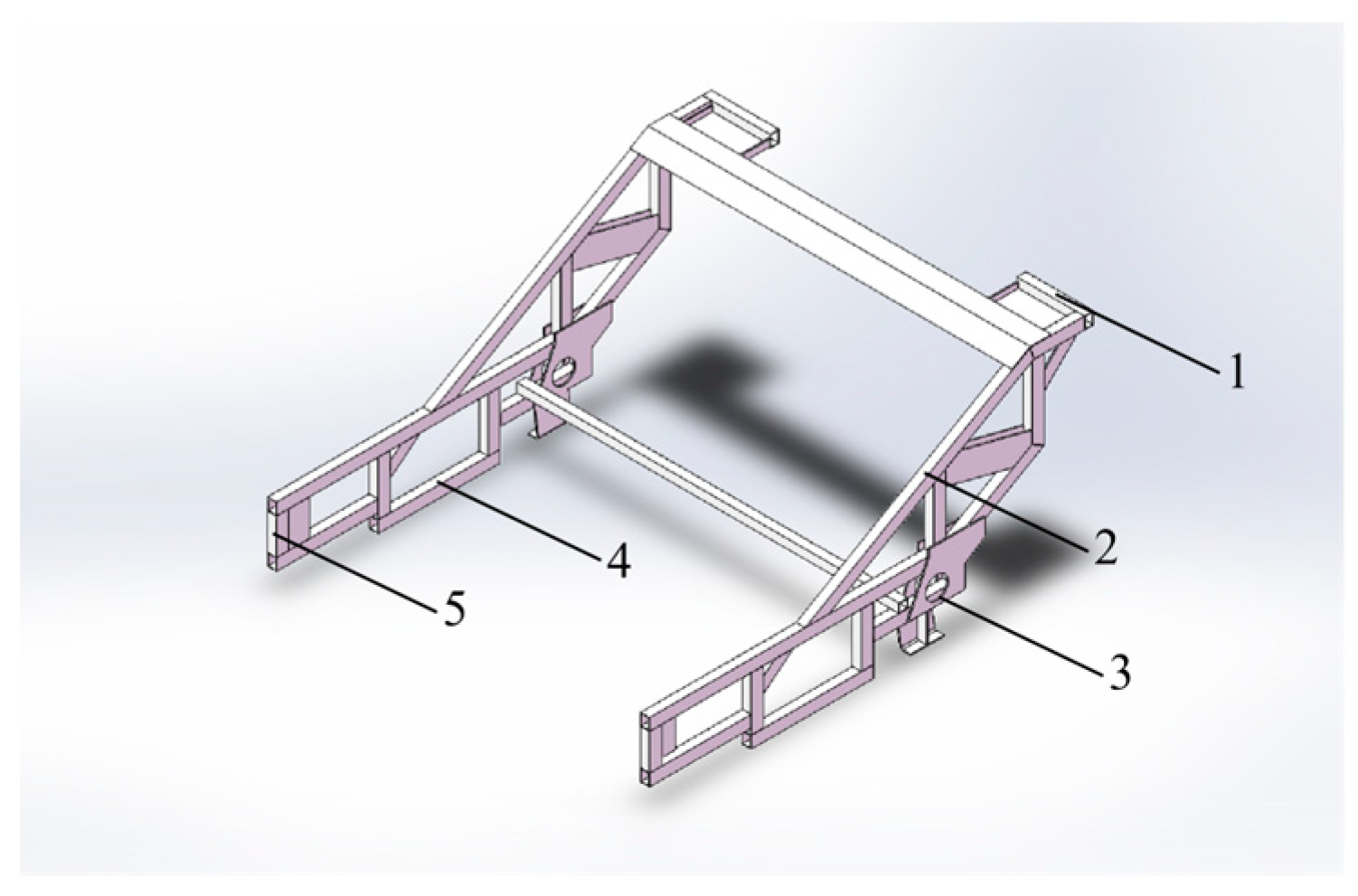
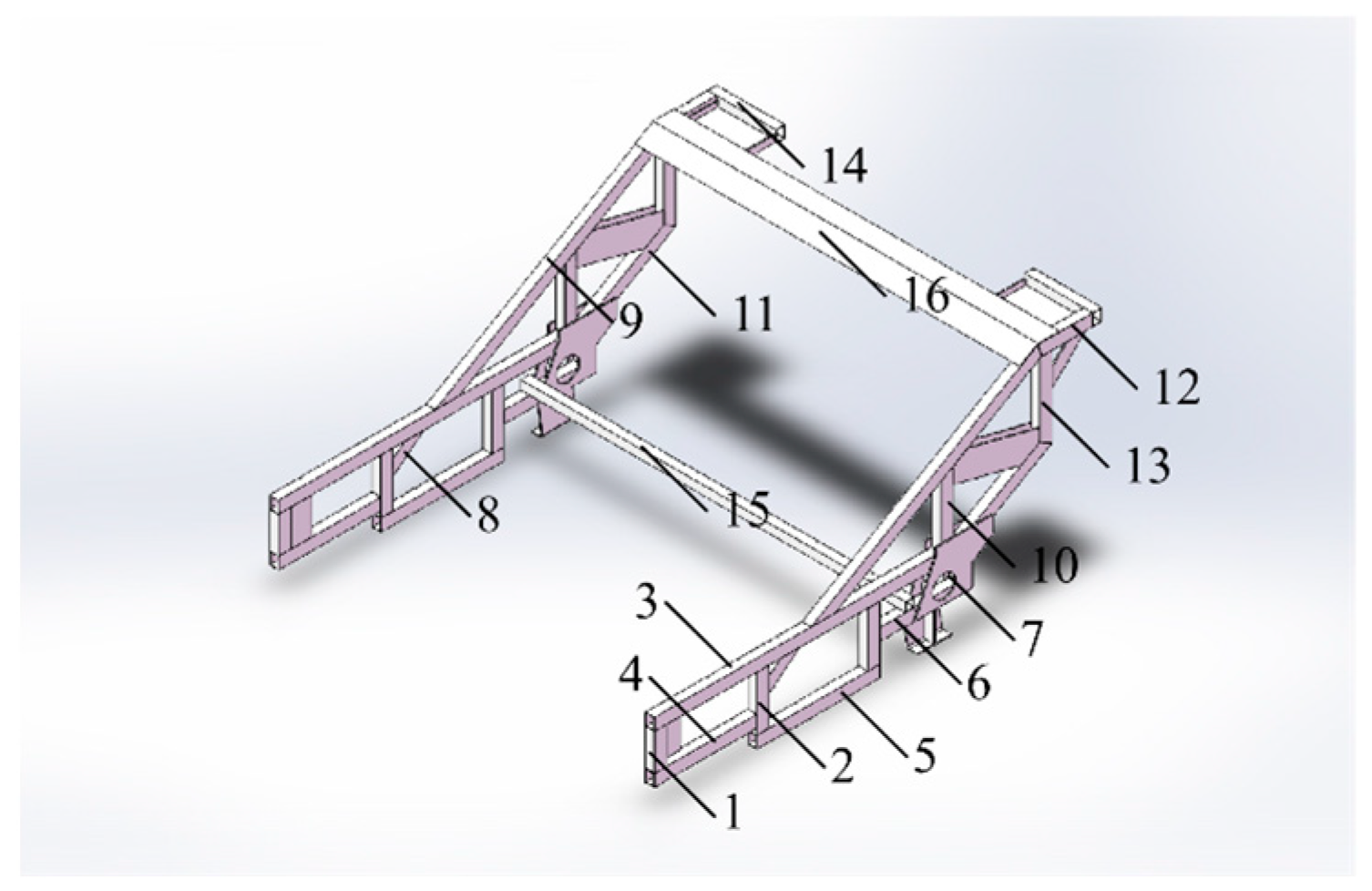
2.1.1. Establishment of Finite Element Model for the Frame
2.1.2. Static Analysis of the Frame
2.2. Modal Analysis of the Frame
2.2.1. Calculated Modal Analysis of the Frame
2.2.2. Test Modal Analysis of the Frame
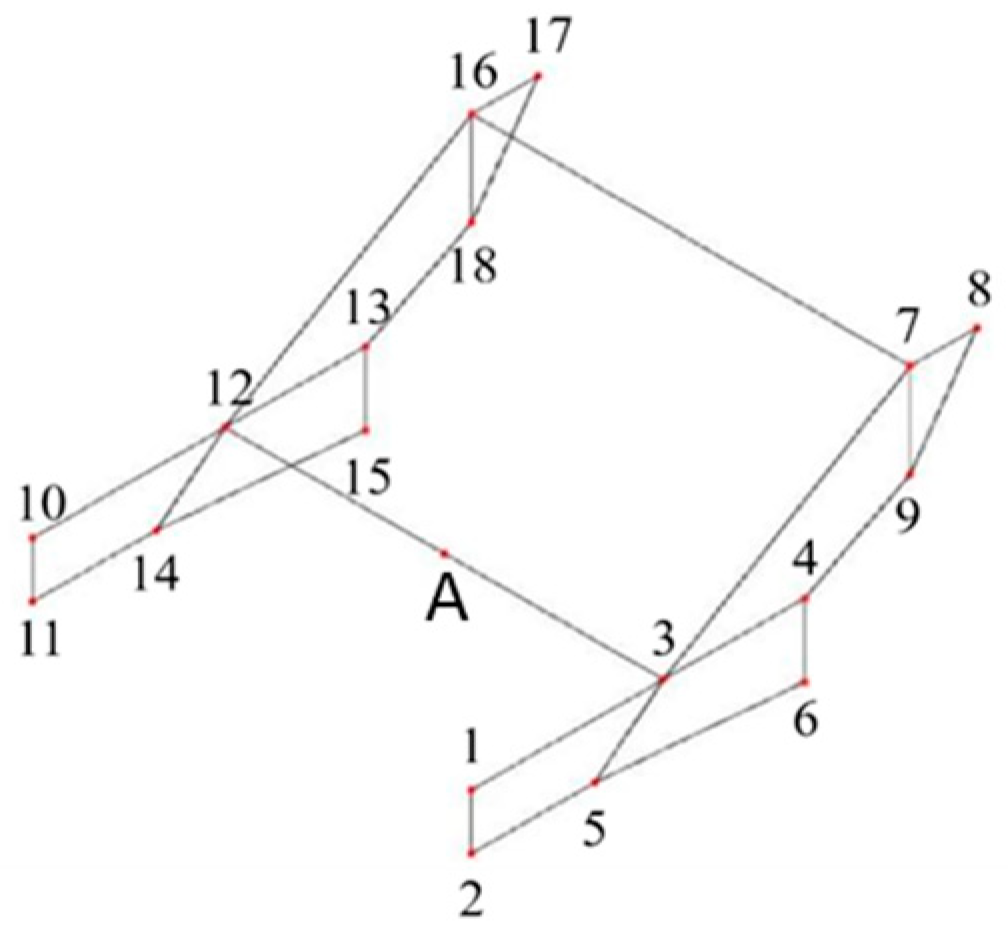
2.3. Optimization of the Framework Dimensions
3. Results
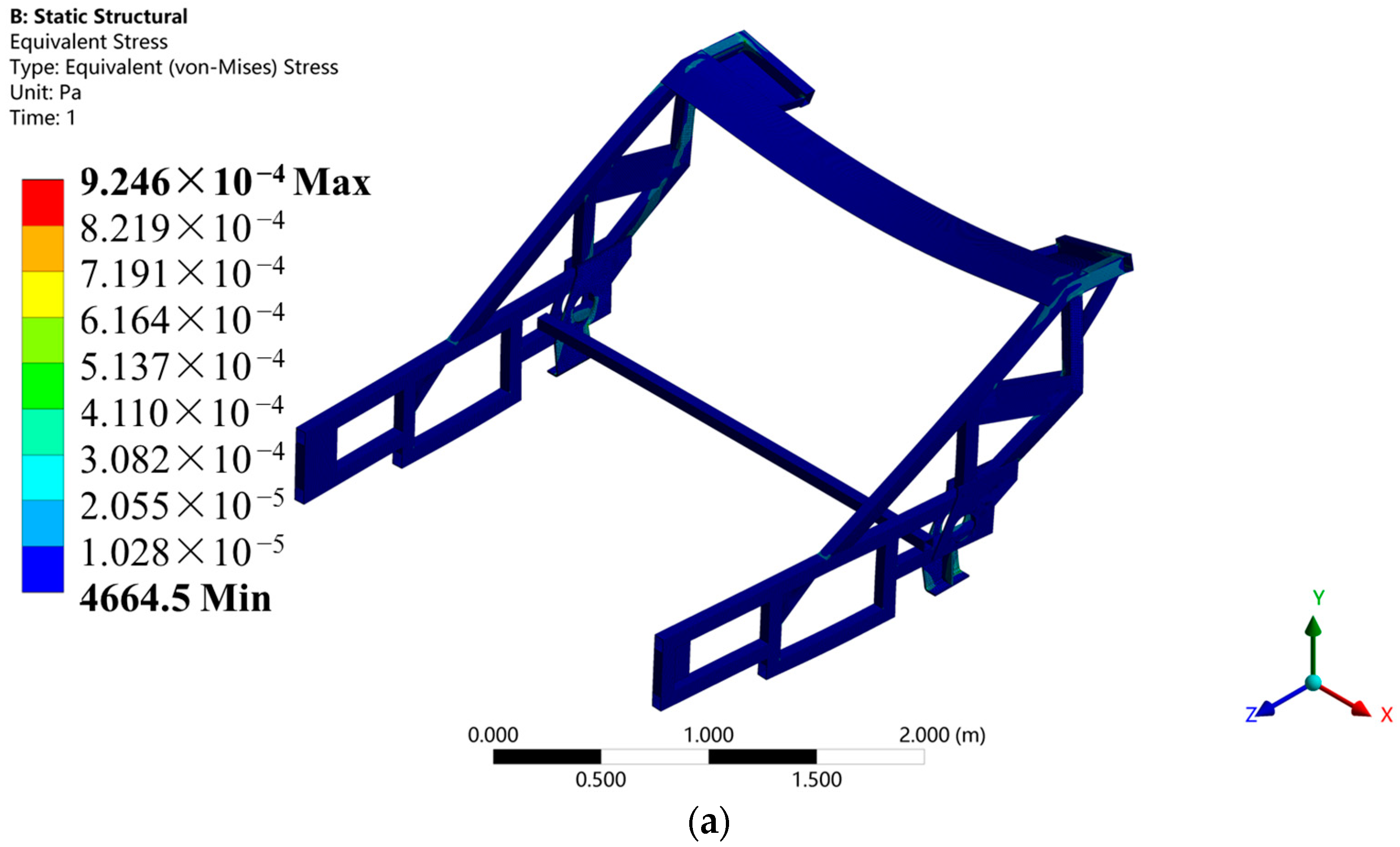
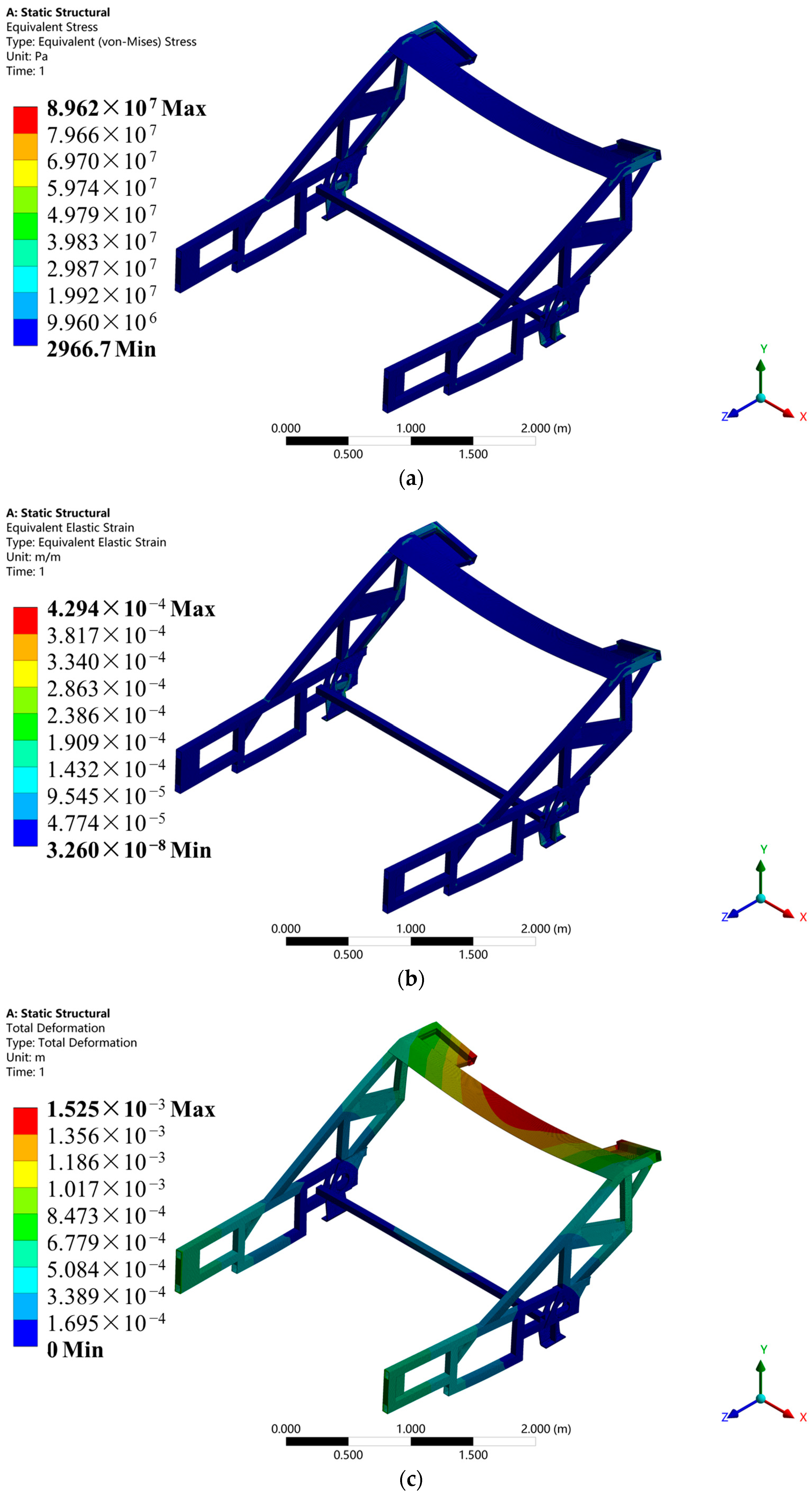
3.1. Results of Static Analysis
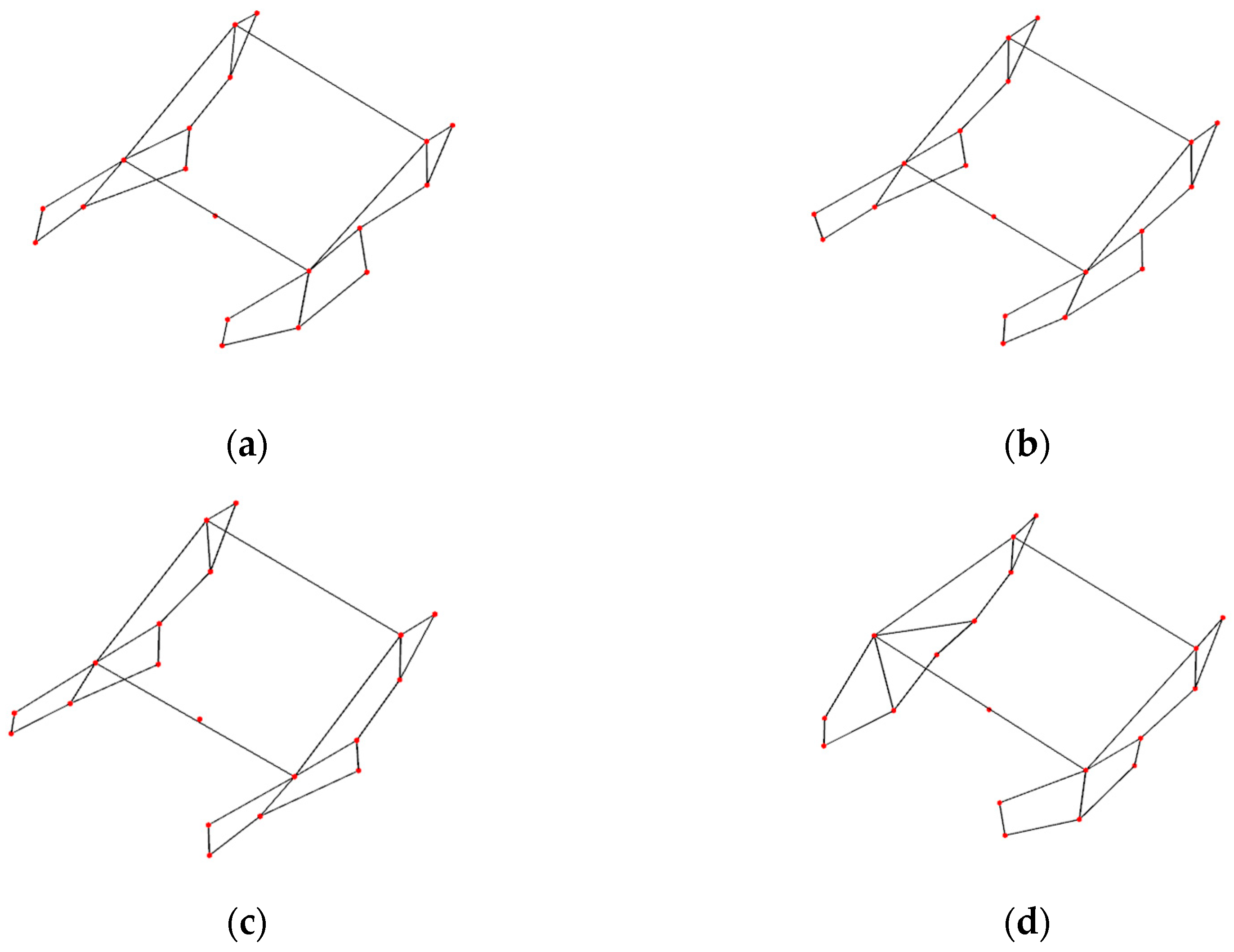
3.2. Results of Modal Analysis
3.3. Results of Dimensional Optimization
3.4. Comparison of the Frame before and after Optimization
3.4.1. Comparison of Static Analysis Results
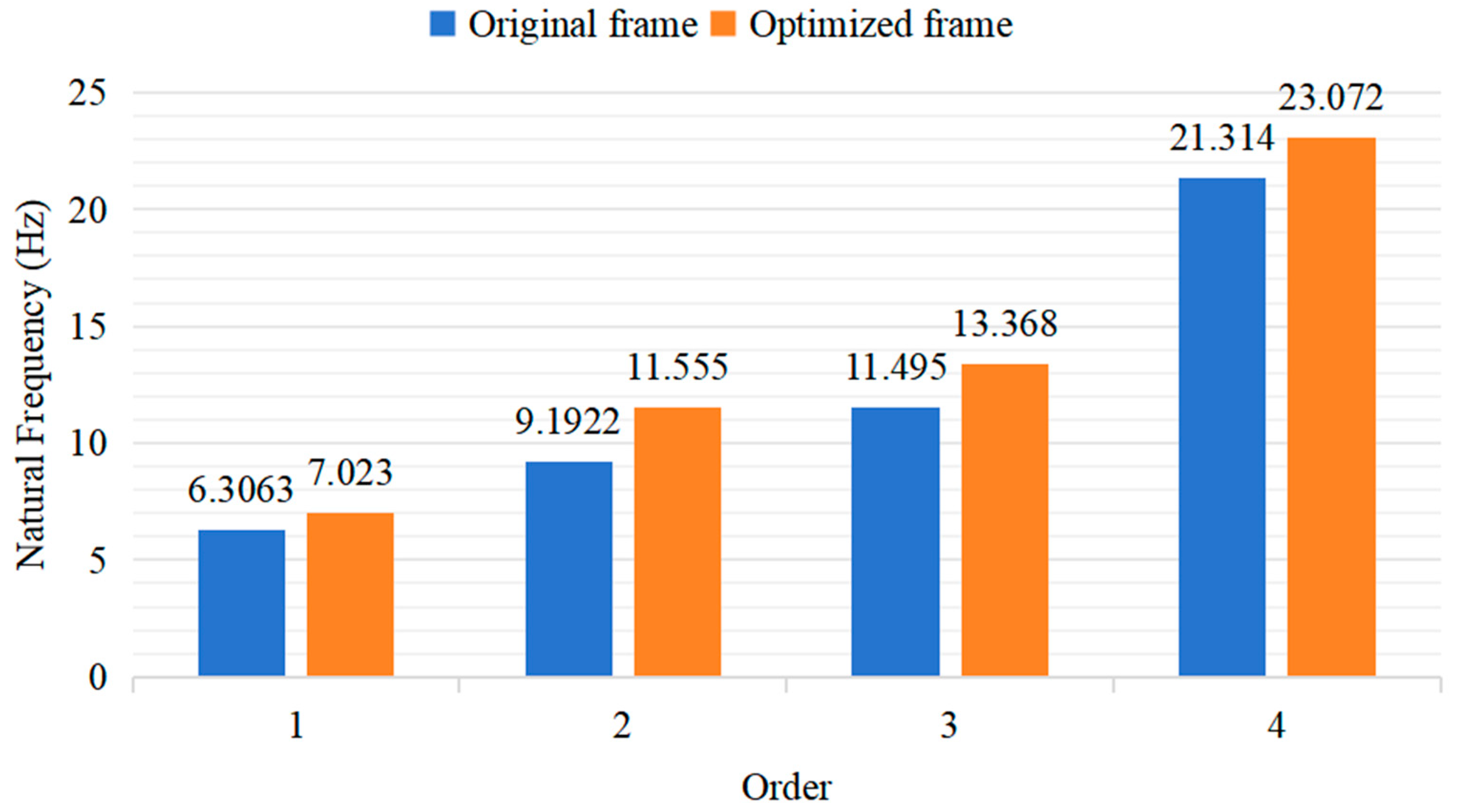
3.4.2. Comparison of Modal Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chauhan, S.; Basnet, B.; Shrestha, A.K. Innovative farming techniques for superior okra yield in Chitwan, Nepal: The benefits of plastic film mulch and pest exclusion net on soil properties, growth, quality and profitability. Acta Ecol. Sin. 2023, 44, 23–32. [Google Scholar] [CrossRef]
- Liu, J.L.; Huang, X.Y.; Chen, H. Sustaining yield and mitigating methane emissions from rice production with plastic film mulching technique. Agric. Water Manag. 2021, 245, 106667. [Google Scholar] [CrossRef]
- Yang, J.L.; Ren, L.Q.; Zhang, P. Can soil organic carbon sequestration and carbon management index be improved by changing the film-mulching methods in semiarid region? J. Integr. Agric. 2023. [Google Scholar] [CrossRef]
- Yang, Y.; Bai, S.H.; Ma, S.T. Residual Film Recycling Machine Research and Analysis of the Collecting Device. Food Sci. Technol. Econ. 2018, 43, 79–81. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Zhang, Z.; Song, Z.; Liu, Y.; Li, Y.; Xu, L. Durable Testing and Analysis of a Cleaning Sieve Based on Vibration and Strain Signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Hu, Z.C.; You, Z.Y.; Gu, F.W.; Wu, F.; Chen, Y.Q. Comparative study on working performance of two kinds of residue plastic film collectors. Jiangsu Agric. Sci. 2018, 46, 179–182. [Google Scholar] [CrossRef]
- Li, Z.J.; Zheng, K.; Zheng, X.; Hao, Z.Y. Analysis of the Influence of Tooling on Constraint Modal Test of Front End Module. Noise Vib. Control 2019, 39, 150–154. [Google Scholar]
- Li, Y.M.; Sun, P.P.; Pang, J.; Xu, L.Z. Finite element mode analysis and experiment of combine harvester chassis. Trans. Chin. Soc. Agric. Eng. 2013, 29, 38–46+301. [Google Scholar]
- Gao, J.J.; Liu, Z.Y.; Gu, W.; Zhang, F.F.; Zhu, L.P.; Xu, J.X. Modal Analysis and Optimization of Grain Combine Harvester Undercarriage Frame. Mach. Des. Res. 2023, 39, 199–205. [Google Scholar] [CrossRef]
- Zhang, J.M.; Yao, H.P.; Xue, J.L. Vibration characteristics analysis and suspension parameter optimization of tractor/implement system with front axle sus-pension under ploughing operation condition. J. Terramech. 2022, 102, 49–64. [Google Scholar] [CrossRef]
- Wang, X.Z.; Cao, Y.H.; Fang, W.Q.; Sheng, H.R. Vibration Test and Analysis of Crawler Pepper Harvester under Multiple Working Conditions. Sustainability 2023, 15, 8112. [Google Scholar] [CrossRef]
- Liu, Y.C.; Guo, J.X.; Shi, Y.; Xie, J.H.; Qian, X.G.; Han, J. Finite element analysis and optimization of the frame of residual plastic film recycling machine. J. Chin. Agric. Mech. 2023, 44, 189–194. [Google Scholar] [CrossRef]
- Guo, J.X.; Liu, Y.C.; Wei, Y.J.; Zhou, J.; Shi, Y. Ration Characteristics Analysis and Structure Optimization of Integrated Straw Returning and Residual Film Recycling Machine. Trans. Chin. Soc. Agric. Eng. 2024, 40, 155–163. [Google Scholar] [CrossRef]
- Liang, C.J.; Wu, X.M.; Wang, P.Z.; Li, G.C.; Tao, P.J.; Zhang, F.G. Simulation design and experimental on frame and comb teeth of the residual plastic film picker. J. Anhui Agric. Univ. 2019, 46, 203–208. [Google Scholar] [CrossRef]
- Zhong, S.S.; Wang, Q.; Fang, H.F.; Wang, M.D. Modal Analysis of Roller in Used Mulch Shredder. Mech. Eng. 2018, 4, 43–45. [Google Scholar]
- Zhang, P.F.; Hu, C.; Wang, X.F.; Lu, B.; Liu, C.J. Kinetic Analysis of Rotary Tillage Nail Tooth Plastic Film Recycling Machine Hook Film Unit. J. Agric. Mech. Res. 2018, 40, 14–18+25. [Google Scholar] [CrossRef]
- Yu, Z.H.; Xu, G.M.; Wang, H.Y.; Niu, Y.P.; Cao, W.L. Force and modal analysis of film gathering device of residue film recycling machine. China South. Agric. Mach. 2021, 52, 70–71. [Google Scholar]
- Zhang, J.; Wang, T.Y.; Yao, X.X.; Luo, W.G.; Luo, J.G. Modal analysis and physical test verification of a certain type of automobile exhaust system. J. Guangxi Univ. Sci. Technol. 2023, 34, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.L.; Dai, X.D.; Xie, Y.B. Modal Analysis of Multi-Cylinder Engine Block. J. Xi’an Jiaotong Univ. 2001, 35, 536–539. [Google Scholar]
- Han, Z.P.; Brownjohn, J.M.W.; Chen, J. Structural modal testing using a human actuator. Eng. Struct. 2020, 221, 111113. [Google Scholar] [CrossRef]
- Liang, J.; Zhao, D.F. Summary of the model analysis method. Mod. Manuf. Eng. 2006, 8, 139–141. [Google Scholar] [CrossRef]
- Zhou, M.; Wei, Z.; Wang, Z.; Sun, H.; Wang, G.; Yin, J. Design and Experimental Investigation of a Transplanting Mechanism for Super Rice Pot Seedlings. Agriculture 2023, 13, 1920. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.X.; Shi, J.S. Research on Subsynchronousr/Supersynchronous Oscillation Parameter Identification Based on Fundamental Synchrophasor: Spectrum Characteristics and Essential Issues. Trans. China Electrotech. Soc. 2024. [Google Scholar] [CrossRef]
- Cai, S.; Luo, Y.H.; Li, Q.L. State of the Art of Lightweight Technology in Agricultural Machinery and Its Development Trend. J. Mech. Eng. 2021, 57, 35–52. [Google Scholar]
- Liao, Y.Y.; Liao, B.Y. Lightweight Design of Hydro-Generator Upper Bracket Based on Sizing Optimization. Water Power 2019, 45, 91–94+117. [Google Scholar]
- Cao, Y.; Yu, Y.; Tang, Z.; Zhao, Y.; Gu, X.; Liu, S.; Chen, S. Multi-Tooth Cutting Method and Bionic Cutter Design for Broccoli Xylem (Brassica oleracea L. var. Italica Plenck). Agriculture 2023, 13, 1267. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Y.; Li, Y.; Ji, K. Research and Experiment on Variable-Diameter Threshing Drum with Movable Radial Plates for Combine Harvester. Agriculture 2023, 13, 1487. [Google Scholar] [CrossRef]
- Zhu, M.T.; He, Z.G.; Xu, L.; Li, Z.B. Mode Analysis of Car-body and Its Correlative Research Shape. Trans. Chin. Soc. Agric. Mach. 2004, 3, 13–15+19. [Google Scholar]
- Palumbo, A.; Polito, T.; Marulo, F. Experimental modal analysis and vibro-acoustic testing at leonardo laboratories. Mater. Today Proc. 2021, 34, 24–30. [Google Scholar] [CrossRef]
- Zhang, K.P.; Shao, L.; Lv, J.C.; Deng, C. Modal Analysis on the Frame of Tractor. Automob. Appl. Technol. 2012, 1, 35–39. [Google Scholar]
- Hao, S.; Tang, Z.; Guo, S.; Ding, Z.; Su, Z. Model and Method of Fault Signal Diagnosis for Blockage and Slippage of Rice Threshing Drum. Agriculture 2022, 12, 1968. [Google Scholar] [CrossRef]
- Fang, C.; Zhao, S.Y.; Yan, G.; Qing, G.F. Multi-Objective Topology Optimization, Size Optimization and Detailed Design of Frame for an Electric Car. Mach. Des. Manuf. 2023, 8, 16–22. [Google Scholar] [CrossRef]










| Positions | Magnitudes/N | Directions | Loading Modes |
|---|---|---|---|
| Picking support side plate | 7298 | Vertical downward | Uniformly distributed load |
| Picking support side plate | 2500 | Horizontal backward | Uniformly distributed load |
| Peel-off roller bearing seat | 3310 | Vertical downward | Uniformly distributed load |
| Baling machine bearing seat | 8388 | Vertical downward | Uniformly distributed load |
| Transport roller bearing seat | 2992 | Vertical downward | Uniformly distributed load |
| Straw grinder connection hole | 2500 | Horizontal forward | Uniformly distributed load |
| Order | Calculated Modal Analysis | Test Modal Analysis | Relative Error/% | ||
|---|---|---|---|---|---|
| Calculated Frequency | Mode Shapes | Test Frequency | Mode Shapes | ||
| 1 | 6.306 | Torsion | 5.859 | Torsion | 7.093 |
| 2 | 9.192 | Bending | 7.813 | Bending | 5.004 |
| 3 | 11.495 | Bending | 11.603 | Bending | −0.940 |
| 4 | 21.314 | Bending | 21.908 | Bending | −2.787 |
| 5 | 35.302 | Bending | 35.157 | Bending | 0.411 |
| 6 | 42.909 | Bending | 41.415 | Bending | 3.482 |
| 7 | 50.949 | Bending | 51.055 | Bending | −0.208 |
| 8 | 53.713 | Bending | 54.751 | Bending | −1.932 |
| 9 | 61.642 | Bending | 61.908 | Bending | −0.432 |
| 10 | 69.063 | Torsion, Bending | 67.563 | Bending | 2.172 |
| 11 | 76.664 | Bending | 76.730 | Bending | −0.086 |
| 12 | 83.454 | Torsion | 82.028 | Torsion | 1.709 |
| 13 | 92.378 | Bending | 92.631 | Bending | −0.274 |
| 14 | 95.845 | Torsion, Bending | 95.334 | Bending | 0.533 |
| Design Variables | Before Optimization/mm | After Optimization/mm | Increment/mm |
|---|---|---|---|
| Steel Tubes 1 | 5 | 5 | 0 |
| Steel Tubes 2 | 5 | 7 | 2 |
| Steel Tubes 3 | 5 | 5 | 0 |
| Steel Tubes 4 | 5 | 4 | −1 |
| Steel Tubes 5 | 5 | 4 | −1 |
| Steel Tubes 6 | 5 | 5 | 0 |
| Steel Tubes 7 | 5 | 4 | −1 |
| Steel Tubes 8 | 5 | 7 | 2 |
| Steel Tubes 9 | 5 | 7 | 2 |
| Steel Tubes 10 | 5 | 6 | 1 |
| Steel Tubes 11 | 5 | 6 | 1 |
| Steel Tubes 12 | 5 | 5 | 0 |
| Steel Tubes 13 | 5 | 5 | 0 |
| Steel Tubes 14 | 5 | 5 | 0 |
| Steel Tubes 15 | 5 | 5 | 0 |
| Steel Tubes 16 | 5 | 5 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hong, T.; Fang, W.; Chen, X. Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis. Agriculture 2024, 14, 543. https://doi.org/10.3390/agriculture14040543
Wang X, Hong T, Fang W, Chen X. Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis. Agriculture. 2024; 14(4):543. https://doi.org/10.3390/agriculture14040543
Chicago/Turabian StyleWang, Xinzhong, Tianyu Hong, Weiquan Fang, and Xingye Chen. 2024. "Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis" Agriculture 14, no. 4: 543. https://doi.org/10.3390/agriculture14040543
APA StyleWang, X., Hong, T., Fang, W., & Chen, X. (2024). Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis. Agriculture, 14(4), 543. https://doi.org/10.3390/agriculture14040543






