Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm
Abstract
:1. Introduction
2. Materials and Methods
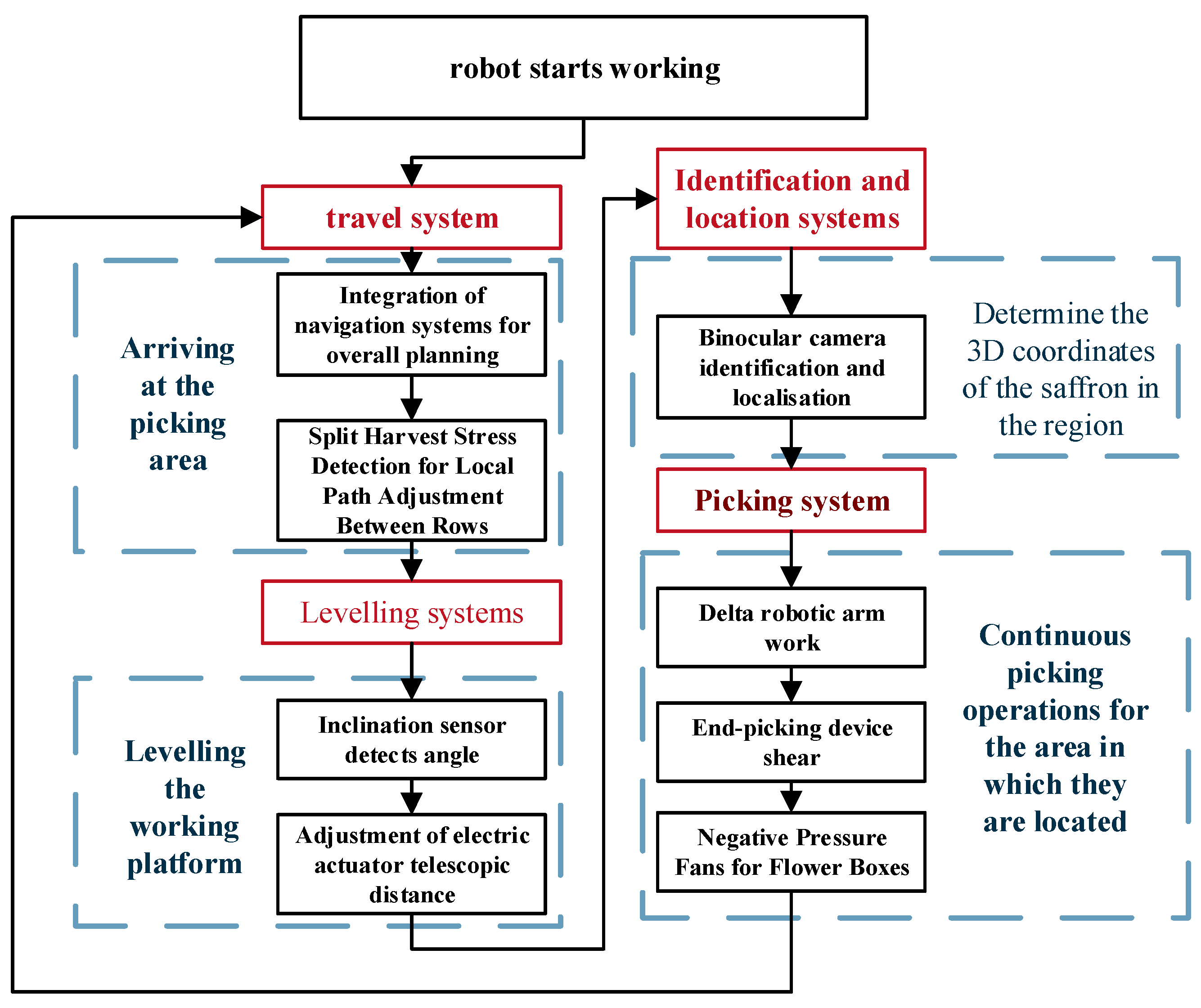
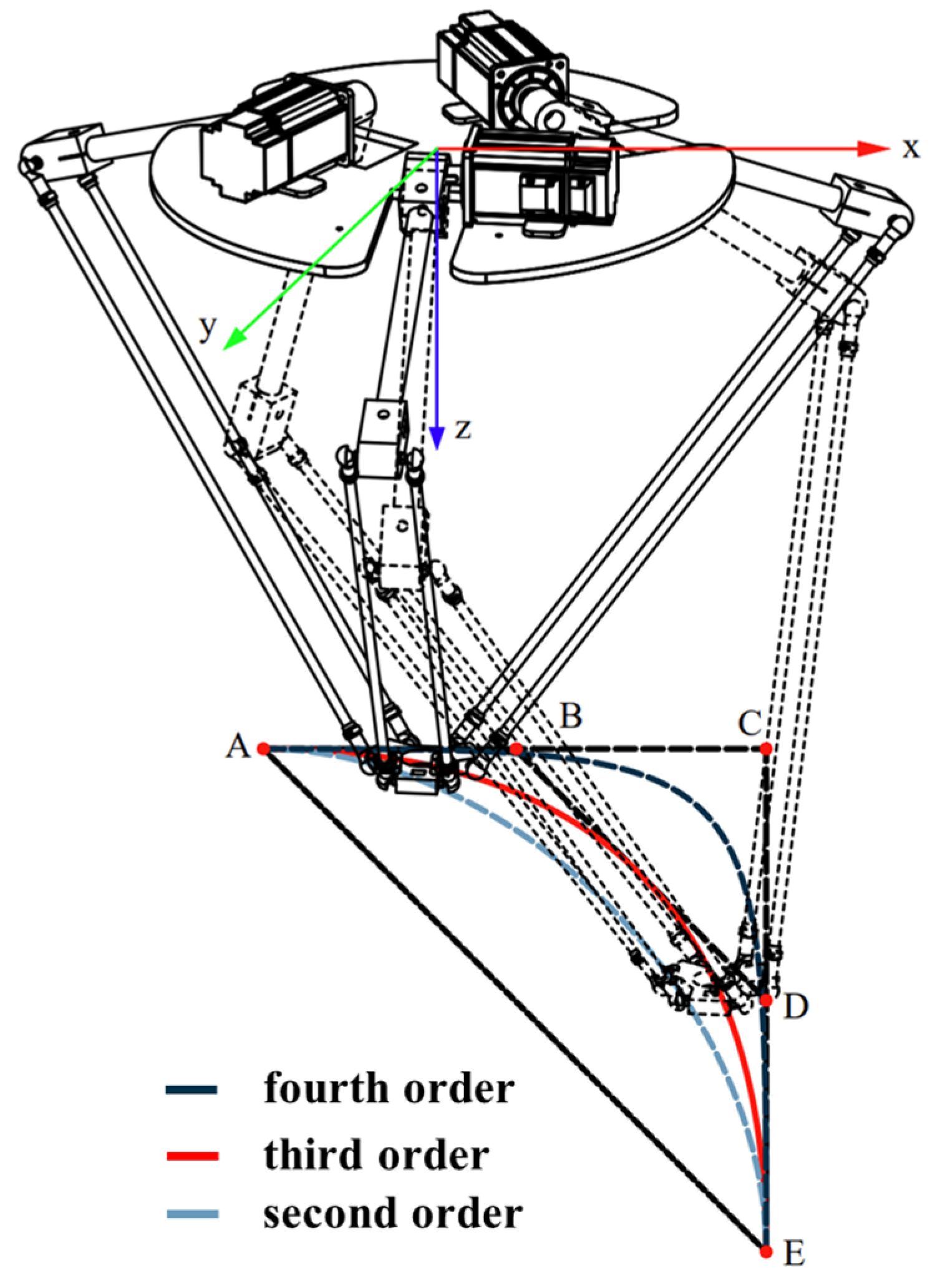
2.1. Safflower-Picking Robot Working Principle
2.2. Laws of Motion Analysis
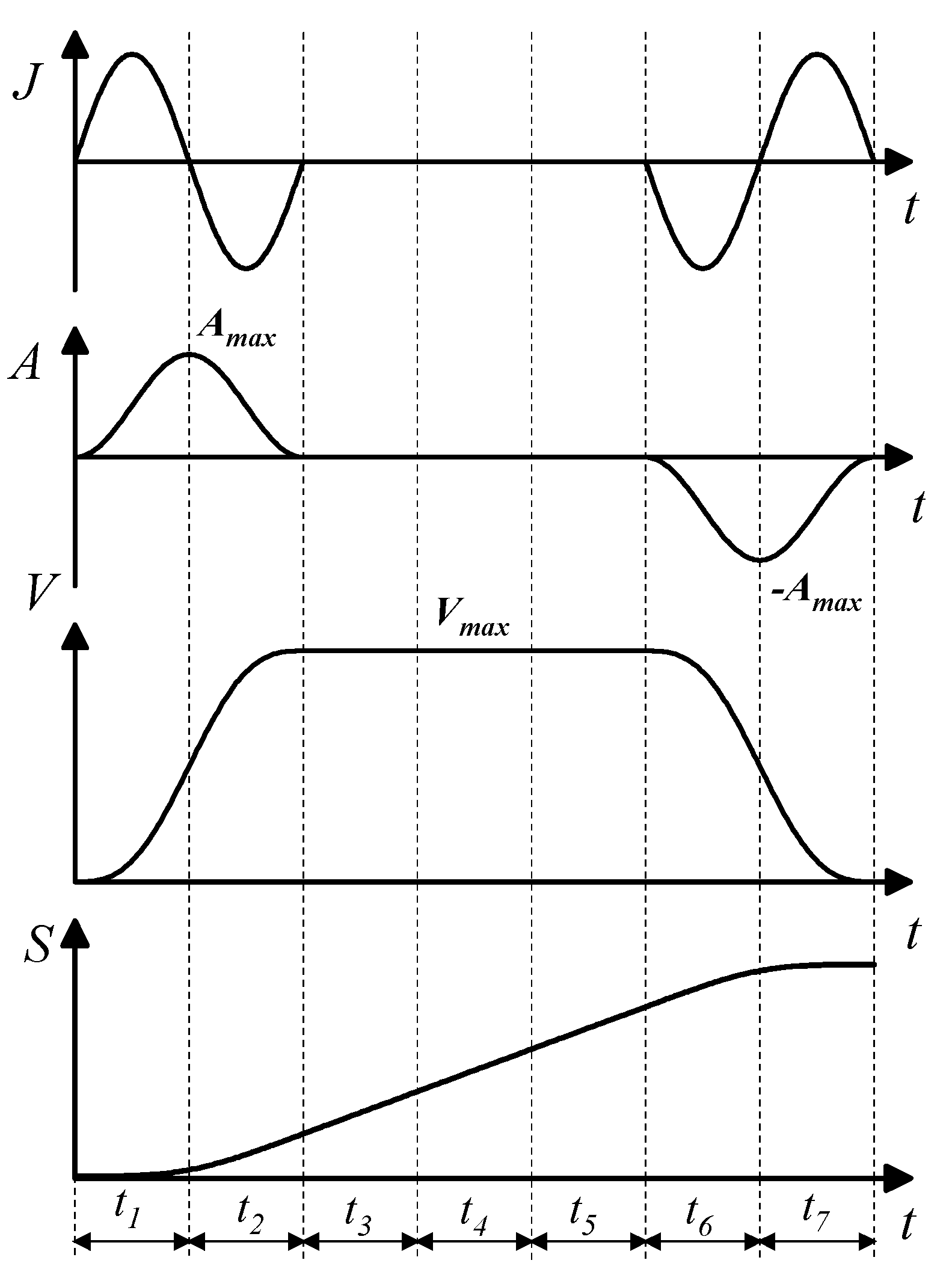
2.2.1. Improved S-Type Velocity Curve Model
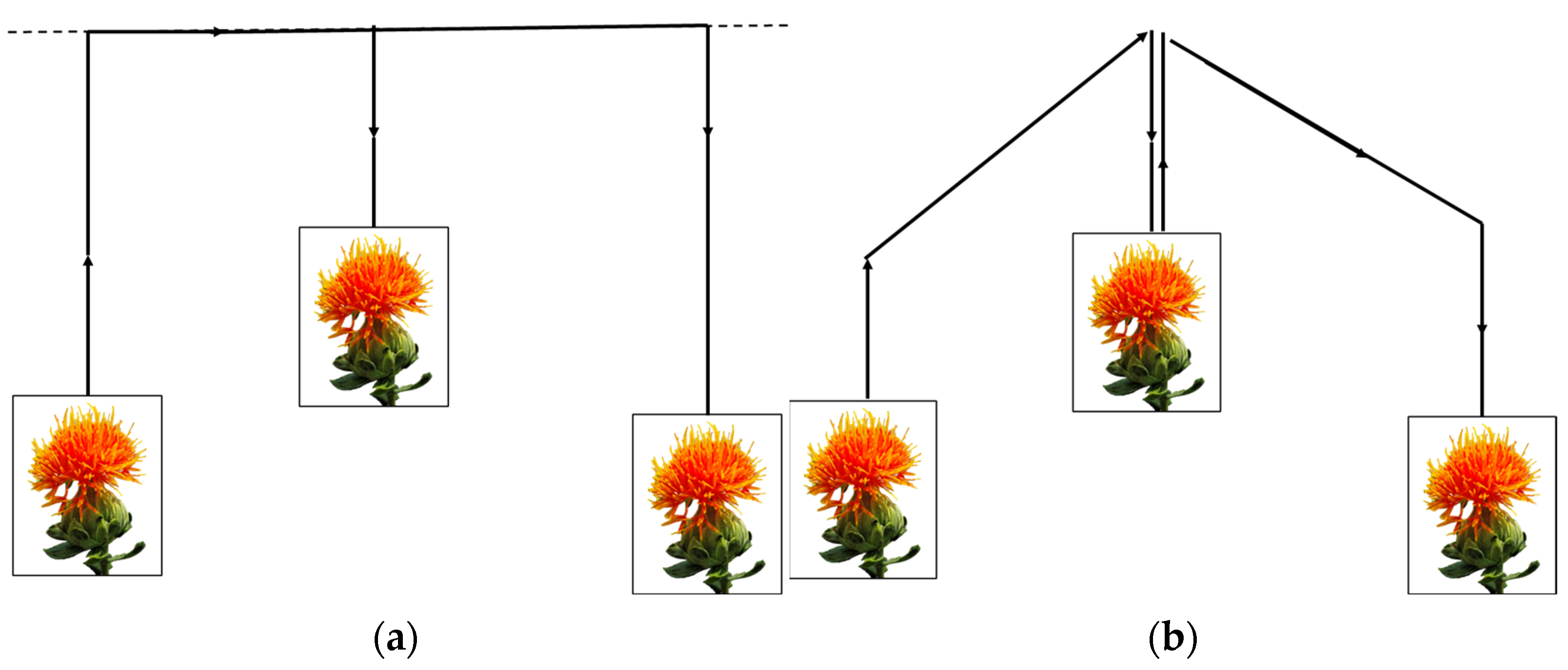
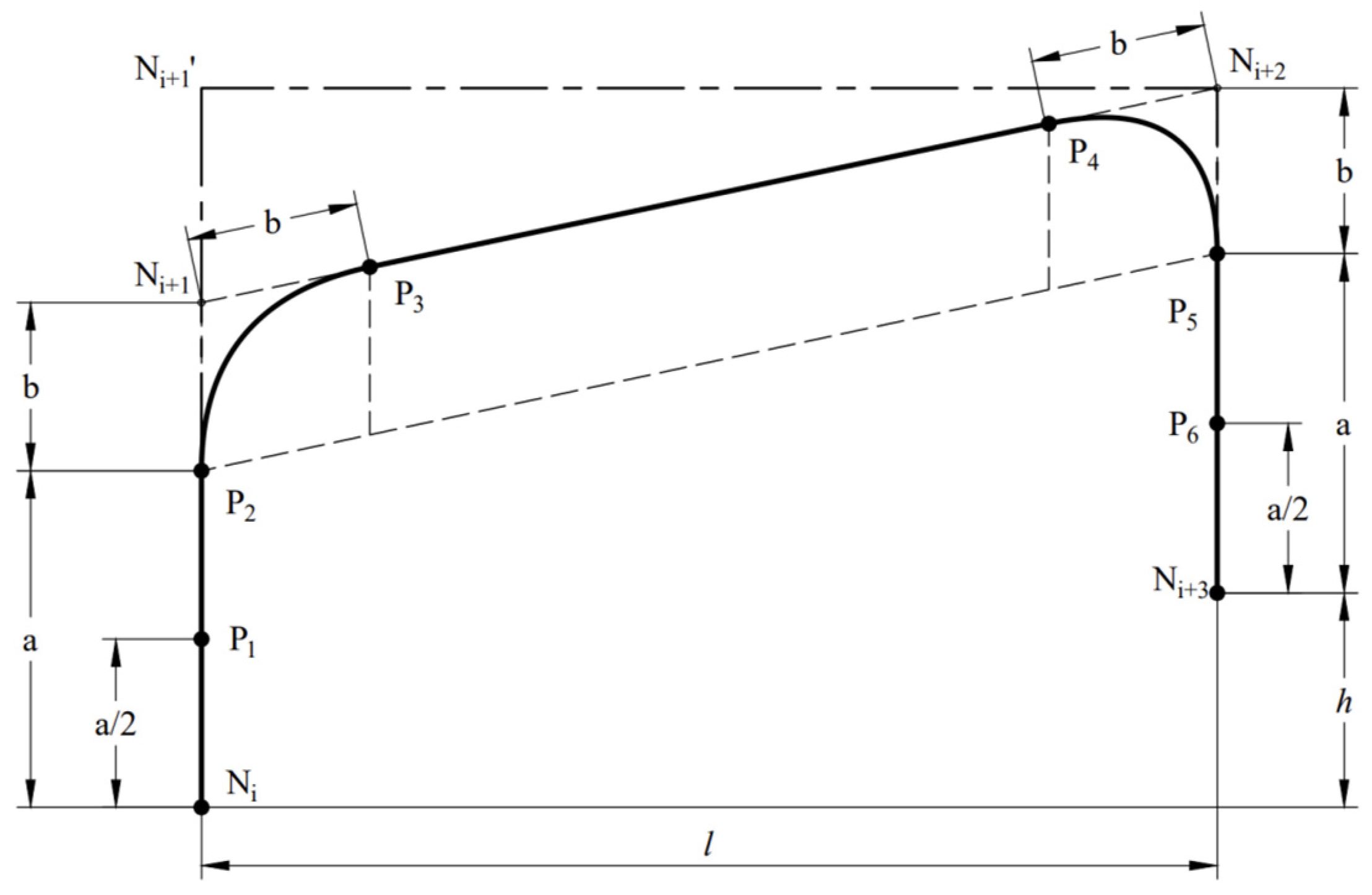
2.2.2. Improved Analysis of Picking Trajectories
- (1)
- The motion accelerates with an increasing acceleration from “” to “”.
- (2)
- The motion continues to accelerate, but with a decreasing acceleration from “” to “”.
- (3)
- After reaching point “”, the motion transitions into a uniform speed or constant velocity motion from “” to “”.
- (4)
- As the motion approaches point “”, it starts to decelerate with an increasing acceleration.
- (5)
- As the motion approaches point “”, it decelerates with a decreasing acceleration until reaching point “”.
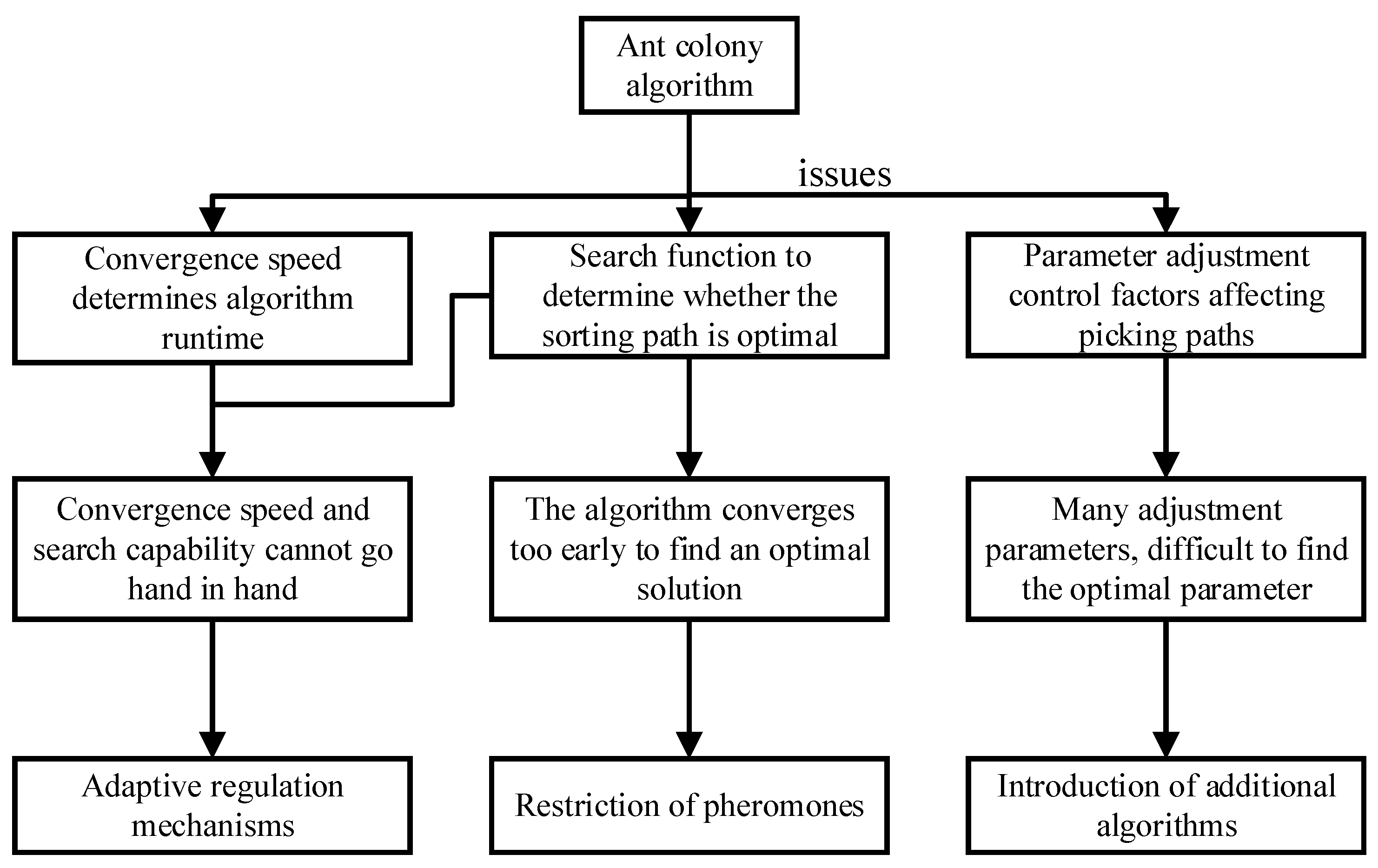
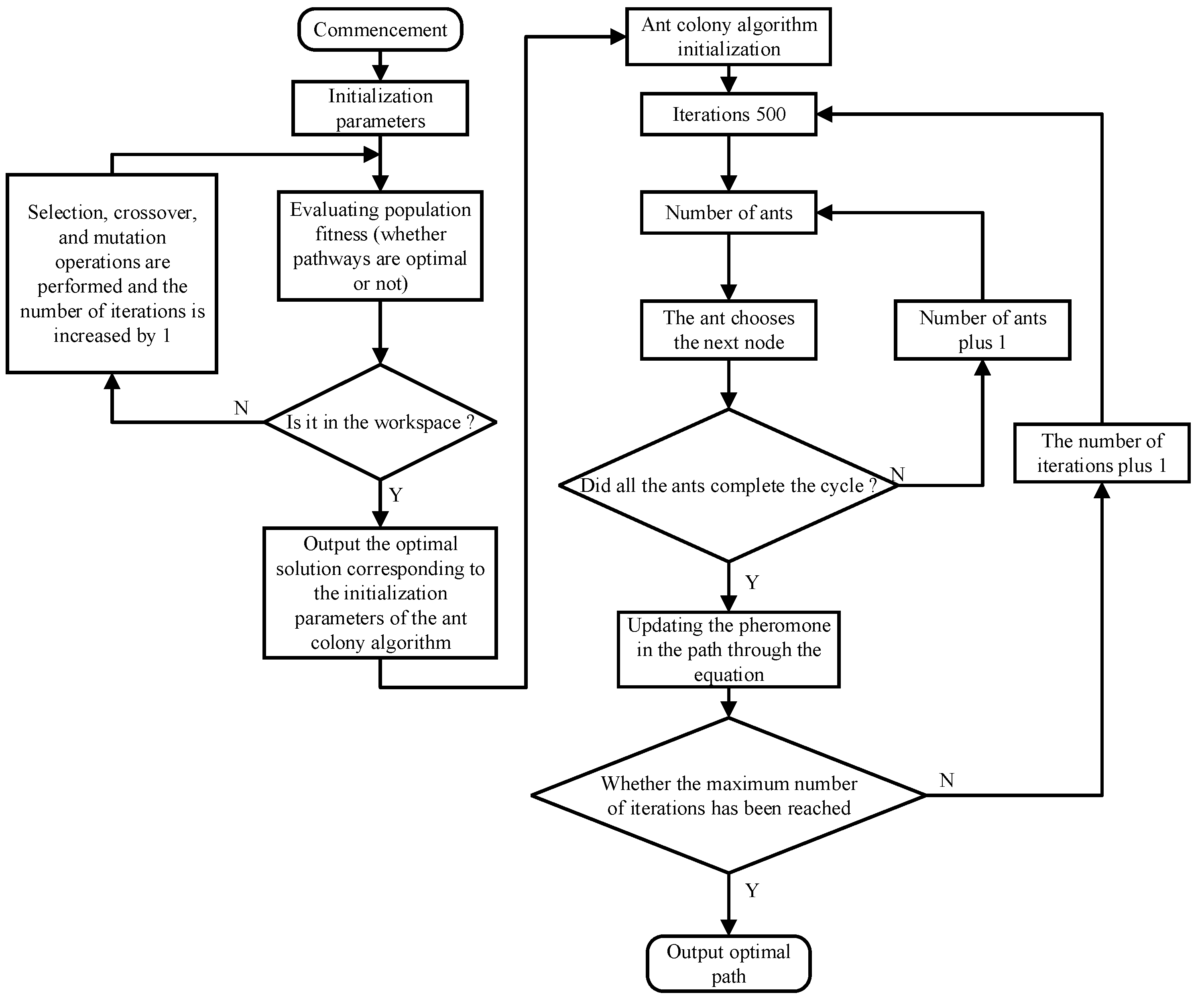
2.3. Improved Ant Colony Genetic Fusion Algorithm
2.3.1. Adaptive Regulation Mechanisms
2.3.2. Limiting Pheromones
2.3.3. Parameter Optimization of the Ant Colony Algorithm Based on Genetic Algorithm
- (1)
- Initializing the population: The genetic algorithm initially generates a certain number of initial populations randomly and encodes them, representing the parameters , , , and with four binary code strings , , , , respectively. These are then combined into a single binary code string. Moreover, based on the findings of previous researchers, it is known that the overall performance of the algorithm is better when is in the range in , and in .
- (2)
- Adaptive function: Genetic algorithms simulate natural genetic mechanisms to tackle optimization problems, where “fitness” serves as a crucial metric for evaluating the extent to which a solution addresses the problem. The fitness function is tailored according to the optimization objective, assessing the effectiveness of each solution. The algorithm selects and propagates optimal solutions based on their fitness, generally without requiring additional information. In this study, the optimal solution is defined as the one that enables the robotic arm to harvest safflower filaments via the shortest possible path. Therefore, the fitness function is formulated as follows:
- (3)
- Genetic operators: Consistent with the ant colony algorithm, the selection operation employs the roulette wheel method; the crossover and mutation operations utilize the methods described in Equations (14) and (15), respectively.
- (4)
- Algorithm parameter configuration: For the improved ant colony algorithm, the parameter settings are as follows: the number of ants m = 50 and the maximum number of iterations G = 300. For the genetic algorithm, the parameter settings include population size P = 40, the number of iterations set to 200, initial crossover probability = 0.7, and initial mutation probability .
3. Results
3.1. Comparative Analysis of Velocity Profile Models
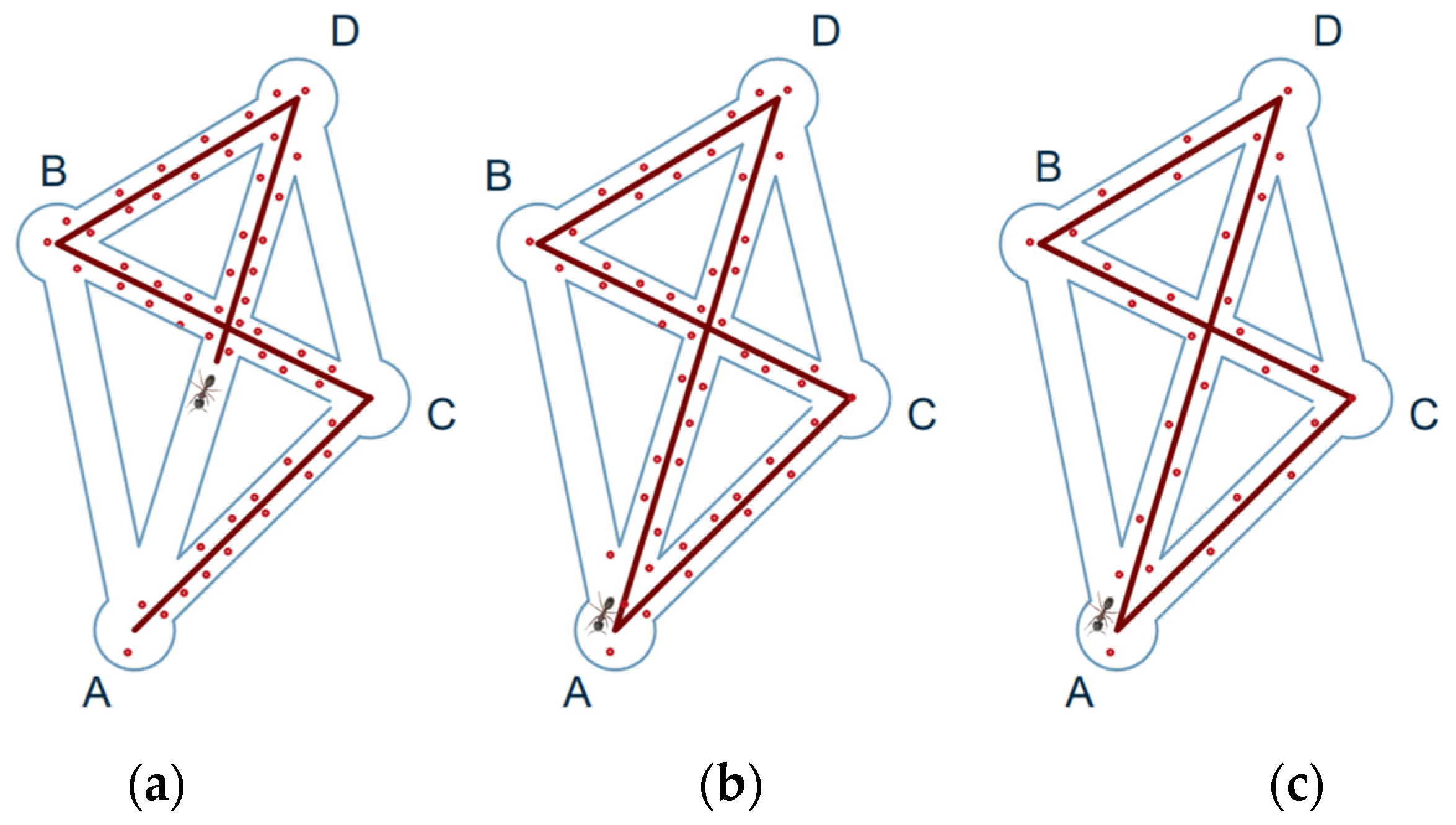
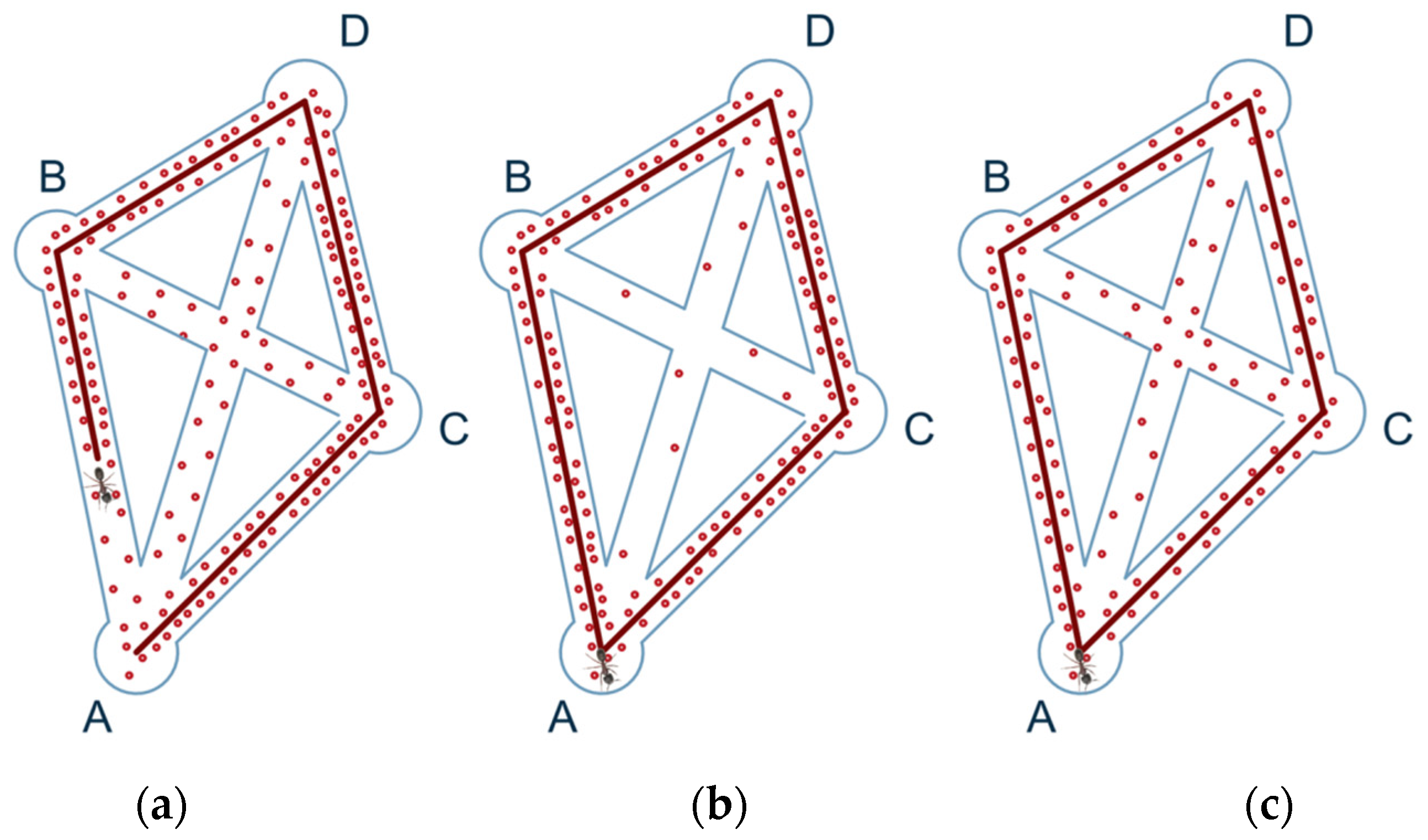
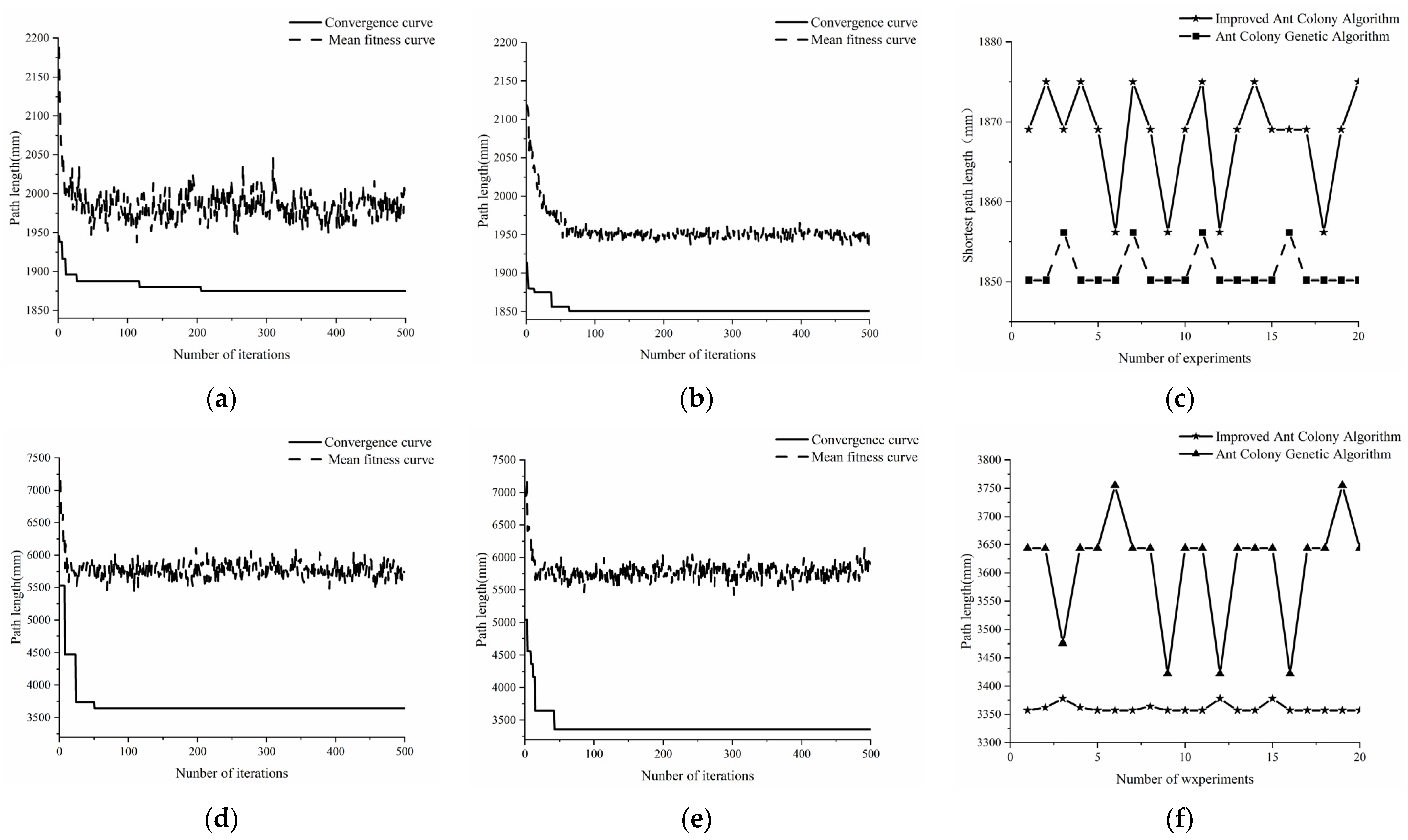
3.2. Comparative Analysis of Path Planning Algorithms
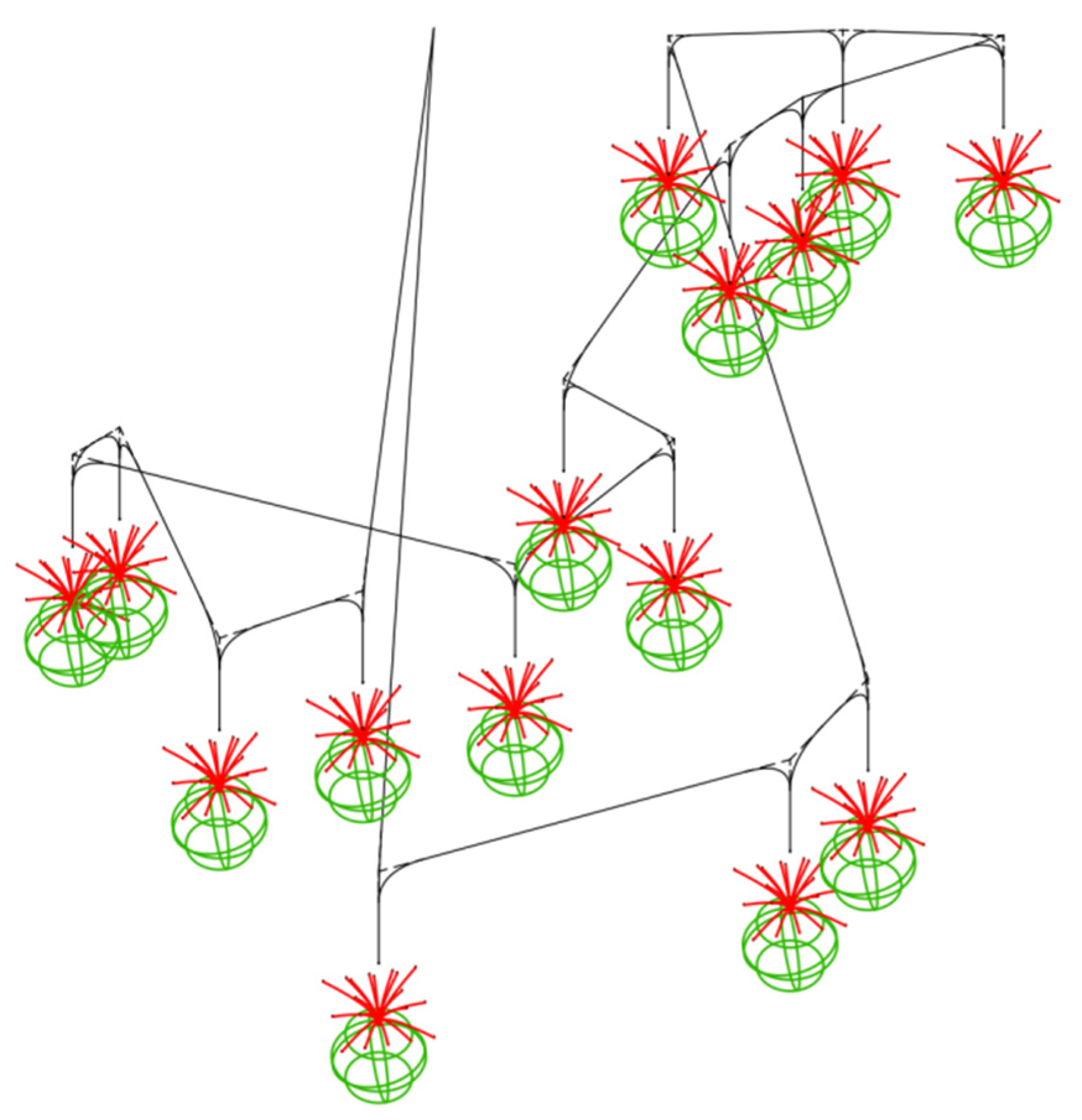
3.3. Field Experiment Validation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.H.; Guo, J.F.; Ma, X.L.; Fan, X.Q.; Chen, Y.; Lin, M. Research on Current Situation and Development Countermeasures of Xinjiang Safflower Production. J. Anhui Agric. Sci. 2021, 49, 199–201, 217. [Google Scholar]
- Yang, H. Research Status of Mechanized Harvesting of Safflower Silk in Xinjiang. J. Agric. Mech. Res. 2020, 5, 34–37. [Google Scholar]
- Hatim, M.; Majidian, M.; Tahmasebi, M.; Nabavi-Pelesaraei, A. Life cycle assessment, life cycle cost, and exergoeconomic analysis of different tillage systems in safflower production by micronutrients. Soil Tillage Res. 2023, 233, 105795. [Google Scholar] [CrossRef]
- Mani, V.; Lee, S.K.; Yeo, Y.; Hahn, B.S. A Metabolic Perspective and Opportunities in Pharmacologically Important Safflower. Metabolites 2020, 10, 253. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, Y.; Sun, C.; Zeng, H.; Liu, N. Picking path planning method of dual rollers type safflower picking robot based on improved ant colony algorithm. Processes 2022, 10, 1213. [Google Scholar] [CrossRef]
- Gao, G.; Guo, H.; Zhou, W.; Luo, D.; Zhang, J. Design of a control system for a safflower picking robot and research on multisensor fusion positioning. Eng. Agrícola 2023, 43, e20210238. [Google Scholar] [CrossRef]
- Cao, R.Y.; Zhang, Z.Q.; Li, S.C.; Zhang, M.; Li, H.; Li, Z.M. Multi-machine Cooperation Global Path Planning Based on A-star Algorithm and Bezier Curve. Trans. Chin. Soc. Agric. Mach. 2021, 52, 548–554. [Google Scholar]
- Li, G.; Wang, Y. Time-optimal trajrctory planning of robots based on B-spline and improved grnrtic algorithm. Comput. Appl. Softw. 2020, 37, 215–223+279. [Google Scholar]
- Liu, C.; Cao, G.H.; Qu, Y.Y.; Cheng, Y.M. An improved PSO algorithm for time-optimal trajectory planning of Delta robot in intelligent packaging. Int. J. Adv. Manuf. Technol. 2020, 107, 1091–1099. [Google Scholar] [CrossRef]
- Wu, M.; Mei, J.; Zhao, Y.; Niu, W. Vibration reduction of delta robot based on trajectory planning. Mech. Mach. Theory 2020, 153, 104004. [Google Scholar] [CrossRef]
- Fang, S.; Cao, J.; Zhang, Z.; Zhang, Q.; Cheng, W. Study on high-speed and smooth transfer of robot motion trajectory based on modified s-shaped acceleration/deceleration algorithm. IEEE Access 2020, 8, 199747–199758. [Google Scholar] [CrossRef]
- Lu, S.; Ding, B.; Li, Y. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1687814020913667. [Google Scholar] [CrossRef]
- Qi, M.; Dou, L.; Xin, B. 3D Smooth Trajectory Planning for UAVs under Navigation Relayed by Multiple Stations Using Bézier Curves. Electronics 2023, 12, 2358. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, T.; Bai, G.; Wang, Y.; Wang, S.; Tan, M. Stepwise Cooperative Trajectory Planning for Multiple BUVs Based on Temporal–Spatial Bezier Curves. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Ren, L.; Wang, N.; Cao, W.; Li, J.; Ye, X. Trajectory planning and motion control of full-row seedling pick-up arm. Int. J. Agric. Biol. Eng. 2020, 13, 41–51. [Google Scholar] [CrossRef]
- Lai, R.; Wu, Z.; Liu, X.; Zeng, N. Fusion Algorithm of the Improved A* Algorithm and Segmented Bézier Curves for the Path Planning of Mobile Robots. Sustainability 2023, 15, 2483. [Google Scholar] [CrossRef]
- Yao, X.; Li, Z.; Cheng, X. Research on Robot Path Planning Based on Improved Ant Colony Algorithm. Comput. Simul. 2021, 38, 379–383. [Google Scholar]
- Ren, T.; Luo, T.; Li, X.; Xiang, S.; Xiao, H.L.; Xing, L.N. Knowledge based ant colony algorithm for cold chain logistics distribution path optimization. Control Decis. 2022, 37, 545–554. [Google Scholar]
- Hu, Z.; Luo, L.; Lv, Y.; Luo, Y. Path planning of mobile robot based on potential field oriented logarithmic ant colony algorithm. J. Chongqing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2021, 33, 498–506. [Google Scholar]
- Zhao, W.; Zhou, D. An Improved Path Planning Algorithm Based on the Fusion of A* and Third-order Bessel Curves. J. Anhui Univ. Technol. (Nat. Sci.) 2023, 40, 333–338. [Google Scholar]
- de Winkel, K.N.; Irmak, T.; Happee, R.; Shyrokau, B. Standards for passenger comfort in automated vehicles: Acceleration and jerk. Appl. Ergon. 2023, 106, 103881. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Wang, N.; Cao, R.; Zhang, Z.; Ji, Y.; Li, H.; Wang, H. Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm. Comput. Electron. Agric. 2023, 204, 107532. [Google Scholar] [CrossRef]
- Comert, S.E.; Yazgan, H.R. A new approach based on hybrid ant colony optimization-artificial bee colony algorithm for multi-objective electric vehicle routing problems. Eng. Appl. Artif. Intell. 2023, 123, 106375. [Google Scholar] [CrossRef]




| Mandates | Working Condition 1 | Working Condition 2 |
|---|---|---|
| Coordinate Value | Motor Running Angle | |
| Starting coordinate value | (0, 0, 0) | (, , ) |
| Endpoint coordinate value | (100, 50, 50) | (, , ) |
| Speed limit | 10 (mm/s) | 1.8 (rad/s) |
| Acceleration constraint | 30 (mm/s2) | 10 (rad/s2) |
| Jerk constraints | 30 (mm/s3) | 50 (rad/s3) |
| Speed Curve | Time/s | |
|---|---|---|
| Working condition 1 | S-curve model | 5.728 |
| Improved S-curve model | 5.032 | |
| Working condition 2 | S-curve model | 3.988 |
| Improved S-curve model | 3.088 |
| Algorithm | Maximum Jerk | Average Jerk | |||||
|---|---|---|---|---|---|---|---|
| Joints 1 | Joints 2 | Joints 3 | Joints 1 | Joints 2 | Joints 3 | ||
| (mm/s3) | |||||||
| Working condition 1 | S-curve model | 27.3 | 21.4 | 20.2 | 17.54 | 16.88 | 18.92 |
| Improved S-curve model | 7.3 | 7.8 | 6.8 | 6.81 | 7.22 | 6.42 | |
| Working condition 2 | S-curve model | 48.2 | 49.5 | 45.8 | 28.24 | 24.58 | 27.35 |
| Improved S-curve model | 25.3 | 25.0 | 24.8 | 15.42 | 14.08 | 14.22 | |
| Safflower Count | Models | Time/s | |
|---|---|---|---|
| 15 | Improved S-curve model | 44.2642 | 10.4342 |
| S-curve model | 51.5422 | 23.4251 | |
| 30 | Improved S-curve model | 76.4586 | 13.6485 |
| S-curve model | 98.3549 | 28.4265 |
| Count | Considerations | |||
|---|---|---|---|---|
| 15 | 2.46 | 8.99 | 1734.80 | 25.69 |
| 30 | 2.30 | 8.85 | 387.59 | 59.54 |
| Amount of Safflower | Average Working Time/s | ||
|---|---|---|---|
| Imitate Manual Picking | Basic Ant Colony Algorithm | Ant Colony Genetic Algorithm | |
| small amount (15) | 64.354 | 46.172 | 43.244 |
| large amount (30) | 111.465 | 77.524 | 72.246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Qiu, Z.; Gao, G.; Wu, T.; Chen, H.; Wang, X. Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm. Agriculture 2024, 14, 622. https://doi.org/10.3390/agriculture14040622
Guo H, Qiu Z, Gao G, Wu T, Chen H, Wang X. Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm. Agriculture. 2024; 14(4):622. https://doi.org/10.3390/agriculture14040622
Chicago/Turabian StyleGuo, Hui, Zhaoxin Qiu, Guomin Gao, Tianlun Wu, Haiyang Chen, and Xiang Wang. 2024. "Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm" Agriculture 14, no. 4: 622. https://doi.org/10.3390/agriculture14040622
APA StyleGuo, H., Qiu, Z., Gao, G., Wu, T., Chen, H., & Wang, X. (2024). Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm. Agriculture, 14(4), 622. https://doi.org/10.3390/agriculture14040622







