A Cooperative Scheduling Based on Deep Reinforcement Learning for Multi-Agricultural Machines in Emergencies

Abstract

Effective scheduling of multiple agricultural machines in emergencies can reduce crop losses to a great extent. In this paper, cooperative scheduling based on deep reinforcement learning for multi-agricultural machines with deadlines is designed to minimize makespan. With the asymmetric transfer paths among farmlands, the problem of agricultural machinery scheduling under emergencies is modeled as an asymmetric multiple traveling salesman problem with time windows (AMTSPTW). With the popular encoder-decoder structure, heterogeneous feature fusion attention is designed in the encoder to integrate time windows and asymmetric transfer paths for more comprehensive and better feature extraction. Meanwhile, a path segmentation mask mechanism in the decoder is proposed to divide solutions efficiently by adding virtual depots to assign work to each agricultural machinery. Experimental results show that our proposal outperforms existing modified baselines for the studied problem. Especially, the measurements of computation ratio and makespan are improved by 26.7% and 21.9% on average, respectively. The computation time of our proposed strategy has a significant improvement over these comparisons. Meanwhile, our strategy has a better generalization for larger problems.

1. Introduction

Agriculture is the foundation of our economy and material production, of which the significant feature is crop production. Extreme weather (e.g., strong wind, sands, and dust storms) often occurs in the northwest of China, which has a great and severe influence on crops. Economic losses from meteorological disasters account for 70% of those from all agricultural natural disasters. The scheduling of agricultural machinery in emergencies can reduce the area affected by crop damage and then reduce economic losses. With the advantages of extracting weather reports, governments and farmers always need to process these emergencies as soon as possible.

Generally speaking, agricultural machinery managers provide service for farmers with small-scale farms. Figure 1 shows an example of agricultural machinery scheduling; the blue bars are the required time windows for different farmlands. Assume $b_i(i\in \{1,\dots ,10\})$ and $e_i(i\in \{1,\dots ,10\})$ represent the beginning and the ending of the time window. There are three agricultural machines assigned to 10 farmlands. Each piece of agricultural machinery departs from the depot, and after processing several farmlands, it is required to return to the depot. For instance, agricultural machine 1 departs from the depot and subsequently processes fields No. 10, No. 9, and No. 8 before returning to the depot. From the perspective of farmers, time windows are best to satisfy while minimizing makespan for machine managers. In general, the path among farmlands is always asymmetric with different road conditions, such as uphill and fall pavement. Therefore, it is a valuable study to investigate how to schedule agricultural machinery in extreme weather and other emergencies to complete all farmlands on time.

In general, the transfer time of an agricultural machine depends on the speed and path of the machine. With homogeneous machines, the speed of all machines is the same. The transfer time between farmlands is asymmetric due to the complex road conditions and traffic effects in the real scenario. Meanwhile, in emergencies, there is always a certain time window required for each farmland. The asymmetric transfer time and the time window make the agricultural machinery scheduling complex to solve. Generally speaking, there are two steps in scheduling agricultural machinery. The first step involves assigning each machine to the farmland, and the second step is to plan the sequence of farm machines. It is a great challenge to synthesize the above two steps to obtain a solution with excellent performance. All the above challenges make agricultural machinery scheduling in emergencies harder to solve.

With the agricultural machinery scheduling, researchers usually model it as a combinatorial optimization problem (COP) [1,2,3,4,5,6,7,8,9,10,11,12]. In particular, Huang et al. [1] modeled an agricultural machinery scheduling problem as a multi-depot vehicle routing problem with time windows (MDVRPTW) problem and proposed a hybrid particle swarm optimization (PSO) algorithm for solving it. Zhou et al. [2] considered the problem of scheduling operations in farmland with the irregular shape of the farmland and obstacles in the farmland; a travelling salesman problem (TSP) and an ant colony optimization (ACO) algorithm were used as the solutions. Jensen et al. [4] transformed the scheduling problem in fertilizer application operations into a TSP-based model and proposed a coverage planning algorithm. Pitakaso et al. [8] proposed an adaptive large neighborhood search (ALNS) algorithm for the mechanical harvester allocation and time window routing problem to maximize the total area served by mechanical harvesters under a shared infield resource system. All the above agricultural machinery scheduling problems are always converted into TSP-problems, and some of them consider time window constraints. The asymmetric paths among farmlands in the real scenario have not been studied.

The exact algorithms, such as dynamic programming [13] and branch and bound algorithms [14], are usually used in agricultural machinery scheduling problems. Although approximate optimal solutions can be obtained using the exact algorithm, they take a long time to solve and cannot be well applied to large-scale problems. Heuristic algorithms such as genetic algorithms [15], tabu search algorithms [16], and simulated annealing algorithms [17] are the most commonly used in the field of agricultural machinery scheduling. However, it relies on experts to construct rules manually to solve the problem, and it is easy to fall into the local optimal solution. In recent years, more and more deep-learning (DL)-based methods have been used for COP. Among them, the neural networks to solve COP are of emerging interest. Vinyals et al. [18], based on the classical sequence-to-sequence (Seq2Seq) mapping model in the field of machine translation, proposed Pointer Network (Ptr-Net) for solving COPs. The model is trained by supervised learning and achieves good results on the TSP. Supervised learning necessitates a significant quantity of labeled data for its training, which poses a significant challenge owing to the NP-hard complexity of COP. Deep reinforcement learning (DRL) can be trained without labeled data, and more and more methods use DRL to study COPs [19,20,21,22,23,24,25]. In particular, Bello et al. [19] formulated the TSP problem as a Markov decision process(MDP) for the first time and trained the pointer network model as a strategy using the REINFORCE algorithm. Additionally, inspired by Transformer [26], Kool et al. [21] proposed attention-based frameworks, which show significant performance improvements. Some work also considers other settings such as time windows, i.e., traveling salesman problem with time windows (TSPTW), which is first mentioned in [27]. The authors propose a framework to solve the traveling salesman problem with time windows and rejection (TSPTWR) problem in [24]. Zhang et al. [25] proposed a manager-worker framework for multiple traveling salesman problem with time windows and rejection (MTSPTWR), which is a complex variant of TSP. In the MTSPTWR problem, customers who fail to receive service by the specified deadline are subject to being rejected. In agricultural machine scheduling, the general reinforcement learning methods considering Euclidean distance cannot work well because the transfer times among farmlands are asymmetric, which makes the studied problem more complex. As we know, there are two papers that consider the asymmetric paths [28,29] in the TSP-problem. Gao et al. [28] converted a multi-robot task allocation into an open-path multi-depot asymmetric traveling salesman problem (OPMATSP). A genetic algorithm is designed to minimize the total cost of completing all tasks with asymmetric cost. Kris et al. [29] consider an asymmetric multiple vehicle TSP with time windows. A two-phase hybrid deterministic annealing and tabu search algorithm are proposed to minimize the number of vehicles deployed and the total travel distance. Though the above papers consider asymmetric paths in the TSP-problem, some of them ignore the time window constraint. While the solver with DL in this paper is different from the existing methods for papers considering asymmetric paths and time window. Meanwhile, the objective of CR and MS in our paper is different from the above two papers.

In this paper, the studied problem is named asymmetric multiple traveling salesman problem with time windows (AMTSPTW), i.e., MTSPTW with asymmetry paths. In order to finish farmlands with time windows in emergencies, the objectives of the scheduling of agricultural machinery (e.g., leveling machines, ploughs) are to maximize the number of finished farmlands in the given time window and to minimize makespan. We propose a DRL framework to provide an end-to-end solution for the studied problem. Specifically, our DRL framework utilizes an encoder-decoder structure for the policy network. Inspired by the excellent performance of attention mechanisms in feature extraction for solving vehicle routing problem (VRP) problems as demonstrated in [21,30], we propose a heterogeneous feature fusion attention mechanism that integrates time window information with asymmetric path information to enhance the feature extraction capability of the policy network. By incorporating virtual depots and mask mechanisms, we design a path segmentation mask mechanism to partite solutions for each agricultural machinery more efficiently. We summarize the main contributions of this study as follows:

• We transform the emergency agricultural machinery scheduling problem into a class of AMTSPTW problems, taking into account the asymmetry of field transfer time and time windows.
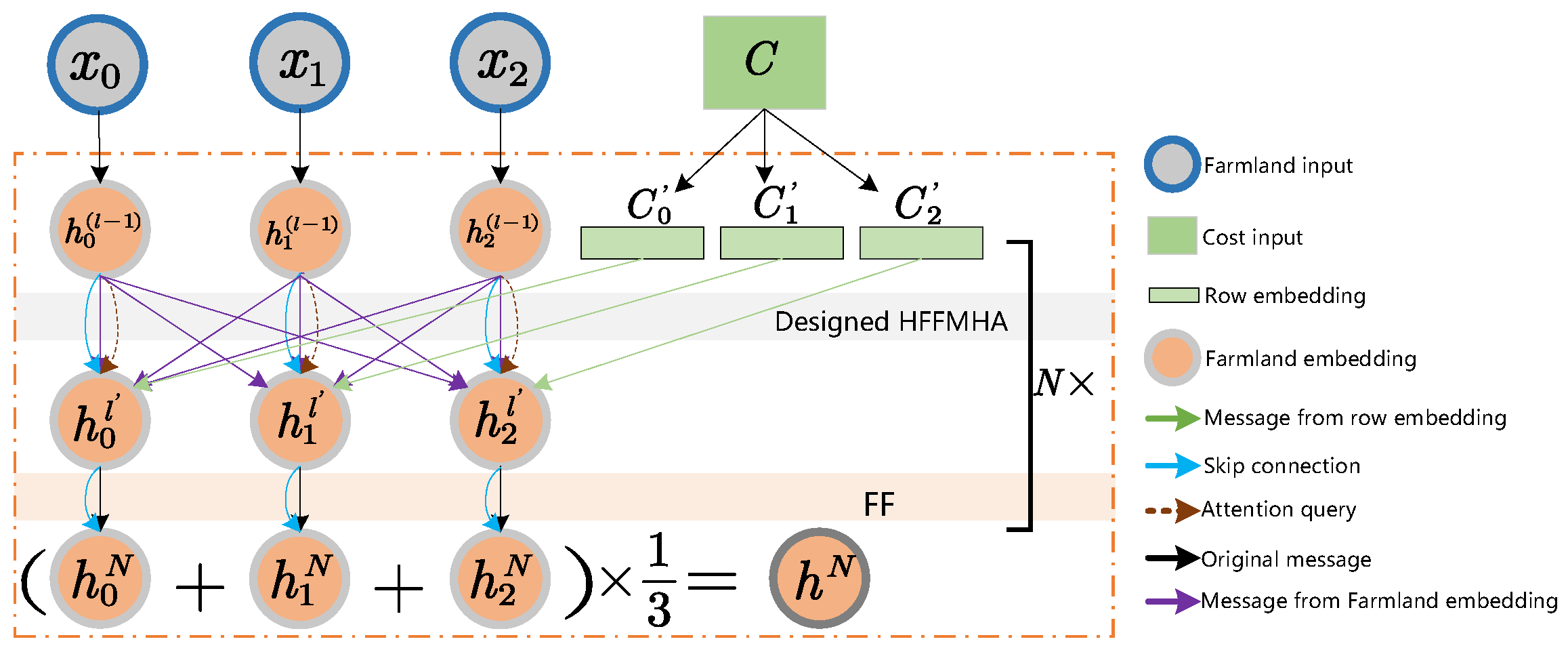
• We propose a DRL framework for end-to-end solving of the AMTSPTW problem. The framework employs an encoder-decoder structure. We propose a heterogeneous feature fusion attention mechanism in the encoder that allows the policy network to integrate time windows and path features for decision-making.
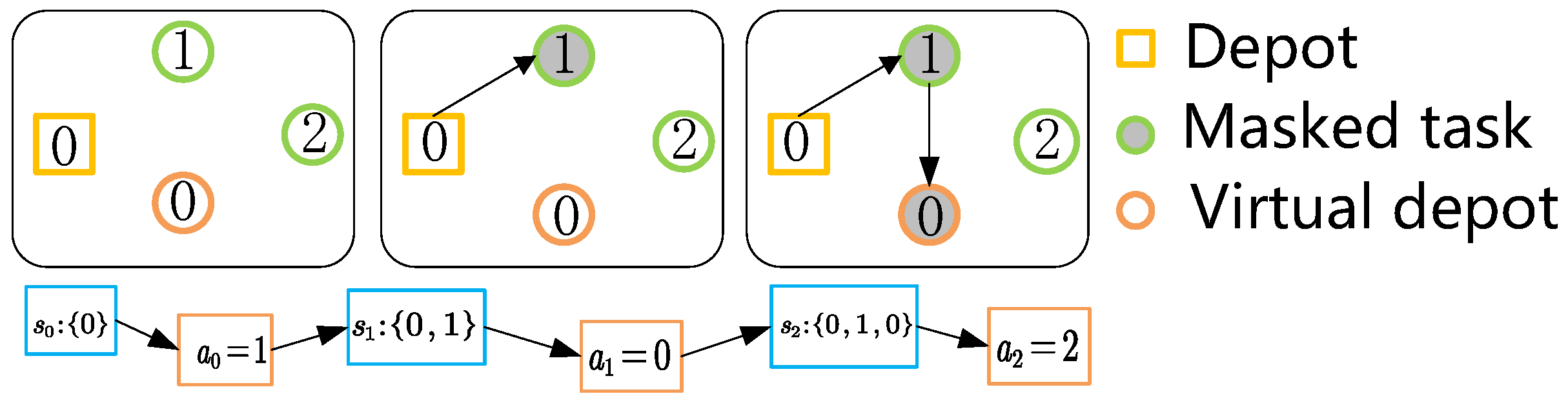
• In the decoder, we add virtual depots to assign farmlands to each agricultural machinery. We design a path segmentation mask mechanism to enable the policy to utilize the virtual depots and mask mechanism to partition the solutions efficiently.

Section 2 describes the problem description. Section 3 introduces a DRL approach for the studied problem. Section 4 investigates the experimental results. And Section 5 concludes the paper and shows our future work.

2. Problem Description

Based on practical investigations and theoretical analysis, the studied problem is based on the following assumptions:

• The location of the agricultural machinery depot, the farmlands, and their entry and exit points are known and fixed.
• The number of agricultural machines is known, and they have the same parameters. The influence of machinery lifespan on power is ignored.
• The transfer time of agricultural machinery from one farmland to another farmland is known, and the time windows for each farmland are also known.
• Agricultural machinery departs from the depot. Each farmland can only be served by one agricultural machine once, and the machine needs to return to the depot after completing its farmlands.
• There are no capacity restrictions for the agricultural machinery. It is assumed that they can complete all their tasks, such as leveling machines, ploughs, and so on.

Under the aforementioned assumptions, the agricultural machinery scheduling problem can be formulated as the AMTSPTW problem. The objectives are to meet the time windows and minimize the makespan. Let $\chi =\left\{x_0,\dots ,x_n\right\}$ represents the time windows of farmlands with n farmlands and $x_i=\left(b_i,e_i\right)(i\in \{0,1\dots ,n\})$. Specially, $x_0\in (0,+\infty )$ represents the time windows of the depot and virtual depot used in Section 3.2.1. $M=\left\{v_1,\dots ,v_{\lambda }\right\}$ is the agricultural machines set with $\lambda$ identical machines. For each farmland, if the machine arrives earlier than the start time $b_i$, it will wait. A $n\times n$ asymmetric matrix $\tau$ represents the transfer time among the farmlands. $\varsigma =\left\{{\varsigma }_0,\dots ,{\varsigma }_n\right\}$ denotes the processing time required for each farmland, and ${\varsigma }_0=0$. Different from vehicles arriving in time of VRP, the studied problem requires agricultural machinery to complete farmlands in time windows. Therefore, we make the following adjustments:

$$\left(b_i,e_i^{\prime }\right)=\left(b_i,e_i-{\varsigma }_i\right),i\in \{0,1\dots ,n\}$$

(1)

Subsequently, we calculate the cost matrix C as the transfer cost for the agricultural machines:

$$C_i={\tau }_i+{\varsigma }_i,i\in \{0,1\dots ,n\}$$

(2)

where $C_i$ and ${\tau }_i$ represent the $i\mathrm{th}$ row of cost matrix C and the $i\mathrm{th}$ row of matrix $\tau$, respectively. Let $y_{mj}$ be a binary variable to indicate whether the time window constraint of farmland i is met by the agricultural machine $v_m(v_m\in M)$. Assume $x_{mij}$ is a binary variable to indicate whether agricultural machine $v_m$ is processing farmland $x_j$ from farmland $x_i$. $\ell a_{mi}$ is the arrival time of agricultural machinery $v_m$ to i, and $w_{mi}$ is the waiting time of agricultural machinery $v_m$ at farmland i. Assume $\alpha$ is the weight of the sub-tour length. The objective of AMTSPTW is defined as:

$$\mathbf{min}\left(-\sum _{m=1}^{\lambda }\sum _{\mathit{i}=\mathit{1}}^{\mathit{n}}{\mathit{y}}_{\mathit{mi}}+\right.\left.\alpha \times \underset{m}{max}\sum _{j=1}^n{x}_{mj0}\left(a_{mj}+w_{mj}+C_{j0}\right)\right)$$

(3)

where $C_{ij}$ represents the transfer cost from farmland $x_i$ to farmland $x_j$.

Assume P represent an extreme large positive number; the AMTSPTW satisfies the following constraints:

$$\sum _{m=1}^{\lambda }\sum _{j=1}^n{x}_{m0j}+x_{mj0}=2\lambda$$

(4)

$$\sum _{m=1}^{\lambda }\sum _{i\ne k}{x}_{mik}=1,\left(k=1,\dots ,n\right)$$

(5)

$$\sum _{m=1}^{\lambda }\sum _{j\ne k}xmkj=1,\left(k=1,\dots ,n\right)$$

(6)

$$\sum _{m=1}^{\lambda }\sum _{i\ne j;i,j\in S}{x}_{mij}\le \left|S\right|-1,(2\le \left|S\right|\le n-1,S\subseteq \left\{1,\dots ,n\right\})$$

(7)

$$\sum _{m=1}^{\lambda }\sum _{i=1}^N{y}_{mi}\le n$$

(8)

$$\ell a_{mi}+w_{mi}+C_{ij}+P(1-x_{mij})\le \ell a_{mi},(i=1,\dots n,m=1,\dots ,\lambda )$$

(9)

$$b_i\le \ell a_{mi}+w_{mi},(i=1,\dots n,m=1,\dots ,\lambda )$$

(10)

$$\ell a_{mi}+w_{mi}\le e_i^{\prime },(i=1,\dots n,m=1,\dots ,\lambda )$$

(11)

Constraint (4) assures that the agricultural machinery must go from depot to depot again. Meanwhile, constraints (5) and (6) ensure each farmland is only visited once. Constraint (7) represents the subtour elimination constraint, which prevents the generation of routes that are disconnected from the depot. Constraint (8) guarantees that the number of finished farmlands in the time window cannot exceed n. Constraints (9)–(11) specify that the agricultural machinery must adhere to the corresponding time window for each farmland.

3. Materials and Methods

3.1. Formulation of MDP

The AMTSPTW can be seen as the process of constructing paths of machines, which is essentially conceptualized as a sequential decision-making process. Such problems can be naturally formulated and solved by reinforcement learning. Then we formulate the process of constructing the paths as an MDP, and Figure 2 illustrates an illustration example with an MDP. Assume $a_i$ denotes the action at step i. The basic components of MDP are defined in the following manner:

State. We set $s_t$ to denote the state at time step t, which denotes the partial solution created at time step t. In other words, the solution is constructed iteratively by $s_t$. Assuming T represents the total time steps, $s_T$ is our final solution. As shown in Figure 2, there are two farmlands and two agricultural machines. Virtual depot 0 and depot 0 both denote the same depot. The initial state $s_0=0$ denotes the current machinery that would depart from the depot. With the action $a_0=1$, we can obtain $s_1=\{0,1\}$. And $s_2=\{0,1,0\}$ is obtained by $a_1=0$, which represents the solution of the current machinery is finished. Since the studied problem includes many machines, $s_0$, $s_1$, and $s_2$ here are just partial solutions. The reason for adding virtual depot 0 is to partite solutions efficiently in the decision-making process, which is elaborately described in Section 3.2.2. The number of virtual depots depends on the number of agricultural machines.

Action. At time step t, the policy selects i from the set $\{0,1,\dots ,n\}$ as the current action.

Transition. The transition between states depends on the current state and the chosen action. The transition matrix is the possibility of moving from the current state to the next state. If the chosen action is 0, the number of 0 needs to reduce 1. In other words, one machine has obtained its solution and returned to the depot.

Reward. The reward function consists of two parts shown in Equation (12). The first part is the reward obtained from each farmland finished in time windows. The negative reward from farmlands violating the deadline is the second part. In Equation (12), assume ${\alpha }_r$ is the weight and $l_m$ denotes the round-trip time of agricultural machinery $v_m$ from depot to depot again. The reward R is calculated as follows:

$$R=\sum _{t=0}^T{r}_t-{\alpha }_r\times \underset{m}{max}{l}_m.$$

(12)

where

$$r_t=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{farmland}\mathrm{satisfies}\mathrm{deadline}\hfill \\ -1\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(13)

Policy. Given a problem instance I, our attention-based encoder-decoder model defines a random policy $p_{\theta }$ to select a feasible solution. $p_{\theta }$ outputs $a_t$ as the current action to satisfy the constraint at each time step until a feasible solution is constructed. Assume the partial solution generated at step i is denoted by ${\pi }_i$, the policy $p_{\theta }$ is obtained as follows:

$$p_{\theta }(\pi \mid I)=\prod _0^{T-1}{p}_{\theta }({\pi }_t\mid I,{\pi }_{0:t-1}).$$

(14)

The action selection at each time step will be based on the learned $p_{\theta }$. Two strategies Greedy and Sampling are used for action selection in this paper, which are shown in Section 4.3.

3.2. Policy Network

In order to obtain a better policy, the similar structure with [21,30] generating by Transformer [26] is used in this paper, which is shown in Figure 3. The encoder generates embeddings for all input farmlands. $x_i\in \chi$ is linearly mapped to obtain the embedding, and the C is obtained by Equation (2). Subsequently, the embedding of the obtained C matrix and $x_i\in \chi$ is fed into the encoder. The encoder consists of multiple blocks; each block has an attention layer, addition and normalization layer, feed-forward layer, and addition and normalization layer. $h_i^N$ and $h^N$ are the values of each farmland and the mean values of all farmlands after N encoders. Since the study problem considers not only the time window but also transfer costs among farmlands, these heterogeneous features make the existing feature fusion [21,26,30] not work well. Therefore, we designed a heterogeneous feature fusion attention mechanism. After going through multiple encoder blocks, the feature vectors, including time windows and the transfer cost of each farmland, are obtained. Since the obtained solution consists of paths of many agriculture machinery, dividing the solution efficiently for each machinery is difficult in the decoder. As aforementioned, the virtual depot added to solutions can make the partition solution just by removing the representing 0, which leads to great efficiency. Because the mask mechanism can effectively avoid invalid action selections, we designed the path segmentation mask mechanism based on the solutions with a virtual depot in the decoder for solution partition in the decoder.

3.2.1. Encoder

Existing heterogeneous feature fusion based on attention is always used in image processing, which segments images into grids and calculates the weights of a grid and its neighborhoods for feature fusion. Since the study problem considers not only the time window but also the transfer cost among farmlands, these heterogeneous features make the existing feature fusion not work well. Furthermore, with the asymmetric paths in our paper, the transfer cost of each farmland from the cost matrix needs to be exactly selected for feature fusion, which is ignored in existing feature fusion. In this paper, we design a heterogeneous feature fusion attention mechanism in the encoder to fuse the asymmetric paths and the transfer cost efficiently. In Figure 4, the input farmland time windows $x_i\in \chi$ and the cost matrix C are linearly mapped into initial embeddings with a dimension of 128. Specifically, the cost matrix C needs to be split into rows, where each row corresponds to a respective farmland embedding of transfer cost. Meanwhile, the $C_0^{\prime }$ corresponds to the depot embedding of $x_0$. Then, the embeddings go through the N encoder block, each consisting of a designed multi-head attention sub-layer and a feed-forward sub-layer.

Since the proposed heterogeneous feature fusion is improved by the existing attention mechanism, we introduce the attention mechanism first with the time window $x_i\in \chi$, for example. All $x_i\in \chi$ need to initial embed to sequence $h_i^{l-1},i\in \{0,1,\dots ,n\}$, which represents the farmland embedding $x_i$ of attention layer $l-1$. Assume the multi-head attention consists of D = 8 heads. For the layer embedding $h_i^{l-1}$, the following equation is used for mapping:

$$Q_i=W^Q\times h_i^{l-1},K_i^n=W^K\times h_i^{l-1},V_i^n=W^V\times h_i^{l-1}$$

(15)

where $W^Q,W^K\in R^{d_h\times d_k}$ and $W^V\in R^{d_h\times d_v}$ are trainable parameter matrices and the dimensions of $d_k$ and $d_v$ are $\frac{d_h}{D}$. $Q_i,K_i^n,$ and $V_i^n$ respectively represent Query, Key, and Value. Then the softmax function is processed to calculate the weights $a_{ij}$ between farmland i and farmland j, where a larger value indicates a higher correlation. It is calculated as follows:

$$a_{ij}=softmax(\frac{Q_i\times K_j}{\sqrt{d_k}}),i,j\in \{0,1\dots ,n\}$$

(16)

As shown in the above attention, it just considers one feature, for example, the time window in this paper. It is difficult to incorporate information about the transfer cost of agricultural machinery as it travels from i to j. Furthermore, the transfer cost contains all farmlands, which needs to be split for each farmland for the next calculation. To address the above problem, we propose the heterogeneous feature fusion attention mechanism, which is shown in Figure 4. The FF layer in Figure 4 means the feed-forward layer. Since $h_i^{l-1}$ is the embedding time window for each farmland, we first calculate the embedding of the transfer cost of each farmland. As shown in Equation (17), we compute the key and value of the transfer cost matrix C, which are denoted as $K^e$ and $V^e$.

$$K^e=W^{K_e}\times C,V^e=W^{V_e}\times C$$

(17)

where $W^{K_e}\in R^{d_h\times d_k}$ and $W^{V_e}\in R^{d_h\times d_v}$ are trainable parameter matrices. After obtaining the key and value of the matrix C, we need to split the embedding of the matrix according to the row for each farmland’s embedding. Assume $e_{ij}$ and $a_{i{e}_{ij}}^{\prime }$ denote the $j\mathrm{th}$ element in each row $C_i$ of C and the weight of $e_{ij}$, respectively. The calculation of $a_{i{e}_{ij}}^{\prime }$ is processed as follows:

$$a_{i{e}_{ij}}^{\prime }=softmax(\frac{Q_i\times K_{e_{ij}}^e}{\sqrt{d_k}}),i,j\in \{0,1,\dots ,n\}$$

(18)

After the obtained weights $a_{ij}$ and $a_{i{e}_{ij}}^{\prime }$, both the time window $x_i$ and the transfer cost $C_i$ are fused to calculate embedding by Equation (19).

$$h_i^d=a_{ij}{V}_j^n+a_{i{e}_{ij}}^{\prime }{V}_j^e,d\in \left\{1,\dots ,D\right\}$$

(19)

With the $h_i^d$, all features of time window and transfer cost are considered to have a better feature representation. The above process is the computation process of a single head in the attention mechanism, and the concatenating from D heads as follows:

$$\begin{array}{ccc}\hfill & MultiHead(Q_i,K_j^y,V_j^y)=Concat(h_i^1,\dots ,h_i^D),\hfill & \hfill y\in \left\{e,n\right\}\end{array}$$

(20)

Finally, each layer works as follows,

$${\widehat{h}}_i=B{N}^l(h_i^{l-1}+MultiHea{d}_i^l(Q_i,K_j^y,V_j^y))$$

(21)

$$h_i^l=B{N}^l({\widehat{h}}_i+F{F}^l({\widehat{h}}_i))$$

(22)

where $B{N}^l$ and $F{F}^l$ is batch normalization and feed forward at layer l. After passing through N layers, the graph embeddings $h^N$ are calculated as the mean of the farmland embedding at the last layer, i.e., $h^N=\frac{1}{n+1}\times {\sum }_{i=0}^n{h}_i^N$. Meanwhile ${\overline{h}}^N=\frac{1}{n+1}\times {\sum }_{i=0}^n{h}_i^N+V^v,$ where $V^v$ is the embedding of the number of agricultural machines.

3.2.2. Decoder

In MTSP and its variants, the solution to the problem always adds extra nodes [31] to simplify the solution partition for different travelers. While in our policy network, the method of adding additional nodes can greatly increase the complexity of the solution partition, which makes the problem size grow. In this paper, we invite the virtual depot to provide solutions for a more efficient solution partition. In other words, except for the first 0 in a solution, when another virtual depot 0 emerges, the path of one machine is obtained. Since the solution obtained from the policy network consists of the paths of many agriculture machinery, the actions used in the constructed paths of some machinery need to be removed from the solution, which can efficiently calculate the path of the next machine. Because the mask mechanism can effectively avoid invalid action selections, we designed the path segmentation mask mechanism based on the solutions with a virtual depot in the decoder for solution partition. The decoder takes ${\overline{h}}^N$ and $h_i^N$ from the encoder as input, and each time step it will generate a probability vector. A context $h^c$ is always required at the beginning of each time step, which is shown below:

$$V^r=W^r\times v$$

(23)

$$h^c=Concat({\overline{h}}^N,h_{{\pi }_{t-1}}^N,V^r)$$

(24)

where $V^r$ and v are the embeddings of the number of remaining agricultural machines and the number of virtual depots in the unmasked part of the solution, respectively. Similar to glimpse [30], we use the following equation to compute the context $h_t^N$:

$$h_t^N=MultiHead(W^q{h}^c,W^k{h}_i^N,W^v{h}_i^N)$$

(25)

In this equation, $W^q,W^k\in R^{d_h\times d_k},W^v\in R^{d_h\times d_v}$ are trainable parameters.

In order to partite the solution efficiently, we invite the virtual depot to represent a path for the agricultural machine. In other words, except for the first 0 in a solution, when another virtual depot 0 emerges, the path of one machine is obtained. Assume $q^T=W^{q^{\prime }}\times h_t^N$ and $k_j=W^{k^{\prime }}\times h_j^N$, where the $W^{q^{\prime }},W^{k^{\prime }}\in R^{d_h\times d_k}$ are trainable parameters. We need to calculate the compatibility of $h_j^t$ between $q^T$ and $k_j$. If the current farmland j is not the virtual depot and it has not been selected, $h_j^t$ is calculated by $\frac{q^T{k}_j}{\sqrt{d_k}}$. Especially when $j=0$, the number of currently available virtual depots v must be larger than 0, and $h_j^t$ can be calculated by $\frac{q^T{k}_j}{\sqrt{d_k}}$ too. Because the actions used in the constructed paths of some machinery need to be removed from the solution, the mask mechanism is adopted with $h_j^t=-\infty$ to avoid this invalid information. In other words, some virtual depots need to be masked for the path of the next machine. As aforementioned, the compatibility $h_j^t$ is calculated as follows:

$$h_j^t=\left\{\begin{array}{cc}\frac{q^T{k}_j}{\sqrt{d_k}}\hfill & \mathrm{if}j\ne 0andj\ne {\pi }_{t^{\prime }},\forall t^{\prime }<torj=0,\forall t^{\prime }<t\hfill \\ -\infty \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(26)

In order to smooth the probability distribution of output, we clip the result into $\left[-G,G\right]$ for a better exploration, which is similar to [19]. G is set to 10.

$$\widehat{h_j^t}=G\times tanh(h_j^t)$$

(27)

As aforementioned, the path segmentation mask mechanism can divide the solution by the number of 0 that have been selected, and the mask mechanism implies the assignments between farmlands and agricultural machines.

Finally, we use the softmax function to output the probability vector.

$$p({\pi }_t\mid I,{\pi }_{0:t-1})=softmax(\widehat{h^t})$$

(28)

3.3. Training Method

Since sparse rewards always exist in agricultural machinery scheduling, the REINFORCE [32] algorithm is used to update parameters, which minimizes losses through Monte Carlo sampling. Meanwhile, for the significant variance in policy gradients often generated by Monte Carlo sampling, we subtract the mean of batch reward ${\overline{R}}_B$ from an episode reward $R^{\varrho }$ to reduce the variance during the calculation of policy gradient, which is similar to [33]. The loss function is initialized as $E_{p_{\theta }(\pi \mid I^{\varrho })}\left[R^{\varrho }\left(\pi \right)-{\overline{R}}_B\right]$, which represents the expected reward for a given instance $I^{\varrho }$ with the parameter $p_{\theta }$. Assume B is the batch size. We compute the policy gradient using the following equation:

$$\nabla L\leftarrow \frac{1}{B}\sum _{\varrho =1}^B(R^{\varrho }-{\overline{R}}_B){▽}_{\theta }log{p}_{\theta }({\pi }^{\varrho }\mid I^{\varrho })$$

(29)

4. Results

4.1. Experimental Environment

Following the settings of the existing DRL’s work to solve VRP problems [21,25,34,35], we randomly generate instances of problems with varying sizes of tasks, denoted by n. Specifically, we consider $n=\left\{21,51,101\right\}$ to train and test our method. We use uniform distribution to sample the working time of each farmland from $U\left[0,10\right]$ with the unit hour. For the transfer times between farmlands, we also use uniform distribution to sample from $U\left[0,1\right]$ with the unit hour for the agriculture scenario. The cost matrix is constructed using the above two data points. For the generation of the time window, the start time is considered as $b_i\sim U\left[0,\frac{11\times n}{5}\right]$, and the end time is $e_i=b_i+6$, with $U\left[·\right]$ denoting the uniform distribution. The working time of the special depot is set to 0, and the time window is set to $\left[0,+\infty \right]$. In particular, the number of agricultural machines is set at 5. The problem sizes range from 21 farmlands to 101 farmlands to indicate both small and large-scale problems in reality. It is noteworthy that AMTSPTW is an NP-hard problem, and as the scale of the problem increases, the computational complexity rises exponentially.

During the training phase, all instances are generated on the fly. We primarily referred to [21] for the selection of hyperparameters. For instances of problem sizes 21 and 51, we train 100 epochs, and for instances of problem size 101, we also train 100 epochs. In each epoch, there are 1000 batches, each containing 256 instances. For each instance, the farmland and matrix information is linearly projected onto a 128-dimensional vector and processed through 3 attention layers of the encoder before entering the decoder. At the same time, we use the Adam optimizer to train the policy network. The learning rate is fixed at ${10}^{-4}$. During training, the test instances of our method are fixed, where each problem size generates 100 instances, using the same distribution as for training. The hardware we use is a single GPU RTX A5000 (24 GB), an Intel(R) Xeon(R) Platinum 8358P CPU with 30 GB memory. The evaluation metrics include CR (computation ratio), MS (makespan), and CT (computation time), in which CR is calculated as the ratio of the number of farmlands finished by the deadline to the number of whole farmlands.

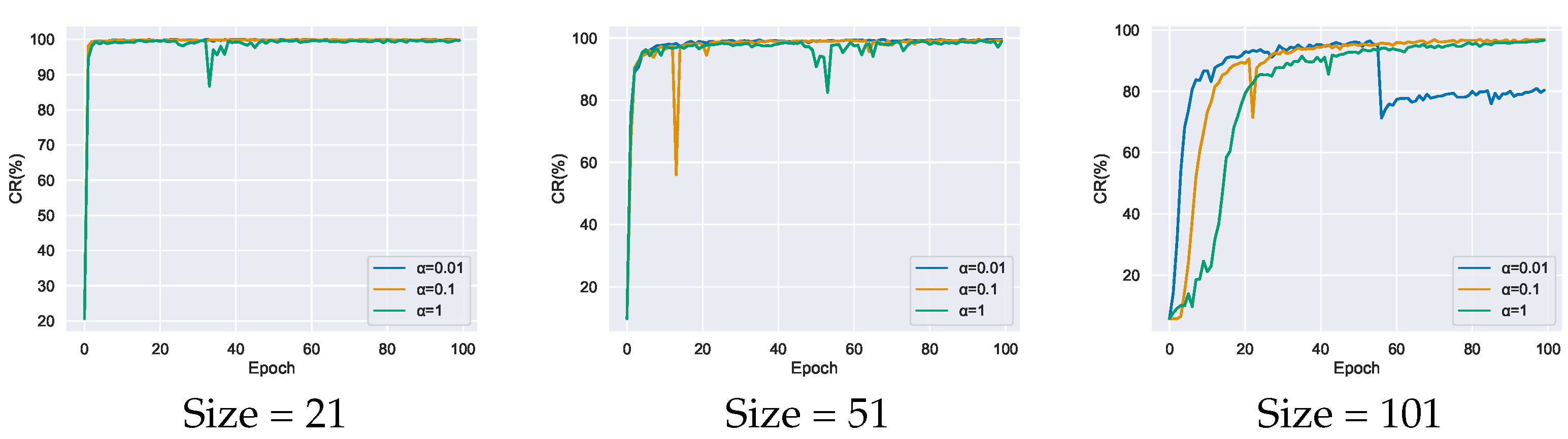
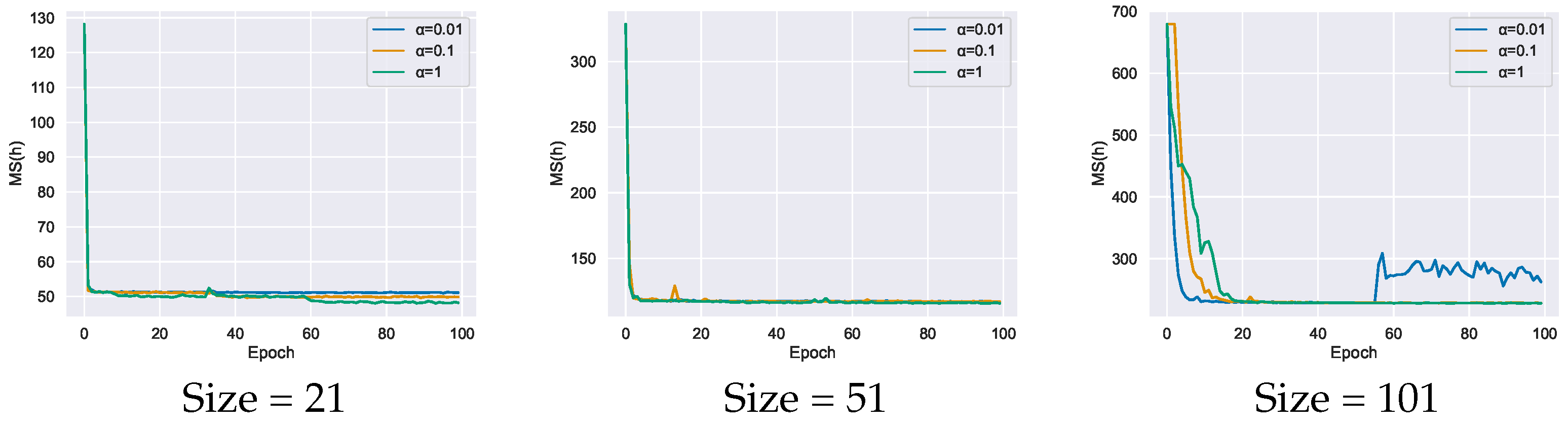
4.2. Parameter Analysis

Before making comparisons with the baseline, our DRL method’s training curves are detailed for every size of the problem. We analyze the effect of parameter $\alpha$ in the objective function on the training process. We test the model at the end of each epoch and record the results in Figure 5 and Figure 6. The test set is fixed to a batch.

In Figure 6, although $\alpha =1$ achieves the minimum in makespan at problem size 21, the completion rate fluctuates more at $\alpha =1$. As the problem size increases, $\alpha =0.1$ and $\alpha =1$ have almost the same makespan. In Figure 5, $\alpha =0.1$ has a slightly higher completion rate than $\alpha =1$. $\alpha =0.01$ is less effective than either of the above cases. This is because when $\alpha =0.01$, makespan takes less weight, resulting in the policy network paying more attention to the completion rate of the time window. When $\alpha =1$, the policy network paid too much attention to makespan. Therefore, through comprehensive consideration, we fixed $\alpha =0.1$ in the subsequent experiments.

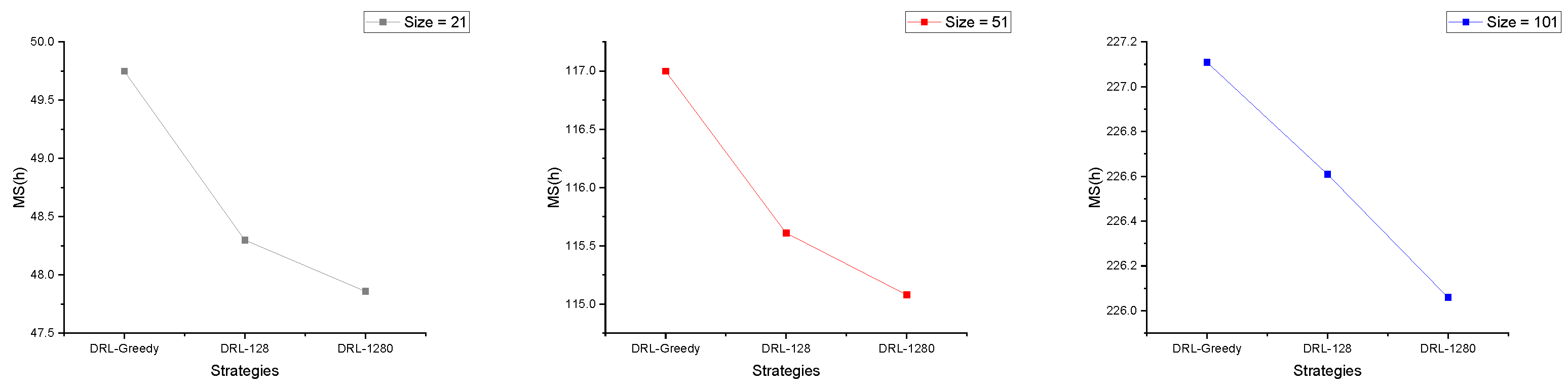
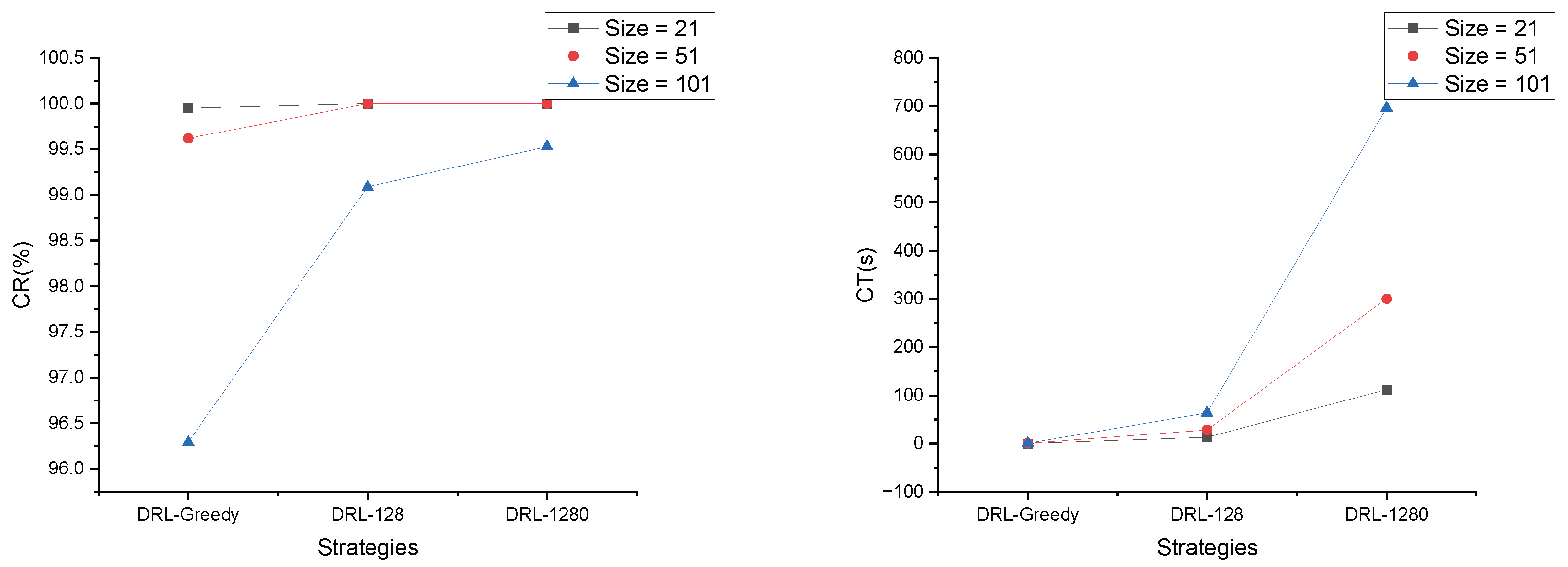
4.3. Strategy Analysis

For the proposed DRL model, two strategies were employed during the testing phase.

• Greedy strategy, we consistently select the farmland with the greatest probability for each decoding action.
• Sampling, sampling through the probability distribution generated by the decoder, generates ℜ solutions for each instance and selects the best solution, where ℜ is set to 128 and 1280, called DRL-128 and DRL-1280, respectively.

We test the performance of different strategies by randomly sampling 100 instances and solving them with different strategies. The average performance after solving for these 100 instances is recorded in Figure 7 and Figure 8.

As shown in Figure 7, we record the effects on makespan under different strategies. In Figure 7, the sampling strategy’s performance is better than the greedy strategy’s performance, and the more sampling times, the better its performance. Similarly, in Figure 8, the completion rate increases with the number of sampling times. However, the computation time also increases with the number of sampling times, especially when the problem size increases. This is because there will be some errors when using neural networks to fit data, which is difficult to avoid. Therefore, the optimal solution obtained by using the Greedy strategy is not necessarily the optimal solution. The policy network generates a policy distribution at each time step, and the more times of sampling strategies, the more candidate solutions can be obtained, so that the optimal solution can be selected. The increasing number of sample times also leads to an increase in computation time. Therefore, the solution of DRL-1280 is the best among all strategies, but it also consumes the most computation time. The greedy strategy is noteworthy for its ability to quickly obtain high-quality solutions, making it particularly suitable for scenarios with strict time constraints, such as agricultural machinery scheduling.

4.4. Comparision Analysis

We embrace three highly competitive and widely recognized conventional metaheuristic algorithms, notably the genetic algorithm $\left(GA\right)$ [15], tabu search $\left(TS\right)$ [36] and simulated annealing $\left(SA\right)$ [17] as baselines. We adapt the AM [21] method to the asymmetric MTSPTW, a well-established state-of-the-art approach within DRL for addressing TSP problems. We sampled 100 instances for testing. During the testing process, we use DRL-1280 and baselines to calculate each of the 100 instances 5 times and take the average to evaluate the average performance of the algorithm.

In

Table 1. CR, MS and CT of compared strategies with different problem sizes.

Method	Measurement	Size = 21	Size = 51	Size = 101
GA	CR (%)	95.47%	36.99%	22.04%
	MS (h)	52.39	155.13	306.87
	CT (s)	≥2000	≥2000	≥2000
SA	CR (%)	94.84%	72.34%	44.40%
	MS (h)	53.51	134.21	287.05
	CT (s)	602.71	1163.58	≥2000
TS	CR (%)	99.98%	99.70%	97.13%
	MS (h)	50.812	116.57	226.53
	CT (s)	156.29	722.24	≥2000
AM-1280	CR (%)	100.00%	65.68%	50.03%
	MS (h)	47.48	130.21	258.06
	CT (s)	90.59	204.85	461.14
DRL-1280	CR (%)	100.00%	100%	99.50%
	MS (m)	47.77	115.14	225.97
	CT (s)	97.28	221.25	534.48

Bold indicates the best value in all methods.

, we record the performance of the DRL methods and all baselines for all problem sizes. The evaluation is based on the completion rate, the makespan, and the computation time. Through the analysis of Figure 7 and Figure 8, it can be concluded that the quality of the solution can be effectively improved by increasing the sampling times. So the strategy we used in the baseline comparison is DRL-1280. For AM, we also sample 1280 times and then get the optimal solution, which is called AM-1280. In all baselines, AM-1280 achieves the makespan with optimal performance on the test with problem size 21, but AM-1280’s performance decreases very quickly as the problem size increases. This is because the AM-1280 cannot effectively fuse the two heterogeneous features when the problem size increases, resulting in a sharp performance degradation. GA performs well on problems with a problem size of 21, but as the problem size grows, the performance starts to degrade drastically. This is because, with the increase in the problem size, the search space of the solution also increases greatly, resulting in a decline in performance. SA outperforms GA, but again, a dramatic drop in performance is found. Performance degrades for the same reasons as GA, but SA is more efficient for searching solution spaces. TS is optimal in all baselines on the rest of the tests due to its large search space and very adequate search of the space, which also leads to a long computation time. Compared to AM-1280, our method has a slightly worse length metric on the problem size of 21 but still has a very competitive performance. As the problem size grows, AM-1280’s performance decreases drastically, while our method can be well adapted to larger problems.

4.5. Generalization Analysis

We demonstrate the generalization of our approach by applying the learned strategy to larger problems. We increased the problem size to 31, 71, and 121, respectively, and experimented with the corresponding problems using the learned strategy. We also set the same settings for AM-1280. We evaluate the average performance of each algorithm by calculating 5 times for each of the 100 instances and taking the mean value.

With the increase in problem size, the performances of all comparisons decreased in

Table 2. CR, MS and CT of compared strategies with larger problem sizes for generalization.

Method	Measurement	Size = 31	Size = 71	Size = 121
GA	CR(%)	72.81%	28.96%	18.75%
	MS (h)	83.29	215.08	370.35
	CT (s)	≥2000	≥2000	≥2000
SA	CR (%)	88.40%	58.73%	37.97%
	MS (h)	78.86	195.26	351.95
	CT (s)	790.00	1538.21	≥2000
TS	CR (%)	99.98%	98.79%	95.88%
	MS (h)	72.89	161.11	270.93
	CT (s)	332.67	1166.87	≥2000
AM-1280	CR (%)	99.23%	49.58%	42.34%
	MS (h)	72.40	192.09	318.69
	CT (s)	130.87	272.84	614.41
DRL-1280	CR (%)	99.94%	98.36%	97.54%
	MS (h)	71.27	161.02	271.14
	CT (s)	140.10	333.36	718.21

Bold indicates the best value in all methods.

. While our proposal has the fewest differences among all problem sizes. Compared to the AM-1280, our method outperforms the AM-1280 for all problem sizes, proving that our method generalizes better than AM-1280. This is because as the problem scale increases, the processing requirements for $\chi$ and C heterogeneous features become higher, while the AM-1280 is insufficient for heterogeneous features, resulting in rapid performance degradation. Compared to the meta-heuristic baselines, DRL-1280 outperforms TS on makespan metrics at 31 problem sizes, achieves competitive results at 71 problem sizes, and outperforms TS on time-window completion rate metrics at 121 problem sizes. Therefore, we can conclude that our method has good generalization. Meanwhile our proposal is focused on algorithm improvement in a special scenario, so it can solve any other problems with the same features (e.g., time window, transfer cost, and asymmetric paths) as the studied problem, which just needs to retrain the policy network without any changes.

5. Conclusions

In this study, the agricultural machinery scheduling problem with asymmetric paths among farmlands and the given time windows of farmlands is named the AMTSPTW problem, which is more suitable for the real scenario. We formulated the studied problem to AMTSPTW and introduced a deep reinforcement learning framework to solve the above problem. A heterogeneous feature fusion attention mechanism considers the transfer cost, and the asymmetric paths are designed in the encoder of policy networks. Meanwhile, we design a path segmentation mask mechanism based on a virtual depot and a mash mechanism to allocate the farmlands for dividing the solutions of each agricultural machinery efficiently. Experimental results show that our proposal outperforms existing modified baselines for the studied problem. Especially, the measurements of computation ratio and makespan are improved by 26.7% and 21.9% at average, respectively. The computation time of our proposed strategy has a significant improvement over these comparisons. Meanwhile, our strategy has a better generalization for larger problems. In the future, we will extend our framework to real-world data sets and other more complex and realistic scenarios.