Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery
Abstract
:1. Introduction
2. Materials and Methods
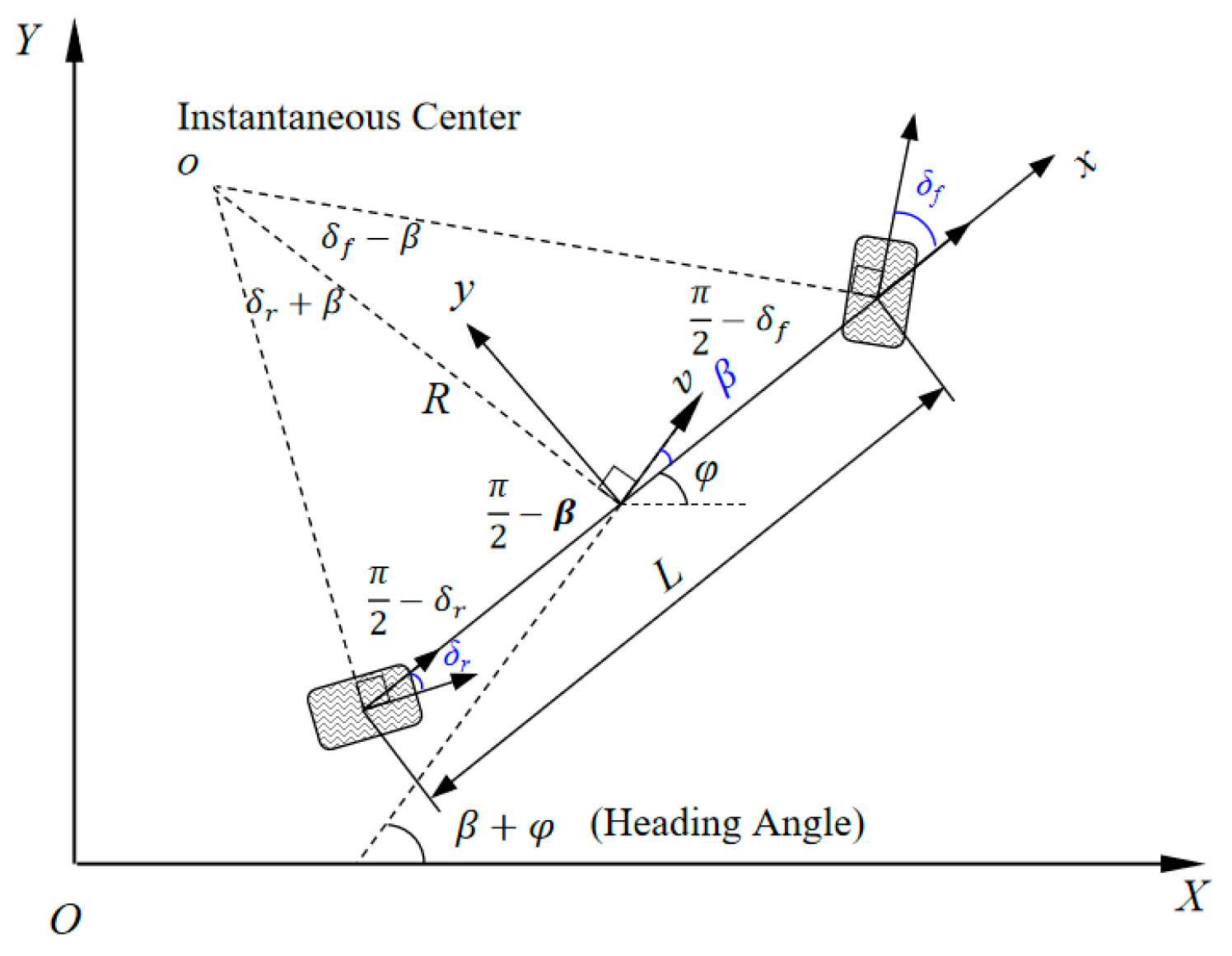
2.1. Vehicle Model of Rear-Wheel-Steering Agricultural Machinery
2.1.1. Kinematic Model
2.1.2. Dynamic Model
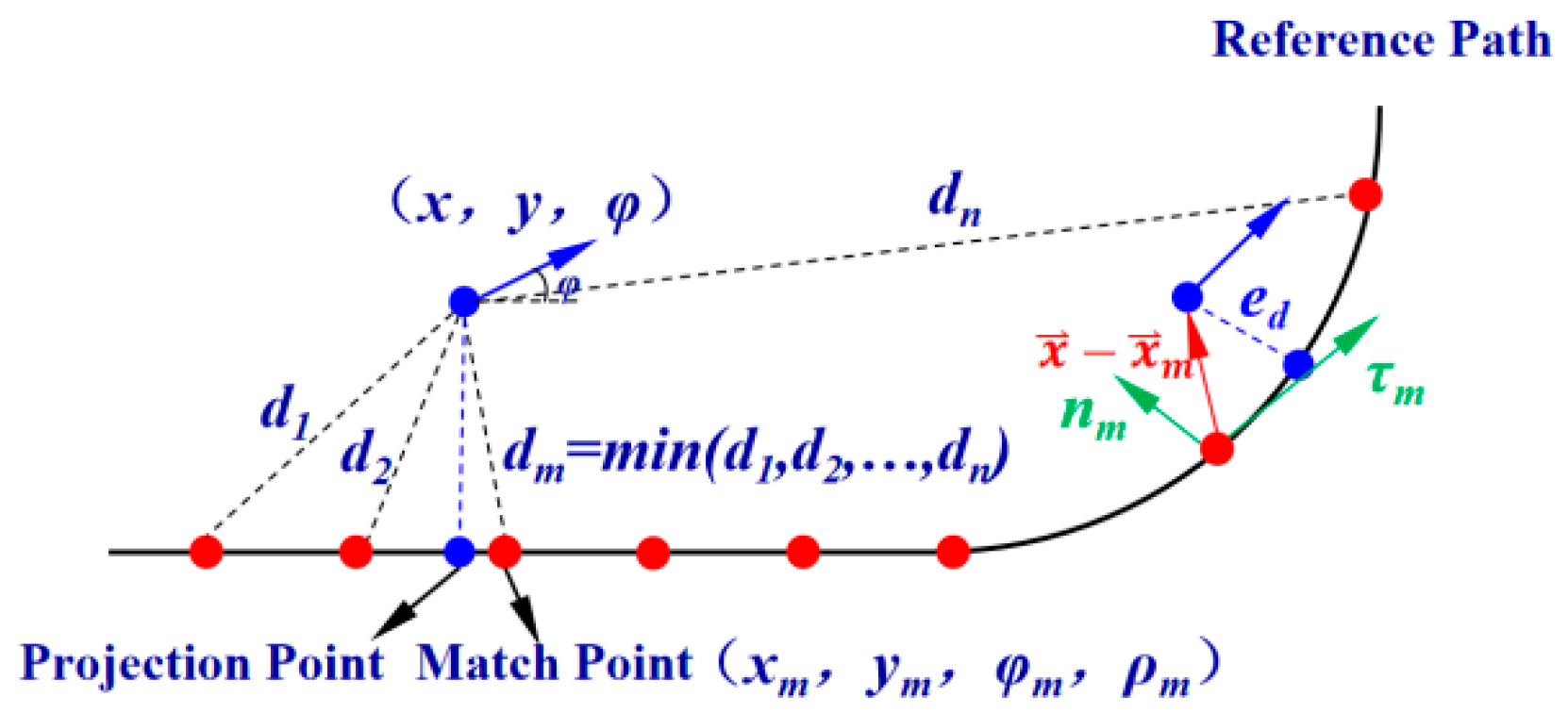
2.2. Model Predictive Control
2.2.1. Objective Function
2.2.2. Constraint Condition
2.3. Analysis of Factors Influencing MPC Tracking Performance
2.3.1. Impact of Wheelbase on Tracking Effect
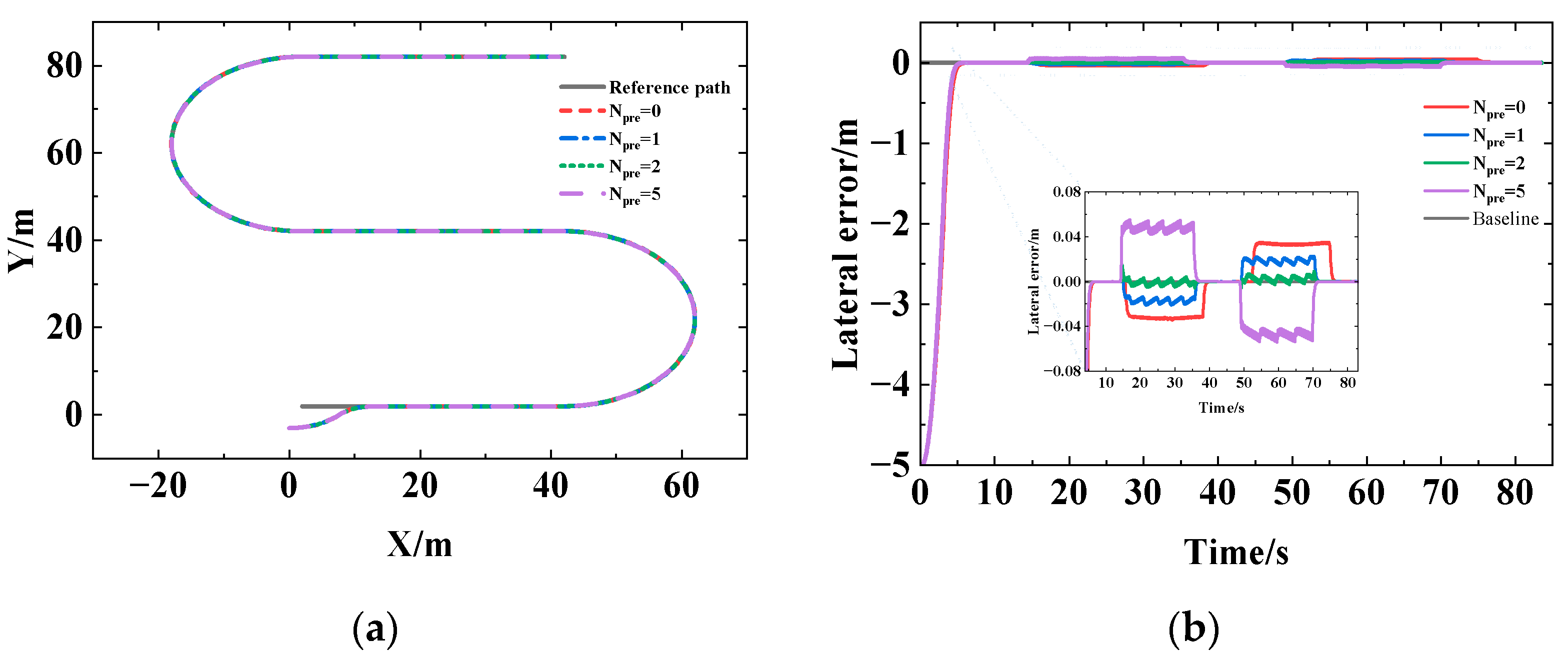
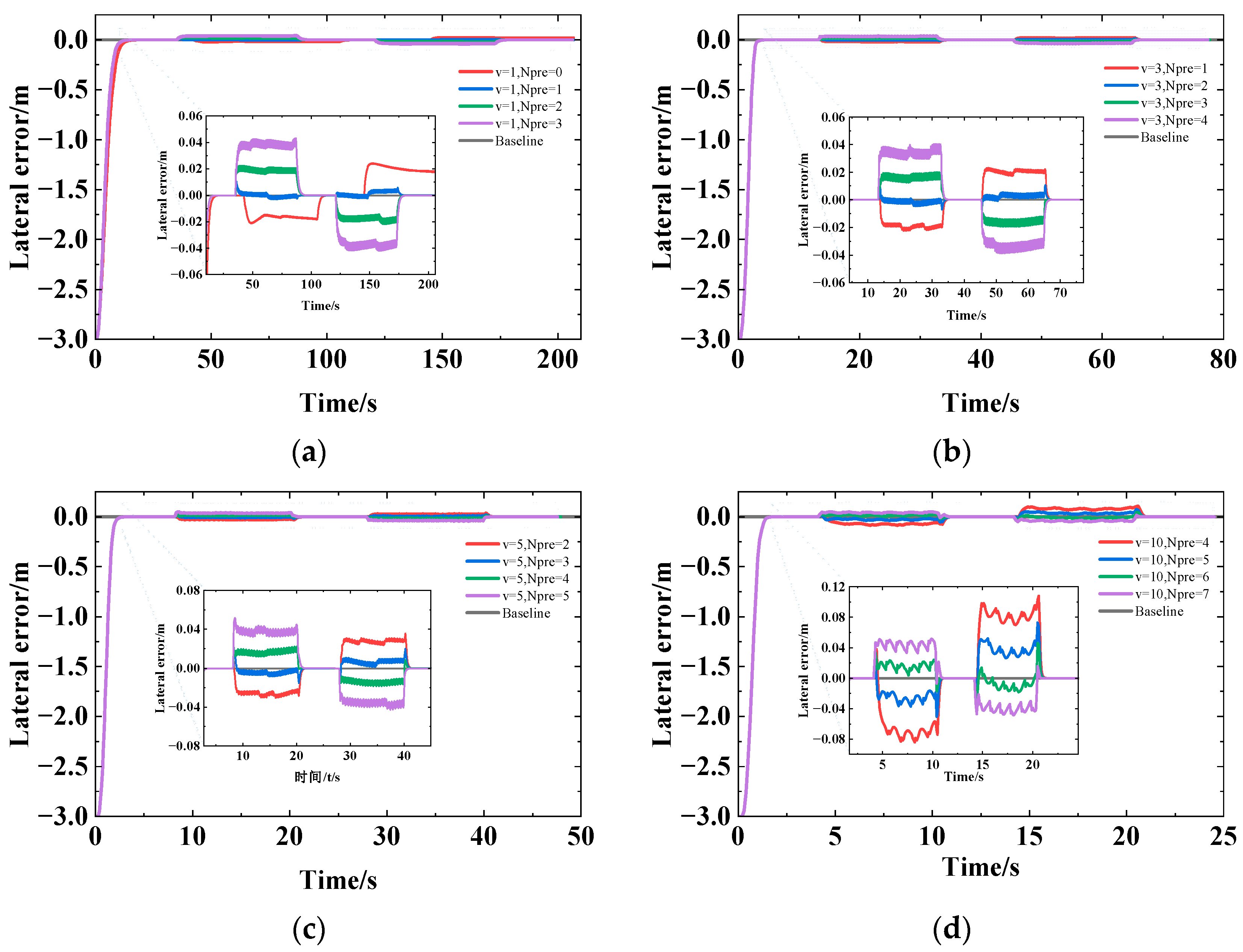
2.3.2. Impact of Preview on Tracking Effect
- Impact of reference path curvature on the value of Npre
- 2.
- Impact of velocity on the value of Npre
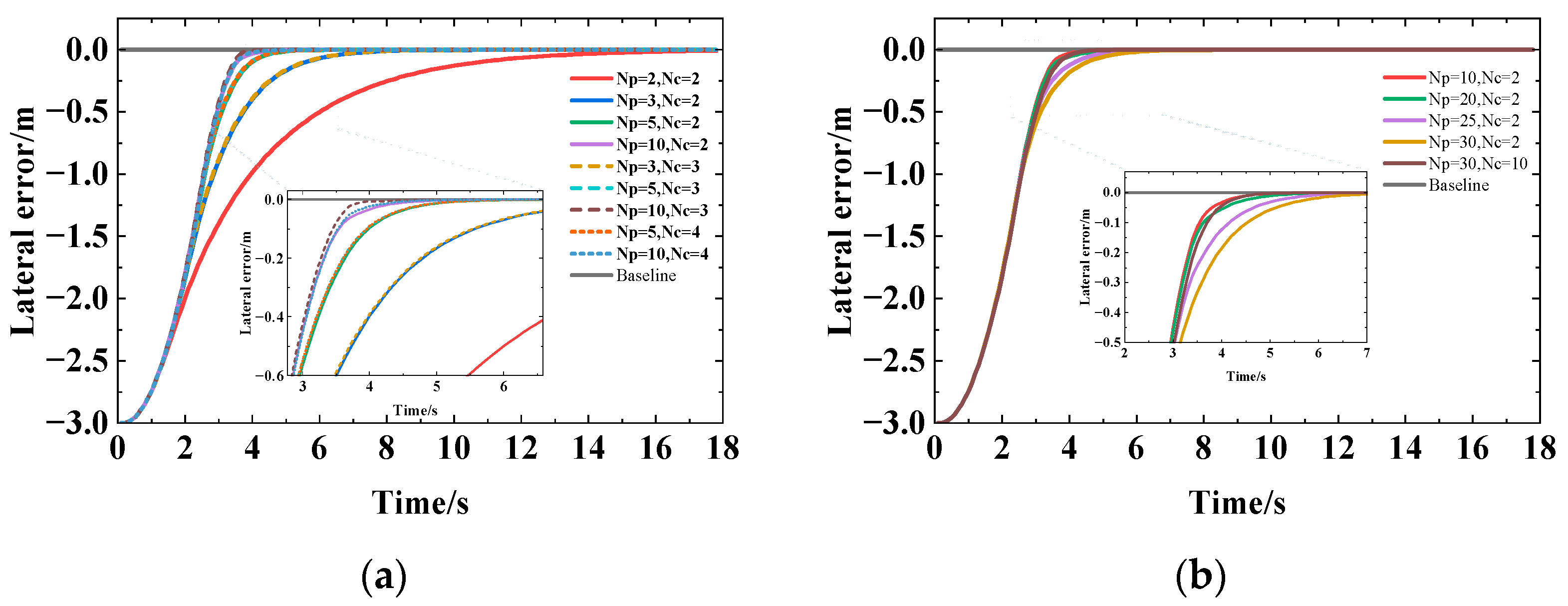
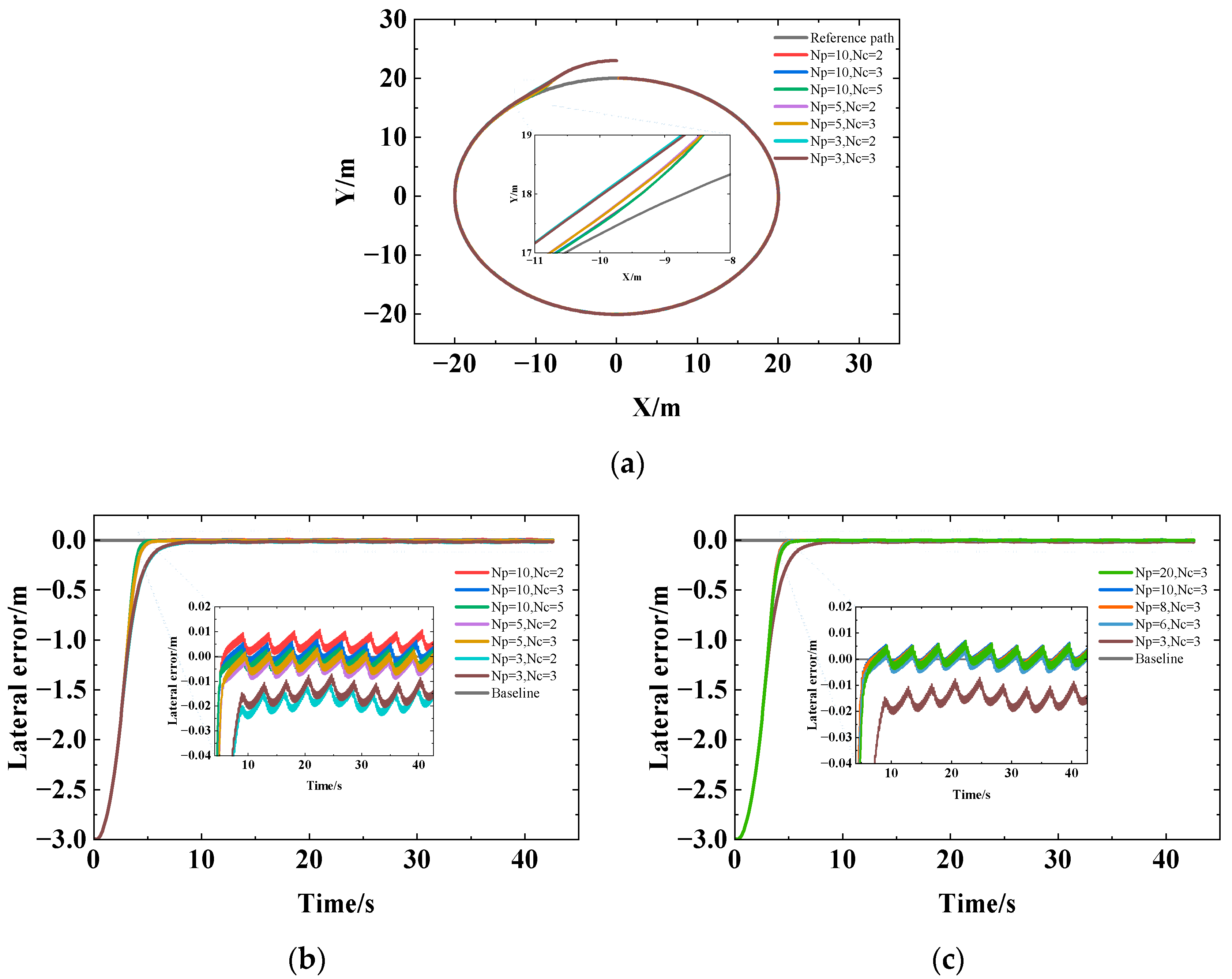
2.3.3. Impact of the Predictive Horizon and Control Horizon on Tracking Effect
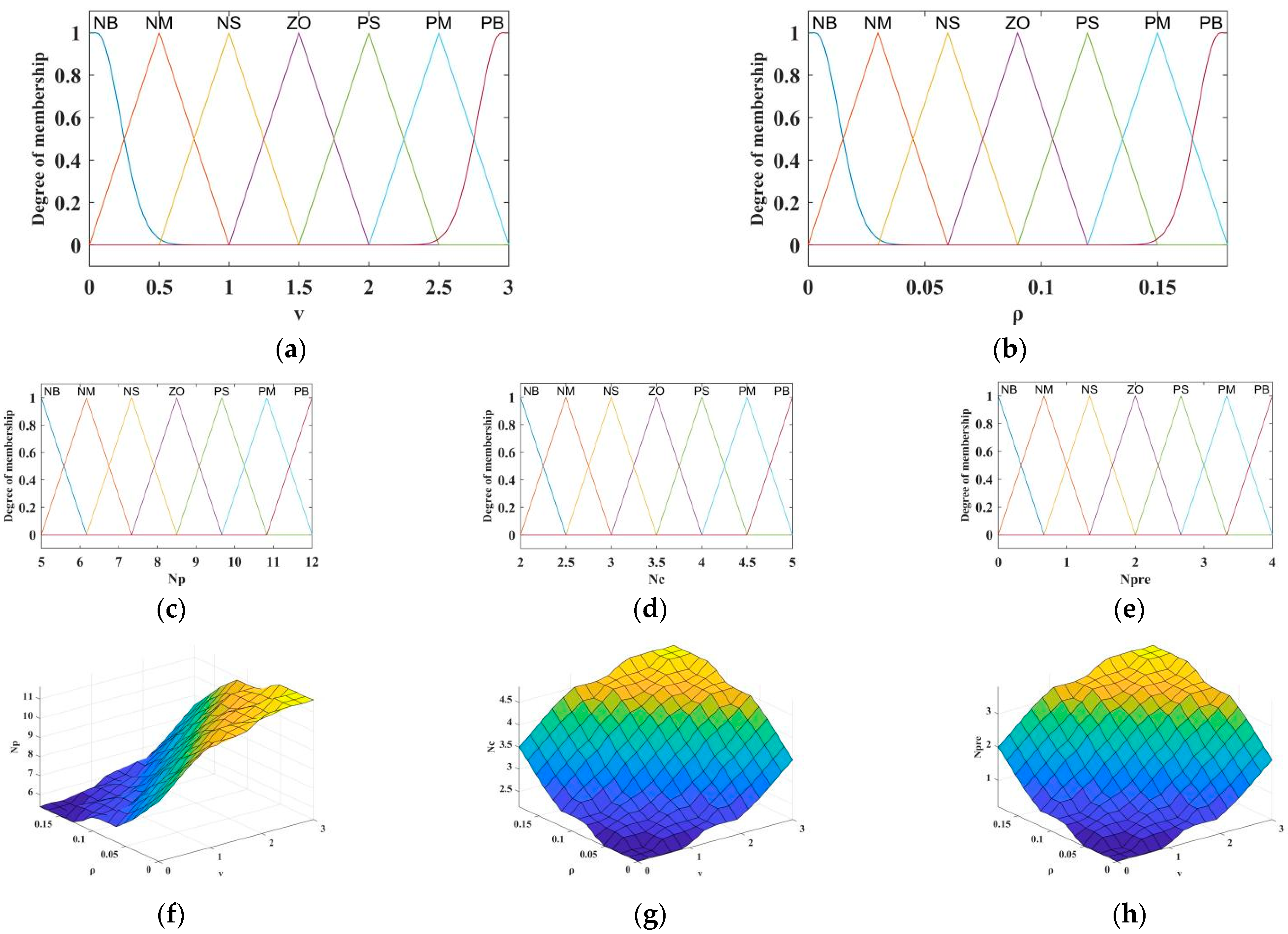
2.4. Parameter Adaptive MPC
2.4.1. Parameter Adaptive MPC Based on Fuzzy Control
2.4.2. Parameter Adaptive MPC Based on PSO
3. Results and Discussion
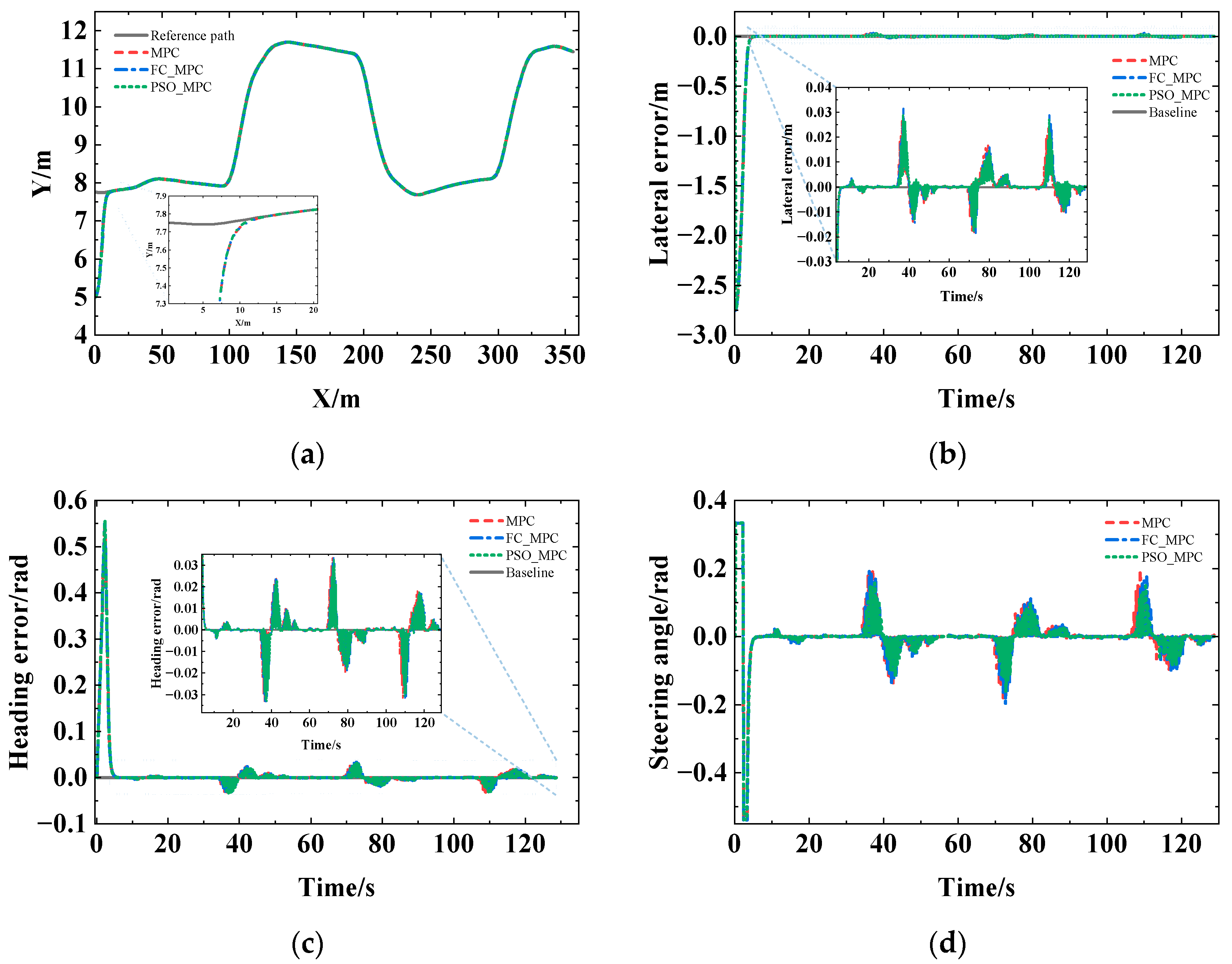
3.1. Simulation Test Results
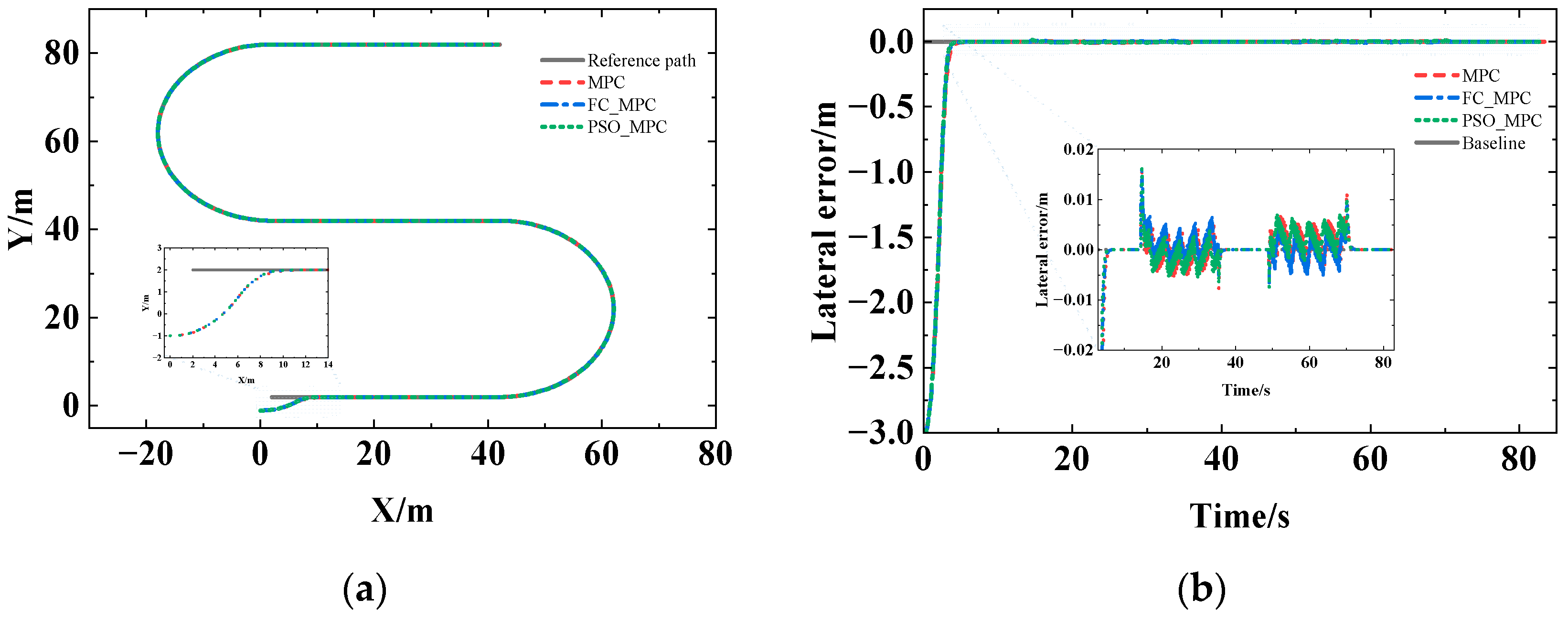
3.1.1. U-Shaped Path Simulation Test
3.1.2. Complex Curve Path Simulation Test
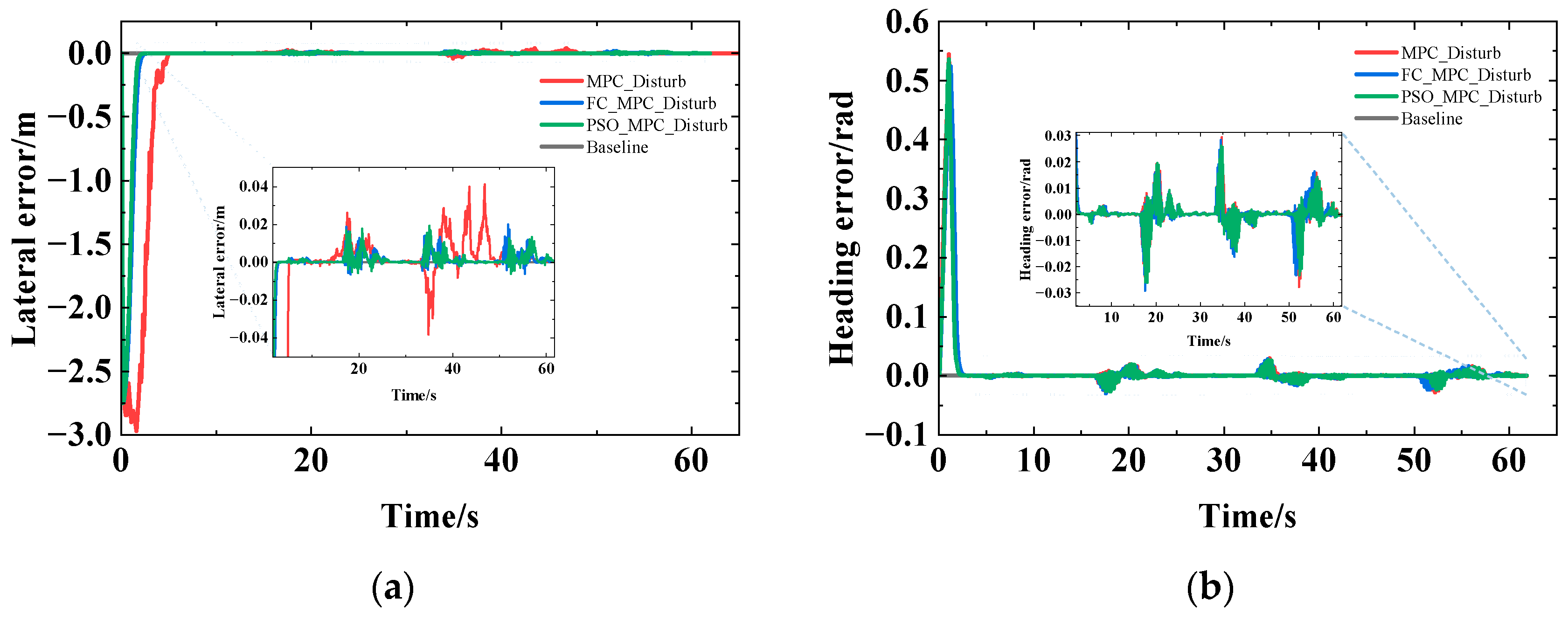
3.2. Discussion
4. Conclusions
- Since the vehicle model is a vital part of implementing MPC, the kinematic and dynamic error state–space equations for rear-wheel-steering agricultural machinery were established, which can directly apply to the design of MPC controllers.
- The factors impacting the MPC control effect were simulated and analyzed using the kinematic model as the control model. (a) The larger the unique vehicle intrinsic physical quantity wheelbase incorporated by the kinematic model, the larger the online time and distance. (b) Increasing Npre was favorable to improving the curve tracking effect, and Npre was correlated positively with the curvature and speed changes. Preferred values of Npre for the U-shaped path were 1, 2, 3, and 6, respectively, at speeds of 1 m/s, 3 m/s, 5 m/s, and 10 m/s. (c) The tracking effect was affected by the parameter settings of Np and Nc, which were influenced by the curvature and speed. Np should be increased appropriately and Nc should be decreased appropriately in straight path tracking, while Np should be decreased appropriately and Nc should be increased appropriately in curve tracking. Np and Nc should be increased appropriately when the vehicle speed increases.
- Fuzzy control and the PSO algorithm were used to establish the adaptive MPC parameters (Np, Nc, and Npre) under different curvatures and velocities, and then the simulation platform was built based on MATLAB for simulation and analysis under U-shaped and complex curve paths. The results indicated that the differences among the manual tuning MPC, the FC_MPC, and the PSO_MPC were small under no disturbance, and the tracking effects were all better. The mean absolute value of lateral error was ≤0.0018 m, with the maximum error <0.0315 m, while the mean absolute value of heading error was ≤0.0096 rad, with the maximum error <0.0325 rad. Laterally, this implies that manual tuning can obtain an optimal parameters combination, but with high uncertainty and low efficiency. The tracking effect of FC_MPC and PSO_MPC was significantly better than that of the manual tuning MPC under random velocity disturbance, and the difference between FC_MPC and PSO_MPC was not significant. As a result, FC_MPC and PSO_MPC are more anti-interference compared to the manual tuning MPC with fixed horizon, and more adaptable to complex field scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, X.; Liao, J.; Hu, L.; Zhou, Z.; Zhang, Z.; Zang, Y.; Wang, P.; He, J. Research progress of intelligent agricultural machinery and practice of unmanned farm in China. J. South China Agric. Univ. 2021, 42, 8–17+5. [Google Scholar]
- Meng, Z.; Wang, H.; Fu, W.; Liu, M.; Yin, Y.; Zhao, C. Research Status and Prospects of Agricultural Machinery Autonomous Driving. Trans. Chin. Soc. Agric. Mach. 2023, 54, 1–24. [Google Scholar]
- Macenski, S.; Singh, S.; Martín, F.; Ginés, J. Regulated Pure Pursuit for Robot Path Tracking. Auton. Robot. 2023, 47, 685–694. [Google Scholar] [CrossRef]
- Wang, L.; Zhai, Z.; Zhu, Z.; Mao, E. Path Tracking Control of an Autonomous Tractor Using Improved Stanley Controller Optimized with Multiple-Population Genetic Algorithm. Actuators 2022, 11, 22. [Google Scholar] [CrossRef]
- Han, G.; Fu, W.; Wang, W.; Wu, Z. The Lateral Tracking Control for the Intelligent Vehicle Based on Adaptive PID Neural Network. Sensors 2017, 17, 1244. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Jeon, S.; Kim, H.; Kum, D. Optimal Path Tracking Control of Autonomous Vehicle: Adaptive Full-State Linear Quadratic Gaussian (LQG) Control. IEEE Access 2019, 7, 109120–109133. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Wang, M.; Chen, J.; Yang, H.; Wu, X.; Ye, L. Path Tracking Method Based on Model Predictive Control and Genetic Algorithm for Autonomous Vehicle. Math. Probl. Eng. 2022, 2022, e4661401. [Google Scholar] [CrossRef]
- Arifin, B.; Suprapto, B.Y.; Prasetyowati, S.A.D.; Nawawi, Z. Steering Control in Electric Power Steering Autonomous Vehicle Using Type-2 Fuzzy Logic Control and PI Control. World Electr. Veh. J. 2022, 13, 53. [Google Scholar] [CrossRef]
- Li, H.; Gao, F.; Zuo, G. Research on the Agricultural Machinery Path Tracking Method Based on Deep Reinforcement Learning. Sci. Program. 2022, 2022, e6385972. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Chen, P.; Zhang, X.; Li, Q. Overview of the application of neural networks in the motion control of unmanned vehicles. Chin. J. Eng. 2022, 44, 235–243. [Google Scholar]
- A Survey on Industry Impact and Challenges Thereof [Technical Activities]. IEEE Control Syst. 2017, 37, 17–18. [CrossRef]
- Liu, J.; Yang, Z.; Huang, Z.; Li, W.; Dang, S.; Li, H. Simulation Performance Evaluation of Pure Pursuit, Stanley, LQR, MPC Controller for Autonomous Vehicles. In Proceedings of the 2021 IEEE International Conference on Real-time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; pp. 1444–1449. [Google Scholar]
- Diaz-del-Rio, F.; Sanchez-Cuevas, P.; Iñigo-Blasco, P.; Sevillano-Ramos, J.L. Improving Tracking of Trajectories through Tracking Rate Regulation: Application to UAVs. Sensors 2022, 22, 9795. [Google Scholar] [CrossRef]
- Xue, P.; Wu, Y.; Yin, G.; Liu, S.; Shi, Y. Path Tracking of Orchard Tractor Based on Linear Time-Varying Model Predictive Control. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 5489–5494. [Google Scholar]
- He, J.; Hu, L.; Wang, P.; Liu, Y.; Man, Z.; Tu, T.; Yang, L.; Li, Y.; Yi, Y.; Li, W.; et al. Path Tracking Control Method and Performance Test Based on Agricultural Machinery Pose Correction. Comput. Electron. Agric. 2022, 200, 107185. [Google Scholar] [CrossRef]
- Zhou, B.; Su, X.; Yu, H.; Guo, W.; Zhang, Q. Research on Path Tracking of Articulated Steering Tractor Based on Modified Model Predictive Control. Agriculture 2023, 13, 871. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path Tracking Control for Autonomous Vehicles Based on an Improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Shi, P.; Chang, H.; Wang, C.; Ma, Q.; Zhou, M. Research on Path Tracking Control of Autonomous Vehicles Based on PSO-BP Optimized MPC. Automob. Technol. 2023, 7, 38–46. [Google Scholar]
- Guan, L.; Liao, P.; Wang, A.; Shi, L.; Zhang, C.; Wu, X. Path tracking control of intelligent vehicles via a speed-adaptive MPC for a curved lane with varying curvature. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 802–824. [Google Scholar] [CrossRef]
- Liang, J.; Zhu, F.; Cai, Y.; Chen, X.; Chen, L. Intelligent Vehicle Path Tracking Control Based on Complex Curvature Variation. Automot. Eng. 2021, 43, 1771–1779. [Google Scholar]
- Lin, X.; Tang, Y.; Zhou, B. Improved Model Predictive Control Path Tracking Strategy Based on an Online Updating Algorithm With Cosine Similarity and a Horizon Factor. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12429–12438. [Google Scholar] [CrossRef]
- Dai, C.; Zong, C.; Chen, G. Path Tracking Control Based on Model Predictive Control With Adaptive Preview Characteristics and Speed-Assisted Constraint. IEEE Access 2020, 8, 184697–184709. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, W.; Yoo, J. A Variable Horizon Model Predictive Control Based on Curvature Properties of Vehicle Driving Path. Trans. KSAE 2021, 29, 1147–1159. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Cheng, K.W.E. A Two-Layer Model Predictive Path-Tracking Control With Curvature Adaptive Method for High-Speed Autonomous Driving. IEEE Access 2023, 11, 89228–89239. [Google Scholar] [CrossRef]
- Jing, L.; Zhang, Y.; Shen, Y.; He, S.; Liu, H.; Cui, Y. Adaptive Trajectory Tracking Control of 4WID High Clearance Unmanned Sprayer. Trans. Chin. Soc. Agric. Mach. 2021, 52, 408–416. [Google Scholar]
- Shen, Y.; Zhang, Y.; Liu, H.; He, S.; Feng, R.; Wan, Y. Research Review of Agricultural Equipment Automatic Control Technology. Trans. Chin. Soc. Agric. Mach. 2023, 54, 1–18. [Google Scholar]
- Belman-Flores, J.M.; Rodríguez-Valderrama, D.A.; Ledesma, S.; García-Pabón, J.J.; Hernández, D.; Pardo-Cely, D.M. A Review on Applications of Fuzzy Logic Control for Refrigeration Systems. Appl. Sci. 2022, 12, 1302. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Li, D.; Wang, L.; Guo, W.; Zhang, M.; Hu, B.; Wu, Q. A Particle Swarm Optimizer with Dynamic Balance of Convergence and Diversity for Large-Scale Optimization. Appl. Soft Comput. 2023, 132, 109852. [Google Scholar] [CrossRef]
- ISO 12188-2:2012(E); Tractors and Machinery for Agriculture and Forestry-Test Procedures for Positioning and Guidance Systems in Agriculture-Part 2: Testing of Satellite-Based Auto-Guidance Systems during Straight and Level Travel. International Organization for Standardization: Geneva, Switzerland, 2012.
- GB/T 37164-2018; Work Performance Requirements and Evaluation Method of Auto-Guidance Systems for Self-Propelled Agricultural Machinery. State Administration for Market Regulation. China National Standardization Administration: Beijing, China, 2018.







| Parameters | Values |
|---|---|
| Prediction horizon Np | Dynamic adjustment |
| Control horizon Nc | |
| Preview value Npre | |
| State quantity weight Q | 100 |
| Control increment weight R | 1 |
| Relaxation factor | 10 |
| Control minimum /rad | |
| Control maximum /rad | |
| Control increment minimum /rad | |
| Control increment maximum /rad | |
| Sampling period T/s | 0.1 |
| Wheelbase /m | Online Time /s | Online Distance /m | Absolute Value of Lateral Error | ||
|---|---|---|---|---|---|
| Mean Value /m | Standard Deviation/m | Maximum Error/m | |||
| L = 1.5 | 3 | 8.7 | 0.0005 | 0.0027 | 0.0216 |
| L = 2.9 | 3.6 | 10.7 | 0.0007 | 0.0029 | 0.0232 |
| L = 3.7 | 3.9 | 11.7 | 0.0007 | 0.0031 | 0.0243 |
| Parameters | Np | Nc | Npre | |
|---|---|---|---|---|
| ρ | ↑ | ↓ | ↑ | ↑ |
| ↓ | ↑ | ↓ | ↓ | |
| v | ↑ | ↑ | ↑ | ↑ |
| ↓ | ↓ | ↓ | ↓ | |
| Np = [5, 12] | v = [0, 3] | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| ρ = [0, 0.18] | NB | ZO | PS | PM | PM | PB | PB | PB |
| NM | NS | ZO | PS | PM | PM | PB | PB | |
| NS | NM | NS | ZO | PS | PM | PM | PB | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NB | NM | NM | NS | ZO | PS | PM | |
| PM | NB | NB | NM | NM | NS | ZO | PS | |
| PB | NB | NB | NB | NM | NM | NS | ZO | |
| Nc = [2, 5] | v = [0, 3] | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| ρ = [0, 0.18] | NB | NB | NB | NB | NM | NM | NS | ZO |
| NM | NB | NB | NM | NM | NS | ZO | PS | |
| NS | NB | NM | NM | NS | ZO | PS | PM | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NM | NS | ZO | PS | PM | PM | PB | |
| PM | NS | ZO | PS | PM | PM | PB | PB | |
| PB | ZO | PS | PM | PM | PB | PB | PB | |
| Npre = [0, 4] | v = [0, 3] | |||||||
| NB | NM | NS | ZO | PS | PM | PB | ||
| ρ = [0, 0.18] | NB | NB | NB | NB | NM | NM | NS | ZO |
| NM | NB | NB | NM | NM | NS | ZO | PS | |
| NS | NB | NM | NM | NS | ZO | PS | PM | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NM | NS | ZO | PS | PM | PM | PB | |
| PM | NS | ZO | PS | PM | PM | PB | PB | |
| PB | ZO | PS | PM | PM | PB | PB | PB | |
| Parameters | Values |
|---|---|
| Particle dimension D | 3 |
| Pop size | 1 |
| Maximum number of iterations | 100 |
| Individual learning factor c1 | 0.8 |
| Global learning factor c2 | 1 |
| VarSize of Np | [5, 12] |
| VarSize of Nc | [2, 5] |
| VarSize of Npre | [0, 4] |
| ωinit | 0.9 |
| ωend | 0.4 |
| Control Algorithm | Online Time /s | Online Distance/m | Absolute Value of Lateral Error | Absolute Value of Heading Error | ||||
|---|---|---|---|---|---|---|---|---|
| Mean Value /m | Standard Deviation /m | Maximum Error /m | Mean Value /rad | Standard Deviation /rad | Maximum Error /rad | |||
| MPC | 4.1 | 11.29 | 0.0016 | 0.0023 | 0.0238 | 0.0096 | 0.0091 | 0.0325 |
| FC_MPC | 3.9 | 10.67 | 0.0014 | 0.0021 | 0.0214 | 0.0095 | 0.0091 | 0.0321 |
| PSO_MPC | 3.7 | 10.10 | 0.0003 | 0.0028 | 0.0168 | 0.0095 | 0.0091 | 0.0326 |
| Control Algorithm | Online Time /s | Online Distance /m | Absolute Value of Lateral Error | Absolute Value of Heading Error | ||||
|---|---|---|---|---|---|---|---|---|
| Mean Value /m | Standard Deviation /m | Maximum Error /m | Mean Value /rad | Standard Deviation /rad | Maximum Error /rad | |||
| MPC_Disturb | 2.1 | 11.67 | 0.0189 | 0.0181 | 0.0561 | 0.0060 | 0.0076 | 0.0502 |
| FC_MPC_Disturb | 1.9 | 9.93 | 0.0047 | 0.0059 | 0.0498 | 0.0160 | 0.0153 | 0.0471 |
| PSO_MPC_Disturb | 1.7 | 10.44 | 0.0049 | 0.0056 | 0.0244 | 0.0159 | 0.0151 | 0.0463 |
| Control Algorithm | Online Time /s | Online Distance/m | Absolute Value of Lateral Error | Absolute Value of Heading Error | ||||
|---|---|---|---|---|---|---|---|---|
| Mean Value /m | Standard Deviation /m | Maximum Error /m | Mean Value /rad | Standard Deviation /rad | Maximum Error /rad | |||
| MPC | 4.2 | 10.57 | 0.0017 | 0.0035 | 0.0269 | 0.0021 | 0.0046 | 0.0334 |
| FC_MPC | 4.3 | 10.81 | 0.0018 | 0.0037 | 0.0315 | 0.0022 | 0.0046 | 0.0334 |
| PSO_MPC | 4.2 | 10.45 | 0.0016 | 0.0034 | 0.0290 | 0.0022 | 0.0046 | 0.0330 |
| Control Algorithm | Online Time /s | Online Distance/m | Absolute Value of Lateral Error | Absolute Value of Heading Error | ||||
|---|---|---|---|---|---|---|---|---|
| Mean Value /m | Standard Deviation /m | Maximum Error /m | Mean Value /rad | Standard Deviation /rad | Maximum Error /rad | |||
| MPC_Disturb | 4.9 | 26.59 | 0.0072 | 0.0137 | 0.1625 | 0.0022 | 0.0046 | 0.0293 |
| FC_MPC_Disturb | 2.3 | 11.12 | 0.0020 | 0.0033 | 0.0200 | 0.0020 | 0.0033 | 0.0200 |
| PSO_MPC_Disturb | 2.3 | 13.14 | 0.0018 | 0.0031 | 0.0193 | 0.0021 | 0.0044 | 0.0263 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Niu, C.; Wang, Z.; Jiang, Y.; Jian, J.; Tang, X. Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery. Agriculture 2024, 14, 823. https://doi.org/10.3390/agriculture14060823
Wang M, Niu C, Wang Z, Jiang Y, Jian J, Tang X. Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery. Agriculture. 2024; 14(6):823. https://doi.org/10.3390/agriculture14060823
Chicago/Turabian StyleWang, Meng, Changhe Niu, Zifan Wang, Yongxin Jiang, Jianming Jian, and Xiuying Tang. 2024. "Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery" Agriculture 14, no. 6: 823. https://doi.org/10.3390/agriculture14060823
APA StyleWang, M., Niu, C., Wang, Z., Jiang, Y., Jian, J., & Tang, X. (2024). Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery. Agriculture, 14(6), 823. https://doi.org/10.3390/agriculture14060823





