Modeling Reliability Analysis for the Branch-Based Irrigation Water Demands Due to Uncertainties in the Measured Surface Runoff

Abstract

This study aims to model the uncertainty and reliability quantification of estimating the planning irrigation water demands in the multi-canal irrigation zone, named the RA_IWD_Canal model. The proposed RA_IWD_Canal could estimate the zone-based and branch-based water demands and quantify their uncertainties and reliabilities via the weighted frequency quantile curves. The historical planning irrigation water demands and measured surface runoff from 2019 to 2024 in the Zhudong irrigation zone are utilized in the model development and application. Using the proposed RA_IWD_Canal model, the estimated branch-based irrigation water demands exhibit a significant variation (on average, from 0.02 m³/s to 1.7 m³/s) in time and space attributed to uncertainties in the historical gauged surface runoff. Also, the Zhudong Canal zone is demonstrated to be sufficiently supplied irrigation water subject to existing introduced water demands with a high reliability of 0.85; instead, the associated branches have considerable difficulty achieving the expected irrigation efficiency based on the desired water requirements with low reliability (nearly 0.25). To keep all branches in the irrigation zone consistent in irrigation efficiency, the probabilistic-based water demands could be introduced via the proposed RA_IWD_Canal model with the desired reliability.

1. Introduction

Recently, irrigation water allocation systems could be grouped into schedule-based and object-based water supply [1]. According to the locations of the irrigation branches, the allocated irrigation water could be achieved from upstream to downstream in schedule-based systems [1,2]; on the contrary, within object-based systems, the irrigation water should be optimally allocated subject to the priorities given in advance [1]. The minimum water requirements are commonly given in the growing seasons to achieve the expected crop production among the above irrigation systems with various water allocation strategies [2,3,4]. Also, irrigation water demands frequently vary with the crop types [5]. However, if the upstream inflow is less than the desired irrigation water demands, the shortage risk of irrigation water might be induced. On the contrary, sufficient irrigation water over water demands could be supplied with high reliability. Therefore, introducing available water demands and requirements is vital for modern irrigation systems.

However, climate change significantly triggers the water-related shortage risk [6,7,8,9,10]; additionally, increasing industrial and domestic water frequently raises the complexity of irrigation water use due to the irrigation zone utilization [1,3]; it is more likely to lead to shortage risk to the irrigation regions lacking sufficient water supply subject to the existing water demands for the crop growing. To facilitate irrigating efficiency, the reliability of existing irrigation water demands should be necessarily quantified and evaluated to introduce reasonable ones, considering the effect of uncertainties in climatic and hydrological features and land use. In general, the irrigation water demands in the irrigation zones could be introduced by the deterministic models (e.g., CROPWAT model, Penman–Monteith method, SWAT model, and WBM model) subject to the crop types and climatic as well as the hydrological features in the irrigation zones [1,11,12,13,14,15,16,17]. For instance, Hussain et al. [16] employed an experiment to estimate the water requirement for crops during the growth seasons based on the difference in the water depths calculated via the deterministic equations with the change in evapotranspiration and soil moisture. Dang et al. [17] estimated the water requirements based on the difference in the historical surface runoff and evapotranspiration during crop growth. In addition, the irrigation water demands could be set based on the sources of the surface runoff and cultivation extents [2,18,19,20]. For example, Zhang et al. [9] simulated the surface runoff via the hydrological model with the observed hydrological data, such as rainfall, evapotranspiration, and soil moisture, as the boundary condition of the crop growth model to estimate the water demands. In addition to the crop type, hydrological data, and cultivated area, irrigation water demands could be introduced subject to the crop economic values [21,22].

Overall, as mentioned above, irrigation water demands were mainly introduced via the hydrological models with the crop-related factors (crop type and price as well as the cultivation area) and hydrological data (rainfall, evapotranspiration, and soil moisture). However, the resulting irrigation water demands were estimated without considering the temporal and space changes and induced uncertainties in the measurements of irrigation-related surface runoff. Also, in contrast with the zone-based irrigation water demands comprehensively provided, the branch-based ones within multi-canal irrigation zones are rarely introduced, so as to be approximated based on the corresponding cultivation extents to the branches [1,6]; namely, the irrigation water demands probably have uncertainty in space. Accordingly, the above uncertainties are highly likely to impact the availability of irrigation water demand, further reducing irrigation reliability. Nevertheless, a number of investigations have assessed irrigation reliability [13,14]; they mainly focused on evaluating the effect of rainfall variation on irrigation efficiency and reliability. Therefore, this study aims to develop an optimization and uncertainty analysis-derived model for estimating branch-based irrigation water demands and quantifying their quantiles with gauged historical surface runoffs within multi-canal irrigation zones, named the RA_IWD_Canal model; it is expected that the resulting water demand quantiles could not only describe the uncertainties in the estimated branch-based irrigation water demands due to surface-runoff variation but also apply to the reliability quantification of the zone-based and branch-based irrigation water demands of interest.

2. Methodology

The proposed RA_IWD_Canal model is mainly developed to estimate branch-based irrigation water demands, quantify uncertainties, and induce reliability in the multi-branch irrigation zone. Thus, within the proposed RA_IWD_Canal model, the optimization and uncertainty analysis should be configured with the observed surface runoff at the discharge gauges within the study area. Accordingly, the detailed model concepts and methods regarding the optimization and uncertainty analysis for the irrigation water could be addressed below.

2.1. Model Concept

The proposed RA_IWD_canal model could consist of three components: data collection, estimation of branch-based irrigation water demands, and uncertainty and reliability quantification of irrigation water demands. At the data collection step, in addition to the measured surface runoff at all discharge gauges and upstream inflow, the historical irrigation water demands introduced should be required in the model development and validation. After that, to estimate the branch-based water demands in the multi-canal irrigation zone via the proposed RA_IWD_Canal model, an optimization-based model for allocating the branch-based irrigation water supplies (OPA_IWS_Canal) [2] is adopted under consideration of the historical runoff data recorded at the discharge gauges. In detail, if the discharge gauge is installed at the branch, the corresponding measured surface runoff could be regarded as the branch-based irrigation water demand; alternatively, at the branch in the middle of two discharge gauges, its irrigation water demands could be estimated with the difference of surface runoff at two discharge gauges. In the case of several branches in the middle of two discharge gauges, their irrigation water demands could be achieved via the OPA_IWS_Canal model with the difference of gauged surface runoff.

Eventually, to quantify and assess the reliabilities of the specific irrigation water demands, the proposed RA_IWD_Canal model proceeds with the uncertainty analysis via weighted frequency curves [23], consisting of quantiles under the desired probabilities, established using the L-Moment approach, estimated via the L-Moment method; thus, the dispersion of estimated branch-based water demands could be quantified in terms of the L-mean and L-CV; accordingly, the exceedance probability of the specific water demands (e.g., introduced planning magnitudes) could be extrapolated from the resulting quantile curves, called overestimated risk as a reference to the reliability.

2.2. Optimization Estimation of Irrigation Water Demands

Within the optimization water allocation model (OPA_IWA_Canal model) proposed by Wu et al. [1], schedule-based water allocation is adopted to distribute the upstream inflow in the main canal to the target branches located from upstream to downstream; thus, the irrigation water supplied at the target branch (named the branch-based irrigation water supply) could be estimated by comparing the remaining canal-based water supply with the corresponding maximum delivered water volume:

$$Q_{S,IBL}=min\left\{Q_{S,Canal},Q_{MDF,IBL}\right\}$$

(1)

where $Q_{S,IBL}$ denotes the irrigation water supply obtained at the ith branch (called branch IBL); $Q_{S,IBL canal}$ stands for the water supply that could be provided from the main canal for the branch IBL; and $Q_{MDF,IBL}$ serves as the maximum delivered water supply at the target branch IBL. The above water supply provided from the main canal to the branch IBL $Q_{s,IBL,canal}$ could be calculated by the following equation under consideration of the water supplies received by the branches and water-intake hydraulic structures located both upstream of the canal-based irrigation zone:

$$Q_{S,IBL,canal}=Q_{IN,Canal-{\sum }_{I=1=1}^{IBL}{Q}_{S,IBL,canal}-Q_{S,HYST}}$$

(2)

in which $Q_{IN,Canal}$ stands for the resulting upstream inflow from the upstream boundary in the canal; $Q_{s,IBL,canal}$ serves as the branch-based irrigation water supply obtained at the upstream IBL branch; and $Q_{S,HYST}$ is the total water intake of the hydraulic structures upstream calculated using the following equation:

$$Q_{S,HYST}={Q_{D,HYST}\times \beta }_{IRR,HYST}$$

(3)

where $Q_{D,HYST}$ is the expected water demands of the hydraulic structures and ${\beta }_{IRR,HYST}$ stands for the corresponding water-intake reduction ratios of the hydraulic structures. Also, the maximum derived water volume at the target IBL branch ($Q_{MDF,IBL}$) could be computed as [20]

$$Q_{MDF,IBL}=Q_{D,IBL}\times {\mathsf{\alpha }}_{SR,IBL}$$

(4)

where $Q_{D,IBL}$ and ${\mathsf{\alpha }}_{MDR,IBL}$ denote the corresponding irrigation water demand at the branch IBL (named the branch-based irrigation water demand) and the maximum derived supply to the target branch (IBL), respectively. In reference to the branch-based irrigation water demand, it is more likely to be determined based on the type of the crop and expected cultivation extent; it is commonly introduced for all of the canal-based irrigation zones, comprising a group of trenches [20]. Accordingly, in this study, the branch-based irrigation water demand ($Q_{D,IBL}$) could be approximated subject to the canal-based irrigation water demand and the cultivation area of the branches as

$$Q_{D,IBL}=Q_{D,Canal}\times \frac{{CA}_{IBL}}{{CA}_{Canal}}$$

(5)

where $Q_{D,Canal}$ is the planning irrigation water demand for the canal-based zone; and ${CA}_{IBL}$ and ${CA}_{Canal}$ account for the cultivation extents of the target i^th branch (IBL) and canal-based zone, respectively.

Within the OPA_IWD_Canal model, achieving the optimal branch-based irrigation water supply ($Q_{S,IBL}$) and demand ($Q_{D,IBL}$), the branch-based supplying satisfaction index (${\mathrm{S}\mathrm{I}}_{IBL}$) is required to evaluate the irrigation efficiency at the branch IBL as [2,20,24]

$${\mathrm{S}\mathrm{I}}_{IBL}=\frac{Q_{S,IBL}}{Q_{D,IBL}}$$

(6)

in which $Q_{S,IBL}$ and $Q_{D,IBL}$ account for the branch-based irrigation water supply and demand, respectively; in the case of ${\mathrm{S}\mathrm{I}}_{IBL}$ approaching the expected value (e.g., 1.0), the optimal water supply at the target branch is achieved with an acceptable satisfaction index ${\mathrm{S}\mathrm{I}}_{IBL}$ given a desired water demand. The detailed concepts of the OPA_IWS_Canal model can be referred to Wu’s investigation [2].

2.3. Uncertainty and Reliability Quantification of Estimated Irrigation Water Demands

Uncertainties in the hydrological data and relevant deterministic models are frequently caused by a lack of information on hydrologic-related phenomena, which might induce the failure risk of the expected performance regarding the hydraulic structures. In general, the uncertainties could be described in terms of the statistical moments of various orders, including the mean, variance, and coefficients of skewness as well as kurtosis; also, the detailed information on the data and model inputs as well as the outputs could refer to the quantiles under consideration of the various occurrence probabilities. However, the resulting quantiles should be calculated via the identified best-of-fit probability density functions (PDF), which significantly change with the goodness-of-fit criteria adopted [17]. To reduce the uncertainties attributed to the selection of the goodness-of-fit criteria, Wu et al. [23] presented a weighted frequency curve method to produce quantities of the desired occurrence probabilities.

Apart from the uncertainty due to PDF selection, the PDF parameters are commonly calibrated by the conventional produce-moment approach; however, the worse bias of the resulting statistical properties and quantiles might be induced with the moment orders; thus, Hosking [25] proposed the L-moments to significantly reduce the above bias attributed to the orders of statistical moments as to provide more accurate quantiles. Therefore, within the proposed RA_IWD_Canal model, the weighted frequency curve approach with the L-moment could be employed in the uncertainty and reliability quantification of the estimated branch-based irrigation water demands. Thus, within the proposed RA_IWD_Canal model, the reliability of the estimated irrigation water demand could be represented in terms of the exceedance probability concerning the specific demand, which could be defined as [2,14]

$$\mathrm{R}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}=P_r(W_D\ge w_d)$$

(7)

where $W_D$ accounts for the quantiles in the weighted frequency curve; and $w_d$ serves as the specific demand, such as the estimated branch-based irrigation water demands or the introduced planning irrigation water demand. The concept regarding the weighted frequency curves is briefly introduced as follows.

To reduce uncertainty in the quantiles attributed to the inappropriate probability distributions selected, Tung [26] proposed a weighted frequency curve (WFC) method by collaborating the multiple probability distributions; when deriving the WFC model, the commonly used probability distributions are considered, including the normal and log-normal distributions, Pearson and log-Pearson distributions, Gamma distribution, generalized extreme value distribution, generalized Pareto distribution, and generalized logistic distribution. In detail, the above-considered probability distributions are assumed to be suitable for estimating the quantiles of given probabilities, which are calculated via the plotting position formula. After that, the weighted quantiles can be obtained by the following equation:

$$X_{p,w}=\sum _{i=1}^M\left(w_i\times X_{p,i}\right)$$

(8)

where $X_{p,w}$ accounts for the weighted quantiles of a given probability (p); $X_{p,i}$ and $w_i$stand for the quantiles of a given probability (p) and the corresponding weighted factors under the ith probability distribution concerned, respectively. Note that the weighted factors of the candidate probability distributions are calculated based on their fitness performance in terms of the mean square error ($MS{E}_i$) as

$$MS{E}_i=\frac{1}{n}{{\displaystyle \sum }}_{j=1}^n(X_{\left(j\right)}-Y_{\left(i,j\right)}{)}^2$$

(9)

in which n denotes as the sample size; $X_{\left(j\right)}$ and $Y_{\left(i,j\right)}$ and serve as the ascending sample data and corresponding quantile coming from the ith candidate probability distribution. Eventually, the resulting weighted factors of the candidate probability distributions are computed via the following equation:

$$w_i=\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$MS{E}_i$}\right.}{{\sum }_{i=1}^n\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$MS{E}_i$}\right.\right)}$$

(10)

where $w_i$ is treated as the weighted factor of the ith candidate probability distirouion.

In total, the quantile curves of the estimated branch-based irrigation water demands via the OPA_IWD_Canal model can be established through the weighted frequency curve methods to proceed with the reliability quantification of the specific irrigation water demands within the proposed RA_IWD_Canal model. In particular, the parameter calibration of the candidate probability distributions should be carried out via the L-moment method with a group of estimated branch-based irrigation water demands. Also, the uncertainties of the estimated branch-based irrigation water demands could be quantified using L-moment ratios of the first four orders as

$$L\text{-}CV: {\tau }_2=\frac{{\lambda }_2}{{\lambda }_1}$$

(11)

$$L\text{-}\mathit{Skewness}: {\tau }_2=\frac{{\lambda }_3}{{\lambda }_2}$$

(12)

$$L\text{-}\mathit{Kurtosis}: {\tau }_2=\frac{{\lambda }_4}{{\lambda }_2}$$

(13)

where ${\lambda }_i$ stands for the ith order L-moment, which could be obtained via the following equation proposed by Hosking [18]:

$${\lambda }_r=\frac{1}{r}{{\displaystyle \sum }}_{k=1}^{r-1}\left[(-1)\left(\begin{array}{c}r-1\\ k\end{array}\right)E\left(X_{r-k:r}\right)\right],r=1,2,\dots$$

(14)

where $E\left(X_{r-k:r}\right)$ denotes the expected value of the kth ascending sample datum among the r sample data extracted from the population.

2.4. Model Framework

To summarize the relevant concepts, the proposed RA_IWD_Canal model can be configured using optimal irrigation water allocation and uncertainty quantification methods. Therefore, developing the proposed RA_IWD_Canal model could refer to the following steps:

Step [1]

Collecting information on the irrigation system, including the system structure, cultivation extents, and the number and location of the irrigation branches, discharge gauges, and water-intake hydraulic structures; geometric and hydrologic data are also necessary to apply to model development, upstream inflow, gauged surface runoff, and irrigation water demand planning.

Step [2]

Carrying out the uncertainty analysis to quantify the stochastic properties of the gauged surface runoff and planning irrigation water demands.

Step [3]

Calculating the differences in the measured surface runoffs among the discharge gauges.

Step [4]

Grouping the irrigation branches into various clusters based on their locations compared with the spots of the discharge gauges.

Step [5]

The observed surface runoff is treated as the estimated water demand at the branch with the single discharge gauge.

Step [6]

The difference in the gauged surface runoffs is the estimated water demands in the cluster with a single irrigation branch.

Step [7]

Estimating the optimal water supplies based on the water demand at more than one irrigation branch within the cluster via the OPA_IWS model with the difference in the corresponding gauged surface runoffs.

Step [8]

Quantifying the uncertainties in the estimations of the branch-based water demands to calculate their corresponding quantiles under the desired probabilities.

Step [9]

Quantifying the corresponding reliabilities to the existing water zone-based and branch-based water demands and serve the probabilistic-based water demand estimates under a desired reliability as the introduced ones. The above model development framework could refer to Figure 1.

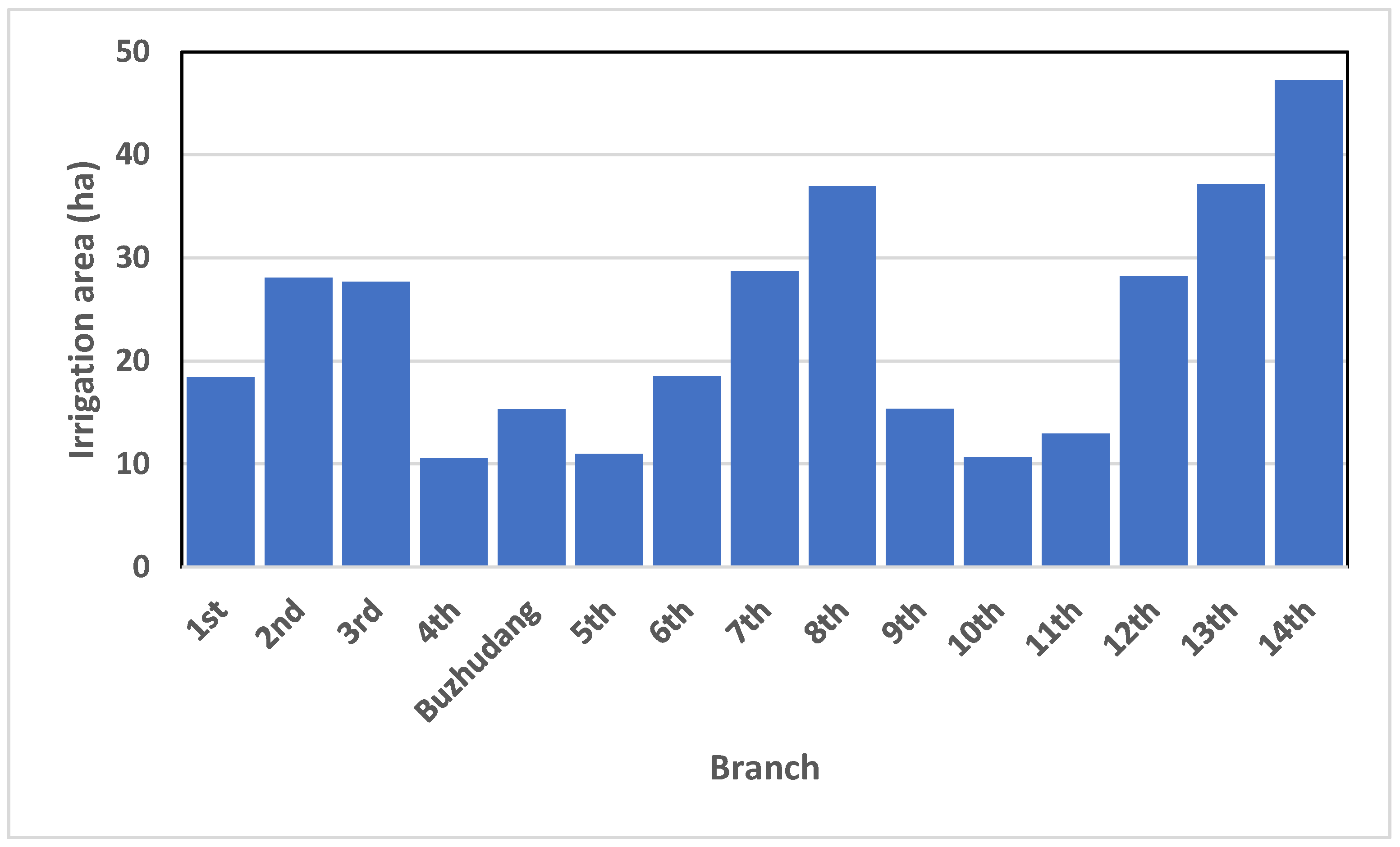
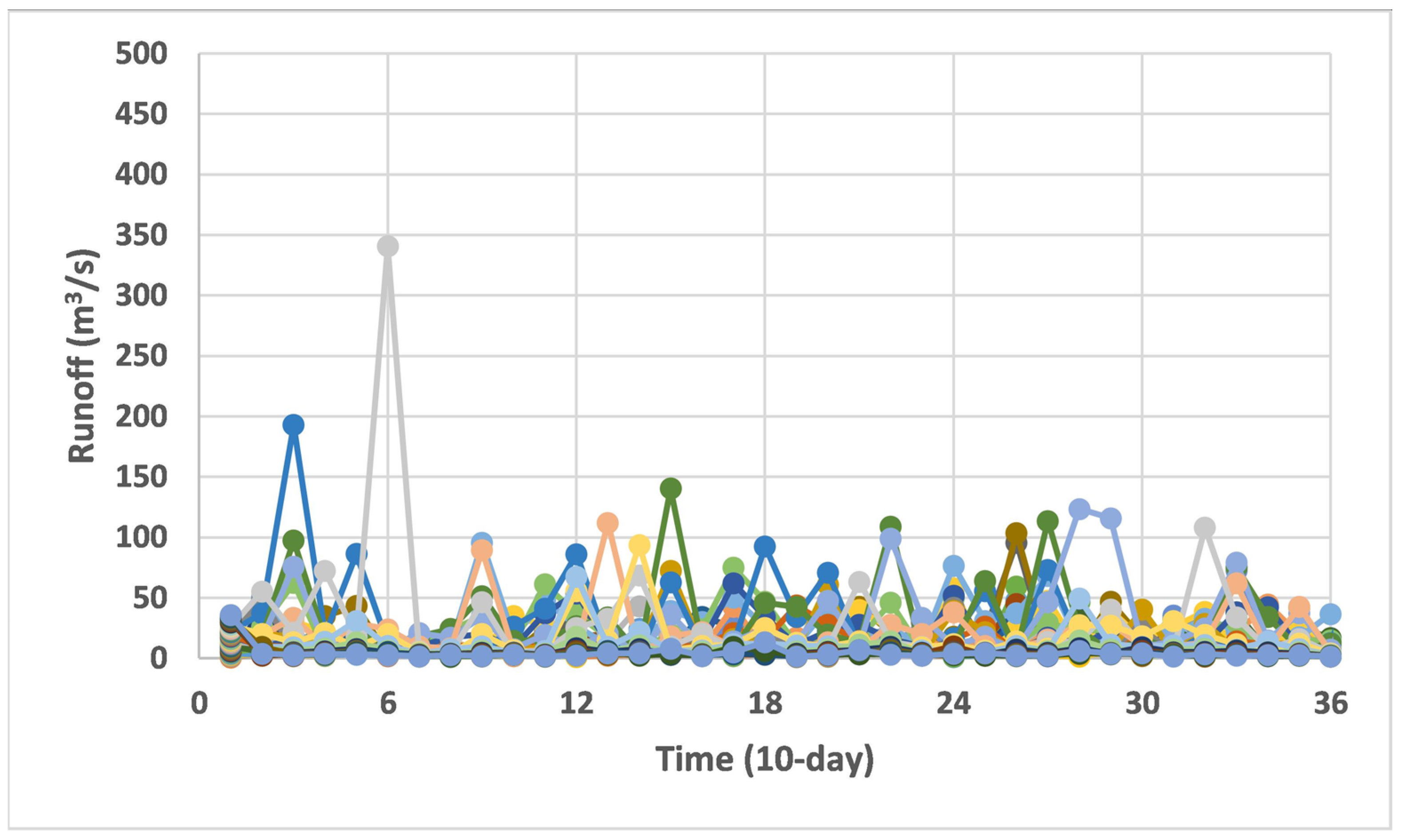
3. Study Area and Data

To express the development and application of the proposed RA_IWD_Canal model for estimating branch-based irrigation water demands, a multi-branch irrigation zone, Zhudong Canal irrigation zone, is selected in this study. The Zhudong Canal irrigation zone, whose cultivation extent is nearly 800 ha, is located in Northern Taiwan (see Figure 2). The main crop is rice, which grows from the middle of February to the end of November. Within the study area, 15 branches (BL1-BL14 and Bazhuang branch), whose irrigation extents vary from 10 ha to 50 ha (see Figure 3), as well as the two water intake structures, including Baoshan Reservoir located between the 7^th seventh and 8^th eighth (i.e., BL7 and BL8) branches and the Yuandon treatment plant situated between the 2^nd nd and 3^rd branches.; their detailed physical characteristics and operational rules could be referred to in Wu’s investigation [2]. Also, to effectively capture the spatial and temporal changes in the irrigation water in the Zhudong Canal zone, 15 discharge gauges (G1–G15) were set up.

The Zhudong canal zone supplied the irrigation water converted from upstream inflow at the Shanping Weir. Namely, the upstream inflow mainly comes from the Shanping River, whose historical 10-day surface runoff at the Shaning water-level gauge in 1959–2022 changes from 1 m³/s to 400 m³/s (see Figure 4). In addition, to effectively measure the spatial change of the surface runoff in the Zhudong Canal zone, 15 discharge gauges were installed from upstream to downstream in the Zhudong Canal zone to measure the surface runoff, as shown in Figure 2. Among 15 discharge gauges, the gauges G2, G3, G6, G8, G10, and G11 are located in the main channel, and the remaining gauges are set up in the branches, which could directly measure water intake to the branches. Thus, given Figure 5, the 10-day surface runoffs at 15 discharge gauges were measured from 2019 to 2022, indicating that the observed surface runoff at the 4^th to 33^rd 10-day period (on average 0.5 m³/s) markedly exceeds the observations at the remaining 10-day periods (nearly 0.14 m³/s); in particular, at the 3^rd, 5^th, 7^th and 9^th discharge gauges, their observed surface runoffs are considerably over observations at the remaining gauges by 63%; this indicates that the observations of surface runoff within the study area (Zhudong Canal zone) are associated with a significant variation in time and space. Moreover, the 4^th to 33^rd 10-day periods could be regarded as the rainy seasons, with the remaining 10-day period being treated as the drought season. Therefore, this study focuses on the uncertainty quantification and reliability assessment of the irrigation water demands in the rainy season (i.e., 4^th–33^rd 10-day period).

In general, ahead of supplying irrigation water, the planning irrigation water demands should be given as the criterion for evaluating the irrigation performance [1,15]. Subsequently, the irrigation water supplies and requirements are represented in 10-day periods (Wu et al., 2023). Therefore, the planning irrigation water demands at various 10-day periods in the Zhudong Canal zone from 2015 to 2024 were introduced for evaluating irrigation performance as shown in Figure 6 (roughly from 0.85 to 1.5 m³/s); this unveils the intro irrigation water demands in the Zhudong Canal zone reach the maximum (approximately 1.8 m³/s) at the 23^rd 10-day periods. Note that within the Zhudong Canal zone, the third branch (Su-Qi-Lin) was also given the planning irrigation water demand as shown in Figure 6b with the significantly less introduced ones (about 0.11 m³/s).

4. Results and Discussion

Regarding the development framework of the RA_IWD_Canal model (see Figure 1), the irrigation-related data in the study area (Zhudong Canal zone) should be collected in advance. Then, the proposed RA_IWD_Canal model could estimate the branch-based irrigation water demands, quantify their uncertainties, and include reliabilities. The detailed model development and evaluation of application results can be found below.

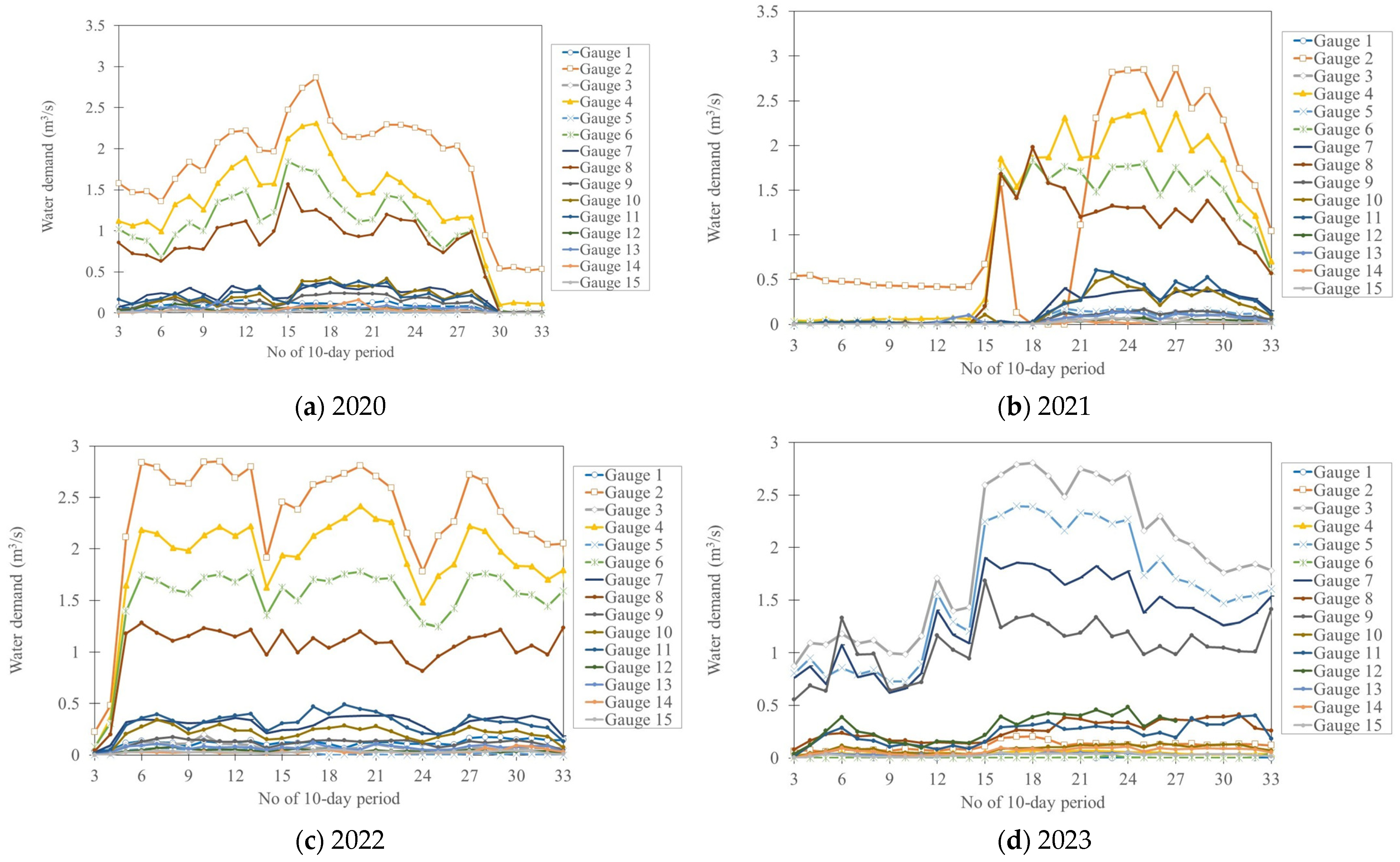
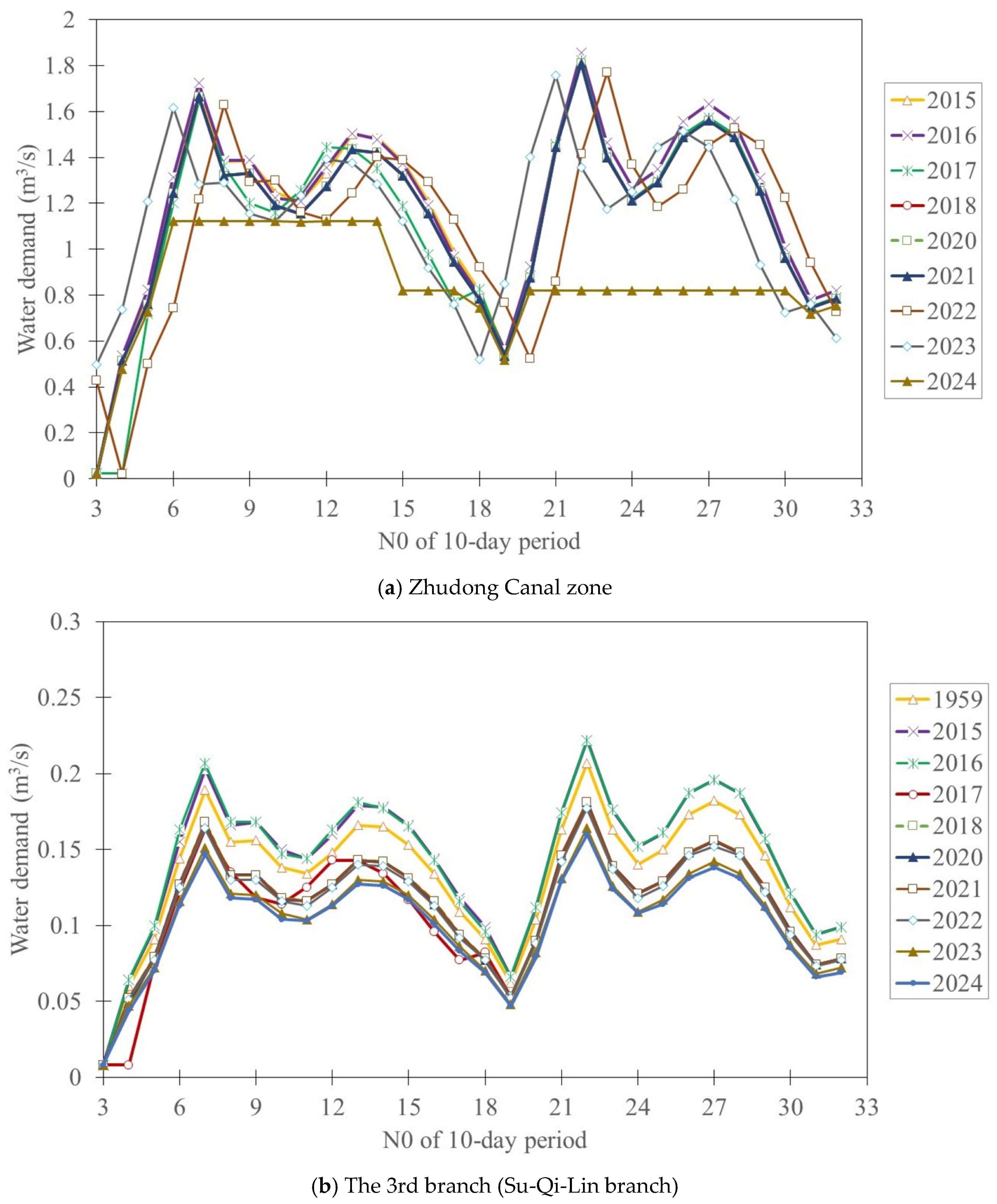
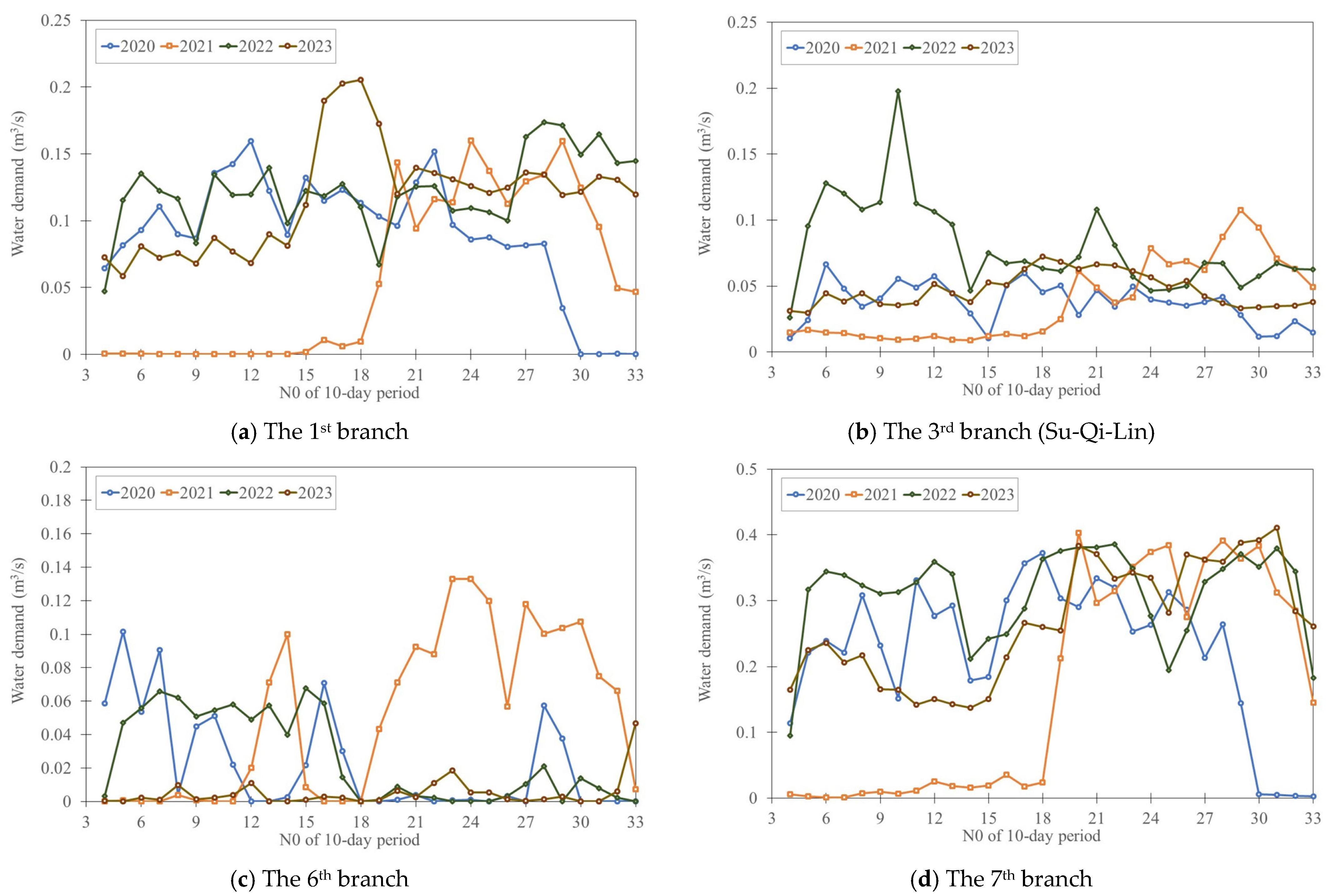
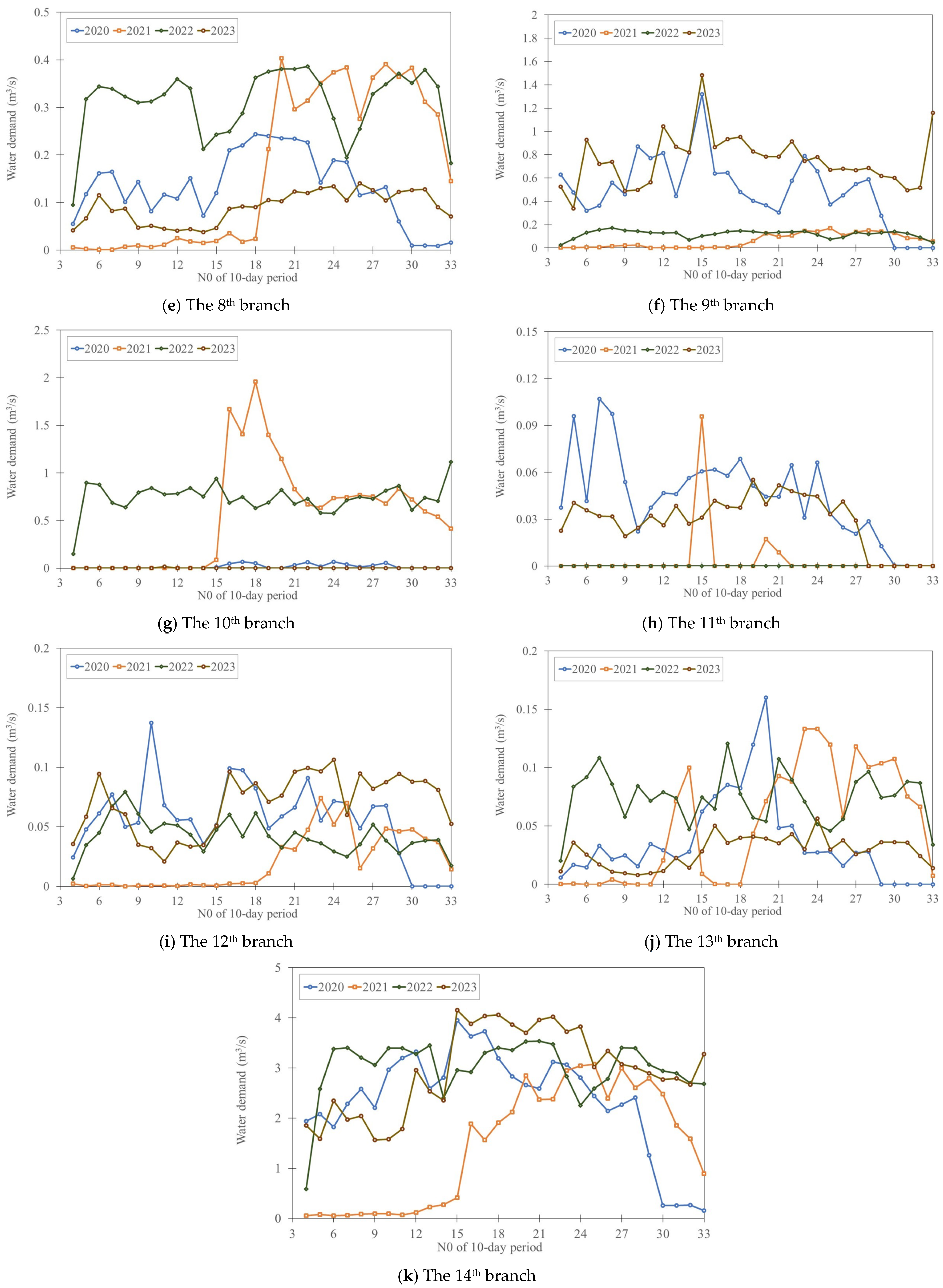
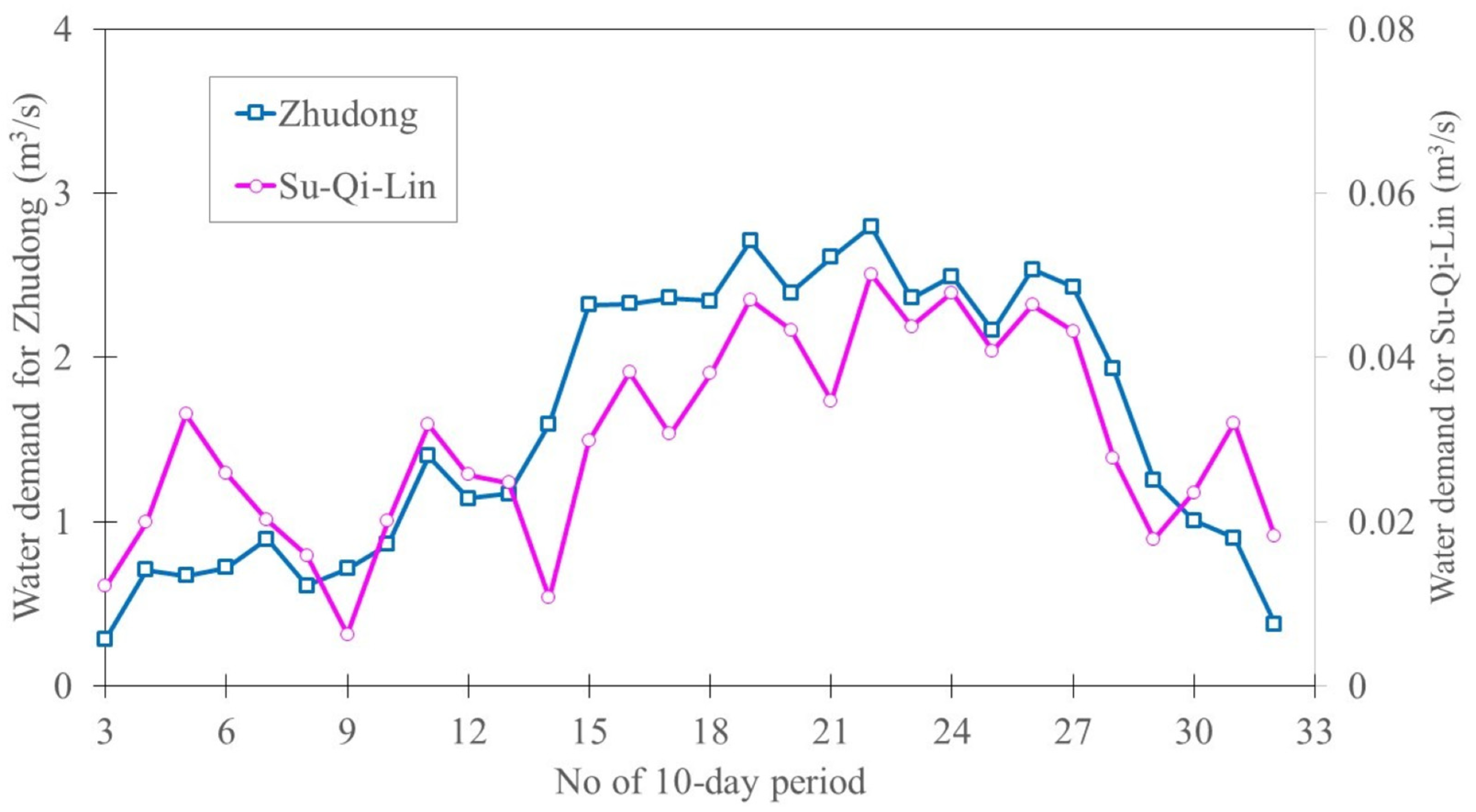
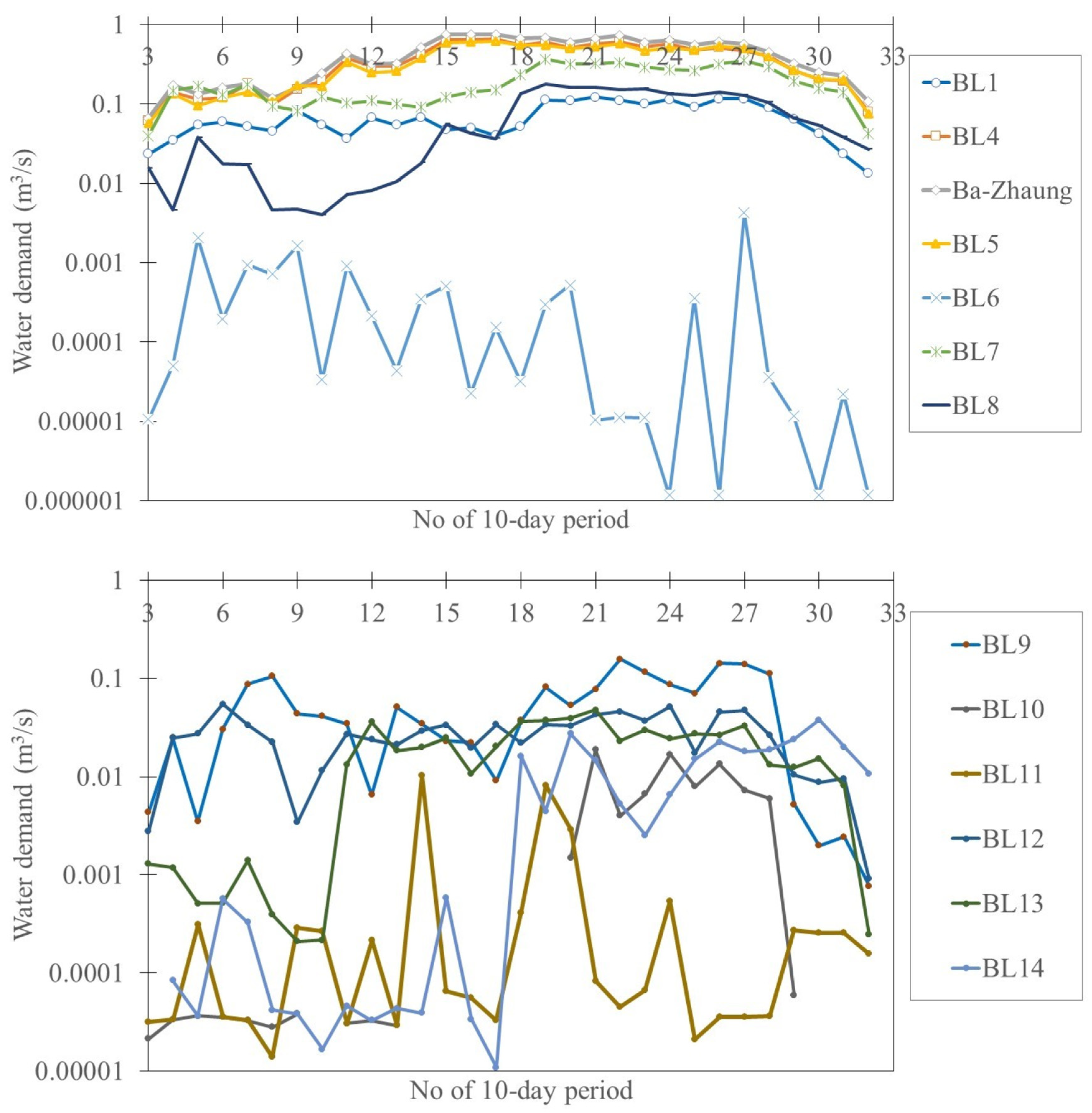
4.1. Establishment of the Relationship between the Branch-Based Water Demand and Gauged Runoff

Relying on Figure 1, before developing the proposed RA_IWD_Canal model, the irrigation branches should be grouped into the desired cluster based on the locations of the irrigation branches and discharge gauges. As shown in Figure 2, a group of discharge gauges are installed at the 1^st, 6^th, and 8^th branches and from the 11^th to 14^th branches; their irrigation water demands could be given the measurements of gauged surface runoff. In addition, the irrigation water demands at the 9^th and 10^th branches could be achieved by calculating the difference in the observed surface runoffs at the two discharge gauges as

$$Q_{D,9th}=Q_{G,8th}-Q_{D,8th}$$

(15)

$$Q_{D,10th}=Q_{G,10th}-Q_{G,11th}$$

(16)

where $Q_{D,9th}$ and $Q_{D,10th}$ account for the estimated irrigation water demands at the 9th and 10th branches, respectively; and $Q_{G,8th}$,$Q_{G,10th}$ and $Q_{G,11th}$ serve as the observed surface runoffs at the 8^th, 10^th, and 11^th water-level gauges. Thus, estimating the irrigation water demands directly with the measurements of gauged surface runoff is called a data-derived approach. Regarding the remaining branches (i.e., the 4^th branch, fifth branch, and the Ba-Zhuang branches), their irrigation water demands should be obtained via the OPA_IWS_Canal model with the difference in the gauged surface runoffs at the 4^th and 5^th discharge gauges (i.e., $Q_{G,4th}$ and $Q_{G,5th}$), named the model-derived approach. In summary,

Table 1. Formulae for estimating the branch-based irrigation water demands via the proposed RA_IWD_Canal model.

No of Branch	Gauged Surface Runoff Is Used	Formula
$\mathrm{The} 1^{\mathrm{st}}\mathrm{branch} Q_{D,1st}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,1st}$	$Q_{D,1st}$ = $Q_{G,1st}$
$\mathrm{The} 3^{\mathrm{rd}} \mathrm{branch} \left(\text{Shu-Qi-Lin}\right) Q_{D,3rd}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,3rd}$	$Q_{D,3rd}$ = $Q_{G,3rd}$
$\mathrm{The} 4^{\mathrm{th}} \mathrm{branch} Q_{D,4th}$	$\mathrm{Difference} \mathrm{in} \mathrm{gauged} \mathrm{discharges} Q_{G,4th}$ and $Q_{G,5th}$	OPA_IWS_Canal model
$\mathrm{The} 5^{\mathrm{th}} \mathrm{branch} Q_{D,5th}$
$\mathrm{The} \mathrm{branch} \text{Ba-Zhuang} Q_{D,BZ}$
$\mathrm{The} 6^{\mathrm{th}} \mathrm{branch} Q_{D,6th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,3rd}$	$Q_{D,3rd}$ = $Q_{G,3rd}$
$\mathrm{The} 7^{\mathrm{th}} \mathrm{branch} Q_{D,7th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,7th}$	$Q_{D,7th}$ = $Q_{G,7th}$
$\mathrm{The} 8^{\mathrm{th}} \mathrm{branch} Q_{D,8th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,9th}$	$Q_{D,8th}$ = $Q_{G,9th}$
$\mathrm{The} 9^{\mathrm{th}} \mathrm{branch} Q_{D,9th}$	$\mathrm{Difference} \mathrm{in} \mathrm{gauged} \mathrm{discharges} Q_{G,8th}$ and $Q_{G,9th}$	$Q_{D,7th}$ = $Q_{G,8th}$ − $Q_{G,9th}$
$\mathrm{The} {10}^{\mathrm{th}} \mathrm{branch} Q_{D,10th}$	$\mathrm{Difference} \mathrm{in} \mathrm{gauged} \mathrm{discharges} Q_{G,10th}$ and $Q_{G,11th}$	$Q_{D,10th}$ = $Q_{G,10th}$ − $Q_{G,11h}$
$\mathrm{The} {11}^{\mathrm{th}} \mathrm{branch} Q_{D,11th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,12th}$	$Q_{D,11th}$ = $Q_{G,12th}$
$\mathrm{The} {12}^{th} \mathrm{branch} Q_{D,12th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,13th}$	$Q_{D,12th}$ = $Q_{G,13th}$
$\mathrm{The} {13}^{\mathrm{th}} \mathrm{branch} Q_{D,13th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,14th}$	$Q_{D,13th}$ = $Q_{G,14th}$
$\mathrm{The} {14}^{\mathrm{th}} \mathrm{branch} Q_{D,14th}$	$\mathrm{Gauged} \mathrm{discharge} Q_{G,15th}$	$Q_{D,14th}$ = $Q_{G,7th}$

lists the formulas to estimate the irrigation water demands at all branches in the study area. Flowing the estimations of the branch-based irrigation water demands, the zone-based water demand ($Q_{D,zone}$) could be estimated with the water demands at all branches, excluding the 3^rd branch (i.e., Su-Qi-Lin), which is given separately, as

$$Q_{D,zone}={\sum }_{i=1,i\ne 3}^{14}{Q}_{D,i}$$

(17)

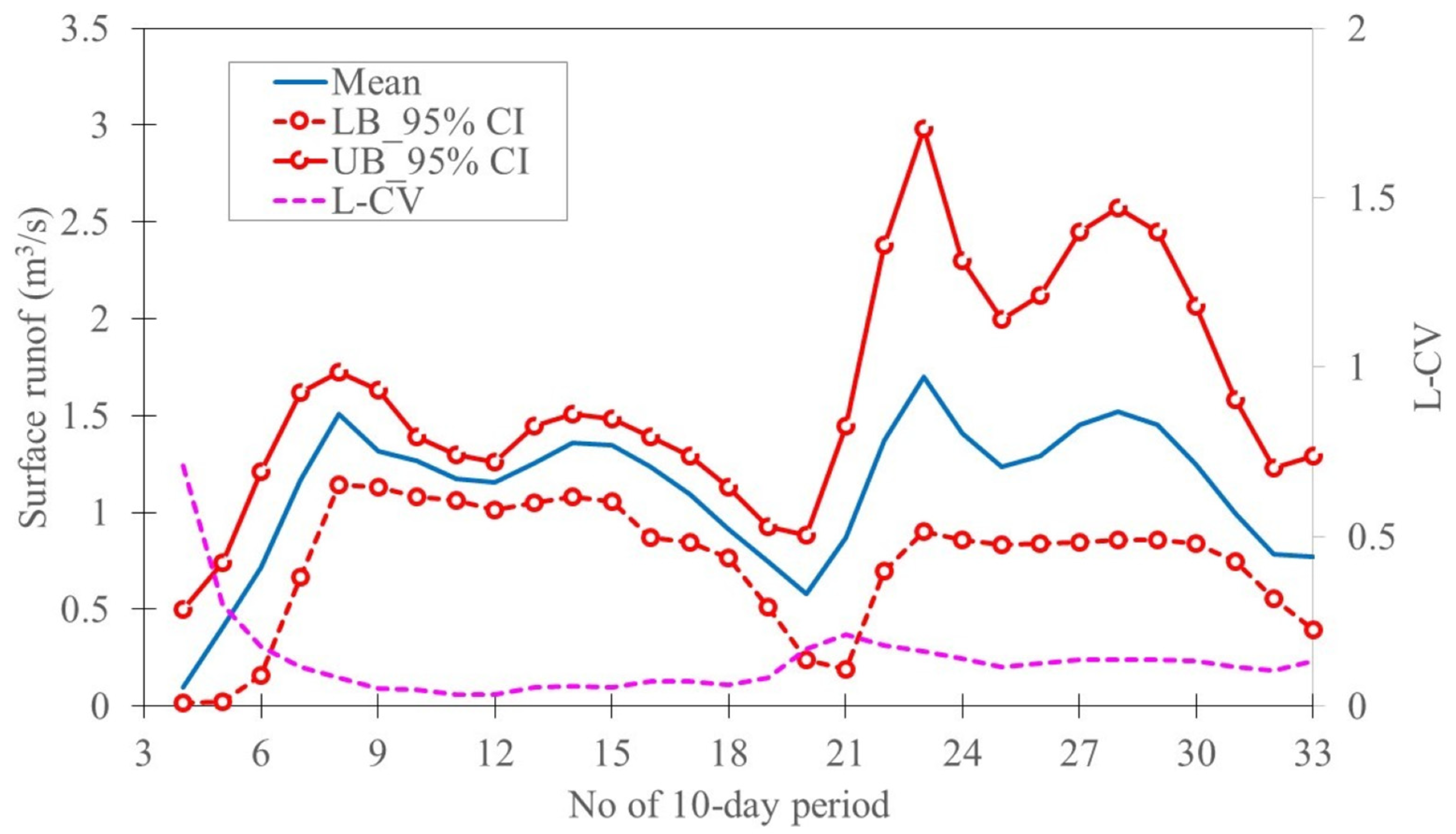
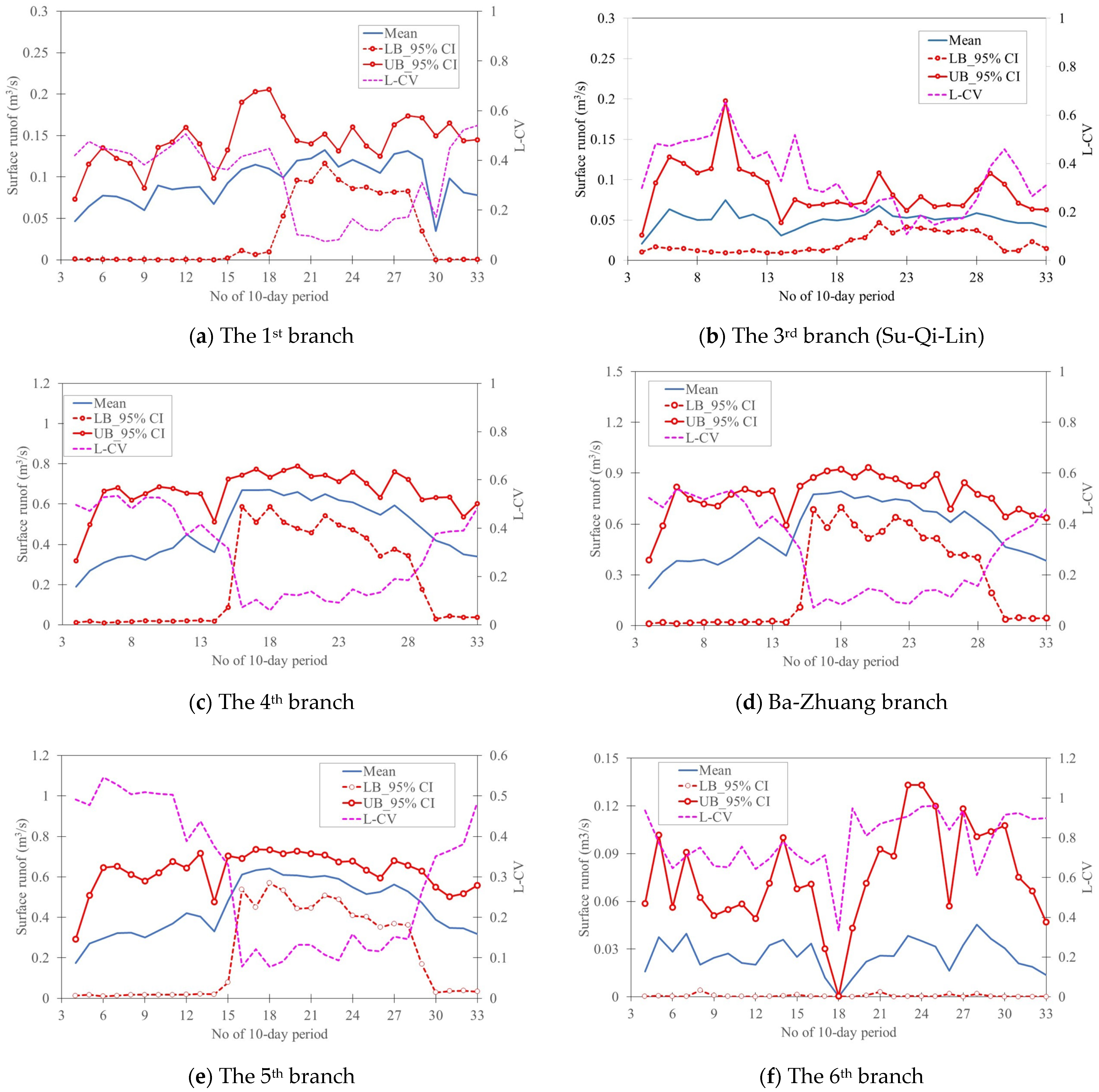
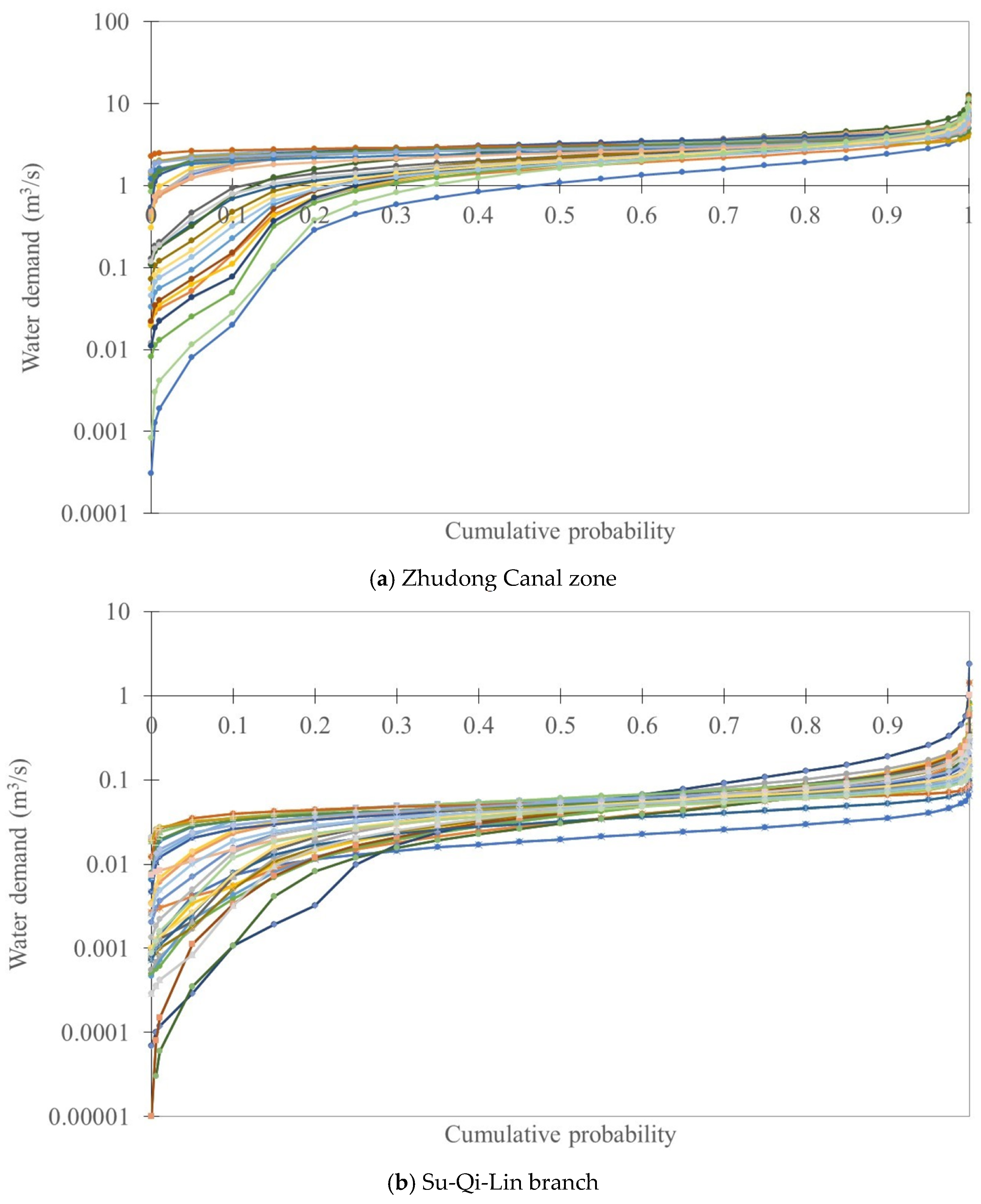
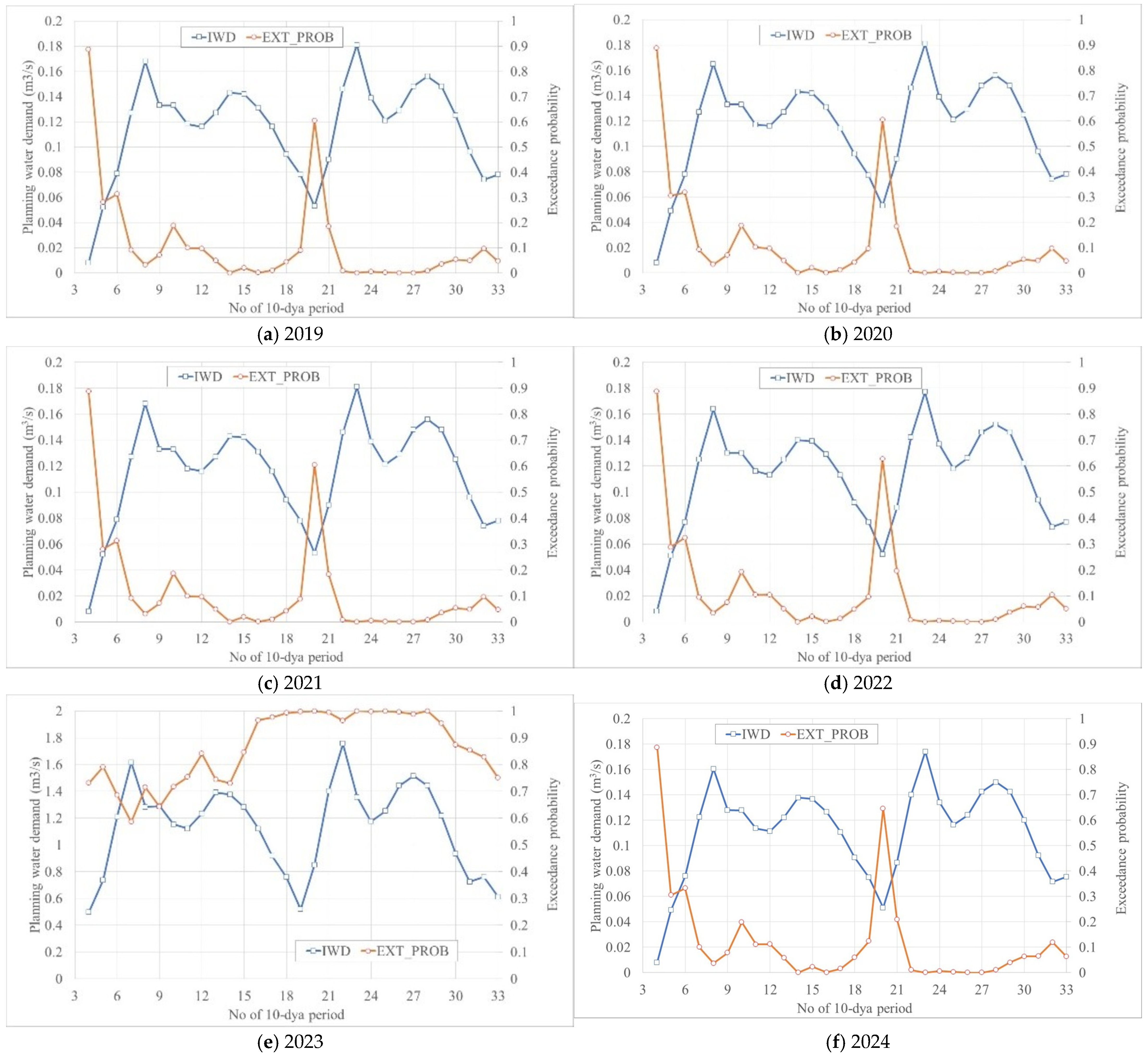
4.2. Uncertainty Quantification End Assessment of Introduced Planning Irrigation Water Demands

Before carrying out the reliability analysis for the branch-based irrigation water demands in the study area, the uncertainties in the officially-introduced water demands for the study area (Zhudong irrigation zone) and the 3rd branch (Su-Qi-Lin) (see Figure 5) should be quantified; Figure 7 shows that their L-moment ratios at 30 10-day periods are calculated via the proposed RA_IWD_Canal model, as shown in Figure 7 and Figure 8, in which the corresponding 95% confidence intervals could also be found. Observed from Figure 7, the mean values of introduced planning irrigation water demands for the Zhuang Canal zone vary from 0.02 m³/s to 1.7 m³/s, with a noticeable L-CV value (on average, 0.13) and a large confidence interval of around 0.8 m³/s; in detail, the 7^th–33^rd 10-day periods were given high irrigation water demands, on average from 0.8 m³/s to 1.5 m³/s. In summary, the introduced planning irrigation water demands are more likely to have temporal variations in the various 10-day periods; this indicates that the current planning water demands possibly hardly reflect the variations attributed to climate change and extreme events. A similar varying trend could be referred to in Figure 8, showing that the planning water demands at the 3^rd branch (Su-Qi-Lin) have a low average of 1.2 m³/s with a considerable L-CV of around 0.1 m³/s.

Therefore, by proceeding with the proposed RA_IWD_Canal model, it could be known that finalizing the irrigation water demands associated with the desired uncertainties is necessary in response to the variations due to the temporal and spatial change in hydrological features. Accordingly, the proposed RA_IWD_Canal model is supposed to proceed with quantifying the reliabilities of introduced irrigation water demands subject to the uncertainties in the surface runoff-related irrigation water supplies.

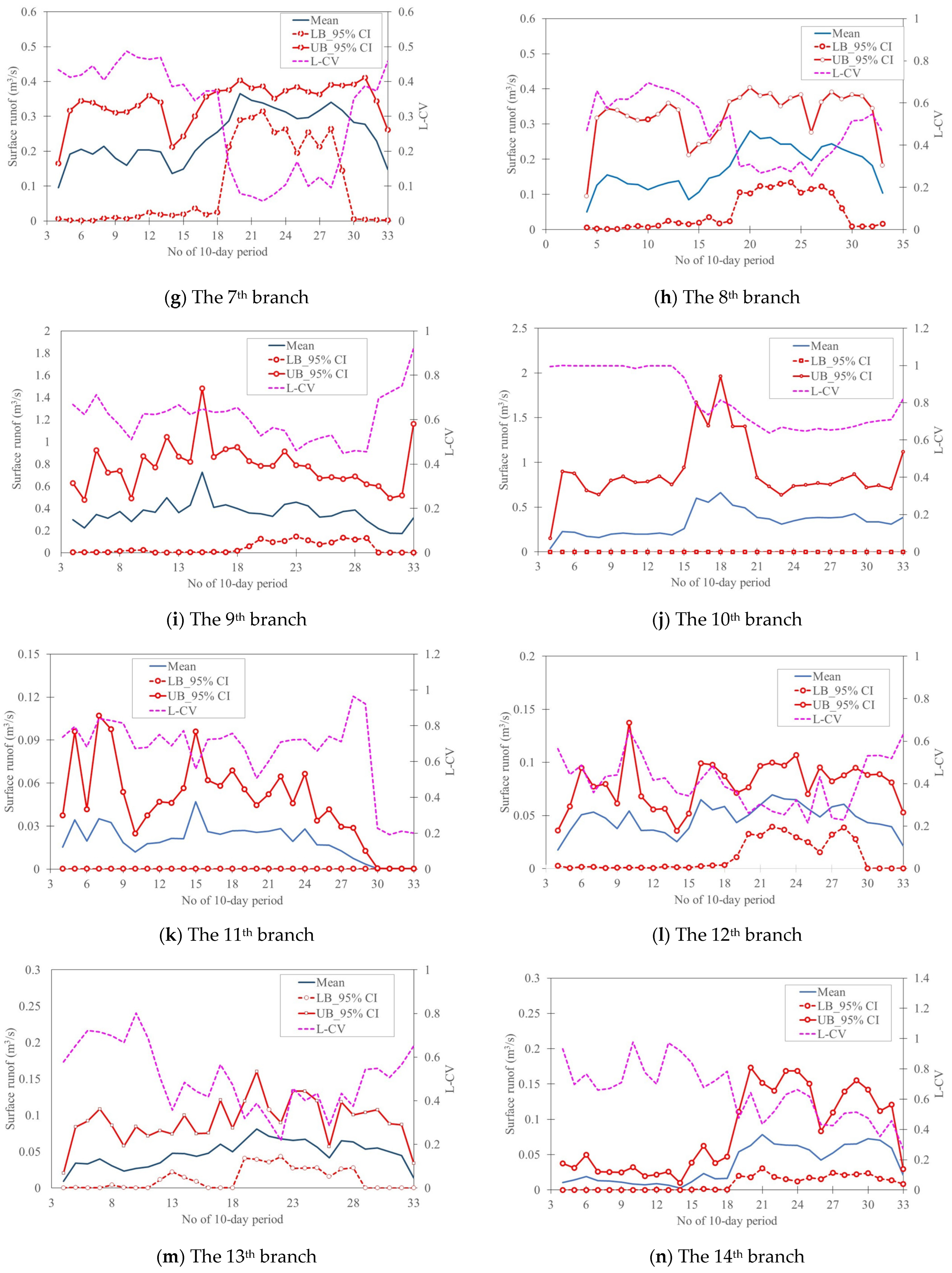
4.3. Uncertainty Quantification and Assessment of Branch-Based Irrigation Water Demands

Concerning Table 1, for a group of the branches in the study area, their corresponding irrigation water demands could be obtained via the data-derived approach with the gauged surface runoffs as shown in Figure 9; alternatively, the branch-based irrigation water demands (i.e., the four and fifth as well as the Ba-Zhang branches) are estimated using the OPA_IWS_Canal model, with a given supplying satisfaction index (see Equation (6)) (i.e., ${\mathrm{S}\mathrm{I}}_{IBL}$ = 1.0) set up in the proposed RA_IWD_Canal model (see Figure 10). Comparing the results from Figure 9 and Figure 10, the data-derived branch-based water demands exhibit a considerable change in time; for example, concerning the 3^rd branch (i.e., Su-Qi-Lin), the resulting irrigation water demands have a significant change, roughly from 0.4 m³/s to 0.8 m³/s in 2020–2023. Nevertheless, the above branches are nearly consistent with the spatial distributions of the data-derived irrigation water demands markedly; for instance, in 2023, the more significant estimated water demands (around from 0.03 m³/s to 0.3 m³/s) could be found at the 18^th–30^th 10-day periods. Instead, the 4^th, 5^th, and Ba-Zhuang branches include a similar spatial and temporal varying trend in the model-derived irrigation water demands; for example, in 2000, their estimated irrigation water demands significantly increase from 0.4 to 0.7, which reach the maximum at the 14^th–17^th 10-day periods and then gradually decline to 0.03 at the 30^th–33^rd 10-day periods; as comparable to Figure 5, the above varying trend in time resembles the change in the difference in the gauged discharges at the 4^th and 5^th discharge gauges.

Using the proposed RA_IWD_Canal model, the uncertainties of estimated branch-based irrigation water demands could be represented in terms of the L-moment ratio calculated, as shown in Figure 11. It can be seen that the estimated branch-based irrigation water demands during the rainy seasons (4^th–33^rd 10-day periods) display a considerable variation in space due to a large L-CV (on average, from 0.2 to 0.8). It concludes that branch-based irrigation water demands noticeably rely on the measurements of the gauged surface runoff. By doing so, the variations in the observed surface runoff significantly lead to uncertainties in the estimations of the branch-based branches.

Altogether, the regulation of the branch-based irrigation water demands should be considered based not only on irrigation features (e.g., cultivation extents and crop types), but also on the change of measured surface runoff supplied in time and space. That is to say, the discharge gauges comprehensively installed within the irrigation zones play a vital role in accurately and reliably estimating the irrigation water requirements with high spatial resolution.

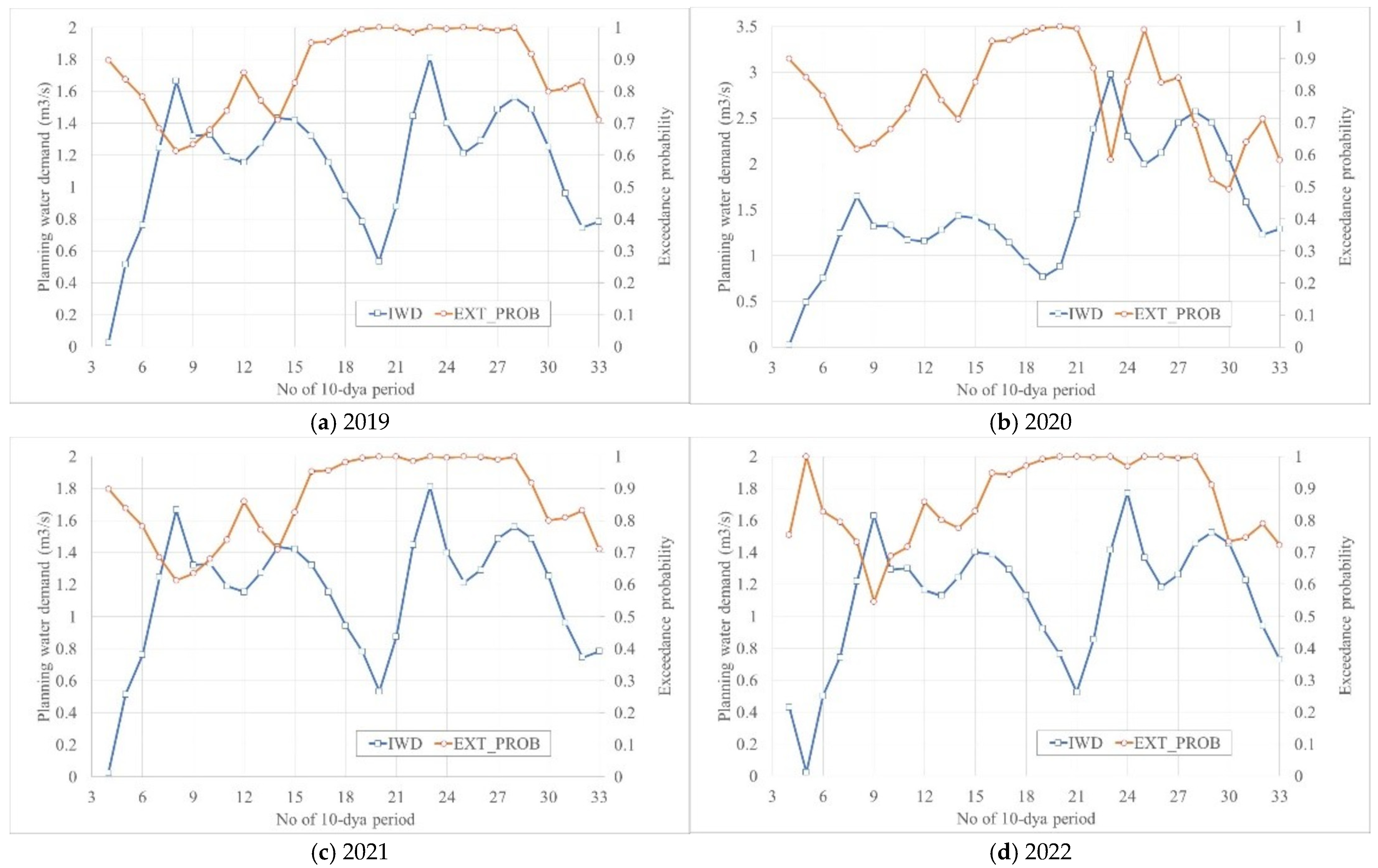
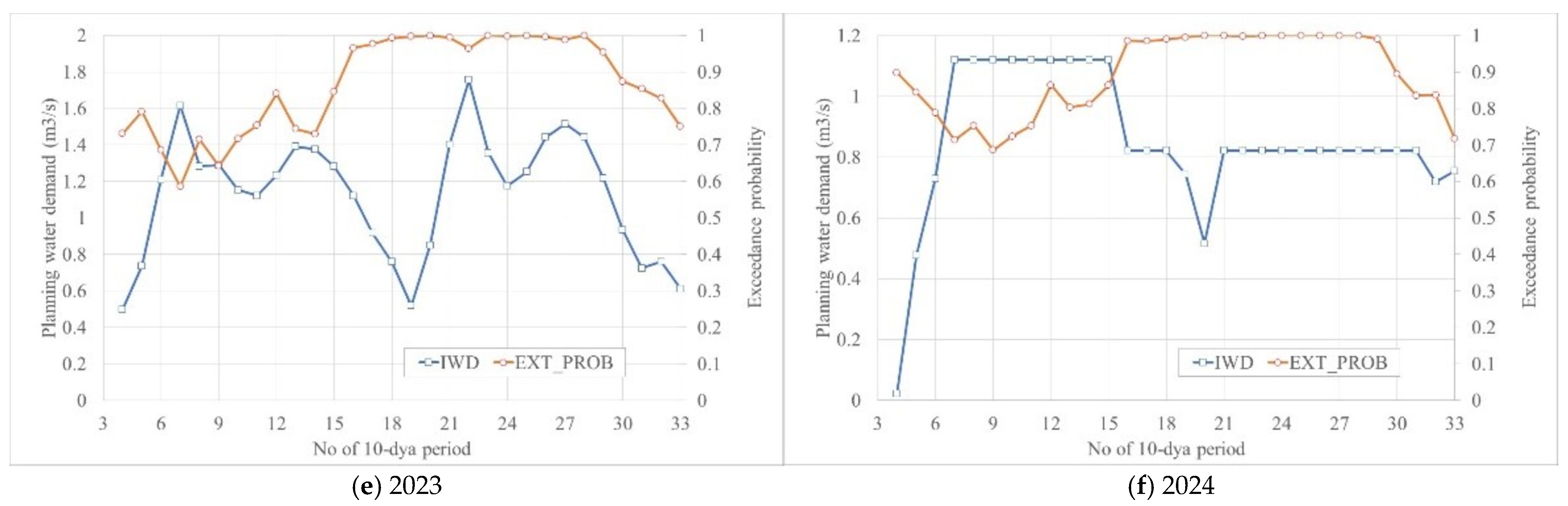
4.4. Reliability Quantification of Irrigation Water Demands

As well as estimating the branch-based irrigation water demands, the proposed RA_IWD_Canal model could be applied in the reliability analysis for the introduced planning irrigation water demand by establishing the weighted quantile curves, consisting of the quantiles under the desired probability. Since the two planning irrigation water demands were issued for the study area, including the Zhudong Canal zone and the 3^rd branch (Su-Qi-Lin), the irrigation water demands for the Zhudong Canal zone should be achieved by summing up all the resulting branch-based ones via Equation (17). Figure 12 shows the estimated irrigation water demands for the Zhudong Canal zone at the 30 10-day periods in 2020–2024, indicating that the spatial varying trend of the one-based irrigation water demands significantly change with time (year); in detail, the more significant water demands (about from 2 m³/s to 4 m³/s) could be observed at the 4^th–20^th 10-day period in 2020 in contrast with results at the 20^th and 30^th periods, varying from 1.8 m³/s to 2 m³/s. This unveils that considerable spatial and temporal variation exists in the zone-based irrigation water demands, indicating that the reliabilities are supposed to be quantified to evaluate their irrigation efficiency. Alternatively, the estimated irrigation water demands at the Su-Qi-Lin branch could be referred to in Figure 11b.

Accordingly, to proceed with the reliability assessment of the desired irrigation water demands, the corresponding quantile curves should be established via the weighted frequency curve methods within the proposed RA_IWD_Canal model, as shown in Figure 13. Given Figure 13, the resulting quantiles from the estimated water demands for the Zhudong Canal zone commonly exceed those at the 3^rd branch, especially for the lower cumulative probabilities of less than 0.1. By doing so, the corresponding exceedance probabilities to the introduced irrigation water demands in 2019–2024 (i.e., reliability) could be calculated with the above-resulting quantile curves as shown in Figure 14 and Figure 15; it can be seen that the exceedance probabilities of the introduced water demands for the Zhudong irrigation zone (see Figure 14), on average, approximate 0.85; specifically, in the 16^th–28^th 10-day periods, the corresponding reliability (exceedance probability) reaches 0.97. Moreover, in the 7^th–10^th 10-day periods, the corresponding introduced water demands could be given with an exceedance probability (i.e., reliability) of less than 0.7. It concludes that the study area (Zhudong Canal zone) could be sufficiently supplied irrigation water higher than the introduced ones in 2019–2024 with a high likelihood. In contrast, the Zhudong Canal zone, the exceedance probabilities of the introduced irrigation water demands at the Su-Qi-Lin (the 3^rd branch) (see Figure 15), on average, are noticeably less than 0.25 with a minimum approaching 0.00001 one at the 14^th 10-day period, namely treated as the fallow period; this is because surface runoff has been probably converted to the upstream 1^st branch to hardly supply the expected water amount to the 3^rd branch (Su-Qi-Lin). Namely, the current introduced irrigation water demands at the Su-Qi-Lin branch are markedly overestimated, making it difficult to achieve the desired irrigation requirements. That is to say, the introduced water demands for the Su-Qi-Lin branch should be necessarily declined to boost the irrigation efficiency.

Altogether, despite the recently introduced irrigation water demands for the Zhudong Canal zone with an average reliability of higher than 0.9, the irrigation water is hardly supplied subject to the introduced water demands at the specific 10-day periods (7^th–10^th periods) merely with a reliability of nearly 0.7. In addition, the introduced ones for the Su-Qi-Lin branch exhibit a low irrigation efficiency with a reliability of less than 0.3, indicating that the introduced water demands at the Su-Qi-Line branch area are considerably overestimated to lead to a shortage risk. To enhance the reliability of the introduced irrigation water demands for the entire branches within the study area, the probabilistic-based irrigation water could be provided by calculating the quantiles of the irrigation water demands under a desired exceedance probability (i.e., reliability) as the introduced magnitudes. Figure 16 illustrates the probabilistic-based irrigation water demands at 30 10-day periods for the Zhudong Canal zone as well as the third branch under a desired reliability of 0.8; also, it could be seen that the above probabilistic-based irrigation water demands are mutually correlated in time with a high correlation coefficient of roughly 0.8, indicating that it is necessary to take the spatiotemporal correlation of irrigation water as setting the introduced water demands into account. As well as the zone-based irrigation water demands, the proposed RA_IWD_Canal could provide the probabilistic-based irrigation water demands with high spatial resolution, revealing that the irrigation water demands at all branches could be quantified under an accepted reliability of 0.8 as shown in Figure 17. According to Figure 17, the 6^th and 11^th branches are associated with significantly low probabilistic-based water demands (approximately 0.000001 m³/s), revealing that they could be treated as non-irrigation branches in case of insufficient irrigation water supplies.

5. Conclusions

This study aims to model reliability analysis for estimating the branch-based irrigation water demands in a multi-canal irrigation zone subject to the uncertainties in the observations of gauged surface runoff, named the RA_IWD_Canal model. Within the proposed RA_IWD_Canal model, the corresponding uncertainties to the estimated irrigation water demands are quantified in terms of L-moment ratios, and induced reliabilities of the introduced irrigation water demands could be achieved by calculating the exceedance probabilities via the weighted quantile-curve method. Additionally, the probabilistic-based branch-based irrigation water demands could be accordingly provided with the desired reliability to boost irrigation performance.

The Zhudong Canal irrigation zone located in Northern Taiwan, with fifteen branches, is selected as the study area, and the associated observed surface runoff at the fifteen discharge gauges from 2019 to 2023 is adopted in the model development and application. As well as the historical gauged surface runoffs, the introduced 10-day irrigation water demands set for the Zhudong irrigation zone and the 3rd branch (Su-Qi-Lin) set from 2019 to 2024 are utilized in the reliability quantification. The application results indicate that the introduced irrigation water demands at the 30 10-day periods exhibit significant variation (on average, from 0.02 m³/s to 1.7 m³/s) with a noticeable 95% confidence interval of nearly 0.8 m³/s. Also, the average of their corresponding reliabilities approaches 0.85 but with a significant change in time (from 0.63 m³/s to 0.999 m^d/s). In contrast with the Zhudong Canal zone, the introduced irrigation water demands at the Su-Qi-Lin branch, on average, are approximately less than 0.12 m³/s with a significantly low reliability (around 0.25). This implies that the introduced irrigation water demands within the study area were set without considering the variations of the climatic and hydrological features that impact irrigation reliability and efficiency. Subsequently, quantified via the proposed RA_IWD_Canal model with a desired and acceptable reliability, the resulting probabilism-based irrigation water demand could be treated as the introduced water demands to enable all branches in the study area to achieve high irrigation efficiency consistently.

Although the proposed RA_IWD_Canal model could effectively be applied in estimating the branch-based irrigation water demands, the measured surface runoffs for the four years are adopted in the model development and application. Hence, to reduce the effect of the record length of gauge surface off on the model applicability, more observations of the gauged runoff data are desirably required. In addition, the estimation of the branch-based irrigation water demands is demonstrated via the proposed RA_IWD_Canal model only with the surface runoff observations to have a significant correlation in time. However, the other hydrological features (e.g., rainfall, evapotranspiration, and soil moisture) should impact the irrigation water supplies and requirements [6,10,27,28]. Also, AI-created models have recently been comprehensively applied in irrigation water allocation and management [29,30]. Thus, using the resulting probabilistic-based irrigation water demands under different conditions of gauged surface runoffs, future work could be performed by training AI-derived models to estimate probabilistic-based irrigation water demands with the surface runoff and hydroclimatic features of interest given.