Farm Plot Boundary Estimation and Testing Based on the Digital Filtering and Integral Clustering of Seeding Trajectories
Abstract
1. Introduction
2. Materials and Methods
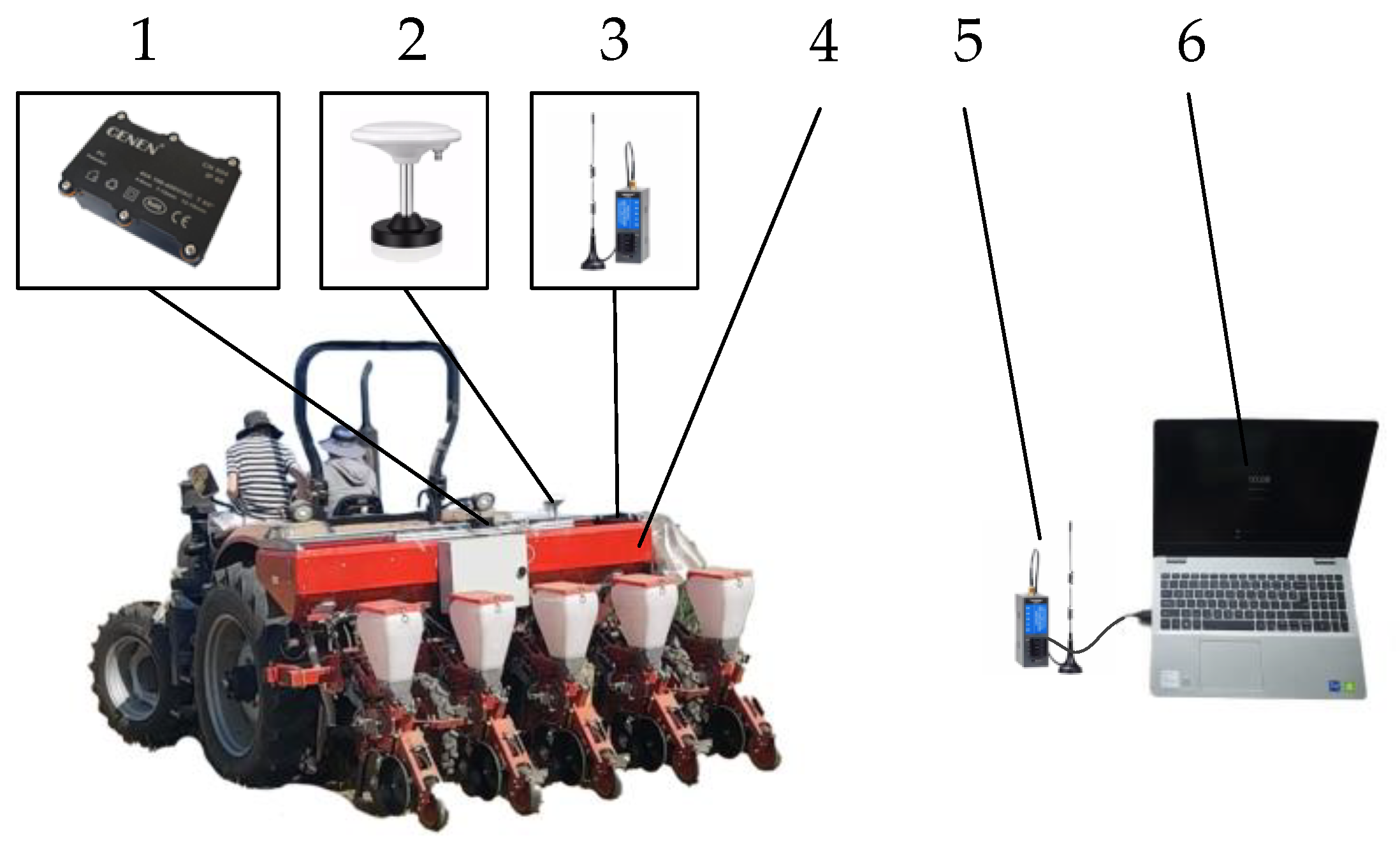
2.1. Hardware
2.1.1. Seeding Machine
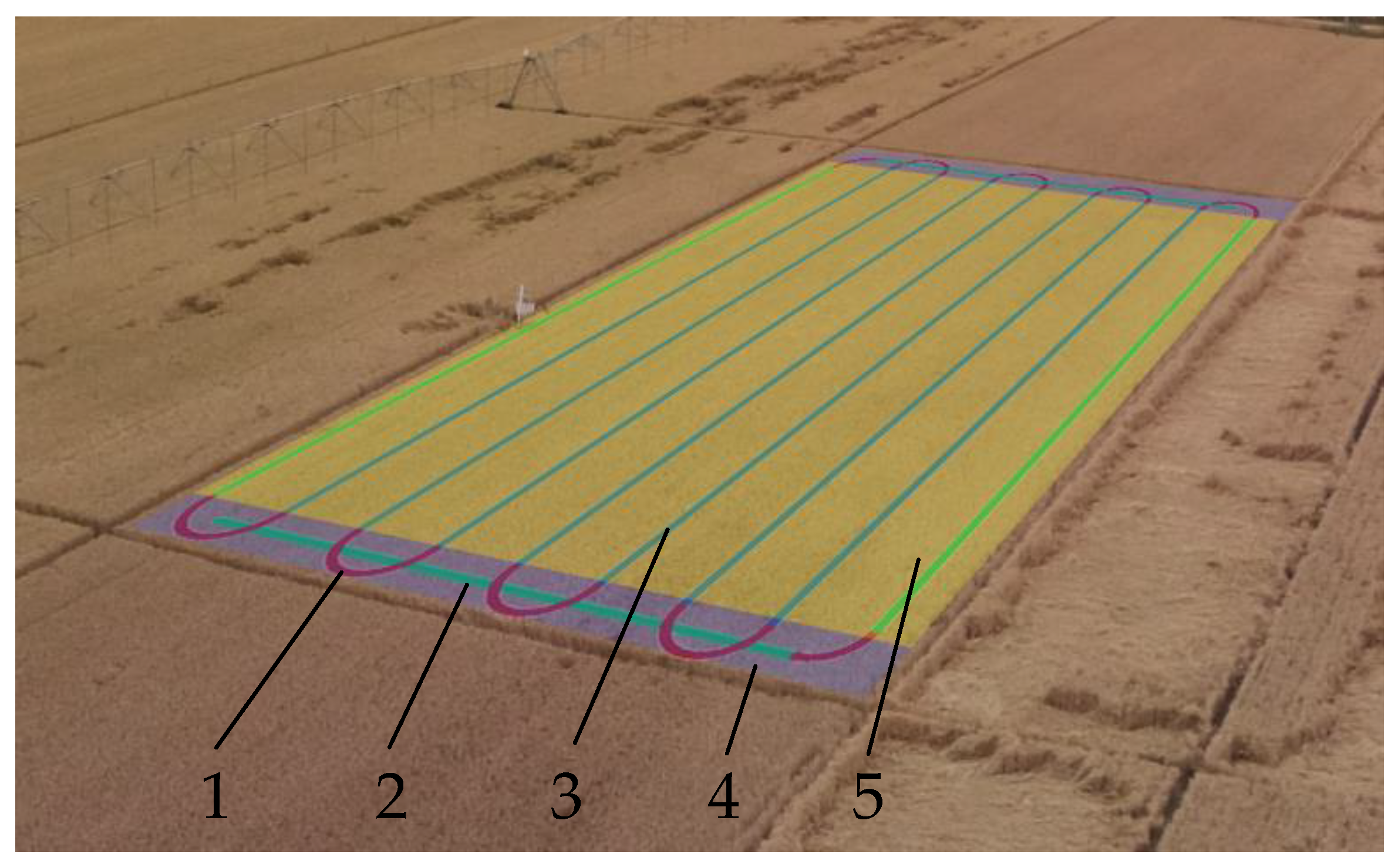
2.1.2. Trajectory Characteristics
2.2. Boundary Extraction Based on Low-Pass Filter and Integral Clustering
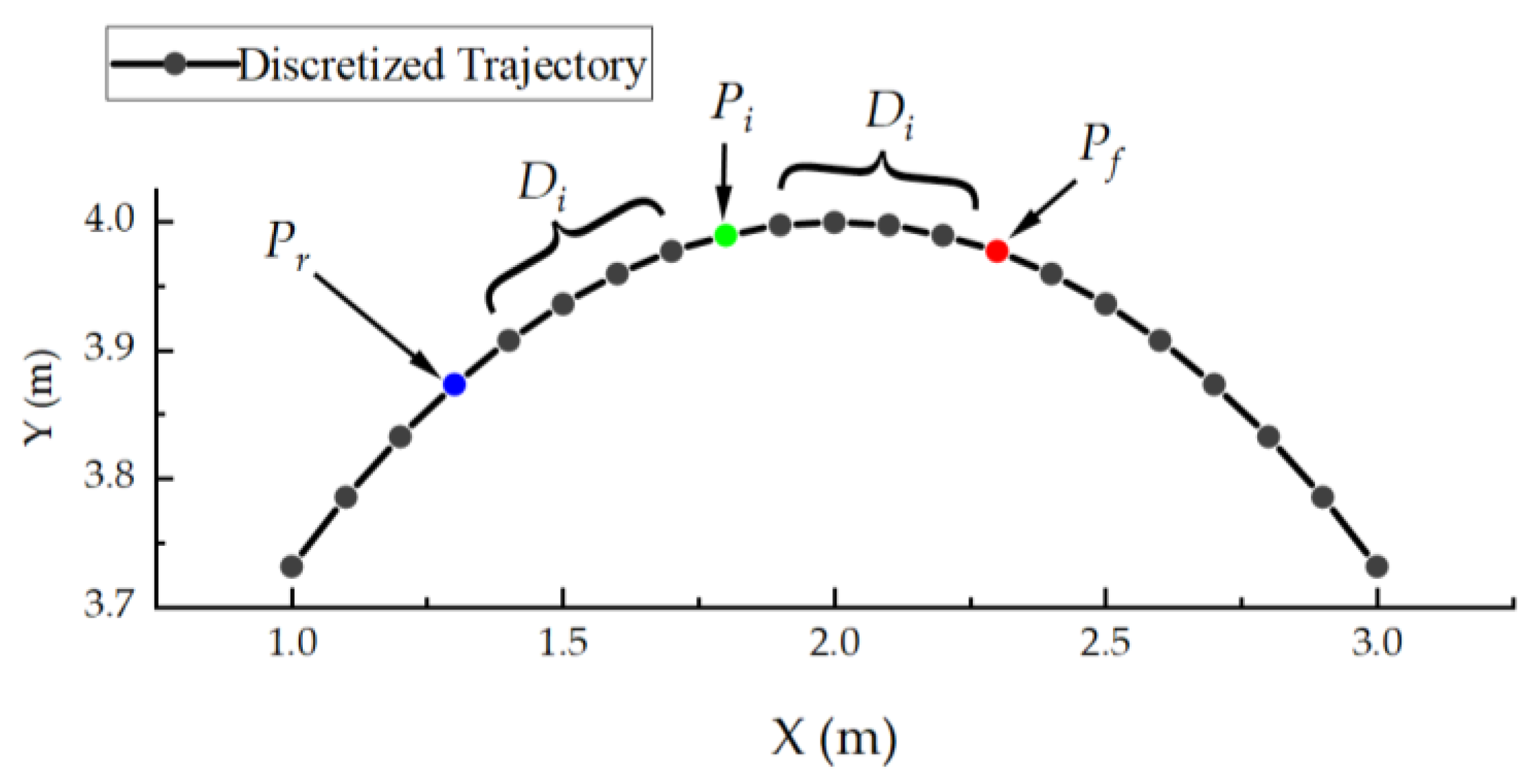
2.2.1. Path Curvature Calculation
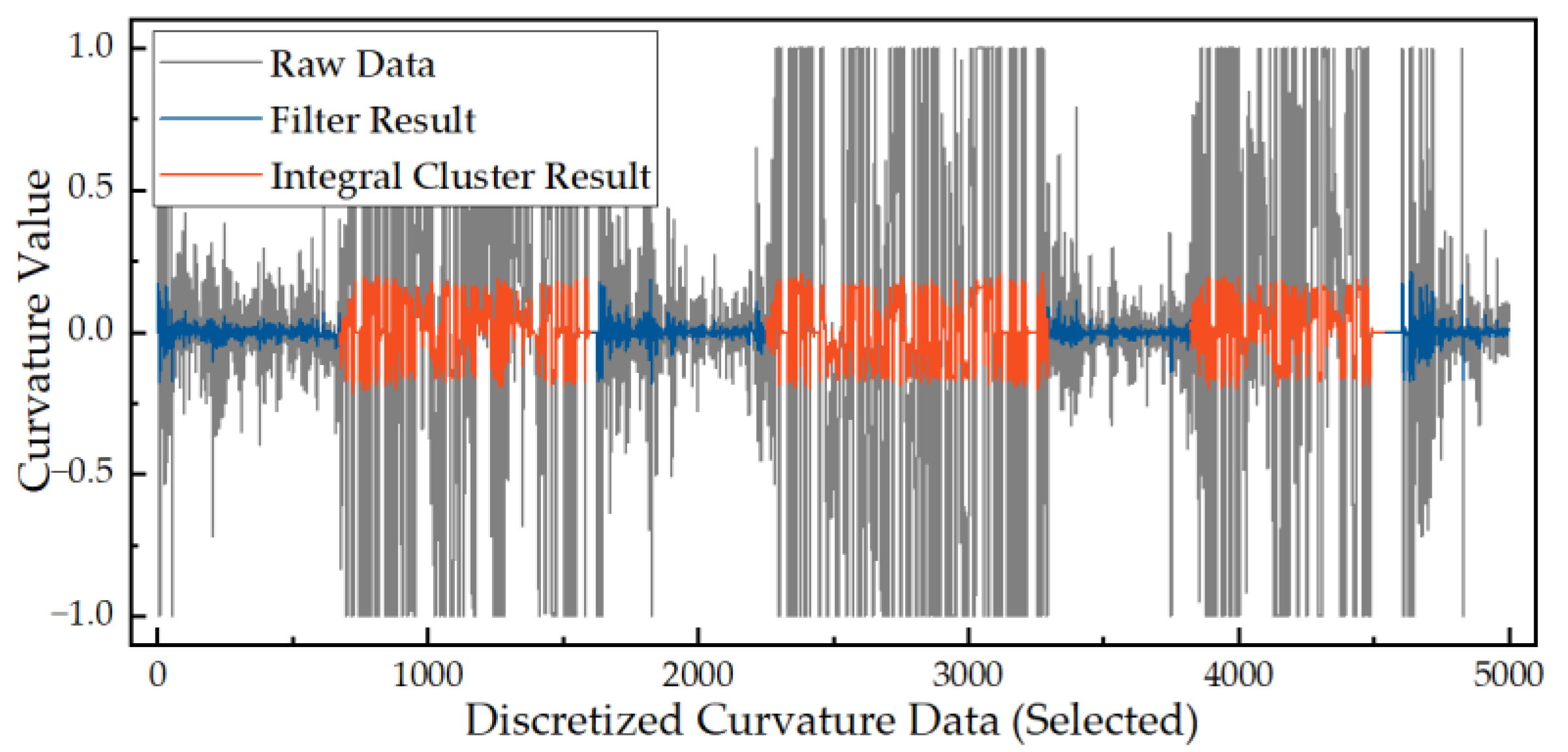
2.2.2. Discrete Data Low-Pass Filtering
2.2.3. Integral Clustering
2.2.4. Orthogonal Rotation of Seeding Paths
2.2.5. Orthogonal Rotation of Seeding Paths
2.2.6. Orthogonal Rotation of Seeding Paths
3. Results
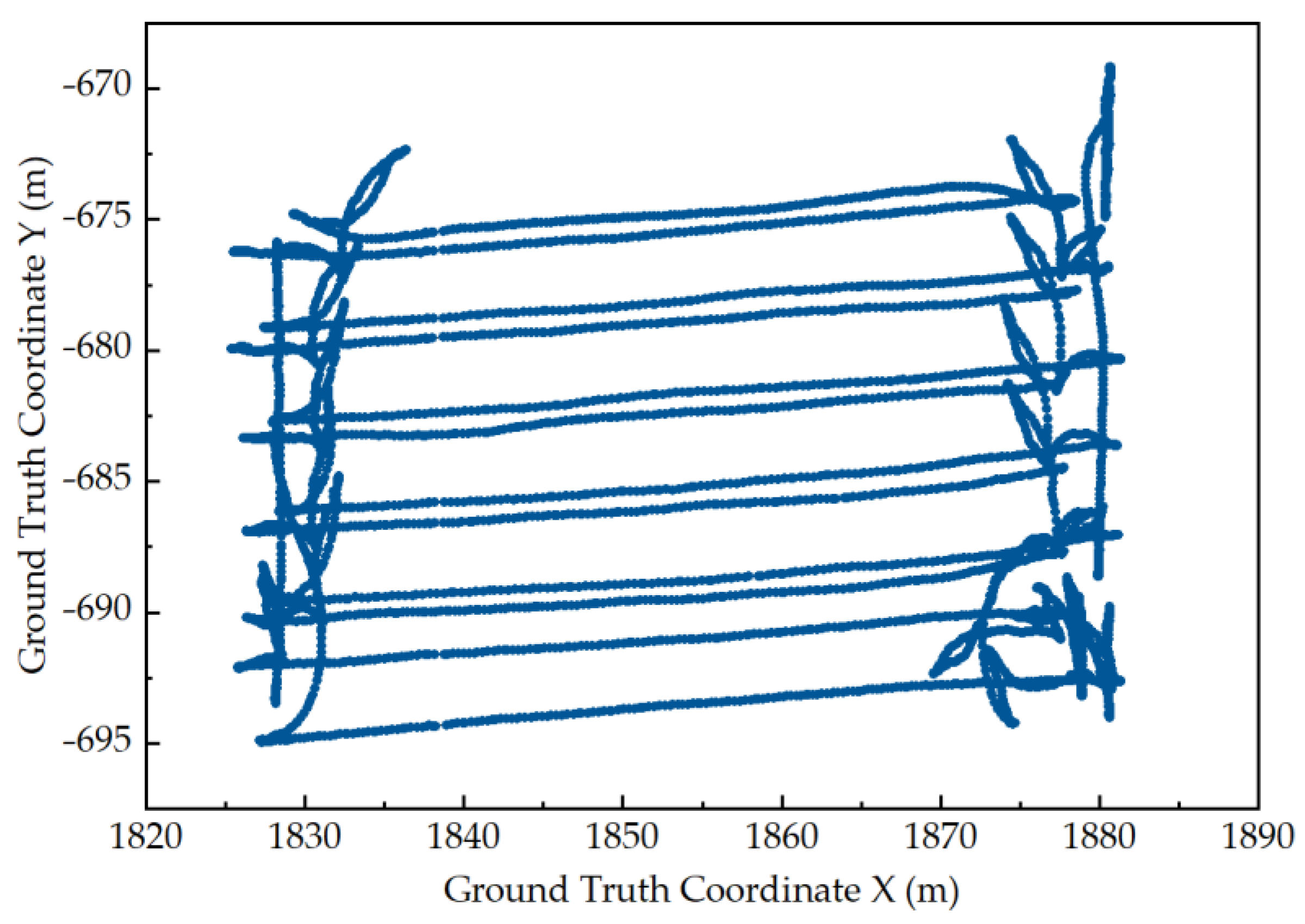
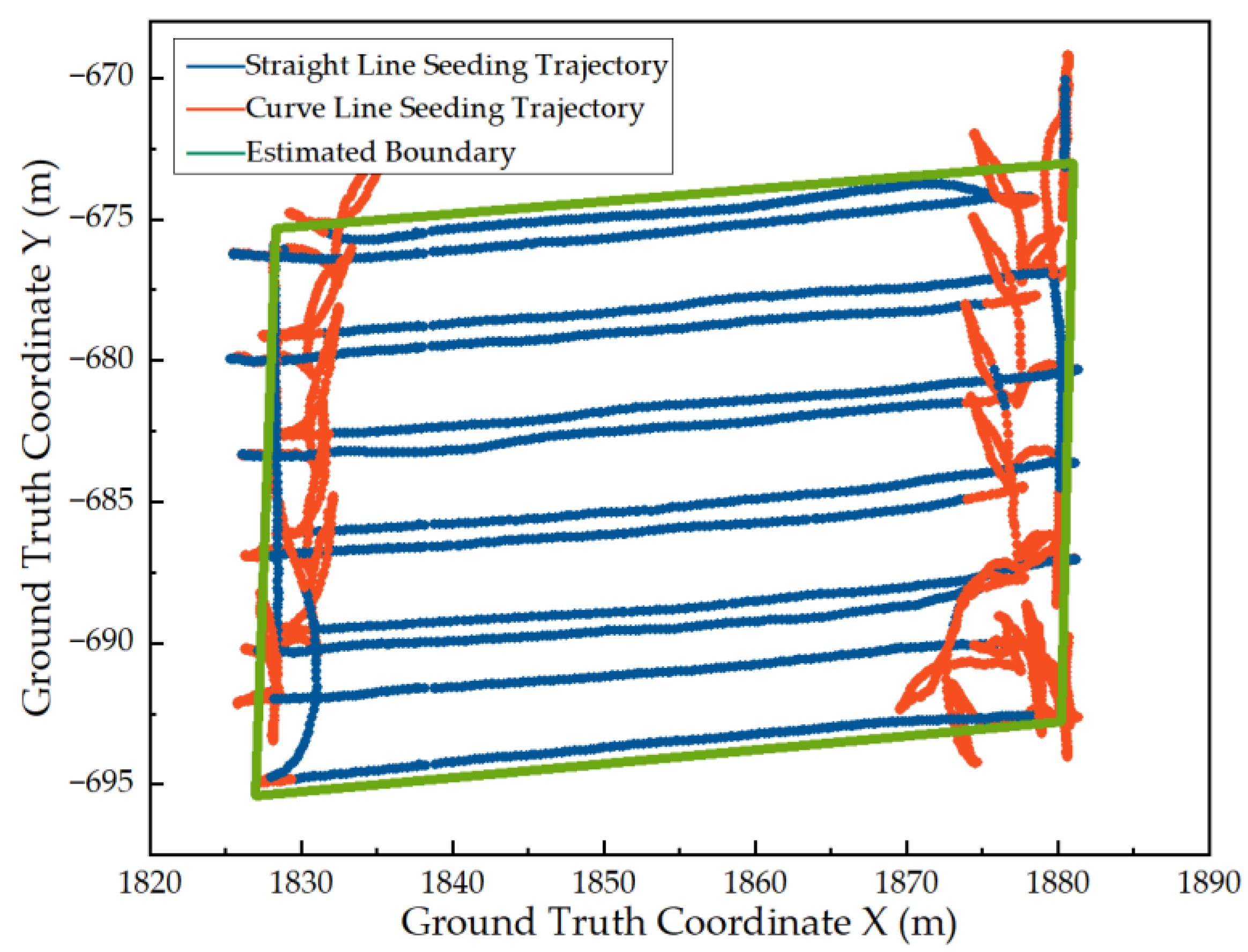
3.1. Trajectory Data Acquisition
3.2. Calculating Results
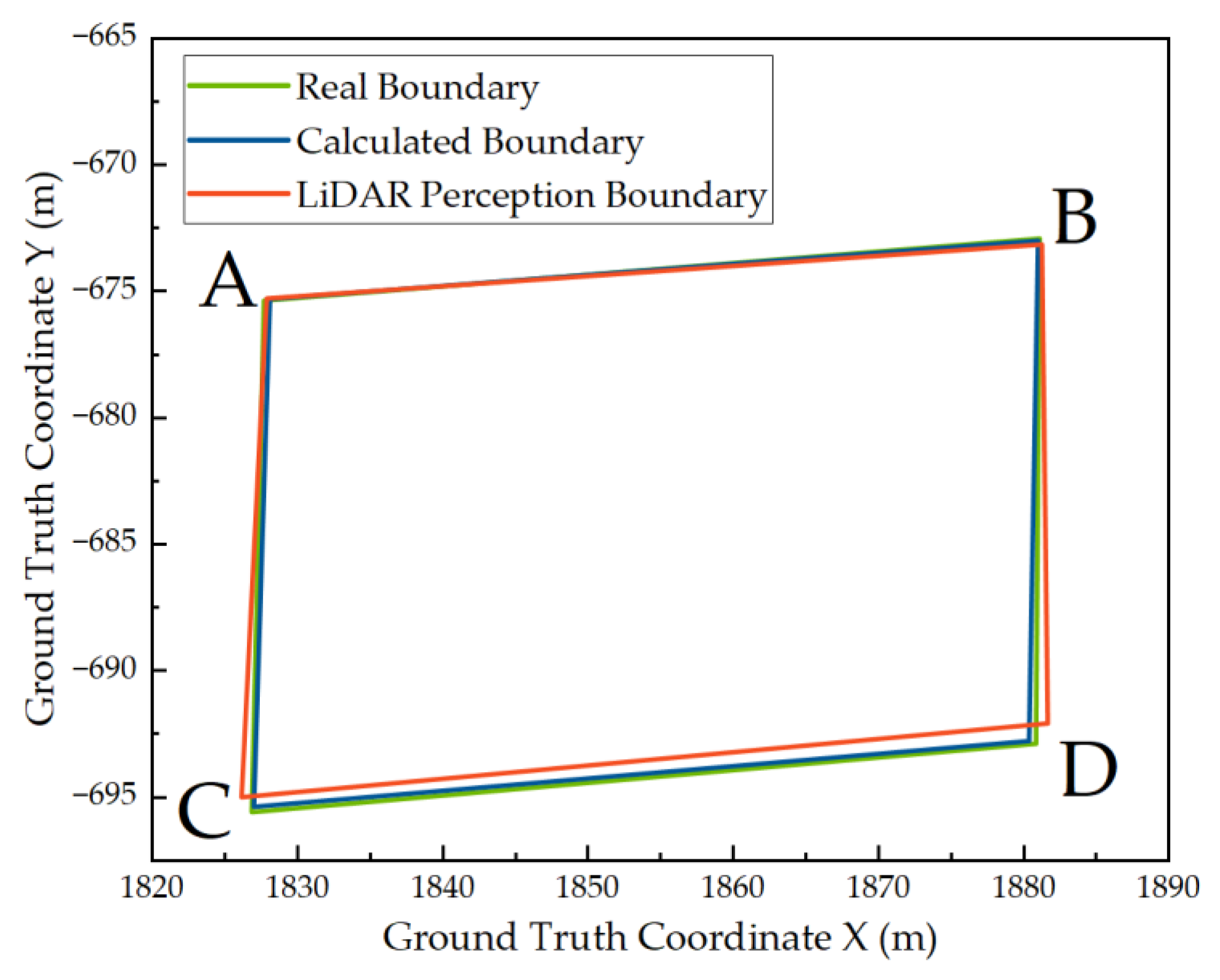
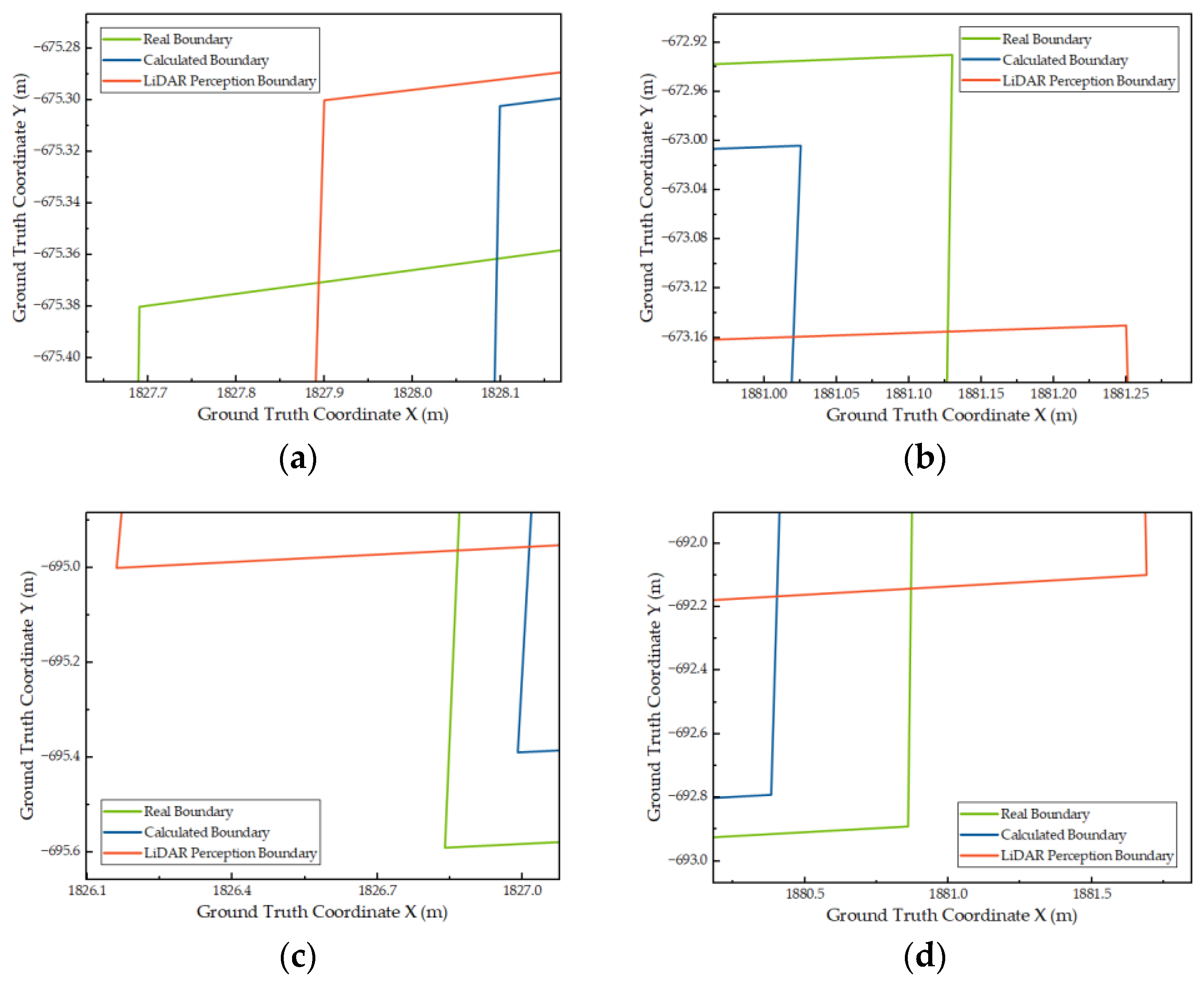
3.3. Results Comparison
3.4. Results Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, C. Current situations and prospects of smart agriculture. J. South China Agric. Univ. 2021, 42, 1–7. [Google Scholar]
- Zhao, C. State-of-the-art and recommended developmental strategic objectives of smart agriculture. Smart Agric. 2019, 1, 1–7. [Google Scholar]
- Kamilaris, A.; Kartakoullis, A.; Prenafeta-Boldú, F.X. A Review on the Practice of Big Data Analysis in Agriculture. Comput. Electron. Agric. 2017, 143, 23–37. [Google Scholar] [CrossRef]
- Wang, T.; Xu, X.; Wang, C.; Li, Z.; Li, D. From Smart Farming towards Unmanned Farms: A New Mode of Agricultural Production. Agriculture 2021, 11, 145. [Google Scholar] [CrossRef]
- Ma, Z.; Chong, K.; Zhao, X.; Zhao, J.; Zhao, S.; Yu, H. Research on the work precision of farm machinery driven by automatic navigation tractors. J. Hebei Agric. Univ. 2022, 45, 109–114. [Google Scholar] [CrossRef]
- Lu, B.; Dong, W.; Ding, Y.; Sun, Y.; Li, H.; Zhang, C. An rapeseed unmanned seeding system based on cloud-terminal high precision maps. Smart Agric. 2023, 5, 33–44. [Google Scholar]
- Ju, J.; Chen, G.; Lv, Z.; Zhao, M.; Sun, L.; Wang, Z.; Wang, J. Design and Experiment of an Adaptive Cruise Weeding Robot for Paddy Fields Based on Improved YOLOv5. Comput. Electron. Agric. 2024, 219, 108824. [Google Scholar] [CrossRef]
- Zhao, C.; Fan, B.; Li, J.; Feng, Q. Technology progress, challenges and trends. Smart Agric. 2023, 5, 1–15. [Google Scholar]
- Wang, N.; Yang, X.; Wang, T.; Xiao, J.; Zhang, M.; Wang, H.; Li, H. Collaborative Path Planning and Task Allocation for Multiple Agricultural Machines. Comput. Electron. Agric. 2023, 213, 108218. [Google Scholar] [CrossRef]
- Zhang, Y. Monitoring maize evapotranspiration and soil water content in farmland based on UAV multi-source remote sensing data. Ph.D. Thesis, Research Center of Soil and Water Conservation and Ecological Environment, Chinese Academy of Sciences and Ministry of Education, Xianyang, China, 2024. [Google Scholar]
- Xu, J.; Liu, Y.; Yan, C.; Yuan, J. Estimation of Soil Organic Matter Based on Spectral Indices Combined with Water Removal Algorithm. Remote Sens. 2024, 16, 2065. [Google Scholar] [CrossRef]
- Zhang, K.; Gong, L.; He, Z.; Huo, P. Crop yield prediction based on 3DCNN-TCN model. Microelectron. Comput. 2023, 40, 83–89. [Google Scholar] [CrossRef]
- Wang, H.; Ma, Z.; Ren, Y.; Du, S.; Lu, H.; Shang, Y.; Hu, S.; Zhang, G.; Meng, Z.; Wen, C.; et al. Interactive Image Segmentation Based Field Boundary Perception Method and Software for Autonomous Agricultural Machinery Path Planning. Comput. Electron. Agric. 2024, 217, 108568. [Google Scholar] [CrossRef]
- Chen, L.; Si, Y.; Tian, B.; Tan, Z.; Wang, Y. Boundary detection of mine drivable area based on 3D LiDAR. J. China Coal Soc. 2020, 45, 2140–2146. [Google Scholar] [CrossRef]
- Zhan, J.; Guo, C.; Lei, T.; Qu, Y.; Wu, H.; Liu, J. Comparative study on data standards of autonomous driving map. J. Image Graph. 2021, 26, 36–48. [Google Scholar]
- Ma, Z.; Chong, K.; Ma, S.; Fu, W.; Yin, Y.; Yu, H.; Zhao, C. Control Strategy of Grain Truck Following Operation Considering Variable Loads and Control Delay. Agriculture 2022, 12, 1545. [Google Scholar] [CrossRef]
- Aguiar, A.S.; dos Santos, F.N.; Cunha, J.B.; Sobreira, H.; Sousa, A.J. Localization and Mapping for Robots in Agriculture and Forestry: A Survey. Robotics 2020, 9, 97. [Google Scholar] [CrossRef]
- Liu, Z. Research on Visual Slam of Inspection Robot Based on Image Defogging and Semantic Mapping. Master Thesis, Shandong University, Jinan, China, 2021. [Google Scholar]
- Wagner, M.P.; Oppelt, N. Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction. Remote Sens. 2020, 12, 1990. [Google Scholar] [CrossRef]
- Gafurov, A. Automated Mapping of Cropland Boundaries Using Deep Neural Networks. AgriEngineering 2023, 5, 1568–1580. [Google Scholar] [CrossRef]
- Borowiec, N.; Marmol, U. Using LiDAR System as a Data Source for Agricultural Land Boundaries. Remote Sens. 2022, 14, 1048. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Liu, X.; Tao, J.; Liu, C.; Li, R. An Automatic Drive Control Technique for Rice Drill Seeder in Uneven Paddy Fields. Trans. Chin. Soc. Agric. Mach. 2018, 49, 15–22. [Google Scholar]
- Cai, D.; Li, Y.; Qin, C.; Liu, C. Detection Method of Boundary of Paddy Fields Using Support Vector Machine. Trans. Chin. Soc. Agric. Mach. 2019, 50, 22–27. [Google Scholar]
- Zhai, W.; Xiong, X.; Mo, G.; Xiao, Y.; Wu, C.; Xu, Z.; Pan, J. A Bagging-SVM Field-Road Trajectory Classification Model Based on Feature Enhancement. Comput. Electron. Agric. 2024, 217, 108635. [Google Scholar] [CrossRef]
- He, X.; Zhu, J.; Li, P.; Zhang, D.; Yang, L.; Cui, T.; Zhang, K.; Lin, X. Research on a Multi-Lens Multispectral Camera for Identifying Haploid Maize Seeds. Agriculture 2024, 14, 800. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, H. Performance Evaluation of 2D LiDAR SLAM Algorithms in Simulated Orchard Environments. Comput. Electron. Agric. 2024, 221, 108994. [Google Scholar] [CrossRef]
- Naich, A.Y.; Carrión, J.R. LiDAR-Based Intensity-Aware Outdoor 3D Object Detection. Sensors 2024, 24, 2942. [Google Scholar] [CrossRef]


| Parameter Name | Value |
|---|---|
| Curvature Calculation Points Interval Di | 5 |
| System Cut-off Frequency ω0 | 2π |
| Integral Step Length Δs | 100 |
| Integral Threshold S | 8 |
| Heading Resolution R | 0.1 |
| Continuous Boundary Dots Set Amount P | 100 |
| Corner | Real Boundary | Calculated Boundary | LiDAR Perception Boundary | |||
|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | |
| A | 1827.69 | −675.38 | 1828.09 | −675.30 | 1827.90 | −675.30 |
| B | 1881.13 | −672.93 | 1881.02 | −673.00 | 1881.25 | −673.15 |
| C | 1826.84 | −695.59 | 1826.99 | −695.38 | 1826.16 | −695.00 |
| D | 1880.86 | −692.89 | 1880.38 | −692.79 | 1881.69 | −693.26 |
| LiDAR Perception | Trajectory Estimation | |
|---|---|---|
| Calculated area | 1048.52 | 1061.10 |
| Missing area | 41.49 | 17.64 |
| Exceeded area | 12.27 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Ma, S.; Zhao, J.; Wang, W.; Yu, H. Farm Plot Boundary Estimation and Testing Based on the Digital Filtering and Integral Clustering of Seeding Trajectories. Agriculture 2024, 14, 1238. https://doi.org/10.3390/agriculture14081238
Ma Z, Ma S, Zhao J, Wang W, Yu H. Farm Plot Boundary Estimation and Testing Based on the Digital Filtering and Integral Clustering of Seeding Trajectories. Agriculture. 2024; 14(8):1238. https://doi.org/10.3390/agriculture14081238
Chicago/Turabian StyleMa, Zhikai, Shiwei Ma, Jianguo Zhao, Wei Wang, and Helong Yu. 2024. "Farm Plot Boundary Estimation and Testing Based on the Digital Filtering and Integral Clustering of Seeding Trajectories" Agriculture 14, no. 8: 1238. https://doi.org/10.3390/agriculture14081238
APA StyleMa, Z., Ma, S., Zhao, J., Wang, W., & Yu, H. (2024). Farm Plot Boundary Estimation and Testing Based on the Digital Filtering and Integral Clustering of Seeding Trajectories. Agriculture, 14(8), 1238. https://doi.org/10.3390/agriculture14081238






