Optimization of Operation Parameters and Performance Prediction of Paddy Field Grader Based on a GA-BP Neural Network
Abstract
:1. Introduction
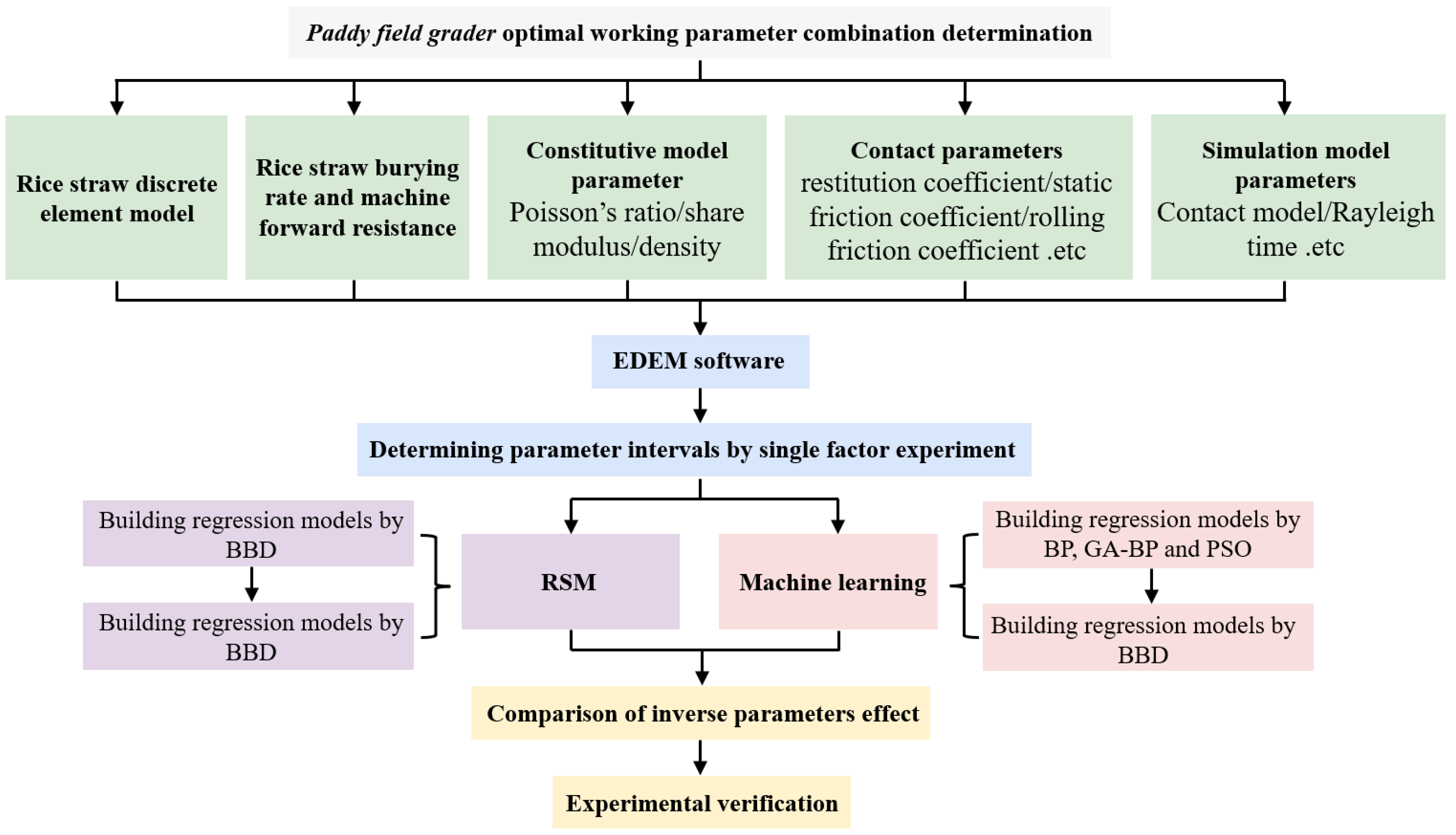
2. Materials and Methods
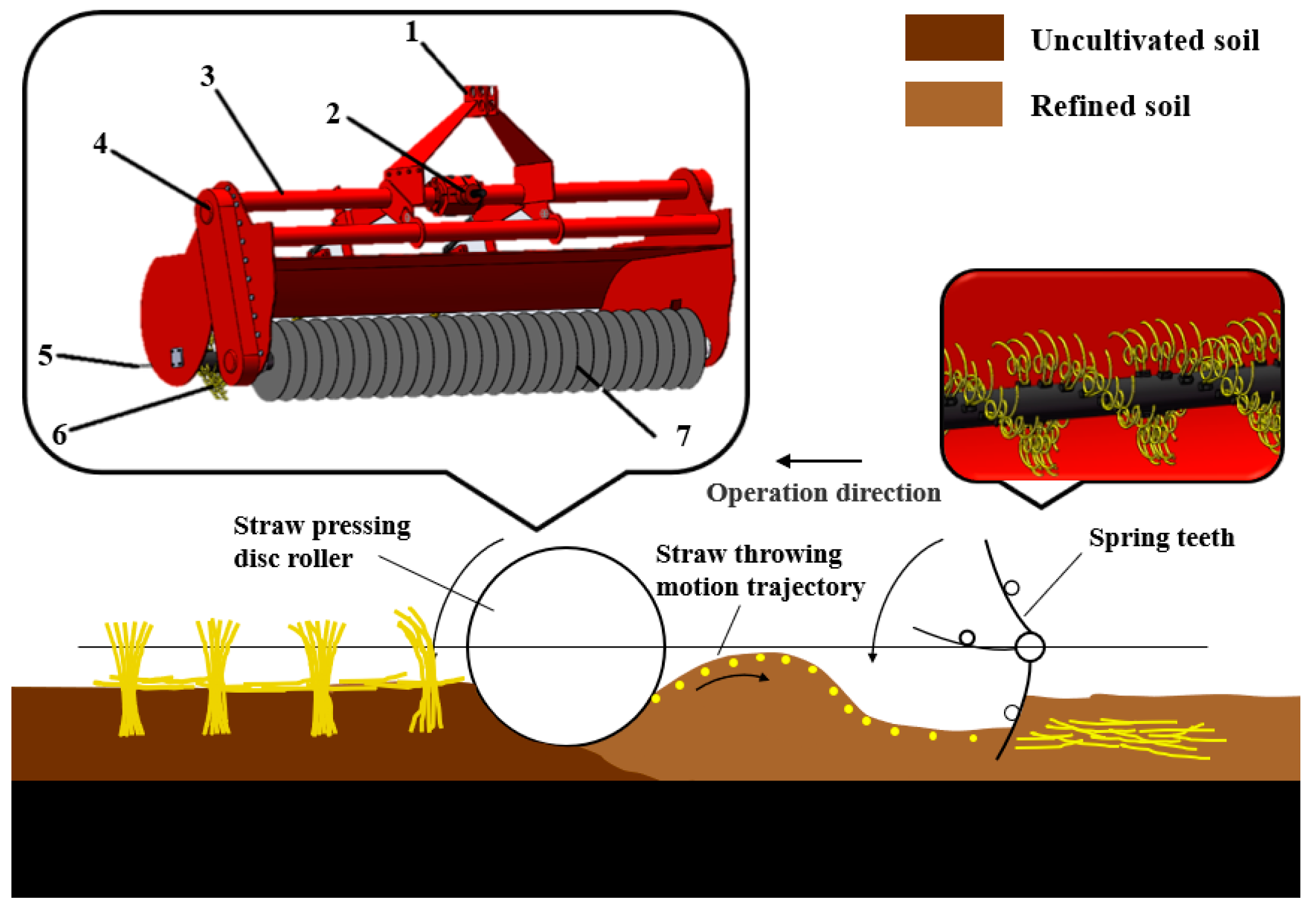
2.1. Structure and Working Principle
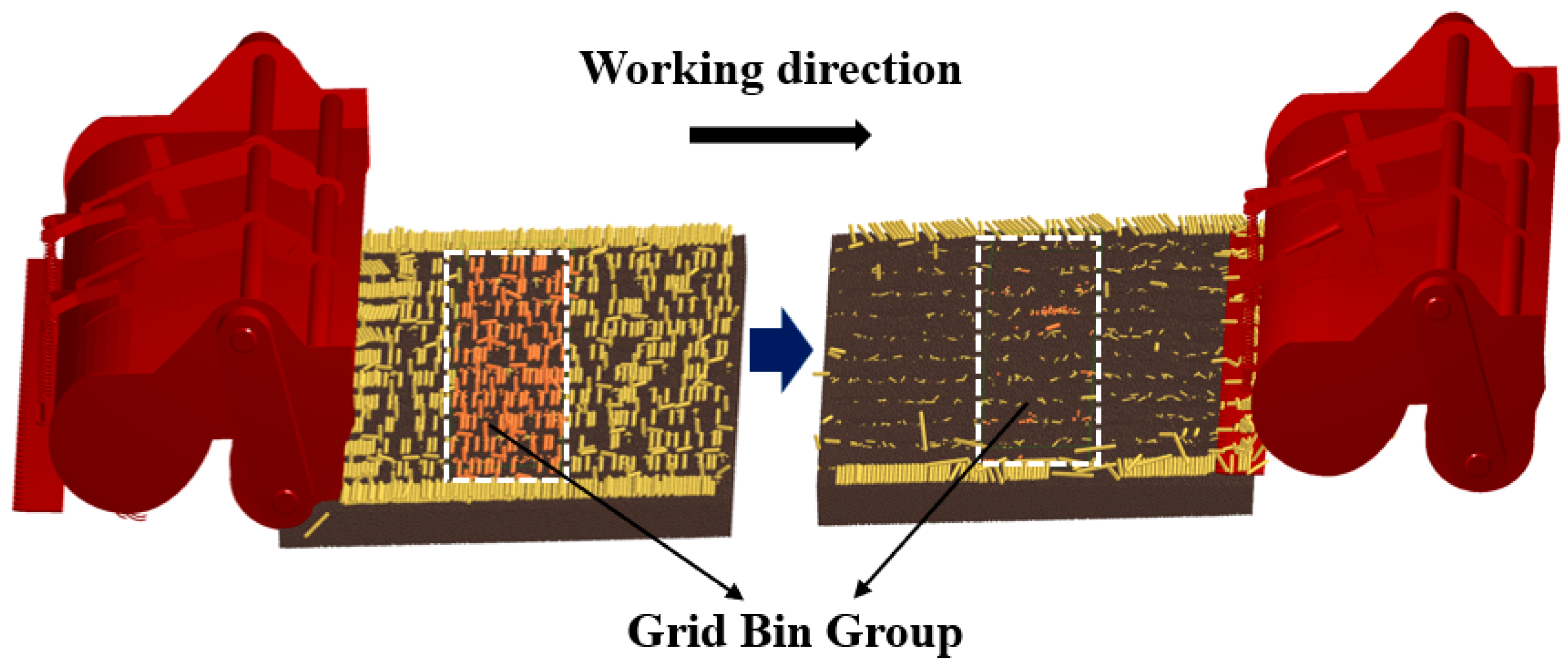
2.2. Discrete Element Simulation Modeling
2.3. RSM Test Design
2.3.1. Single-Factor Test
2.3.2. Box–Behnken Test
2.4. Regression Fitting Modeling Based on Machine Learning Algorithm
2.4.1. BP Algorithm
2.4.2. GA-BP Algorithm
2.4.3. PSO Algorithm
2.5. Data Analysis and Processing
3. Results and Discussion
3.1. Analysis of Single-Factor Experiment Results
3.2. Analysis of Box–Behnken Test Results
3.3. Machine Learning Regression Model
3.3.1. Model Comparison
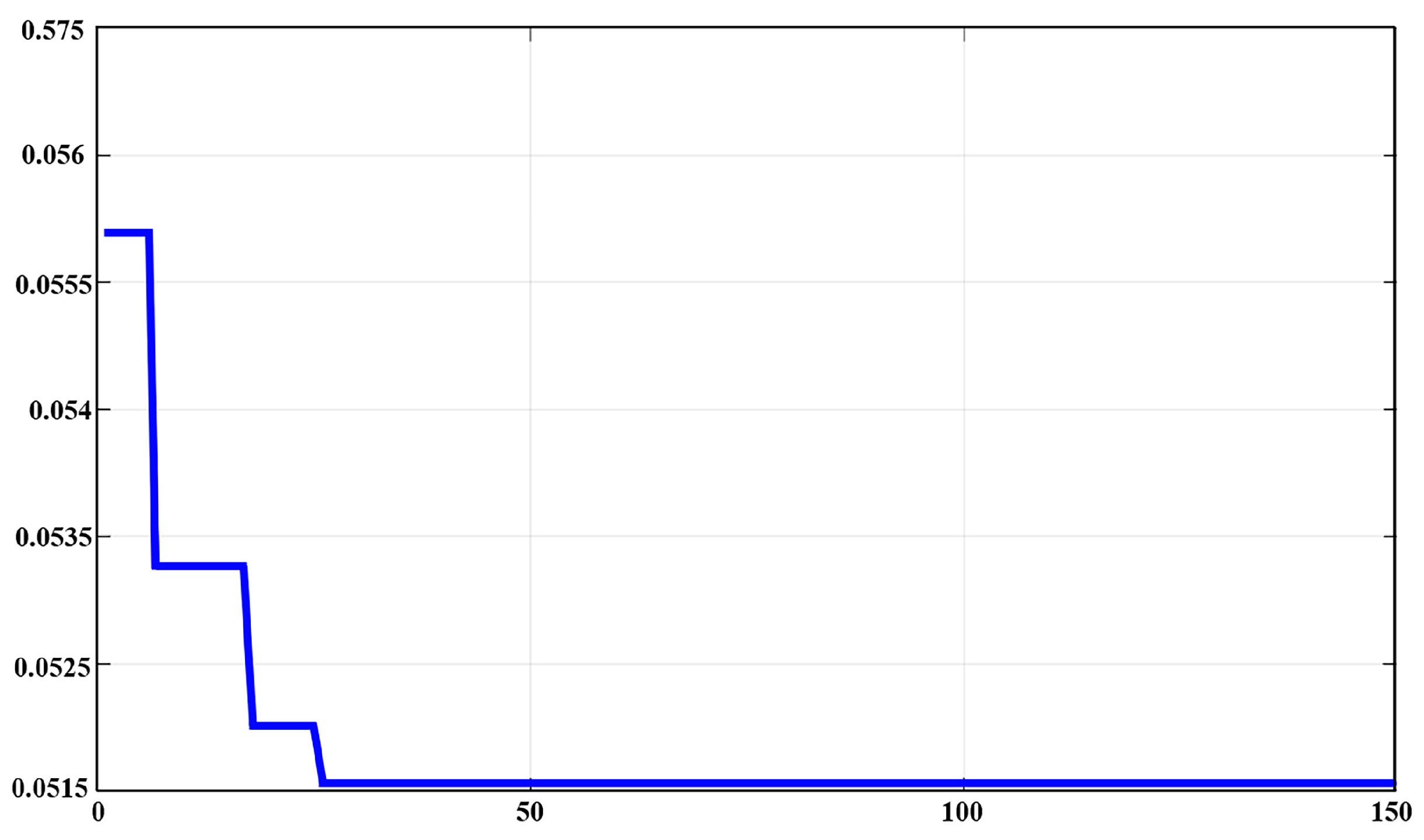
3.3.2. GA-BP Parameter Optimization
3.3.3. Inversion of Parameters in GA-BP-GA
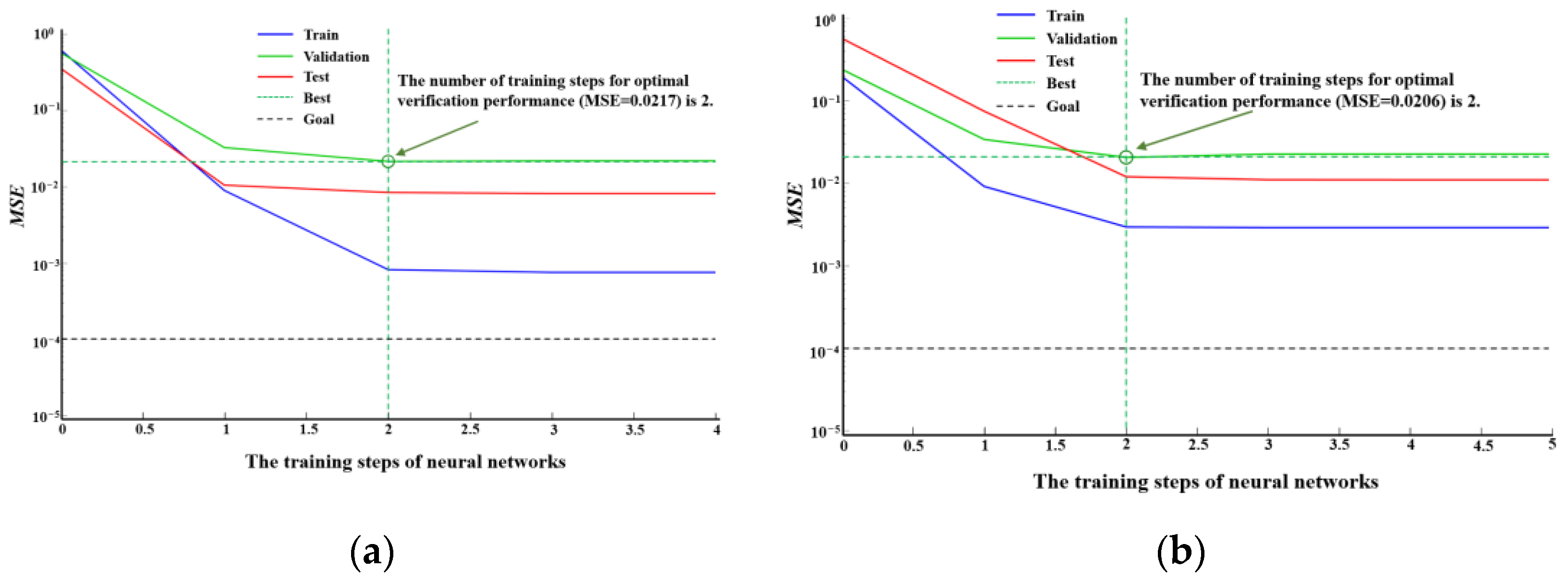
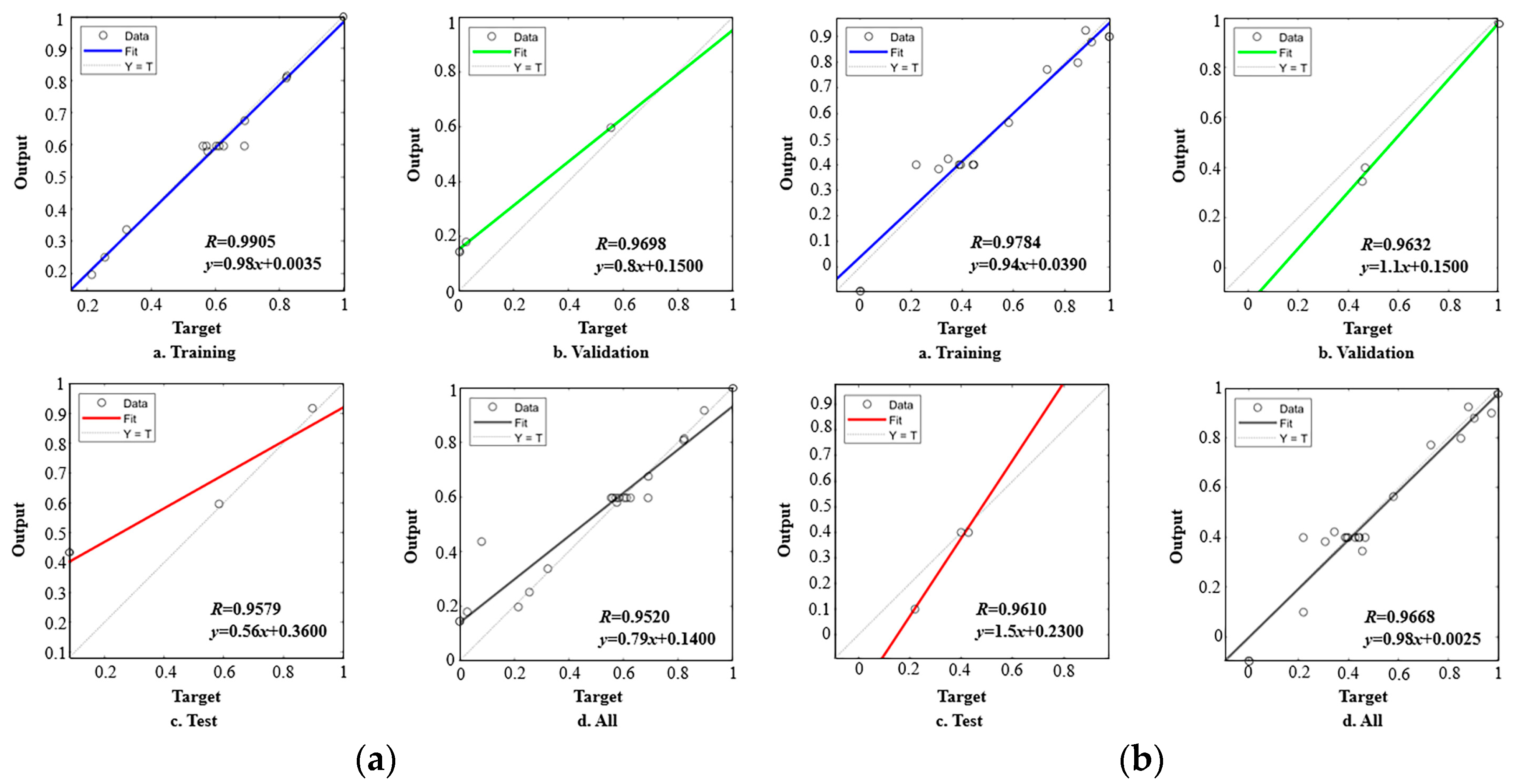
3.3.4. Model Evaluation
3.3.5. Experimental Verification
4. Discussion
5. Conclusions
- (1)
- The discrete element software is used to establish a simulation model to simulate the straw-burying process of the disc spring–tooth-combined paddy field grader. The single-factor test was carried out, and the operating speed of the machine, the operating depth of the burying mechanism, and the speed of the knife roller were used as the test factors. The straw-burying rate and the forward resistance of the machine were used as indicators to optimize the range of test factors. The BB test was carried out, and the data were fitted and analyzed by RSM to explore the influence of the interaction of various factors on the operation effect.
- (2)
- Three machine learning regression models are compared: standard back propagation neural network (BP), back propagation neural network optimized by genetic algorithm (GA-BP), and particle swarm optimization algorithm (PSO) to evaluate their performance in the prediction of working parameters of disc spring–tooth-combined paddy field grader. The evaluation criteria include the determination coefficient (R2), mean absolute error (MAE), and mean square error (MSE). The results show that the GA-BP model has the lowest error value in both MAE and MSE indicators, and its R2 value is closest to 1, indicating that the model is superior to BP and PSO models in terms of prediction accuracy and stability. The GA-BP regression model will be used as a prediction model for the working parameters of the disc spring–tooth-combined paddy field grader.
- (3)
- The optimized GA-BP model is used for parameter inversion, and the parameter combination obtained by GA-BP and RSM models is compared. The analysis results show that the GA-BP model is superior to the RSM model in terms of model accuracy, stability, and data fitting. The results validate the feasibility of using the GA-BP model to optimize the working parameters of the machine, and this method can provide a reference for the optimization of related working parameters in other fields as well as the calibration of discrete element simulation parameters.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.Y.; Chen, W.H.; Yuan, W.; Zhou, Z.P.; Liu, S.P. Nitrogen Diagnosis Model of Vegetation Indices Based on Canopy Hyperspectral Remote Sensing for Hybrid Rice. China Rice 2021, 27, 17–20+29. [Google Scholar]
- Liu, M.H.; Li, H.Y.; Du, J.; Chen, L.; Lin, X.Y.; Zhao, H.C.; Zhang, Y.; Zhang, G.L. Effect of straw returning and increasing nitrogen of tillering fertilizer on rice yield and nitrogen uptake and utilization in cold region. J. China Agric. Univ. 2023, 28, 49–59. [Google Scholar]
- Ge, X.L.; Qian, C.R.; Li, L.; Jiang, Y.B.; Gong, X.J.; Lv, G.Y. Effects of straw returning cooperated with fertilizer practice on yield of maize and soil quality of tillage layer. Soil Fertil. Sci. China 2021, 1, 131–136. [Google Scholar]
- Zhai, S.L.; Xu, C.F.; Wu, Y.C.; Liu, J.; Meng, Y.L.; Yang, H.S. Long-term ditch-buried straw return alters soil carbon sequestration, nitrogen availability and grain production in a rice–wheat rotation system. Crop Pasture Sci. 2021, 72, 245–254. [Google Scholar] [CrossRef]
- Song, J.; Huang, J.; Gao, J.S.; Wang, Y.N.; Wu, C.X.; Bai, L.Y.; Zeng, X.B. Effects of green manure planted in winter and straw returning on soil aggregates and organic matter functional groups in double cropping rice area. Chin. J. Appl. Ecol. 2021, 32, 564–570. [Google Scholar]
- Pei, Y.N.; Lv, W.G.; Guo, T.; Bai, N.L.; Li, S.X.; Zhang, J.Q.; Zhang, H.Y.; Zhang, H.L. Effeets of straw-returning combined with application of microbial inoculants on soil aggregates and related nutrients. Chin. J. Appl. Ecol. 2023, 34, 3357–3363. [Google Scholar]
- Sun, N.N.; Wang, X.Y.; Li, H.W.; Wang, J.; Jiang, H.; Tan, D.Y. Study on the Technology and Equipment of Rice Straw Direct Returning. J. Agric. Mech. Res. 2019, 41, 1–7. [Google Scholar]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Sadek, M.A. Modelling of soil-seed contact using the Discrete Element Method (DEM). Biosyst. Eng. 2014, 121, 56–66. [Google Scholar] [CrossRef]
- Mustafa, U.; John, M.; Fielke, C.S. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesione. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar]
- Wang, J.L. Discrete Element Method Deep-Buried Blade Roller Assembly Based on Optimum Design and Experimental of Rice Straw. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2019. [Google Scholar]
- Zhang, J.; Min, X.; Wei, C.; Dong, Y.; Wu, C.Y.; Zhu, J.P. Simulation Analysis and Experiments for Blade-Soil-Straw Interaction under Deep Ploughing Based on the Discrete Element Method. Agriculture 2023, 13, 136. [Google Scholar] [CrossRef]
- Hadi, A.N.; Seyed, H.K.; Mojtaba, N.B. Weed seed burial as affected by mouldboard design parameters, ploughing depth and speed: DEM simulations and experimental validation. Biosyst. Eng. 2022, 216, 79–92. [Google Scholar]
- Chen, G.B.; Wang, Q.J.; Li, H.W.; He, J.; Wang, X.H.; Zhang, X.Y.; He, D. Experimental research on vertical straw cleaning and soil tillage device based on Soil-Straw composite model. Comput. Electron. Agric. 2024, 216, 108510. [Google Scholar] [CrossRef]
- Han, M. Artificial Neural Network Basis; Dalian University of Technology Press: Dalian, China, 2014. [Google Scholar]
- Bai, H.B. Collision Damage Test and Prediction Model Establishment of Plug Seedling Based on Hanging Cup Transplanter. Master’s Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2023. [Google Scholar]
- Holzinger, A.; Fister, I., Jr.; Fister, I.; Kaul, H.-P.; Asseng, S. Human-centered ai in smart farming: Towards agriculture 5.0. IEEE Access 2024, 12, 62199–62214. [Google Scholar] [CrossRef]
- Yan, W.Y. Noise Benefits for Image Recognition in BP Neural Networks; Nanjing University of Posts and Telecommunications: Nanjing, China, 2023. [Google Scholar]
- Chen, L.N. Experimental Study on Coal Flotation Based RSM and BP Neural Network. Multipurp. Util. Miner. Resour. 2018, 5, 28–32. [Google Scholar]
- Veza, I.; Spraggon, M.; Fattah, I.M.R. Response surface methodology (RSM) for optimizing engine performance and emissions fueled with biofuel: Review of RSM for sustainability energy transition. Results Eng. 2023, 18, 101213. [Google Scholar] [CrossRef]
- Bourquin, J.; Schmidli, H.; Van, H.P. Advantages of Artificial Neural Networks (ANNs) as alternative modelling technique for data sets showing non-linear relationships using data from a galenical study on a solid dosage form. Eur. J. Pharm. Sci. 1998, 7, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Hammoudi, A.; Moussaceb, K.; Belebchouche, C. Comparison of artificial neural network (ANN) and response surface methodology (RSM) prediction in compressive strength of recycled concrete aggregates. Constr. Build. Mater. 2019, 209, 425–436. [Google Scholar] [CrossRef]
- Najet, G.; Mahmoud, M.; Talel, B.; Kamel, N.; Ali, F. Modeling and optimization of capsaicin extraction from Capsicum annuum L. using response surface methodology (RSM), artificial neural network (ANN), and Simulink simulation. Ind. Crops Prod. 2021, 171, 113869. [Google Scholar]
- Fetimi, A.; Dâas, A.; Benguerba, Y. Optimization and prediction of safranin-O cationic dye removal from aqueous solution by emulsion liquid membrane (ELM) using artificial neural network-particle swarm optimization (ANN-PSO) hybrid model and response surface methodology (RSM). J. Environ. Chem. Eng. 2021, 9, 105837. [Google Scholar] [CrossRef]
- Ma, X.J.; Guo, M.J.; Tong, X.; Hou, Z.F.; Liu, H.Y.; Ren, H.Y. Calibration of Small-Grain Seed Parameters Based on a BP Neural Network: A Case Study with Red Clover Seeds. Agronomy 2023, 13, 2670. [Google Scholar] [CrossRef]
- Zhao, J.K.; Song, W.B.; Li, J.J. Modeling and Mechanical Analysis of Rice Straw Based on Discrete Element Mechanical Model. Chin. J. Soil Sci. 2020, 51, 1086–1093. [Google Scholar]
- Ma, Z.T.; Zhao, Z.H.; Quan, W.; Shi, F.G.; Gao, C.; Wu, M.L. Calibration of Discrete Element Parameter of Rice Stubble Straw Based on EDEM. J. Agric. Sci. Technol. 2023, 25, 103–113. [Google Scholar]
- Tang, Z.Y.; Gong, H.; Wu, S.L.; Zeng, Z.W.; Wang, Z.Q.; Zhou, Y.H.; Fu, D.B.; Liu, C.; Cai, Y.H.; Qi, L. Modelling of paddy soil using the CFD-DEM coupling method. Soil Tillage Res. 2023, 226, 105591. [Google Scholar] [CrossRef]
- Ding, Q.S.; Ren, J.; Belal, E.A.; Zhao, J.K.; Ge, S.Y.; Li, Y. Discrete Element Analysis of Subsoiling Process of Wet Clay Paddy Soil. Agric. Mach. 2017, 48, 38–48. [Google Scholar]
- Zhou, J.; Sun, W.T.; Liang, Z.A. Construction of Discrete Element Flexible Model for Jerusalem Artichoke Root-Tuber at Harvest Stage. Trans. Chin. Soc. Agric. Mach. 2023, 54, 124–132. [Google Scholar]
- Ding, X.T.; Li, K.; Hao, W.; Yang, Q.C.; Yan, F.X.; Cui, Y.J. Calibration of Simulation Parameters of Camellia oleifera SeedsBased on RSM and GA-BP-GA Optimization. Trans. Chin. Soc. Agric. Mach. 2023, 54, 139–150. [Google Scholar]
- Gai, L. Exploration of Manufaturing Technique and Mechanical Performance Prediction of Reconsolidated Square Materials of Cotton Stalk. Master’s Thesis, Northwest A&F University, Xianyang, China, 2015. [Google Scholar]
- Ren, K.; Jia, L.; Huang, J.T.; Wu, M. Research on cutting stock optimization of rebar engineering based on building information modeling and an improved particle swarm optimization algorithm. Dev. Built Environ. 2023, 13, 100121. [Google Scholar] [CrossRef]
- Bu, X.Y.; Xu, Y.Q.; Zhao, M.M.; Li, D.L.; Zhou, J.H.; Wang, L.B.; Bai, J.W.; Yang, Y. Simultaneous extraction of polysaccharides and polyphenols from blackcurrant fruits: Comparison between response surface methodology and artificial neural networks. Ind. Crops Prod. 2021, 170, 113682. [Google Scholar] [CrossRef]
- Nanvakenari, S.; Movagharejad, K.; Latifi, A. Evaluating the fluidized-bed drying of rice using response surface methodology and artificial neural network. LWT—Food Sci. Technol. 2021, 147, 111589. [Google Scholar] [CrossRef]




| Factors | Value |
|---|---|
| soil–soil restitution coefficient | 0.6 |
| soil–soil static friction coefficient | 0.5 |
| soil–soil rolling friction coefficient | 0.4 |
| soil–machine restitution coefficient | 0.6 |
| soil–machine static friction coefficient | 0.5 |
| soil–machine rolling friction coefficient | 0.04 |
| soil–rice straw restitution coefficient | 0.6 |
| soil–rice straw static friction coefficient | 0.5 |
| soil–rice straw rolling friction coefficient | 0.2 |
| rice straw–rice straw restitution coefficient | 0.6 |
| rice straw–rice straw static friction coefficient | 0.5 |
| rice straw–rice straw rolling friction coefficient | 0.01 |
| rice straw–machine restitution coefficient | 0.6 |
| rice straw–machine static friction coefficient | 0.3 |
| rice straw–machine rolling friction coefficient | 0.01 |
| JKR surface energy | 0.15 |
| Level | Operating Speed (km/h) | Buried Depth (mm) | Working Speed (r/min) |
|---|---|---|---|
| 1 | 2 | 160 | 200 |
| 2 | 2.5 | 170 | 220 |
| 3 | 3 | 180 | 240 |
| 4 | 3.5 | 190 | 260 |
| 5 | 4 | 200 | 280 |
| Level Code | Operating Speed (km/h) | Buried Depth (mm) | Working Speed (r/min) |
|---|---|---|---|
| −1 | 2 | 170 | 240 |
| 0 | 2.5 | 180 | 260 |
| 1 | 3 | 190 | 280 |
| No. | A | B | C | Straw-Burying Rate (%) | Machine Forward Resistance (N) |
|---|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 89.33 | 5647 |
| 2 | 1 | −1 | 0 | 86.77 | 7196 |
| 3 | −1 | 1 | 0 | 95.03 | 6206 |
| 4 | 1 | 1 | 0 | 92.55 | 7251 |
| 5 | −1 | 0 | −1 | 87.57 | 6047 |
| 6 | 1 | 0 | −1 | 88.92 | 7467 |
| 7 | −1 | 0 | 1 | 95.77 | 6704 |
| 8 | 1 | 0 | 1 | 90.01 | 7420 |
| 9 | 0 | −1 | −1 | 87.04 | 6273 |
| 10 | 0 | 1 | −1 | 93.71 | 6977 |
| 11 | 0 | −1 | 1 | 95.01 | 6477 |
| 12 | 0 | 1 | 1 | 96.8 | 7294 |
| 13 | 0 | 0 | 0 | 92.4 | 6426 |
| 14 | 0 | 0 | 0 | 92.63 | 6457 |
| 15 | 0 | 0 | 0 | 92.34 | 6046 |
| 16 | 0 | 0 | 0 | 93.05 | 6498 |
| 17 | 0 | 0 | 0 | 92.91 | 6351 |
| 18 | 0 | 0 | 0 | 93.7 | 6374 |
| 19 | 0 | 0 | 0 | 92.51 | 6449 |
| 20 | 0 | 0 | 0 | 92.82 | 6362 |
| Source | Mean Square | Degree of Freedom | Sum of Square | p-Value |
|---|---|---|---|---|
| Model | 17.15 | 9 | 154.3100 | <0.0001 |
| A | 11.1600 | 1 | 11.1600 | 0.0001 |
| B | 49.7000 | 1 | 49.7000 | <0.0001 |
| C | 51.7700 | 1 | 51.7700 | <0.0001 |
| AB | 0.0016 | 1 | 0.0016 | 0.9428 |
| AC | 12.6400 | 1 | 12.6400 | <0.0001 |
| BC | 5.9500 | 1 | 5.9500 | 0.0012 |
| A2 | 22.6100 | 1 | 22.6100 | 0.1605 |
| B2 | 0.5560 | 1 | 0.5560 | 0.1998 |
| C2 | 0.0001 | 1 | 0.0001 | 0.9885 |
| Residual | 0.2951 | 10 | 2.9500 | |
| Lack of fit | 0.5271 | 3 | 1.5800 | 0.1265 |
| Pure error | 0.1956 | 7 | 1.3700 | |
| Sum | 19 | 157.2600 |
| Source | Mean Square | Degree of Freedom | Sum of Square | p-Value |
|---|---|---|---|---|
| Model | 513,400 | 9 | 4,620,000 | <0.0001 |
| A | 2,797,000 | 1 | 2,797,000 | <0.0001 |
| B | 569,800 | 1 | 569,800 | 0.0010 |
| C | 159,900 | 1 | 159,900 | 0.0349 |
| AB | 63,504 | 1 | 63,504 | 0.1553 |
| AC | 123,900 | 1 | 123,900 | 0.0574 |
| BC | 3192.25 | 1 | 3192.25 | 0.7375 |
| A2 | 22.6100 | 1 | 22.6100 | 0.0413 |
| B2 | 147,200 | 1 | 147,200 | 0.7493 |
| C2 | 2900.16 | 1 | 2900.16 | 0.0009 |
| Residual | 591,400 | 10 | 268,800 | |
| Lack of fit | 26,878.76 | 3 | 130,000 | 0.1775 |
| Pure error | 19,820.84 | 7 | 138,700 | |
| Sum | 19 | 4,889,000 |
| Model | Parameter | Values |
|---|---|---|
| BP | training steps | 50 |
| learning rate | 0.001 | |
| number of neurons in the hidden layer | 9 | |
| GA-BP | iteration times | 200 |
| population size | 100 | |
| number of neurons in the hidden layer | 9 | |
| PSO | learning rate | 0.6 |
| Initialize the population number | 50 | |
| iteration times | 100 | |
| inertia factor | 0.1 |
| Model | R2 | MSE | MAE | |||
|---|---|---|---|---|---|---|
| SBR | MER | SBR | MER | SBR | MER | |
| BP | 0.8645 | 0.9399 | 1.1385 | 14,406.5899 | 0.6157 | 78.6879 |
| GA-BP | 0.9814 | 0.9601 | 0.1394 | 10,681.5752 | 0.2281 | 50.3941 |
| PSO | 0.8624 | 0.9477 | 1.1031 | 12,531.1535 | 0.5486 | 66.0054 |
| Value | R2 | MSE | MAE | |||
|---|---|---|---|---|---|---|
| SBR | MER | SBR | MER | SBR | MER | |
| 3 | 0.8180 | 0.8269 | 1.7049 | 38,777.4200 | 0.9739 | 124.8300 |
| 4 | 0.8422 | 0.8296 | 1.5617 | 54,210.8800 | 0.9190 | 151.3200 |
| 5 | 0.9149 | 0.8369 | 0.7147 | 39,771.5900 | 0.5411 | 141.4400 |
| 6 | 0.9045 | 0.8872 | 0.7203 | 28,001.9100 | 0.5606 | 126.7800 |
| 7 | 0.9392 | 0.8826 | 0.4457 | 22,984.2700 | 0.3949 | 96.7060 |
| 8 | 0.9357 | 0.9059 | 0.5056 | 23,214.9600 | 0.3449 | 98.8310 |
| 9 | 0.9677 | 0.9701 | 0.2609 | 9520.4390 | 0.2615 | 57.6210 |
| 10 | 0.9235 | 0.8943 | 0.4807 | 27,517.5100 | 0.4005 | 102.0500 |
| 11 | 0.9003 | 0.8834 | 0.7077 | 28,375.1100 | 0.5014 | 115.2600 |
| 12 | 0.8706 | 0.8897 | 0.6581 | 22,633.1100 | 0.4786 | 107.7600 |
| 13 | 0.8606 | 0.8716 | 0.8225 | 30,916.0500 | 0.6006 | 100.1100 |
| Value | R2 | MSE | MAE | |||
|---|---|---|---|---|---|---|
| SBR | MER | SBR | MER | SBR | MER | |
| 25 | 0.8325 | 0.8597 | 1.2412 | 35,402.22 | 0.7804 | 107.5754 |
| 50 | 0.9389 | 0.8997 | 0.4503 | 27,862.13 | 0.4843 | 119.3024 |
| 75 | 0.8608 | 0.9225 | 1.1332 | 18,955.8 | 0.6646 | 78.8395 |
| 100 | 0.9206 | 0.9264 | 0.6238 | 18,222.21 | 0.3652 | 88.5078 |
| 125 | 0.9119 | 0.9113 | 0.6929 | 16,788.64 | 0.4636 | 96.9820 |
| 150 | 0.9765 | 0.9701 | 0.2094 | 5652.656 | 0.2564 | 56.8173 |
| 175 | 0.8986 | 0.9044 | 0.7971 | 23,358.52 | 0.4933 | 87.8477 |
| 200 | 0.8385 | 0.9275 | 1.2696 | 17,722.82 | 0.5367 | 71.7827 |
| Value | R2 | MSE | MAE | |||
|---|---|---|---|---|---|---|
| SBR | MER | SBR | MER | SBR | MER | |
| 100 | 0.8589 | 0.8251 | 1.2827 | 42,743.3500 | 0.7841 | 137.2596 |
| 150 | 0.8847 | 0.8892 | 1.1515 | 21,678.3500 | 0.7043 | 95.9713 |
| 200 | 0.9862 | 0.9667 | 0.0853 | 6979.6340 | 0.1622 | 61.7603 |
| 250 | 0.8804 | 0.9168 | 0.9402 | 20,344.9900 | 0.595 | 80.3930 |
| 300 | 0.8562 | 0.8214 | 1.2565 | 43,864.0800 | 0.7221 | 174.7358 |
| Parameters | Value |
|---|---|
| Machine size (L × W × H)/mm | 3068 × 1004 × 1175 |
| Working width/mm | 2800 |
| Number of discs | 34 |
| Number of spring teeth | 76 |
| Matching traction power requirement/kw | ≥66 |
| Hydraulic cylinder extension/mm | 100 |
| Diameter of the grass pressure disk/mm | 500 |
| Depth of burial/mm | ≥160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Ma, X.; Feng, W.; Jing, H.; Shi, Q.; Wang, Y.; Huang, D.; Wang, J. Optimization of Operation Parameters and Performance Prediction of Paddy Field Grader Based on a GA-BP Neural Network. Agriculture 2024, 14, 1283. https://doi.org/10.3390/agriculture14081283
Liu M, Ma X, Feng W, Jing H, Shi Q, Wang Y, Huang D, Wang J. Optimization of Operation Parameters and Performance Prediction of Paddy Field Grader Based on a GA-BP Neural Network. Agriculture. 2024; 14(8):1283. https://doi.org/10.3390/agriculture14081283
Chicago/Turabian StyleLiu, Min, Xuejie Ma, Weizhi Feng, Haiyang Jing, Qian Shi, Yang Wang, Dongyan Huang, and Jingli Wang. 2024. "Optimization of Operation Parameters and Performance Prediction of Paddy Field Grader Based on a GA-BP Neural Network" Agriculture 14, no. 8: 1283. https://doi.org/10.3390/agriculture14081283
APA StyleLiu, M., Ma, X., Feng, W., Jing, H., Shi, Q., Wang, Y., Huang, D., & Wang, J. (2024). Optimization of Operation Parameters and Performance Prediction of Paddy Field Grader Based on a GA-BP Neural Network. Agriculture, 14(8), 1283. https://doi.org/10.3390/agriculture14081283








