Simulation and Optimization of a Rotary Cotton Precision Dibbler Using DEM and MBD Coupling
Abstract
1. Introduction
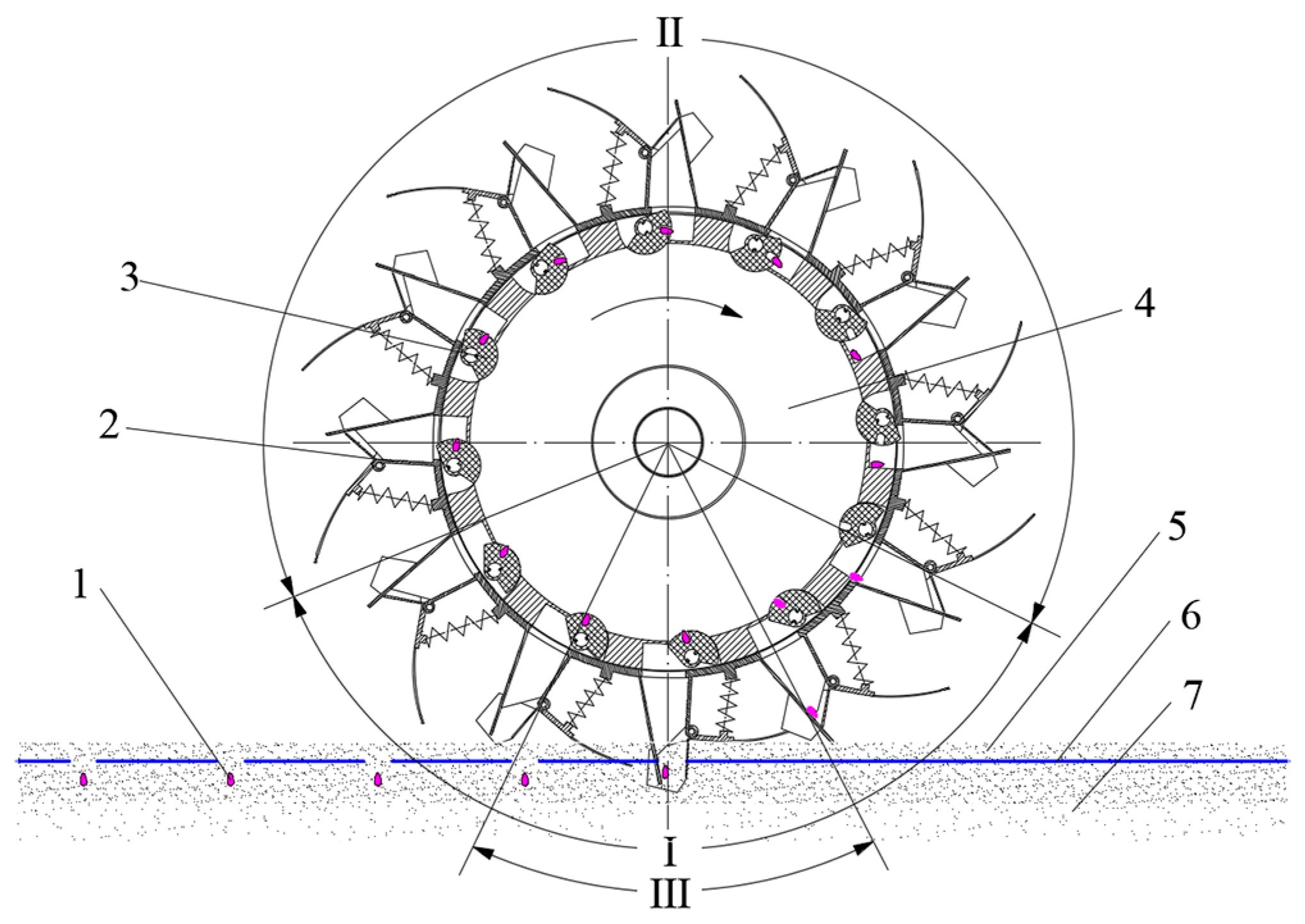
2. Structure Analysis and Modeling of the Dibbler
2.1. Working Principle of the Rotary Type-Hole Dibbler
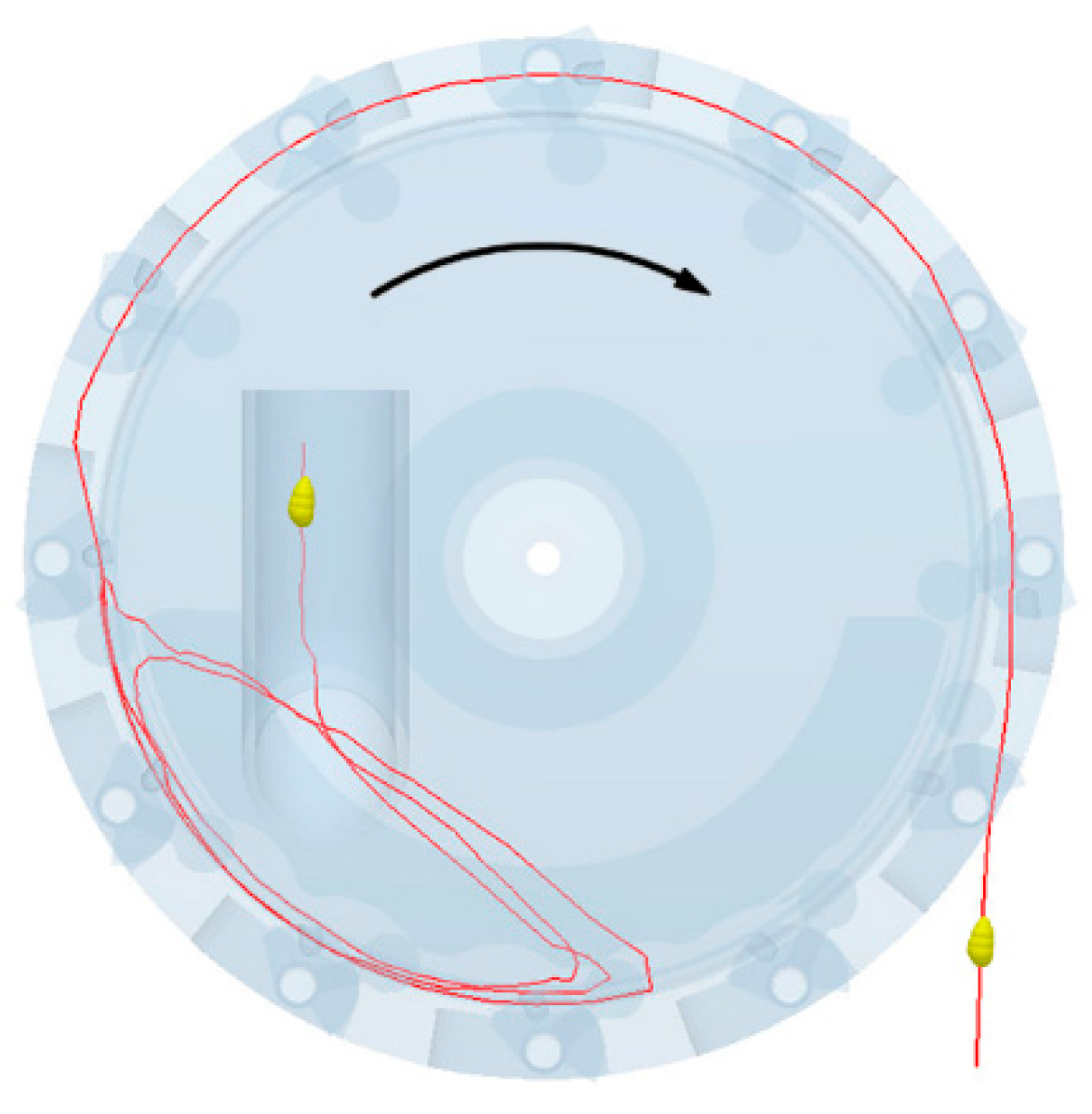
2.2. Analysis of the Seed-Picking Movement of the Type-Hole Wheel
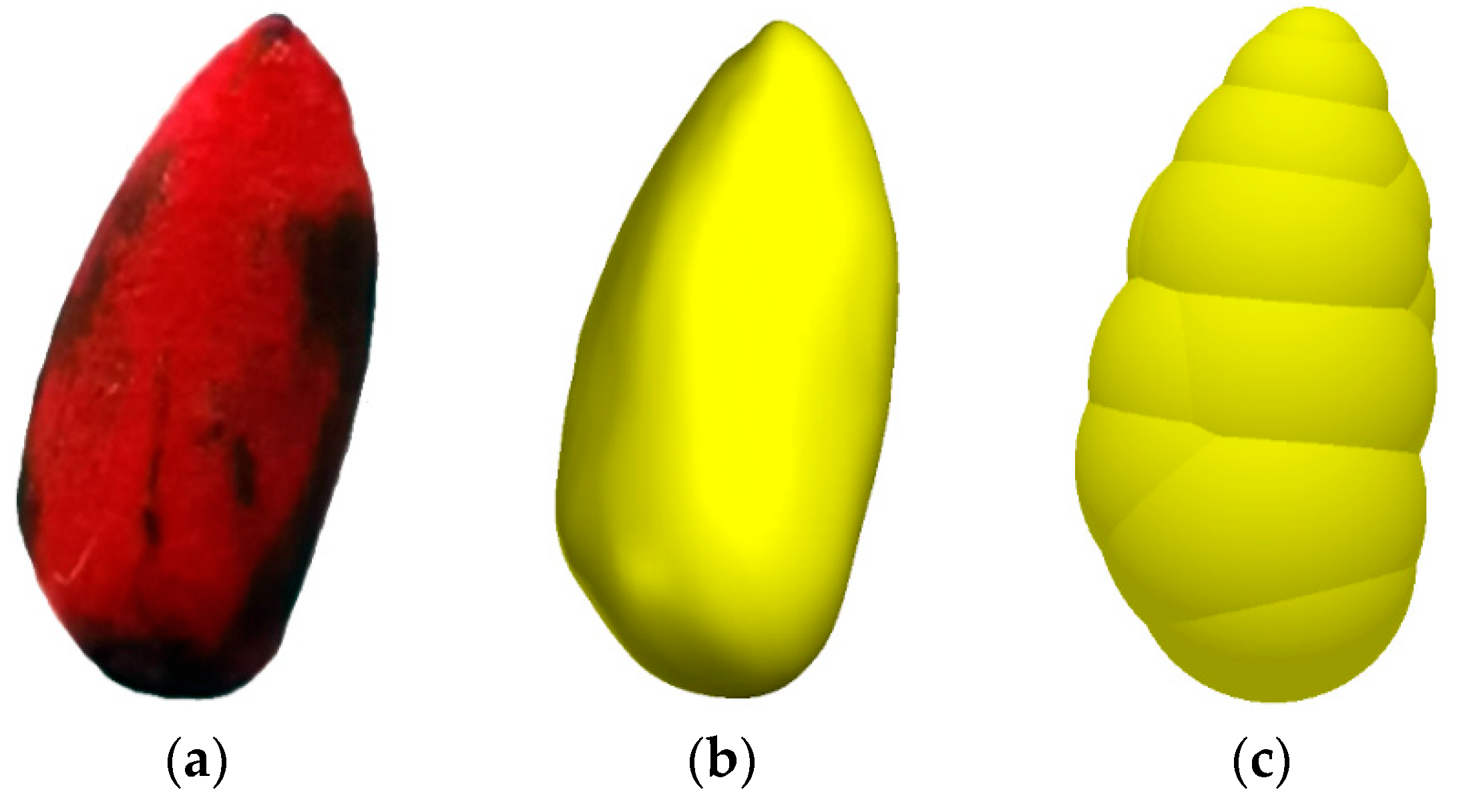
2.3. Establishment of a Discrete Element Model for Coated Cotton Seeds
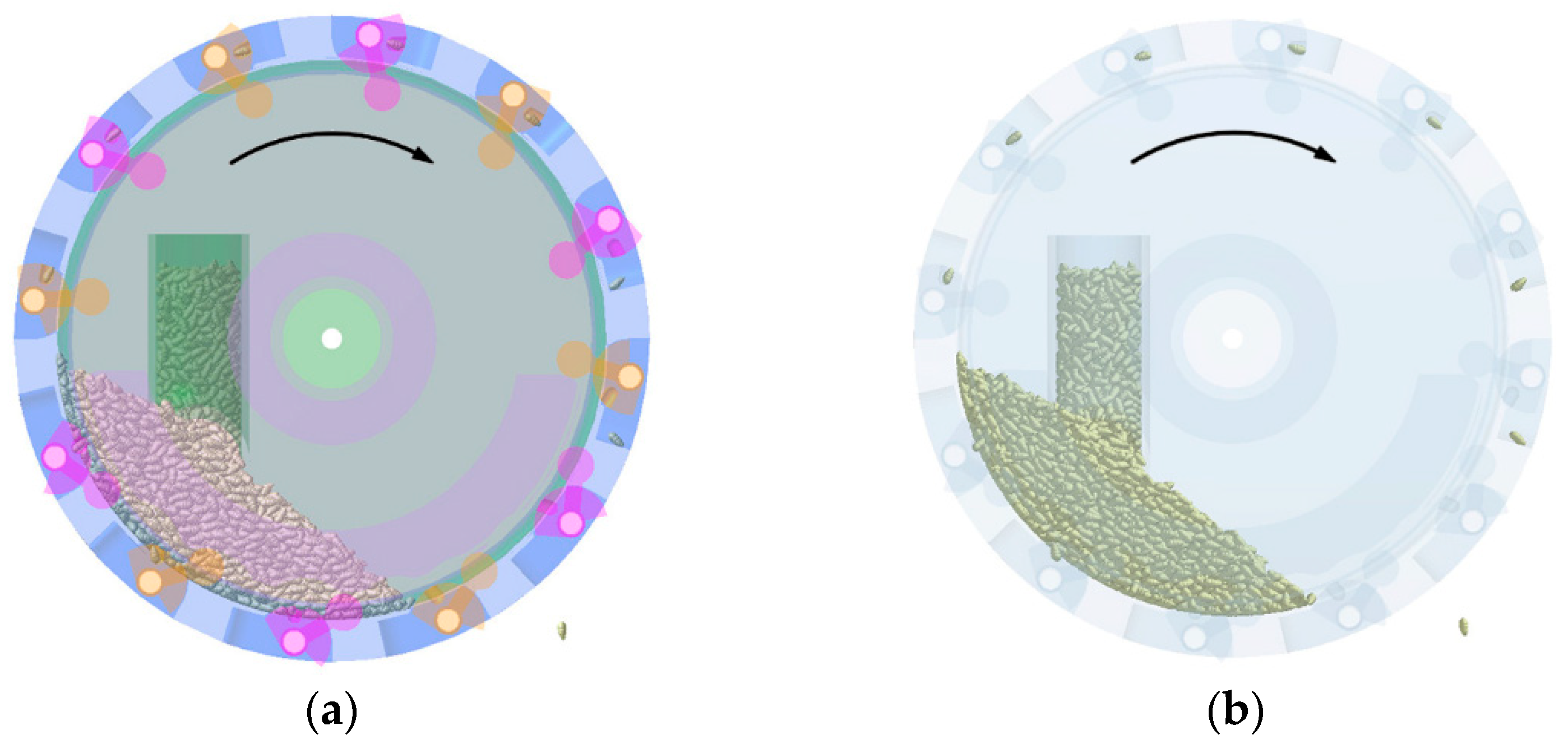
2.4. Establishment of the DEM-MBD Coupling Simulation Model
3. Simulation and Bench Tests
3.1. Simulation Test
3.2. Bench Test
4. Results and Discussion
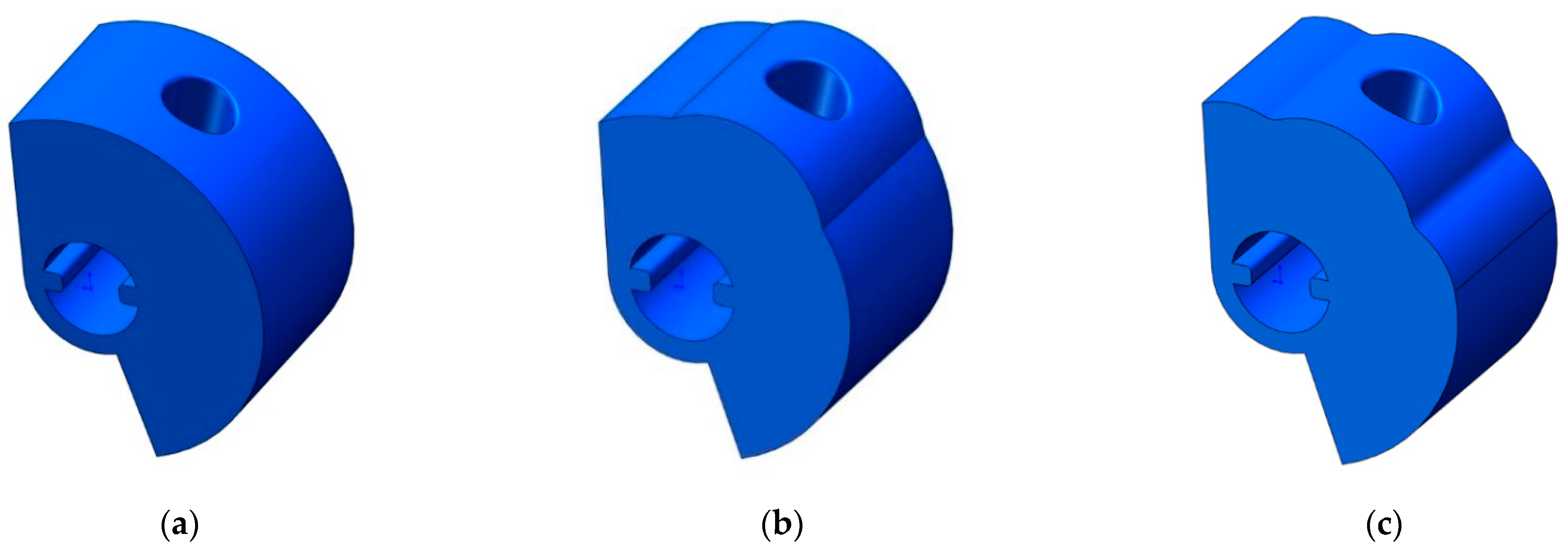
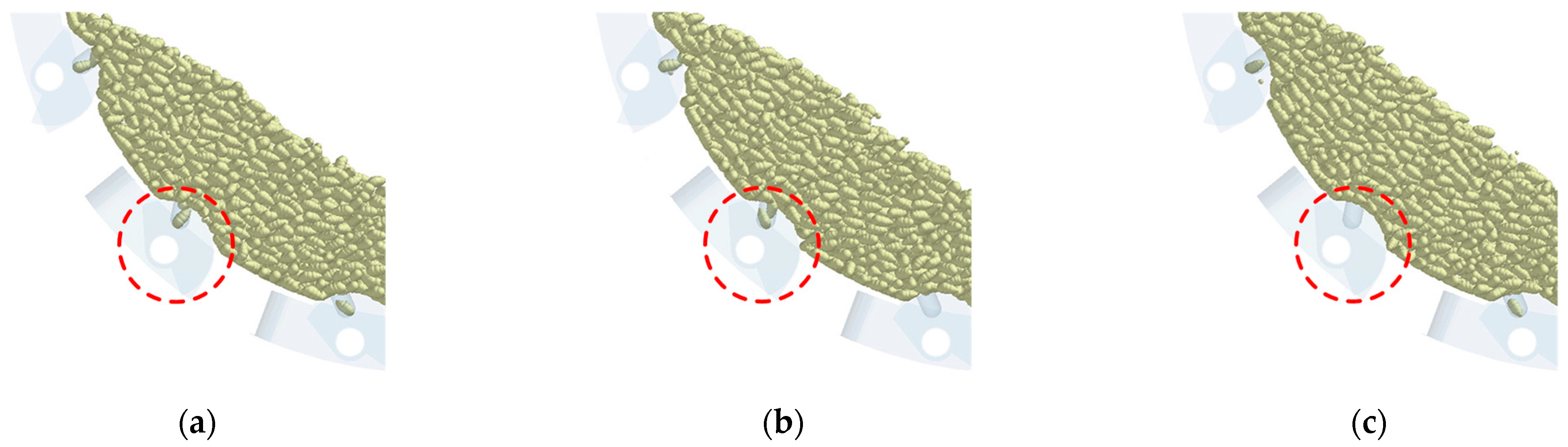
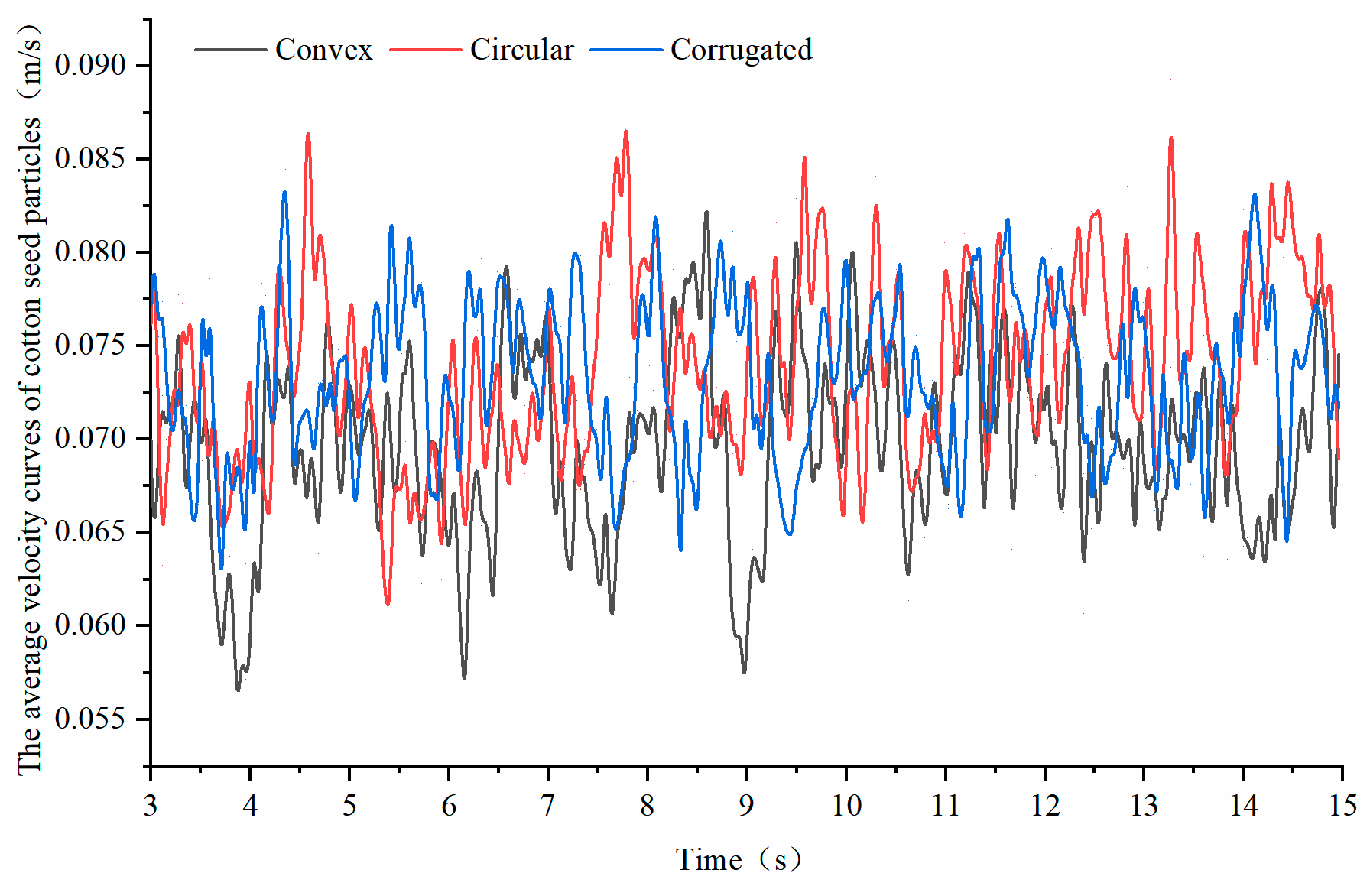
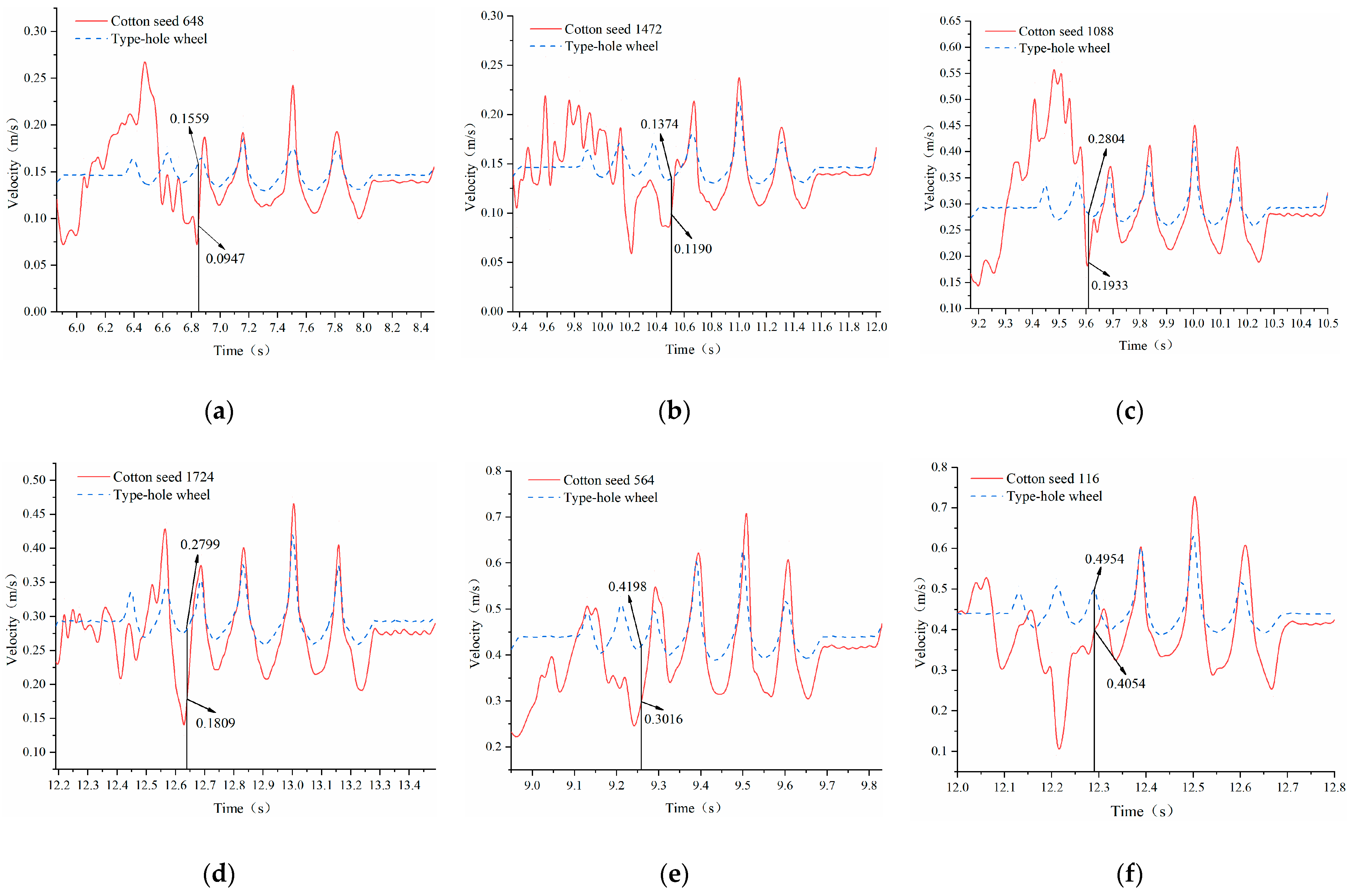
4.1. Impact of the Type-Hole Wheel Structure on the Seeding Performance
4.2. Influence of the Dibbler Rotation Speed on Seeding Performance
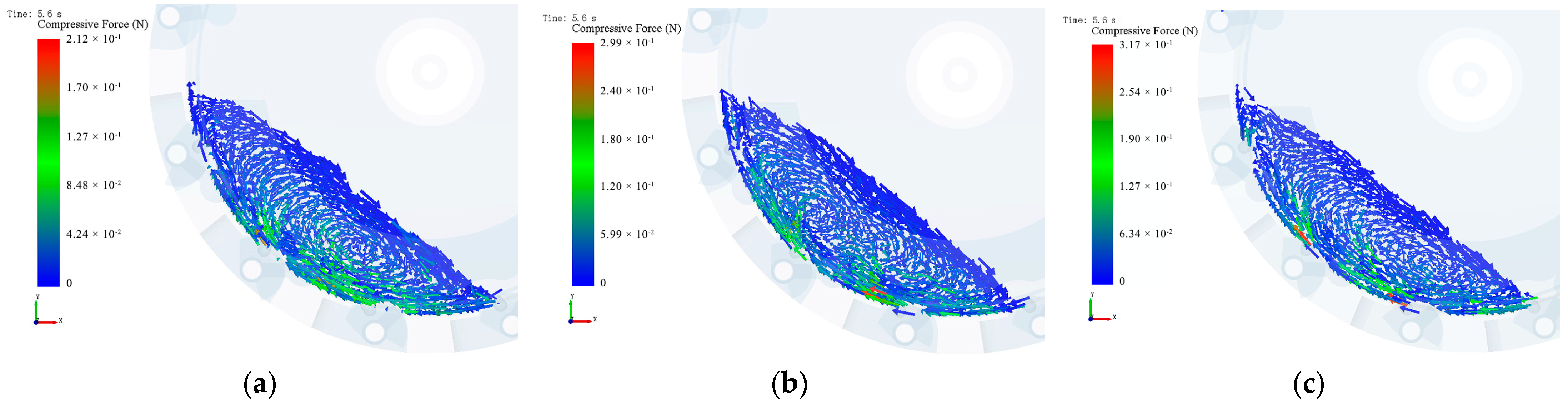
4.3. Effects of the Motion Parameters of the Type-Hole Wheel on Seeding Performance
4.4. Optimization and Validation of Seeder Performance in Bench Tests
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Wu, B.; Niu, L.K.; Xiong, X.Y.; Dong, Z.X. Dynamic characteristics of two-way coupling between flip-flow screen and particles based on DEM. Chin. Coal Soc. 2019, 44, 1930–1940. [Google Scholar]
- Gan, J.Q.; Zhou, Z.Y.; Yu, A.B.; Ellis, D.; Attwood, R.; Chen, W. Co-simulation of multibody dynamics and discrete element method for hydraulic excavators. Powder Technol. 2023, 414, 118001. [Google Scholar] [CrossRef]
- Fang, J.; Zhao, C.F.; Lu, X.Y.; Xiong, W.H.; Shi, C. Dynamic behavior of railway Vehicle-Ballasted track system with unsupported sleepers based on the hybrid DEM-MBD method. Constr. Build. Mater. 2023, 394, 132091. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Els, D.N.J.; Dymond, G.F. Discrete element parameter calibration and the modelling of dragline bucket filling. J. Terramech. 2010, 47, 33–44. [Google Scholar] [CrossRef]
- Lommen, S.; Lodewijks, G.; Schott, D.L. Co-simulation framework of discrete element method and multibody dynamics models. Eng. Comput. 2018, 35, 1481–1499. [Google Scholar] [CrossRef]
- Lu, Z.; Lu, X.L.; Lu, W.S.; Masri, S.F. Studies of the performance of particle dampers under dynamic loads. J. Sound Vib. 2010, 329, 5415–5433. [Google Scholar] [CrossRef]
- Ahmad, N.; Ranganath, R.; Ghosal, A. Modeling and experimental study of a honeycomb beam filled with damping particles. J. Sound Vib. 2017, 391, 20–34. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; Tavares, L.M. A preliminary model of high pressure roll grinding using the discrete element method and multi-body dynamics coupling. Int. J. Miner. Process. 2016, 156, 32–42. [Google Scholar] [CrossRef]
- Ji, S.Y.; Liang, S.M. DEM-FEM-MBD coupling analysis of landing process of lunar lander considering landing mode and buffering mechanism. Adv. Space Res. 2021, 68, 1627–1643. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; de Kluijver, W.; Helmons, R.L.J.; van Rhee, C.; Schott, D.L. A validated co-simulation of grab and moist iron ore cargo: Replicating the cohesive and stress behaviour of bulk solids. Adv. Powder Technol. 2021, 32, 1157–1169. [Google Scholar] [CrossRef]
- Shi, S.W.; Gao, L.; Xiao, H.; Xu, Y.; Yin, H. Research on ballast breakage under tamping operation based on DEM-MBD coupling approach. Constr. Build. Mater. 2021, 272, 1810–1822. [Google Scholar] [CrossRef]
- Shi, S.W.; Gao, L.; Cai, X.P.; Yin, H.; Wang, X.L. Effect of tamping operation on mechanical qualities of ballast bed based on DEM-MBD coupling method. Comput. Geotech. 2020, 124, 103574. [Google Scholar] [CrossRef]
- Xiao, W.Q.; Huang, Y.X.; Jiang, H.; Lin, H.; Li, J.L. Energy dissipation mechanism and experiment of particle dampers for gear transmission under centrifugal loads. Particuology 2016, 27, 40–50. [Google Scholar] [CrossRef]
- Xiao, W.Q.; Li, J.N.; Pan, T.L.; Zhang, X.; Huang, Y.X. Investigation into the influence of particles’ friction coefficient on vibration suppression in gear transmission. Mech. Mach. Theory 2017, 108, 217–230. [Google Scholar] [CrossRef]
- Chung, Y.C.; Wu, Y.R. Dynamic modeling of a gear transmission system containing damping particles using coupled multi-body dynamics and discrete element method. Nonlinear Dyn. 2019, 98, 129–149. [Google Scholar] [CrossRef]
- Wu, Y.R.; Chung, Y.C.; Wang, I.C. Two-way coupled MBD-DEM modeling and experimental validation for the dynamic response of mechanisms containing damping particles. Mech. Mach. Theory 2021, 159, 104257. [Google Scholar] [CrossRef]
- Curry, D.R.; Deng, Y. Optimizing Heavy Equipment for Handling Bulk Materials with Adams-EDEM Co-simulation. In Proceedings of the 7th International Conference on Discrete Element Methods (DEM), Dalian, China, 15 December 2017. [Google Scholar]
- Hu, J.P.; Pan, J.; Chen, F.; Yue, R.C.; Yao, M.J.; Li, J. Simulation Optimization and Experiment of Finger-clamping Seedling Picking Claw Based on EDEM RecurDyn. Chin. Soc. Agric. Mach. 2022, 53, 75–85+301. [Google Scholar]
- Xu, T.Y.; Zhang, R.X.; Wang, Y.; Jiang, X.M.; Feng, W.Z.; Wang, J.L. Simulation and Analysis of the Working Process of Soil Covering and Compacting of Precision Seeding Units Based on the Coupling Model of DEM with MBD. Processes 2022, 10, 1103. [Google Scholar] [CrossRef]
- Yan, D.X.; Xu, T.Y.; Yu, J.Q.; Wang, Y.; Guan, W.; Tian, Y.; Zhang, N. Test and Simulation Analysis of the Working Process of Soybean Seeding Monomer. Agriculture 2022, 12, 1464. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.P.; Zhang, T. Load Analysis of Rotary Cutter Shaft for Power Tiller Based on DEM and MBD Theory. J. Agric. Sci. Technol. 2020, 22, 79–86. [Google Scholar]
- Lai, Q.H.; Jia, G.X.; Su, W.; Zhao, L.J.; Qiu, X.B.; Lu, Q. Design and Test of Chain Spoom Type Precision Seed Metering Device for Ginseng Based onDEM-MBD Coupling. Chin. Soc. Agric. Mach. 2022, 53, 91–104. [Google Scholar]
- Kim, Y.S.; Lee, S.D.; Baek, S.M.; Baek, S.Y.; Jeon, H.H.; Lee, J.H.; Siddique, M.A.; Kim, Y.J.; Kim, W.S.; Sim, T.; et al. Development of DEM-MBD coupling model for draft force prediction of agricultural tractor with plowing depth. Comput. Electron. Agric. 2022, 202, 107405. [Google Scholar] [CrossRef]
- Dong, X.Q.; Su, C.; Zheng, H.N.; Han, R.Q.; Li, Y.L.; Wan, L.P.C.; Song, J.N.; Wang, J.C. Analysis of soil disturbance process by vibrating subsoiling based on DEM-MBD coupling algorithm. Transact. Chin Soc. Agric. Eng. 2022, 38, 34–43. [Google Scholar]
- Yu, Q.X.; Liu, Y.; Chen, X.B.; Sun, K.; Lai, Q.H. Calibration and Experiment of Simulation Parameters for Panax notoginseng Seeds Based on DEM. Chin. Soc. Agric. Mach. 2020, 51, 123–132. [Google Scholar]
- Abbaspour-Fard, M.H. Theoretical validation of a multi-sphere discrete element model suitable for biomaterials handling simulation. Biosyst. Eng. 2004, 88, 153–161. [Google Scholar] [CrossRef]
- Wang, L.; He, X.W.; Hu, C.; Guo, W.S.; Wang, X.F.; Xing, J.F. Measurement of physical parameters of coated cotton seed and parameter calibration of discrete element. Chin. Agric. Univ. 2022, 27, 71–82. [Google Scholar]
- Wang, L.; Hu, C.; He, X.W.; Guo, W.S.; Hou, S.L. A general modelling approach for coated cotton-seeds based on the discrete element method. Inmateh-Agric. Eng. 2021, 63, 219–228. [Google Scholar]




| Parameter | Value |
|---|---|
| Density of cotton seed (g/cm3) | 0.981 |
| Poisson’s ratio of cotton seed | 0.27 |
| Shear modulus of cotton seed (MPa) | 1.4 × 107 |
| Density of resin (g/cm3) | 1.18 |
| Poisson’s ratio of resin | 0.38 |
| Shear modulus of resin (MPa) | 177 |
| Seed-to-seed static friction coefficient | 0.130 |
| Seed-to-seed dynamic friction coefficient | 0.225 |
| Seed-to-seed collision restoration coefficient | 0.185 |
| Seed-to-resin static friction coefficient | 0.49 |
| Seed-to-resin dynamic friction coefficient | 0.21 |
| Seed-to-resin collision restoration coefficient | 0.25 |
| Level | Rotation Speed of Dibbler X1 (r/min) | Number of Teeth on the Gear Plate X2 | Oscillation Amplitude of the Type-Hole Wheel X3 (mm) |
|---|---|---|---|
| −1 | 10 | 4 | 7 |
| 0 | 20 | 6 | 10 |
| 1 | 30 | 8 | 13 |
| No. | Rotation Speed of Dibbler X1 (r/min) | Number of Teeth on the Gear Plate X2 | Oscillation Amplitude of Type-Hole Wheel X3 (mm) | Qualified Index Y1 (%) | Re-Sowing Index Y2 (%) | Skip Sowing Index Y3 (%) |
|---|---|---|---|---|---|---|
| 1 | −1 | 1 | 0 | 89.69 | 7.25 | 3.06 |
| 2 | 0 | −1 | −1 | 89.16 | 5.39 | 5.45 |
| 3 | 0 | −1 | 1 | 89.22 | 4.16 | 6.62 |
| 4 | −1 | 0 | 1 | 90.43 | 6.52 | 3.05 |
| 5 | 0 | 1 | −1 | 88.48 | 6.34 | 5.18 |
| 6 | 0 | 0 | 0 | 91.65 | 3.88 | 4.47 |
| 7 | 0 | 0 | 0 | 91.57 | 4.32 | 4.11 |
| 8 | 1 | −1 | 0 | 86.58 | 4.49 | 8.93 |
| 9 | 0 | 1 | 1 | 86.96 | 6.89 | 6.15 |
| 10 | 0 | 0 | 0 | 91.52 | 4.21 | 4.27 |
| 11 | 1 | 0 | −1 | 87.77 | 4.54 | 7.69 |
| 12 | 1 | 0 | 1 | 85.31 | 4.85 | 8.84 |
| 13 | −1 | 0 | −1 | 90.96 | 6.26 | 2.78 |
| 14 | 0 | 0 | 0 | 92.19 | 3.75 | 4.06 |
| 15 | −1 | −1 | 0 | 90.45 | 6.38 | 3.17 |
| 16 | 1 | 1 | 0 | 86.48 | 5.23 | 8.29 |
| 17 | 0 | 0 | 0 | 91.96 | 3.65 | 4.39 |
| Source of Variance | Sum of Squares | Degrees of Freedom | F | p | Significance |
|---|---|---|---|---|---|
| Model | 74.67 | 9 | 42.97 | <0.0001 | ** |
| X1 | 29.61 | 1 | 153.33 | <0.0001 | ** |
| X2 | 1.81 | 1 | 9.35 | 0.0184 | * |
| X3 | 2.48 | 1 | 12.82 | 0.0090 | ** |
| X1X2 | 0.1089 | 1 | 0.5640 | 0.4771 | |
| X1X3 | 0.9312 | 1 | 4.82 | 0.0641 | |
| X2X3 | 0.6241 | 1 | 3.23 | 0.1152 | |
| X1X1 | 11.57 | 1 | 59.93 | 0.0001 | ** |
| X2X2 | 13.95 | 1 | 72.25 | <0.0001 | ** |
| X3X3 | 9.51 | 1 | 49.24 | 0.0002 | ** |
| Residual | 1.35 | 7 | |||
| Lack of fit | 1.02 | 3 | 4.14 | 0.1017 | |
| Error | 0.3291 | 4 | |||
| Sum | 76.02 | 16 |
| Source of Variance | Sum of Squares | Degrees of Freedom | F | p | Significance |
|---|---|---|---|---|---|
| Model | 21.69 | 9 | 15.29 | 0.0008 | ** |
| X1 | 6.66 | 1 | 42.26 | 0.0003 | ** |
| X2 | 3.50 | 1 | 22.19 | 0.0022 | ** |
| X3 | 0.0015 | 1 | 0.0096 | 0.9247 | |
| X1X2 | 0.0042 | 1 | 0.0268 | 0.8746 | |
| X1X3 | 0.0006 | 1 | 0.0040 | 0.9516 | |
| X2X3 | 0.7921 | 1 | 5.03 | 0.0599 | |
| X1X1 | 3.12 | 1 | 19.82 | 0.0030 | ** |
| X2X2 | 4.33 | 1 | 27.46 | 0.0012 | ** |
| X3X3 | 2.18 | 1 | 13.81 | 0.0075 | ** |
| Residual | 1.10 | 7 | |||
| Lack of fit | 0.7647 | 3 | 3.01 | 0.1574 | |
| Error | 0.3387 | 4 | |||
| Sum | 22.79 | 16 |
| Source of Variance | Sum of Squares | Degrees of Freedom | F | p | Significance |
|---|---|---|---|---|---|
| Model | 69.15 | 9 | 270.38 | <0.0001 | ** |
| X1 | 58.81 | 1 | 2069.37 | <0.0001 | ** |
| X2 | 0.2775 | 1 | 9.77 | 0.0167 | * |
| X3 | 1.58 | 1 | 55.75 | 0.0001 | ** |
| X1X2 | 0.0702 | 1 | 2.47 | 0.1599 | |
| X1X3 | 0.1936 | 1 | 6.81 | 0.0349 | * |
| X2X3 | 0.0100 | 1 | 0.3519 | 0.5717 | |
| X1X1 | 1.90 | 1 | 66.76 | <0.0001 | ** |
| X2X2 | 3.65 | 1 | 128.49 | <0.0001 | ** |
| X3X3 | 1.83 | 1 | 64.30 | <0.0001 | ** |
| Residual | 0.1989 | 7 | |||
| Lack of fit | 0.0753 | 3 | 0.8126 | 0.5498 | |
| Error | 0.1236 | 4 | |||
| Sum | 69.35 | 16 |
| Rotation Speed of the Dibbler (r/min) | Qualified Index (%) | Re-Sowing Index (%) | Skip Sowing Index (%) |
|---|---|---|---|
| 12 | 91.78 | 6.64 | 1.58 |
| 16 | 93.28 | 4.35 | 2.37 |
| 20 | 92.95 | 3.98 | 3.07 |
| 24 | 92.17 | 3.04 | 4.79 |
| 28 | 90.71 | 2.82 | 6.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Ran, X.; Shi, L.; Xing, J.; Wang, X.; Hou, S.; Li, H. Simulation and Optimization of a Rotary Cotton Precision Dibbler Using DEM and MBD Coupling. Agriculture 2024, 14, 1411. https://doi.org/10.3390/agriculture14081411
Wang L, Ran X, Shi L, Xing J, Wang X, Hou S, Li H. Simulation and Optimization of a Rotary Cotton Precision Dibbler Using DEM and MBD Coupling. Agriculture. 2024; 14(8):1411. https://doi.org/10.3390/agriculture14081411
Chicago/Turabian StyleWang, Long, Xuyang Ran, Lu Shi, Jianfei Xing, Xufeng Wang, Shulin Hou, and Hong Li. 2024. "Simulation and Optimization of a Rotary Cotton Precision Dibbler Using DEM and MBD Coupling" Agriculture 14, no. 8: 1411. https://doi.org/10.3390/agriculture14081411
APA StyleWang, L., Ran, X., Shi, L., Xing, J., Wang, X., Hou, S., & Li, H. (2024). Simulation and Optimization of a Rotary Cotton Precision Dibbler Using DEM and MBD Coupling. Agriculture, 14(8), 1411. https://doi.org/10.3390/agriculture14081411





