Design and Optimization of Power Harrow Soil Crushing Components for Coastal Saline–Alkali Land
Abstract
:1. Introduction
2. Materials and Methods
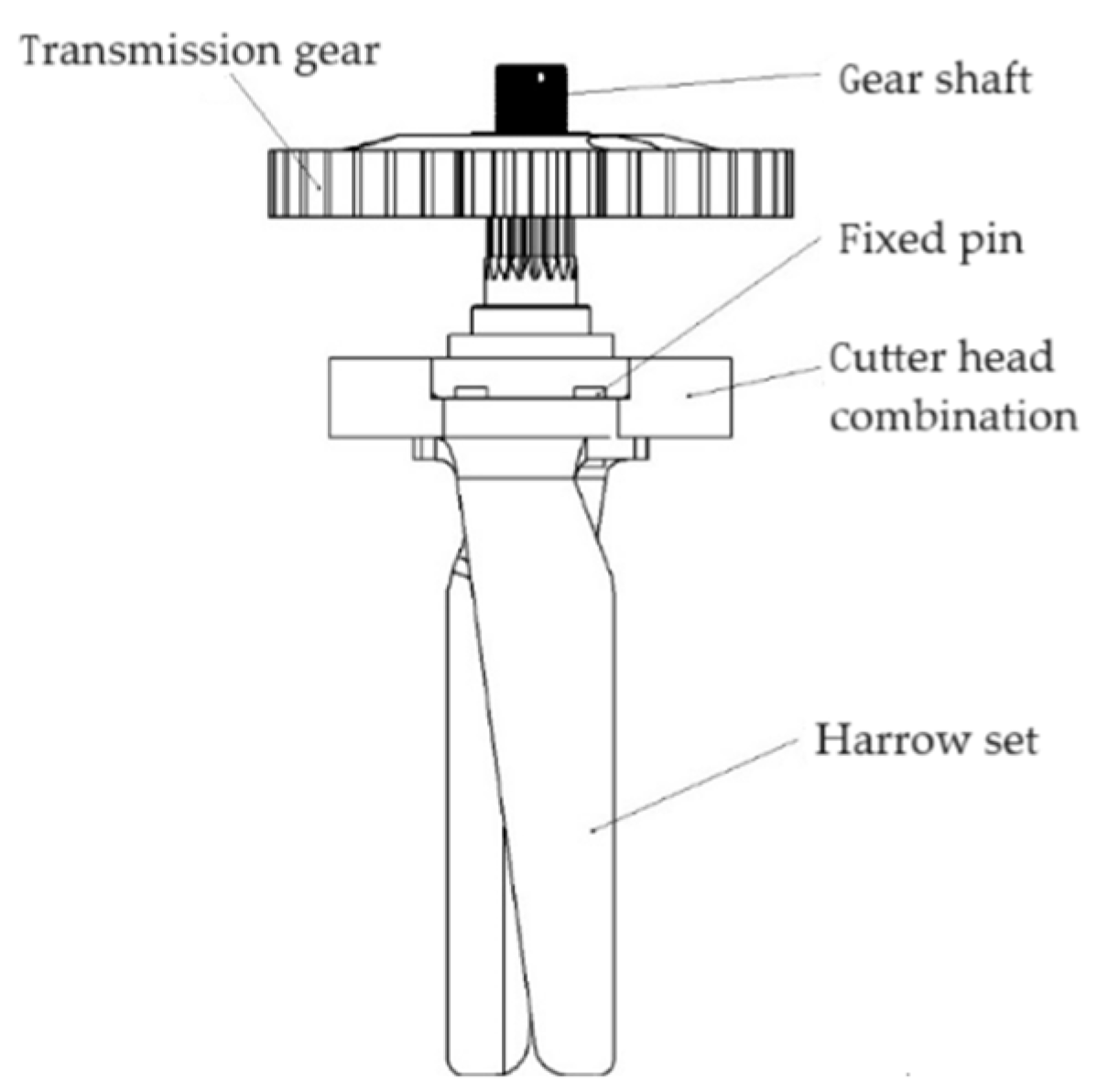
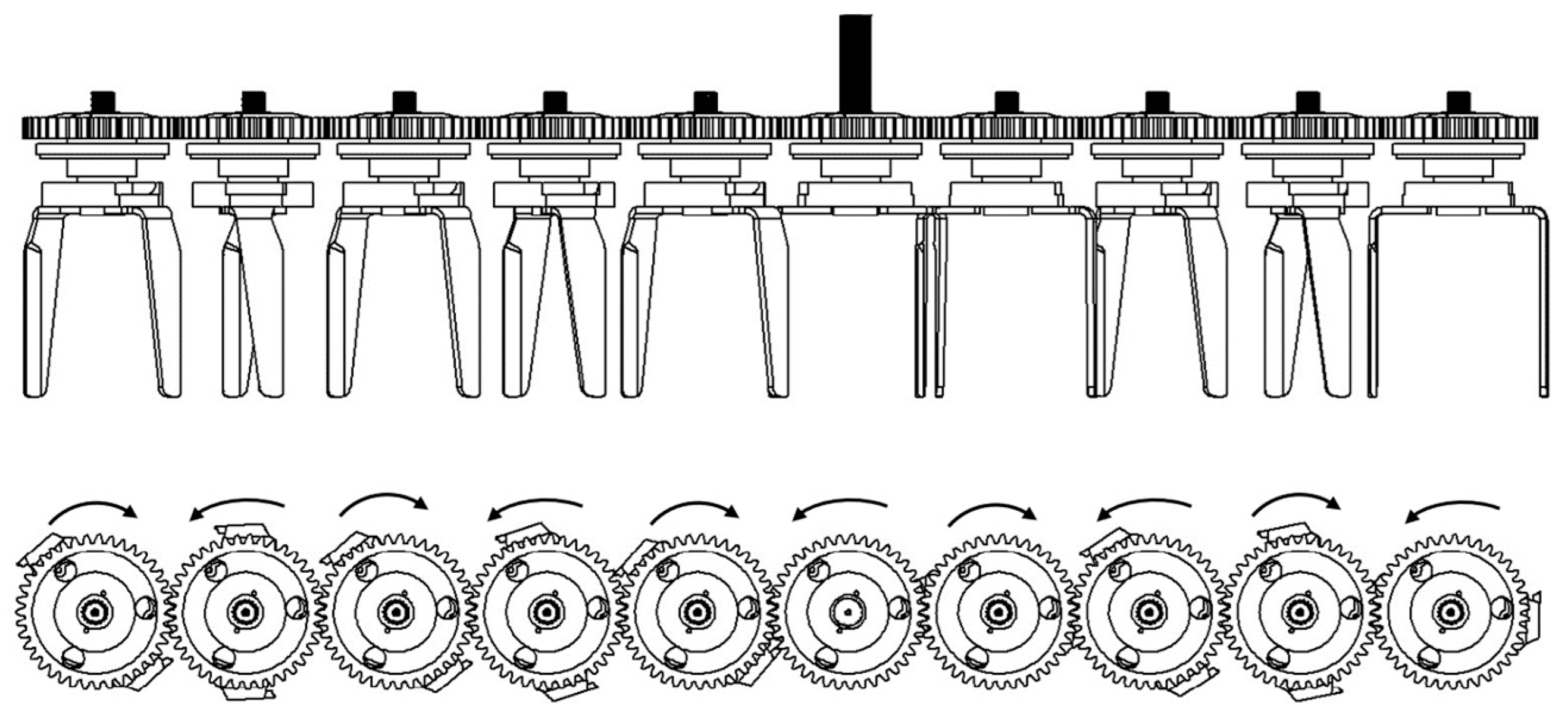
2.1. Machine Structure and Working Principle
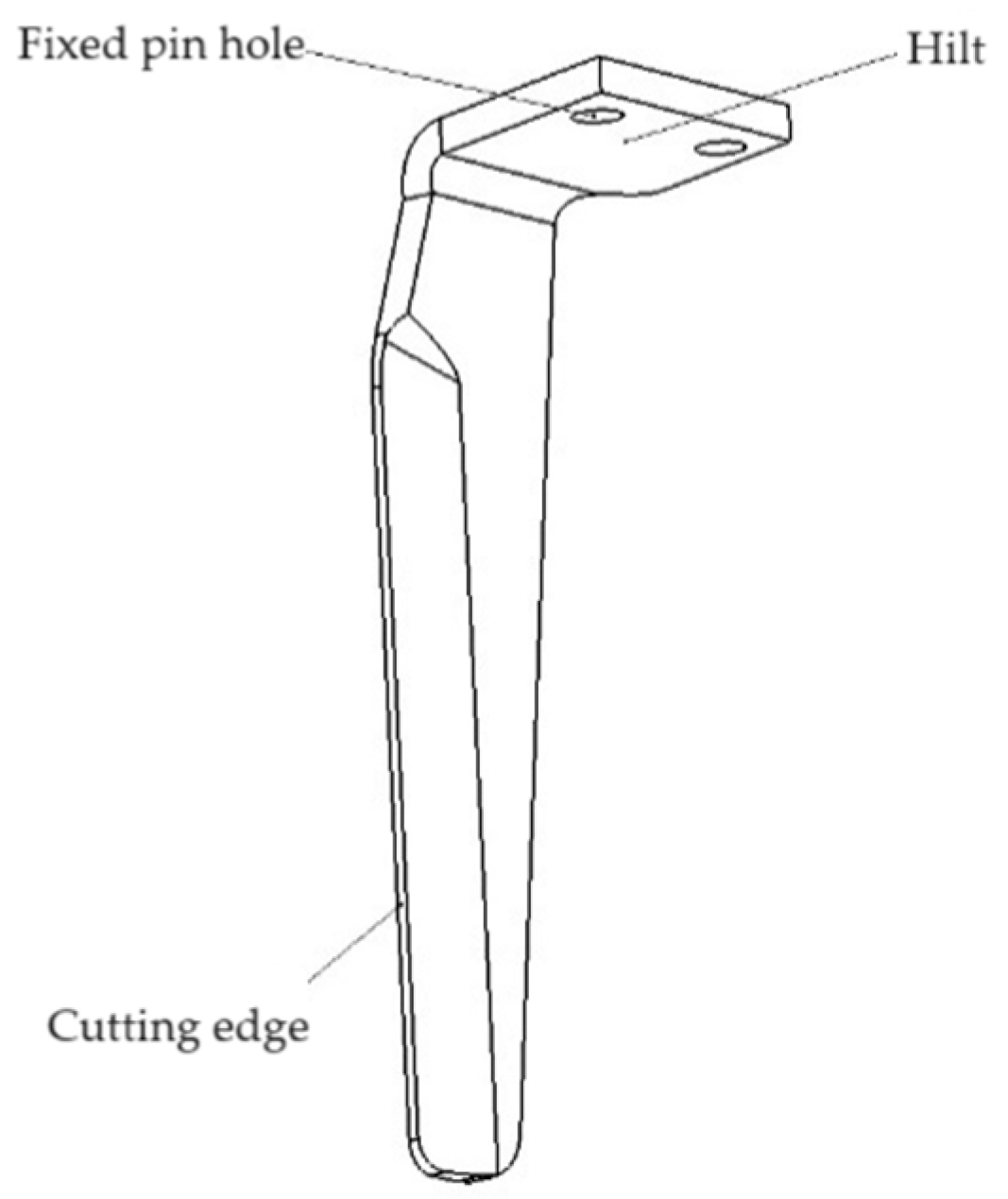
2.2. Design of the Soil Crushing Components of the Power Harrow
- (1)
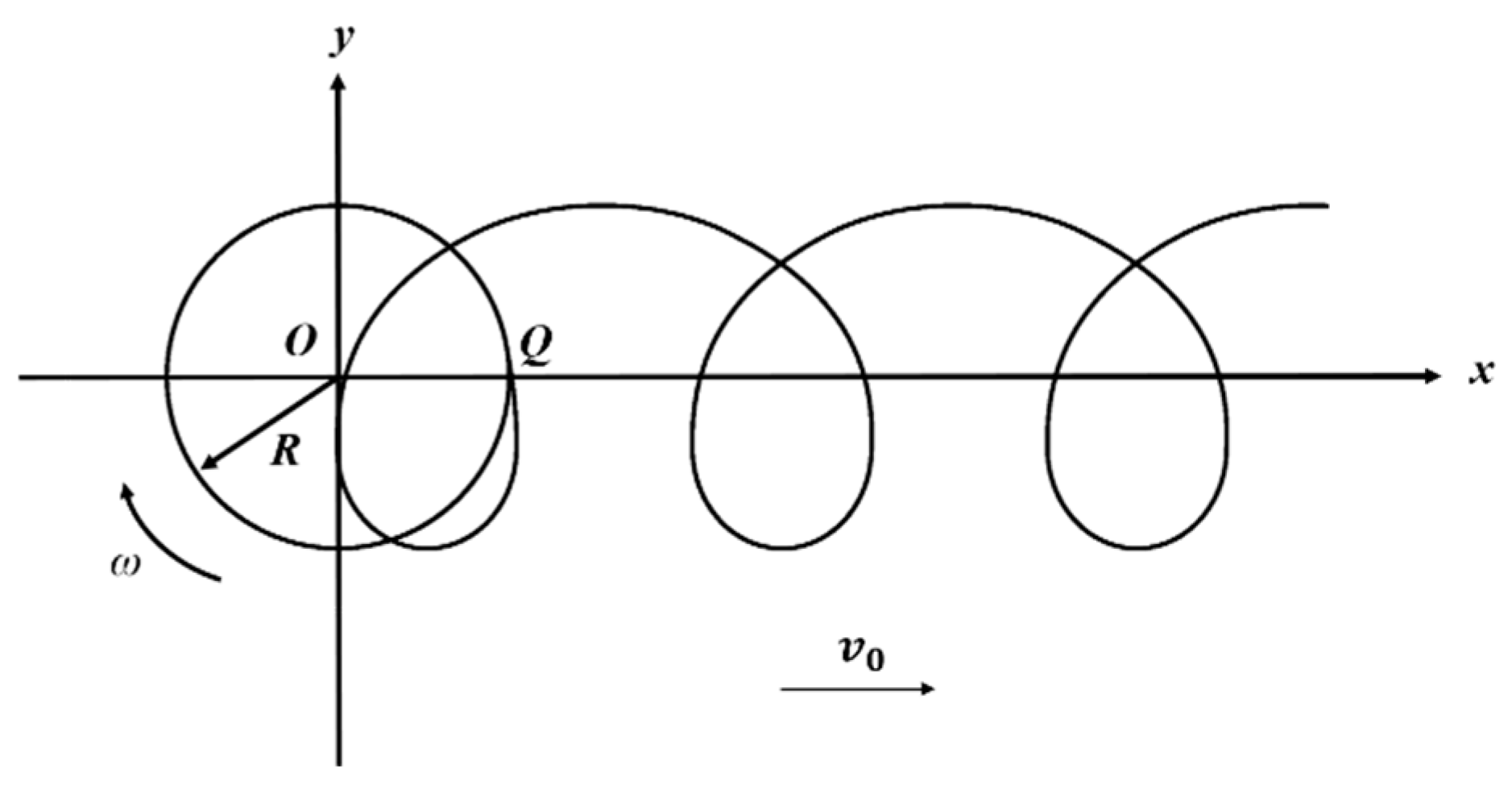
- Study on kinematic parameter relationship.
- (2)
- Structural parameter design research.
2.3. Establishment of the Discrete Element Simulation Model
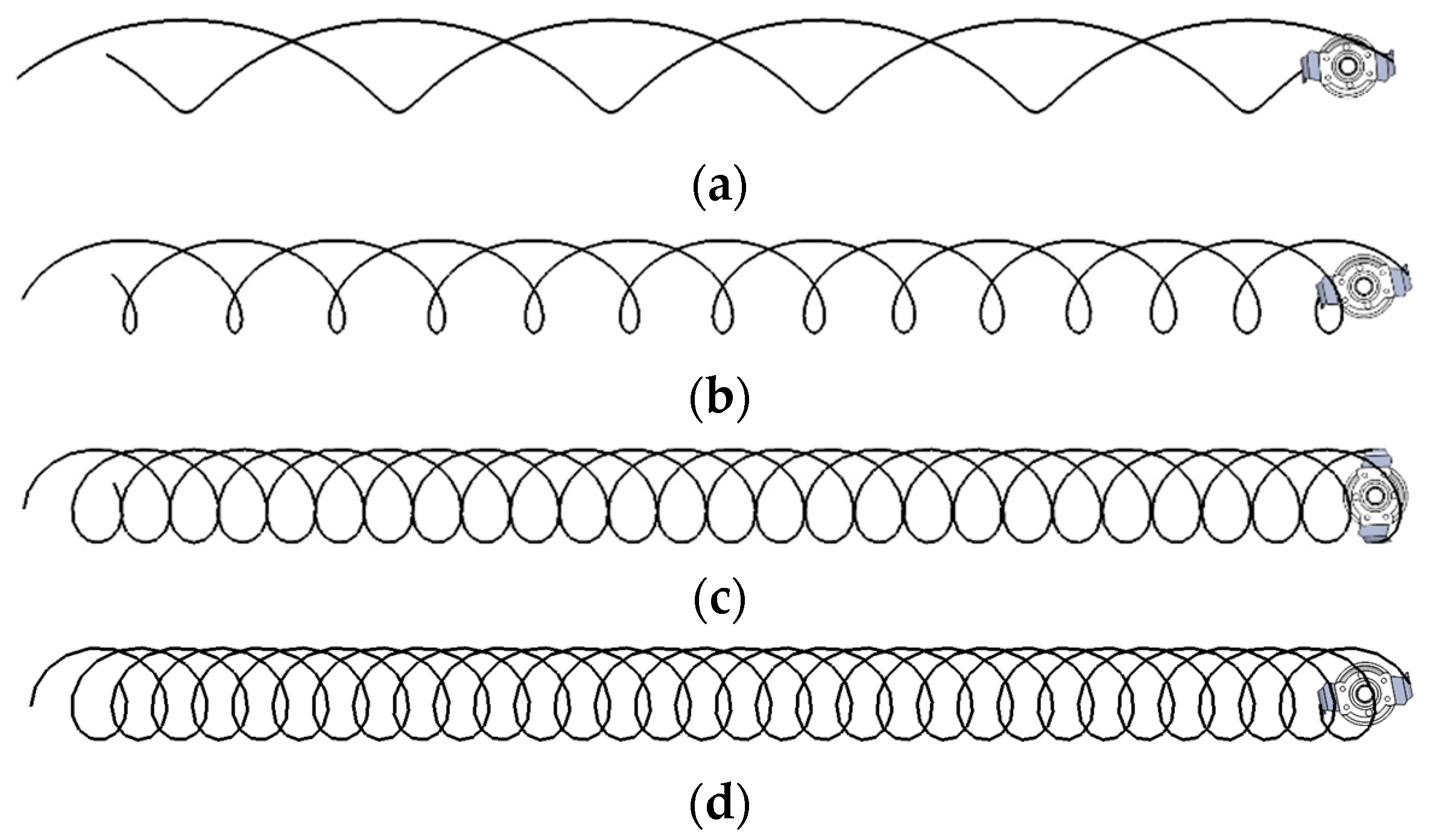
2.3.1. Geometric Simulation Model of the Vertical Rotor of the Power Harrow
2.3.2. Parameter Setting of Discrete Element Simulation Test
2.3.3. The Whole Simulation Model of Discrete Element Is Established
2.4. Discrete Element Simulation Test Scheme
- (1)
- Influence of harrow cutting edge angle on working effect of vertical rotor.
- (2)
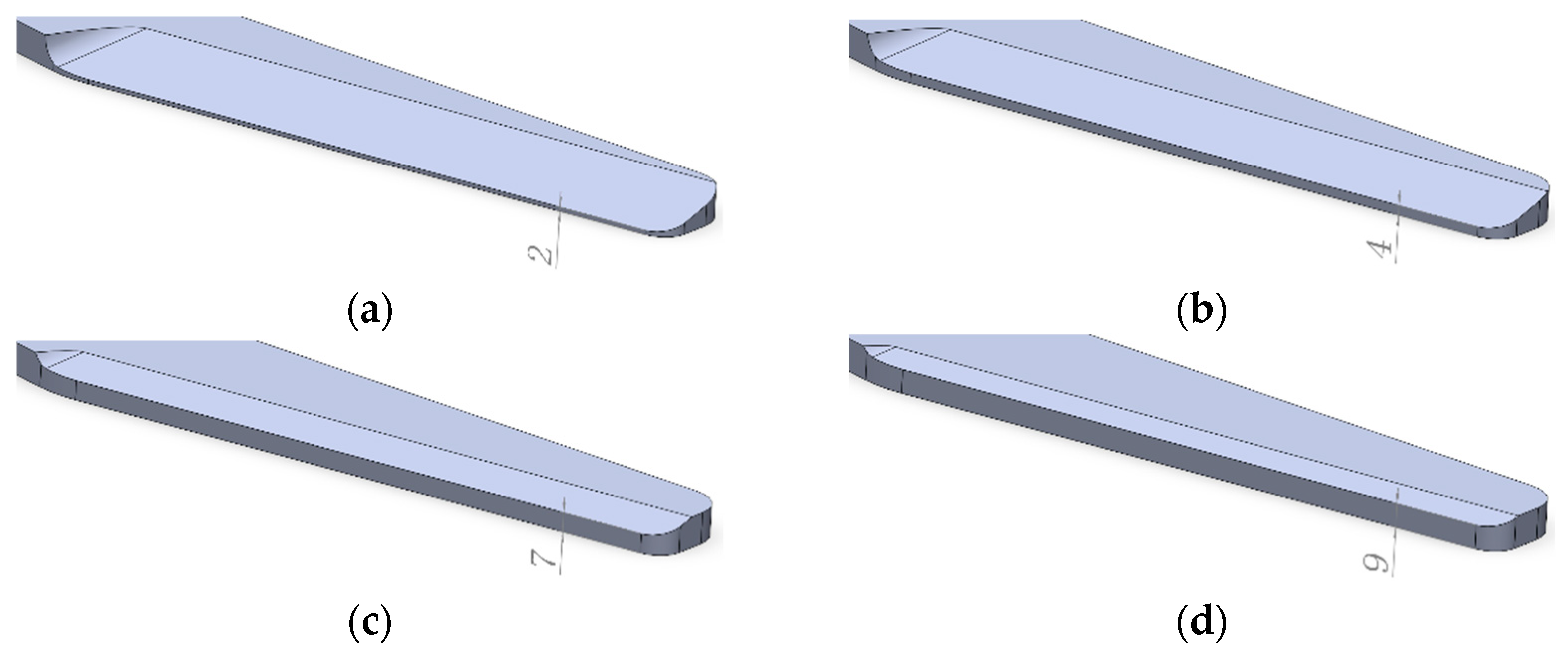
- Influence of cutting edge thickness of harrow cutter on the working effect of the vertical rotor.
- (3)
- Influence of the ratio of circular speed to forward speed of the vertical axis rotor on the operating effect.
- (4)
- Orthogonal experimental design for the multi-factor soil crushing operation of the vertical rotor.
2.5. Field Trial Scheme
- (1)
- Field test plan for soil crushing rate.
- (2)
- Test location and time.
3. Results and Discussion
3.1. Discrete Element Simulation Results
- (1)
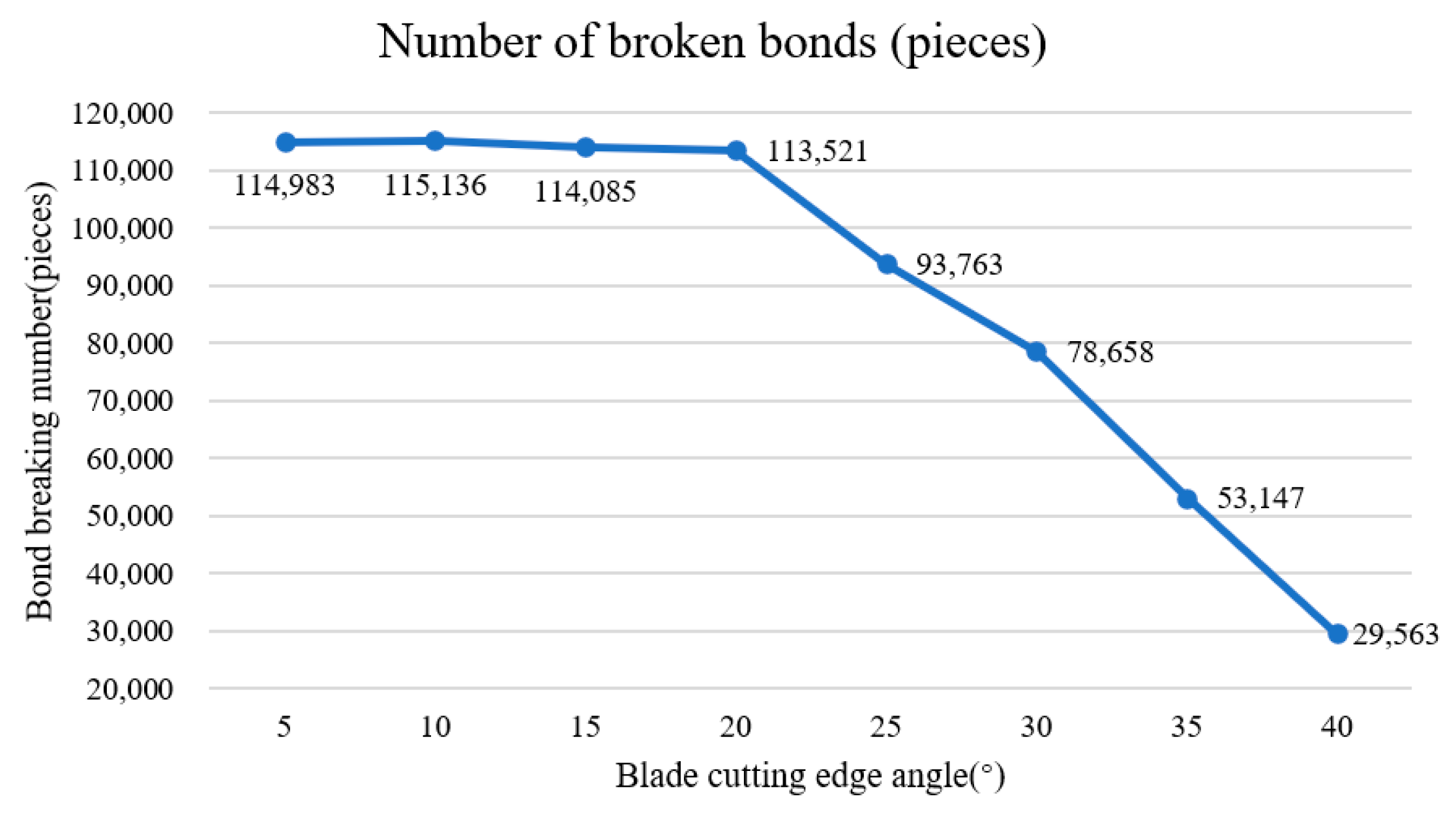
- Results of the influence of the cutting edge angle of the rake knife on the operation effect of the vertical rotor.
- (2)
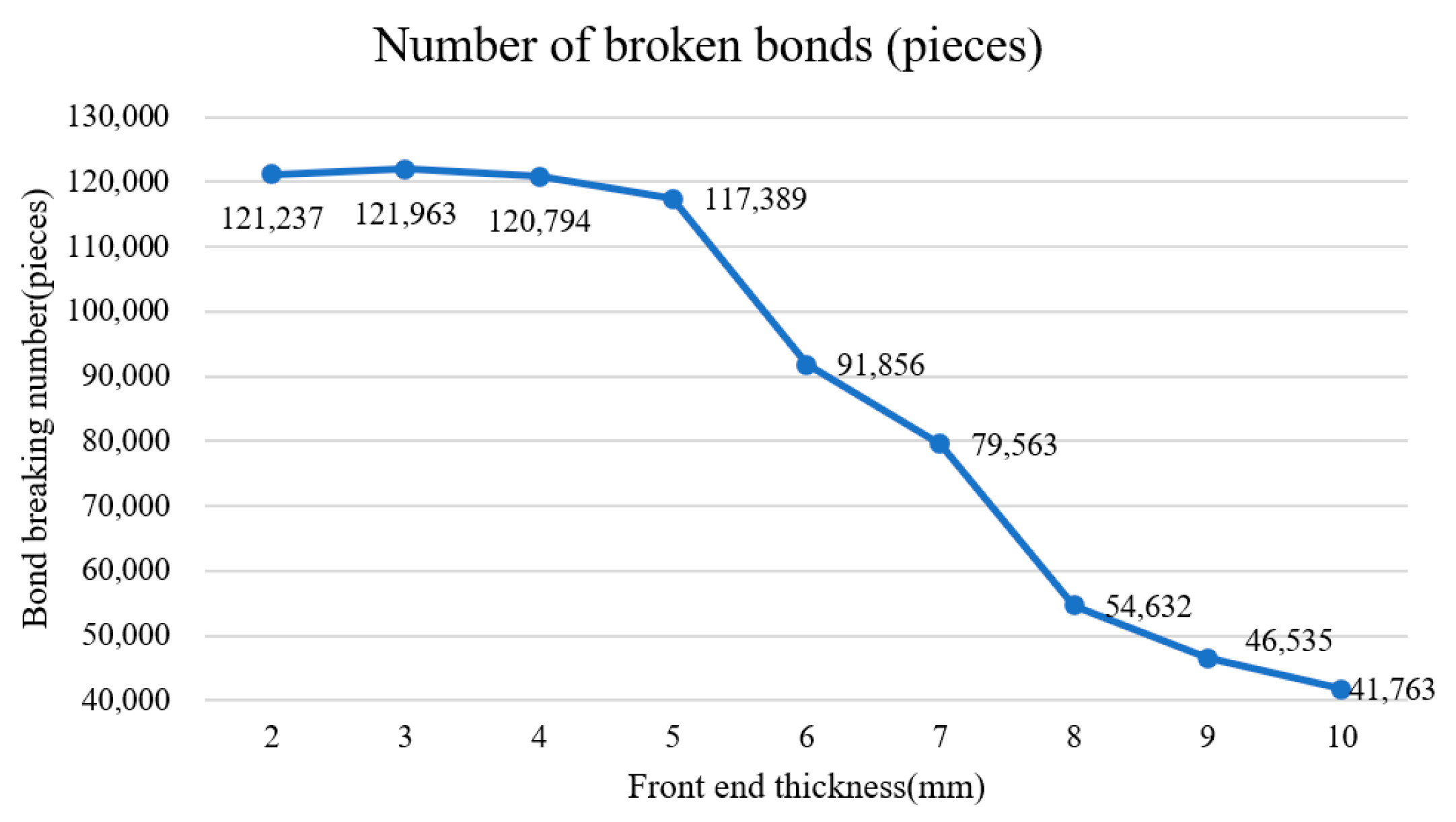
- Influence of the thickness of the front end of the rake knife’s cutting edge on the operation effect of the vertical-shaft rotor.
- (3)
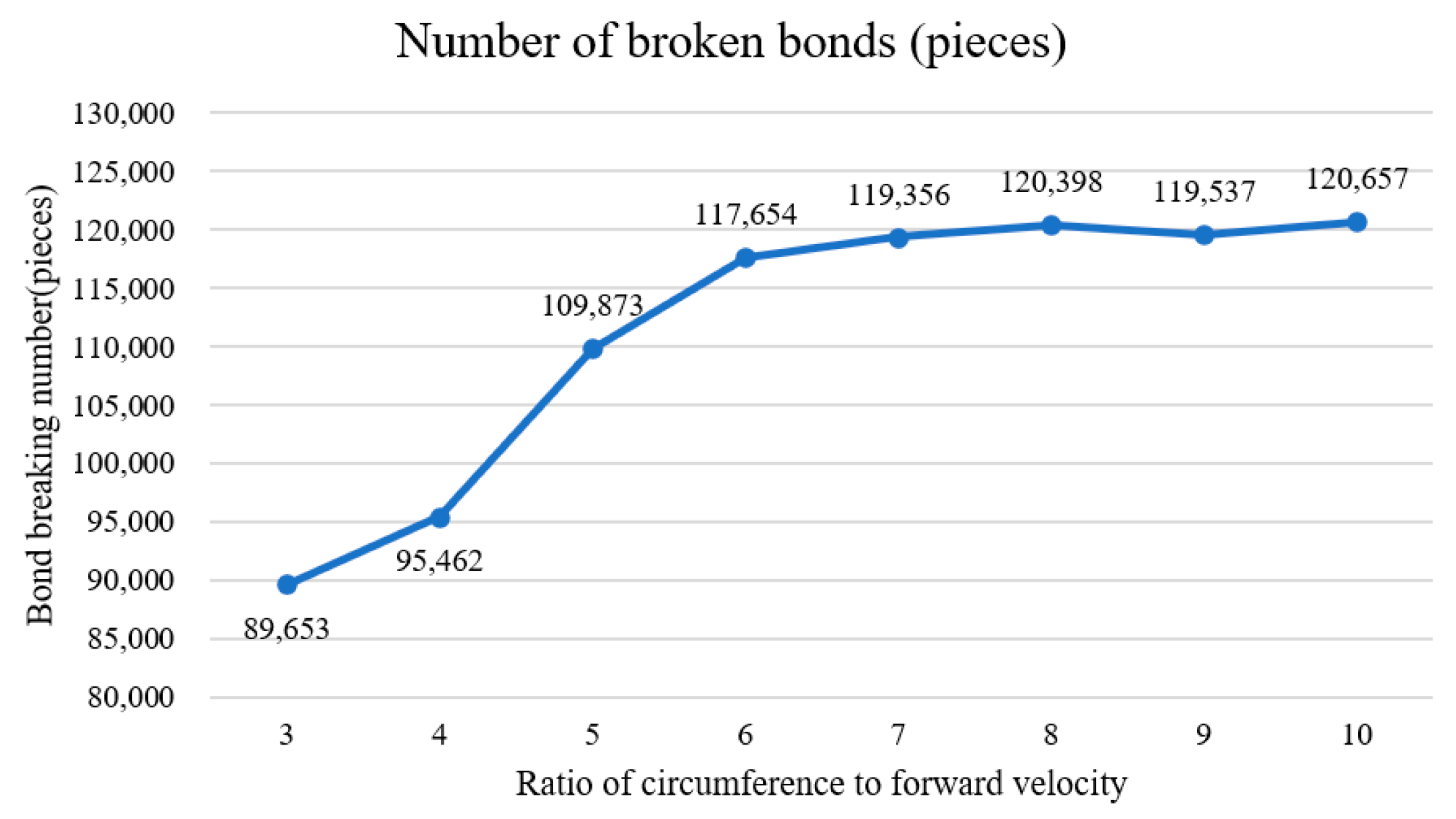
- Results of the influence of the ratio of the circumferential speed of the vertical rotor to the forward speed on the operation effect of the vertical rotor.
- (4)
- Results of the multi-factor orthogonal test for the soil crushing operation of the vertical-rotor.
3.2. Analysis and Discussion
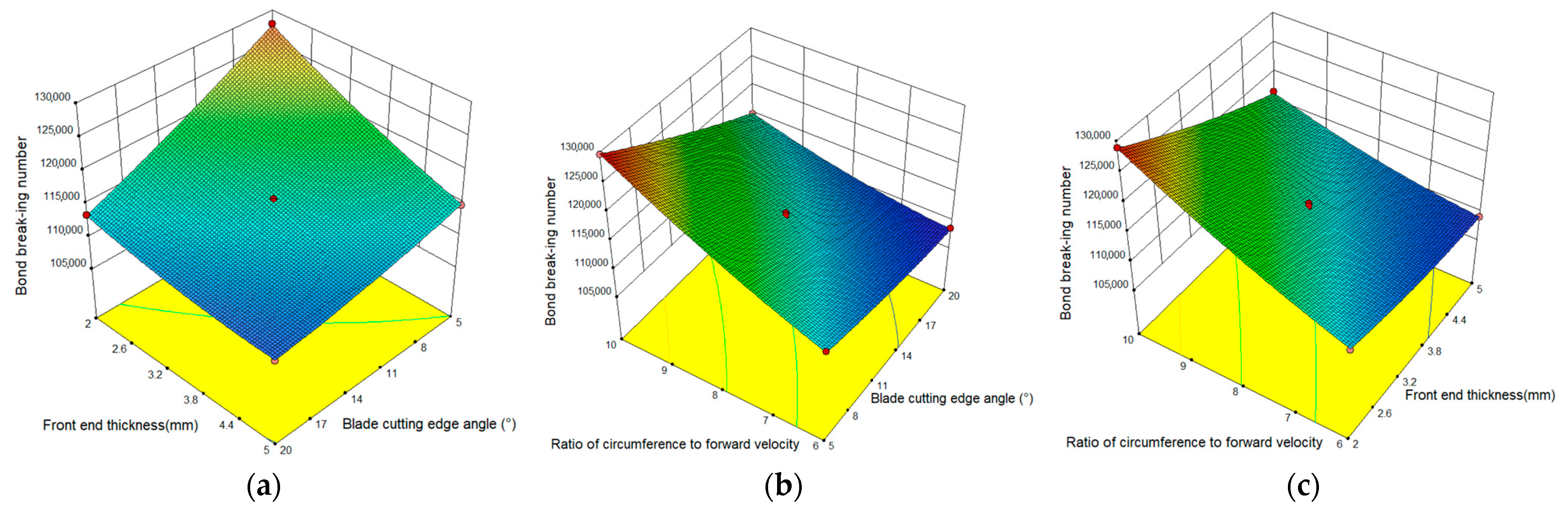
3.2.1. Response Surface Regression Analysis
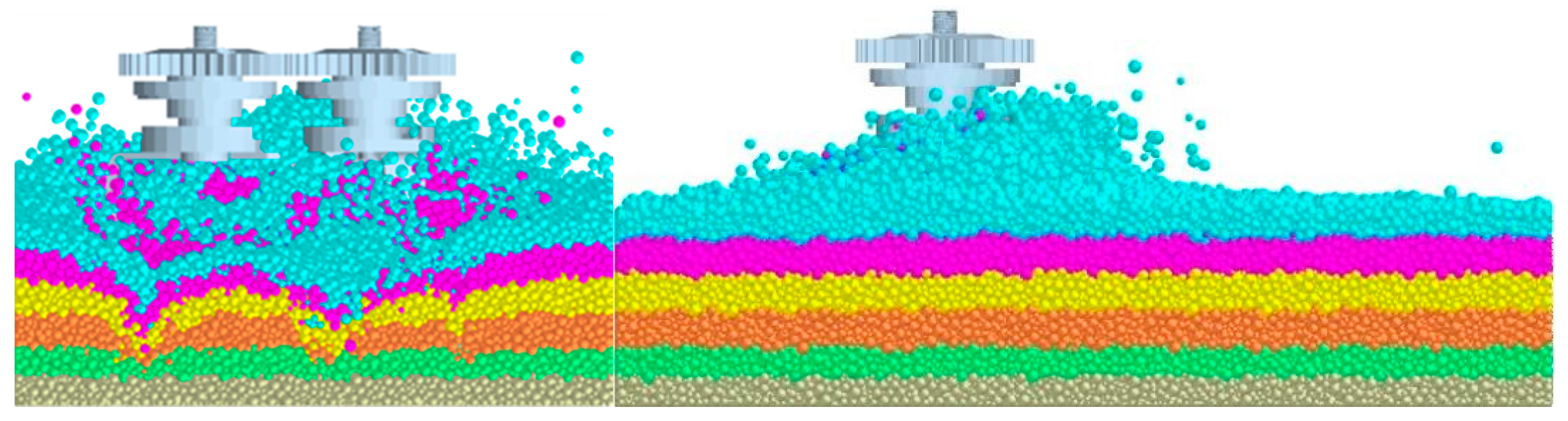
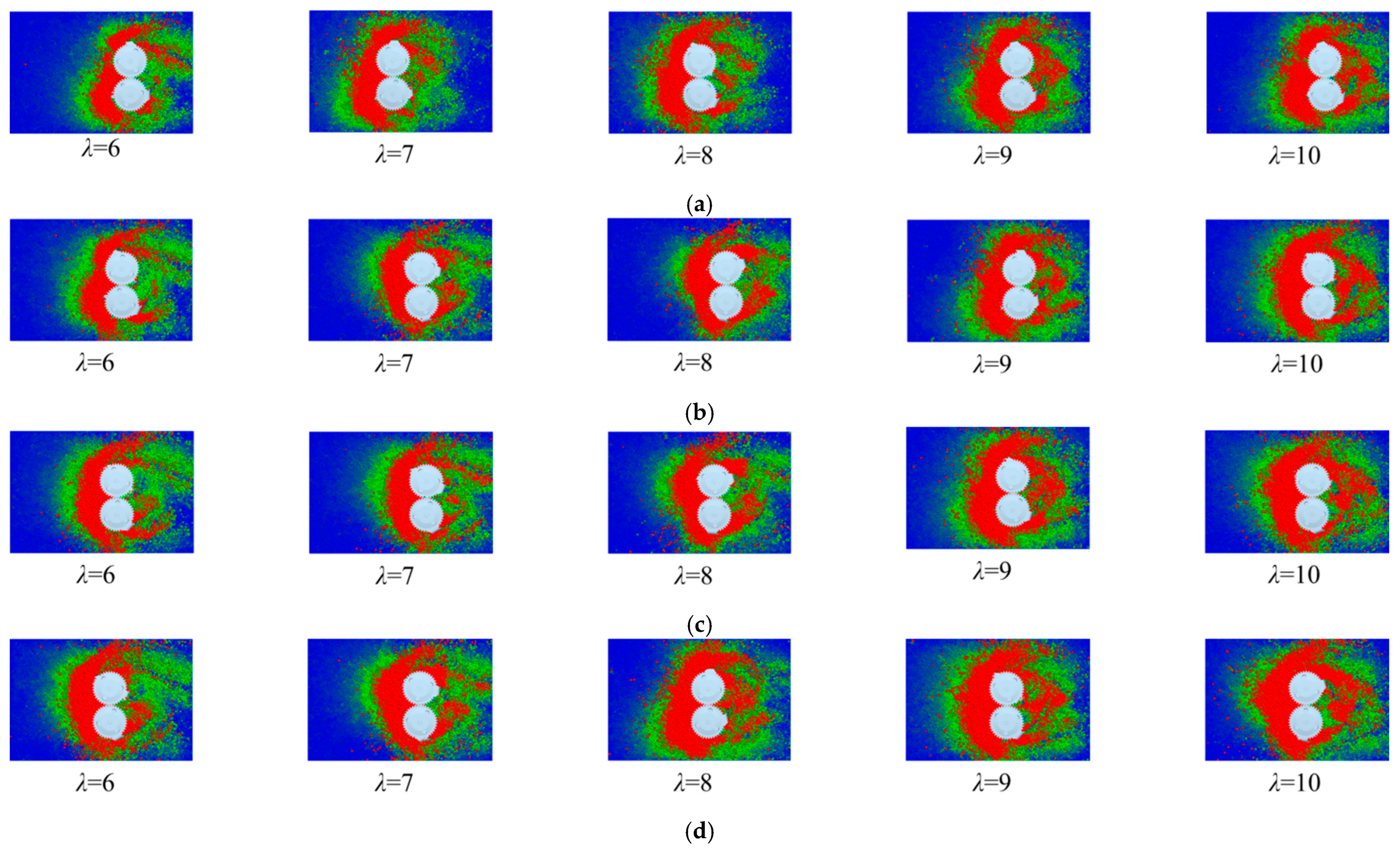
3.2.2. Analysis of Soil Disturbance and Soil Blockage
3.3. Field Test Results
4. Conclusions
- (1)
- The overall structure and key components of the power harrow were meticulously designed through the profound integration of agricultural machinery and agronomy concepts. This design process primarily entailed several crucial steps. First, kinetic research was carried out to precisely determine the parameters that have a direct impact on the soil crushing effect of the harrow blades. Then, in close combination with agronomic requirements, the reasonable range of structural parameters was preliminarily ascertained. Moreover, kinematics was employed to conduct a detailed analysis of the motion parameters influencing the soil crushing effect. Through this in-depth analysis, a reasonable parameter range was successfully obtained. All these efforts provide solid data support for subsequent simulation-based optimization, which is essential for enhancing the overall performance and efficiency of the power harrow in soil crushing operations.
- (2)
- The Discrete Element Method (DEM) was employed to simulate the soil crushing process of the vertical-shaft rotor. Taking the number of key fractures as the test index, and considering the cutting edge angle of the harrow blade, the thickness of the front end of the harrow blade’s cutting edge, and the ratio of the circumferential speed to the forward speed as the test factors, an in-depth analysis of the interactions among these test factors was conducted. Subsequently, a regression equation was established, and the optimal combination of the test factors was determined. Based on these findings, the trial production of the soil crushing device was successfully completed.
- (3)
- Field tests were conducted in strict accordance with agronomic requirements. The test results reveal that the soil crushing rate exceeds 85%, with an average soil crushing rate of 88.66%. These test results have successfully achieved the predetermined objectives and fulfill the design requirements. The research and development of the power harrow, along with its crucial soil crushing components, have significantly enhanced the quality of land-preparation operations in saline–alkali land. This not only has the potential to increase crop yields, but also offers essential equipment support for the comprehensive development and utilization of saline–alkali land, thus contributing to the expansion and optimization of agricultural activities in such challenging terrains.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bulletin on the main data of the Third National Land Survey. In Proceedings of the 2021 Office of the Leading Group of the Third National Land Survey of the State Council, Ministry of Natural Resources, National Bureau of Statistics, Beijing, China, 25 August 2021.
- Bao, X.M.; Hua, Y.W.; Song, X.L.; Niu, J.P.; Cai, D.H. Design Development and Structure Analysis of 1BQ–4.0 Power Drive Harrow. TAFE 2021, 48, 55–57. [Google Scholar]
- Anup, B.; Hifjur, R.; Thomas, E.V. A comparative study on tillage performance of rota-cultivator (a passive-active combination tillage implement) with rotavator (an active tillage implement). Soil Till. Res. 2021, 207, 104861. [Google Scholar]
- Han, Y.J.; Li, Y.W.; Zhao, H.H.; Chen, H.; Liu, D.X. Simulation of Soil Cutting by Vertical Rotary Blade Based on SPH Method. J. Southwest Univ. 2016, 38, 150–155. [Google Scholar]
- Fang, H.M. Research on the Straw-Soil-Rotary Blade Interaction Using Discrete Element Method. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2016. [Google Scholar]
- He, C. Design and Research of Deep Loosening and Vertical Rotary Tillage and Wheat Wide-Narrow-Row Sowing Compound Machine. Master’s Thesis, Henan Agricultural University, Zhengzhou, China, 2019. [Google Scholar]
- Zheng, K. Study on Subsoiling and Rotary Tillage Operation Adjustable Combine Machine. Ph.D. Thesis, China Agricultural University, Beijing, China, 2019. [Google Scholar]
- Zhang, H. Experimental Study on Vibrating Subsoiling Components in Soda Saline Alkali Soil. Master’s Thesis, Henan Agricultural University, Zhengzhou, China, 2019. [Google Scholar]
- Hu, W.H.; Yang, F.Z.; Zhao, G.D.; Lin, Y.L.; Huang, K. Analysis and Optimization of Working Parameters of Vertical Rotary Tiller Blade Based on Didcrete Element Method. J. China Agric. Mach. 2022, 43, 25–41. [Google Scholar]
- Tian, Y.F. Design and Test of Vertical Strip Rotary Cultivator in Straw Return Mode. Master’s Thesis, Jilin Agricultural University, Changchun, China, 2023. [Google Scholar]
- Wang, Y.B.; Rong, G.; Li, H.W. Design and Parameter Optimization of Vertical Driving-Type Surface Rotary Tillage Machine. Trans. Chin. Soc. Agric. Eng. 2019, 35, 38–47. [Google Scholar]
- Massimiliano, V.; Michele, M.; Giovanni, M.; Alessandro, B.; Lorenzo, C. Correlation between power harrow energy demand and tilled soil aggregate dimensions. Biosyst. Eng. 2023, 225, 54–68. [Google Scholar]
- Tang, W.B.; Liu, E.G.; He, C.; Jin, C.; Liu, C.X. Design and Experiment of Vertical Rotary Cultivator. Agric. Mach. Res. 2022, 10, 77–87. [Google Scholar]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Discrete Element Modelling of Top Soil Burial Using a Full Scale Mouldboard Plough under Field Conditions. Biosyst. Eng. 2017, 160, 140–153. [Google Scholar] [CrossRef]
- Asaf, Z.; Rubinstein, D.; Shmulevich, I. Determination of Discrete Element Model Parameters Required for Soil Tillage. Soil Till. Res. 2007, 92, 227–242. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the Effect of Harrow Angle on Narrow Opener Performance with the Discrete Element Method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Mustafa, U.; Chris, S.; Peilin, L.; Sang-Heon, L.; Jacky, M.A.D. Analyzing the Mixing Performance of A Rotary Spader Using Digital Image Processing and Discrete Element Modelling (DEM). Comput. Electron. Agric. 2018, 151, 1–10. [Google Scholar]
- Cao, L.F.; Zhang, C.C.; Zhang, J.H.; Liu, C.X.; Zhao, H. Design and Analysis of the Rotary Blade System of Y-Shaped Vertical Rotary Cultivator. Agric. Mach. Res. 2018, 8, 47–51. [Google Scholar]
- Zhang, J. Design and Experimental Study on Driving Target and Plastic Film Collecting Combined Operation Machine. Master’s Thesis, Xinjiang Agricultural University, Ürümqi, China, 2013. [Google Scholar]
- Ahmet, C.; Sefa, A. The effect of power harrow on the wheat residue cover and residue incorporation into the tilled soil layer. Soil Till. Res. 2022, 215, 105202. [Google Scholar]
- Balsari, P.; Biglia, A.; Comba, L.; Sacco, D.; Eloi, A.L.; Varani, M.; Mattetti, M.; Barge, P.; Tortia, C.; Manzone, M.; et al. Performance Analysis of a Tractor-Power Harrow System Under Different Working Conditions. Biosyst. Eng. 2021, 202, 28–41. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, C.Y.; Chen, C.L. Drive System Design and Blade Motion Analysis of Vertical Rotary Cultivator. J. China Agric. Mach. 2013, 34, 66–69. [Google Scholar]
- Wang, M.; Li, P.P.; Wang, J.H.; Li, K.; Xiao, H.G. Simulation of Soil Cutting Process of Vertical Rotary Tillage Tool in Tea Plantation Based on LS-DYNA. J. Anal. At. Spectrom. 2015, 9, 422–425. [Google Scholar]
- Liu, F.J.; Mi, Y.; Liao, N.; Di, M.L.; Liu, Y.D.; Liu, H.K. Research Design of Vertical Rotary Cultivator and Experiment. Agric. Mach. Res. 2017, 11, 81–84. [Google Scholar]
- Sun, J.; Wang, Y.; Ma, Y.; Tong, J.; Zhang, Z. DEM Simulation of Bionic Subsoilers (Tillage Depth > 40 cm) with Drag Reduction and Lower Soil Disturbance Characteristics. Adv. Eng. Softw. 2018, 119, 30–37. [Google Scholar] [CrossRef]
- Gao, M.Y.; Liu, E.H.; Zhang, B.K. Design and Testing of a Soil Stratification on-Demand Tillage Compound Cultivator. Modern Agric. 2014, 8, 55–56. [Google Scholar]
- Zhang, X.Y.; Zhang, L.X.; Hu, X.; Wang, H.; Shi, X.B.; Ma, X. Simulation of Soil Cutting and Power Consumption Optimization of a Typical Rotary Tillage Soil Blade. Appl. Sci. 2022, 12, 8177. [Google Scholar] [CrossRef]
- Power-Driven Harrow; Ministry of Agriculture and Rural Development of the People’s Republic of China: Beijing, China, 2019; Volume 3, p. 8.
- Yang, S. Optimal Design and Experimental on Rotary Harrow in Mulberry Field. Master’s Thesis, Shandong Agricultural University, Taian, China, 2020. [Google Scholar]
- Zhang, Q.B.; Liu, Y.G.; Zhang, R.; Zhao, W.; Yang, X.W.; Li, R.Y.; Hu, C.Q. Simulation and Analysis of Driving Harrowing Load of Combined Soil Preparation Machine Based on Discrete Element Method. Agric. Mach. Res. 2021, 4, 167–173. [Google Scholar]
- Wang, L.Y.; Yang, F.Z.; Li, W.H.; Jiang, F.L.; Jian, S.C. Simulation Research on the Performance of Vertical Rotary Tillage Cutter Based on Discrete Element Method. Agric. Mach. Res. 2023, 2, 9–20. [Google Scholar]
- Xu, B. Design and Experiment on Seedbed Arrangement of Rape Seeding Transplater and Matching Device. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2018. [Google Scholar]
- Wang, L.Y. Research on The Development and Operation Stability of Seed and Fertilizer Precision Sowing and Tillage Integreted Machine. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2021. [Google Scholar]
- Zhao, J.F.; Wang, W.; Sun, Z.X.; Su, X.J. Improvement and Verification of Pressure-Sinkage Model in Homogeneous Soil. Trans. Chin. Soc. Agric. Eng. 2016, 32, 60–66. [Google Scholar]
- Xu, N.; Xin, Z.B.; Yuan, J.; Gao, Z.H.; Tian, Y.; Xia, C.; Liu, X.M.; Wang, D.W. Calibration of Discrete Element Simulation Parameters and Model Construction for the Interaction Between Coastal Saline Alkali Soil and Soil-Engaging Components. Agricultueral 2024, 15, 7. [Google Scholar] [CrossRef]









| Contact Model Parameters | Parameter Ranges | |||||
|---|---|---|---|---|---|---|
| Depth/cm | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 |
| Bond radius/mm | 5.16 | 5.16 | 5.16 | 5.29 | 5.29 | 5.29 |
| Normal stiffness/N·m−3 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 |
| Critical normal stress/Pa | 3.05 × 104 | 3.05 × 104 | 3.05 × 104 | 4.03 × 104 | 4.03 × 104 | 4.03 × 104 |
| Shear stiffness/N·m−3 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 5 × 107 |
| Critical tangential stress/Pa | 3.05 × 104 | 3.05 × 104 | 3.05 × 104 | 4.03 × 104 | 4.03 × 104 | 4.03 × 104 |
| Poisson’s ratio of saline–alkali soil | 0.38 | 0.38 | 0.37 | 0.37 | 0.37 | 0.36 |
| Shear modulus of saline–alkali soil/Pa | 1 × 106 | 1 × 106 | 1.01 × 106 | 1.02 × 106 | 1.02 × 106 | 1.05 × 106 |
| Saline soil density/g·cm−3 | 1.653 | 1.682 | 1.725 | 1.746 | 1.775 | 1.793 |
| Soil intergranular recovery coefficient | 0.42 | 0.39 | 0.38 | 0.36 | 0.35 | 0.35 |
| Coefficient of static friction between soil particles | 0.35 | 0.42 | 0.52 | 0.64 | 0.78 | 0.96 |
| Coefficient of dynamic friction between soil particles | 0.055 | 0.058 | 0.062 | 0.071 | 0.080 | 0.0885 |
| Harrow knife Poisson ratio | 0.30 | |||||
| Harrow knife shear modulus/Pa | 7.9 × 1010 | |||||
| Harrow density/kg·m−3 | 7860 | |||||
| Soil–harrow recovery coefficient | 0.48 | 0.45 | 0.43 | 0.40 | 0.38 | 0.35 |
| Coefficient of static friction between soil and harrow | 0.43 | 0.46 | 0.474 | 0.512 | 0.534 | 0.556 |
| Coefficient of dynamic friction between soil and harrow | 0.0454 | 0.0492 | 0.0528 | 0.0552 | 0.0580 | 0.0608 |
| Depth | Soil Compactness/kg.cm−2 | Soil Density/g.cm−3 | Soil Moisture Content/% |
|---|---|---|---|
| 0–5 cm | 19.10 | 1.653 | 16.82 |
| 5–10 cm | 18.42 | 1.682 | 21.35 |
| 10–15 cm | 18.06 | 1.725 | 22.52 |
| 15–20 cm | 17.36 | 1.746 | 24.08 |
| 20–25 cm | 16.93 | 1.775 | 24.68 |
| 25–30 cm | 16.15 | 1.793 | 26.28 |
| Serial Number | Harrow Cutting Edge Angle (°) | Bond Break Number |
|---|---|---|
| 1 | 5 | 114,983 |
| 2 | 10 | 115,136 |
| 3 | 15 | 114,085 |
| 4 | 20 | 113,521 |
| 5 | 25 | 93,763 |
| 6 | 30 | 78,658 |
| 7 | 35 | 53,147 |
| 8 | 40 | 29,563 |
| Serial Number | Harrow Cutting Edge Thickness (mm) | Bond Break Number |
|---|---|---|
| 1 | 2 | 121,237 |
| 2 | 3 | 121,963 |
| 3 | 4 | 120,794 |
| 4 | 5 | 117,389 |
| 5 | 6 | 91,856 |
| 6 | 7 | 79,563 |
| 7 | 8 | 54,632 |
| 8 | 9 | 46,535 |
| 9 | 10 | 41,763 |
| Serial Number | The Ratio of the Circumference Velocity to the Forward Velocity | Bond Break Number |
|---|---|---|
| 1 | 3 | 89,653 |
| 2 | 4 | 95,462 |
| 3 | 5 | 109,873 |
| 4 | 6 | 117,654 |
| 5 | 7 | 119,356 |
| 6 | 8 | 120,398 |
| 7 | 9 | 119,537 |
| 8 | 10 | 120,657 |
| Level | A Blade Cutting Edge Angle/° | B Front End Thickness/mm | C Ratio of Circumference to Forward Velocity |
|---|---|---|---|
| −1 | 5 | 2 | 6 |
| 0 | 12.5 | 3.5 | 8 |
| 1 | 20 | 5 | 10 |
| Serial Number | A | B | Y Bond Breaking Number | |
| Blade Cutting Edge Angle/° | Front End Thickness/mm | Ratio of Circumference to Forward Velocity | ||
| 1 | 12.5 | 3.5 | 8 | 114,963 |
| 2 | 5 | 2 | 8 | 127,865 |
| 3 | 12.5 | 3.5 | 8 | 115,087 |
| 4 | 5 | 3.5 | 10 | 129,564 |
| 5 | 12.5 | 2 | 6 | 112,873 |
| 6 | 20 | 5 | 8 | 109,876 |
| 7 | 12.5 | 5 | 10 | 116,832 |
| 8 | 20 | 2 | 8 | 113,549 |
| 9 | 12.5 | 3.5 | 8 | 115,321 |
| 10 | 20 | 3.5 | 6 | 108,678 |
| 11 | 12.5 | 3.5 | 8 | 115,783 |
| 12 | 12.5 | 5 | 6 | 109,107 |
| 13 | 20 | 3.5 | 10 | 115,079 |
| 14 | 12.5 | 3.5 | 8 | 115,398 |
| 15 | 5 | 3.5 | 6 | 113,496 |
| 16 | 12.5 | 2 | 10 | 128,963 |
| 17 | 5 | 5 | 8 | 114,836 |
| Polynomial Regression | Quadratic Sum | Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 6.568 × 108 | 9 | 7.298 × 107 | 720.24 | <0.0001 |
| A | 1.860 × 108 | 1 | 1.860 × 108 | 1836.06 | <0.0001 |
| B | 1.328 × 108 | 1 | 1.328 × 108 | 1310.97 | <0.0001 |
| C | 2.678 × 108 | 1 | 2.678 × 108 | 2642.69 | <0.0001 |
| AB | 2.188 × 107 | 1 | 2.188 × 107 | 215.97 | <0.0001 |
| AC | 2.336 × 107 | 1 | 2.336 × 107 | 230.57 | <0.0001 |
| BC | 1.749 × 107 | 1 | 1.749 × 107 | 172.64 | <0.0001 |
| A2 | 1.014 × 106 | 1 | 1.014 × 106 | 10.01 | 0.0158 |
| B2 | 2.246 × 106 | 1 | 2.246 × 106 | 22.16 | 0.0022 |
| C2 | 3.434 × 106 | 1 | 3.434 × 106 | 33.89 | 0.0006 |
| Residue | 7.093 × 105 | 7 | 1.013 × 105 | — | — |
| Lack of fit | 3.076 × 105 | 3 | 1.025 × 105 | 1.02 | 0.4719 |
| Error | 4.017 × 105 | 4 | 1.004 × 105 | — | — |
| Aggregate | 6.575 × 108 | 16 | — | — |
| Testing Order Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Percentage of soil breaking (%) | 87.6 | 86.9 | 88.2 | 90.3 | 88.5 | 91.8 | 89.2 | 88.3 | 86.2 | 89.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, N.; Xin, Z.; Yuan, J.; Gao, Z.; Tian, Y.; Xia, C.; Liu, X.; Wang, D. Design and Optimization of Power Harrow Soil Crushing Components for Coastal Saline–Alkali Land. Agriculture 2025, 15, 206. https://doi.org/10.3390/agriculture15020206
Xu N, Xin Z, Yuan J, Gao Z, Tian Y, Xia C, Liu X, Wang D. Design and Optimization of Power Harrow Soil Crushing Components for Coastal Saline–Alkali Land. Agriculture. 2025; 15(2):206. https://doi.org/10.3390/agriculture15020206
Chicago/Turabian StyleXu, Nan, Zhenbo Xin, Jin Yuan, Zenghui Gao, Yu Tian, Chao Xia, Xuemei Liu, and Dongwei Wang. 2025. "Design and Optimization of Power Harrow Soil Crushing Components for Coastal Saline–Alkali Land" Agriculture 15, no. 2: 206. https://doi.org/10.3390/agriculture15020206
APA StyleXu, N., Xin, Z., Yuan, J., Gao, Z., Tian, Y., Xia, C., Liu, X., & Wang, D. (2025). Design and Optimization of Power Harrow Soil Crushing Components for Coastal Saline–Alkali Land. Agriculture, 15(2), 206. https://doi.org/10.3390/agriculture15020206







