Multi Standardized Precipitation Evapotranspiration Index (Multi-SPEI-ETo): Evaluation of 40 Empirical Methods and Their Influence in SPEI
Abstract
1. Introduction
2. Materials and Methods
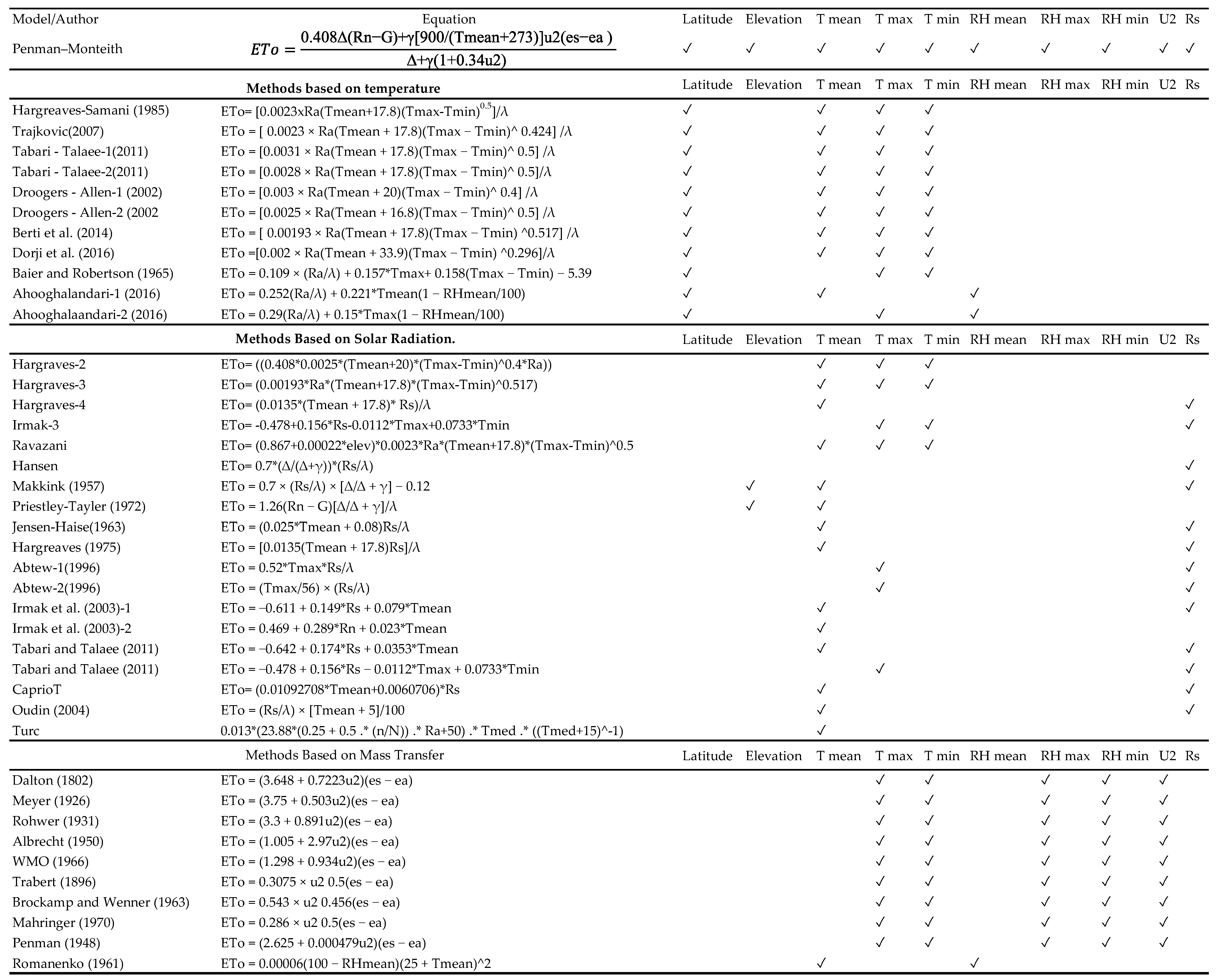
2.1. Methods Based on Temperature (°C)
2.2. Methods Based on Solar Radiation
2.3. Methods Based on Mass Transfer
2.4. SPEI: Temporal Analysis
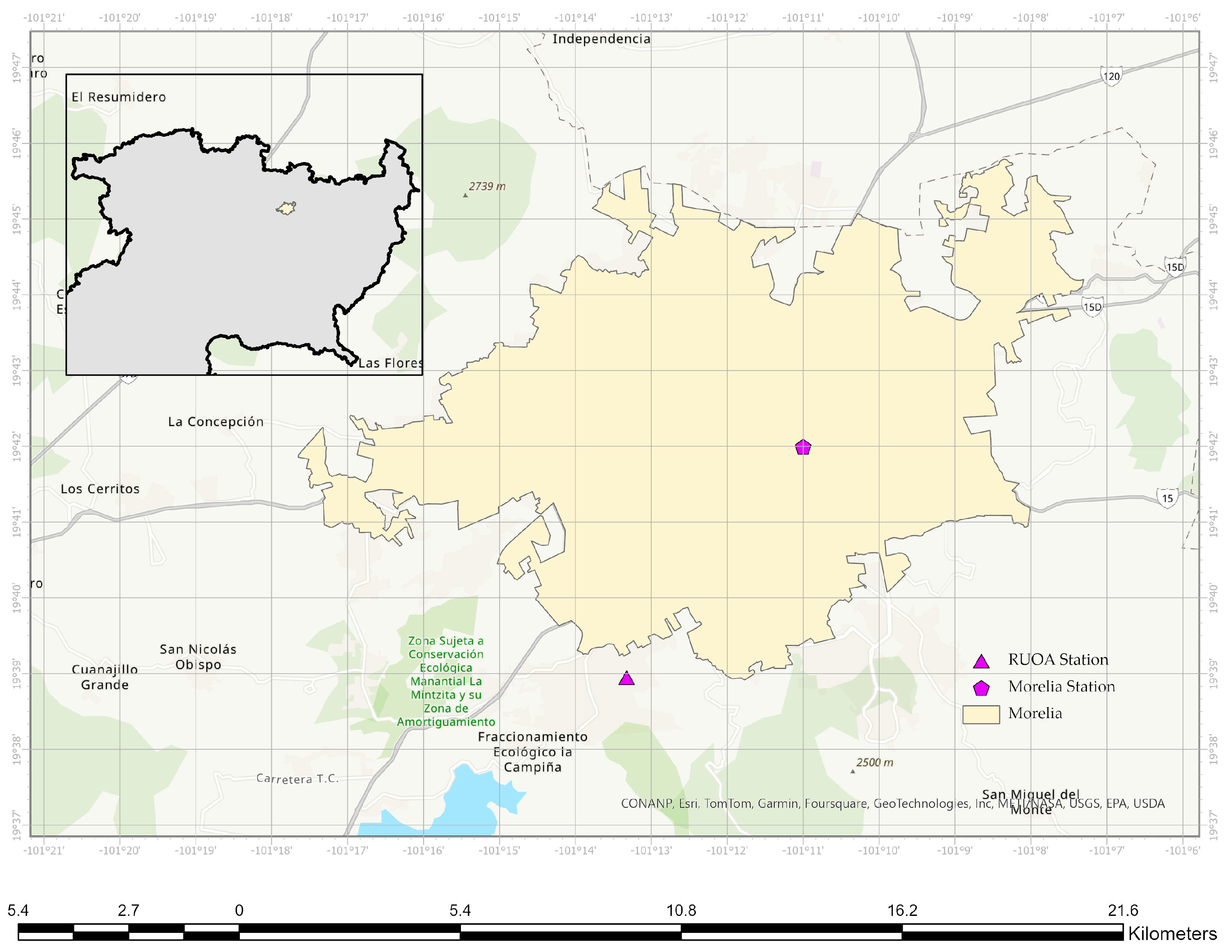
2.5. Study Area
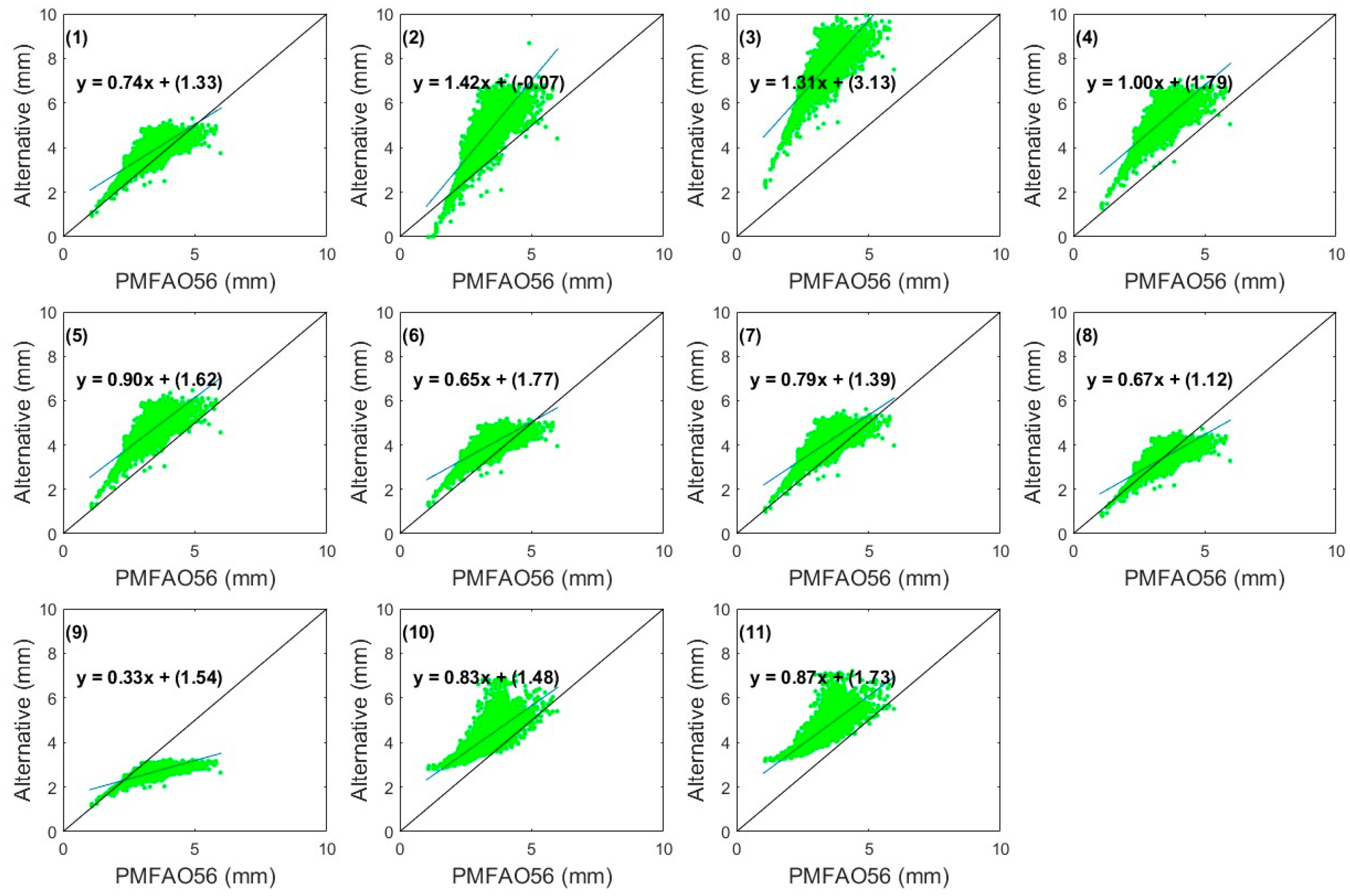
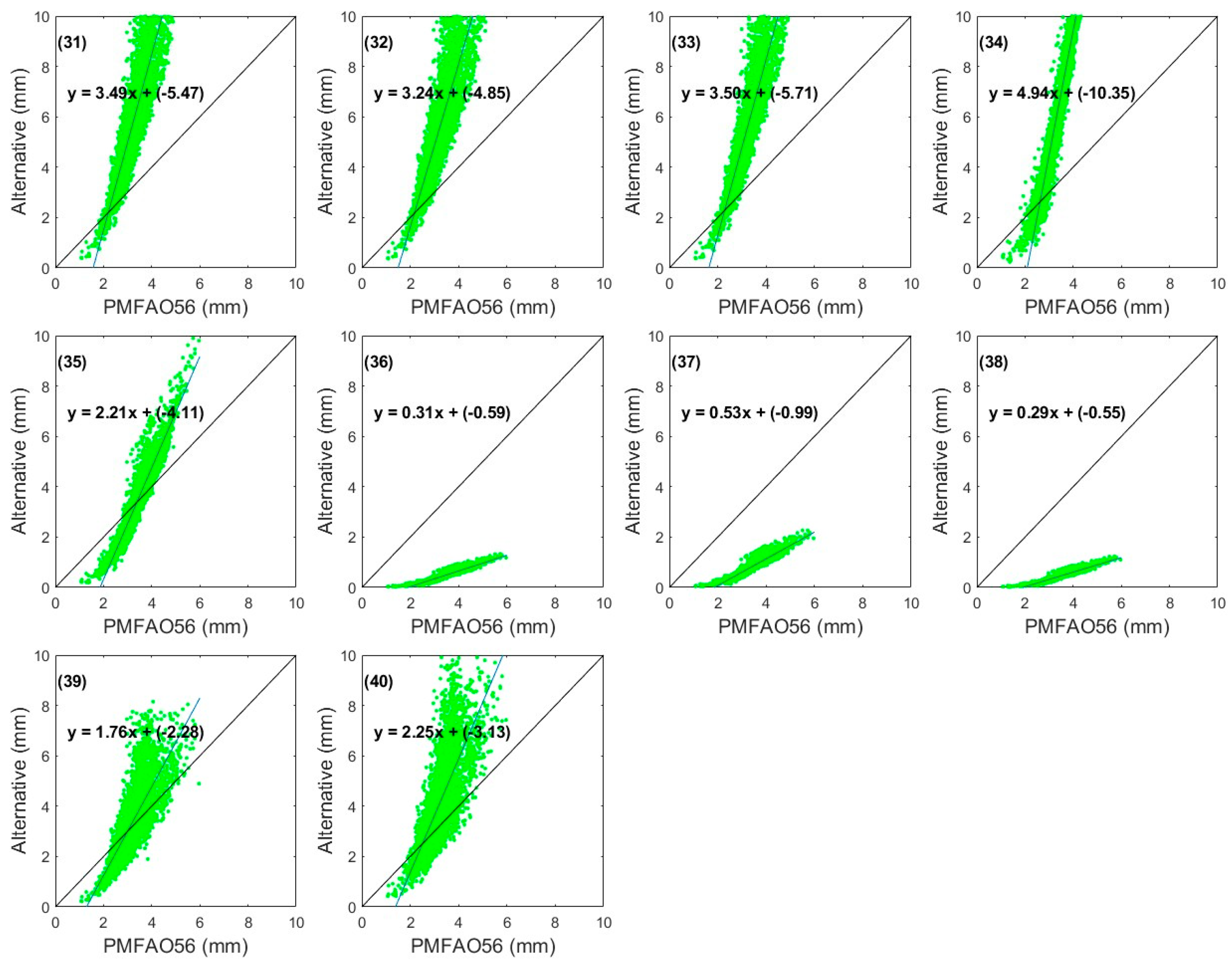
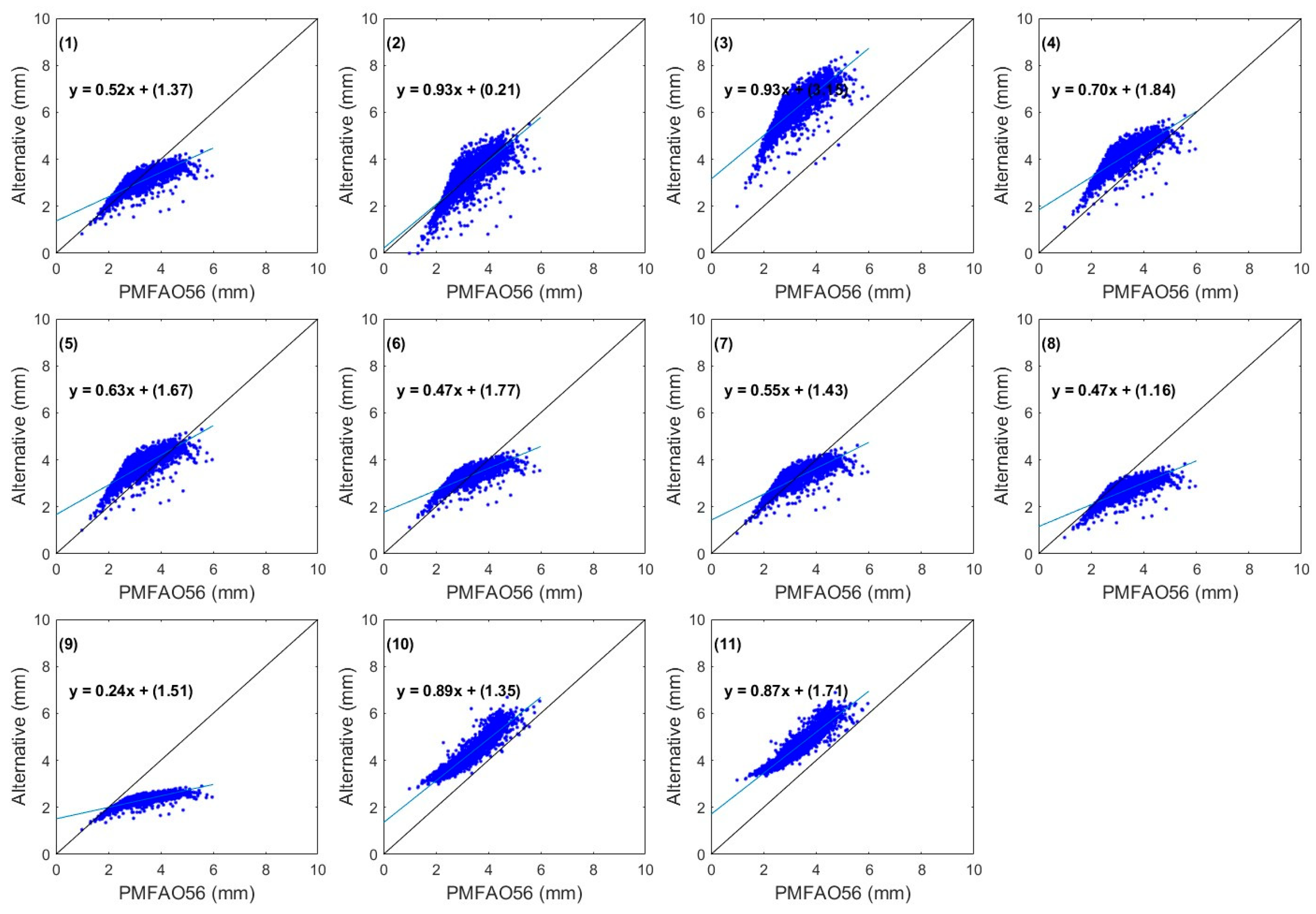
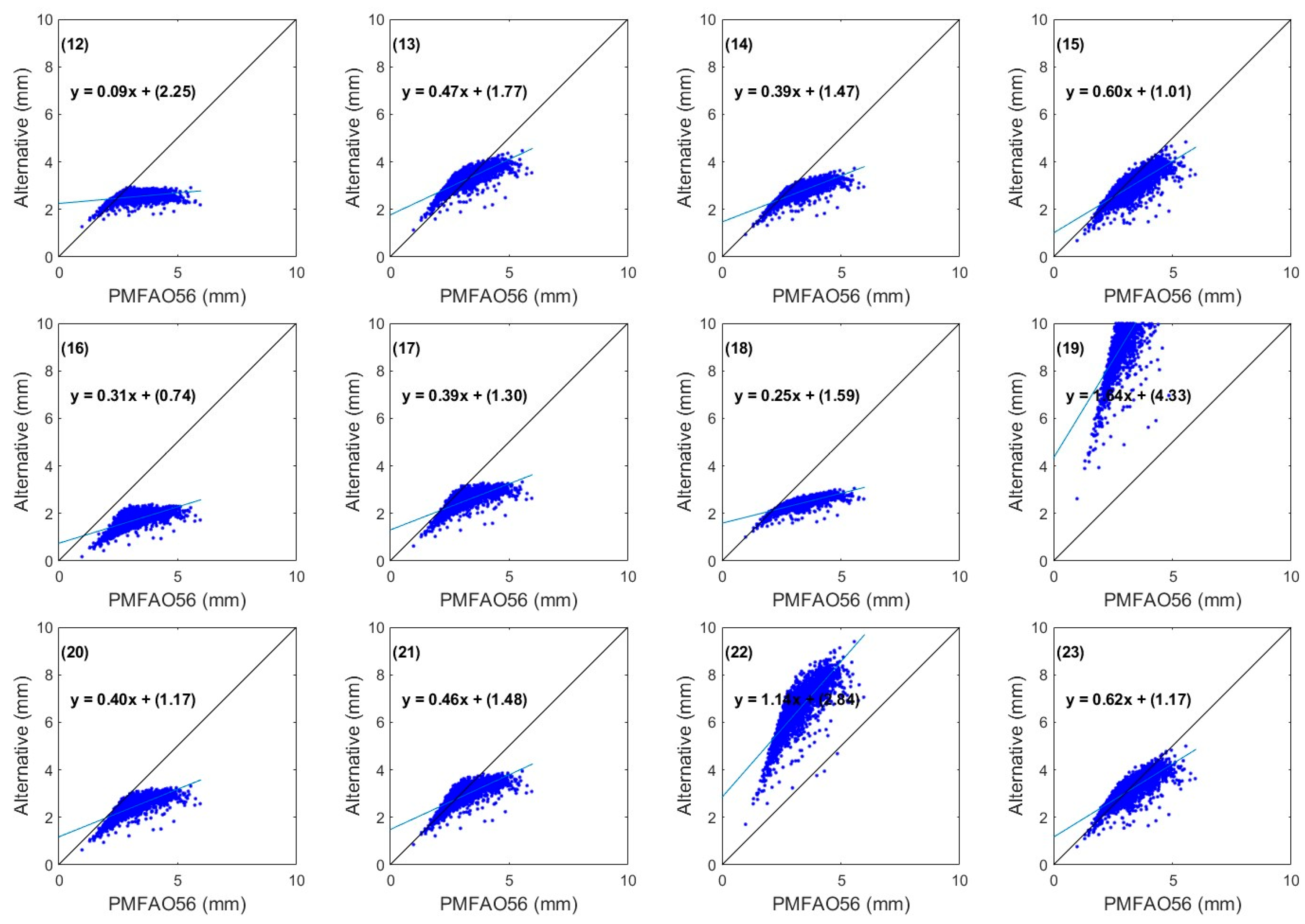
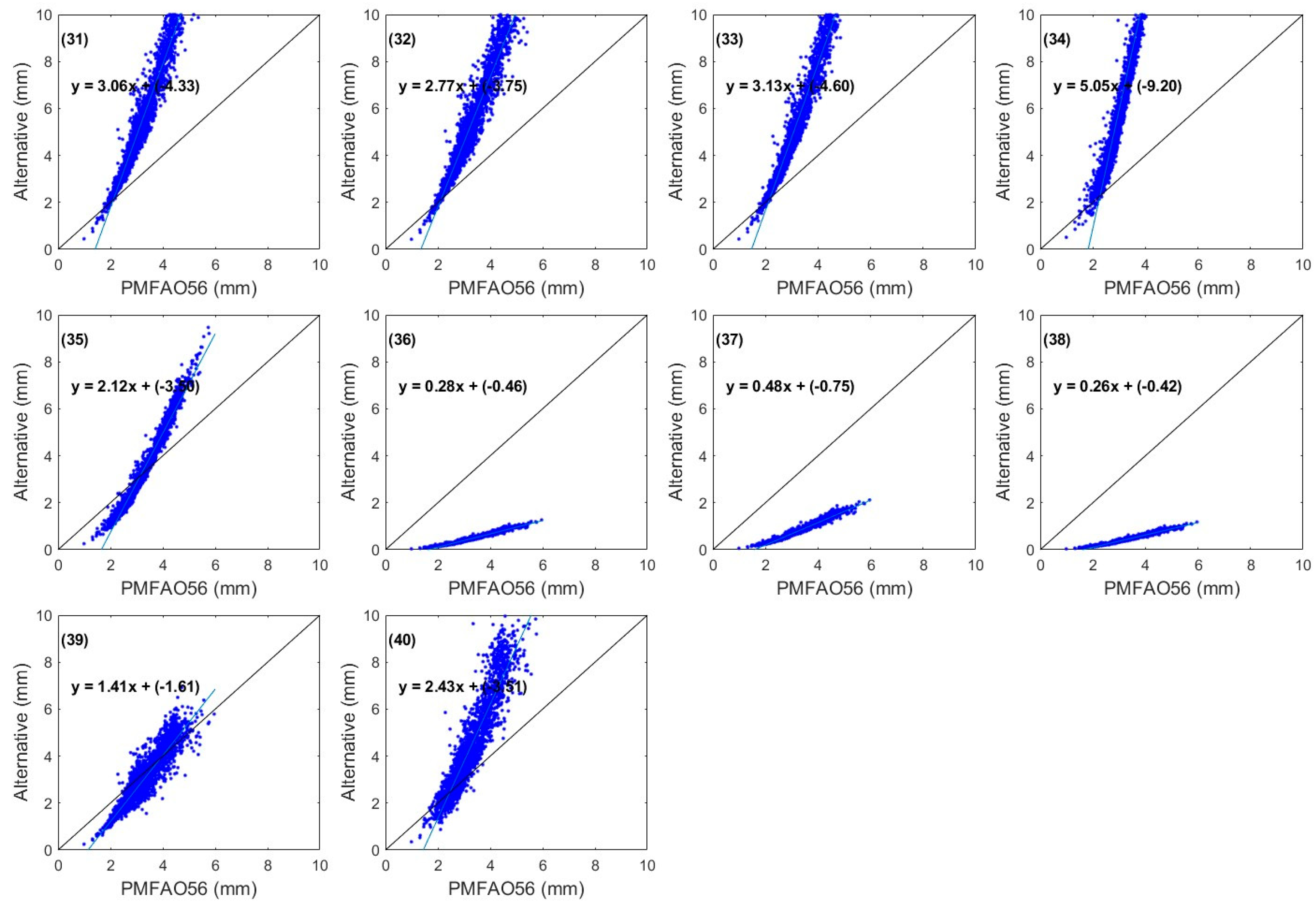
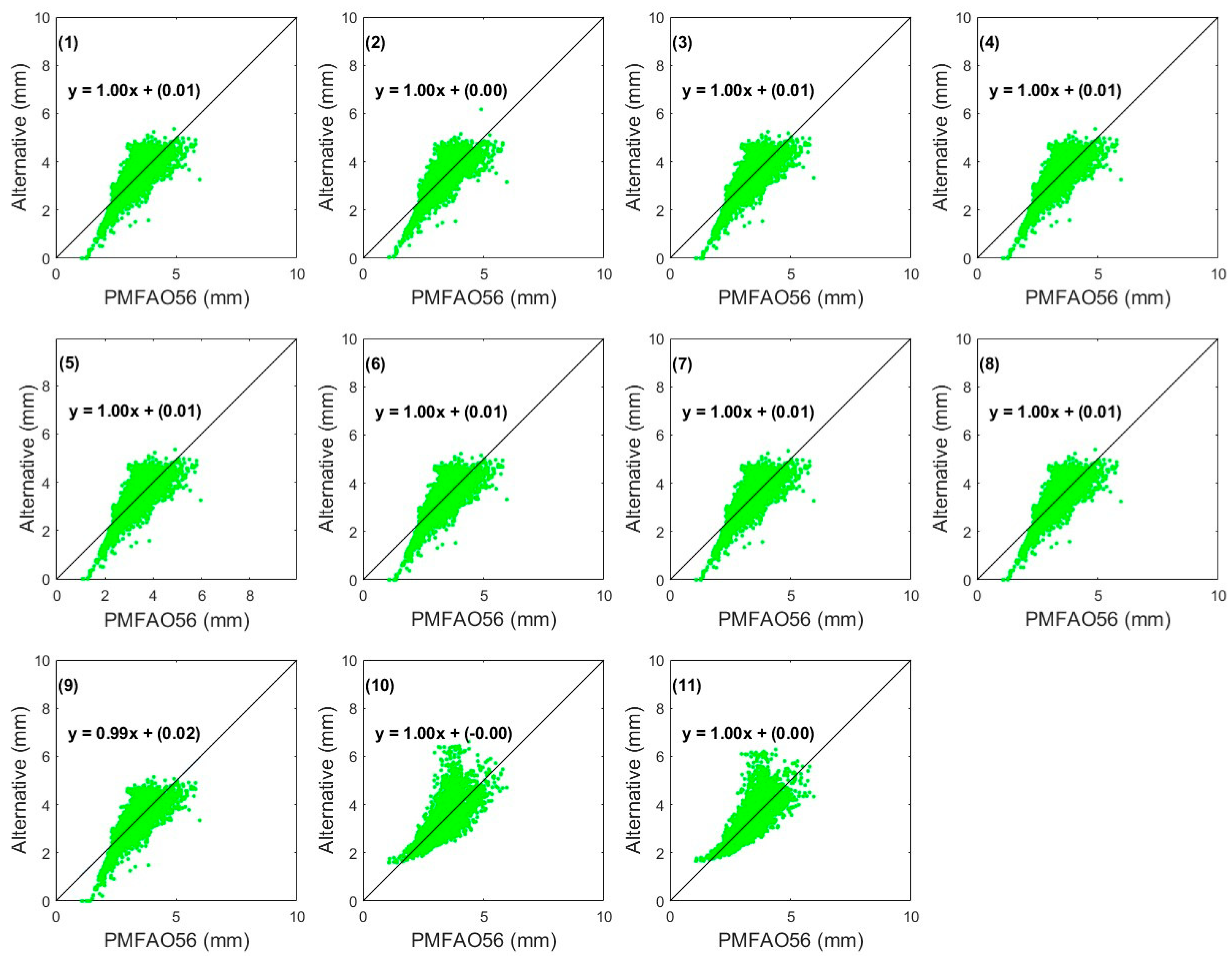
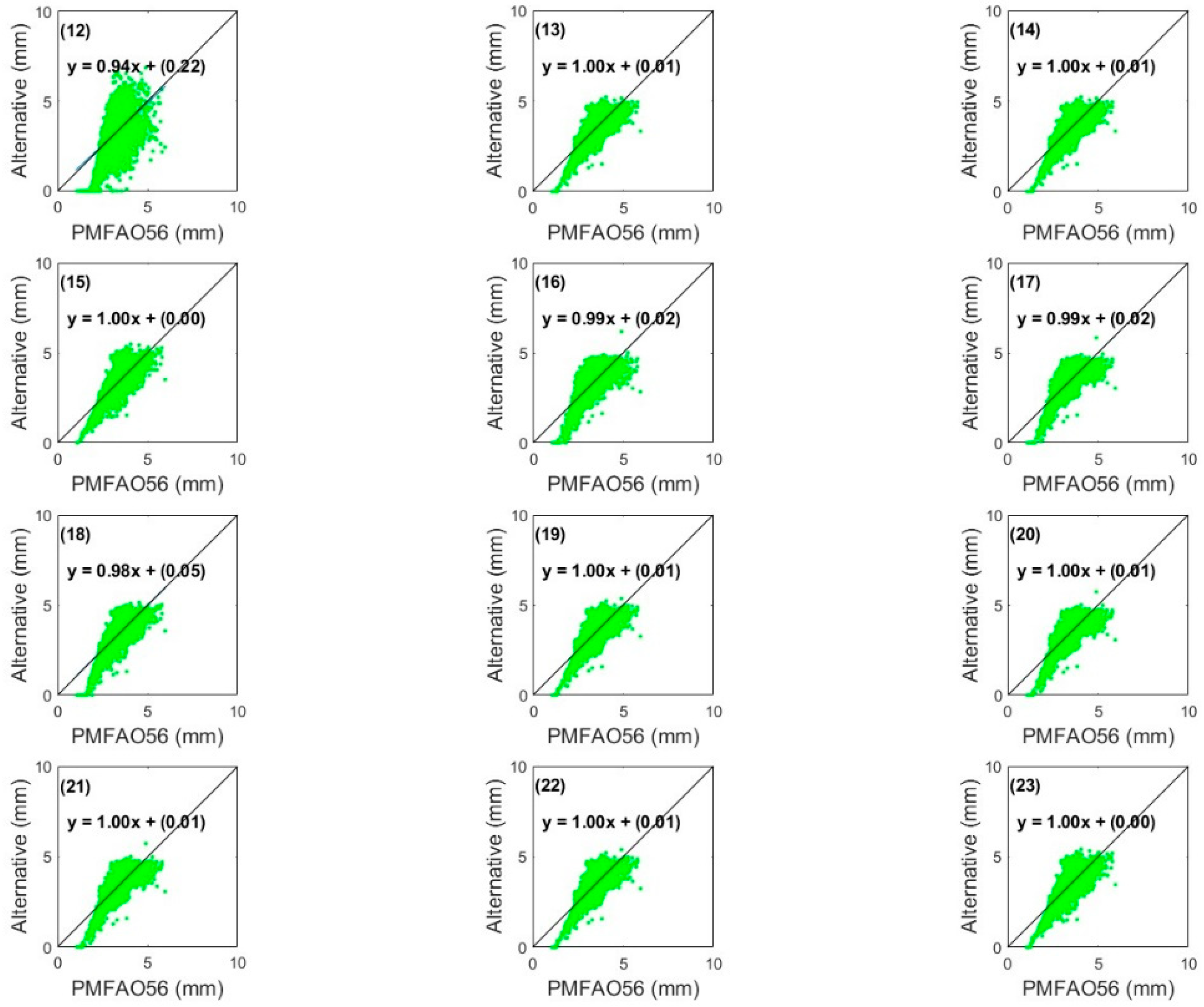
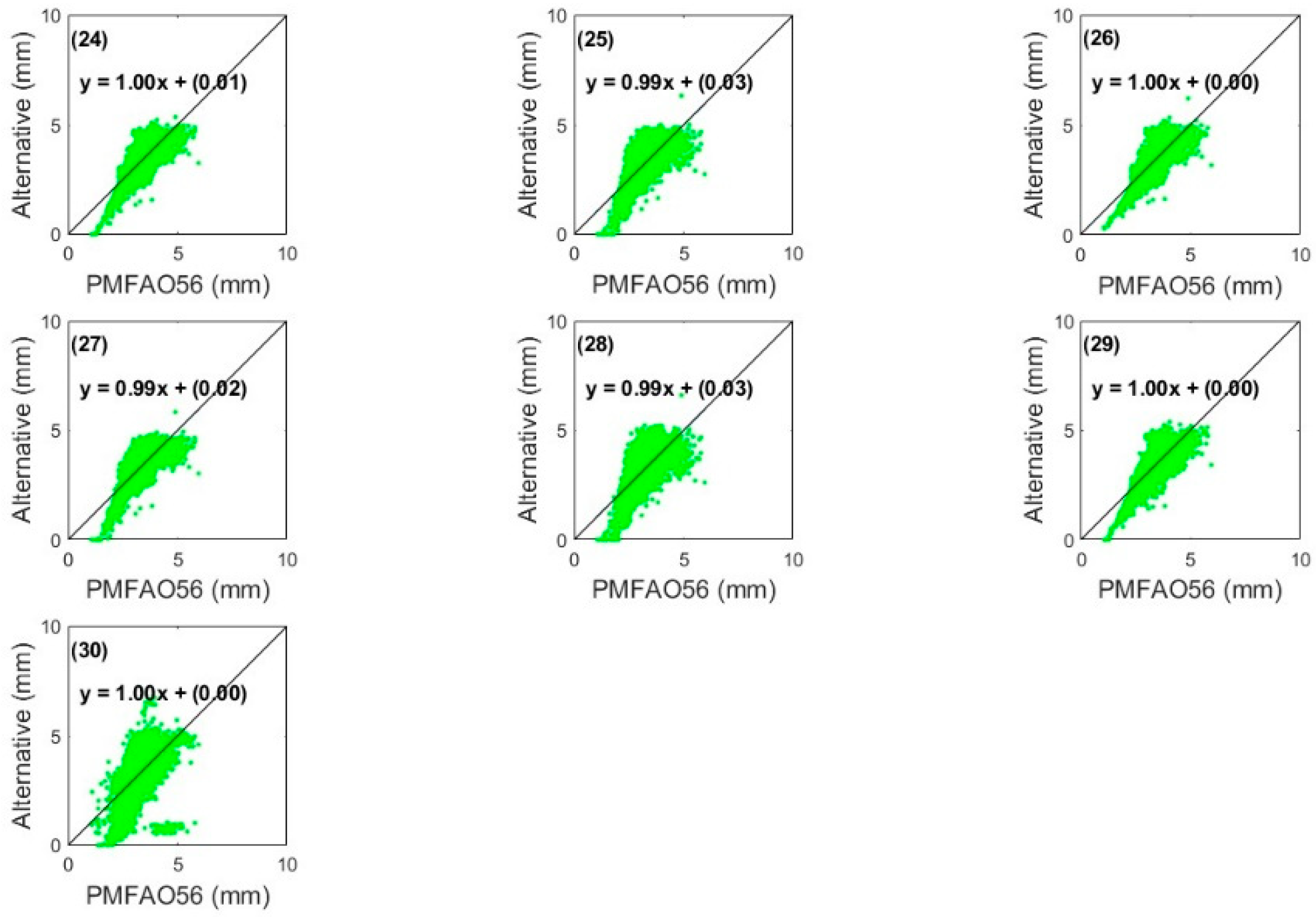
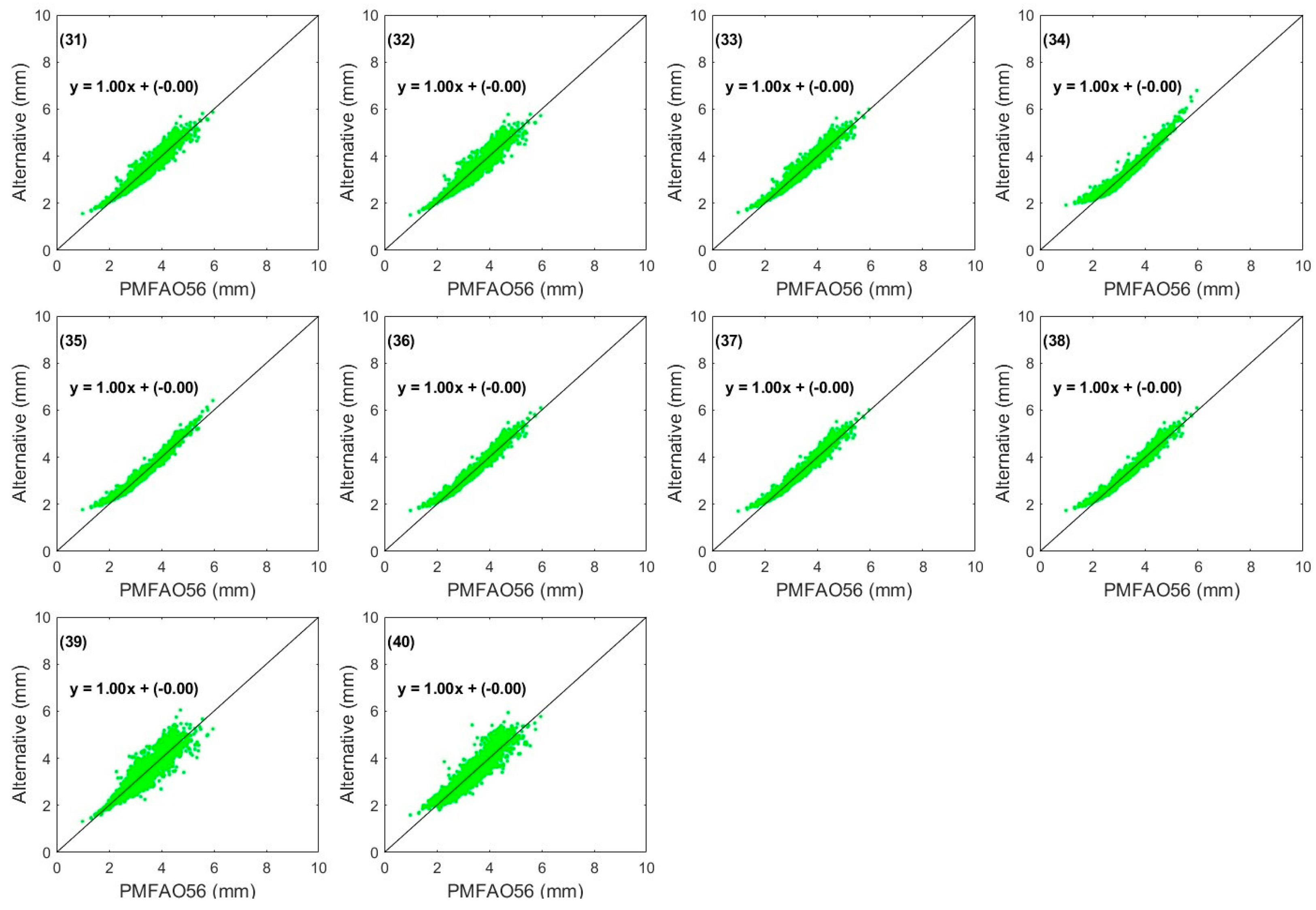
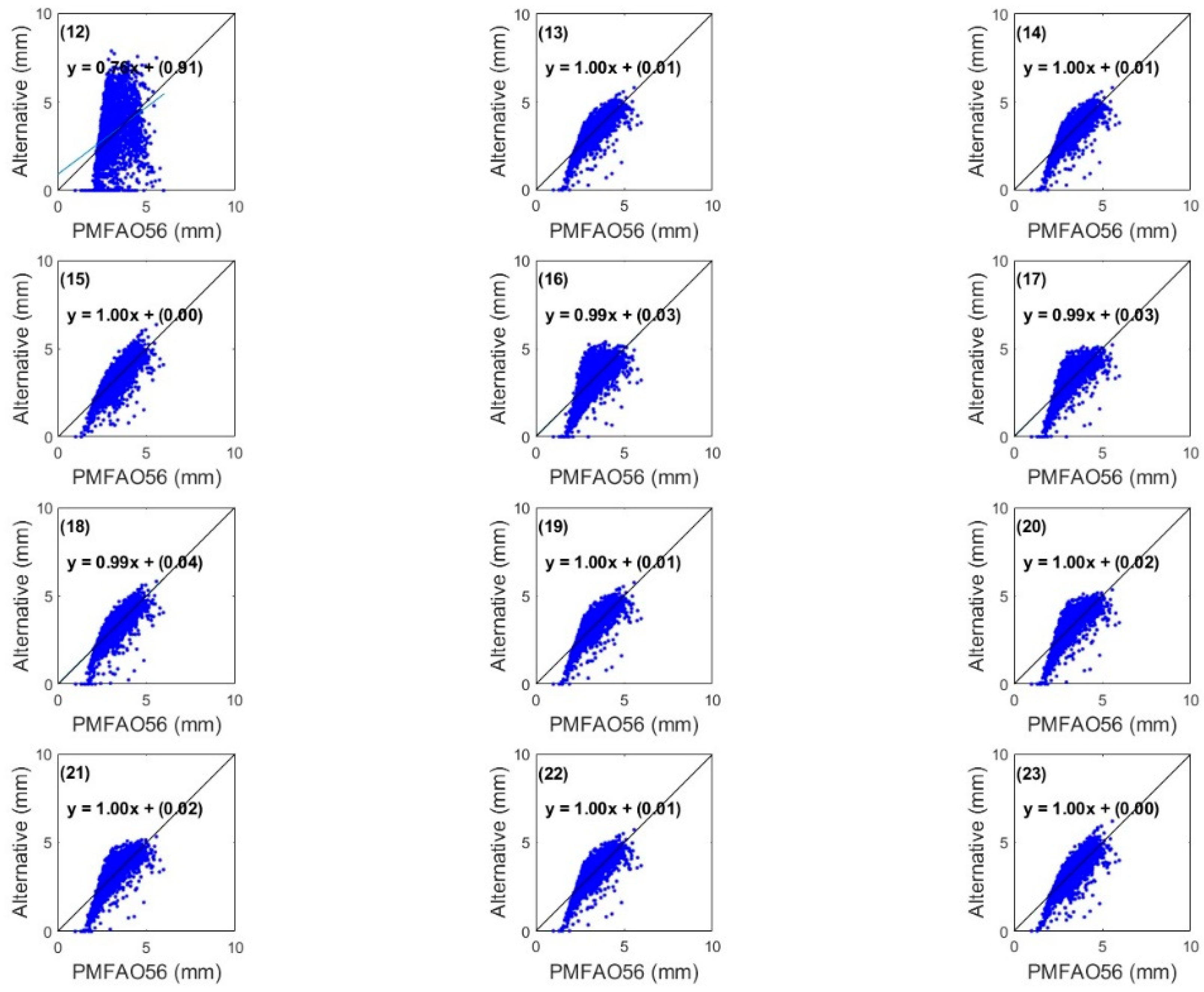
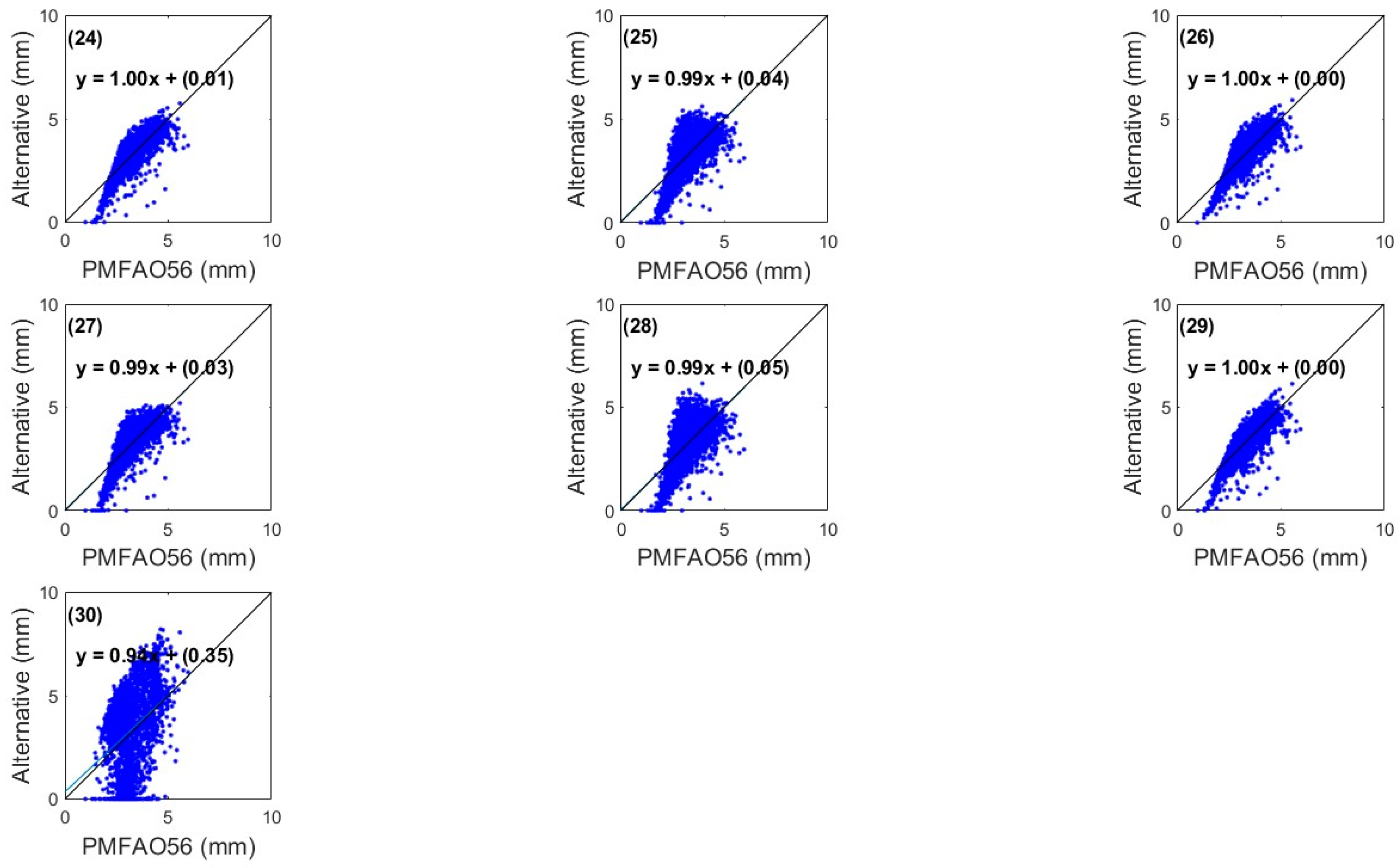
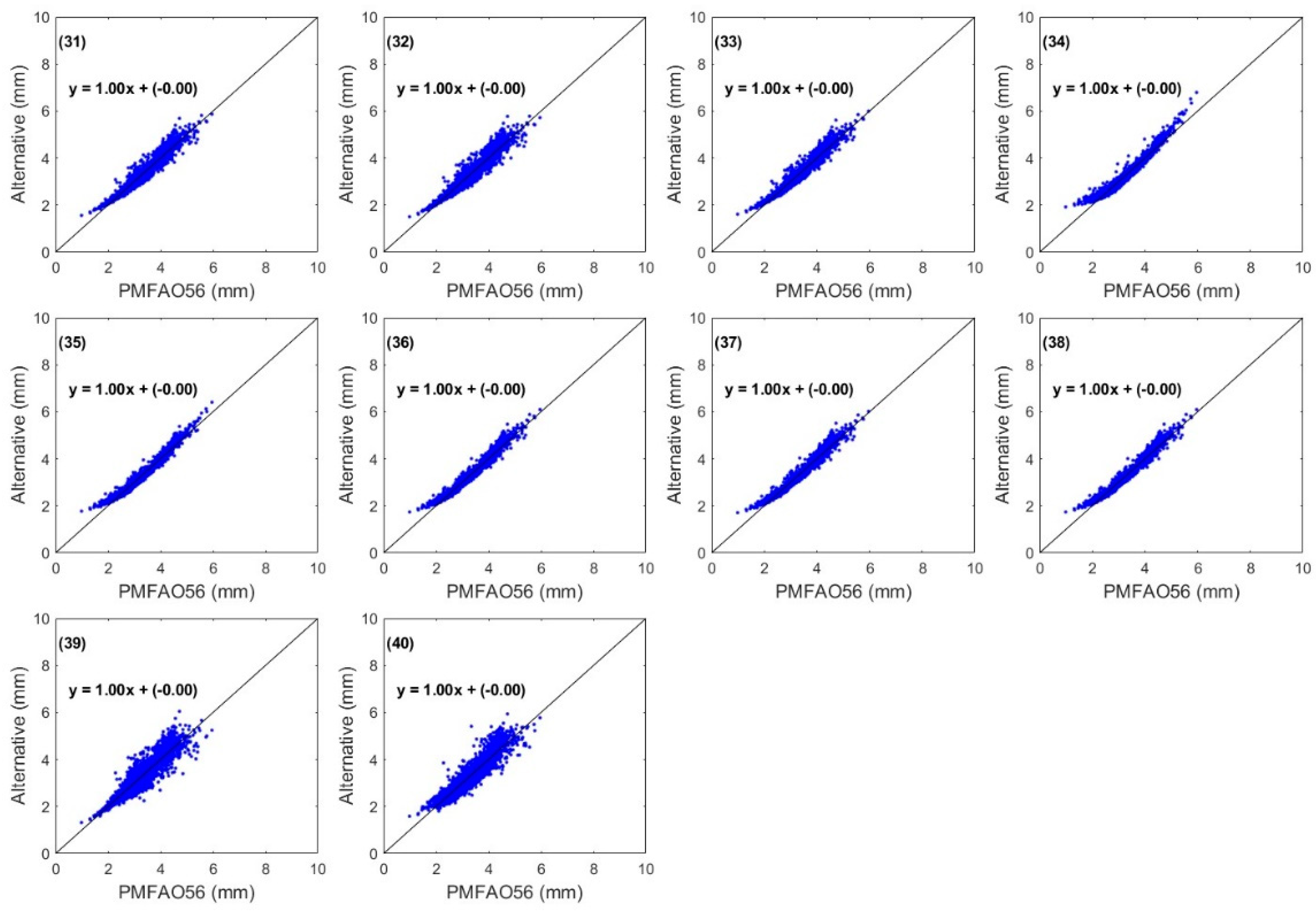
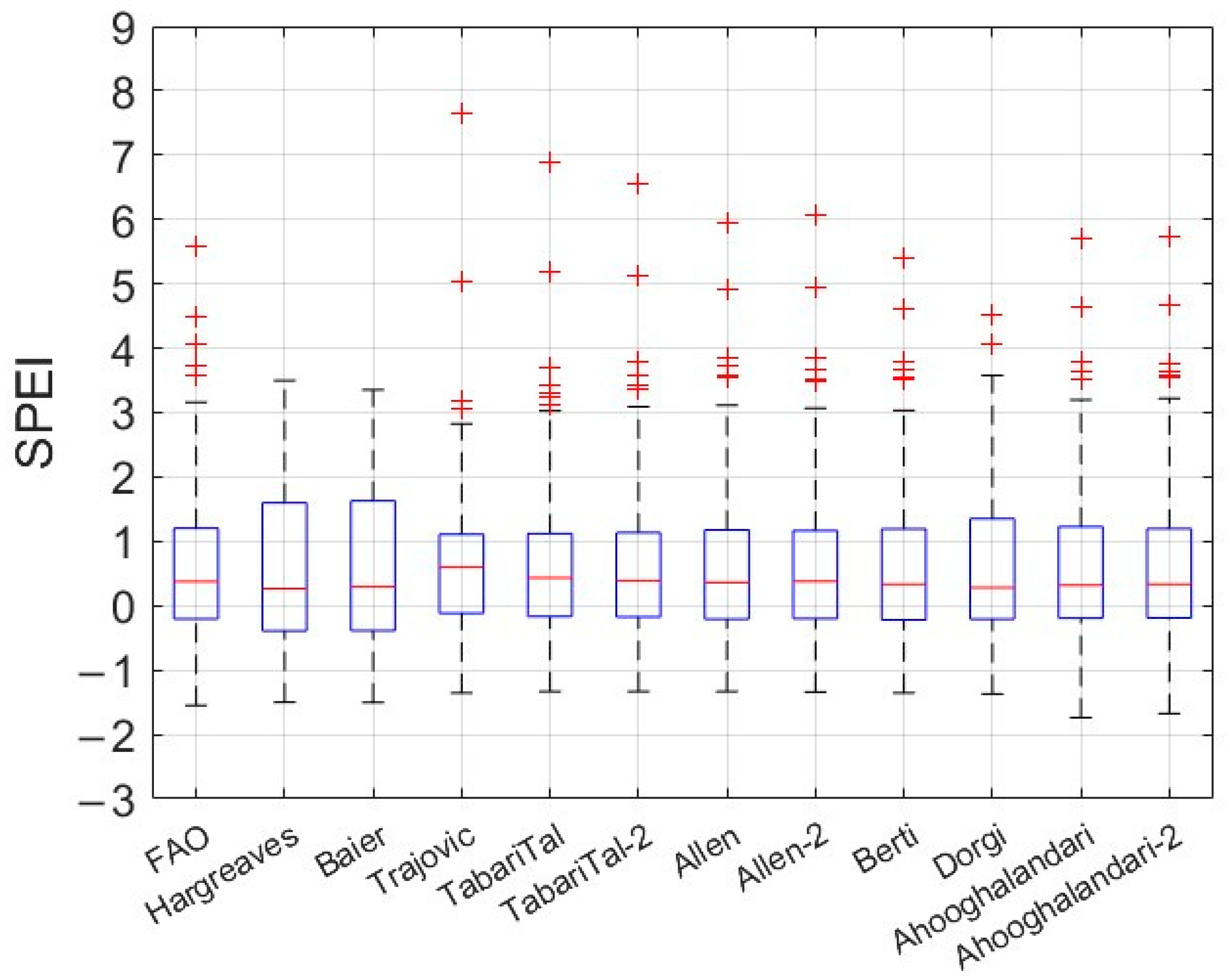
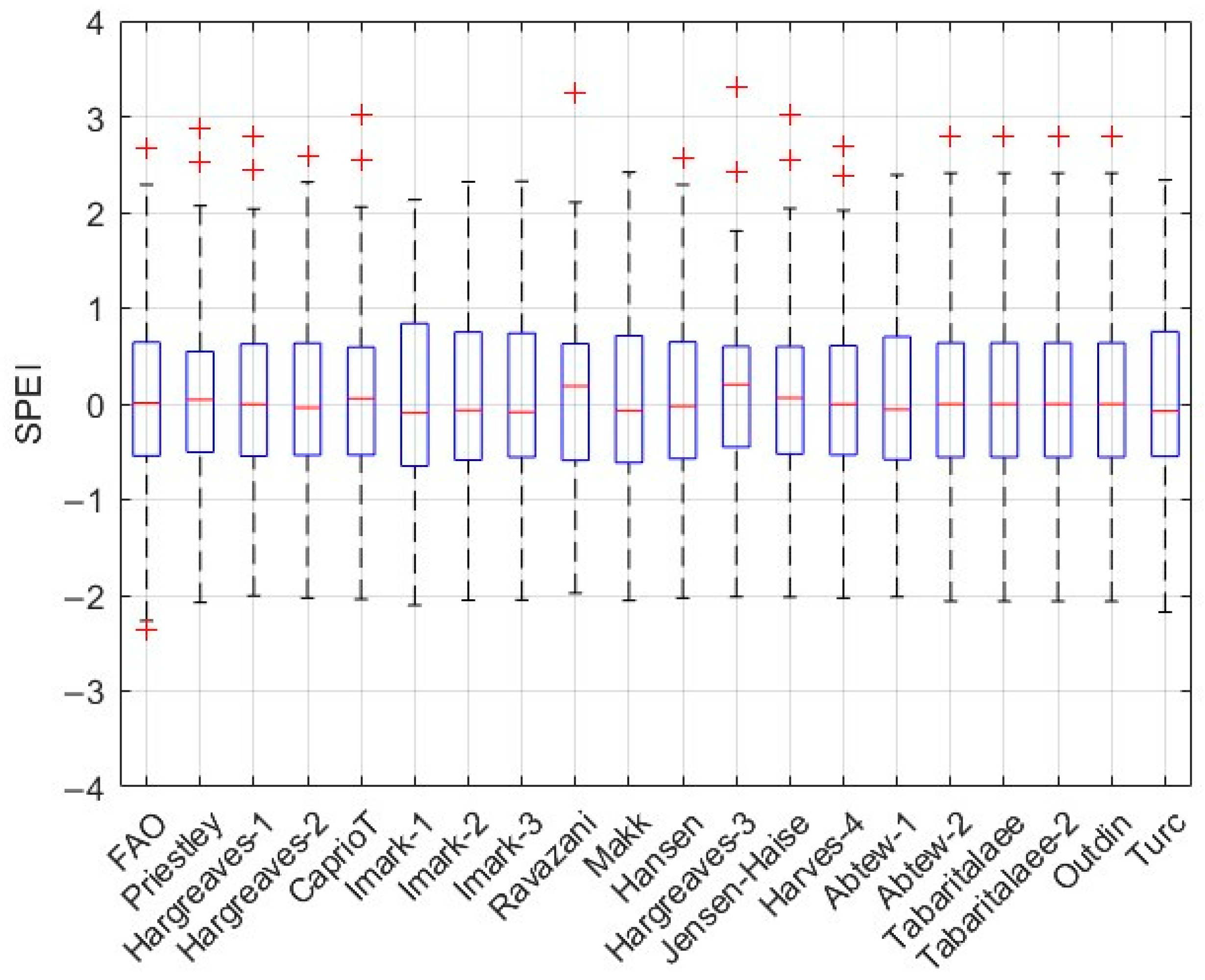
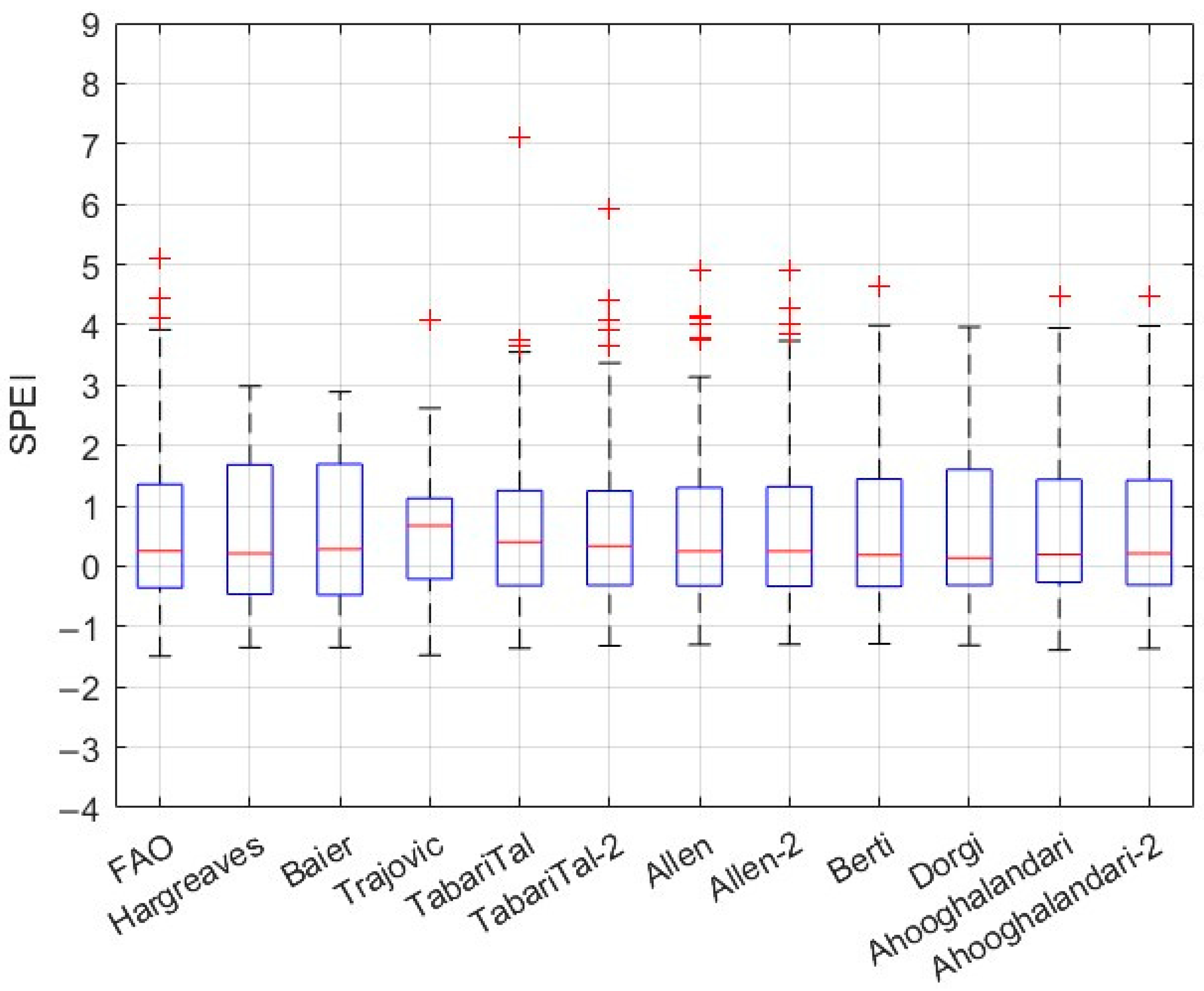
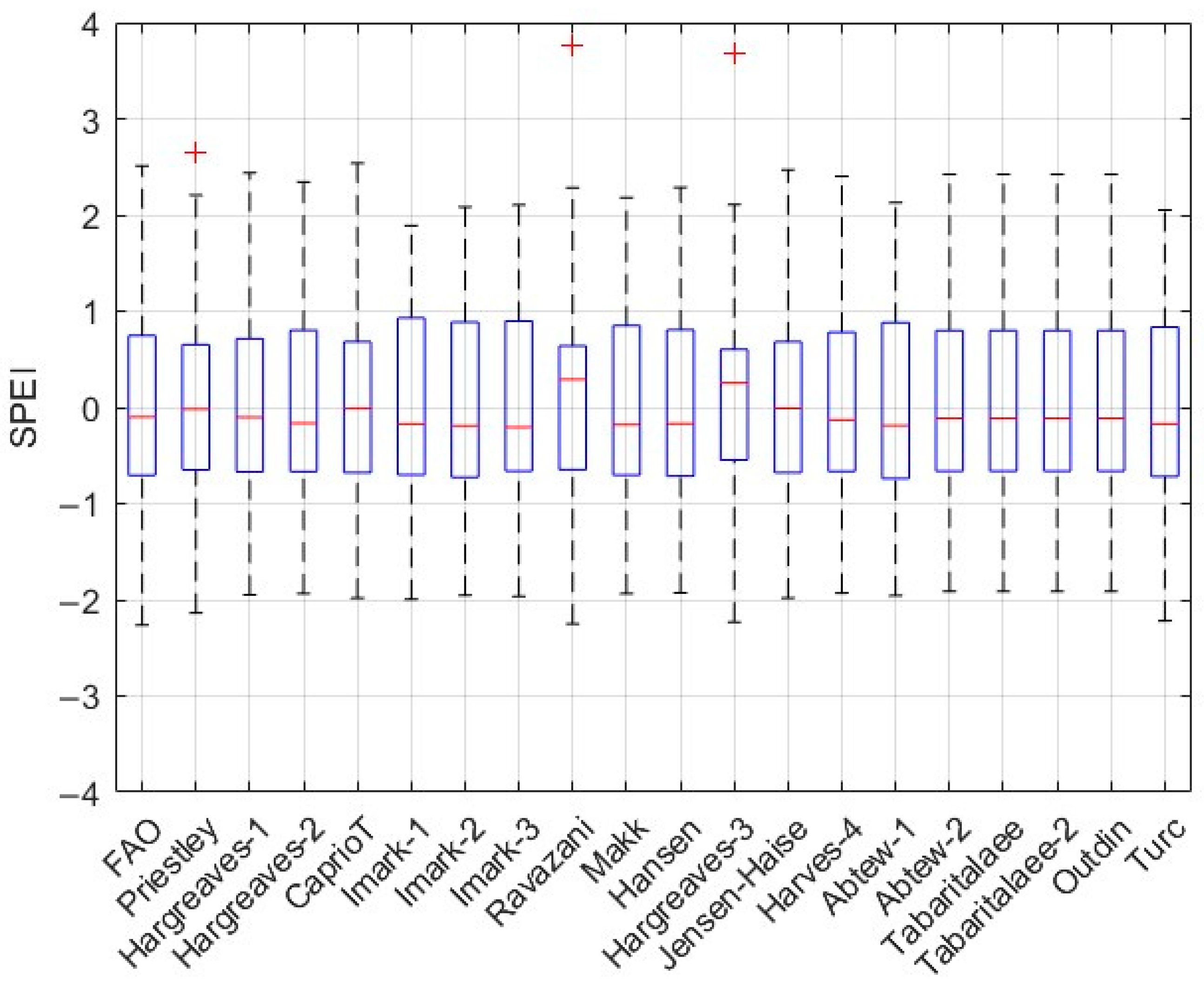
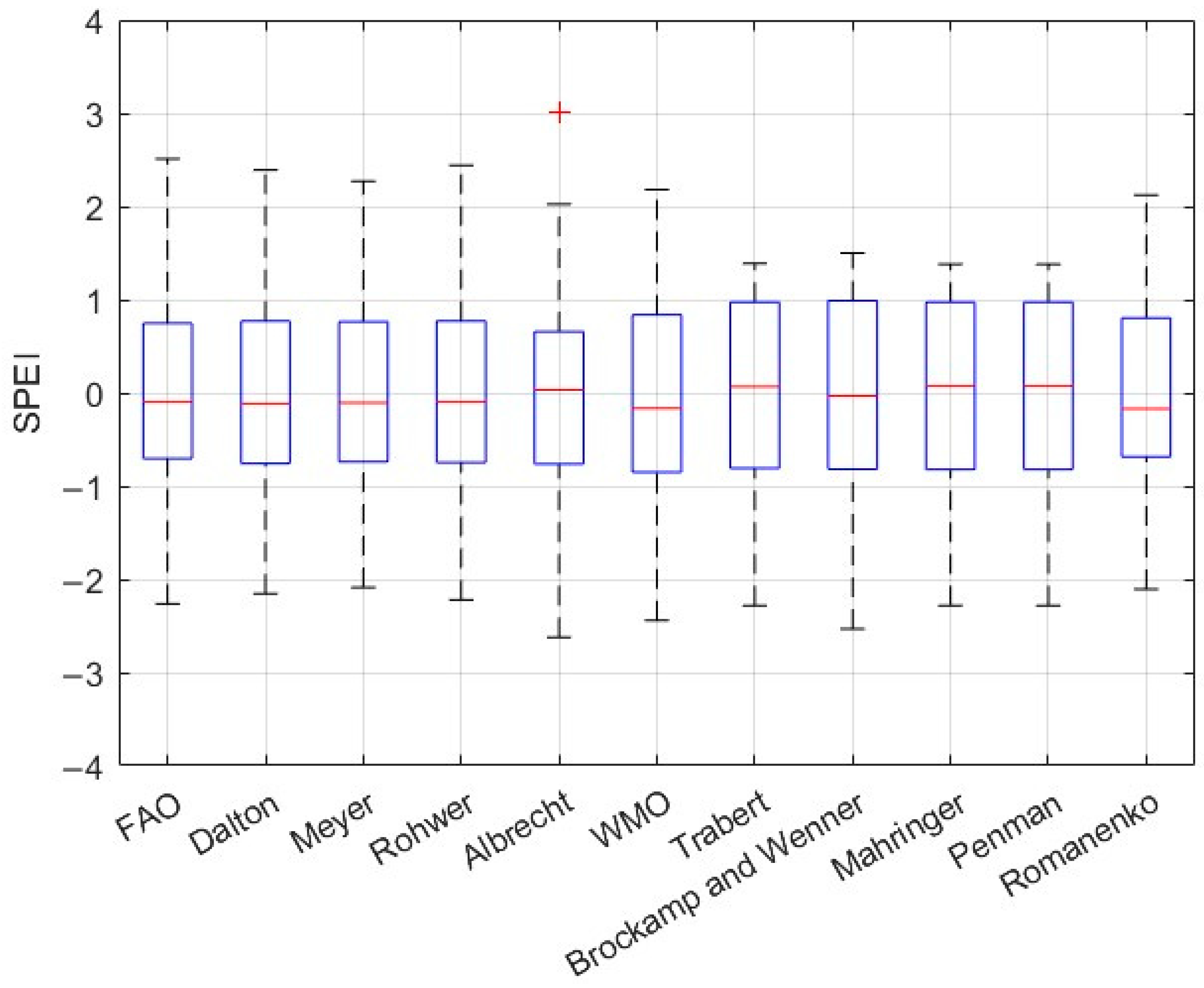
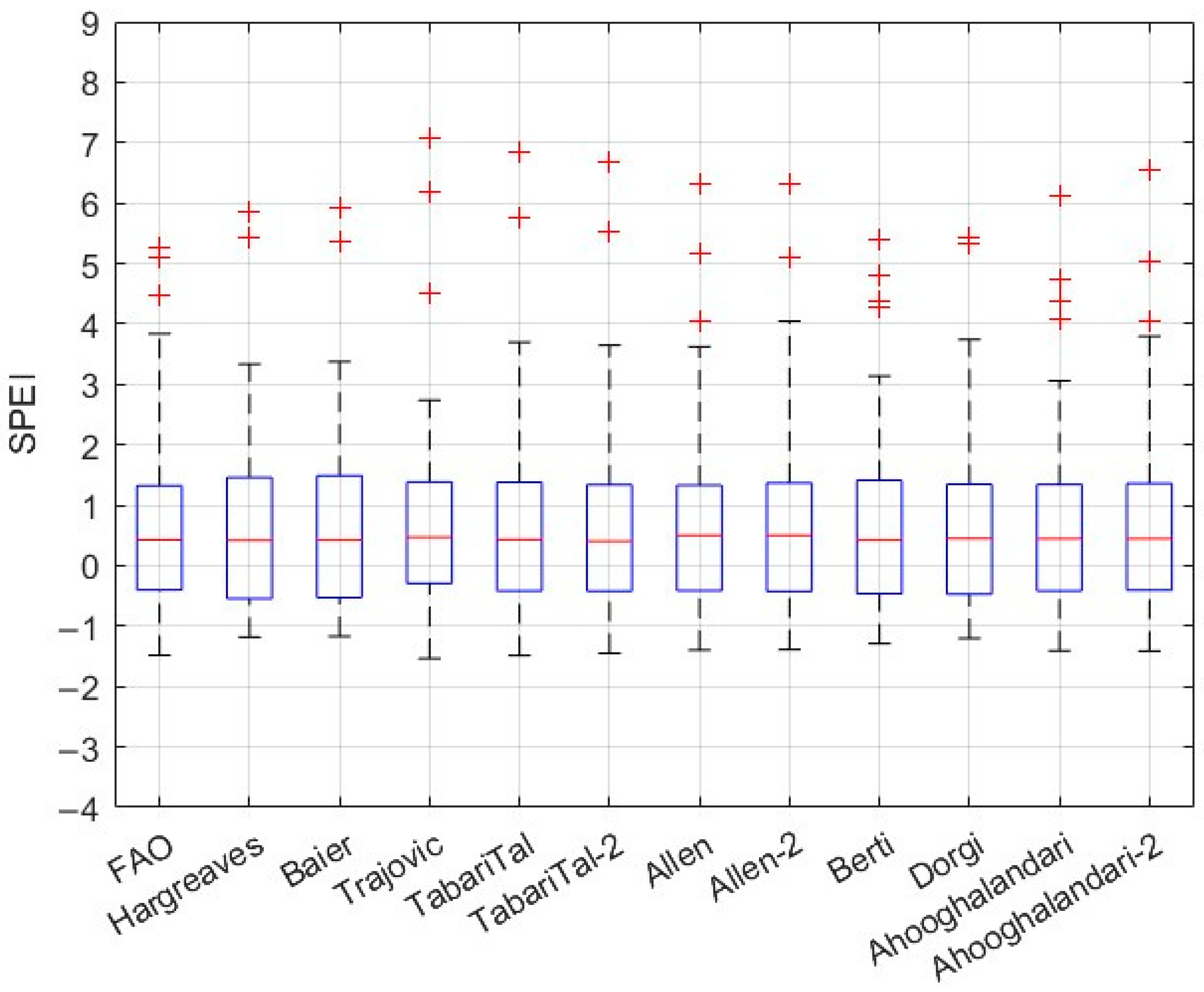
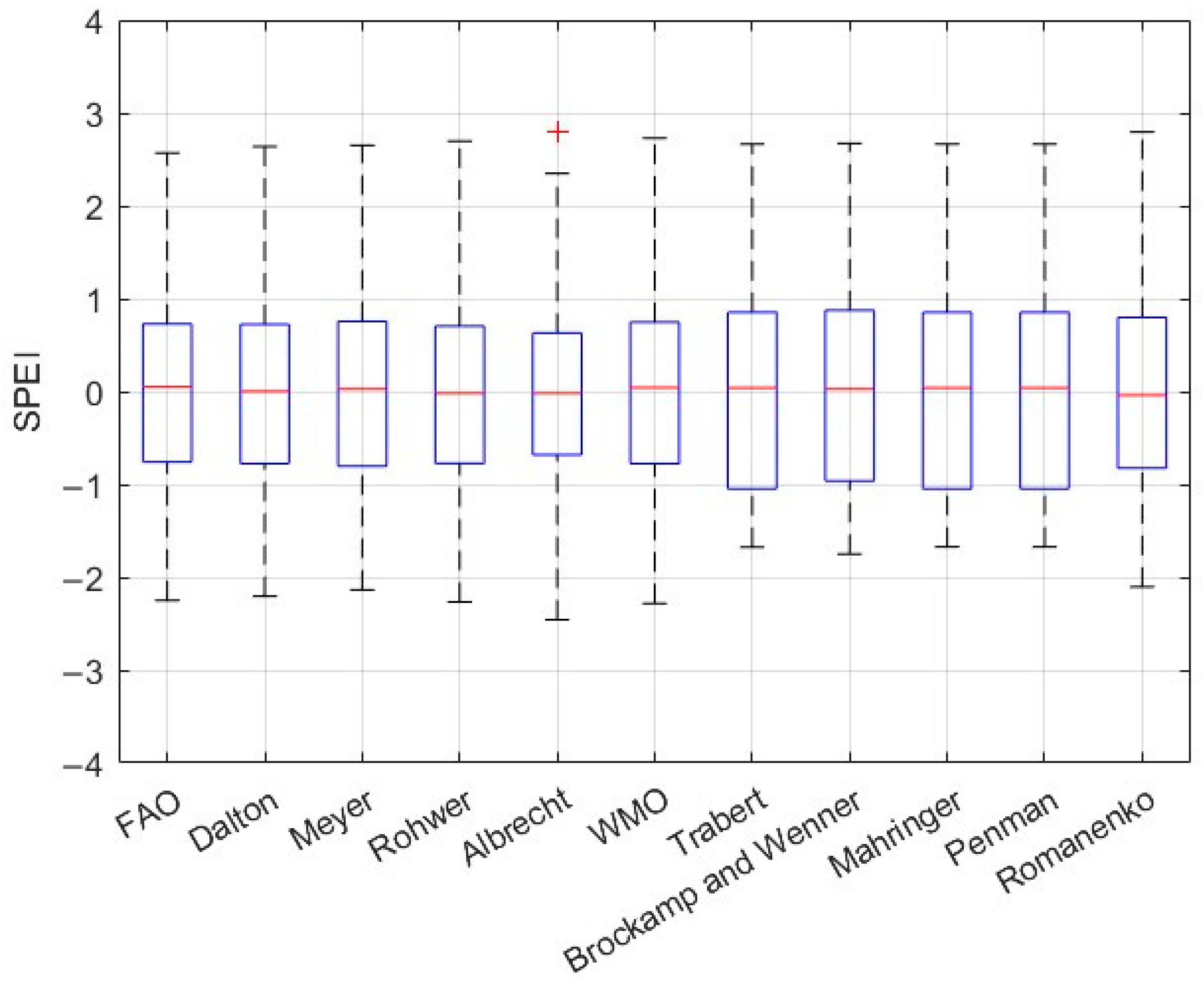
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z. Estimating Land Evapotranspiration from Potential Evapotranspiration Constrained by Soil Water at Daily Scale. Sci. Total Environ. 2022, 834, 155327. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and Difference of Potential Evapotranspiration and Reference Crop Evapotranspiration—A Review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar]
- FAO. Guidelines for Designing and Evaluating Surface Irrigation System: Irrigation and Drainage Paper 45; FAO: Rome, Italy, 1989. [Google Scholar]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- FAO. Irrigation Management|Land & Water. Available online: https://www.fao.org/land-water/water/water-management/irrigation-management/en/ (accessed on 23 November 2023).
- Hou, P.S.; Fadzil, L.M.; Manickam, S.; Al-Shareeda, M.A. Vector Autoregression Model-Based Forecasting of Reference Evapotranspiration in Malaysia. Sustainability 2023, 15, 3675. [Google Scholar] [CrossRef]
- Nie, T.; Yuan, R.; Liao, S.; Zhang, Z.; Gong, Z.; Zhao, X.; Chen, P.; Li, T.; Lin, Y.; Du, C.; et al. Characteristics of Potential Evapotranspiration Changes and Its Climatic Causes in Heilongjiang Province from 1960 to 2019. Agriculture 2022, 12, 2017. [Google Scholar] [CrossRef]
- Kim, H.J.; Chandrasekara, S.; Kwon, H.H.; Lima, C.; Kim, T. woong A Novel Multi-Scale Parameter Estimation Approach to the Hargreaves-Samani Equation for Estimation of Penman-Monteith Reference Evapotranspiration. Agric. Water Manag. 2023, 275, 108038. [Google Scholar] [CrossRef]
- Sutapa, I.W.; Saparuddin, Y.A.; Lipu, S.; Rustiati, N.B.; Adi, I.P.H. The Performance of Thirty-Eight Evapotraspiation Methods against the Penman Montieth Method. J. Eng. Res. 2023, 11, 13251. [Google Scholar] [CrossRef]
- Filho, L.C.A.L.; Carvalho, L.G.; Evangelista, A.W.P.; Alves, J. Spatial Analysis of the Influence of Meteorological Elements on the Reference Evapotranspiration in the State of Minas Gerais, Brazil. Rev. Bras. Eng. Agric. Ambient. 2010, 14. [Google Scholar] [CrossRef][Green Version]
- Chen, D.; Gao, G.; Xu, C.Y.; Guo, J.; Ren, G. Comparison of the Thornthwaite Method and Pan Data with the Standard Penman-Monteith Estimates of Reference Evapotranspiration in China. Clim. Res. 2005, 2, 28123. [Google Scholar] [CrossRef]
- Cunha, A.C.; Filho, L.R.A.G.; Tanaka, A.A.; Goes, B.C.; Putti, F.F. Influence of the Estimated Global Solar Radiation on the Reference Evapotranspiration Obtained Through the Penman-Monteith Fao 56 Method. Agric. Water Manag. 2021, 243, 106491. [Google Scholar] [CrossRef]
- McColl, K.A. Practical and Theoretical Benefits of an Alternative to the Penman-Monteith Evapotranspiration Equation. Water Resour. Res. 2020, 56, e2020WR027106. [Google Scholar] [CrossRef]
- Beven, K. A Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. Sensitivity of Potential Evapotranspiration to Changes in Climate Variables for Different Australian Climatic Zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L. Analysis of the Variation in Potential Evapotranspiration and Surface Wet Conditions in the Hancang River Basin, China. Sci. Rep. 2021, 11, 8607. [Google Scholar] [CrossRef]
- Thorp, K.R. Pyfao56: FAO-56 Evapotranspiration in Python. SoftwareX 2022, 19, 101208. [Google Scholar] [CrossRef]
- El-Rawy, M.; Batelaan, O.; Al-Arifi, N.; Alotaibi, A.; Abdalla, F.; Gabr, M.E. Climate Change Impacts on Water Resources in Arid and Semi-Arid Regions: A Case Study in Saudi Arabia. Water 2023, 15, 606. [Google Scholar] [CrossRef]
- Das, S.; Kaur Baweja, S.; Raheja, A.; Gill, K.K.; Sharda, R. Development of Machine Learning-Based Reference Evapotranspiration Model for the Semi-Arid Region of Punjab, India. J. Agric. Food Res. 2023, 13, 100640. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. Evaluation and Generalization of Temperature-Based Methods for Calculating Evaporation. Hydrol. Process. 2001, 15, 305–319. [Google Scholar]
- Aparicio, F.J. Fundamentos de Hidrología de Superficie; Noriega: San Francisco, CA, USA, 1989; ISBN 9681830148. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Tam, B.Y.; Cannon, A.J.; Bonsal, B.R. Standardized Precipitation Evapotranspiration Index (SPEI) for Canada: Assessment of Probability Distributions. Can. Water Resour. J. 2023, 48, 283–299. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Chen, Z.; Ren, Z. Assessment of Candidate Distributions for SPI/SPEI and Sensitivity of Drought to Climatic Variables in China. Int. J. Climatol. 2019, 39, 4392–4412. [Google Scholar] [CrossRef]
- Zhang, P.; Cai, Y.; Cong, P.; Xie, Y.; Chen, W.; Cai, J.; Bai, X. Quantitation of Meteorological, Hydrological and Agricultural Drought under Climate Change in the East River Basin of South China. Ecol. Indic. 2024, 158, 111304. [Google Scholar] [CrossRef]
- Yimer, E.A.; Van Schaeybroeck, B.; Van de Vyver, H.; van Griensven, A. Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere 2022, 13, 364. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Response to Comment on “Candidate Distributions for Climatological Drought Indices (SPI and SPEI)”. Int. J. Climatol. 2016, 36, 2132–2138. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, B.; Jia, L.; Huang, H. Conditional Distribution Selection for SPEI-Daily and Its Revealed Meteorological Drought Characteristics in China from 1961 to 2017. Atmos. Res. 2020, 246, 105108. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S. Comment on “Candidate Distributions for Climatological Drought Indices (SPI and SPEI)” by James, H. Stagge et al. Int. J. Climatol. 2016, 36, 2120–2131. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Bai, Y.; Zhang, S.; Yang, S.; Henchiri, M.; Seka, A.M.; Nanzad, L. Drought Monitoring and Performance Evaluation Based on Machine Learning Fusion of Multi-Source Remote Sensing Drought Factors. Remote Sens. 2022, 14, 6398. [Google Scholar] [CrossRef]
- Fan, L.; Wang, H.; Liu, Z.; Li, N. Quantifying the Relationship between Drought and Water Scarcity Using Copulas: Case Study of Beijing-Tianjin-Hebei Metropolitan Areas in China. Water 2018, 10, 1622. [Google Scholar] [CrossRef]
- Jensen, M.E.; Burmann, R.D.; Allen, R.G. Evaporation and Irrigation Water Requirements. In ASCE Manual and Reports on Engineering Practice; American Society of Civil Engineers: Reston, VA, USA, 1990; p. 332. [Google Scholar]
- The MathWorks Inc. MATLAB version: 9.14.0 (R2023a); The MathWorks Inc. 2022. Available online: https://www.mathworks.com (accessed on 25 March 2025).
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A.; Abstract, A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 2, 96–99. [Google Scholar]
- Trajkovic, S. Hargreaves versus Penman-Monteith under Humid Conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Local Calibration of the Hargreaves and Priestley-Taylor Equations for Estimating Reference Evapotranspiration in Arid and Cold Climates of Iran Based on the Penman-Monteith Model. J. Hydrol. Eng. 2011, 16, 837–845. [Google Scholar] [CrossRef]
- Arteaga-Ramírez, R.; Vázquez-Peña, M.A.; Ibáñez-Castillo, L.A. Agrociencia; Colegio de Postgraduados, Escuela Nacional de Agricultura (Mexico): Mexico City, Mexico, 2015; Volume 49. [Google Scholar]
- Salam, R.; Islam, A.R.M.T.; Pham, Q.B.; Dehghani, M.; Al-Ansari, N.; Linh, N.T.T. The Optimal Alternative for Quantifying Reference Evapotranspiration in Climatic Sub-Regions of Bangladesh. Sci. Rep. 2020, 10, 20171. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration under Inaccurate Data Conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar]
- Ortiz-Gómez, R.; Flowers-Cano, R.S.; Medina-García, G. Sensitivity of the RDI and SPEI Drought Indices to Different Models for Estimating Evapotranspiration Potential in Semiarid Regions. Water Resour. Manag. 2022, 36, 2471–2492. [Google Scholar] [CrossRef]
- Peng, L.; Li, Y.; Feng, H. The Best Alternative for Estimating Reference Crop Evapotranspiration in Different Sub-Regions of Mainland China. Sci. Rep. 2017, 7, 5458. [Google Scholar] [CrossRef]
- Majidi, M.; Alizadeh, A.; Vazifedoust, M.; Farid, A.; Ahmadi, T. Analysis of the Effect of Missing Weather Data on Estimating Daily Reference Evapotranspiration Under Different Climatic Conditions. Water Resour. Manag. 2015, 29, 2107–2124. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing Reference Evapotranspiration by the Hargreaves Method in North-Eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Dorji, U.; Olesen, J.E.; Seidenkrantz, M.S. Water Balance in the Complex Mountainous Terrain of Bhutan and Linkages to Land Use. J. Hydrol. Reg. Stud. 2016, 7, 55–68. [Google Scholar] [CrossRef]
- Robertson, W.; Baier, W. Estimation of Latente Evaporation from Simple Weather Observations. Can. J. Plant Sci. 1965, 45, 276–284. [Google Scholar]
- Ahooghalandari, M.; Khiadani, M.; Jahromi, M.E. Developing Equations for Estimating Reference Evapotranspiration in Australia. Water Resour. Manag. 2016, 30, 3815–3828. [Google Scholar] [CrossRef]
- Celestin, S.; Qi, F.; Li, R.; Yu, T.; Cheng, W. Evaluation of 32 Simple Equations against the Penman–Monteith Method to Estimate the Reference Evapotranspiration in the Hexi Corridor, Northwest China. Water 2020, 12, 2772. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Singh Rawat, K.; Kumar Singh, S.; Bala, A.; Szabó, S. Estimation of Crop Evapotranspiration through Spatial Distributed Crop Coefficient in a Semi-Arid Environment. Agric. Water Manag. 2019, 213, 922–933. [Google Scholar] [CrossRef]
- López-Urrea, R.; Martín de Santa Olalla, F.; Fabeiro, C.; Moratalla, A. Testing Evapotranspiration Equations Using Lysimeter Observations in a Semiarid Climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, W.; Huang, B. Seasonal Variation of Evapotranspiration, Priestley-Taylor Coefficient and Crop Coefficient in Diverse Landscapes. Geogr. Sustain. 2021, 2, 224–233. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating Evapotranspiration from Solar Radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Asae, M. Moisture Availability and Crop Production. Trans. ASAE 1975, 18, 980–984. [Google Scholar] [CrossRef]
- Abtew, W. Water Resources Bulletin Evapotranspiration Measurements and Modeling for Three Wetland Systems in South Florida. J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
- Abtew, W. Evapotranspiration in the Everglades: Comparison of Bowen Ratio Measurements and Model Estimations. In 2005 ASAE Annual International Meeting; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2005; p. 1. [Google Scholar] [CrossRef]
- Irmak, S.; Irmak, A.; Allen, R.G.; Jones, J.W. Solar and Net Radiation-Based Equations to Estimate Reference Evapotranspiration in Humid Climates. J. Irrig. Drain. Eng. 2003, 129, 336–347. [Google Scholar] [CrossRef]
- Kodja, D.J.; Akognongbé, A.J.S.; Amoussou, E.; Mahé, G.; Vissin, E.W.; Paturel, J.E.; Houndénou, C. Calibration of the Hydrological Model GR4J from Potential Evapotranspiration Estimates by the Penman-Monteith and Oudin Methods in the Ouémé Watershed (West Africa). Proc. Int. Assoc. Hydrol. Sci. 2020, 383, 163–169. [Google Scholar] [CrossRef]
- Dalton, J. Experimental Essays, on the Constitution of Mixed Gases. Manch. Soc. 1785–1879 1802, 5, 535–602. [Google Scholar]
- Albrecht, F. Die Methoden Zur Bestimmung Der Verdunstung Der Natürlichen Erdoberfläche. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1950, 2, 1–38. [Google Scholar] [CrossRef]
- Meyer, A. Ueber Einige Zusammenhänge Zwischen Klima Und Boden in Europa. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1926. [Google Scholar] [CrossRef]
- Muhammad, M.K.I.; Nashwan, M.S.; Shahid, S.; Ismail, T.b.; Song, Y.H.; Chung, E.S. Evaluation of Empirical Reference Evapotranspiration Models Using Compromise Programming: A Case Study of Peninsular Malaysia. Sustainability 2019, 11, 4267. [Google Scholar] [CrossRef]
- Rohwer, C.; Rohwer, G. Evaporation from Free Water Surfaces; US Department of Agriculture: Washington, DC, USA, 1931. [Google Scholar]
- Yang, Y.; Chen, R.; Han, C.; Liu, Z. Evaluation of 18 Models for Calculating Potential Evapotranspiration in Different Climatic Zones of China. Agric. Water Manag. 2021, 244, 106545. [Google Scholar] [CrossRef]
- WMO. Measurement and Estimation of Evaporation and Evapotranspiration; WMO: Geneva, Switzerland, 1966. [Google Scholar]
- Bormann, H. Sensitivity Analysis of 18 Different Potential Evapotranspiration Models to Observed Climatic Change at German Climate Stations. Clim. Change 2011, 104, 729–753. [Google Scholar] [CrossRef]
- Ghiat, I.; Govindan, R.; Al-Ansari, T. Evaluation of Evapotranspiration Models for Cucumbers Grown under CO2 Enriched and HVAC Driven Greenhouses: A Step towards Precision Irrigation in Hyper-Arid Regions. Front. Sustain. Food Syst. 2023, 7, 1155443. [Google Scholar] [CrossRef]
- Sweers, H.E. A Nomogram to Estimate the Heat-Exchange Coefficient at the Air-Water Interface as a Function of Wind Speed and Temperature; a Critical Survey of Some Literature. J. Hydrol. 1976, 30, 375–401. [Google Scholar] [CrossRef]
- Rezaei, M.; Valipour, M.; Valipour, M. Modelling Evapotranspiration to Increase the Accuracy of the Estimations Based on the Climatic Parameters. Water Conserv. Sci. Eng. 2016, 1, 197–207. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of Sixteen Reference Evapotranspiration Methods under Sahelian Conditions in the Senegal River Valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating Daily Reference Evapotranspiration Based on Limited Meteorological Data Using Deep Learning and Classical Machine Learning Methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Farg, E.; Arafat, S.M.; Abd El-Wahed, M.S.; El-Gindy, A.M. Estimation of Evapotranspiration ETc and Crop Coefficient K c of Wheat, in South Nile Delta of Egypt Using Integrated FAO-56 Approach and Remote Sensing Data. Egypt. J. Remote Sens. Space Sci. 2012, 15, 83–89. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Al-Juboori, A.M.; Beyaztas, U.; Al-Ansari, N.; Chau, K.W.; Qi, C.; Ali, M.; Salih, S.Q.; Shahid, S. Prediction of Evaporation in Arid and Semi-Arid Regions: A Comparative Study Using Different Machine Learning Models. Eng. Appl. Comput. Fluid. Mech. 2020, 14, 70–89. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, J.; Lei, T.; He, B.; Wu, Z.; Liu, M.; Mo, X.; Geng, G.; Li, X.; Zhou, H.; et al. Temporal-Spatial Characteristics of Severe Drought Events and Their Impact on Agriculture on a Global Scale. Quat. Int. 2014, 349, 10–21. [Google Scholar] [CrossRef]
- INEGI. Uso de Suelo y Vegetación. Available online: https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=702825568580 (accessed on 3 August 2023).






| Categorization | SPEI Values |
|---|---|
| Extreme drought | ≤−2 |
| Severe drought | −2 |
| Moderate drought | −1.5 |
| Mild drought | −1 |
| Normal | ±≤0.5 |
| Mildly wet | 0.5 |
| Moderately wet | 1≤ |
| Severely wet | 1.5≤ |
| Extremely wet | ≥2 |
| Latitude | Longitude | Altitude |
|---|---|---|
| 19.7030° N | 101.1920° W | 1920 mbsl |
| Station Data | Annual Mean Climatic Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Latitude | Longitude | Period | T Mean (°C) | T max (°C) | T min (°C) | RH Mean (%) | RH max (%) | RH min (%) | U2 (m/s) |
| Morelia, Michoacán | 19.7214 | −101.1828 | 2010–2022 | 18.786 | 27.9734 | 11.4 | 66.8674 | 89.9603 | 39.126 | 1.063 |
| Red Universitaria de Observatorios Atmosfericos (RUOA) | 19.6493 | −101.222 | 2016–2022 | 17.402 | 23.3321 | 11.58 | 61.225 | 83.4486 | 35.369 | 1.702 |
| Methods Based on Temperature | Mean Error (mm/day) | Standard Deviation Error (mm/Day) | Correlation Coefficient (Dimensionless) | RMSE | MAE | PE |
|---|---|---|---|---|---|---|
| Hargreaves–Samani | −0.0003 | −0.1350 | 0.8130 | 0.4238 | 0.3256 | 0.0001 |
| Baier–Robertson | 0.0000 | −0.1411 | 0.8078 | 0.4326 | 0.3366 | 0.0000 |
| Trajovic | −0.0005 | −0.1356 | 0.8116 | 0.4256 | 0.3243 | 0.0001 |
| Tabari–Tale | −0.0003 | −0.1350 | 0.8130 | 0.4238 | 0.3256 | 0.0001 |
| Tabari–Tale-2 | −0.0003 | −0.1350 | 0.8130 | 0.4238 | 0.3256 | 0.0001 |
| Droogers–Allen | −0.0006 | −0.1354 | 0.8113 | 0.4257 | 0.3244 | 0.0002 |
| Droogers–Allen-2 | −0.0003 | −0.1349 | 0.8131 | 0.4236 | 0.3250 | 0.0001 |
| Berti | −0.0003 | −0.1352 | 0.8129 | 0.4240 | 0.3265 | 0.0001 |
| Dorji | −0.0011 | −0.1343 | 0.8102 | 0.4263 | 0.3247 | 0.0003 |
| Ahooghalandari | 0.0000 | −0.1962 | 0.7514 | 0.5206 | 0.3678 | 0.0000 |
| Ahooghalandari-2 | 0.0000 | −0.1792 | 0.7679 | 0.4945 | 0.3539 | 0.0000 |
| Priestley | −0.0136 | −0.4542 | 0.5300 | 0.8888 | 0.6947 | 4.27 × 10−3 |
| Hargreaves-1 | −0.0006 | −0.1354 | 0.8113 | 0.4257 | 0.3244 | 1.79 × 10−4 |
| Hargreaves-2 | −0.0006 | −0.1354 | 0.8113 | 0.4257 | 0.3244 | 1.79 × 10−4 |
| CaprioT | 0.0000 | −0.1626 | 0.7846 | 0.4684 | 0.3520 | 7.60 × 10−6 |
| Imark-1 | −0.0013 | −0.2196 | 0.7244 | 0.5600 | 0.4552 | 4.10 × 10−4 |
| Imark-2 | −0.0012 | −0.1641 | 0.7778 | 0.4758 | 0.3791 | 3.85 × 10−4 |
| Imark-3 | −0.0028 | −0.1496 | 0.7862 | 0.4589 | 0.3471 | 8.83 × 10−4 |
| Ravazani | −0.0003 | −0.1350 | 0.8130 | 0.4238 | 0.3256 | 1.02 × 10−4 |
| Makk | −0.0007 | −0.1530 | 0.7919 | 0.4555 | 0.3604 | 2.05 × 10−4 |
| Hansen | −0.0007 | −0.1530 | 0.7919 | 0.4555 | 0.3604 | 2.05 × 10−4 |
| Hargreaves-3 | −0.0003 | −0.1352 | 0.8129 | 0.4240 | 0.3265 | 9.32 × 10−5 |
| Jensen–Haise | −0.0001 | −0.1518 | 0.7958 | 0.4509 | 0.3395 | 2.30 × 10−5 |
| Harves-4 | −0.0003 | −0.1350 | 0.8130 | 0.4238 | 0.3256 | 1.02 × 10−4 |
| Abtew-1 | −0.0014 | −0.2491 | 0.6988 | 0.6022 | 0.4922 | 4.29× 10−4 |
| Abtew-2 | 0.0000 | −0.1367 | 0.8126 | 0.4252 | 0.3279 | 8.37 × 10−16 |
| Tabaritalaee | −0.0012 | −0.1641 | 0.7778 | 0.4758 | 0.3791 | 3.85 × 10−4 |
| Tabaritalaee-2 | −0.0017 | −0.3077 | 0.6523 | 0.6826 | 0.5609 | 5.29 × 10−4 |
| Outdin | −0.0001 | −0.1465 | 0.8013 | 0.4423 | 0.3337 | 3.45 × 10−5 |
| Turc | 0.0000 | −0.4777 | 0.5538 | 0.8913 | 0.6669 | 4.04 × 10−6 |
| Dalton | 0.0000 | −0.0729 | 0.8905 | 0.3029 | 0.2155 | 1.39 × 10−16 |
| Meyer | 0.0000 | −0.0889 | 0.8697 | 0.3365 | 0.2406 | 4.18 × 10−16 |
| Rohnwer | 0.0000 | −0.0602 | 0.9078 | 0.2739 | 0.1941 | 1.39 × 10−16 |
| Albrecht | 0.0000 | −0.0252 | 0.9592 | 0.1748 | 0.1251 | 4.18 × 10−16 |
| WMO | 0.0000 | −0.0301 | 0.9516 | 0.1914 | 0.1354 | 6.97 × 10−16 |
| Trabert | 0.0000 | −0.0279 | 0.9551 | 0.1840 | 0.1293 | 4.18 × 10−16 |
| Brockamp–Wenner | 0.0000 | −0.0308 | 0.9506 | 0.1936 | 0.1355 | 0.00 |
| Mahringer | 0.0000 | −0.0279 | 0.9551 | 0.1840 | 0.1293 | 2.79 × 10−16 |
| Penman | 0.0000 | −0.1459 | 0.8025 | 0.4408 | 0.3189 | 5.58 × 10−16 |
| Romanenko | 0.0000 | −0.1955 | 0.7521 | 0.5196 | 0.3687 | 4.18 × 10−16 |
| Methods Based on Temperature | Mean Error (mm/day) | Standard Deviation Error (mm/Day) | Correlation Coefficient (Dimensionless) | RMSE | MAE | PE |
|---|---|---|---|---|---|---|
| Hargreaves–Samani | −0.0007 | −0.1548 | 0.825220193 | 0.477427537 | 0.3828404 | 0.000224394 |
| Baier–Robertson | −0.0002 | −0.1663 | 0.816209017 | 0.491037418 | 0.3934098 | 6.75 × 10−5 |
| Trajovic | −0.0010 | −0.1494 | 0.829545473 | 2.962091497 | 0.3717325 | 0.0002969 |
| Tabari–Tale | −0.0007 | −0.1548 | 0.825220193 | 0.973372542 | 0.3828404 | 0.000224394 |
| Tabari–Tale-2 | −0.0007 | −0.1548 | 0.825220193 | 0.641185596 | 0.3828404 | 0.000224394 |
| Droogers–Allen | −0.0011 | −0.1498 | 0.828687976 | 0.463349602 | 0.3726154 | 0.000347701 |
| Droogers–Allen-2 | −0.0007 | −0.1533 | 0.826693324 | 0.434204288 | 0.3799169 | 0.000214787 |
| Berti | −0.0007 | −0.1564 | 0.823906742 | 0.719827091 | 0.385891 | 0.000208174 |
| Dorji | −0.0021 | −0.1513 | 0.824613531 | 1.07859283 | 0.3765299 | 0.000659308 |
| Ahooghalandari | 0.0000 | −0.0592 | 0.926079721 | 1.033990958 | 0.2265519 | 1.25 × 10−15 |
| Ahooghalandari-2 | 0.0000 | −0.0586 | 0.926821046 | 1.329602791 | 0.2276466 | 2.77 × 10−16 |
| PMFAO56 | 0 | 0 | 1 | 0 | 0 | 0 |
| Priestley | −0.1275 | −0.9474 | 0.332437136 | 0.968223311 | 1.3150761 | 0.038246666 |
| Hargreaves-1 | −0.0011 | −0.1498 | 0.828687976 | 0.463260988 | 0.3726154 | 0.000347701 |
| Hargreaves-2 | −0.0011 | −0.1498 | 0.828687976 | 0.6939174 | 0.3726154 | 0.000347701 |
| CaprioT | −0.0002 | −0.1691 | 0.813537339 | 0.509345836 | 0.3971055 | 7.64 × 10−5 |
| Imark-1 | −0.0030 | −0.3087 | 0.699388544 | 1.587182557 | 0.6036815 | 0.000944022 |
| Imark-2 | −0.0023 | −0.2217 | 0.763888039 | 0.83641062 | 0.4868398 | 0.000730176 |
| Imark-3 | −0.0034 | −0.1601 | 0.813176993 | 0.991414775 | 0.3874003 | 0.001047757 |
| Ravazani | −0.0007 | −0.1548 | 0.825220193 | 6.464463999 | 0.3828404 | 0.000224394 |
| Makk | −0.0014 | −0.1999 | 0.783853179 | 0.900033036 | 0.4563728 | 0.000447721 |
| Hansen | −0.0014 | −0.1999 | 0.783853179 | 0.54226488 | 0.4563728 | 0.000447721 |
| Hargreaves-3 | −0.0007 | −0.1564 | 0.823906742 | 3.349376127 | 0.385891 | 0.000208174 |
| Jensen–Haise | −0.0003 | −0.1557 | 0.825498561 | 0.427398693 | 0.3771 | 9.77 × 10−5 |
| Harves-4 | −0.0007 | −0.1548 | 0.825220193 | 0.556429119 | 0.3828404 | 0.000224394 |
| Abtew-1 | −0.0034 | −0.3505 | 0.671901998 | 0.55619865 | 0.6549032 | 0.001066803 |
| Abtew-2 | −0.0001 | −0.1549 | 0.827103679 | 0.737458611 | 0.380746 | 1.78 × 10−5 |
| Tabaritalaee | −0.0023 | −0.2217 | 0.763888039 | 0.83641062 | 0.4868398 | 0.000730176 |
| Tabaritalaee-2 | −0.0044 | −0.4273 | 0.626002879 | 1.753167437 | 0.7427538 | 0.001377527 |
| Outdin | −0.0004 | −0.1506 | 0.830097906 | 1.924788073 | 0.3697072 | 0.000110196 |
| Turc | −0.1442 | −1.2336 | 0.351862936 | 1.719438943 | 1.6105994 | 0.043031417 |
| Dalton | 0.0000 | −0.0228 | 0.970227916 | 2.787410828 | 0.1358584 | 5.54 × 10−16 |
| Meyer | 0.0000 | −0.0291 | 0.96229821 | 2.412570555 | 0.1521962 | 9.70 × 10−16 |
| Rohnwer | 0.0000 | −0.0185 | 0.975694912 | 2.765318871 | 0.1235151 | 6.93 × 10−16 |
| Albrecht | 0.0000 | −0.0176 | 0.976863347 | 4.896297446 | 0.1250965 | 8.31 × 10−16 |
| WMO | 0.0000 | −0.0124 | 0.983516927 | 0.879546128 | 0.1047949 | 5.54 × 10−16 |
| Trabert | 0.0000 | −0.0132 | 0.98256795 | 2.80680098 | 0.1067268 | 9.70 × 10−16 |
| Brockamp–Wenner | 0.0000 | −0.0141 | 0.981403162 | 2.462492249 | 0.1088213 | 1.11 × 10−15 |
| Mahringer | 0.0000 | −0.0132 | 0.98256795 | 2.840461287 | 0.1067268 | 8.31 × 10−16 |
| Penman | 0.0000 | −0.0588 | 0.926603426 | 0.601232237 | 0.2154811 | 9.70 × 10−16 |
| Romanenko | 0.0000 | −0.0569 | 0.928758926 | 1.668942635 | 0.2233238 | 1.11 × 10−15 |
| Methods | Mean Error (mm/Day) | Standard Deviation Error (mm/Day) | Correlation Coefficient (Dimensionless) | RMSE | MAE | PE |
|---|---|---|---|---|---|---|
| Temperature | −0.0007 | −0.1371 | 0.8435 | 0.9641 | 0.3530 | 0.0002 |
| Radiation | −0.0145 | −0.3096 | 0.7376 | 1.2094 | 0.5731 | 0.0043 |
| Mass transfer | 0.0000 | −0.0233 | 0.9700 | 2.1928 | 0.1275 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marquez-Alvarez, T.; Bedolla, J.H.; Pardo-Loaiza, J.; Lara-Ledesma, B.; Domínguez-Sánchez, C. Multi Standardized Precipitation Evapotranspiration Index (Multi-SPEI-ETo): Evaluation of 40 Empirical Methods and Their Influence in SPEI. Agriculture 2025, 15, 703. https://doi.org/10.3390/agriculture15070703
Marquez-Alvarez T, Bedolla JH, Pardo-Loaiza J, Lara-Ledesma B, Domínguez-Sánchez C. Multi Standardized Precipitation Evapotranspiration Index (Multi-SPEI-ETo): Evaluation of 40 Empirical Methods and Their Influence in SPEI. Agriculture. 2025; 15(7):703. https://doi.org/10.3390/agriculture15070703
Chicago/Turabian StyleMarquez-Alvarez, Tariacuri, Joel Hernandez Bedolla, Jesus Pardo-Loaiza, Benjamín Lara-Ledesma, and Constantino Domínguez-Sánchez. 2025. "Multi Standardized Precipitation Evapotranspiration Index (Multi-SPEI-ETo): Evaluation of 40 Empirical Methods and Their Influence in SPEI" Agriculture 15, no. 7: 703. https://doi.org/10.3390/agriculture15070703
APA StyleMarquez-Alvarez, T., Bedolla, J. H., Pardo-Loaiza, J., Lara-Ledesma, B., & Domínguez-Sánchez, C. (2025). Multi Standardized Precipitation Evapotranspiration Index (Multi-SPEI-ETo): Evaluation of 40 Empirical Methods and Their Influence in SPEI. Agriculture, 15(7), 703. https://doi.org/10.3390/agriculture15070703







