The Design and Research of the Bolt Loosening Monitoring System in Combine Harvesters Based on Wheatstone Bridge Circuit Sensor
Abstract
:1. Introduction
2. Material and Methods
2.1. Load Analysis of Bolt Structures and Acquisition of Mechanical Parameters
2.2. Design of Wheatstone Bridge-Based Sensor for Monitoring Looseness
2.3. Design of Wireless Monitoring System for Loose Conveying Tank Bolt Structure
2.4. Design of the Sensor Monitoring and Verification Test of the Wireless Monitoring System
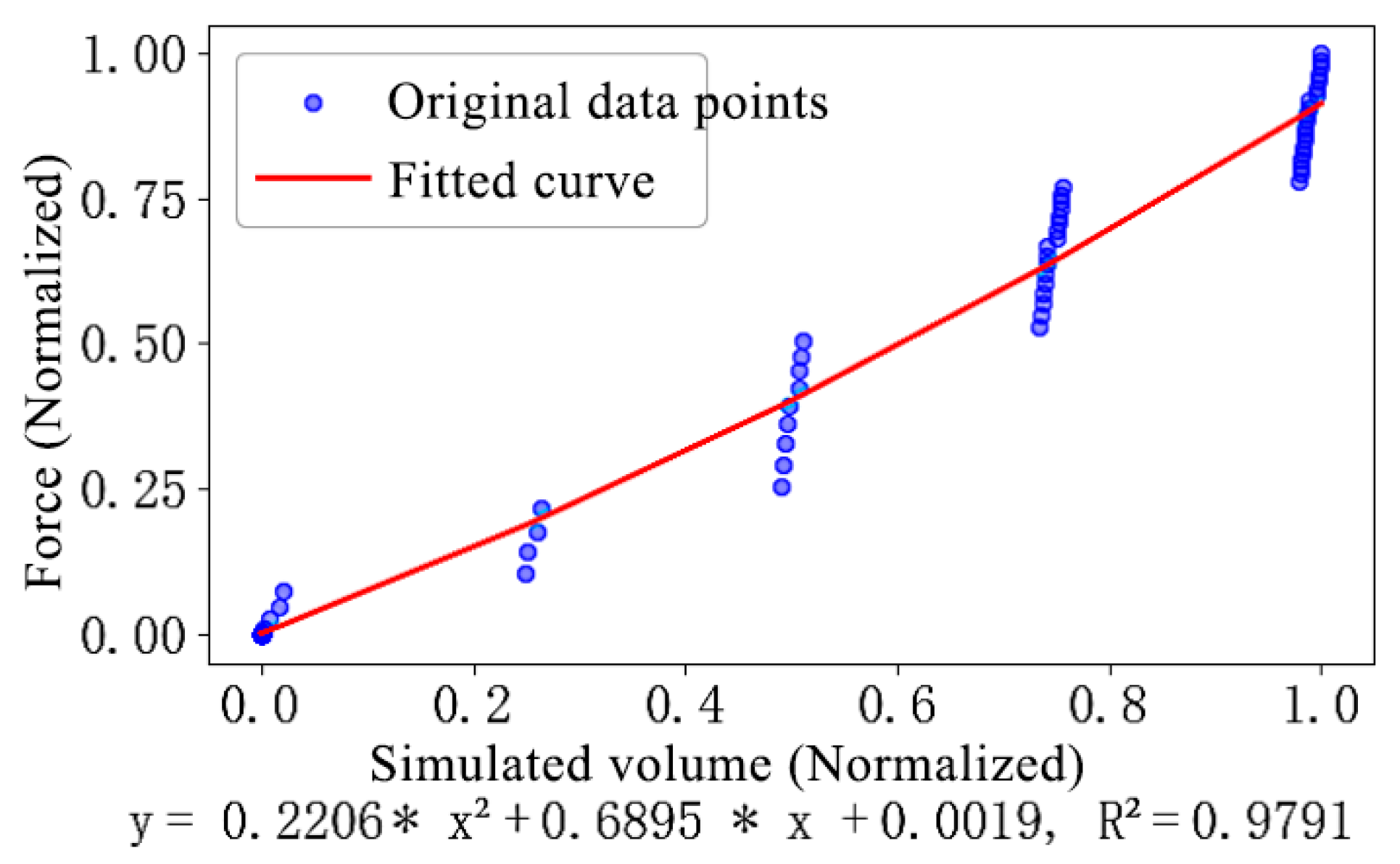
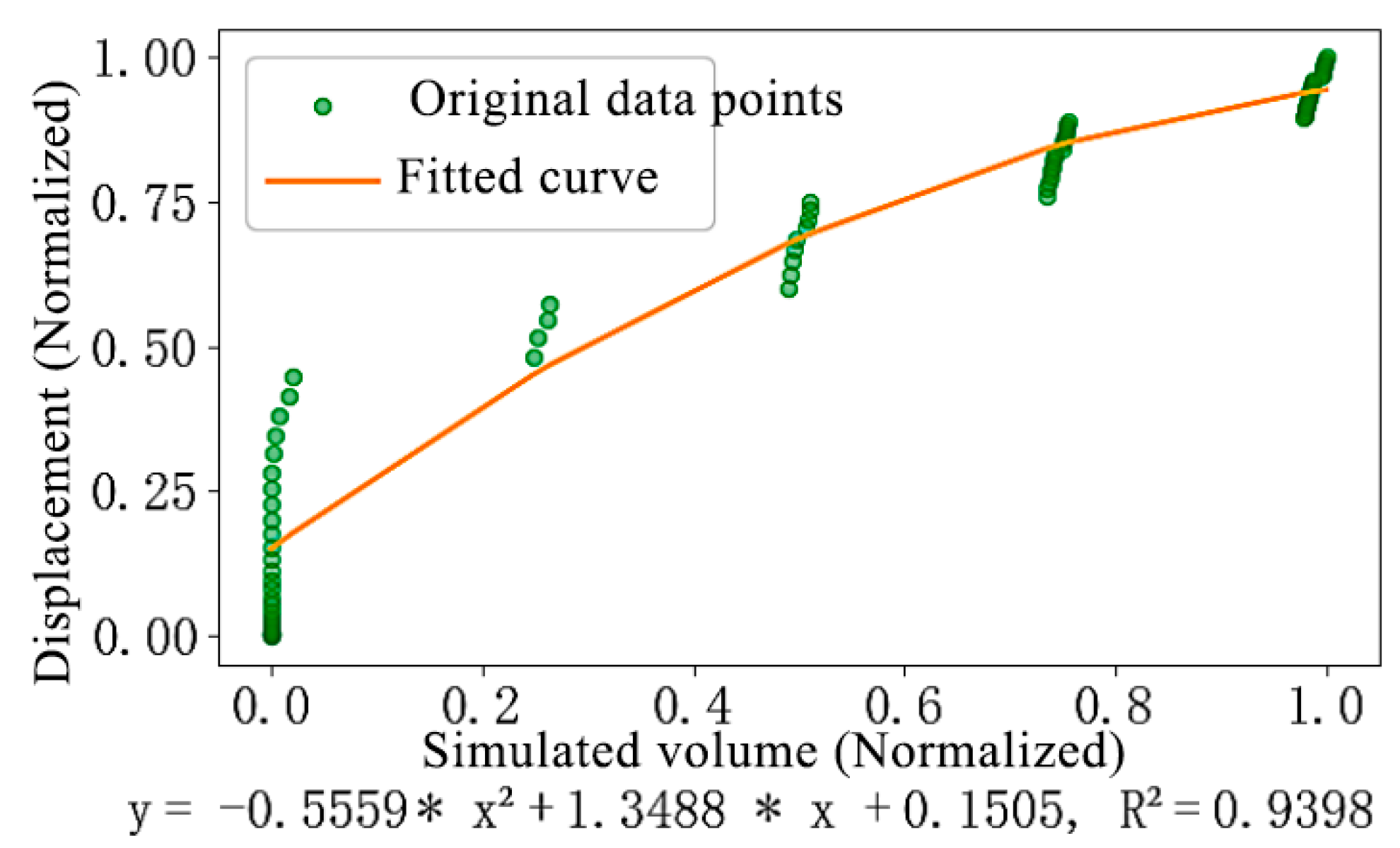
2.5. Data Fitting Method for Sensors in a Conveyor Trough Bolt Structure System
2.6. Sensor Loosening Test Experiment for the Conveyor Trough Bolt Structure System
3. Results and Discussion
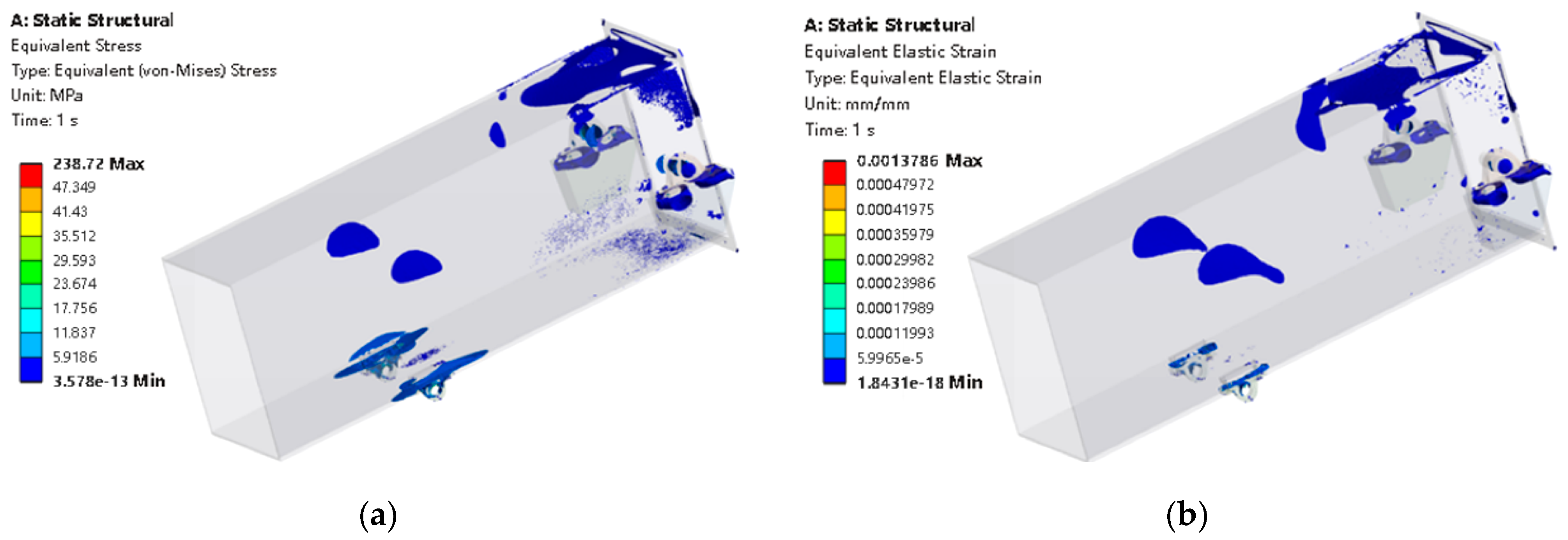
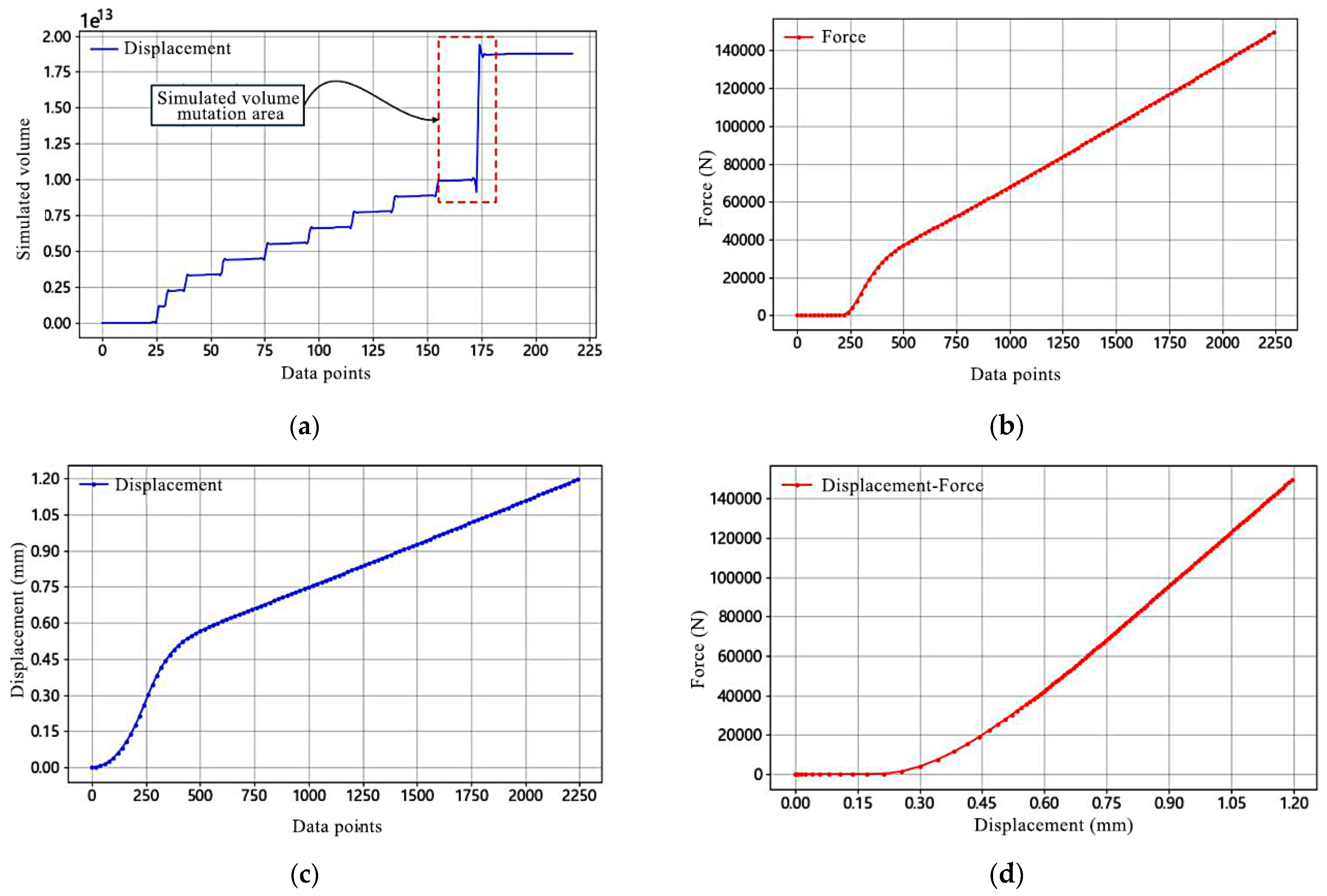
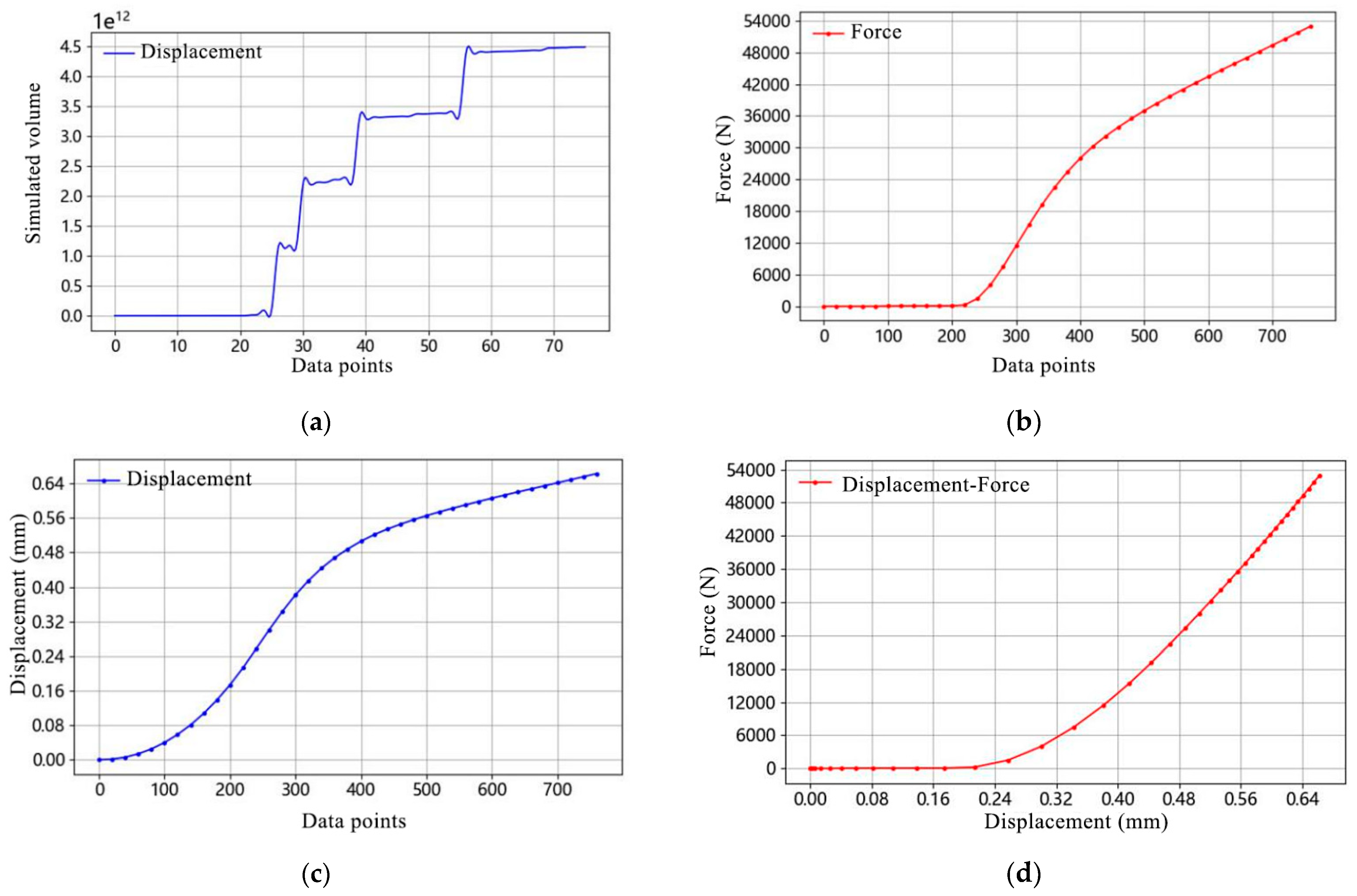
3.1. Load Results of the Bolt Structure at the Connection of the Conveyor Trough Ends
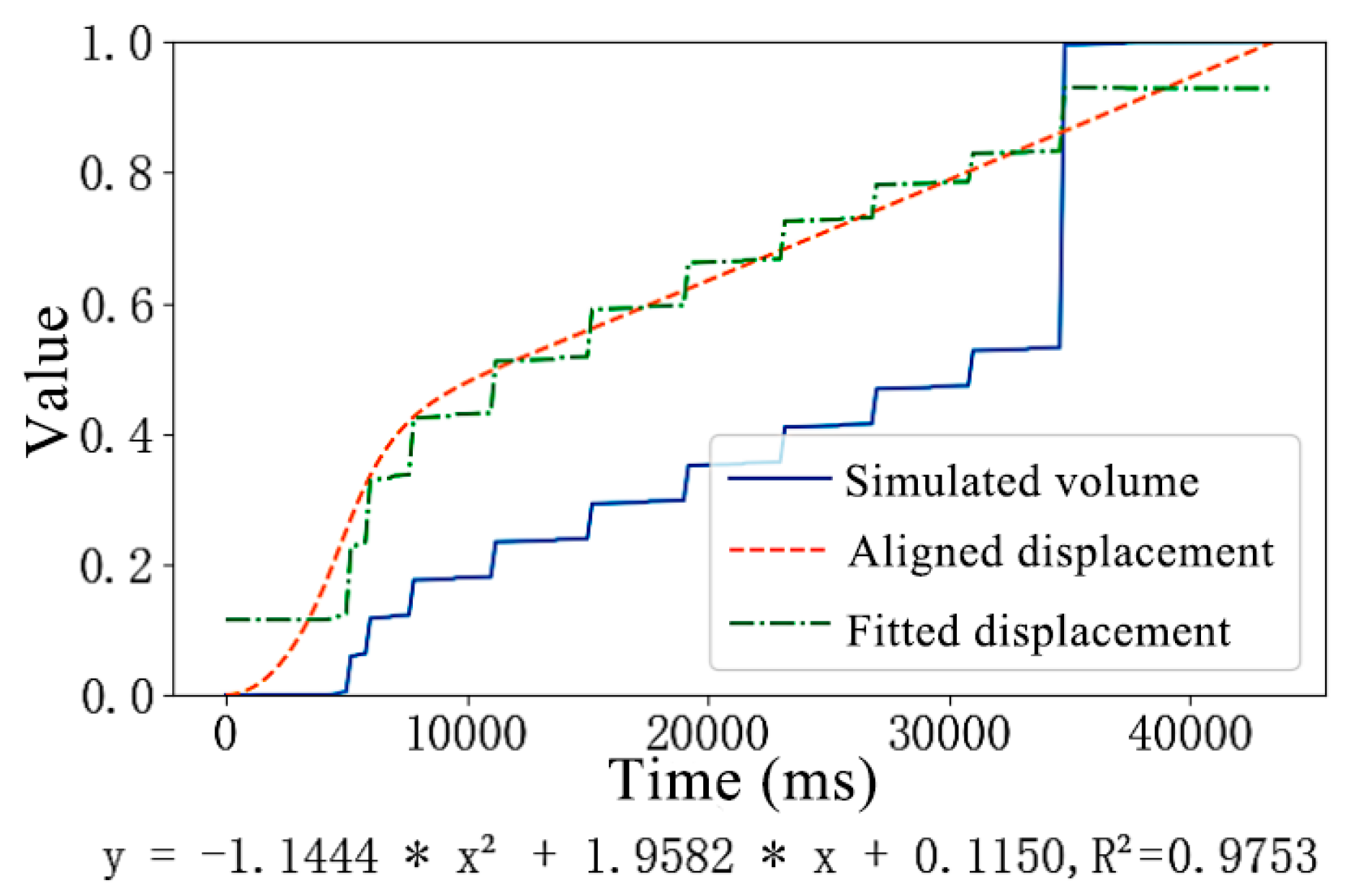
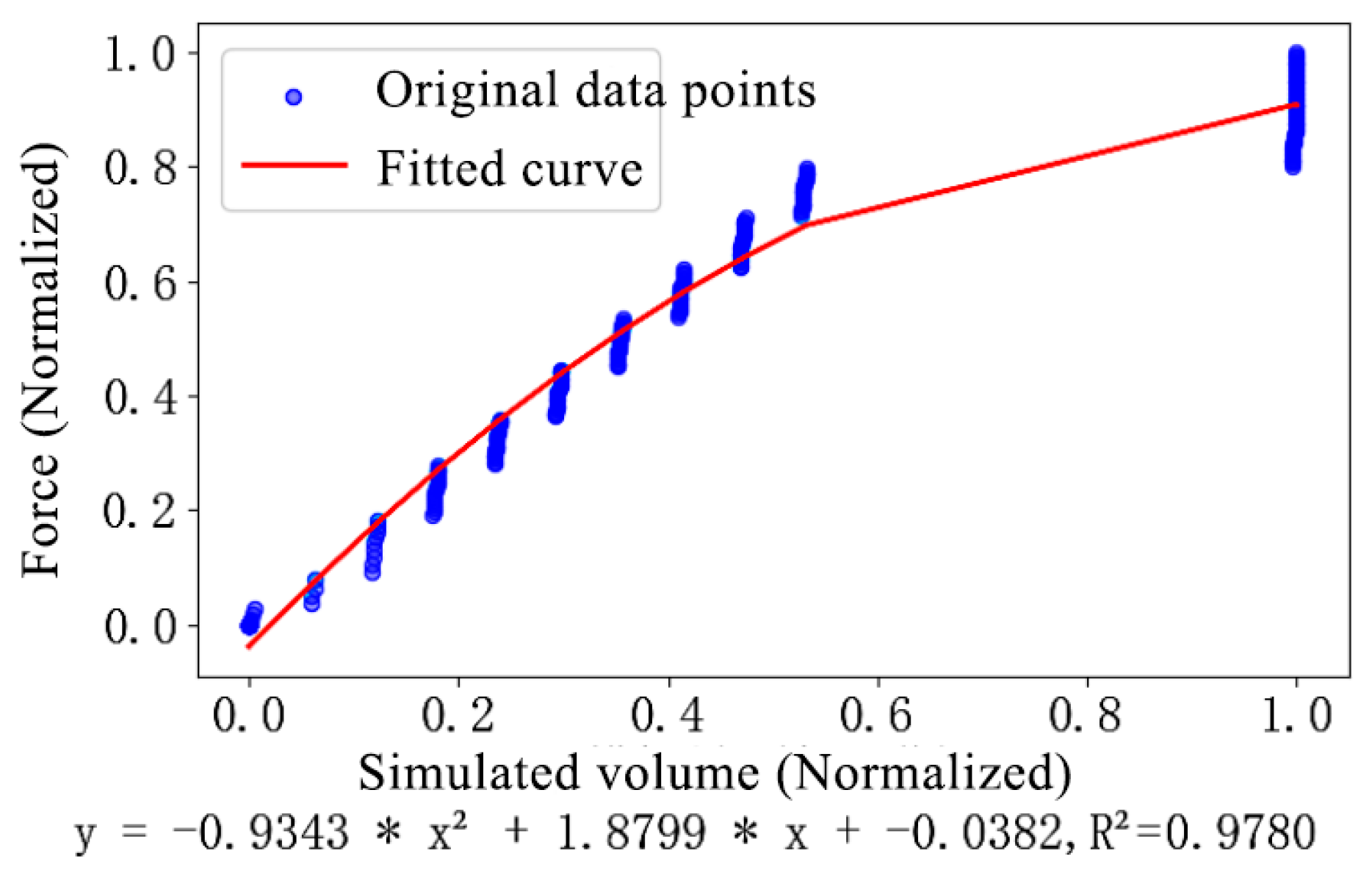
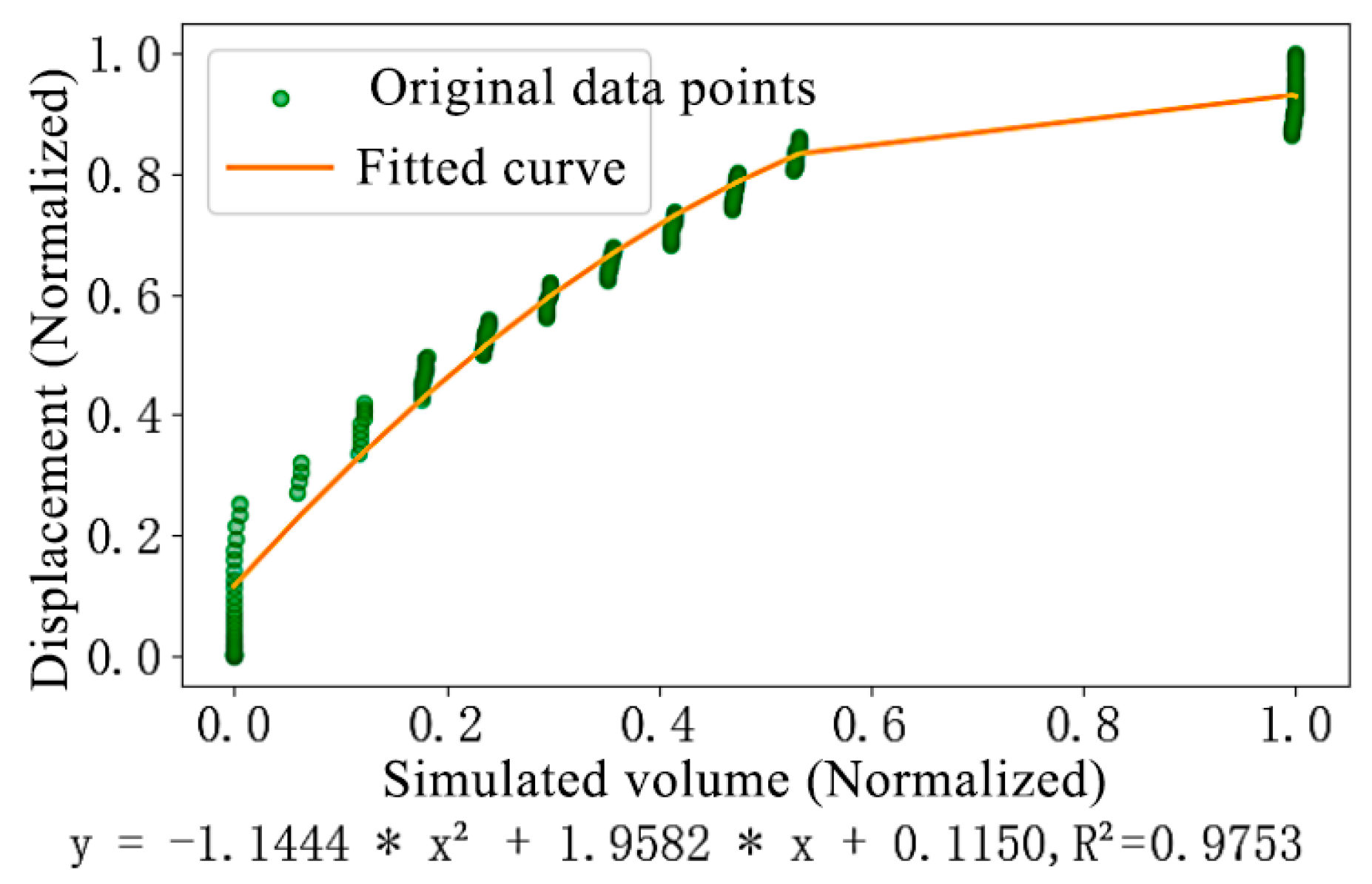
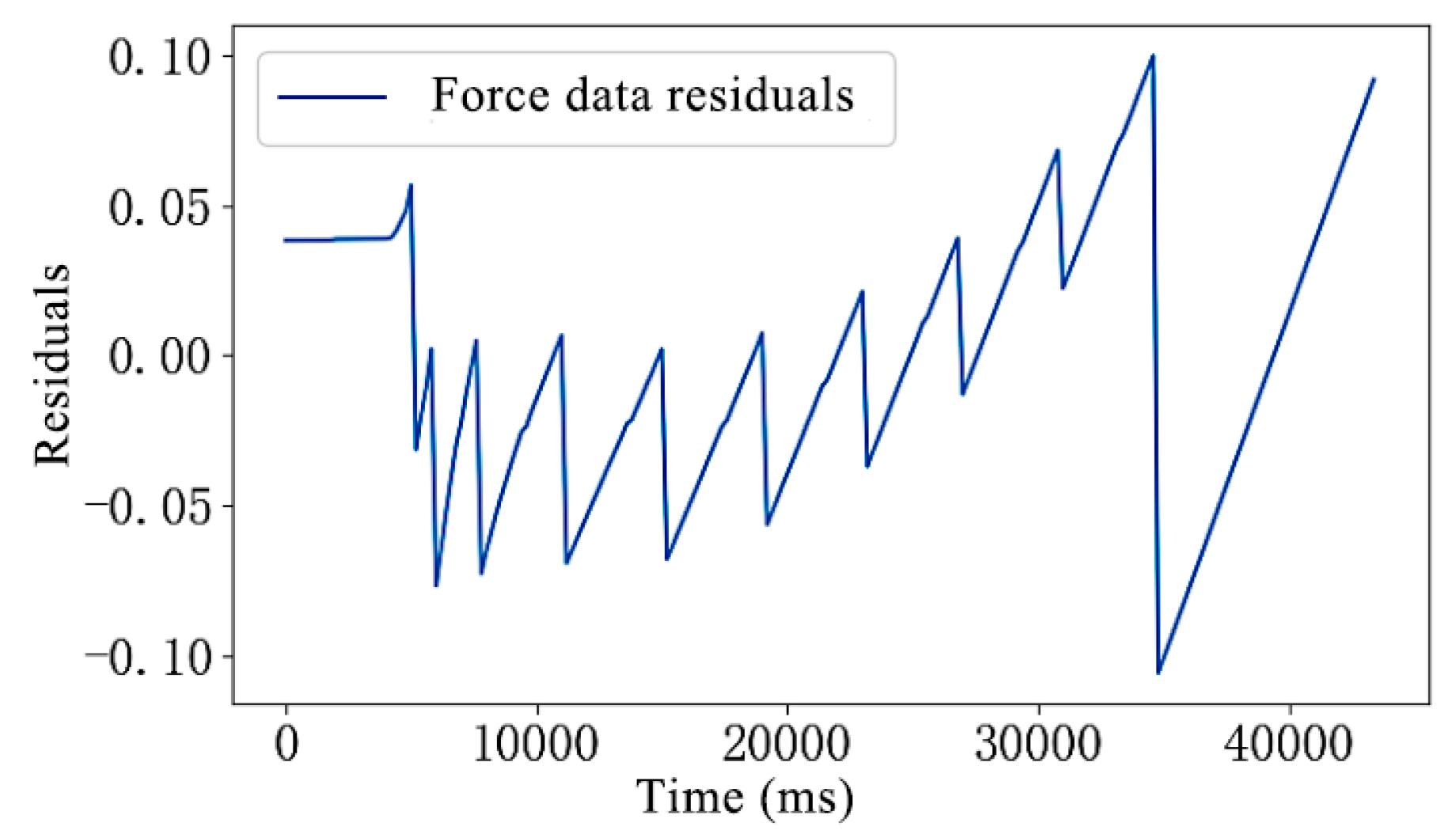
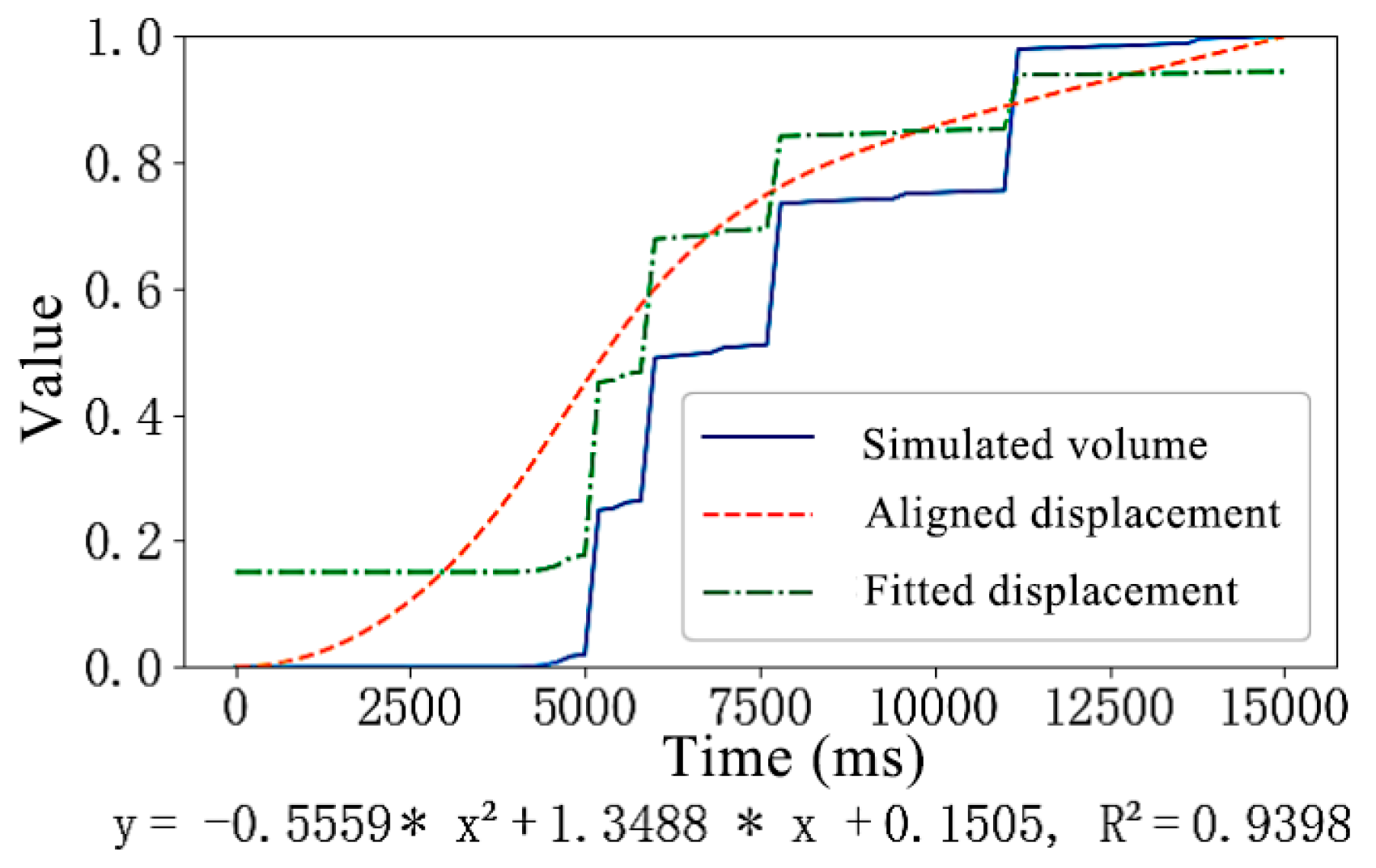
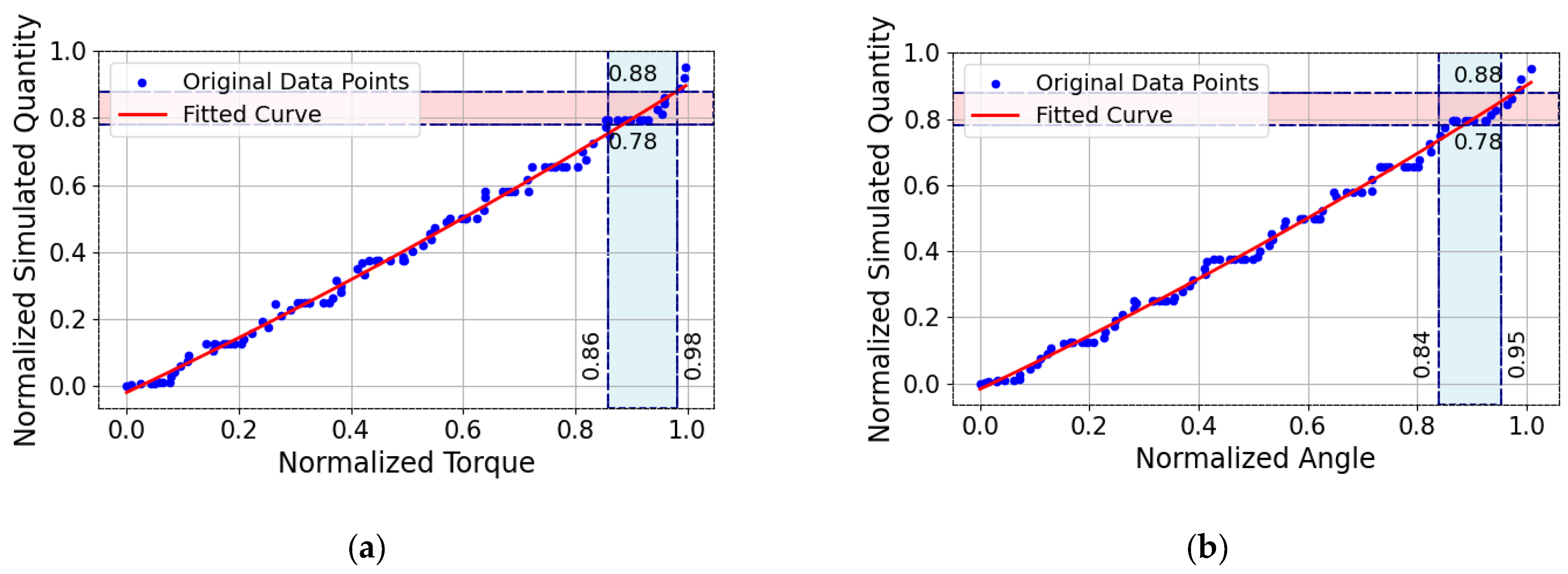
3.2. Analysis of Sensor Data Fitting Results for the Conveyor Trough Bolt Structure System
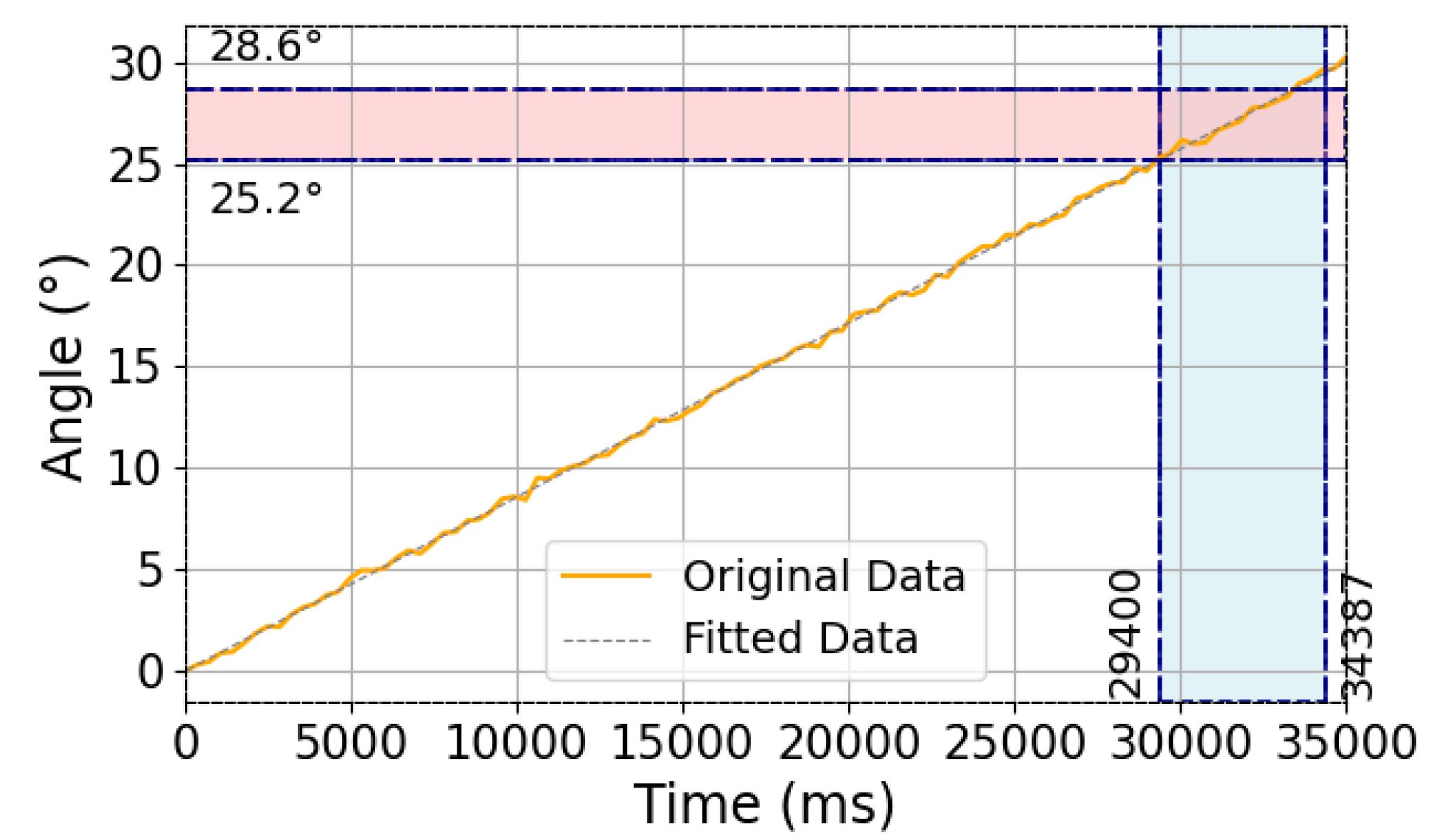
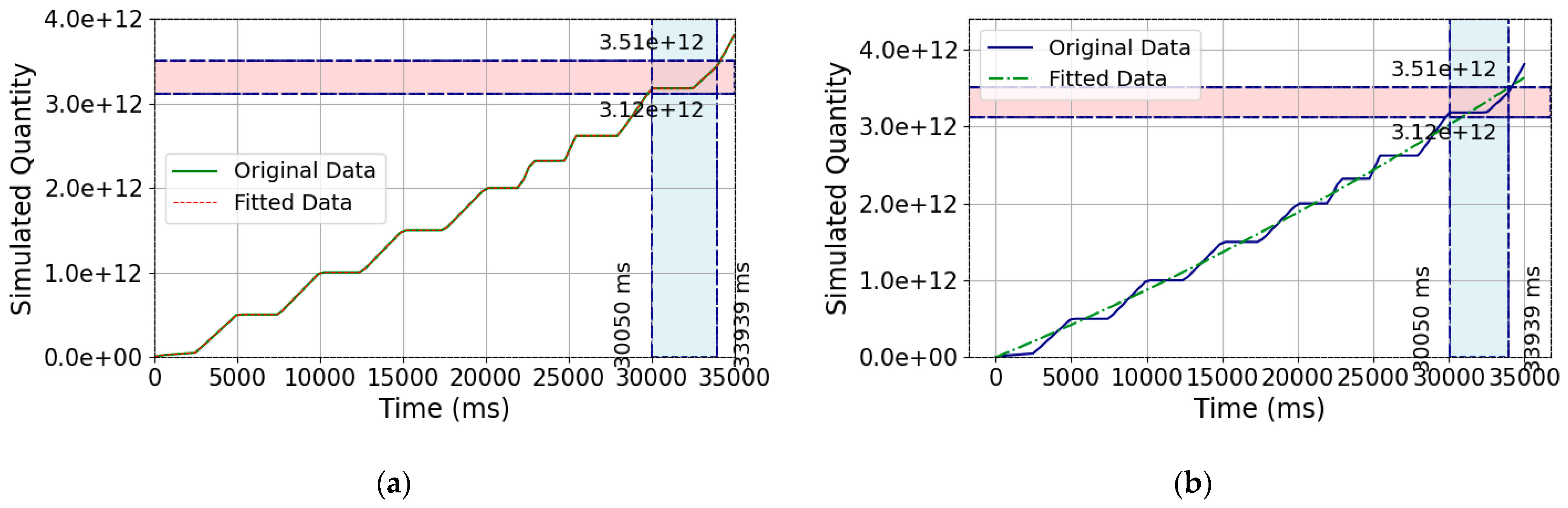
3.3. Analysis of Sensor Loosening Test Results for the Bolt Structure System
3.4. Loosening Monitoring Experiment of Sensor for the Bolt Structure System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Wu, Z.P.; Li, Y.F.; Song, Z.Q.; Yu, J.; Li, Y.M.; Xu, L.Z. Study of the grain particle-conveying performance of a bionic non-smooth-structure screw conveyor. Biosyst. Eng. 2024, 238, 94–104. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.Z.; Lv, L.Y.; Shi, Y.; Yu, X. Study on Modeling Method of a Multi-Parameter Control System for Threshing and Cleaning Devices in the Grain Combine Harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Hou, J.; Xie, F.; Wang, X.; Liu, D.; Ji, B. Design and test of multi-crop harvester header. J. Hunan Agric. Univ. Nat. Sci. 2023, 49, 223–230. [Google Scholar]
- Li, Y.M.; Liu, Y.B.; Ji, K.Z.; Zhu, R.H. A Fault Diagnosis Method for a Differential Inverse Gearbox of a Crawler Combine Harvester Based on Order Analysis. Agriculture 2022, 12, 1300. [Google Scholar] [CrossRef]
- Li, H.B.; Chen, L.W.; Zhang, Z.Y. A Study on the Utilization Rate and Influencing Factors of Small Agricultural Machinery: Evidence from 10 Hilly and Mountainous Provinces in China. Agriculture 2023, 13, 51. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Z.; Tian, R.; Li, Y.; Zhou, J.; Liu, J.; Zhu, M. Effects of Lubricating Greases on Self-loosening Behaviour of Bolted Joints Subject to Dynamic Shear Load. Surf. Technol. 2020, 49, 198. [Google Scholar]
- Chandio, F.A.; Li, Y.; Xu, L.; Ma, Z.; Xu, L.Z. Predicting 3D forces of disc tool and soil disturbance area using fuzzy logic model under sensor based soil-bin. Int. J. Agric. Biol. Eng. 2020, 13, 77–84. [Google Scholar]
- Wang, J.; Hu, B.; Huang, Q.; Zhu, R.; Fu, Q. Simulation analysis and experimental verification on bearings fatigue life of a centrifugal pump. J. Drain. Irrig. Mach. Eng. 2024, 42, 865–871. [Google Scholar]
- Fan, J.; Zhang, W.; Jiao, T.; Zhao, Y. Failure mechanism of fatigue fracture and life analysis for bolted joint of aircraft structure. J. Mech. Strength 2023, 45, 1459–1464. [Google Scholar]
- Fang, P.J.; Cai, Y.F.; Chen, L.; Wang, H.; Li, Y.C.; Sotelo, M.A.; Li, Z.X. A high-performance neural network vehicle dynamics model for trajectory tracking control. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2023, 237, 1695–1709. [Google Scholar] [CrossRef]
- Li, J.; Zhou, F.; Zhang, A.; Sun, Y.; Lei, Z.; Zhu, J. Accurate Finite Element Modeling and Validity Analysis of Thread Structure. Adv. Eng. Sci. 2022, 54, 220–229. [Google Scholar]
- Ma, Z.; Zhang, Z.L.; Zhang, Z.H.; Song, Z.Q.; Liu, Y.B.; Li, Y.M.; Xu, L.Z. Durable Testing and Analysis of a Cleaning Sieve Based on Vibration and Strain Signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, Z.; Zhang, Z.; Sun, Z.; Zhang, H.; Liu, J. Design and Test of Automatic Rubber-tapping Device with Spiral Movement. Trans. Chin. Soc. Agric. Mach. 2023, 54, 169–179. [Google Scholar]
- Teng, S.; Wang, Y.; Wei, X.; Du, D. Optimization of forming process for bracket welded parts based on star point design and response surface method. J. Plast. Eng. 2024, 31, 50–59. [Google Scholar]
- Wang, Y.; Li, H.; Jiang, W.; Wang, R.; Li, Y. Dynamic characteristics of an underframe inerter-based suspended equipment for high speed trains. J. Vib. Shock 2022, 41, 246–254. [Google Scholar]
- Wang, S.; Zhang, Q.; Shi, D.; Yin, C.; Li, C. Analysis of nonlinear vibration response characteristics of hybrid transmission system with dual-planetary gear sets. J. Jilin Univ. Eng. Technol. Ed. 2024, 54, 890–901. [Google Scholar]
- Du, W.; Li, W.; Jiang, S.; Sheng, L. Flexural-torsional coupled vibration analysis of shearer permanent magnet motor rotor system under load excitation. J. Vib. Shock 2023, 42, 237. [Google Scholar]
- Chen, X.; Peng, D.; Hou, Y.; Yang, L. Study on Torsional Vibration Active Control of Hybrid Electric Vehicle Transmission System in Pure Electric Mode. Mech. Sci. Technol. Aerosp. Eng. 2021, 40, 1114–1119. [Google Scholar]
- Ma, Q.J.; Wang, K.; Liu, H.L.; Cheng, Z.M. Influence of shaft combined misalignment on vibration and noise characteristics in a marine centrifugal pump. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1286–1306. [Google Scholar] [CrossRef]
- Ren, N.; Qiu, Z.; Wang, Y.; He, K. Analysis of Acoustic Field Characteristics of Irregular Multi-inclinedWall Cavity Based on Analytical Method. Noise Vib. Control 2020, 40, 54. [Google Scholar]
- Feng, Q.; Yang, Z.; Guo, W.; Lu, J.; Liang, Y.; Lei, X. Analysis of vertical vibration band gap characteristics of periodic discrete support rail. Sci. Sin. Technol. 2020, 50, 1563–1576. [Google Scholar]
- Li, L.; Yue, C.; Fan, J.; Zhou, S. Research on Multi-Axial Excitation Test System and Assembly Deviation Identification of Aero-Engine. Aeronaut. Manuf. Technol. 2022, 65, 86–91. [Google Scholar]
- Hu, S.; Dong, L.; Zhu, J.; Chen, Y.; Cheng, M. Experimental study on typical faults recurrence in vertical centrifugal pump. J. Drain. Irrig. Mach. Eng. 2024, 42, 563–569. [Google Scholar]
- Zhao, B.; Liu, Q.; Fu, Y.; Zhao, Y.; Liao, W.; Xie, Y. Boundary vorticity flux prediction of the centrifugal pump impeller based on artificial neural network. J. Drain. Irrig. Mach. Eng. 2020, 38, 127–132. [Google Scholar]
- Yu, W.; Wang, T.; Deng, S.; Lu, M.; Lu, G.; Yang, D. Bolt Connection State Monitoring Method Based on Fiber Grating Bolt Loosening Angle Measurement. Chin. J. Sens. Actuators 2023, 36, 549–554. [Google Scholar]
- Ma, Z.; Li, B.; Song, Z.; Liu, Y.; Pan, Y. Lightweight Design and Test of Cleaning Sieve for Combine Harvester. Trans. Chin. Soc. Agric. Mach. 2024, 55, 201–211. [Google Scholar]
- Xu, Z.; Wang, C.; Bai, B.; Tu, Y.; Yu, X.; Jia, J. Study of Two Types of Fiber Bragg Grating Strain Sensors Packaged Using Adhesive for Monitoring of Bolt Load in Flange Joints. Intstrument Tech. Sens. 2022, 13, 13–19+24. [Google Scholar]
- Shen, C.; Jin, K.; Zhu, Y.; Hu, Z.; Guo, E. Influence of sensor volume on vortex precession flowmeter based on CFD. J. Drain. Irrig. Mach. Eng. 2024, 42, 895–899. [Google Scholar]
- Wang, C.; Wang, G.; Wang, K. Design and Application of Real-time Monitoring System for Load of Cutter Replacement Device under Atmospheric Pressure of Extra-Large Diameter Slurry Shield. Tunn. Constr. 2021, 41, 1404–1411. [Google Scholar]
- Wang, X.; Chen, Y.; Zhao, G.; Han, Q. Bolts Tightening Technology of Angle-Steel Tower. Trans. Beijing Inst. Technol. 2024, 44, 395–402. [Google Scholar]
- Cai, Y.; Lu, Z.; Li, Y.; Chen, L.; Wang, H. Tightly Coupled SLAM System Based on Multi-Sensor Fusion. Automot. Eng. 2022, 44, 350–361. [Google Scholar]
- Wang, W.; Li, J.; Li, Y.; Wang, Y.; Hua, X.; Ma, Y.; Li, T. On-line alignment method for large-scale thin-walled case based on the laser rapid measurement. J. Solid Rocket Technol. 2020, 43, 237–242. [Google Scholar]
- Wen, H.; Tang, Y.; Tang, L. Program design of pump experiment non-collected data display based on LabVIEW. J. Drain. Irrig. Mach. Eng. 2021, 39, 128–131. [Google Scholar]
- Ge, X.; Zhang, J.; Zhu, S.; Qian, J.; Zhao, L.; Zheng, S.; Zheng, Y.; Xu, X.; Binama, M. Stress characteristics of top cover bolts of hydraulic turbine. J. Vib. Shock 2021, 40, 55–62. [Google Scholar]
- Li, S.; Liu, Y.; Lin, Z.; Shutin, D.; Luo, Y. Rotor vibration signal recognition method based on coupling source error analysis. Chin. J. Sci. Instrum. 2023, 44, 75–83. [Google Scholar]
- Tang, D.; Li, T.; Shi, S. Research on Fault Diagnosis Strategy of Diesel Particulate Filter Coupled with Particle Sensor. J. Xi’an Jiaotong Univ. 2023, 57, 87–97. [Google Scholar]
- Zhu, L.; Liang, H.; Zhang, H.; Shi, J.; Hong, J. Contact Performance Model for Bolted Joint Interfaces Considering Macro-Micro Morphology. J. Xi’an Jiaotong Univ. 2024, 58, 148–159. [Google Scholar]
- Yang, S.; Wang, X.; Gao, Y.; Chen, L.; Zhai, C.; Dou, H. Design of On-line Seed Spacing Monitoring and Miss Seeding Warning System for Maize Precision Planting. Trans. Chin. Soc. Agric. Mach. 2021, 52, 17. [Google Scholar]
- Wu, J.; Shao, J.; Zhou, G.; Yang, D.; Cheng, Y. Detecting Method for Bolt Looseness with Average Vibration Response Energy. Mech. Sci. Technol. Aerosp. Eng. 2022, 41, 992–997. [Google Scholar]
- Tao, H.; He, G.; Yang, J.; Ai, P. Status identification of transmission tower bolts based on MIMU. J. Vib. Shock 2023, 42, 98–104. [Google Scholar]
- Wang, S.; Kong, Q.; Zhou, Y. Percussion-based bolt loosening detection method in a single-row multi-bolted steel beam-column joint. J. Earthq. Eng. Eng. Vib. 2024, 44, 95–103. [Google Scholar]
- Wan, Y.; Xue, J.; Zhang, D.; Han, X.; Lyu, J.; Miao, W. Research on bolts fault diagnosis of diaphragm compressor cylinder head in nuclear power plant based on KPCA. Fluid Mach. 2024, 52, 87–96. [Google Scholar]
- Chen, P.; Shang, Q.; Yu, X.; Yin, A. Ultrasonic multi-feature fusion bolt stress measurement method based on ELM. Chin. J. Sci. Instrum. 2024, 45, 46–56. [Google Scholar]
- Liang, J.; Ge, J.; Song, J.; Xu, Y.; Liu, H.; Zhong, L.; Liu, Q. Looseness detection method of gas insulated switchgear basin insulator bolts based on convolutional neural network. J. Appl. Acoust. 2023, 42, 566–576. [Google Scholar]
- Ge, J.; Wang, W.; Song, J.; Jiao, G.; Li, P.; Gao, J.; Ren, H. Detection on Looseness of Flange Bolt of Insulating Spacer Based on Critical Refraction Longitudinal Wave Method. High Volt. Appar. 2024, 60, 165–172. [Google Scholar]
- Sun, W.; Guan, Z.; Pan, J.; Zeng, Y. Dynamic response analysis of rocket connection structure considering discrepancy of bolt preloads. J. Natl. Univ. Def. Technol. 2024, 46, 59–69. [Google Scholar]
- Sun, A.; Liu, B.; Hu, X. Bolt Loosening Anomaly Detection Method of Solid Motor Vibration Test. Instrum. Tech. Sens. 2024, 12, 112–119. [Google Scholar]
- Jiang, G.; Lu, L.; Zhang, M.; Zeng, D. Study on the characteristic parameters of the loosening of bolt-fastened structures under transverse load. J. Railw. Sci. Eng. 2024, 21, 3310–3320. [Google Scholar]
- Zeng, F.; Liu, X.; Wang, T.; Deng, S.; Yu, W. Bolt-loosening visual detection based on curvature change of elastic line between bolts. Transducer Microsyst. Technol. 2023, 42, 131–134. [Google Scholar]
- Wang, Z.; Gu, F.; Zeng, Z. Research on the Detection Method of Loose Roof Bolts of Low-quality Rail Vehicles. Mach. Des. Res. 2024, 40, 220–224. [Google Scholar]
- Zhou, J.; Liu, Y.; Huo, L. Machine Vision-Based Rotation Angle Measurement of Bolt Looseness. Mach. Des. Res. 2021, 37, 159. [Google Scholar]
- GB/T 16823.2-1997; General Rules of Tightening for Threaded Fasteners. China Machinery Industry Federation: Beijing, China, 2017.
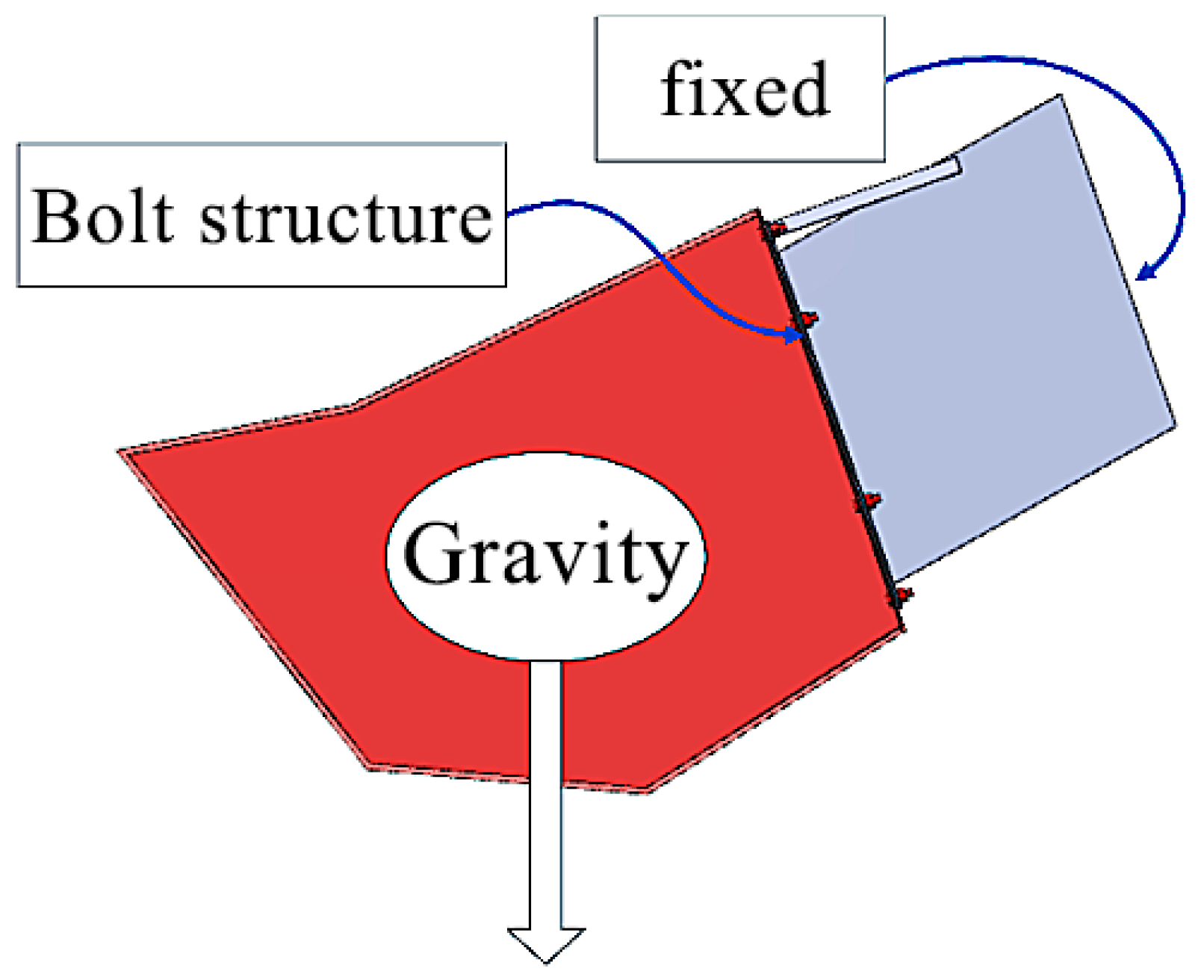
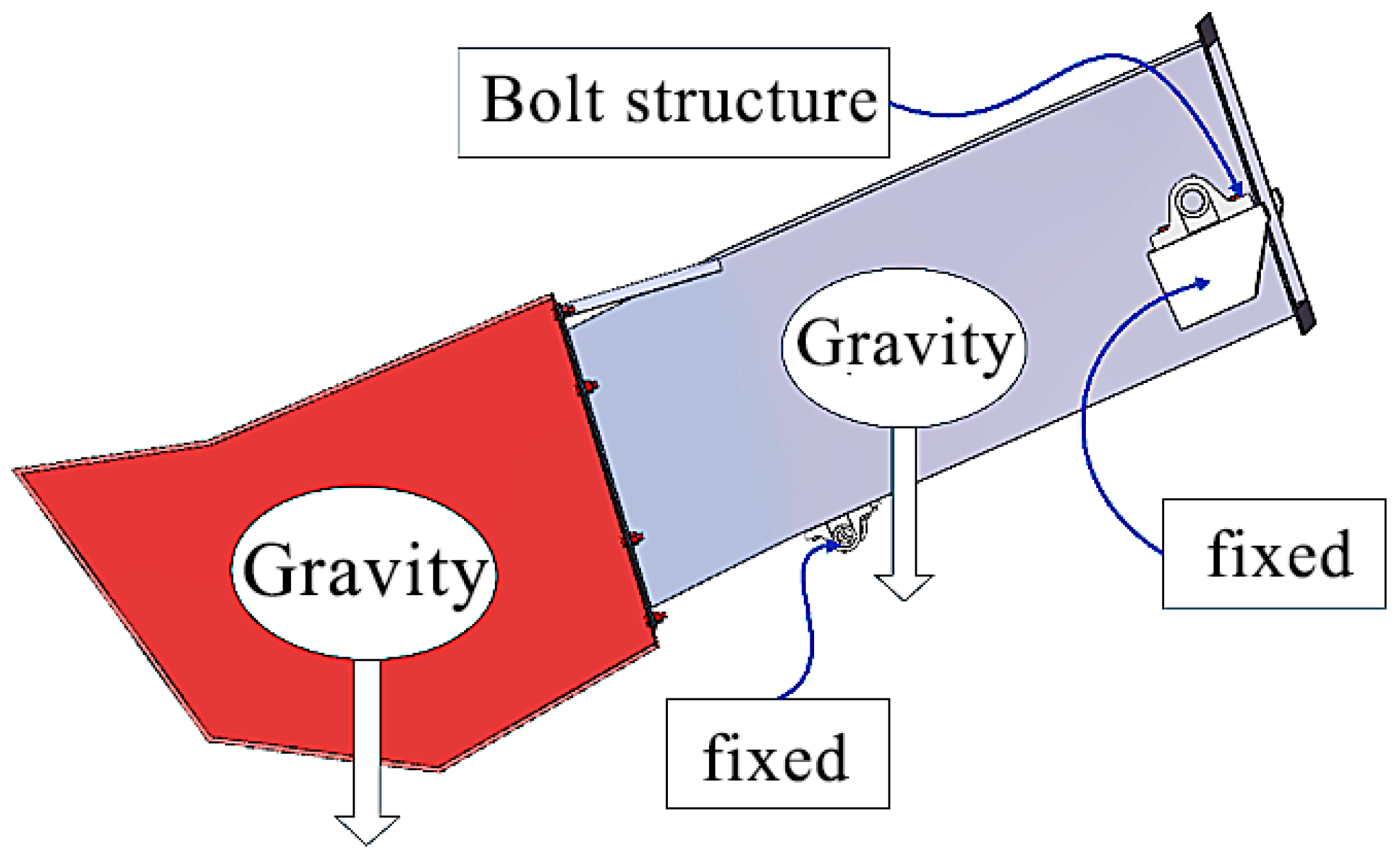
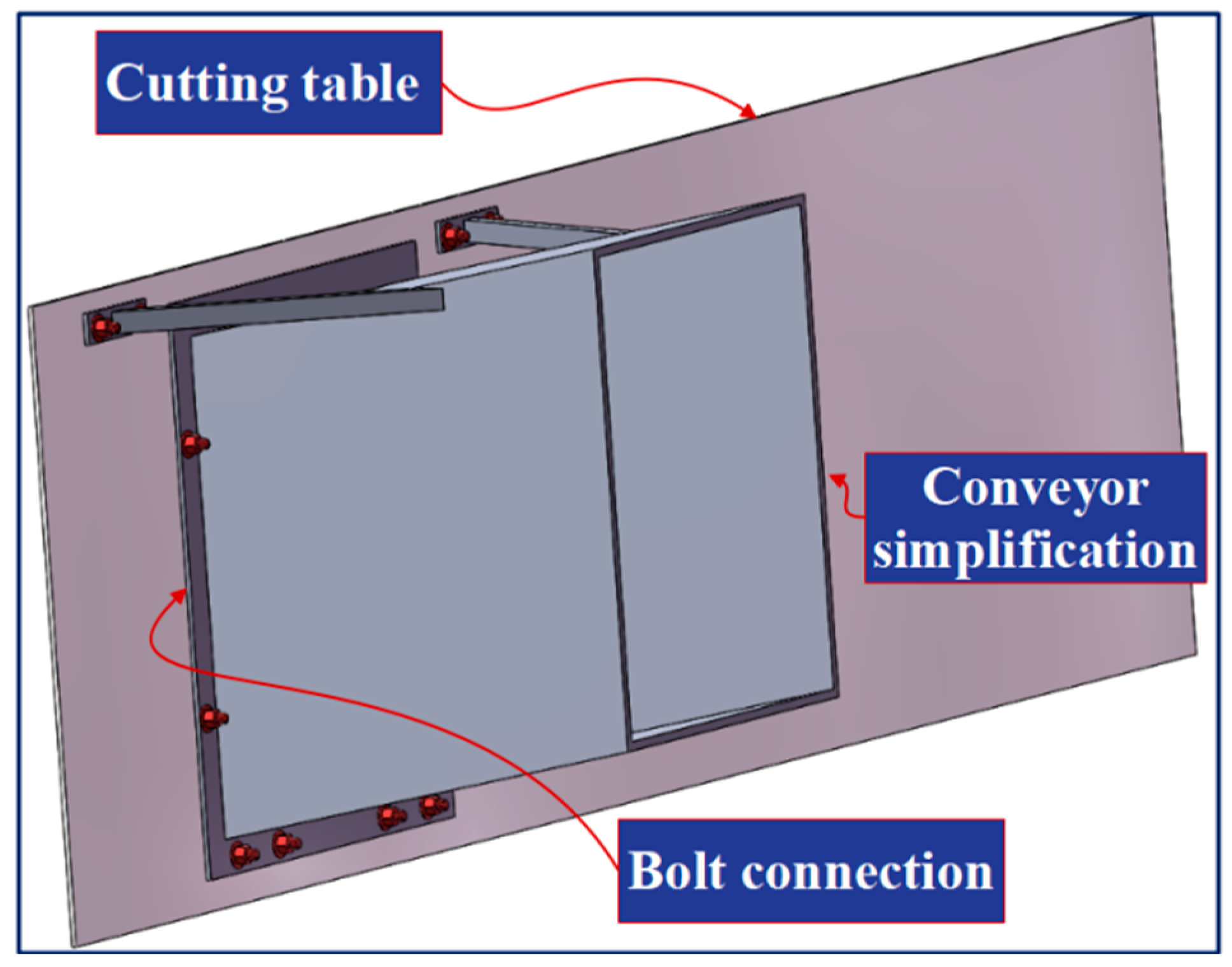
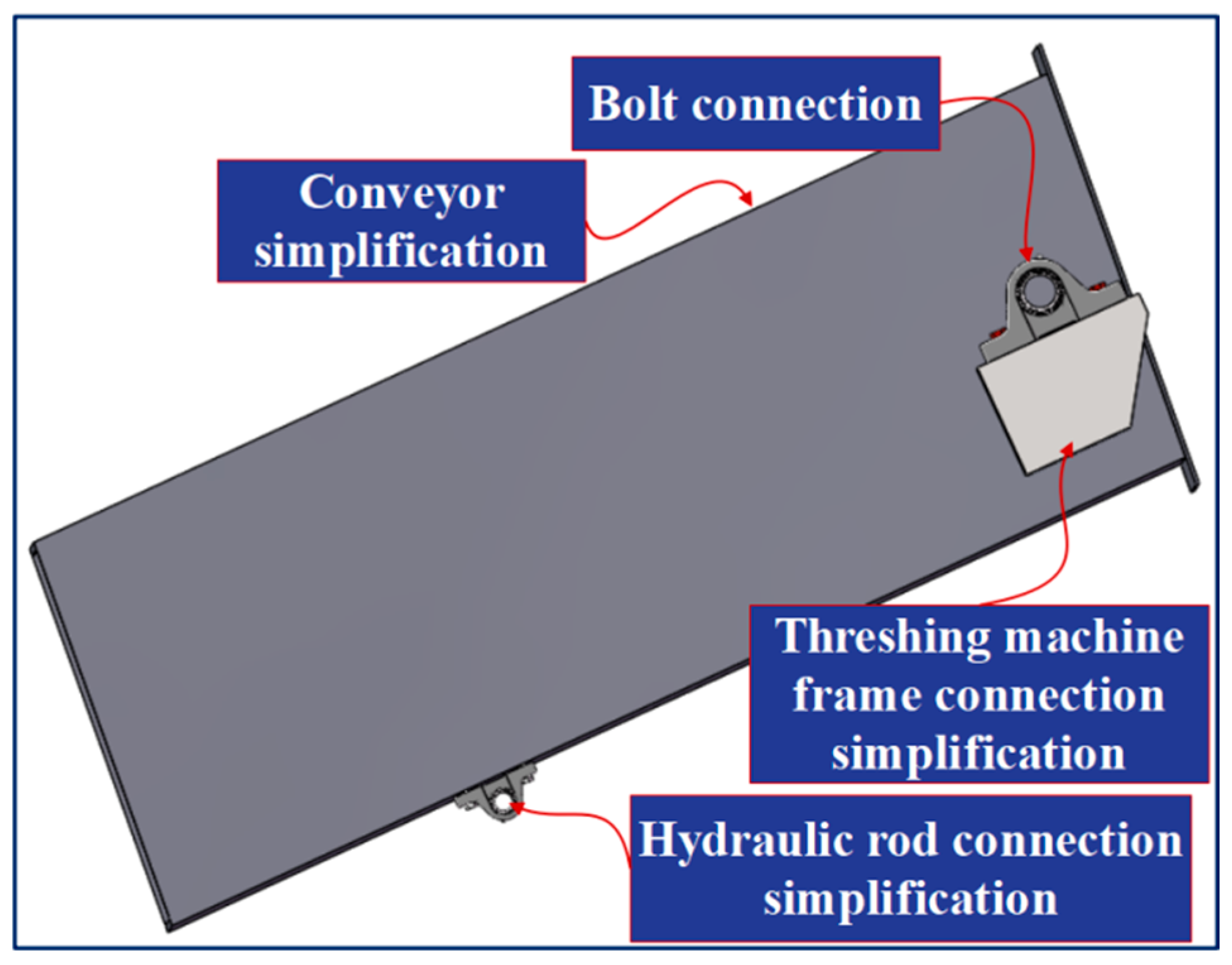
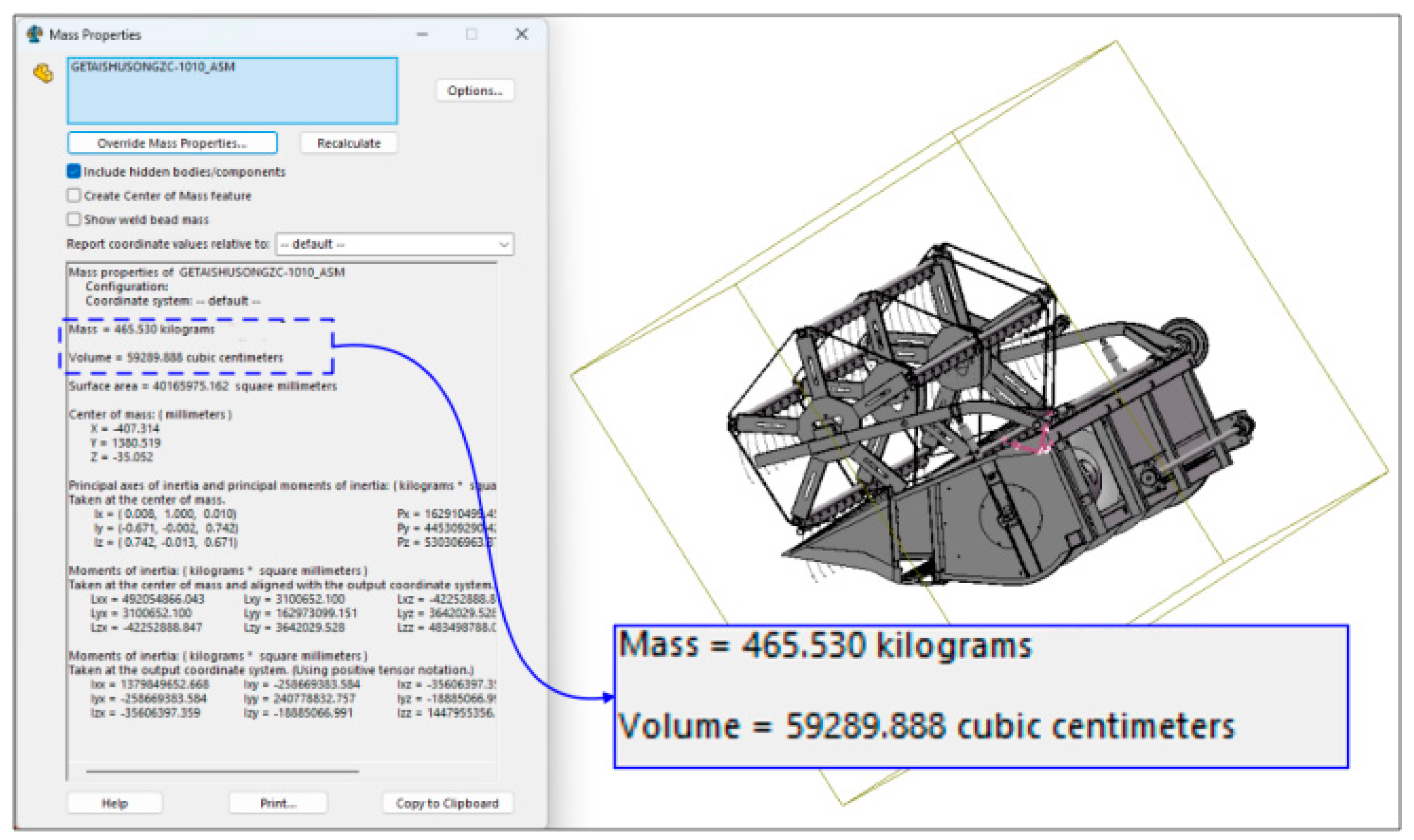

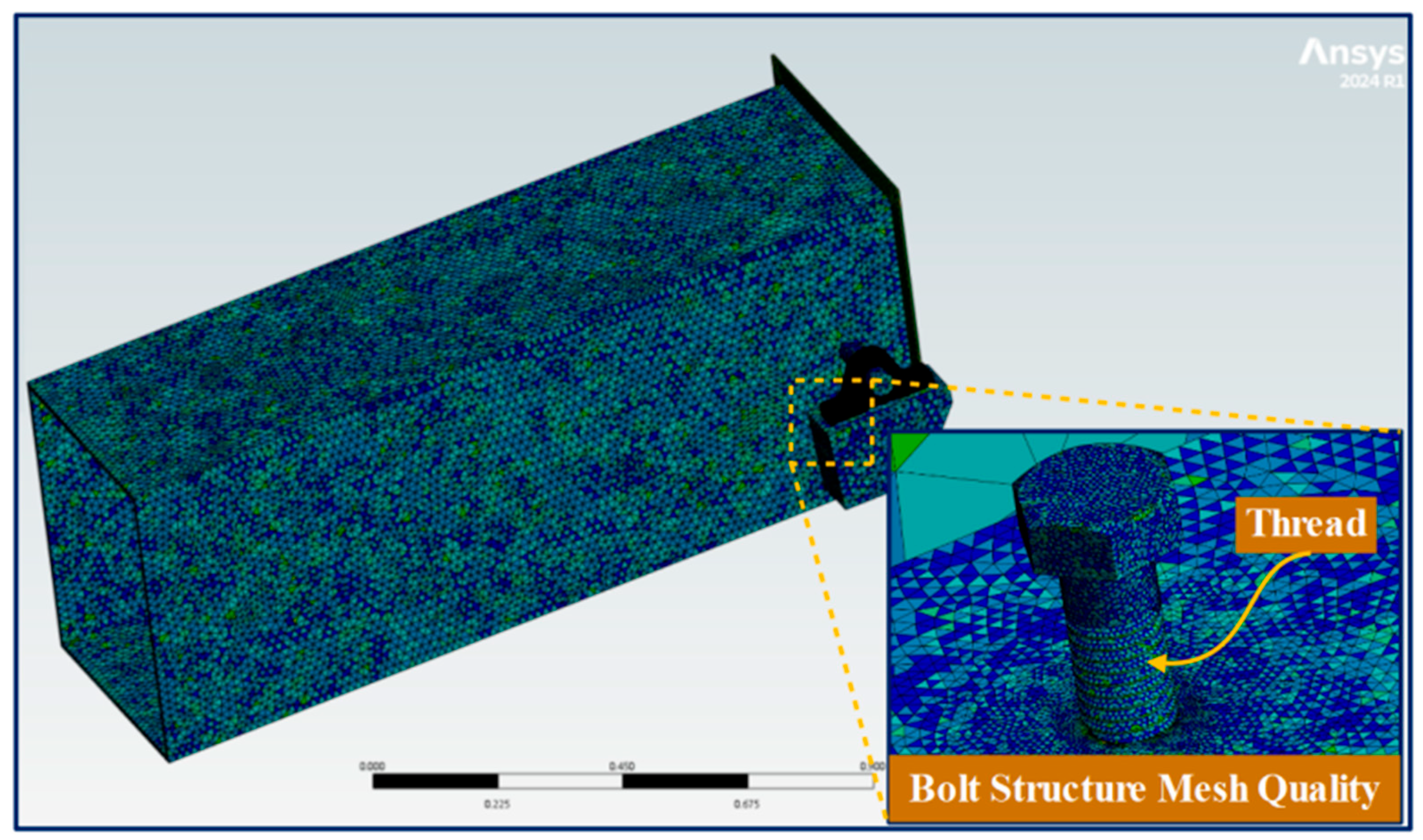

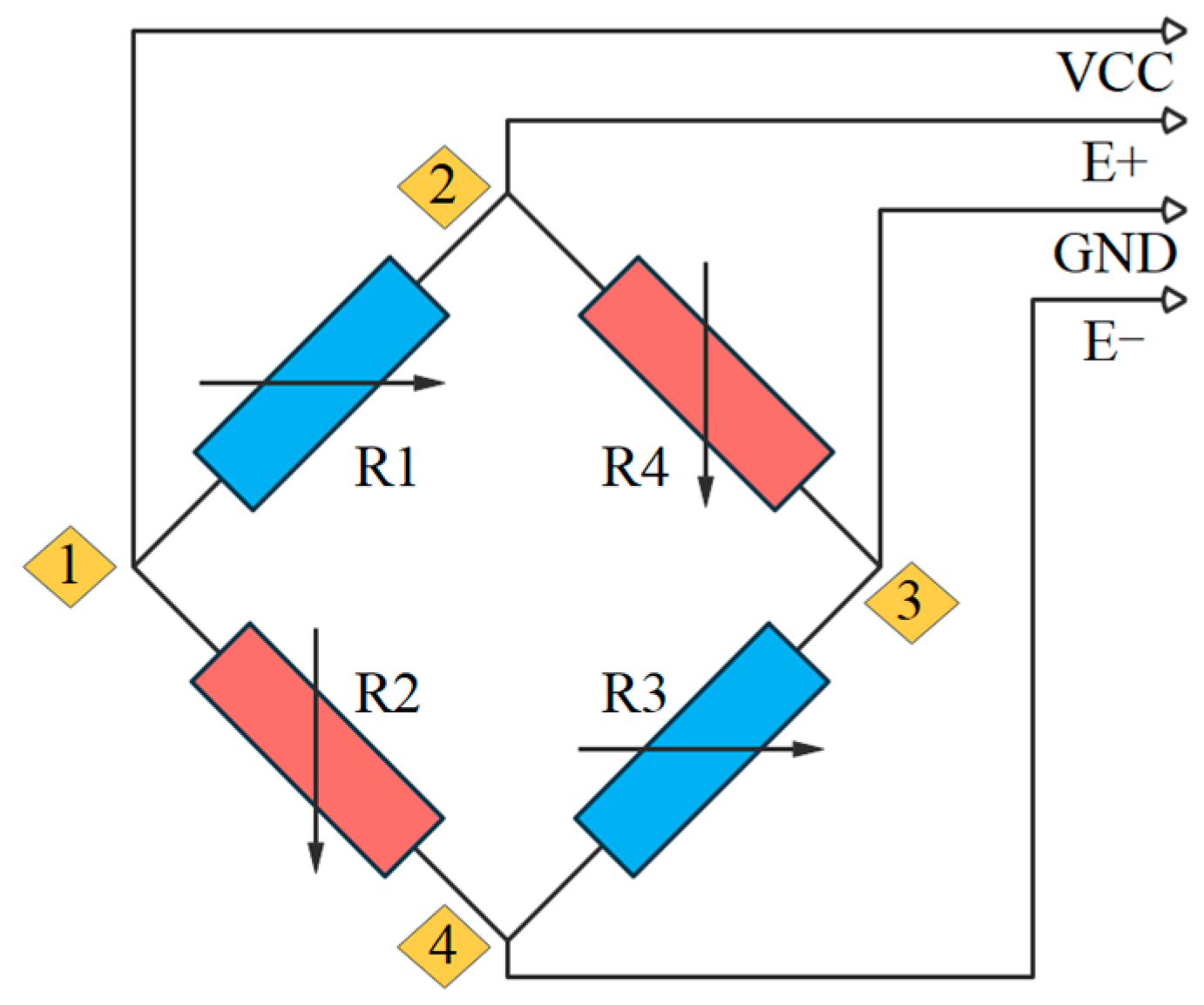


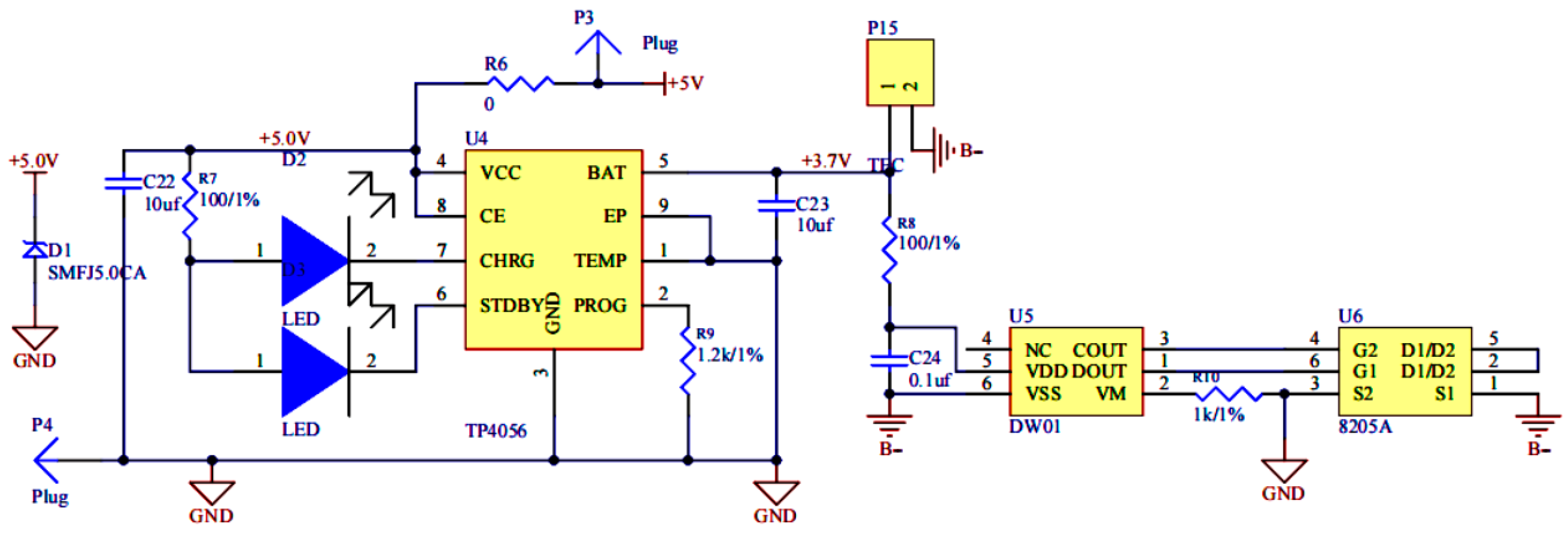
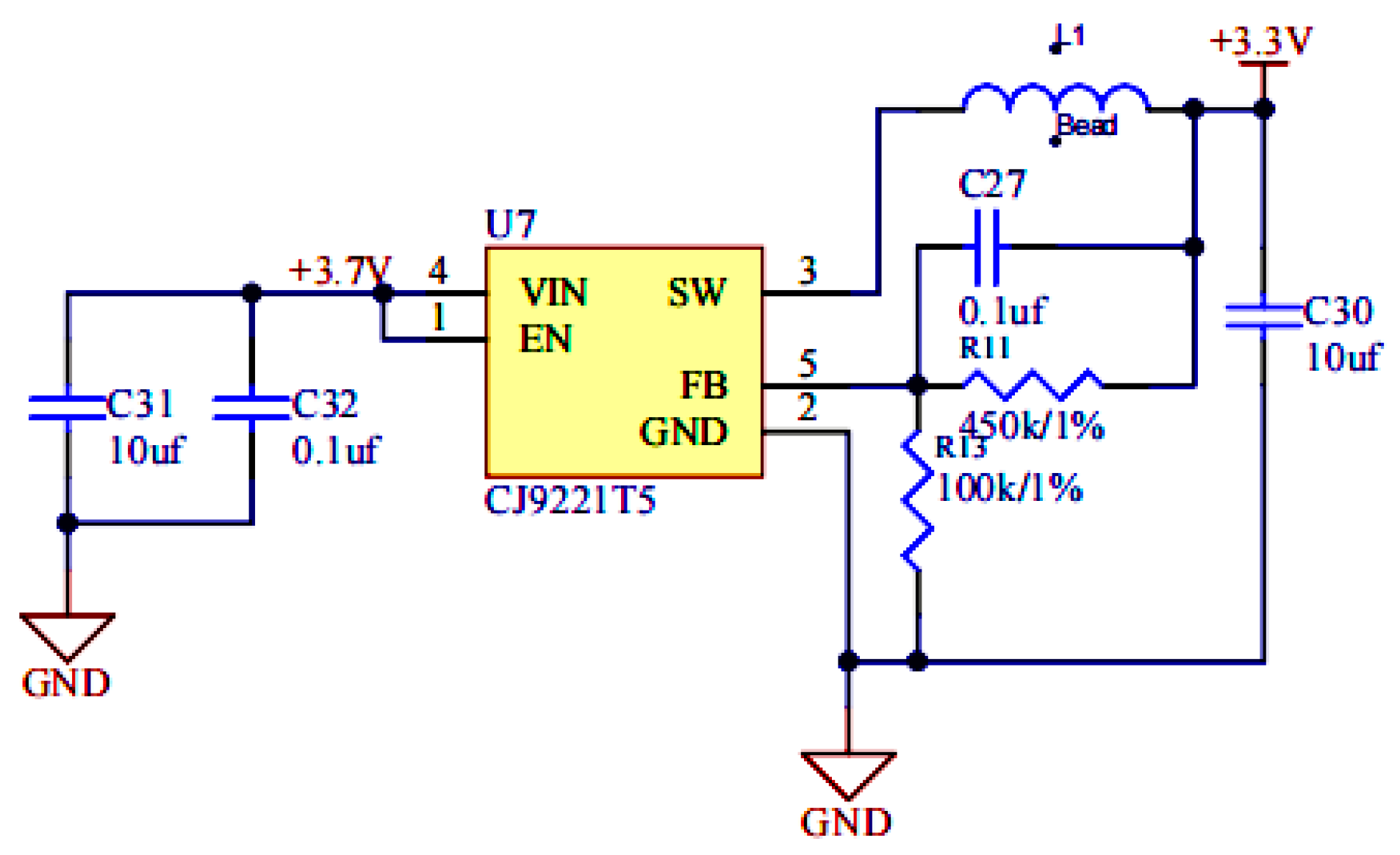

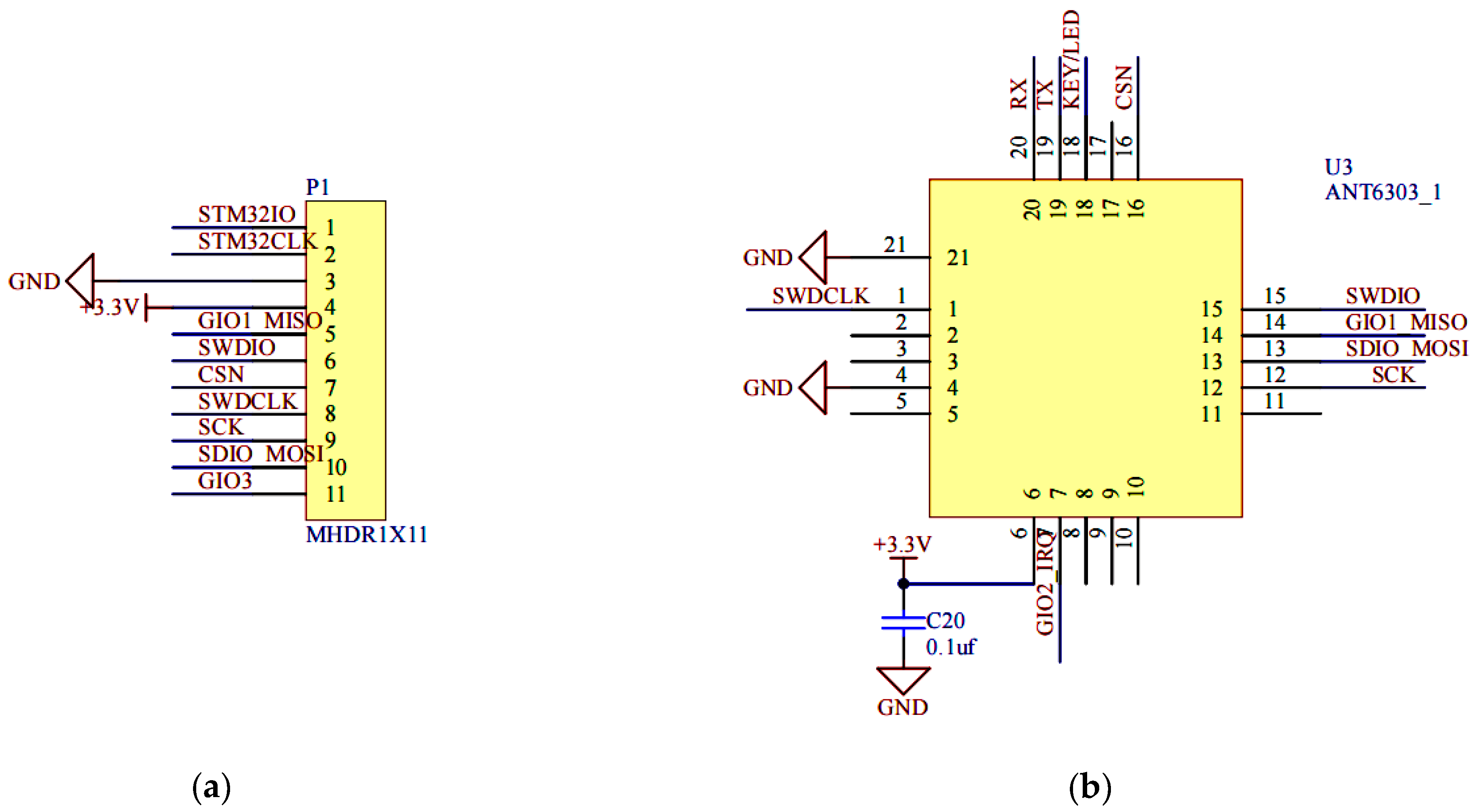
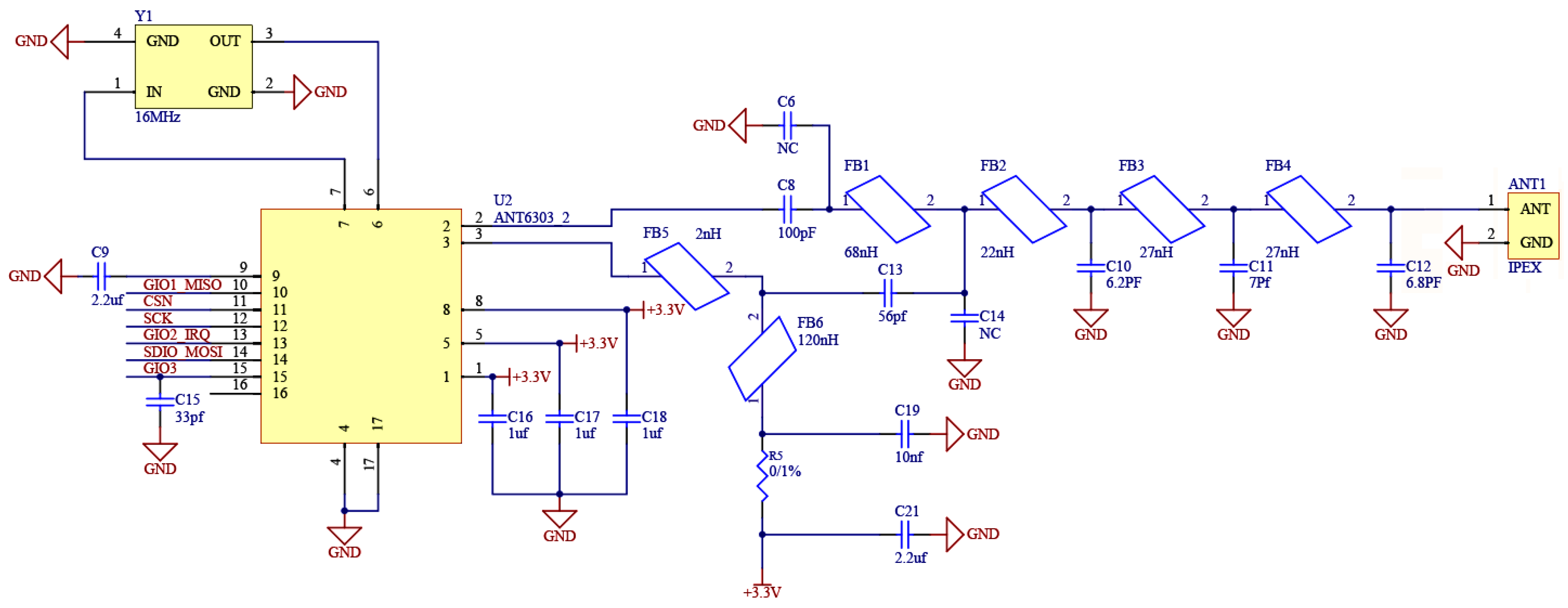

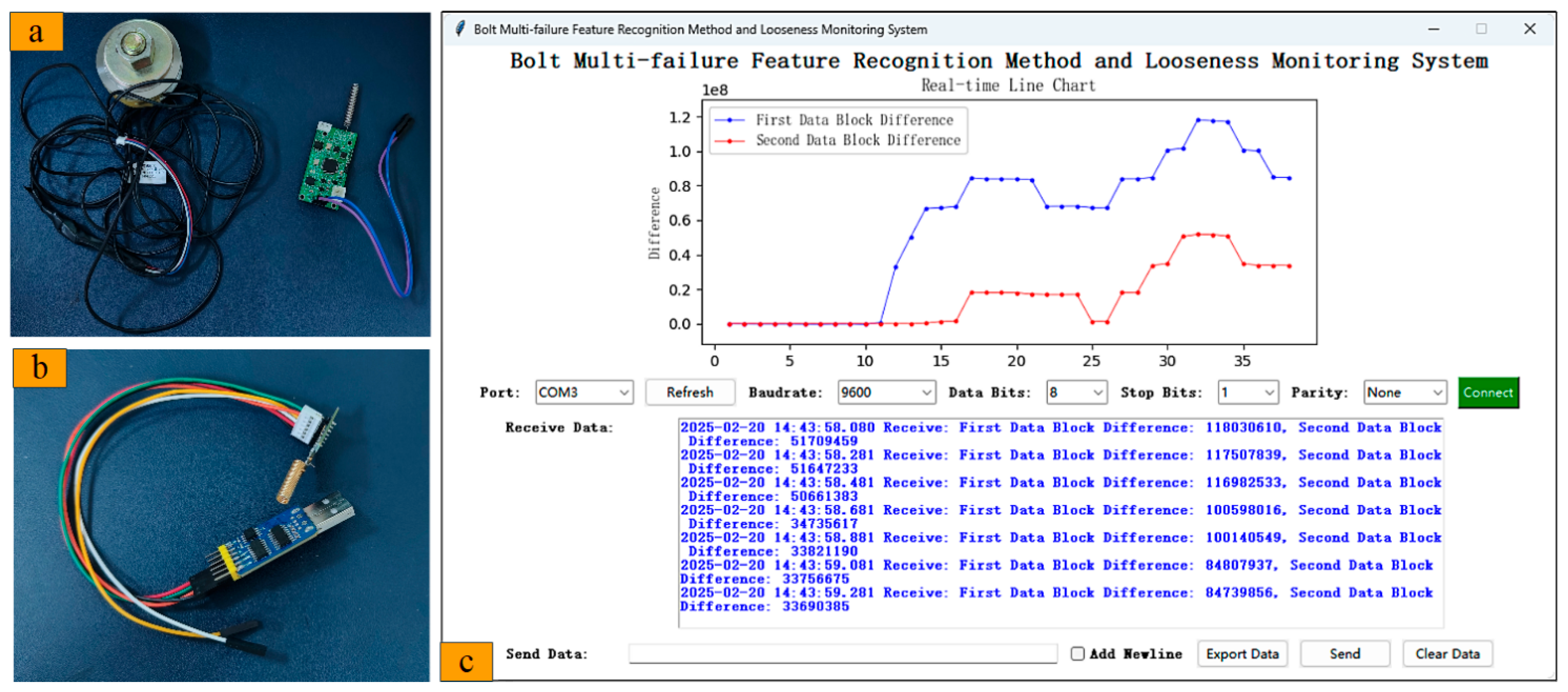
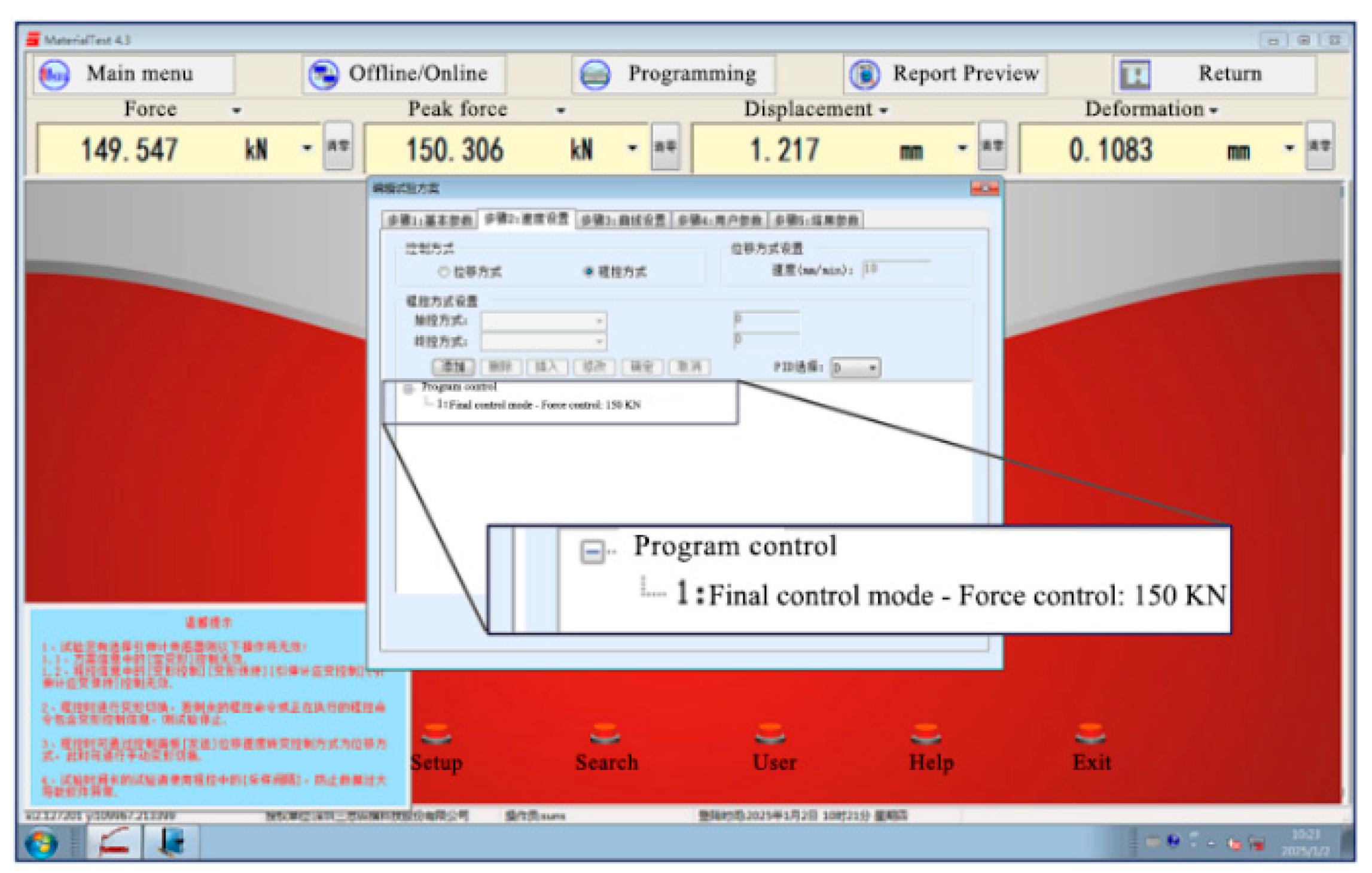
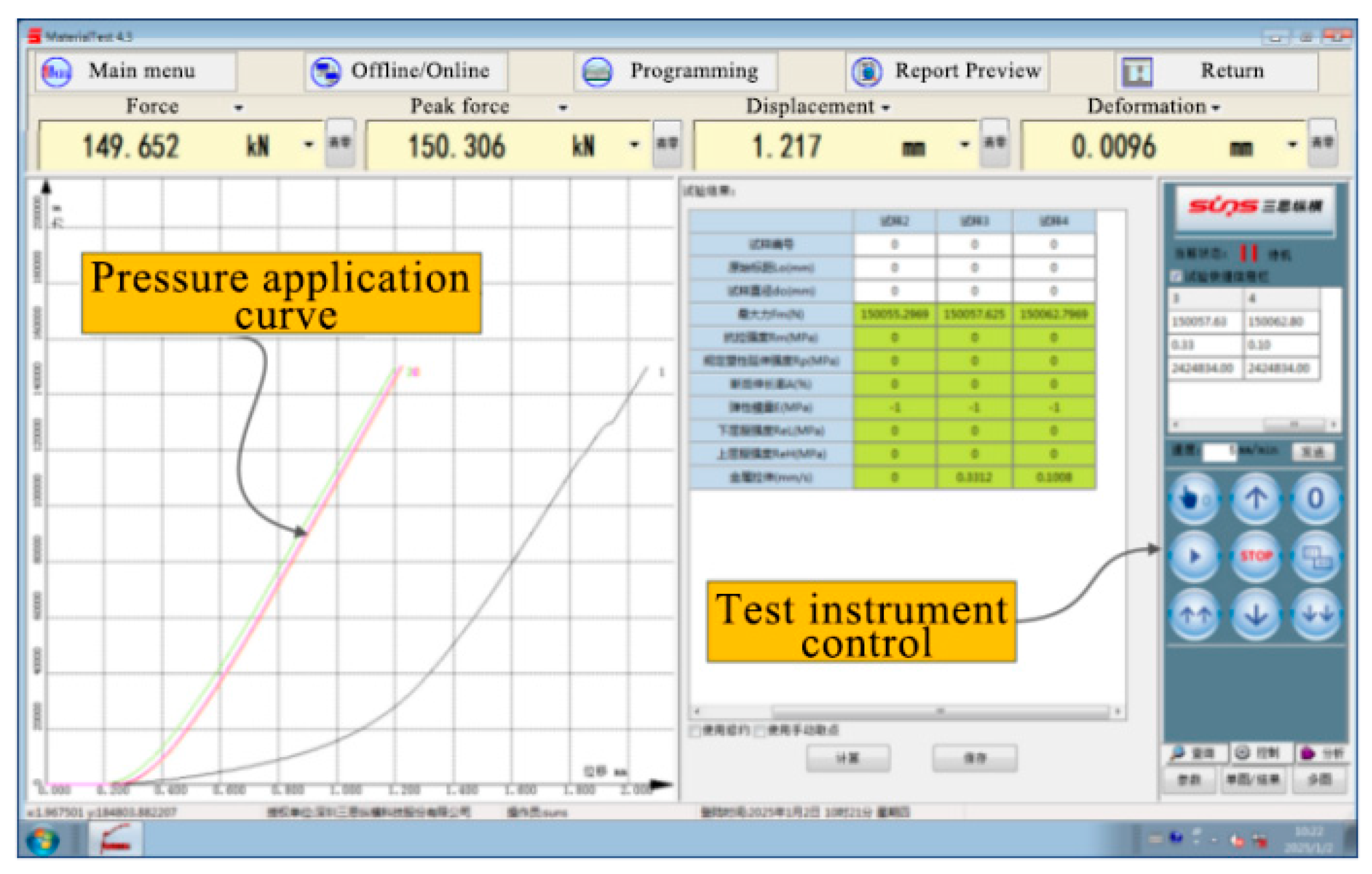

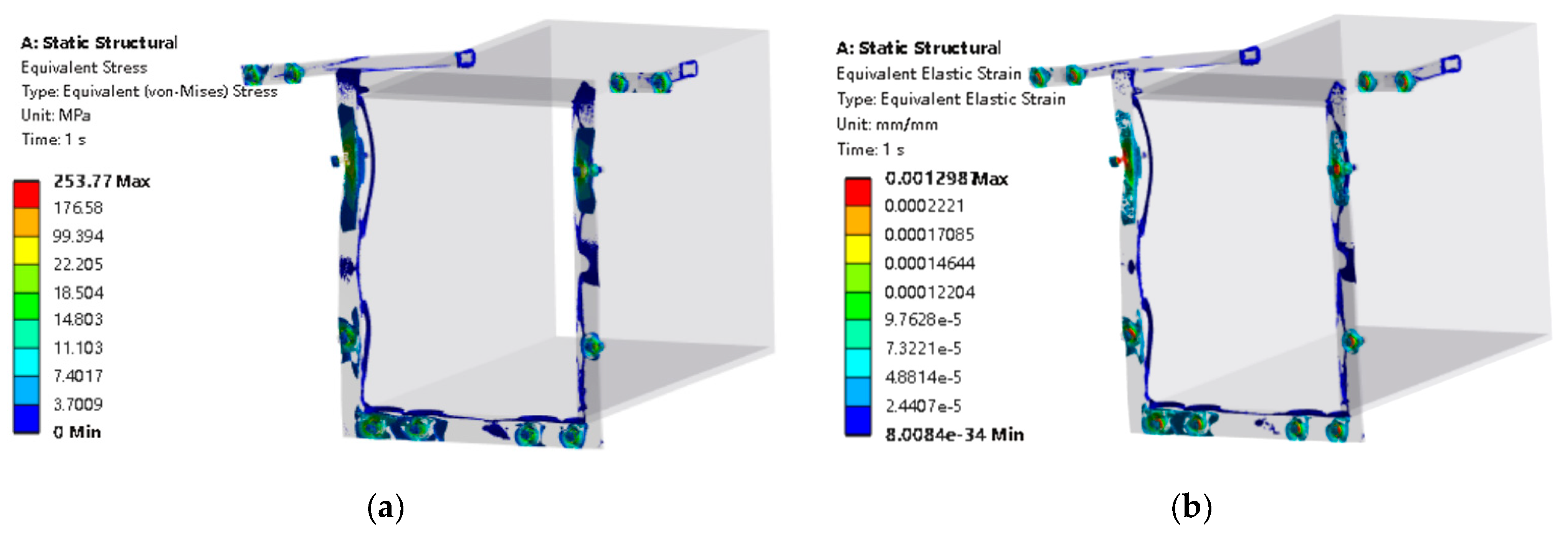





| Structure | () | () | Poisson Ratio | () | () |
|---|---|---|---|---|---|
| Bolts | 7850 | 210 | 0.3 | 640 | 800 |
| Other | 7.850 | 210 | 0.3 | 370 | 630 |
| Order | Qualification | Specifications | Order | Qualification | Specifications |
|---|---|---|---|---|---|
| 1 | Measuring force range | 0~300 kN | 6 | Displacement error | Within ±0.5% of indicated value |
| 2 | Accuracy class | 0.5 | 7 | Displacement resolution | 0.04 μm |
| 3 | Relative error of reading | 0.4~100%f.s. | 8 | Deformation measurement range | 0.2~100%f.s. (Full scale) |
| 4 | Test force error | Within ±0.5% of indicated value | 9 | Deformation error | Within ±0.5% of indicated value |
| 9 | Test force resolution | 1/1,000,000 (No grading throughout the range) |
| Parameter Name | Value | Unit | Parameter Name | Value | Unit |
|---|---|---|---|---|---|
| Torque Range | 8.5~85 | N·m | Working Temperature | −10~50 | °C |
| Resolution | 0.01 | N·m | Accuracy | ±3% (Clockwise), ±4% (Counterclockwise) | |
| Square Drive Size | 3/8 | Unit Conversion | , , , (Four unit conversions) | ||
| Total Length | 271 | Data Storage | Can store 50 sets of torque data | ||
| Weight | 0.52 | Operating Direction | Bidirectional operation | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Y.; Wang, B.; Sun, M.; Que, K.; Xu, S.; Tang, Z.; Huang, Z. The Design and Research of the Bolt Loosening Monitoring System in Combine Harvesters Based on Wheatstone Bridge Circuit Sensor. Agriculture 2025, 15, 704. https://doi.org/10.3390/agriculture15070704
Lian Y, Wang B, Sun M, Que K, Xu S, Tang Z, Huang Z. The Design and Research of the Bolt Loosening Monitoring System in Combine Harvesters Based on Wheatstone Bridge Circuit Sensor. Agriculture. 2025; 15(7):704. https://doi.org/10.3390/agriculture15070704
Chicago/Turabian StyleLian, Yi, Bangzhui Wang, Meiyan Sun, Kexin Que, Sijia Xu, Zhong Tang, and Zhilong Huang. 2025. "The Design and Research of the Bolt Loosening Monitoring System in Combine Harvesters Based on Wheatstone Bridge Circuit Sensor" Agriculture 15, no. 7: 704. https://doi.org/10.3390/agriculture15070704
APA StyleLian, Y., Wang, B., Sun, M., Que, K., Xu, S., Tang, Z., & Huang, Z. (2025). The Design and Research of the Bolt Loosening Monitoring System in Combine Harvesters Based on Wheatstone Bridge Circuit Sensor. Agriculture, 15(7), 704. https://doi.org/10.3390/agriculture15070704







