An Innovative Indoor Localization Method for Agricultural Robots Based on the NLOS Base Station Identification and IBKA-BP Integration
Abstract
1. Introduction
2. Algorithm Design Process
2.1. Base Station Filtering Algorithm
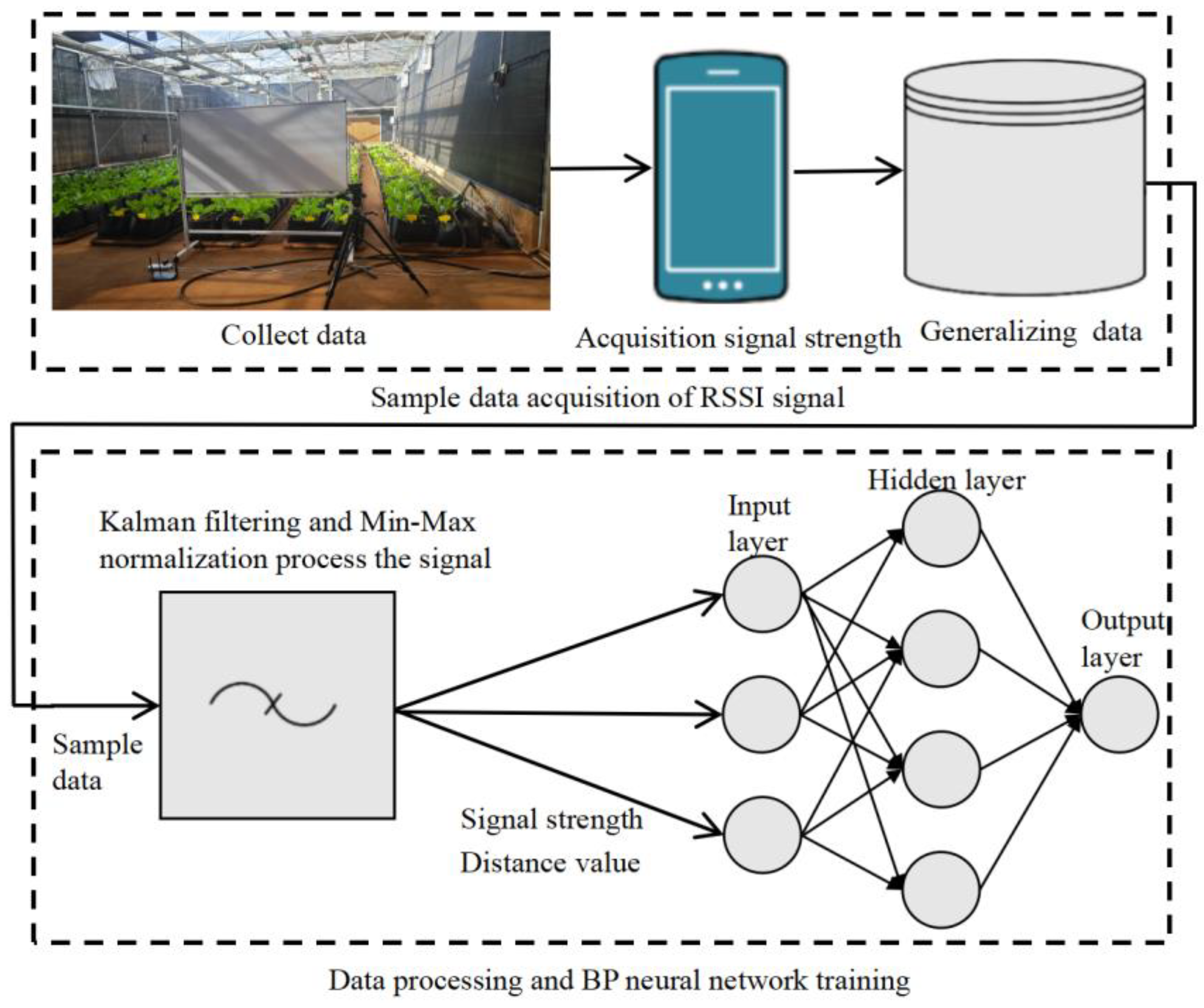
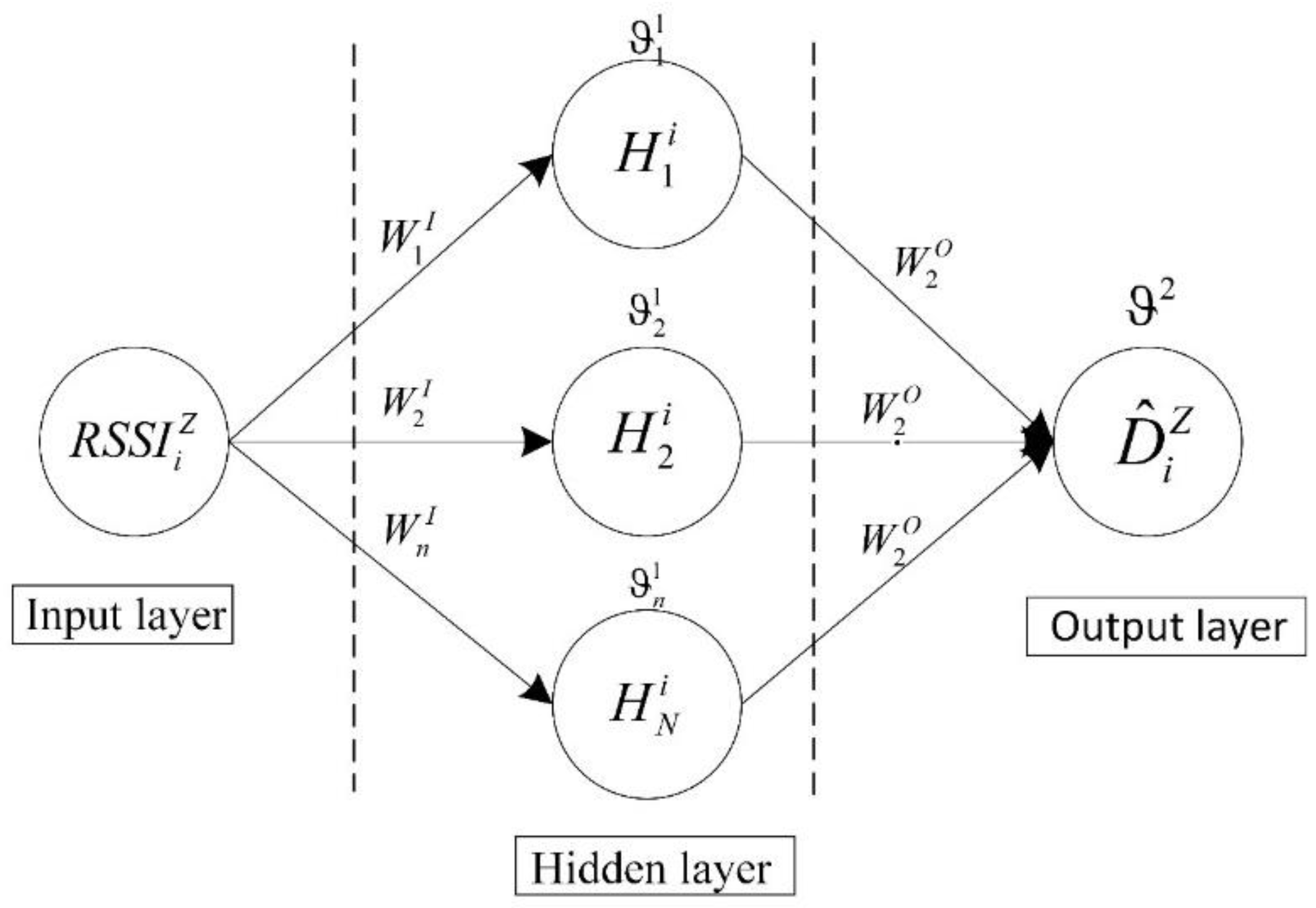
2.2. Distance Measurement Model Based on BP Neural Network
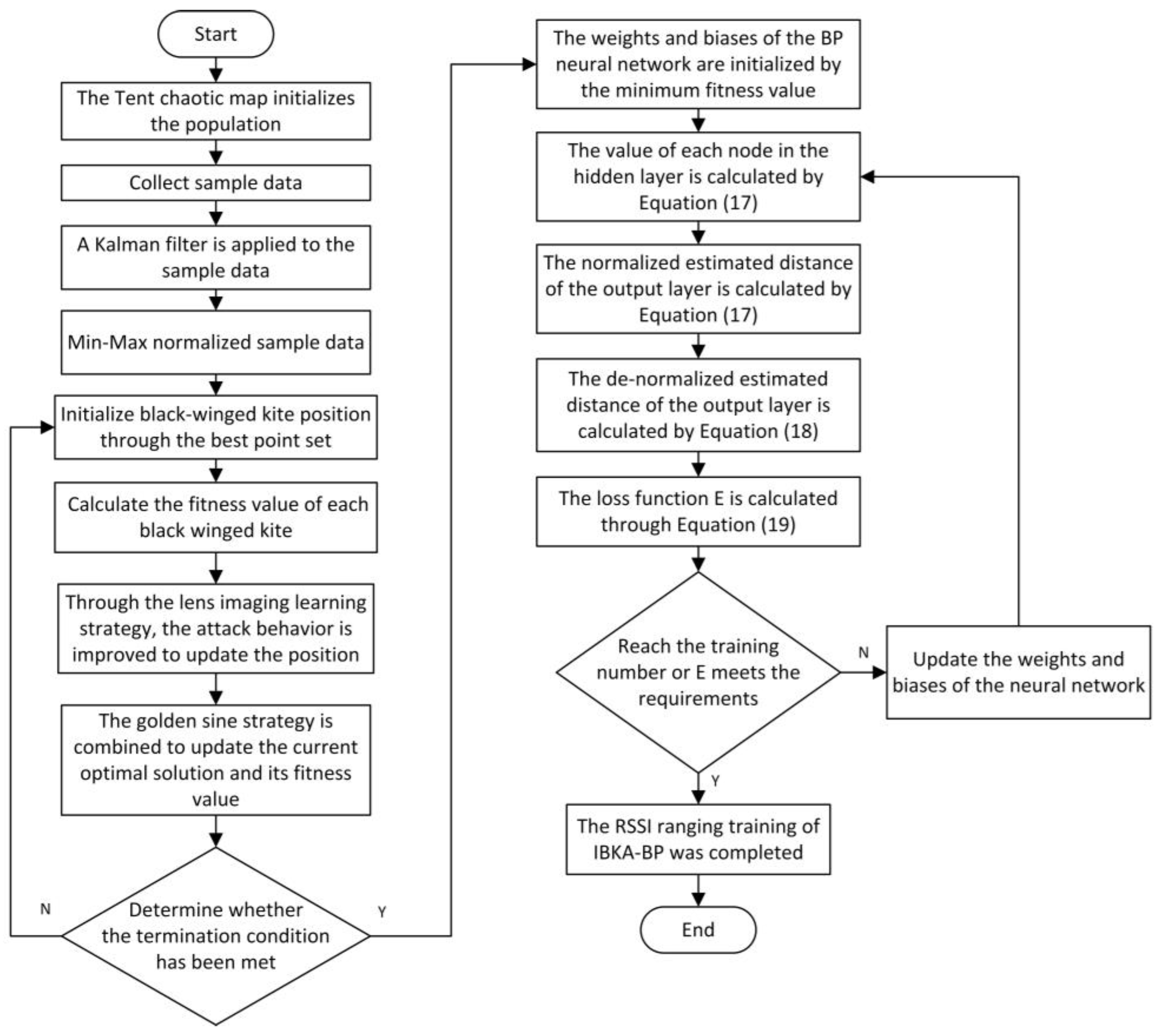
2.3. IBKA-BP Neural Network RSSI Distance Measurement Algorithm
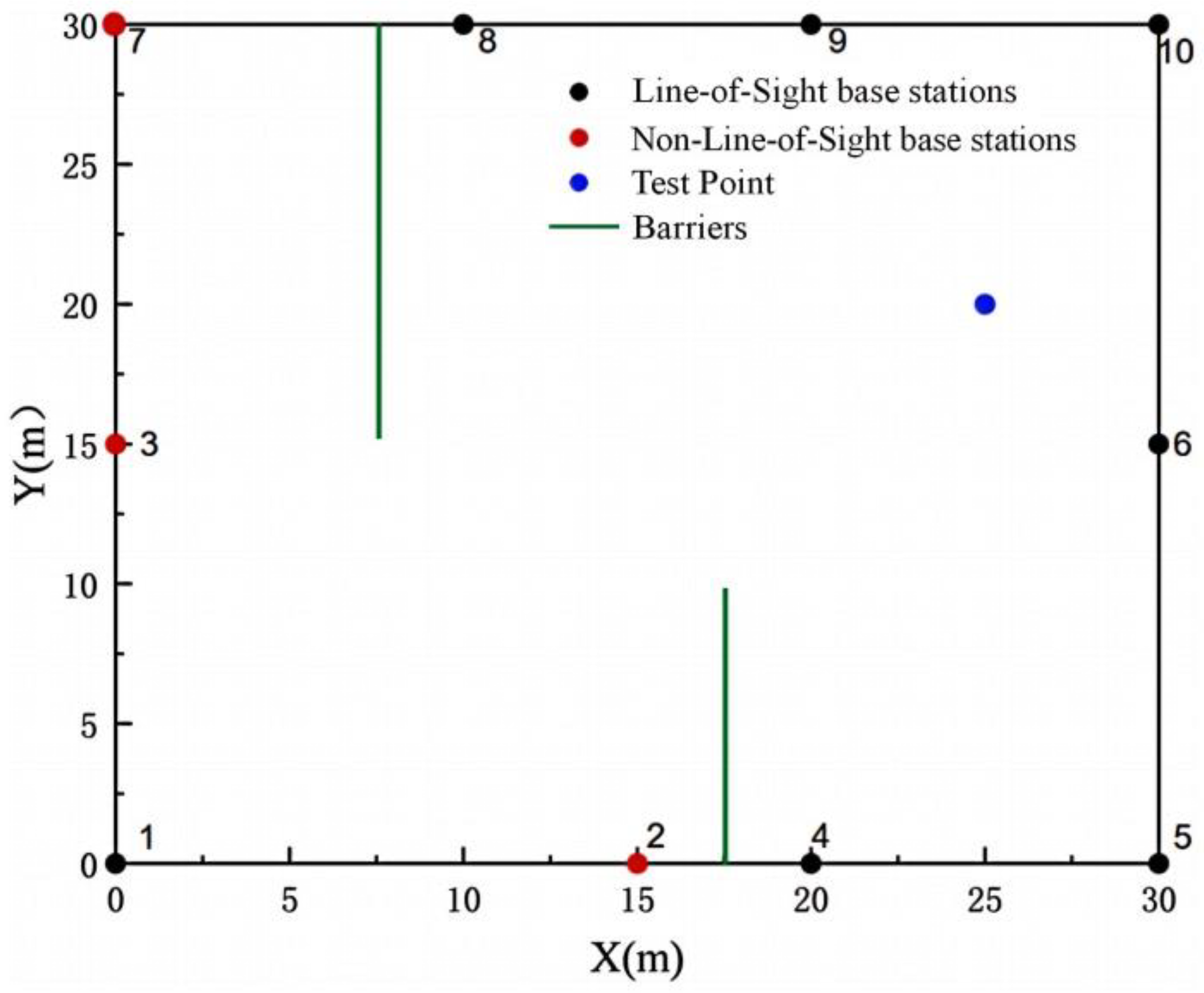
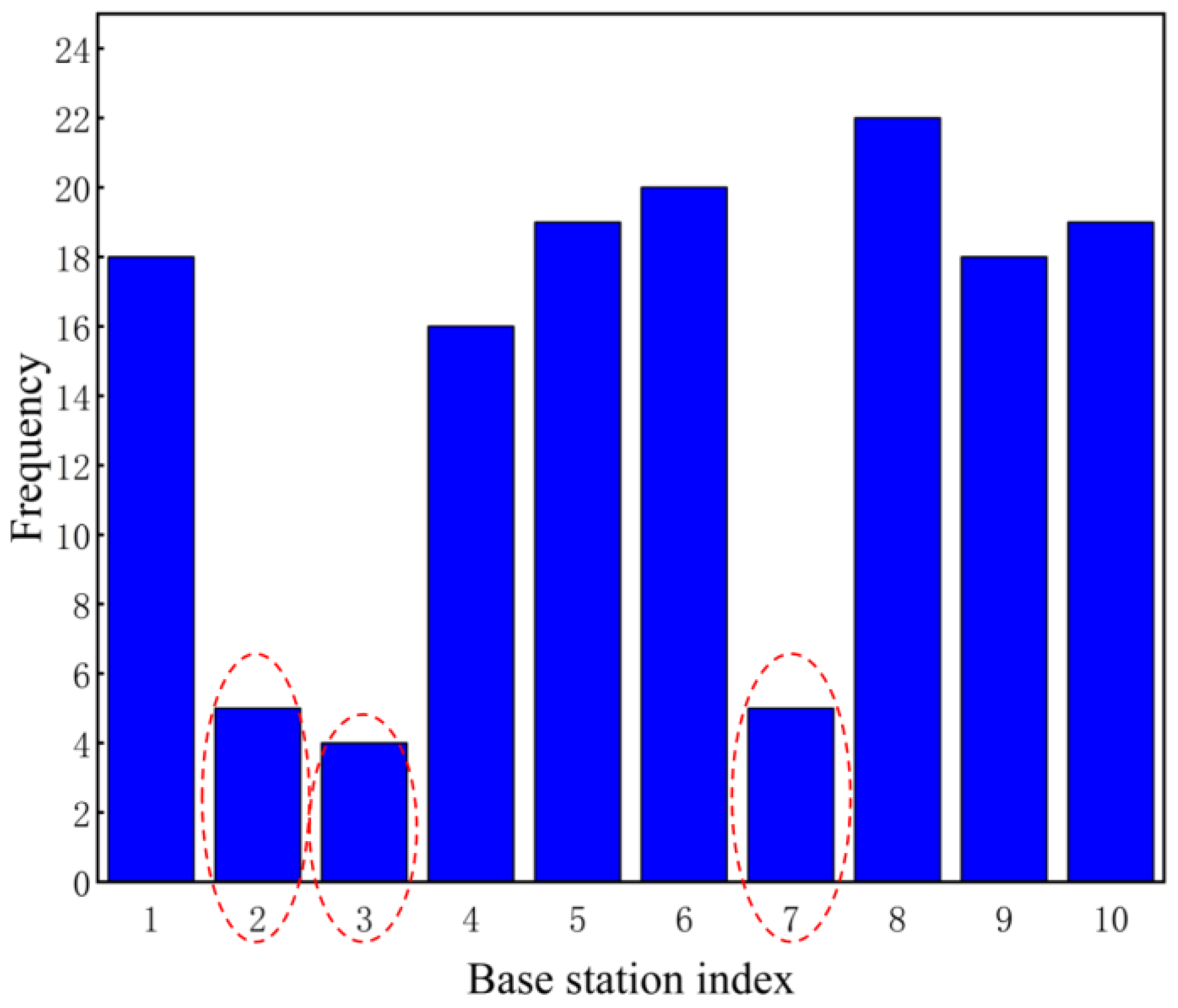
3. NLOS Base Station Identification Algorithm
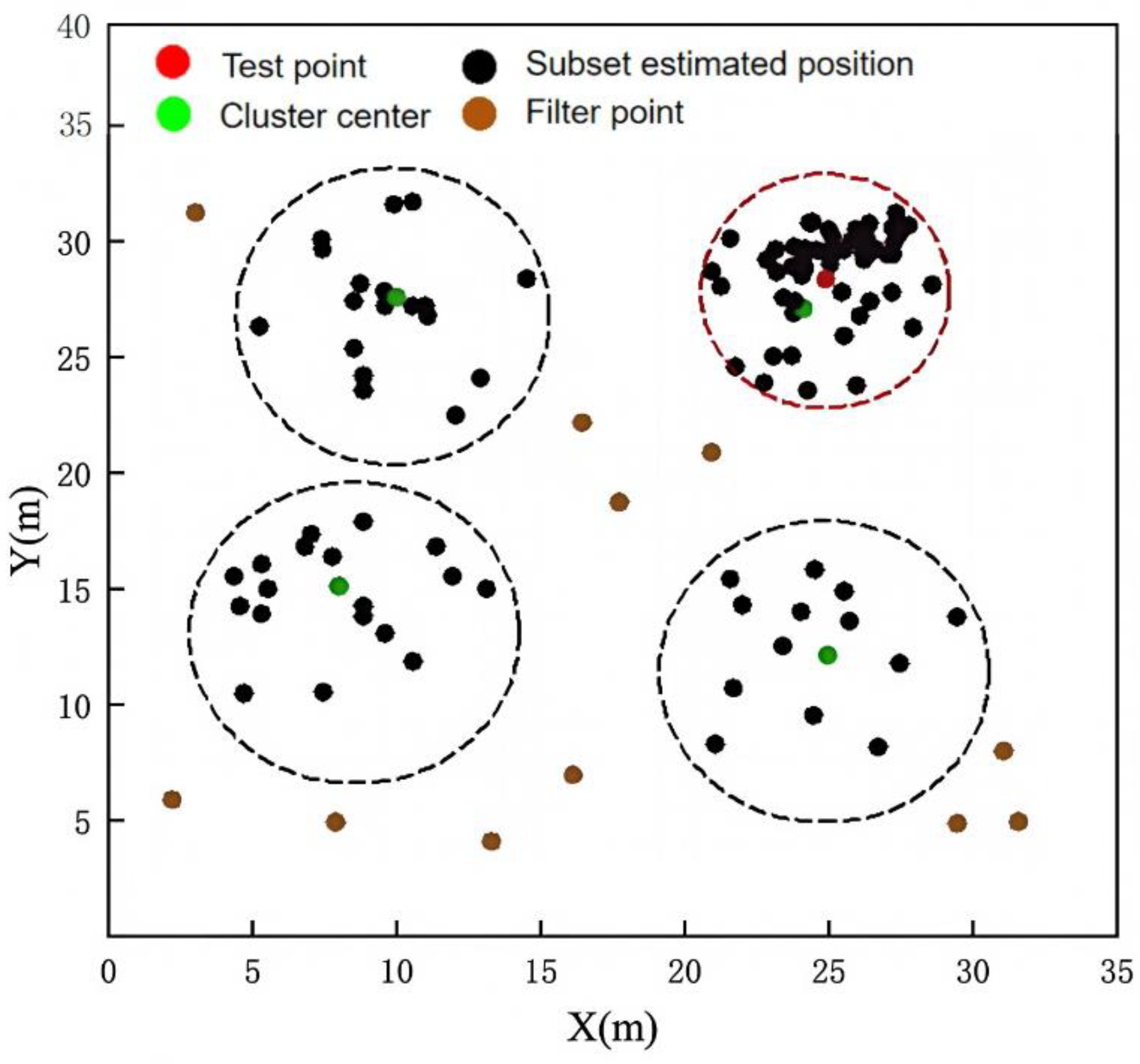
3.1. Subset Division
3.2. Density Peak Detection and Target Localization
3.3. NLOS Base Station Identification
4. Distance Measurement Model Based on BP Neural Network
5. IBKA-BP Neural Network RSSI Ranging Algorithm
5.1. Black Kite Algorithm
5.2. Heuristic Algorithm Improvement Strategy Inspired by Black-Winged Kite
| Algorithm 1 The IBKA-BP algorithm |
| 1: Input: Population size pop, problem dimension dim, maximum iterations T |
| 2: Output: Optimal solution , best fitness value |
| 3: Initialize population using the tent chaotic mapping technique |
| 4: Evaluate initial fitness and select a leader |
| 5: for t = 1 to T do |
| 6: Calculate dynamic parameters: |
| 7: Compute adjustment factor n for position update magnitude |
| 8: for each individual, i do |
| 9: Update position based on the dual predation behaviors: |
| 10: if rand (0, 1) > 0.9, then |
| 11: Update position by the hovering attack strategy using Equation (24) |
| 12: else |
| 13: Update position by the circling attack strategy using Equation (24) |
| 14: end if |
| 15: Calculate an optimal individual by the lens imaging strategy to expand the search space using Equation (32) |
| 16: Assign to the current individual |
| 17: Update individual positions by the golden sine strategy using Equation (36) |
| 18: Incorporate sinusoidal perturbations , , and golden ratio coefficients and |
| 19: Select update mode based on the comparison of constant p and random r |
| 20: end for |
| 21: Update the leader position |
| 22: Update the best fitness value |
| 23: end for |
| 24: return and |
6. Test Results Analysis
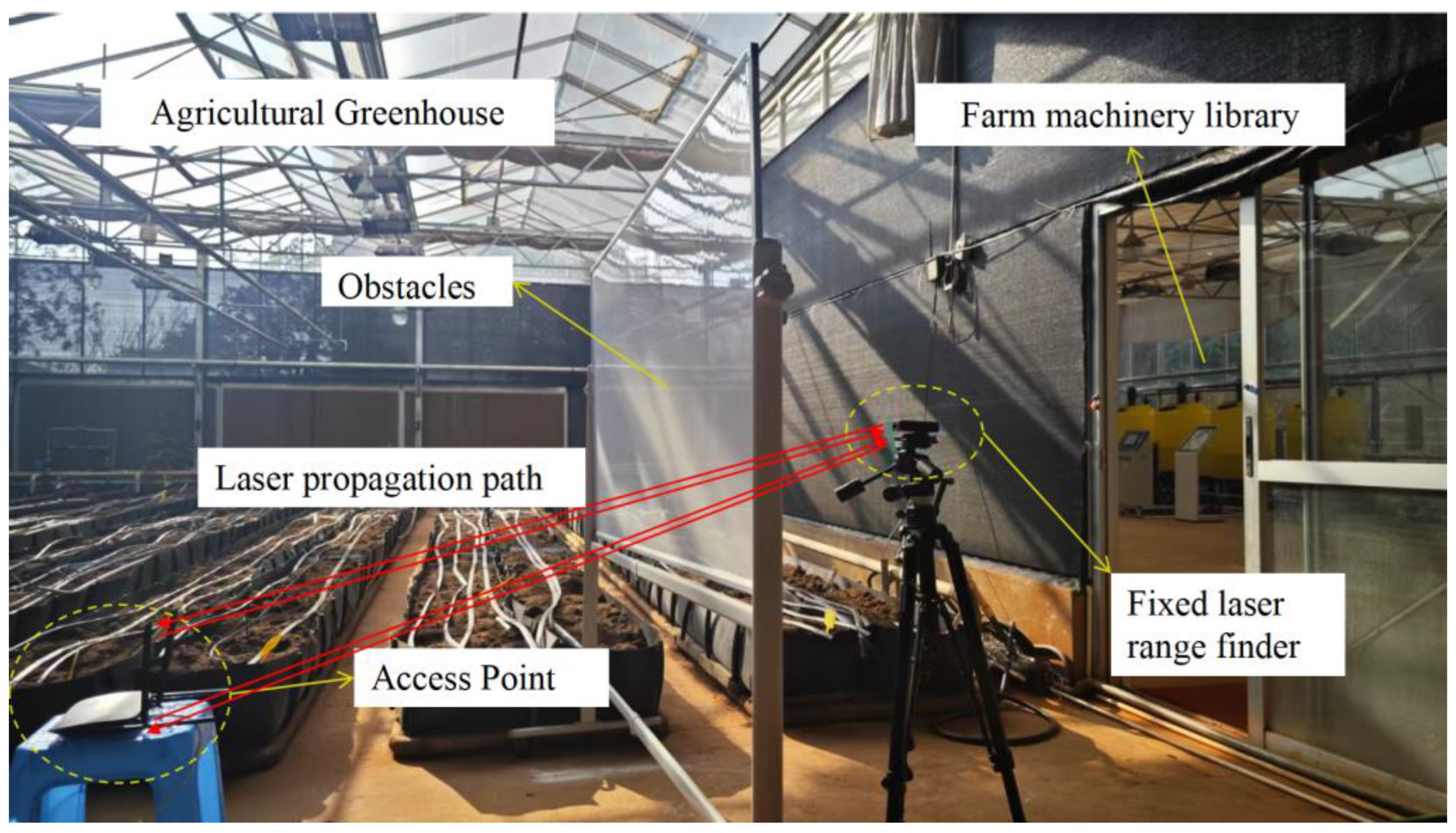
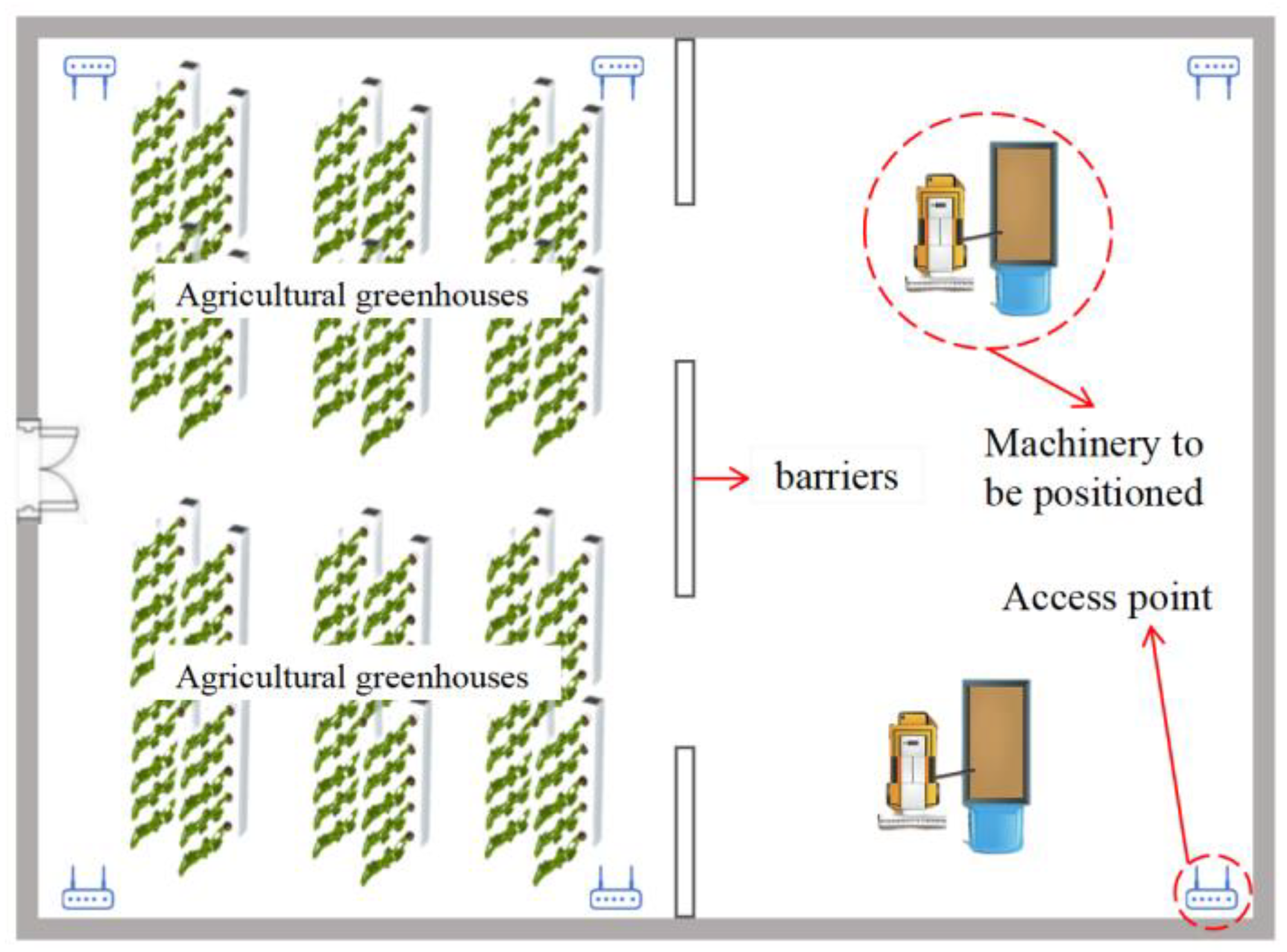
6.1. Test Environmental Setup
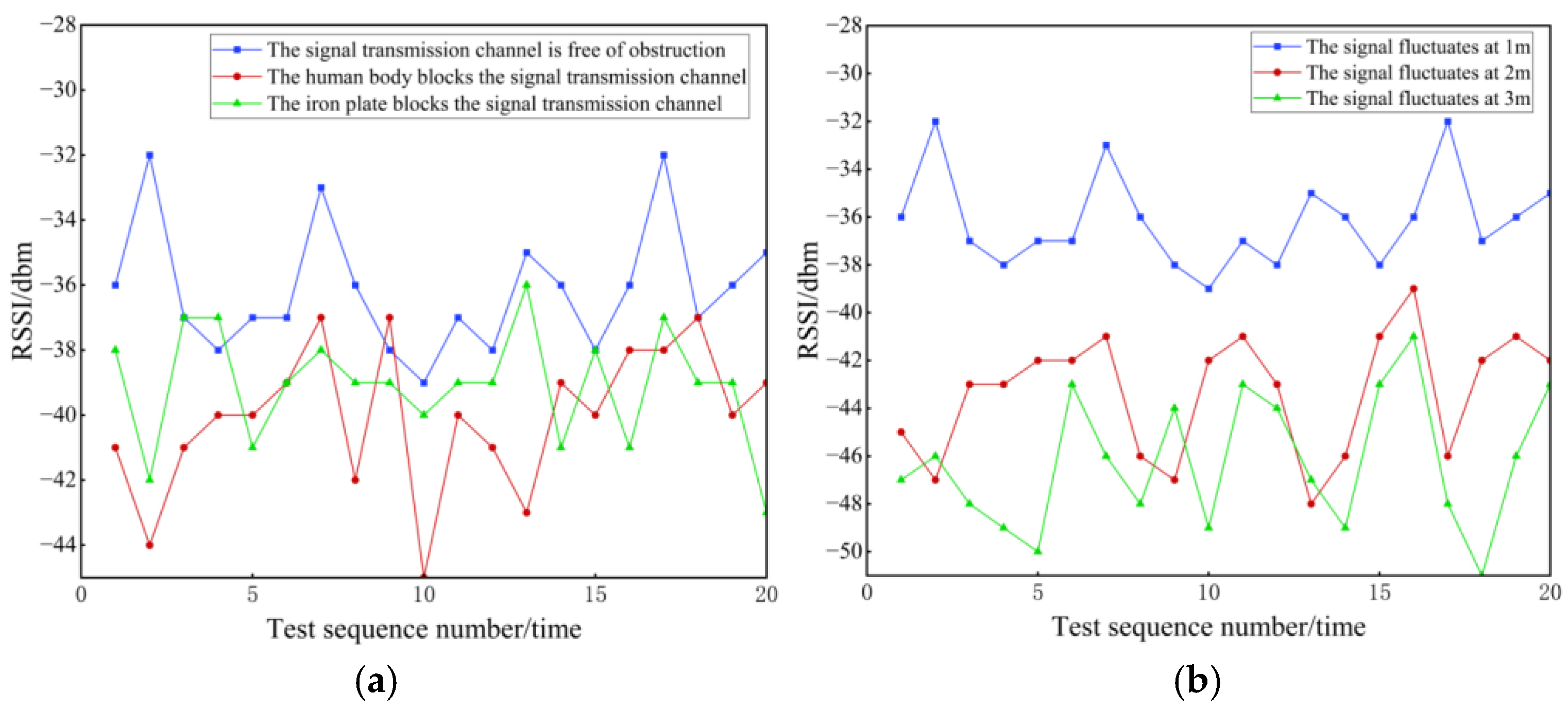
6.2. RSSI Signal Quality Analysis
6.3. Localization Performance Analysis of Different Algorithms
6.4. Comparison of Positioning Accuracy Under WI-FI Radio Frequency Interference
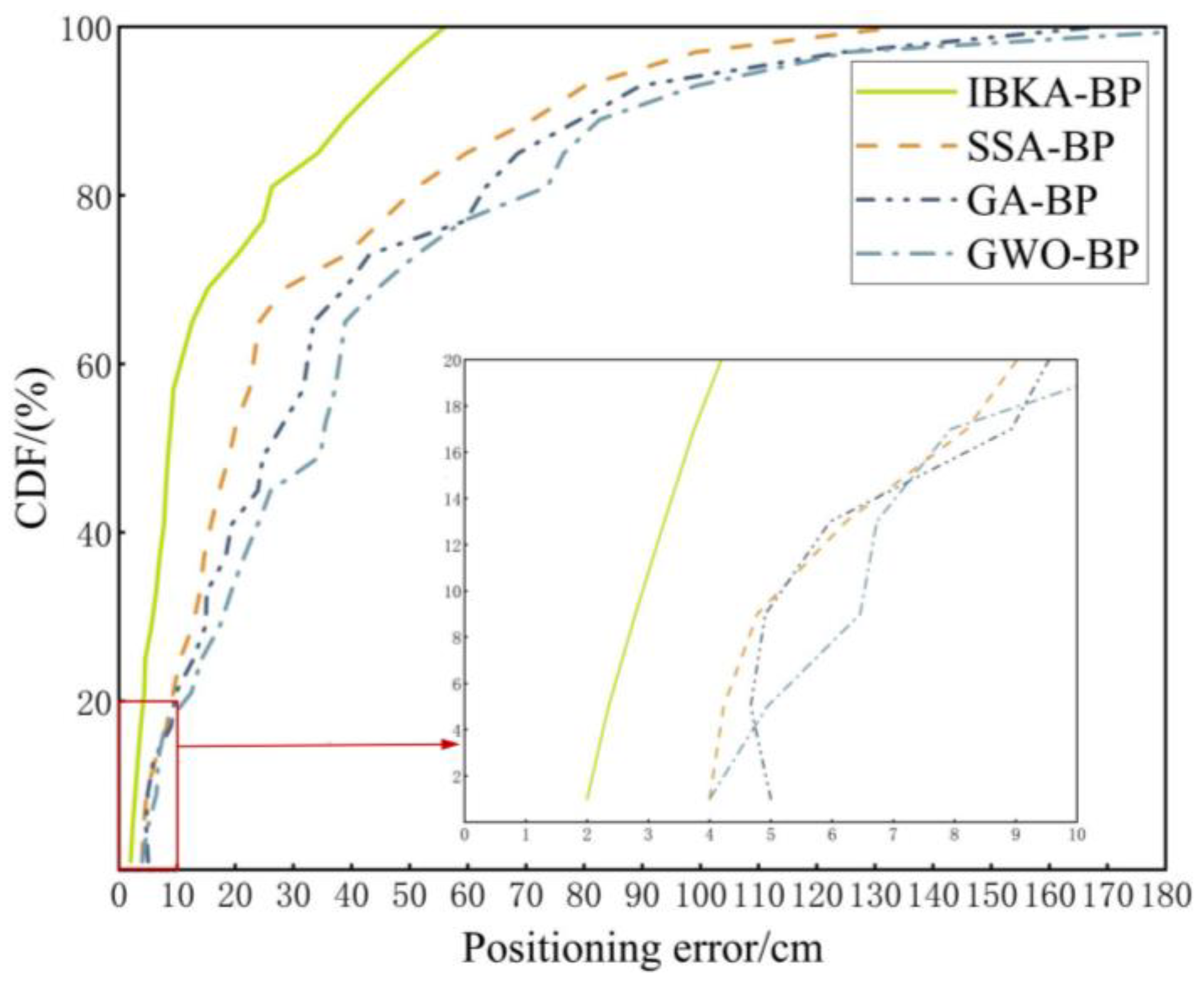
6.5. Positioning Result Comparison of Different Algorithms
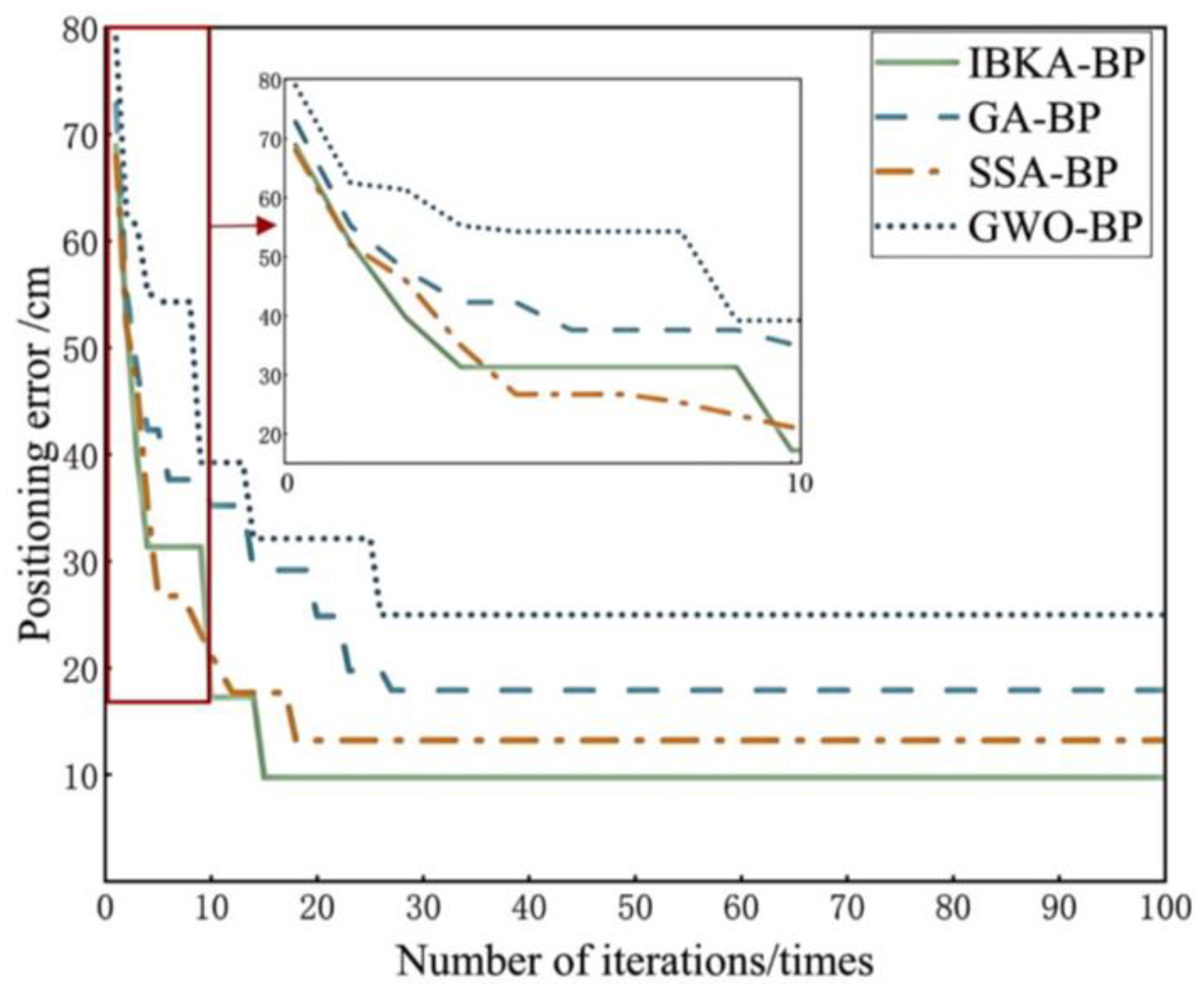
6.6. Algorithm Convergence Analysis
6.7. Comparison with Recent Advancements in AI-Based Localization Field
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RSSI | Received Signal Strength Indication |
| RSS | Received Signal Strength |
| LOS | Line-of-Sight |
| NLOS | Non-Line-of-Sight |
| BKA | Black Kite Algorithm |
| IBKA | Improved Black Kite Algorithm |
| IBKA-BP | Improved Black Kite Algorithm—Back Propagation |
| ISSA-BP | Improved Sparrow Search Algorithm—Back Propagation |
| GWO-BP | Grey Wolf Optimizer—Back Propagation |
| GA-BP | Genetic Algorithm—Back Propagation |
| ME | Mean Error |
| STD | Standard Deviation |
| RMSE | Root Mean Square Error |
| BP | Back Propagation |
| DPC | Density Peaks Clustering |
| GNSS | Global Navigation Satellite System |
| RTT | Round-Trip Time |
| CNNs | convolutional neural networks |
| RNNs | Recurrent Neural Networks |
| IOT | Internet of Things |
| GAN | Generative Adversarial Network |
| CFP | channel frequency Polar-coordinate |
| VAE-CNN | Variational Autoencoder-Convolutional Neural Network |
| RIS | Requires pre-deployed reconfigurable intelligent surface |
| LocDT | localization-oriented DT |
References
- Nijak, M.; Skrzypczyński, P.; Ćwian, K.; Zawada, M.; Szymczyk, S.; Wojciechowski, J. On the Importance of Precise Positioning in Robotised Agriculture. Remote Sens. 2024, 16, 985. [Google Scholar] [CrossRef]
- Qu, J.; Qiu, Z.; Li, L.; Guo, K.; Li, D. Map Construction and Positioning Method for LiDAR SLAM-Based Navigation of an Agricultural Field Inspection Robot. Agronomy 2024, 14, 2365. [Google Scholar] [CrossRef]
- Yang, Q.; Du, X.; Wang, Z.; Meng, Z.; Ma, Z.; Zhang, Q. A review of core agricultural robot technologies for crop productions. Comput Electron. Agric. 2023, 206, 107701. [Google Scholar] [CrossRef]
- Wang, R.; Chen, L.; Huang, Z.; Zhang, W.; Wu, S. A Review on the High-Efficiency Detection and Precision Positioning Technology Application of Agricultural Robots. Processes. 2024, 12, 1833. [Google Scholar] [CrossRef]
- Nimma, D.; Dhanke, J.A.; Murthy, G.; Khandekar, S.D.; Hymavathi, J.; Jangir, P.; Singh, M. Optimization of Crop Yields in Sustainable Agriculture: Application of Big Data Analytics and Artificial Intelligence. Remote. Sens. Earth Syst. Sci. 2025, 1–12. [Google Scholar] [CrossRef]
- Lv, P.; Wang, B.; Cheng, F.; Xue, J. Multi-objective association detection of farmland obstacles based on information fusion of millimeter wave radar and camera. Sensors. 2022, 23, 230. [Google Scholar] [CrossRef]
- Nie, S.; Lunar, M.M.; Bai, G.; Ge, Y.; Pitla, S.; Koksal, C.E.; Vuran, M.C. mmWave on a farm: Channel modeling for wireless agricultural networks at broadband millimeter-wave frequency. In Proceedings of the 2022 19th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Stockholm, Sweden, 25 October 2022. [Google Scholar]
- Ge, H.; Li, B.; Jia, S.; Nie, L.; Wu, T.; Yang, Z.; Shang, J.; Zheng, Y.; Ge, M. LEO enhanced global navigation satellite system (LeGNSS): Progress, opportunities, and challenges. GSIS 2022, 25, 1–13. [Google Scholar] [CrossRef]
- Yao, Z.; Zhao, C.; Zhang, T. Agricultural machinery automatic navigation technology. iScience 2024, 27, 108714. [Google Scholar] [CrossRef]
- Xie, K.; Zhang, Z.; Zhu, S. Enhanced Agricultural Vehicle Positioning through Ultra-Wideband-Assisted Global Navigation Satellite Systems and Bayesian Integration Techniques. Agriculture 2024, 14, 1396. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of WiFi fingerprinting-based indoor positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, K.; Zhu, F.; Bu, J.; Dua, X. The state of the art of deep learning-based Wi-Fi indoor positioning: A review. IEEE Sens. J. 2024, 24, 27076–27098. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W.; Zheng, J.; Lin, A.; Liu, J.; Ge, S.S. Wi-fi-based indoor localization with interval random analysis and improved particle swarm optimization. IEEE Trans. Mob. Comput. 2024, 23, 9120–9134. [Google Scholar] [CrossRef]
- Zheng, J.; Li, K.; Zhang, X. Wi-Fi fingerprint-based indoor localization method via standard particle swarm optimization. Sensors 2022, 22, 5051. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Puspitaningayu, P.; Funabiki, N.; Hamazaki, K.; Kuribayashi, M.; Kojima, K. A proposal of the fingerprint optimization method for the fingerprint-based indoor localization system with IEEE 802.15. 4 devices. Information 2022, 13, 211. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Bi, J.; Zhang, Y.; Yao, G.; Feng, Y.; Si, M. LOS compensation and trusted NLOS recognition assisted WiFi RTT indoor positioning algorithm. Expert Syst. Appl. 2024, 243, 122867. [Google Scholar] [CrossRef]
- Hou, C.; Liu, W.; Tang, H.; Cheng, J.; Zhu, X.; Chen, M.; Gao, C.; Wei, G. Non-Line-of-Sight Positioning Method for Ultra-Wideband/Miniature Inertial Measurement Unit Integrated System Based on Extended Kalman Particle Filter. Drones 2024, 8, 372. [Google Scholar] [CrossRef]
- Kong, Q. NLOS identification for UWB positioning based on IDBO and convolutional neural networks. IEEE Access 2023, 11, 144705–144721. [Google Scholar] [CrossRef]
- Ahirwal, S.; Singh, J. A Review of Range-based RSSI Algorithms for Indoor Wireless Sensor Network Localization. Int. J. Adv. Comput. Technol. 2023, 12, 7–12. [Google Scholar]
- Arigye, W.; Pu, Q.; Zhou, M.; Khalid, W.; Tahir, M.J. RSSI fingerprint height based empirical model prediction for smart indoor localization. Sensors 2022, 22, 9054. [Google Scholar] [CrossRef]
- Du, J.; Yuan, C.; Yue, M.; Ma, T. A novel localization algorithm based on RSSI and multilateration for indoor environments. Electronics 2022, 11, 289. [Google Scholar] [CrossRef]
- Liu, T.; Ji, J.; Pan, D.; Zhao, L.; Li, M. Localization method for agricultural robots based on fusion of LiDAR and IMU. Smart Agric. 2024, 6, 94. [Google Scholar]
- Zhao, L.; Han, Z.; Zhang, F. Research on Stereo Location in Visible Light Room Based on Neural Network. Chin. J. Lasers 2021, 48, 706004. [Google Scholar]
- Tian, Y.; Lian, Z.; Wang, P.; Wang, M.; Yue, Z.; Chai, H. Application of a long short-term memory neural network algorithm fused with Kalman filter in UWB indoor positioning. Sci. Rep. 2024, 14, 1925. [Google Scholar] [CrossRef] [PubMed]
- Gui, L.; Yang, M.; Yu, H.; Li, J.; Shu, F.; Xiao, F. A Cramer-Rao lower bound of CSI-based indoor localization. IEEE Trans. Veh. Technol. 2017, 67, 2814–2818. [Google Scholar] [CrossRef]
- Bi, J.; Wang, Y.; Ning, Y. Indoor rang-based positioning method considering geometry optimization of BLE beacons. J. China Univ. Min. Technol. 2021, 50, 411–416. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Li, G.; Geng, E.; Ye, Z.; Xu, Y.; Lin, J.; Pang, Y. Indoor positioning algorithm based on the improved RSSI distance model. Sensors 2018, 18, 2820. [Google Scholar] [CrossRef]
- Nosrati, L.; Fazel, M.S.; Ghavami, M. Improving indoor localization using mobile UWB sensor and deep neural networks. IEEE Access 2022, 10, 20420–20431. [Google Scholar] [CrossRef]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Feng, D.; Wang, C.; He, C.; Zhuang, Y.; Xia, X.-G. Kalman-filter-based integration of IMU and UWB for high-accuracy indoor positioning and navigation. IEEE Internet Things J. 2020, 7, 3133–3146. [Google Scholar] [CrossRef]
- Xie, Y.; Jiang, L. RSSI Indoor Positioning Algorithm Based on Kalman Filtering. In Proceedings of the 2024 5th International Conference on Electronic Communication and Artificial Intelligence (ICECAI), Shenzhen, China, 24 September 2024. [Google Scholar]
- Shantal, M.; Othman, Z.; Bakar, A.A. A novel approach for data feature weighting using correlation coefficients and min–max normalization. Symmetry 2023, 15, 2185. [Google Scholar] [CrossRef]
- Henderi, H.; Wahyuningsih, T.; Rahwanto, E. Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer. Int. J. Inform. Inf. Syst. 2021, 4, 13–20. [Google Scholar] [CrossRef]
- Mu, C.; Qiu, B.; Liu, X. A new method for figuring the number of hidden layer nodes in BP algorithm. Int. J. Recent Innov. Trends Comput. Commun. 2017, 5, 101–114. [Google Scholar]
- Tian, Y.; Su, D.; Lauria, S.; Liu, X. Recent advances on loss functions in deep learning for computer vision. Neurocomputing 2022, 497, 129–158. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 1–53. [Google Scholar] [CrossRef]
- Choi, T.J.; Togelius, J.; Cheong, Y. Advanced Cauchy mutation for differential evolution in numerical optimization. IEEE Access 2020, 8, 8720–8734. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S. Firefly search algorithm based on leader strategy. Eng. Appl. Artif. Intell. 2023, 123, 106328. [Google Scholar] [CrossRef]
- Su, Y.; Wang, S. Adaptive Hybrid Strategy Sparrow Search Algorithm. Comput. Eng. Appl. 2023, 59, 75–85. [Google Scholar]
- Dexin, Y.; Linna, Z.; Damin, Z. Harris hawks optimization based on chaotic lens imaging learning and its application. Chin. J. Sens. Actuators 2021, 34, 1463–1474. [Google Scholar]
- Liu, C.; He, Q. Golden Sine Chimp Optimization Algorithm Integrating Multiple Strategies. Acta Autom. Sin. 2023, 49, 2360–2373. [Google Scholar]
- Pu, Q.; Yu, W.; Lan, X.; Zhou, M.; Yang, X. A Novel RIS-Aided Indoor Localization in Single Access Point Scenarios via Generative AI. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Yang, C.; Shih, W.; Wen, C.; Tsai, S.; Yuen, C. Enhancing WiFi access point localization with AI-based filtering. IEEE Commun. Letters 2024, 28, 1332–1336. [Google Scholar] [CrossRef]
- Gao, K.; Wang, H.; Lv, H.; Liu, W. Localization-oriented digital twinning in 6G: A new indoor-positioning paradigm and proof-of-concept. IEEE Trans. Wirel. Commun. 2024, 23, 10473–10486. [Google Scholar] [CrossRef]


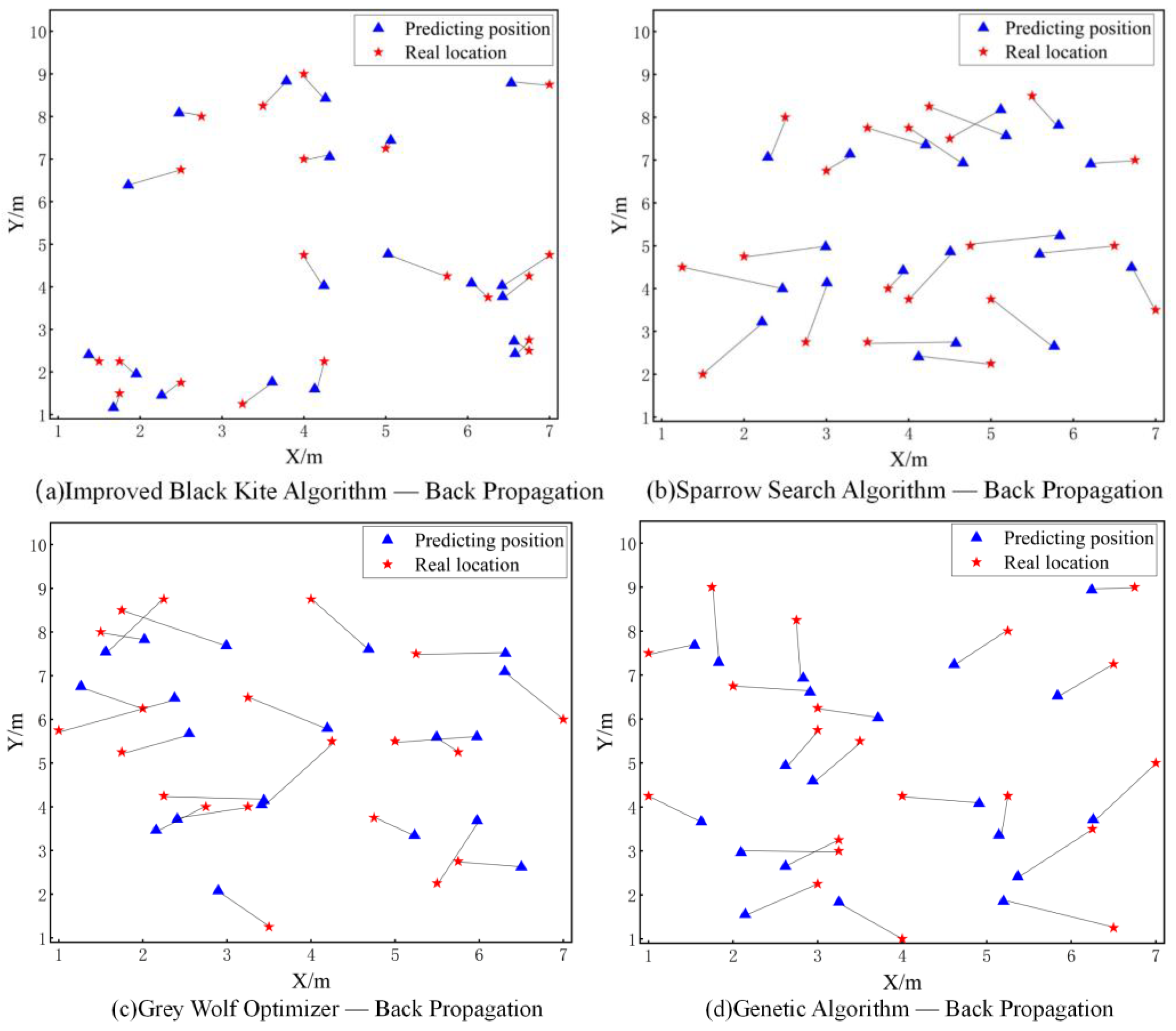
| Algorithm | ME (cm) | SD (cm) | RMSE (cm) |
|---|---|---|---|
| IBKA-BP | 16.34 | 16.32 | 22.87 |
| Sparrow Search Algorithm— Backpropagation | 33.67 | 33.35 | 46.19 |
| Genetic Algorithm—Backpropagation | 39.90 | 40.72 | 56.42 |
| Grey Wolf Optimizer—Backpropagation | 44.76 | 45.56 | 62.67 |
| Algorithm | ME (cm) | SD (cm) | RMSE (cm) |
|---|---|---|---|
| IBKA-BP | 29.71 | 29.13 | 39.86 |
| Sparrow Search Algorithm— Back Propagation | 52.53 | 53.15 | 74.61 |
| Genetic Algorithm—Back Propagation | 61.05 | 61.93 | 85.56 |
| Grey Wolf Optimizer—Back Propagation | 69.75 | 71.27 | 96.37 |
| Algorithm | Strengths | Limitations |
|---|---|---|
| IBKA-BP | 1. Dynamic NLOS base station screening can adapt to multi-obstacle environments (e.g., metal greenhouse frameworks); 2. Kalman filtering can effectively suppress time-varying signal noise caused by temperature/humidity fluctuations | 1. Algorithm performance degrades with sparse Wi-Fi base station deployment; 2. Algorithm lacks multi-band signal fusion capability |
| Reconfigurable intelligent surface-aided localization | 1. Enhancing signal coverage requires pre-deployed reconfigurable intelligent surface (RIS) intelligent reflecting surfaces in single-AP scenarios; 2. Improves NLOS robustness through the VAE-CNN denoising | 1. Expensive RIS hardware; 2. Limited scalability due to dependence on the RIS reflector quantity |
| AI-based filter | 1. Adapts well to low-bandwidth signals (20 MHz) using dynamic AP selection criteria; 2. Adjust filtering thresholds based on known AP locations | 1. Relies on prior AP position knowledge (complex calibration); 2. Neglects dynamic multipath interference effects |
| Localization-oriented digital twinnings | 1. Seven-layer digital twin architecture models physical environments for partial LOS scenarios; 2. Channel frequency polar-coordinate (CFP) polar-coordinate imaging enhances channel fingerprint distinction. | 1. Requires high-precision environmental modeling (high deployment complexity); 2. Dependent on the 6G network infrastructure (currently impractical) |
| Algorithm | Optimization Strategy | Computational Cost |
|---|---|---|
| IBKA-BP | 1. Dynamic base station screening reduces modeling complexity. 2. Min-Max normalization accelerates gradient descent convergence. | Low (minimal hardware requirements) |
| Reconfigurable intelligent surface-aided localization | 1. Semi-tensor product (STP) compresses sparse matrix dimensions. 2. Parallelized VAE-CNN feature extraction. | High (requires generative adversarial network (GAN) training with GPU acceleration) |
| AI-based filter | 1. Progressive accuracy refinement reduces redundant computations. 2. Lightweight AI filter design. | Low (real-time AI-driven parameter filtering) |
| Localization-oriented digital twinnings | 1. Hierarchical digital twin architecture enables phased optimization. 2. SSI-Net attention mechanism minimizes redundant calculations. | Extremely high (real-time environmental modeling + CFP image generation) |
| Algorithm | Advantages | Limitations |
|---|---|---|
| IBKA-BP | 1. Can effectively suppress short-term signal fluctuations by using Kalman filtering and NLOS base station screening; 2. Maintains high positioning accuracy under interference | Lacks the multi-band interference coordination capability |
| Reconfigurable intelligent surface-aided localization | 1. Compensates for the signal loss using the GAN-based data augmentation approach; 2. Dynamic RIS reflector configuration optimizes signal paths | Requires real-time RIS hardware control (high operational costs) |
| AI-based filter | Implements adaptive thresholding to filter anomalous parameters | A lack of a dedicated multipath effect suppression module |
| Localization-oriented digital twinnings | 1. Digital twin-enabled interference prediction improves partial LOS scenarios; 2. Enhances positioning reliability through environmental modeling | Latency in dynamic model updates limits the real-time responsiveness |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wan, L.; Qian, J.; Li, Z.; Mao, Z.; Zhang, X.; Lei, J. An Innovative Indoor Localization Method for Agricultural Robots Based on the NLOS Base Station Identification and IBKA-BP Integration. Agriculture 2025, 15, 901. https://doi.org/10.3390/agriculture15080901
Yang J, Wan L, Qian J, Li Z, Mao Z, Zhang X, Lei J. An Innovative Indoor Localization Method for Agricultural Robots Based on the NLOS Base Station Identification and IBKA-BP Integration. Agriculture. 2025; 15(8):901. https://doi.org/10.3390/agriculture15080901
Chicago/Turabian StyleYang, Jingjing, Lihong Wan, Junbing Qian, Zonglun Li, Zhijie Mao, Xueming Zhang, and Junjie Lei. 2025. "An Innovative Indoor Localization Method for Agricultural Robots Based on the NLOS Base Station Identification and IBKA-BP Integration" Agriculture 15, no. 8: 901. https://doi.org/10.3390/agriculture15080901
APA StyleYang, J., Wan, L., Qian, J., Li, Z., Mao, Z., Zhang, X., & Lei, J. (2025). An Innovative Indoor Localization Method for Agricultural Robots Based on the NLOS Base Station Identification and IBKA-BP Integration. Agriculture, 15(8), 901. https://doi.org/10.3390/agriculture15080901






