Enhancing Agricultural Sustainability Through Intelligent Irrigation Using PVT Energy Applications: Implementing Hybrid Machine and Deep Learning Models
Abstract
:1. Introduction
2. Material and Methods
2.1. Data and Statistical Analysis
2.1.1. Local Weather Information
2.1.2. Evapotranspiration and Water Need Computing
2.1.3. Evaluation Criteria and Statistical Indices
- Mean absolute percentage error (MAPE):
- Root mean square error (RMSE):
- Coefficient of determination (R2):
- Standard deviation (σ):
- Mean bias error (MBE):
2.2. Hybrid ML and DL Models
2.2.1. Machine Learning Models
2.2.2. Integral Feature Selection Method
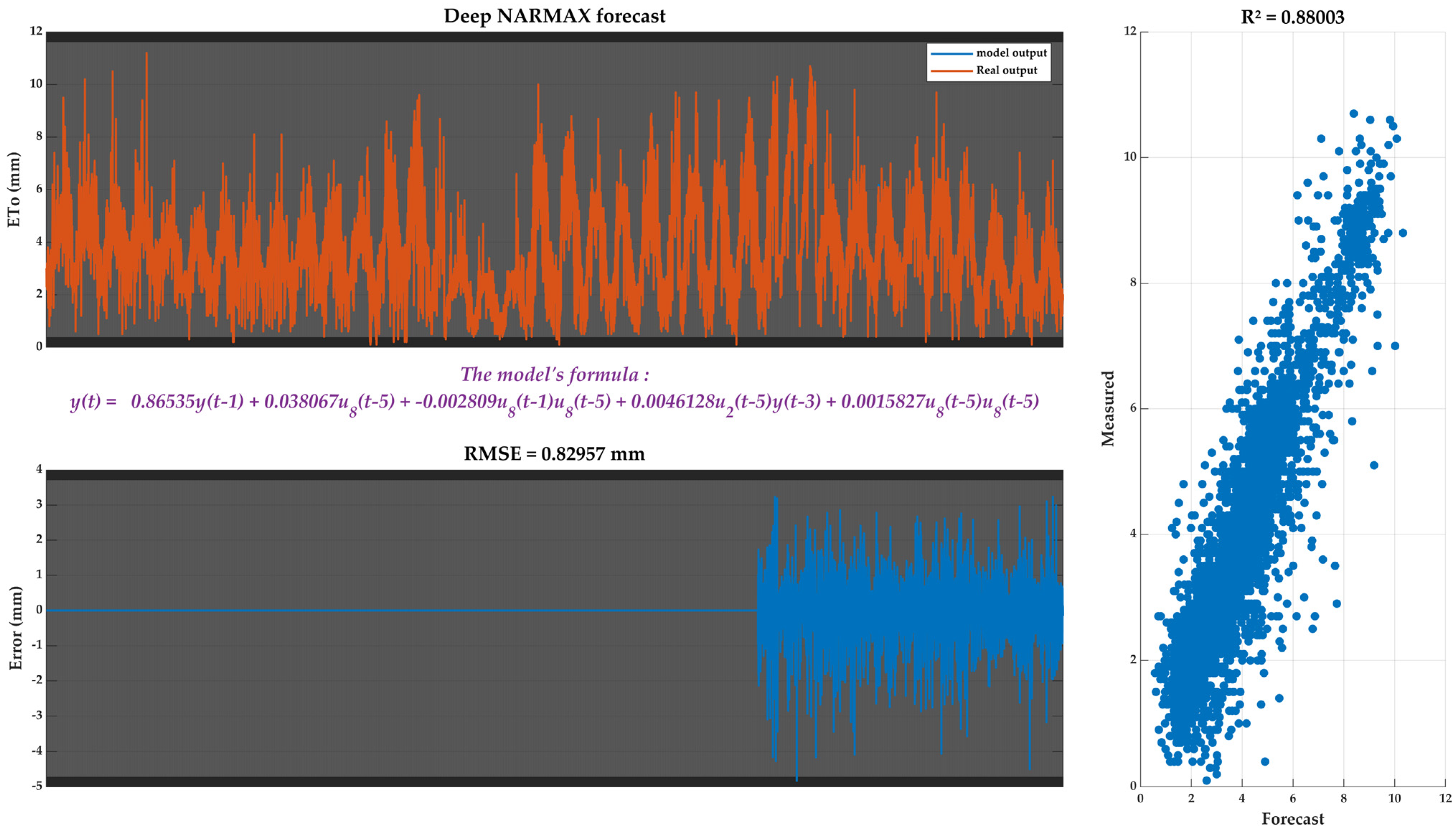
2.2.3. Deep NARMAX Model
2.3. Methodologies
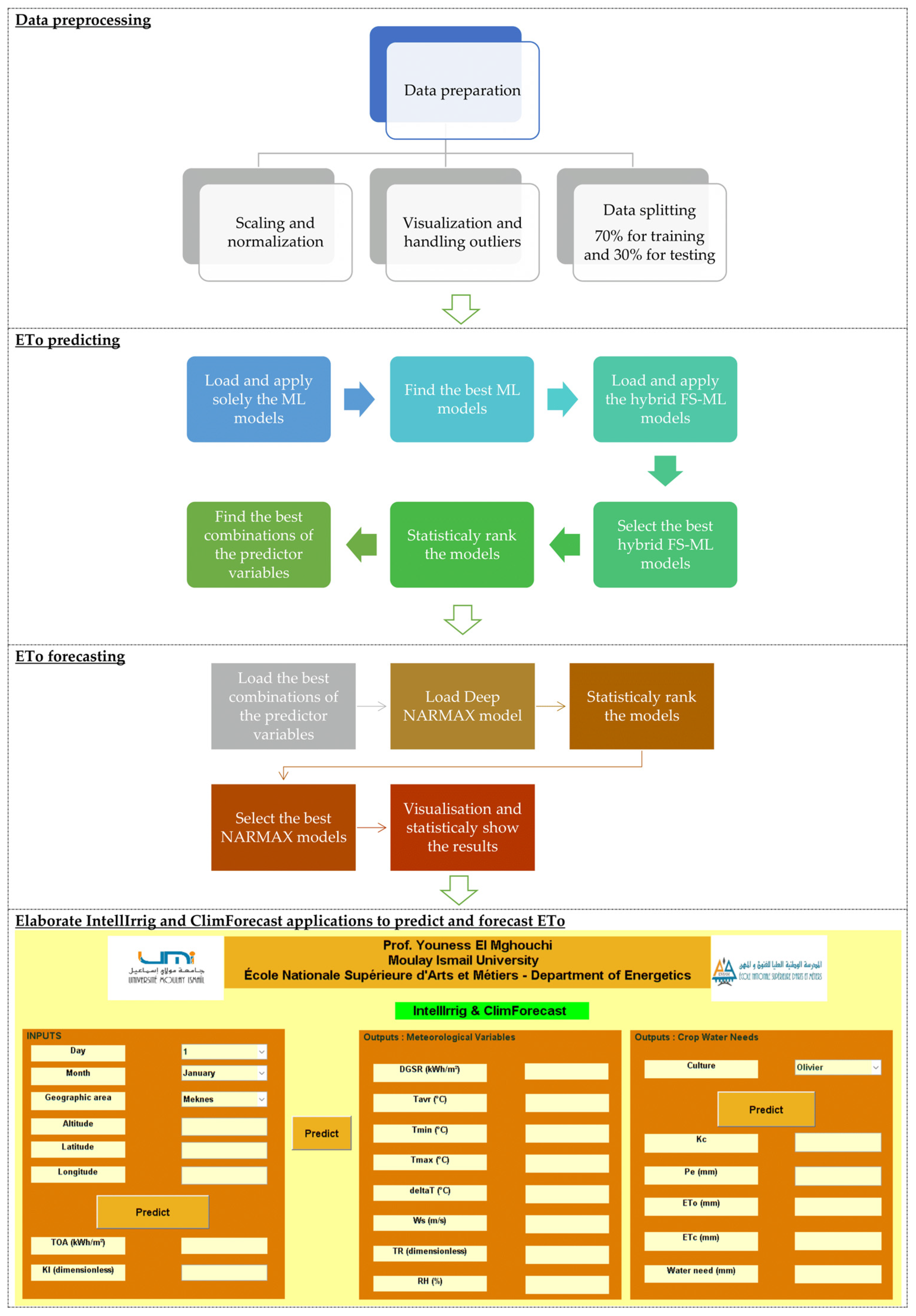
2.3.1. Methodology for Predicting and Forecasting of ETo
- Data Preprocessing: The process begins with loading the complete dataset, which is divided into training (70%) and testing (30%) subsets. Preprocessing steps include normalisation of the data and the application of an autonomous anomaly detection technique to identify and remove anomalous data points, thereby enhancing model reliability and accuracy.
- Machine Learning Model Evaluation: Thirteen machine learning (ML) models are trained and evaluated to determine their effectiveness in predicting and forecasting ETo. This comparative analysis is essential for identifying the most suitable ML model based on prediction performance metrics.
- Hybrid IFS-ML Model Implementation: A hybrid model combining integral feature selection (IFS) with the best-performing ML model is employed to identify the most informative predictor variables. This step involves an exhaustive search across all possible combinations of input features, systematically eliminating irrelevant or redundant combinations and retaining only those that yield the highest predictive accuracy.
- Deep NARMAX Model Integration: The optimal predictor combinations derived from the hybrid IFS-ML model are then fed into a Deep NARMAX model. This integration leverages the strengths of both ML-based feature selection and deep NARMAX’s nonlinear dynamic modelling capability to perform multi-step-ahead forecasting of ETo. Model parameters and forecasting formulas are iteratively refined and adapted during this stage.
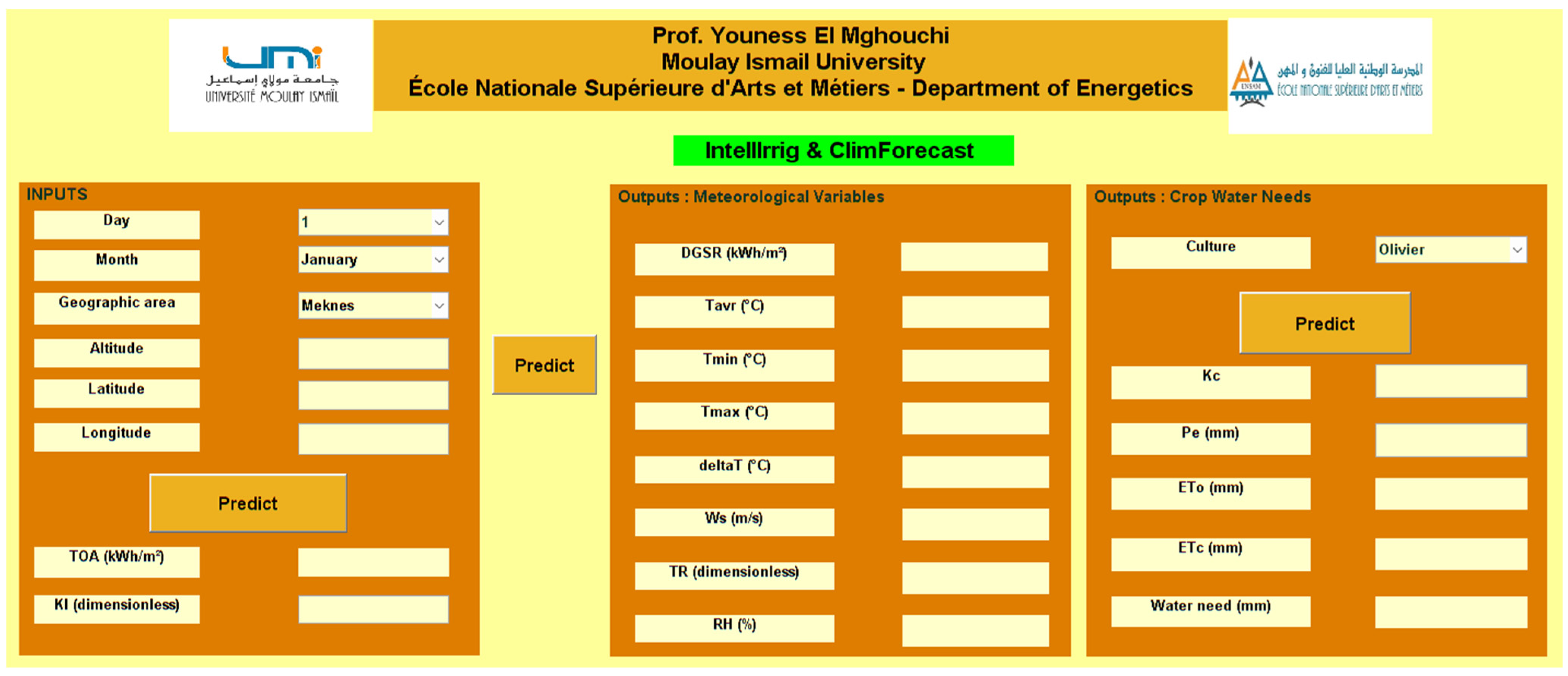
- Application Development and Deployment: Finally, the entire predictive framework is encapsulated into a user-friendly application designed to facilitate efficient and accessible ETo prediction and forecasting. This step involves deploying the trained models into an interactive environment for real-time or batch predictions.
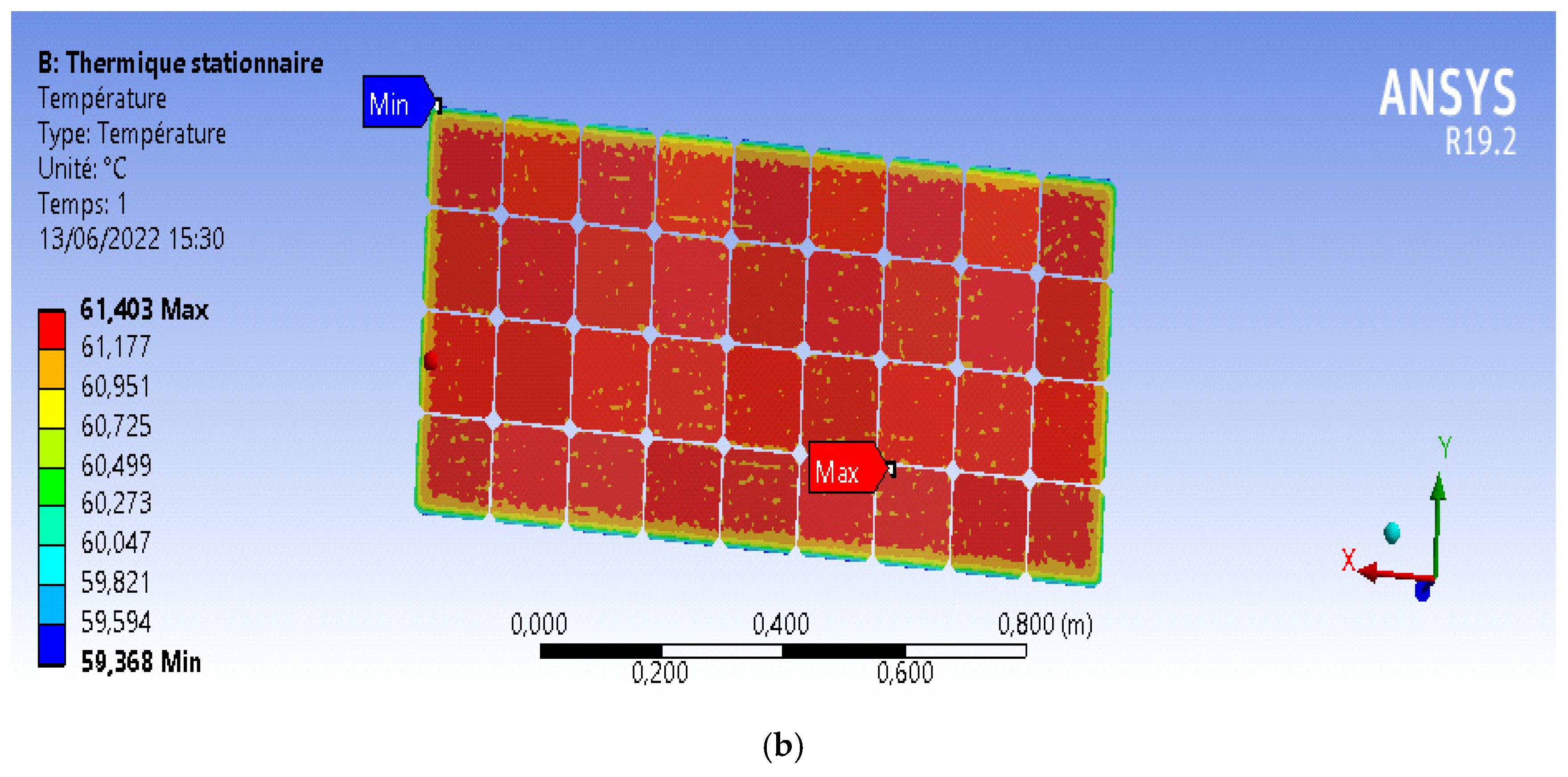
2.3.2. Solar Photovoltaic-Thermal Simulation Using ANSYS Fluent
3. Results and Discussion
3.1. PVT Solutions
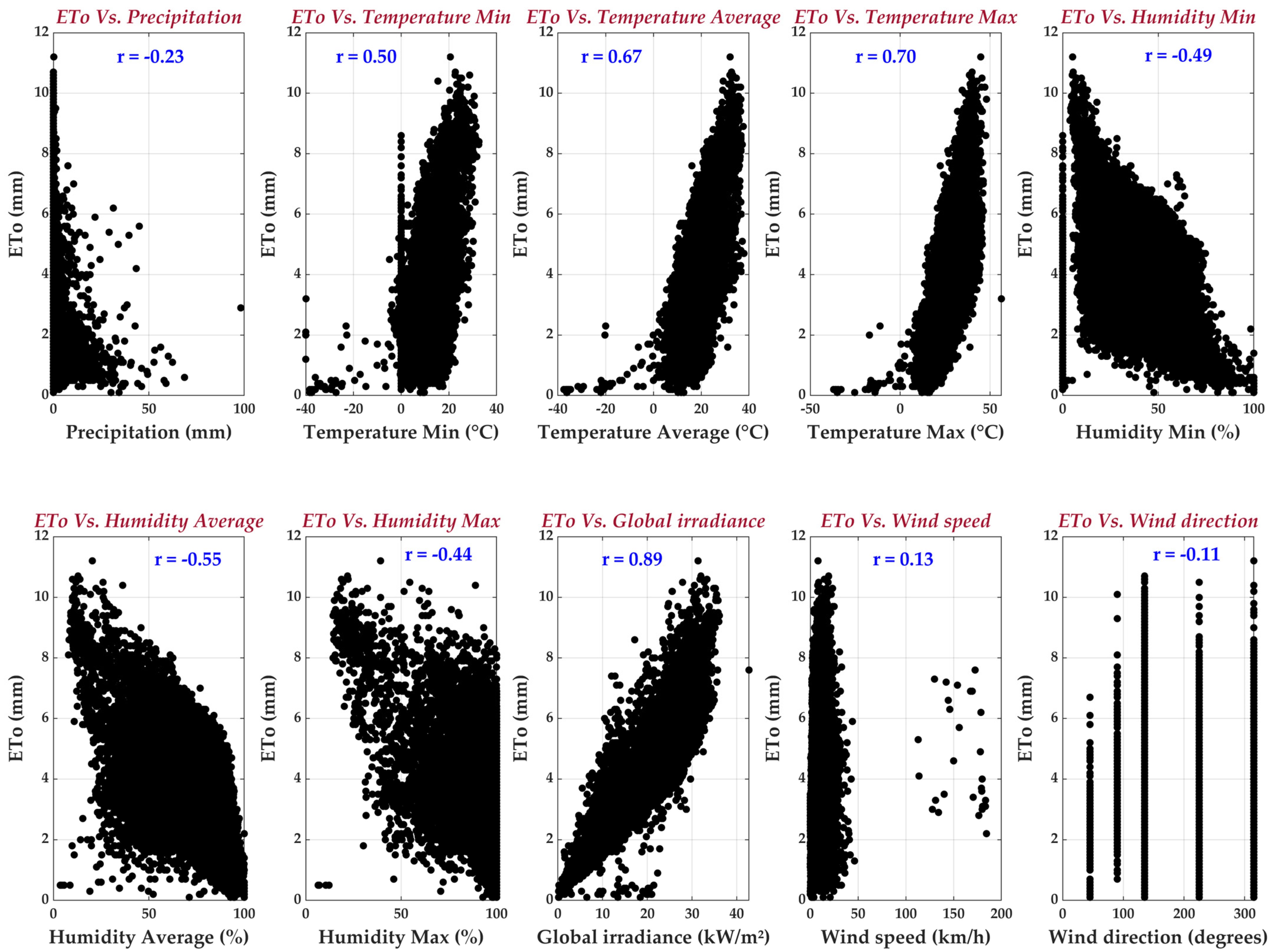
3.2. Correlation Between Variables
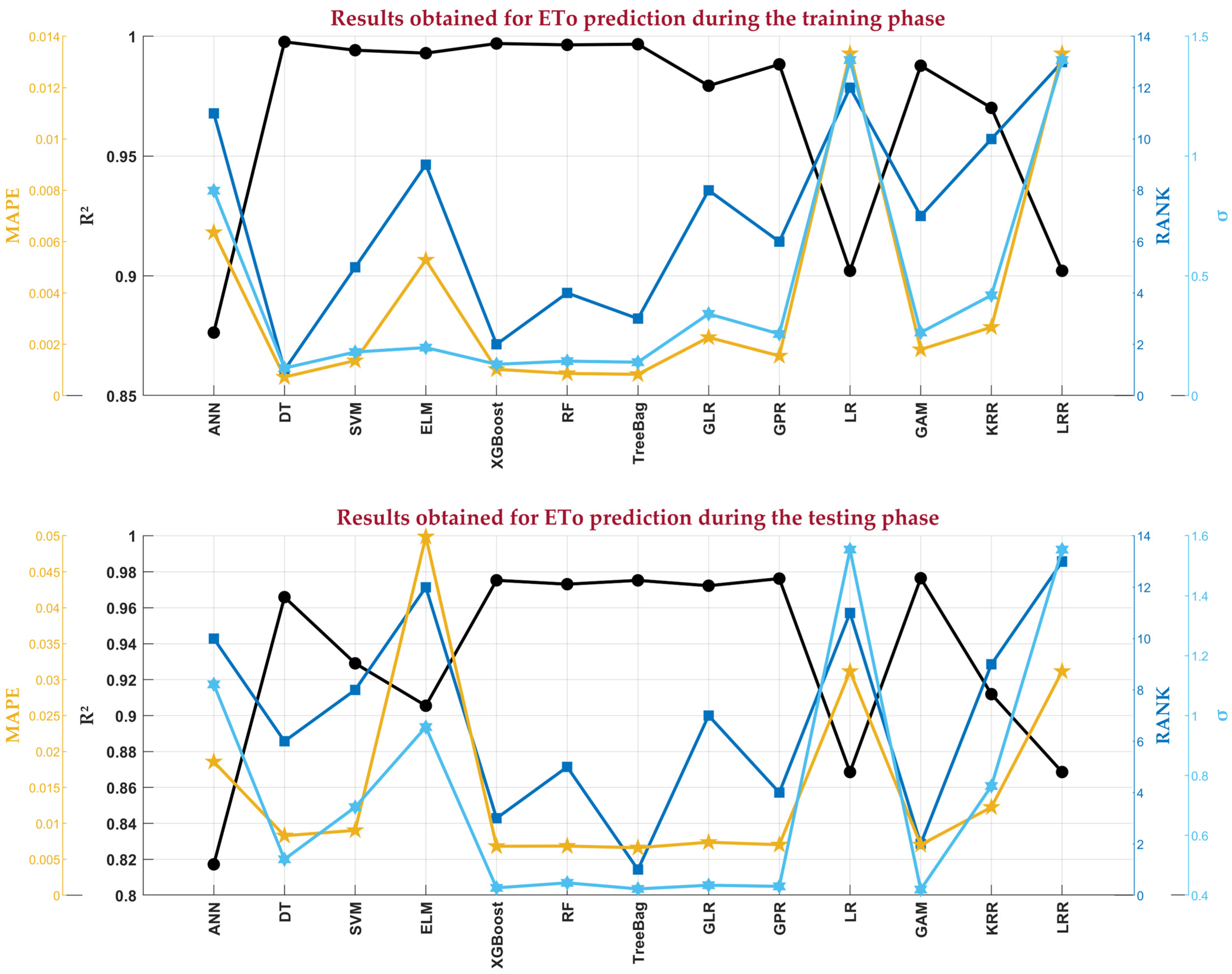
3.3. Best ML Models for Predicting ETo
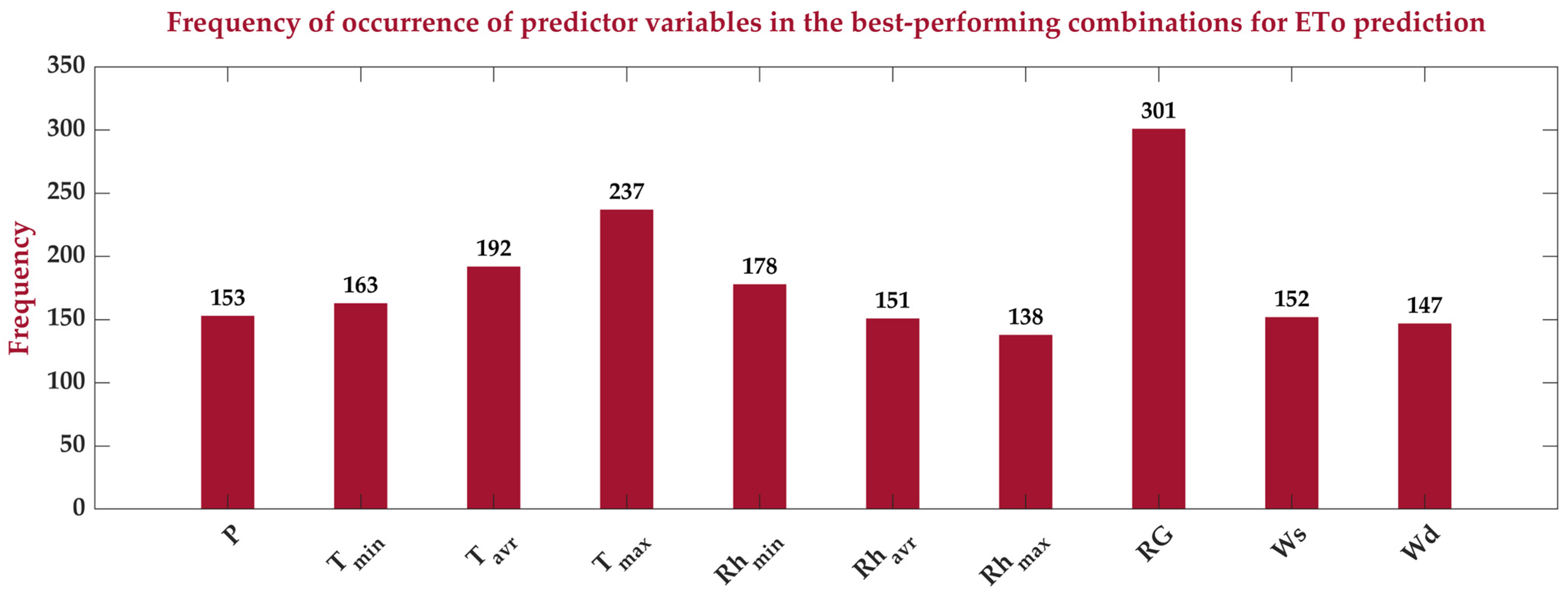
3.4. Best Hybrid IFS-ML Models for Predicting ETo
3.5. Best Models for Forecasting ETo
3.6. Application for Predicting and Forecasting ETo and Water Needs
4. Conclusions
- High Accuracy in ETo Prediction: Among the 13 evaluated models, the hybrid approach integrating feature selection with Deep NARMAX achieved superior forecasting performance, reduced prediction error, and improved reliability in capturing nonlinear temporal dependencies in ETo dynamics.
- Effective Feature Selection for Climate-Driven Forecasting: The integral feature selection method successfully identified the most relevant meteorological variables influencing ETo, enhancing model interpretability and reducing computational complexity without compromising accuracy.
- Potential for Intelligent Irrigation Integration: The proposed predictive model is a foundational component for intelligent irrigation systems. When coupled with real-time sensor data and photovoltaic-thermal (PVT) systems, this model can facilitate dynamic irrigation scheduling, improving water use efficiency in agriculture.
- Implications for Sustainable Agriculture: By incorporating PVT systems into the forecasting and irrigation pipeline, there is potential to utilise renewable energy for both electricity and thermal applications in agriculture. This integration supports sustainable practices by reducing fossil fuel dependence and improving overall system energy efficiency.
- Scalability across Climatic Zones: The framework’s modularity and data-driven nature make it adaptable to diverse agro-climatic regions, allowing for its application in water-scarce and humid environments with appropriate local calibration.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ModelID | a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | MBE | RMSE | MAPE | Sd | R | Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model1 | −1.446 | −0.077 | 0.167 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.049 | 0.499 | 0.003 | 0.497 | 0.959 | 299 |
| Model2 | −1.682 | −0.009 | 0.100 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.035 | 0.492 | 0.002 | 0.490 | 0.960 | 292 |
| Model3 | 0.132 | 0.080 | −0.019 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.418 | 0.002 | 0.418 | 0.971 | 233 |
| Model4 | −0.689 | 0.078 | −0.012 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.017 | 0.439 | 0.002 | 0.439 | 0.968 | 265 |
| Model5 | 0.575 | 0.068 | −0.021 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.380 | 0.002 | 0.380 | 0.976 | 104 |
| Model6 | 0.741 | 0.076 | −0.022 | 0.171 | 0.004 | 0 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.409 | 0.002 | 0.408 | 0.972 | 208 |
| Model7 | 0.750 | 0.069 | −0.022 | 0.165 | −0.001 | 0 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.379 | 0.002 | 0.378 | 0.976 | 115 |
| Model8 | 0.532 | 0.068 | −0.021 | 0.165 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.378 | 0.002 | 0.378 | 0.976 | 83 |
| Model9 | 0.730 | 0.068 | −0.019 | −0.004 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | −0.007 | 0.379 | 0.002 | 0.379 | 0.976 | 100 |
| Model10 | −0.541 | 0.078 | −0.012 | 0.167 | −0.001 | 0 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.436 | 0.002 | 0.435 | 0.969 | 271 |
| Model11 | −0.719 | 0.078 | −0.012 | 0.166 | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.436 | 0.002 | 0.435 | 0.969 | 270 |
| Model12 | 0.884 | 0.071 | −0.007 | −0.018 | 0.169 | 0 | 0 | 0 | 0 | 0 | 0 | −0.004 | 0.394 | 0.002 | 0.394 | 0.974 | 157 |
| Model13 | 0.628 | 0.069 | 0.003 | −0.024 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.379 | 0.002 | 0.378 | 0.976 | 103 |
| Model14 | 0.215 | 0.080 | −0.019 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.417 | 0.002 | 0.417 | 0.971 | 249 |
| Model15 | 0.118 | 0.080 | −0.019 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.417 | 0.002 | 0.417 | 0.971 | 248 |
| Model16 | 1.377 | 0.072 | −0.014 | −0.015 | 0.169 | 0 | 0 | 0 | 0 | 0 | 0 | −0.002 | 0.400 | 0.002 | 0.400 | 0.973 | 173 |
| Model17 | 1.223 | 0.070 | −0.005 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | −0.007 | 0.386 | 0.002 | 0.386 | 0.975 | 132 |
| Model18 | −1.434 | −0.004 | 0.093 | 0.169 | −0.001 | 0 | 0 | 0 | 0 | 0 | 0 | −0.033 | 0.494 | 0.002 | 0.493 | 0.960 | 293 |
| Model19 | −1.742 | −0.014 | 0.104 | 0.170 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0 | −0.039 | 0.490 | 0.002 | 0.489 | 0.960 | 289 |
| Model20 | 0.771 | −0.008 | 0.083 | −0.022 | 0.172 | 0 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.408 | 0.002 | 0.408 | 0.972 | 200 |
| Model21 | 0.797 | 0.028 | 0.043 | −0.023 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.375 | 0.002 | 0.375 | 0.977 | 43 |
| Model22 | −0.176 | 0.056 | 0.026 | −0.016 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.418 | 0.002 | 0.417 | 0.971 | 238 |
| Model23 | −1.639 | −0.017 | 0.105 | 0.169 | −0.001 | 0 | 0 | 0 | 0 | 0 | 0 | −0.039 | 0.486 | 0.002 | 0.484 | 0.961 | 284 |
| Model24 | −1.794 | −0.017 | 0.105 | 0.169 | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | −0.040 | 0.486 | 0.002 | 0.484 | 0.961 | 282 |
| Model25 | 0.702 | −0.011 | 0.084 | −0.022 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.404 | 0.002 | 0.404 | 0.973 | 191 |
| Model26 | 0.699 | 0.008 | 0.062 | −0.022 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.378 | 0.002 | 0.378 | 0.976 | 92 |
| Model27 | −0.299 | 0.020 | 0.059 | −0.015 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.429 | 0.002 | 0.429 | 0.970 | 251 |
| Model28 | −1.418 | −0.077 | 0.167 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.050 | 0.499 | 0.003 | 0.497 | 0.959 | 295 |
| Model29 | −1.476 | −0.078 | 0.168 | 0.171 | 0.003 | 0 | 0 | 0 | 0 | 0 | 0 | −0.051 | 0.499 | 0.003 | 0.497 | 0.959 | 296 |
| Model30 | 0.998 | −0.029 | 0.099 | −0.024 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.382 | 0.002 | 0.382 | 0.976 | 136 |
| Model31 | −0.021 | −0.014 | 0.094 | −0.017 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.417 | 0.002 | 0.417 | 0.971 | 243 |
| Model32 | −1.698 | −0.040 | 0.057 | 0.073 | 0.169 | 0 | 0 | 0 | 0 | 0 | 0 | −0.038 | 0.479 | 0.002 | 0.477 | 0.962 | 279 |
| Model33 | 0.769 | 0.008 | 0.077 | −0.022 | 0.172 | 0 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.409 | 0.002 | 0.409 | 0.972 | 205 |
| Model34 | 0.550 | 0.011 | 0.069 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.377 | 0.002 | 0.377 | 0.976 | 77 |
| Model35 | −0.716 | 0.011 | 0.078 | −0.012 | 0.168 | 0 | 0 | 0 | 0 | 0 | 0 | −0.017 | 0.437 | 0.002 | 0.436 | 0.969 | 266 |
| Model36 | 1.366 | 0.004 | 0.068 | −0.026 | 0.168 | 0 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.393 | 0.002 | 0.393 | 0.974 | 175 |
| Model37 | 0.122 | 0.006 | 0.080 | −0.019 | 0.168 | 0 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.417 | 0.002 | 0.417 | 0.971 | 229 |
| Model38 | −1.717 | 0.007 | −0.011 | 0.102 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | −0.035 | 0.491 | 0.002 | 0.490 | 0.960 | 290 |
| Model39 | −1.773 | 0.008 | −0.016 | 0.105 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | −0.036 | 0.487 | 0.002 | 0.485 | 0.961 | 283 |
| Model40 | −1.456 | 0.002 | −0.077 | 0.167 | 0.172 | 0 | 0 | 0 | 0 | 0 | 0 | −0.049 | 0.499 | 0.003 | 0.497 | 0.959 | 298 |
| Model41 | 0.730 | 0.068 | −0.022 | 0.165 | 0.003 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.378 | 0.002 | 0.378 | 0.976 | 118 |
| Model42 | 0.590 | 0.071 | −0.020 | −0.001 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.018 | 0.377 | 0.002 | 0.377 | 0.976 | 109 |
| Model43 | 0.665 | 0.068 | −0.019 | −0.003 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.378 | 0.002 | 0.378 | 0.976 | 80 |
| Model44 | −0.705 | 0.079 | −0.012 | 0.166 | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | −0.025 | 0.434 | 0.002 | 0.434 | 0.969 | 272 |
| Model45 | 0.579 | 0.076 | −0.007 | −0.015 | 0.169 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.391 | 0.002 | 0.391 | 0.975 | 177 |
| Model46 | 0.792 | 0.071 | −0.007 | −0.017 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.392 | 0.002 | 0.392 | 0.975 | 148 |
| Model47 | 0.306 | 0.075 | 0.002 | −0.021 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.022 | 0.377 | 0.002 | 0.376 | 0.976 | 125 |
| Model48 | 0.579 | 0.069 | 0.003 | −0.024 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.377 | 0.002 | 0.377 | 0.976 | 88 |
| Model49 | 0.552 | 0.070 | 0.003 | −0.024 | 0 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.378 | 0.002 | 0.378 | 0.976 | 98 |
| Model50 | 0.152 | 0.080 | −0.019 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.417 | 0.002 | 0.416 | 0.971 | 254 |
| Model51 | 1.160 | 0.075 | −0.015 | −0.012 | 0.170 | 0 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.398 | 0.002 | 0.398 | 0.974 | 178 |
| Model52 | 1.313 | 0.072 | −0.015 | −0.014 | 0.169 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.005 | 0.399 | 0.002 | 0.399 | 0.974 | 170 |
| Model53 | 0.838 | 0.075 | −0.007 | −0.016 | 0.169 | 0 | 0 | 0 | 0 | 0 | 0 | −0.018 | 0.385 | 0.002 | 0.385 | 0.975 | 167 |
| Model54 | 1.198 | 0.069 | −0.005 | −0.021 | 0.166 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.386 | 0.002 | 0.386 | 0.975 | 134 |
| Model55 | −1.571 | −0.012 | 0.101 | 0.169 | 0.004 | 0 | 0 | 0 | 0 | 0 | 0 | −0.036 | 0.492 | 0.002 | 0.491 | 0.960 | 291 |
| Model56 | 0.253 | −0.014 | 0.095 | −0.018 | 0.172 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.022 | 0.406 | 0.002 | 0.406 | 0.973 | 257 |
| Model57 | 0.682 | −0.012 | 0.086 | −0.022 | 0.171 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.407 | 0.002 | 0.407 | 0.973 | 207 |
| Model58 | 0.551 | 0.019 | 0.057 | −0.020 | 0.165 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.020 | 0.373 | 0.002 | 0.373 | 0.977 | 47 |
| Model59 | 0.732 | 0.025 | 0.046 | −0.022 | 0.165 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.374 | 0.002 | 0.374 | 0.977 | 32 |
| Model60 | 0.671 | 0.027 | 0.045 | −0.023 | 0.001 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.374 | 0.002 | 0.374 | 0.977 | 34 |
| Model61 | −0.097 | 0.053 | 0.029 | −0.016 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.416 | 0.002 | 0.416 | 0.971 | 253 |
| Model62 | −0.238 | 0.051 | 0.030 | −0.016 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.416 | 0.002 | 0.416 | 0.971 | 247 |
| Model63 | 1.014 | 0.031 | 0.042 | −0.010 | −0.016 | 0.169 | 0 | 0 | 0 | 0 | 0 | −0.003 | 0.390 | 0.002 | 0.390 | 0.975 | 140 |
| Model64 | 0.797 | 0.028 | 0.043 | 0 | −0.023 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.375 | 0.002 | 0.375 | 0.977 | 45 |
| Model65 | −1.736 | −0.018 | 0.106 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0 | −0.041 | 0.485 | 0.002 | 0.483 | 0.961 | 281 |
| Model66 | 0.623 | −0.013 | 0.086 | −0.022 | 0.170 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.403 | 0.002 | 0.402 | 0.973 | 199 |
| Model67 | 0.681 | 0.004 | 0.067 | −0.021 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.377 | 0.002 | 0.377 | 0.976 | 101 |
| Model68 | 0.645 | 0.006 | 0.063 | −0.022 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.377 | 0.002 | 0.377 | 0.976 | 78 |
| Model69 | 0.701 | 0.007 | 0.063 | −0.021 | −0.001 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.378 | 0.002 | 0.378 | 0.976 | 87 |
| Model70 | −0.236 | 0.018 | 0.062 | −0.015 | 0.167 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.427 | 0.002 | 0.427 | 0.970 | 264 |
| Model71 | −0.367 | 0.018 | 0.061 | −0.015 | 0.166 | 0.006 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.427 | 0.002 | 0.426 | 0.970 | 261 |
| Model72 | 0.979 | 0.007 | 0.064 | −0.008 | −0.018 | 0.169 | 0 | 0 | 0 | 0 | 0 | −0.002 | 0.394 | 0.002 | 0.394 | 0.974 | 155 |
| Model73 | 0.630 | 0.004 | 0.066 | 0.002 | −0.023 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.378 | 0.002 | 0.378 | 0.976 | 94 |
| Model74 | −1.473 | −0.078 | 0.167 | 0.171 | 0.003 | 0 | 0 | 0 | 0 | 0 | 0 | −0.051 | 0.500 | 0.003 | 0.497 | 0.959 | 300 |
| Model75 | 0.046 | −0.015 | 0.096 | −0.017 | 0.166 | 0 | 0 | 0 | 0 | 0 | 0 | −0.018 | 0.416 | 0.002 | 0.416 | 0.971 | 255 |
| Model76 | −0.048 | −0.015 | 0.095 | −0.017 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.018 | 0.416 | 0.002 | 0.416 | 0.971 | 244 |
| Model77 | 1.181 | −0.022 | 0.095 | −0.012 | −0.015 | 0.169 | 0 | 0 | 0 | 0 | 0 | −0.006 | 0.396 | 0.002 | 0.396 | 0.974 | 161 |
| Model78 | 0.998 | −0.024 | 0.095 | −0.002 | −0.022 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.381 | 0.002 | 0.381 | 0.976 | 119 |
| Model79 | −1.657 | −0.040 | 0.054 | 0.077 | 0.169 | 0 | 0 | 0 | 0 | 0 | 0 | −0.043 | 0.477 | 0.002 | 0.475 | 0.962 | 274 |
| Model80 | −1.759 | −0.040 | 0.053 | 0.077 | 0.168 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.042 | 0.478 | 0.002 | 0.476 | 0.962 | 275 |
| Model81 | 0.546 | −0.029 | 0.040 | 0.065 | −0.021 | 0.170 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.400 | 0.002 | 0.400 | 0.973 | 196 |
| Model82 | 0.725 | −0.014 | 0.050 | 0.035 | −0.022 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.373 | 0.002 | 0.373 | 0.977 | 19 |
| Model83 | −0.221 | −0.008 | 0.067 | 0.023 | −0.016 | 0.166 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.417 | 0.002 | 0.417 | 0.971 | 240 |
| Model84 | 0.783 | 0.010 | 0.069 | −0.022 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.377 | 0.002 | 0.377 | 0.976 | 105 |
| Model85 | 0.492 | 0.009 | 0.069 | −0.021 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.376 | 0.002 | 0.376 | 0.977 | 53 |
| Model86 | 0.694 | 0.010 | 0.069 | −0.019 | −0.003 | 0.168 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.377 | 0.002 | 0.377 | 0.976 | 71 |
| Model87 | −0.547 | 0.011 | 0.078 | −0.012 | 0.167 | −0.001 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.434 | 0.002 | 0.433 | 0.969 | 269 |
| Model88 | −0.741 | 0.010 | 0.078 | −0.012 | 0.167 | 0.006 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.434 | 0.002 | 0.433 | 0.969 | 268 |
| Model89 | 0.862 | 0.010 | 0.071 | −0.007 | −0.018 | 0.170 | 0 | 0 | 0 | 0 | 0 | −0.004 | 0.392 | 0.002 | 0.392 | 0.974 | 152 |
| Model90 | 0.599 | 0.010 | 0.069 | 0.003 | −0.024 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.377 | 0.002 | 0.376 | 0.977 | 68 |
| Model91 | 0.148 | 0.007 | 0.081 | −0.019 | 0.168 | 0 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.416 | 0.002 | 0.416 | 0.971 | 250 |
| Model92 | 0.110 | 0.006 | 0.080 | −0.019 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.416 | 0.002 | 0.416 | 0.971 | 236 |
| Model93 | 1.366 | 0.006 | 0.072 | −0.015 | −0.015 | 0.170 | 0 | 0 | 0 | 0 | 0 | −0.003 | 0.400 | 0.002 | 0.400 | 0.973 | 171 |
| Model94 | 1.201 | 0.006 | 0.070 | −0.005 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.385 | 0.002 | 0.385 | 0.975 | 123 |
| Model95 | −1.639 | 0.006 | −0.013 | 0.105 | 0.171 | 0 | 0 | 0 | 0 | 0 | 0 | −0.038 | 0.490 | 0.002 | 0.489 | 0.960 | 287 |
| Model96 | −1.771 | 0.006 | −0.015 | 0.106 | 0.170 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.039 | 0.490 | 0.002 | 0.489 | 0.960 | 285 |
| Model97 | 0.722 | 0.008 | −0.010 | 0.085 | −0.022 | 0.172 | 0 | 0 | 0 | 0 | 0 | −0.010 | 0.407 | 0.002 | 0.407 | 0.972 | 201 |
| Model98 | 0.759 | 0.009 | 0.026 | 0.045 | −0.023 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.009 | 0.374 | 0.002 | 0.374 | 0.977 | 24 |
| Model99 | −0.213 | 0.008 | 0.054 | 0.028 | −0.016 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.013 | 0.416 | 0.002 | 0.416 | 0.971 | 227 |
| Model100 | −1.830 | 0.007 | −0.018 | 0.106 | 0.170 | 0.006 | 0 | 0 | 0 | 0 | 0 | −0.040 | 0.485 | 0.002 | 0.483 | 0.961 | 280 |
| Model101 | 0.660 | 0.010 | −0.013 | 0.086 | −0.022 | 0.172 | 0 | 0 | 0 | 0 | 0 | −0.011 | 0.403 | 0.002 | 0.403 | 0.973 | 193 |
| Model102 | 0.674 | 0.010 | 0.007 | 0.063 | −0.022 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.008 | 0.377 | 0.002 | 0.377 | 0.976 | 62 |
| Model103 | −0.342 | 0.009 | 0.019 | 0.060 | −0.015 | 0.168 | 0 | 0 | 0 | 0 | 0 | −0.012 | 0.427 | 0.002 | 0.427 | 0.970 | 252 |
| Model104 | −1.424 | 0.002 | −0.077 | 0.167 | 0.172 | 0 | 0 | 0 | 0 | 0 | 0 | −0.050 | 0.500 | 0.003 | 0.497 | 0.959 | 301 |
| Model105 | −1.482 | 0.001 | −0.078 | 0.168 | 0.171 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.052 | 0.499 | 0.003 | 0.497 | 0.959 | 297 |
| Model106 | 0.993 | 0.006 | −0.029 | 0.099 | −0.024 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.014 | 0.381 | 0.002 | 0.381 | 0.976 | 137 |
| Model107 | −0.040 | 0.007 | −0.015 | 0.095 | −0.017 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.015 | 0.416 | 0.002 | 0.416 | 0.971 | 226 |
| Model108 | −1.737 | 0.007 | −0.040 | 0.056 | 0.075 | 0.170 | 0 | 0 | 0 | 0 | 0 | −0.039 | 0.478 | 0.002 | 0.477 | 0.962 | 276 |
| Model109 | 0.196 | 0.078 | −0.007 | −0.012 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.392 | 0.002 | 0.392 | 0.975 | 190 |
| Model110 | 0.642 | 0.071 | 0.003 | −0.023 | 0.166 | 0.003 | −0.001 | 0 | 0 | 0 | 0 | −0.019 | 0.377 | 0.002 | 0.376 | 0.976 | 108 |
| Model111 | 0.534 | 0.072 | 0.003 | −0.025 | 0.002 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | −0.020 | 0.377 | 0.002 | 0.376 | 0.976 | 113 |
| Model112 | 0.579 | 0.069 | 0.003 | −0.023 | −0.001 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | −0.014 | 0.377 | 0.002 | 0.377 | 0.976 | 82 |
| Model113 | 0.379 | 0.080 | −0.015 | −0.006 | 0.170 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.020 | 0.402 | 0.002 | 0.402 | 0.973 | 215 |
| Model114 | 0.777 | 0.075 | −0.007 | −0.016 | 0.169 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.019 | 0.385 | 0.002 | 0.385 | 0.975 | 168 |
| Model115 | 0.666 | −0.002 | 0.077 | −0.021 | 0.176 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.020 | 0.412 | 0.002 | 0.412 | 0.972 | 259 |
| Model116 | 0.525 | 0.017 | 0.058 | −0.020 | 0.166 | 0.003 | −0.001 | 0 | 0 | 0 | 0 | −0.020 | 0.373 | 0.002 | 0.373 | 0.977 | 48 |
| Model117 | 0.167 | 0.022 | 0.056 | −0.022 | 0.005 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | −0.024 | 0.377 | 0.002 | 0.376 | 0.977 | 111 |
| Model118 | 0.677 | 0.024 | 0.047 | −0.022 | 0 | 0.165 | 0.004 | 0 | 0 | 0 | 0 | −0.013 | 0.374 | 0.002 | 0.374 | 0.977 | 27 |
| Model119 | −0.128 | 0.052 | 0.029 | −0.017 | 0.165 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.017 | 0.416 | 0.002 | 0.415 | 0.971 | 237 |
| Model120 | 1.007 | 0.025 | 0.050 | −0.009 | −0.016 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | −0.010 | 0.389 | 0.002 | 0.389 | 0.975 | 142 |
| Model121 | 0.866 | 0.027 | 0.047 | −0.010 | −0.016 | 0.168 | 0.005 | 0 | 0 | 0 | 0 | −0.008 | 0.388 | 0.002 | 0.388 | 0.975 | 126 |
| Model122 | 1.030 | 0.023 | 0.047 | 0.001 | −0.024 | 0.165 | −0.001 | 0 | 0 | 0 | 0 | −0.013 | 0.377 | 0.002 | 0.377 | 0.976 | 99 |
| Model123 | 0.667 | 0.023 | 0.048 | 0 | −0.022 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.013 | 0.374 | 0.002 | 0.374 | 0.977 | 28 |
| Model124 | 0.853 | 0.029 | 0.042 | 0 | −0.023 | 0 | 0.166 | 0 | 0 | 0 | 0 | −0.008 | 0.376 | 0.002 | 0.376 | 0.977 | 54 |
| Model125 | 0.427 | −0.015 | 0.091 | −0.020 | 0.170 | 0.004 | −0.001 | 0 | 0 | 0 | 0 | −0.022 | 0.401 | 0.002 | 0.401 | 0.973 | 235 |
| Model126 | 0.816 | 0.005 | 0.064 | −0.022 | 0.165 | 0.003 | −0.001 | 0 | 0 | 0 | 0 | −0.015 | 0.378 | 0.002 | 0.378 | 0.976 | 110 |
| Model127 | 0.312 | 0.003 | 0.071 | −0.020 | 0.002 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | −0.020 | 0.378 | 0.002 | 0.378 | 0.976 | 120 |
| Model128 | 0.625 | 0.005 | 0.065 | −0.021 | −0.001 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | −0.012 | 0.377 | 0.002 | 0.377 | 0.976 | 67 |
| Model129 | −0.220 | 0.019 | 0.059 | −0.016 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.426 | 0.002 | 0.425 | 0.970 | 262 |
| Model130 | 1.111 | 0.004 | 0.068 | −0.008 | −0.018 | 0.169 | −0.001 | 0 | 0 | 0 | 0 | −0.009 | 0.394 | 0.002 | 0.394 | 0.974 | 163 |
| Model131 | 0.365 | 0.001 | 0.074 | −0.007 | −0.014 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | −0.015 | 0.391 | 0.002 | 0.390 | 0.975 | 165 |
| Model132 | 0.208 | −0.005 | 0.080 | 0.004 | −0.021 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | −0.025 | 0.378 | 0.002 | 0.378 | 0.976 | 150 |
| Model133 | 0.543 | 0.002 | 0.068 | 0.002 | −0.023 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | −0.014 | 0.377 | 0.002 | 0.376 | 0.976 | 76 |
| Model134 | 0.634 | 0.004 | 0.066 | 0.002 | −0.024 | 0 | 0.166 | 0 | 0 | 0 | 0 | −0.009 | 0.378 | 0.002 | 0.378 | 0.976 | 89 |
| Model135 | 0.700 | −0.039 | 0.112 | −0.021 | 0.167 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.026 | 0.381 | 0.002 | 0.380 | 0.976 | 179 |
| Model136 | −0.001 | −0.015 | 0.095 | −0.017 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.019 | 0.416 | 0.002 | 0.415 | 0.971 | 245 |
| Model137 | 0.193 | −0.036 | 0.118 | −0.011 | −0.008 | 0.170 | 0 | 0 | 0 | 0 | 0 | −0.025 | 0.399 | 0.002 | 0.398 | 0.974 | 214 |
| Model138 | 0.969 | −0.026 | 0.100 | −0.012 | −0.014 | 0.168 | 0.004 | 0 | 0 | 0 | 0 | −0.012 | 0.393 | 0.002 | 0.393 | 0.974 | 166 |
| Model139 | 0.795 | −0.034 | 0.109 | −0.002 | −0.020 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | −0.022 | 0.380 | 0.002 | 0.379 | 0.976 | 159 |
| Model140 | 0.967 | −0.025 | 0.095 | −0.002 | −0.022 | 0.166 | 0.003 | 0 | 0 | 0 | 0 | −0.014 | 0.381 | 0.002 | 0.380 | 0.976 | 133 |
| Model141 | −1.187 | −0.040 | 0.060 | 0.062 | 0.165 | 0.001 | −0.001 | 0 | 0 | 0 | 0 | −0.033 | 0.494 | 0.002 | 0.493 | 0.961 | 286 |
| Model142 | 0.307 | −0.031 | 0.038 | 0.073 | −0.018 | 0.170 | −0.001 | 0 | 0 | 0 | 0 | −0.025 | 0.399 | 0.002 | 0.398 | 0.974 | 232 |
| Model143 | 0.604 | −0.029 | 0.037 | 0.067 | −0.021 | 0.170 | 0.004 | 0 | 0 | 0 | 0 | −0.016 | 0.400 | 0.002 | 0.400 | 0.973 | 202 |
| Model144 | 0.105 | −0.021 | 0.047 | 0.053 | −0.017 | 0.167 | −0.001 | 0 | 0 | 0 | 0 | −0.026 | 0.375 | 0.002 | 0.374 | 0.977 | 91 |
| Model145 | 0.515 | −0.015 | 0.047 | 0.041 | −0.021 | 0.165 | 0.004 | 0 | 0 | 0 | 0 | −0.016 | 0.372 | 0.002 | 0.371 | 0.977 | 10 |
| Model146 | 0.700 | −0.014 | 0.050 | 0.036 | −0.021 | 0 | 0.166 | 0 | 0 | 0 | 0 | −0.011 | 0.373 | 0.002 | 0.373 | 0.977 | 12 |
| Model147 | −0.027 | −0.006 | 0.066 | 0.021 | −0.017 | 0.165 | −0.001 | 0 | 0 | 0 | 0 | −0.016 | 0.416 | 0.002 | 0.416 | 0.971 | 228 |
| Model148 | −0.297 | −0.008 | 0.063 | 0.027 | −0.016 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | −0.018 | 0.416 | 0.002 | 0.416 | 0.971 | 242 |
| Model149 | 0.441 | −0.017 | 0.048 | 0.046 | −0.008 | −0.013 | 0.169 | 0 | 0 | 0 | 0 | −0.013 | 0.387 | 0.002 | 0.387 | 0.975 | 143 |
| Model150 | 0.600 | −0.017 | 0.049 | 0.040 | 0.002 | −0.022 | 0.166 | 0 | 0 | 0 | 0 | −0.013 | 0.373 | 0.002 | 0.372 | 0.977 | 15 |
| Model151 | 0.496 | 0.007 | 0.080 | −0.020 | 0.172 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.021 | 0.407 | 0.002 | 0.406 | 0.973 | 256 |
| Model152 | 0.279 | 0.010 | 0.074 | −0.019 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.022 | 0.375 | 0.002 | 0.375 | 0.977 | 81 |
| Model153 | 0.633 | 0.009 | 0.069 | −0.020 | −0.003 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | −0.012 | 0.376 | 0.002 | 0.376 | 0.977 | 50 |
| Model154 | −0.401 | 0.009 | 0.074 | −0.014 | 0.166 | 0.004 | −0.001 | 0 | 0 | 0 | 0 | −0.019 | 0.434 | 0.002 | 0.433 | 0.969 | 267 |
| Model155 | 0.435 | 0.011 | 0.077 | −0.007 | −0.014 | 0.170 | −0.001 | 0 | 0 | 0 | 0 | −0.017 | 0.390 | 0.002 | 0.389 | 0.975 | 181 |
| Model156 | 0.667 | 0.010 | 0.072 | −0.007 | −0.017 | 0.170 | 0.005 | 0 | 0 | 0 | 0 | −0.010 | 0.389 | 0.002 | 0.389 | 0.975 | 141 |
| Model157 | 0.819 | 0.009 | 0.069 | 0.003 | −0.025 | 0.166 | −0.001 | 0 | 0 | 0 | 0 | −0.016 | 0.377 | 0.002 | 0.377 | 0.976 | 112 |
| Model158 | 0.526 | 0.009 | 0.070 | 0.002 | −0.024 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | −0.014 | 0.375 | 0.002 | 0.375 | 0.977 | 55 |
| Model159 | 0.487 | 0.010 | 0.070 | 0.003 | −0.024 | 0 | 0.167 | 0 | 0 | 0 | 0 | −0.013 | 0.376 | 0.002 | 0.376 | 0.977 | 65 |
| Model160 | 0.145 | 0.006 | 0.080 | −0.019 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.016 | 0.416 | 0.002 | 0.415 | 0.971 | 239 |
| Model161 | 1.417 | 0.005 | 0.071 | −0.015 | −0.015 | 0.169 | 0.003 | 0 | 0 | 0 | 0 | −0.003 | 0.400 | 0.002 | 0.400 | 0.973 | 174 |
| Model162 | 0.358 | 0.007 | 0.081 | −0.009 | −0.011 | 0.172 | 0 | 0 | 0 | 0 | 0 | −0.024 | 0.392 | 0.002 | 0.391 | 0.975 | 204 |
| Model163 | 1.102 | 0.005 | 0.071 | −0.006 | −0.020 | 0.167 | 0.003 | 0 | 0 | 0 | 0 | −0.012 | 0.384 | 0.002 | 0.384 | 0.975 | 130 |
| Model164 | −1.677 | 0.005 | −0.014 | 0.104 | 0.170 | 0.004 | 0 | 0 | 0 | 0 | 0 | −0.039 | 0.490 | 0.002 | 0.489 | 0.960 | 288 |
| Model165 | 0.674 | 0.008 | −0.016 | 0.092 | −0.021 | 0.172 | −0.001 | 0 | 0 | 0 | 0 | −0.016 | 0.406 | 0.002 | 0.406 | 0.973 | 213 |
| Model166 | 0.634 | 0.008 | −0.014 | 0.089 | −0.022 | 0.172 | 0.004 | 0 | 0 | 0 | 0 | −0.013 | 0.406 | 0.002 | 0.406 | 0.973 | 206 |
| Model167 | 0.374 | 0.010 | 0.014 | 0.063 | −0.019 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | −0.021 | 0.373 | 0.002 | 0.372 | 0.977 | 49 |
| Model168 | 0.698 | 0.008 | 0.023 | 0.048 | −0.023 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.012 | 0.373 | 0.002 | 0.373 | 0.977 | 14 |
| Model169 | 0.528 | 0.009 | 0.025 | 0.049 | −0.023 | 0.002 | 0.167 | 0 | 0 | 0 | 0 | −0.013 | 0.373 | 0.002 | 0.373 | 0.977 | 11 |
| Model170 | −0.079 | 0.008 | 0.053 | 0.028 | −0.017 | 0.167 | −0.001 | 0 | 0 | 0 | 0 | −0.016 | 0.415 | 0.002 | 0.415 | 0.972 | 216 |
| Model171 | −0.243 | 0.007 | 0.051 | 0.030 | −0.016 | 0.166 | 0.005 | 0 | 0 | 0 | 0 | −0.016 | 0.415 | 0.002 | 0.415 | 0.972 | 220 |
| Model172 | 0.794 | 0.009 | 0.027 | 0.048 | −0.010 | −0.015 | 0.170 | 0 | 0 | 0 | 0 | −0.007 | 0.387 | 0.002 | 0.387 | 0.975 | 124 |
| Model173 | 0.561 | 0.009 | 0.022 | 0.052 | 0 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | −0.012 | 0.373 | 0.002 | 0.372 | 0.977 | 16 |
| Model174 | 0.862 | 0.009 | −0.015 | 0.088 | −0.023 | 0.171 | −0.001 | 0 | 0 | 0 | 0 | −0.017 | 0.405 | 0.002 | 0.405 | 0.973 | 217 |
| Model175 | 0.517 | 0.009 | −0.014 | 0.088 | −0.021 | 0.171 | 0.005 | 0 | 0 | 0 | 0 | −0.016 | 0.401 | 0.002 | 0.400 | 0.973 | 203 |
| Model176 | 0.314 | 0.011 | 0 | 0.075 | −0.019 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | −0.021 | 0.375 | 0.002 | 0.375 | 0.977 | 90 |
| Model177 | 0.573 | 0.009 | 0.005 | 0.065 | −0.022 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.013 | 0.375 | 0.002 | 0.375 | 0.977 | 44 |
| Model178 | 0.648 | 0.010 | 0.006 | 0.065 | −0.021 | −0.001 | 0.168 | 0 | 0 | 0 | 0 | −0.009 | 0.376 | 0.002 | 0.376 | 0.977 | 58 |
| Model179 | −0.248 | 0.009 | 0.018 | 0.062 | −0.015 | 0.168 | −0.001 | 0 | 0 | 0 | 0 | −0.016 | 0.425 | 0.002 | 0.425 | 0.970 | 263 |
| Model180 | −0.396 | 0.008 | 0.017 | 0.062 | −0.015 | 0.167 | 0.005 | 0 | 0 | 0 | 0 | −0.016 | 0.425 | 0.002 | 0.425 | 0.970 | 260 |
| Model181 | 0.916 | 0.010 | 0.006 | 0.066 | −0.008 | −0.017 | 0.170 | 0 | 0 | 0 | 0 | −0.003 | 0.392 | 0.002 | 0.392 | 0.974 | 149 |
| Model182 | 0.637 | 0.010 | 0.003 | 0.066 | 0.002 | −0.024 | 0.167 | 0 | 0 | 0 | 0 | −0.010 | 0.376 | 0.002 | 0.376 | 0.977 | 63 |
| Model183 | −1.488 | 0.001 | −0.078 | 0.168 | 0.171 | 0.003 | 0 | 0 | 0 | 0 | 0 | −0.052 | 0.499 | 0.003 | 0.497 | 0.959 | 294 |
| Model184 | 0.961 | 0.006 | −0.030 | 0.100 | −0.024 | 0.167 | 0.003 | 0 | 0 | 0 | 0 | −0.016 | 0.381 | 0.002 | 0.381 | 0.976 | 147 |
| Model185 | 0.018 | 0.007 | −0.016 | 0.097 | −0.017 | 0.167 | 0 | 0 | 0 | 0 | 0 | −0.018 | 0.415 | 0.002 | 0.415 | 0.972 | 241 |
| Model186 | −0.063 | 0.006 | −0.016 | 0.096 | −0.017 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | −0.018 | 0.415 | 0.002 | 0.415 | 0.972 | 230 |
| Model187 | 1.015 | 0.007 | −0.025 | 0.099 | −0.012 | −0.014 | 0.170 | 0 | 0 | 0 | 0 | −0.009 | 0.393 | 0.002 | 0.393 | 0.974 | 162 |
| Model188 | 0.921 | 0.007 | −0.026 | 0.098 | −0.002 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | −0.014 | 0.379 | 0.002 | 0.379 | 0.976 | 121 |
| Model189 | −1.614 | 0.007 | −0.041 | 0.055 | 0.076 | 0.169 | −0.001 | 0 | 0 | 0 | 0 | −0.041 | 0.478 | 0.002 | 0.476 | 0.962 | 277 |
| Model190 | −1.791 | 0.006 | −0.040 | 0.052 | 0.078 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | −0.043 | 0.477 | 0.002 | 0.475 | 0.962 | 273 |
| Model191 | 0.452 | 0.010 | −0.030 | 0.039 | 0.068 | −0.020 | 0.171 | 0 | 0 | 0 | 0 | −0.016 | 0.398 | 0.002 | 0.398 | 0.974 | 194 |
| Model192 | 0.534 | 0.009 | −0.015 | 0.047 | 0.041 | −0.021 | 0.167 | 0 | 0 | 0 | 0 | −0.013 | 0.371 | 0.002 | 0.370 | 0.977 | 2 |
| Model193 | −0.259 | 0.008 | −0.008 | 0.065 | 0.025 | −0.016 | 0.167 | 0 | 0 | 0 | 0 | −0.015 | 0.416 | 0.002 | 0.416 | 0.971 | 221 |
| Model194 | 0.119 | 0.075 | 0.004 | −0.025 | 0.005 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.025 | 0.379 | 0.002 | 0.378 | 0.976 | 144 |
| Model195 | 0.175 | 0.019 | 0.057 | −0.022 | 0.005 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.023 | 0.376 | 0.002 | 0.375 | 0.977 | 96 |
| Model196 | 0.590 | 0.021 | 0.056 | −0.009 | −0.013 | 0.168 | 0.004 | 0 | 0 | 0 | 0 | −0.016 | 0.387 | 0.002 | 0.387 | 0.975 | 154 |
| Model197 | 0.676 | 0.017 | 0.055 | 0.001 | −0.022 | 0.166 | 0.003 | −0.001 | 0 | 0 | 0 | −0.018 | 0.374 | 0.002 | 0.374 | 0.977 | 61 |
| Model198 | 0.707 | 0.020 | 0.053 | 0.001 | −0.024 | 0.002 | 0.166 | −0.001 | 0 | 0 | 0 | −0.017 | 0.374 | 0.002 | 0.374 | 0.977 | 66 |
| Model199 | 0.651 | 0.024 | 0.048 | 0 | −0.023 | 0.001 | 0.165 | 0.004 | 0 | 0 | 0 | −0.013 | 0.374 | 0.002 | 0.374 | 0.977 | 29 |
| Model200 | 0.935 | 0.004 | 0.065 | −0.021 | −0.003 | 0.165 | 0.003 | −0.001 | 0 | 0 | 0 | −0.014 | 0.379 | 0.002 | 0.378 | 0.976 | 117 |
| Model201 | 0.335 | −0.001 | 0.077 | −0.007 | −0.014 | 0.169 | 0.005 | 0 | 0 | 0 | 0 | −0.019 | 0.391 | 0.002 | 0.391 | 0.975 | 186 |
| Model202 | 0.878 | 0.002 | 0.066 | 0.002 | −0.025 | 0.165 | 0.003 | −0.001 | 0 | 0 | 0 | −0.016 | 0.379 | 0.002 | 0.379 | 0.976 | 127 |
| Model203 | 0.168 | −0.003 | 0.077 | 0.005 | −0.026 | 0.005 | 0.166 | −0.001 | 0 | 0 | 0 | −0.025 | 0.379 | 0.002 | 0.378 | 0.976 | 156 |
| Model204 | 0.346 | 0.001 | 0.071 | 0.003 | −0.024 | 0.002 | 0.166 | 0.005 | 0 | 0 | 0 | −0.017 | 0.377 | 0.002 | 0.376 | 0.976 | 85 |
| Model205 | 0.473 | −0.032 | 0.111 | −0.011 | −0.010 | 0.169 | 0.004 | 0 | 0 | 0 | 0 | −0.021 | 0.394 | 0.002 | 0.393 | 0.974 | 195 |
| Model206 | 1.053 | −0.026 | 0.097 | −0.002 | −0.022 | 0.166 | 0.002 | −0.001 | 0 | 0 | 0 | −0.018 | 0.381 | 0.002 | 0.381 | 0.976 | 153 |
| Model207 | 0.656 | −0.030 | 0.035 | 0.070 | −0.021 | 0.170 | 0.003 | −0.001 | 0 | 0 | 0 | −0.021 | 0.401 | 0.002 | 0.400 | 0.973 | 223 |
| Model208 | 0.406 | −0.018 | 0.045 | 0.048 | −0.019 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.022 | 0.372 | 0.002 | 0.371 | 0.977 | 31 |
| Model209 | 0.561 | −0.016 | 0.047 | 0.043 | −0.021 | 0.001 | 0.165 | −0.001 | 0 | 0 | 0 | −0.020 | 0.372 | 0.002 | 0.371 | 0.977 | 30 |
| Model210 | 0.202 | −0.017 | 0.048 | 0.044 | −0.021 | 0.003 | 0.165 | 0.005 | 0 | 0 | 0 | −0.021 | 0.373 | 0.002 | 0.372 | 0.977 | 38 |
| Model211 | −0.082 | −0.006 | 0.064 | 0.022 | −0.017 | 0.165 | 0.004 | 0 | 0 | 0 | 0 | −0.017 | 0.415 | 0.002 | 0.415 | 0.972 | 224 |
| Model212 | 0.314 | −0.020 | 0.048 | 0.052 | −0.007 | −0.012 | 0.169 | −0.001 | 0 | 0 | 0 | −0.020 | 0.388 | 0.002 | 0.387 | 0.975 | 180 |
| Model213 | 0.452 | −0.017 | 0.047 | 0.047 | −0.008 | −0.014 | 0.168 | 0.005 | 0 | 0 | 0 | −0.016 | 0.385 | 0.002 | 0.385 | 0.975 | 145 |
| Model214 | 0.322 | −0.022 | 0.044 | 0.054 | 0.003 | −0.021 | 0.166 | −0.001 | 0 | 0 | 0 | −0.024 | 0.373 | 0.002 | 0.372 | 0.977 | 56 |
| Model215 | 0.424 | −0.018 | 0.045 | 0.046 | 0.002 | −0.021 | 0.166 | 0.004 | 0 | 0 | 0 | −0.018 | 0.372 | 0.002 | 0.371 | 0.977 | 18 |
| Model216 | 0.630 | −0.016 | 0.049 | 0.039 | 0.002 | −0.023 | 0.001 | 0.166 | 0 | 0 | 0 | −0.013 | 0.373 | 0.002 | 0.373 | 0.977 | 23 |
| Model217 | 0.533 | 0.010 | 0.071 | −0.020 | −0.001 | 0.167 | 0.003 | −0.001 | 0 | 0 | 0 | −0.019 | 0.375 | 0.002 | 0.374 | 0.977 | 73 |
| Model218 | 0.891 | 0.009 | 0.072 | −0.008 | −0.017 | 0.169 | 0.003 | −0.001 | 0 | 0 | 0 | −0.012 | 0.391 | 0.002 | 0.391 | 0.975 | 160 |
| Model219 | 0.741 | 0.009 | 0.070 | 0.003 | −0.024 | 0.166 | 0.003 | −0.001 | 0 | 0 | 0 | −0.018 | 0.376 | 0.002 | 0.376 | 0.977 | 102 |
| Model220 | 0.283 | 0.010 | 0.074 | 0.003 | −0.025 | 0.004 | 0.167 | −0.001 | 0 | 0 | 0 | −0.023 | 0.376 | 0.002 | 0.375 | 0.977 | 106 |
| Model221 | 0.578 | 0.009 | 0.069 | 0.002 | −0.023 | −0.001 | 0.167 | 0.004 | 0 | 0 | 0 | −0.013 | 0.375 | 0.002 | 0.375 | 0.977 | 59 |
| Model222 | 0.407 | 0.006 | 0.080 | −0.016 | −0.006 | 0.171 | 0.004 | 0 | 0 | 0 | 0 | −0.019 | 0.401 | 0.002 | 0.401 | 0.973 | 209 |
| Model223 | 0.469 | 0.004 | 0.080 | −0.006 | −0.014 | 0.171 | 0.003 | 0 | 0 | 0 | 0 | −0.025 | 0.390 | 0.002 | 0.389 | 0.975 | 197 |
| Model224 | 0.424 | 0.006 | 0.077 | −0.004 | −0.025 | 0.010 | 0.168 | 0 | 0 | 0 | 0 | −0.023 | 0.387 | 0.002 | 0.387 | 0.975 | 188 |
| Model225 | 0.659 | 0.009 | −0.017 | 0.093 | −0.021 | 0.172 | 0.003 | −0.001 | 0 | 0 | 0 | −0.020 | 0.406 | 0.002 | 0.406 | 0.973 | 246 |
| Model226 | 0.739 | 0.009 | 0.011 | 0.060 | −0.022 | 0.166 | 0.003 | −0.001 | 0 | 0 | 0 | −0.016 | 0.374 | 0.002 | 0.374 | 0.977 | 46 |
| Model227 | 0.271 | 0.010 | 0.019 | 0.057 | −0.022 | 0.004 | 0.167 | −0.001 | 0 | 0 | 0 | −0.022 | 0.374 | 0.002 | 0.373 | 0.977 | 60 |
| Model228 | 0.658 | 0.008 | 0.022 | 0.049 | −0.022 | 0 | 0.166 | 0.004 | 0 | 0 | 0 | −0.013 | 0.373 | 0.002 | 0.373 | 0.977 | 8 |
| Model229 | −0.239 | 0.007 | 0.048 | 0.033 | −0.016 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.019 | 0.415 | 0.002 | 0.414 | 0.972 | 234 |
| Model230 | 0.250 | 0.010 | 0.017 | 0.064 | −0.008 | −0.011 | 0.171 | 0 | 0 | 0 | 0 | −0.019 | 0.389 | 0.002 | 0.389 | 0.975 | 183 |
| Model231 | 0.670 | 0.009 | 0.023 | 0.053 | −0.009 | −0.015 | 0.169 | 0.004 | 0 | 0 | 0 | −0.011 | 0.386 | 0.002 | 0.386 | 0.975 | 131 |
| Model232 | 0.603 | 0.009 | 0.014 | 0.060 | 0.001 | −0.022 | 0.167 | −0.001 | 0 | 0 | 0 | −0.019 | 0.373 | 0.002 | 0.372 | 0.977 | 42 |
| Model233 | 0.698 | 0.008 | 0.023 | 0.048 | 0 | −0.023 | 0.166 | 0.004 | 0 | 0 | 0 | −0.012 | 0.373 | 0.002 | 0.373 | 0.977 | 13 |
| Model234 | 0.546 | 0.009 | 0.023 | 0.050 | 0.001 | −0.024 | 0.002 | 0.167 | 0 | 0 | 0 | −0.012 | 0.373 | 0.002 | 0.373 | 0.977 | 22 |
| Model235 | 0.642 | 0.009 | −0.016 | 0.090 | −0.021 | 0.171 | 0.003 | −0.001 | 0 | 0 | 0 | −0.020 | 0.402 | 0.002 | 0.401 | 0.973 | 225 |
| Model236 | 0.364 | 0.010 | 0.001 | 0.073 | −0.020 | 0.167 | 0.004 | −0.001 | 0 | 0 | 0 | −0.021 | 0.375 | 0.002 | 0.374 | 0.977 | 72 |
| Model237 | 0.117 | 0.011 | 0.001 | 0.075 | −0.020 | 0.003 | 0.168 | −0.001 | 0 | 0 | 0 | −0.023 | 0.378 | 0.002 | 0.377 | 0.976 | 128 |
| Model238 | 0.514 | 0.009 | 0.004 | 0.067 | −0.021 | −0.001 | 0.167 | 0.004 | 0 | 0 | 0 | −0.014 | 0.375 | 0.002 | 0.375 | 0.977 | 41 |
| Model239 | −0.180 | 0.008 | 0.019 | 0.058 | −0.016 | 0.167 | 0.004 | 0 | 0 | 0 | 0 | −0.015 | 0.424 | 0.002 | 0.424 | 0.970 | 258 |
| Model240 | 0.157 | 0.012 | −0.003 | 0.082 | −0.006 | −0.012 | 0.171 | −0.001 | 0 | 0 | 0 | −0.020 | 0.392 | 0.002 | 0.392 | 0.975 | 192 |
| Model241 | 0.839 | 0.009 | 0.004 | 0.068 | −0.008 | −0.017 | 0.169 | 0.005 | 0 | 0 | 0 | −0.007 | 0.390 | 0.002 | 0.390 | 0.975 | 139 |
| Model242 | 0.408 | 0.011 | −0.003 | 0.077 | 0.003 | −0.022 | 0.168 | −0.001 | 0 | 0 | 0 | −0.022 | 0.375 | 0.002 | 0.374 | 0.977 | 95 |
| Model243 | 0.375 | 0.009 | −0.001 | 0.073 | 0.003 | −0.023 | 0.167 | 0.004 | 0 | 0 | 0 | −0.016 | 0.375 | 0.002 | 0.374 | 0.977 | 51 |
| Model244 | 0.721 | 0.010 | 0.004 | 0.066 | 0.002 | −0.023 | −0.001 | 0.167 | 0 | 0 | 0 | −0.009 | 0.377 | 0.002 | 0.377 | 0.976 | 69 |
| Model245 | 0.717 | 0.006 | −0.038 | 0.112 | −0.021 | 0.168 | 0.002 | 0 | 0 | 0 | 0 | −0.025 | 0.380 | 0.002 | 0.380 | 0.976 | 172 |
| Model246 | −0.002 | 0.006 | −0.015 | 0.095 | −0.018 | 0.166 | 0.004 | 0 | 0 | 0 | 0 | −0.019 | 0.415 | 0.002 | 0.414 | 0.972 | 231 |
| Model247 | 0.193 | 0.008 | −0.036 | 0.118 | −0.011 | −0.008 | 0.171 | 0 | 0 | 0 | 0 | −0.027 | 0.398 | 0.002 | 0.397 | 0.974 | 210 |
| Model248 | 0.587 | 0.007 | −0.031 | 0.108 | −0.012 | −0.011 | 0.170 | 0.004 | 0 | 0 | 0 | −0.020 | 0.392 | 0.002 | 0.392 | 0.974 | 189 |
| Model249 | 0.613 | 0.008 | −0.036 | 0.111 | −0.002 | −0.018 | 0.168 | 0 | 0 | 0 | 0 | −0.025 | 0.379 | 0.002 | 0.378 | 0.976 | 158 |
| Model250 | 0.735 | 0.007 | −0.030 | 0.103 | −0.003 | −0.020 | 0.167 | 0.003 | 0 | 0 | 0 | −0.019 | 0.379 | 0.002 | 0.378 | 0.976 | 138 |
| Model251 | 0.503 | 0.008 | −0.031 | 0.105 | −0.001 | −0.024 | 0.005 | 0.167 | 0 | 0 | 0 | −0.020 | 0.379 | 0.002 | 0.378 | 0.976 | 146 |
| Model252 | −1.661 | 0.002 | −0.039 | 0.053 | 0.075 | 0.169 | 0.004 | 0 | 0 | 0 | 0 | −0.042 | 0.478 | 0.002 | 0.476 | 0.962 | 278 |
| Model253 | 0.471 | 0.010 | −0.031 | 0.036 | 0.073 | −0.020 | 0.171 | −0.001 | 0 | 0 | 0 | −0.023 | 0.398 | 0.002 | 0.398 | 0.974 | 218 |
| Model254 | 0.563 | 0.008 | −0.029 | 0.036 | 0.069 | −0.021 | 0.171 | 0.004 | 0 | 0 | 0 | −0.017 | 0.399 | 0.002 | 0.399 | 0.974 | 198 |
| Model255 | 0.525 | 0.010 | −0.017 | 0.045 | 0.047 | −0.020 | 0.167 | −0.001 | 0 | 0 | 0 | −0.021 | 0.370 | 0.002 | 0.370 | 0.977 | 17 |
| Model256 | 0.610 | 0.008 | −0.015 | 0.046 | 0.040 | −0.022 | 0.166 | 0.004 | 0 | 0 | 0 | −0.014 | 0.371 | 0.002 | 0.371 | 0.977 | 3 |
| Model257 | 0.514 | 0.009 | −0.017 | 0.051 | 0.040 | −0.021 | 0 | 0.167 | 0 | 0 | 0 | −0.014 | 0.371 | 0.002 | 0.370 | 0.977 | 1 |
| Model258 | −0.090 | 0.008 | −0.007 | 0.064 | 0.024 | −0.016 | 0.166 | −0.001 | 0 | 0 | 0 | −0.017 | 0.415 | 0.002 | 0.414 | 0.972 | 219 |
| Model259 | −0.259 | 0.007 | −0.007 | 0.063 | 0.026 | −0.016 | 0.166 | 0.005 | 0 | 0 | 0 | −0.017 | 0.414 | 0.002 | 0.414 | 0.972 | 211 |
| Model260 | 0.436 | 0.010 | −0.020 | 0.055 | 0.043 | −0.008 | −0.014 | 0.170 | 0 | 0 | 0 | −0.013 | 0.385 | 0.002 | 0.385 | 0.975 | 135 |
| Model261 | 0.516 | 0.009 | −0.017 | 0.047 | 0.044 | 0.002 | −0.022 | 0.167 | 0 | 0 | 0 | −0.015 | 0.371 | 0.002 | 0.371 | 0.977 | 4 |
| Model262 | 0.272 | 0.016 | 0.059 | 0.002 | −0.024 | 0.005 | 0.166 | 0.004 | 0 | 0 | 0 | −0.023 | 0.375 | 0.002 | 0.375 | 0.977 | 84 |
| Model263 | 0.225 | −0.003 | 0.076 | 0.004 | −0.025 | 0.003 | 0.166 | 0.004 | −0.001 | 0 | 0 | −0.024 | 0.378 | 0.002 | 0.377 | 0.976 | 129 |
| Model264 | 0.366 | −0.017 | 0.046 | 0.046 | −0.021 | 0.002 | 0.165 | 0.004 | 0 | 0 | 0 | −0.023 | 0.372 | 0.002 | 0.371 | 0.977 | 37 |
| Model265 | 0.141 | −0.020 | 0.046 | 0.054 | −0.007 | −0.012 | 0.168 | 0.005 | 0 | 0 | 0 | −0.023 | 0.388 | 0.002 | 0.387 | 0.975 | 184 |
| Model266 | 0.648 | −0.018 | 0.043 | 0.047 | 0.002 | −0.023 | 0.165 | 0.003 | −0.001 | 0 | 0 | −0.020 | 0.372 | 0.002 | 0.372 | 0.977 | 39 |
| Model267 | 0.894 | −0.016 | 0.044 | 0.043 | 0.002 | −0.023 | −0.001 | 0.165 | −0.001 | 0 | 0 | −0.017 | 0.374 | 0.002 | 0.374 | 0.977 | 70 |
| Model268 | 0.616 | −0.016 | 0.046 | 0.041 | 0.001 | −0.023 | 0 | 0.165 | 0.004 | 0 | 0 | −0.015 | 0.372 | 0.002 | 0.372 | 0.977 | 9 |
| Model269 | 0.109 | 0.010 | 0.075 | 0.003 | −0.025 | 0.005 | 0.167 | 0.004 | 0 | 0 | 0 | −0.025 | 0.377 | 0.002 | 0.376 | 0.977 | 114 |
| Model270 | 0.184 | 0.009 | 0.017 | 0.059 | −0.022 | 0.004 | 0.167 | 0.004 | 0 | 0 | 0 | −0.023 | 0.374 | 0.002 | 0.373 | 0.977 | 64 |
| Model271 | 0.158 | 0.010 | 0.016 | 0.065 | −0.009 | −0.011 | 0.170 | 0.005 | 0 | 0 | 0 | −0.020 | 0.389 | 0.002 | 0.388 | 0.975 | 182 |
| Model272 | 0.148 | 0.010 | 0.008 | 0.069 | 0.001 | −0.019 | 0.168 | 0.004 | 0 | 0 | 0 | −0.025 | 0.375 | 0.002 | 0.374 | 0.977 | 93 |
| Model273 | 0.113 | 0.010 | 0.014 | 0.063 | 0.002 | −0.025 | 0.006 | 0.167 | −0.001 | 0 | 0 | −0.024 | 0.376 | 0.002 | 0.375 | 0.977 | 107 |
| Model274 | 0.441 | 0.008 | 0.020 | 0.053 | 0.001 | −0.023 | 0.002 | 0.166 | 0.004 | 0 | 0 | −0.016 | 0.373 | 0.002 | 0.372 | 0.977 | 20 |
| Model275 | 0.698 | 0.009 | 0.002 | 0.068 | −0.021 | −0.001 | 0.167 | 0.003 | −0.001 | 0 | 0 | −0.017 | 0.375 | 0.002 | 0.375 | 0.977 | 79 |
| Model276 | 0.234 | 0.011 | −0.002 | 0.080 | −0.007 | −0.013 | 0.170 | 0.005 | 0 | 0 | 0 | −0.020 | 0.390 | 0.002 | 0.389 | 0.975 | 185 |
| Model277 | 0.392 | 0.010 | −0.003 | 0.076 | 0.003 | −0.022 | 0.167 | 0.003 | −0.001 | 0 | 0 | −0.022 | 0.375 | 0.002 | 0.374 | 0.977 | 86 |
| Model278 | 0.185 | 0.011 | −0.004 | 0.078 | 0.004 | −0.025 | 0.004 | 0.167 | −0.001 | 0 | 0 | −0.025 | 0.377 | 0.002 | 0.376 | 0.977 | 116 |
| Model279 | 0.472 | 0.009 | 0.001 | 0.069 | 0.002 | −0.023 | 0 | 0.167 | 0.004 | 0 | 0 | −0.015 | 0.375 | 0.002 | 0.375 | 0.977 | 52 |
| Model280 | 0.752 | 0.007 | −0.030 | 0.106 | −0.012 | −0.012 | 0.169 | 0.003 | 0 | 0 | 0 | −0.018 | 0.392 | 0.002 | 0.392 | 0.974 | 187 |
| Model281 | 0.913 | 0.006 | −0.030 | 0.102 | −0.002 | −0.021 | 0.167 | 0.002 | 0 | 0 | 0 | −0.020 | 0.380 | 0.002 | 0.379 | 0.976 | 151 |
| Model282 | 0.139 | 0.009 | −0.032 | 0.035 | 0.076 | −0.018 | 0.171 | 0.004 | 0 | 0 | 0 | −0.027 | 0.397 | 0.002 | 0.396 | 0.974 | 222 |
| Model283 | 0.276 | 0.009 | −0.018 | 0.041 | 0.053 | −0.019 | 0.167 | 0.004 | 0 | 0 | 0 | −0.024 | 0.371 | 0.002 | 0.370 | 0.977 | 25 |
| Model284 | 0.215 | 0.010 | −0.016 | 0.046 | 0.047 | −0.022 | 0.004 | 0.167 | −0.001 | 0 | 0 | −0.024 | 0.372 | 0.002 | 0.371 | 0.977 | 36 |
| Model285 | 0.322 | 0.009 | −0.015 | 0.045 | 0.044 | −0.022 | 0.002 | 0.166 | 0.004 | 0 | 0 | −0.019 | 0.371 | 0.002 | 0.370 | 0.977 | 7 |
| Model286 | −0.127 | 0.007 | −0.007 | 0.064 | 0.024 | −0.017 | 0.166 | 0.004 | 0 | 0 | 0 | −0.017 | 0.414 | 0.002 | 0.414 | 0.972 | 212 |
| Model287 | 0.288 | 0.010 | −0.019 | 0.046 | 0.054 | −0.008 | −0.012 | 0.169 | −0.001 | 0 | 0 | −0.022 | 0.386 | 0.002 | 0.385 | 0.975 | 176 |
| Model288 | 0.748 | 0.009 | −0.014 | 0.042 | 0.046 | −0.009 | −0.016 | 0.169 | 0.004 | 0 | 0 | −0.010 | 0.385 | 0.002 | 0.385 | 0.975 | 122 |
| Model289 | 0.632 | 0.009 | −0.018 | 0.041 | 0.050 | 0.002 | −0.023 | 0.166 | −0.001 | 0 | 0 | −0.020 | 0.371 | 0.002 | 0.371 | 0.977 | 26 |
| Model290 | 0.537 | 0.008 | −0.017 | 0.044 | 0.044 | 0.001 | −0.022 | 0.166 | 0.004 | 0 | 0 | −0.016 | 0.371 | 0.002 | 0.370 | 0.977 | 6 |
| Model291 | 0.658 | 0.009 | −0.016 | 0.047 | 0.040 | 0.001 | −0.023 | 0 | 0.166 | 0 | 0 | −0.012 | 0.372 | 0.002 | 0.371 | 0.977 | 5 |
| Model292 | 0.234 | 0.009 | −0.019 | 0.045 | 0.048 | 0.002 | −0.024 | 0.003 | 0.166 | 0.004 | 0 | −0.021 | 0.371 | 0.002 | 0.370 | 0.977 | 21 |
| Model293 | 0.099 | 0.010 | −0.022 | 0.045 | 0.054 | 0.004 | −0.026 | 0.005 | 0.168 | −0.001 | 0 | −0.027 | 0.373 | 0.002 | 0.372 | 0.977 | 75 |
| Model294 | 0.298 | 0.009 | −0.028 | 0.058 | 0.046 | 0.002 | −0.020 | 0.166 | 0.003 | 0 | 0 | −0.025 | 0.371 | 0.002 | 0.370 | 0.977 | 33 |
| Model295 | 0.294 | 0.010 | −0.019 | 0.044 | 0.054 | −0.008 | −0.013 | 0.169 | 0.004 | 0 | 0 | −0.021 | 0.385 | 0.002 | 0.385 | 0.975 | 164 |
| Model296 | 0.126 | 0.009 | −0.018 | 0.045 | 0.050 | −0.021 | 0.003 | 0.166 | 0.004 | 0 | 0 | −0.025 | 0.372 | 0.002 | 0.371 | 0.977 | 40 |
| Model297 | 0.354 | 0.007 | −0.034 | 0.110 | −0.001 | −0.025 | 0.007 | 0.166 | 0.003 | 0 | 0 | −0.029 | 0.380 | 0.002 | 0.379 | 0.976 | 169 |
| Model298 | 0.336 | 0.010 | −0.002 | 0.075 | 0.003 | −0.024 | 0.002 | 0.167 | 0.003 | −0.001 | 0 | −0.023 | 0.375 | 0.002 | 0.375 | 0.977 | 97 |
| Model299 | 0.361 | 0.009 | 0.015 | 0.060 | 0.002 | −0.024 | 0.004 | 0.167 | 0.003 | 0 | 0 | −0.022 | 0.373 | 0.002 | 0.373 | 0.977 | 57 |
| Model300 | 0.089 | −0.020 | 0.045 | 0.052 | 0.004 | −0.025 | 0.005 | 0.165 | 0.004 | 0 | 0 | −0.028 | 0.374 | 0.002 | 0.373 | 0.977 | 74 |
| Model301 | 0.284 | 0.009 | −0.020 | 0.043 | 0.052 | 0.003 | −0.024 | 0.003 | 0.166 | 0.003 | −0.001 | −0.025 | 0.371 | 0.002 | 0.370 | 0.977 | 35 |
References
- Environment UN. UNEP Annual Report 2000. UNEP-UN Environment Programme. 2017. Available online: https://www.unep.org/resources/annual-report/unep-annual-report-2000 (accessed on 7 February 2022).
- Jury, W.A.; Vaux, H.J. The Emerging Global Water Crisis: Managing Scarcity and Conflict Between Water Users. In Advances in Agronomy; Academic Press: New York, NY, USA, 2007; Volume 95, pp. 1–76. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef]
- Brini, R. Renewable and non-renewable electricity consumption, economic growth and climate change: Evidence from a panel of selected African countries. Energy 2021, 223, 120064. [Google Scholar] [CrossRef]
- Bezyk, Y.; Sówka, I.; Górka, M. Assessment of urban CO2 budget: Anthropogenic and biogenic inputs. Urban Clim. 2021, 39, 100949. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, X.; Zhu, E. Global warming induces significant changes in the fraction of stored precipitation in the surface soil. Glob. Planet. Change 2021, 205, 103616. [Google Scholar] [CrossRef]
- Sillmann, J.; Roeckner, E. Indices for extreme events in projections of anthropogenic climate change. Clim. Change 2008, 86, 83–104. [Google Scholar] [CrossRef]
- Hulme, M.; Doherty, R.; Ngara, T.; New, M.; Lister, D. African climate change: 1900–2100. Clim. Res. 2001, 17, 145–168. [Google Scholar] [CrossRef]
- Douville, H.; Raghavan, K.; Renwick, J.A.; Allan, R.P.; Arias, P.A.; Barlow, M.; Cerezo Mota, R.; Cherchi, A.; Gan, T.Y.; Gergis, J.; et al. Water cycle changes. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Global Warming and Agriculture: Impact Estimates by Country. PIIE. 2016. Available online: https://www.piie.com/bookstore/global-warming-and-agriculture-impact-estimates-country (accessed on 7 February 2022).
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Weather and climate extreme events in a changing climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- World Development Report 2020 Chapters and Data; World Bank: Washington, DC, USA, 2020; Available online: https://www.worldbank.org/en/publication/wdr2020/brief/world-development-report-2020-data (accessed on 7 February 2022).
- Making Waves: Integrating Coastal Conservation and Development; Routledge; CRC Press: New York, NY, USA, 2002; Available online: https://www.routledge.com/Making-Waves-Integrating-Coastal-Conservation-and-Development/Brown-Tompkins-Adger/p/book/9781853839122 (accessed on 7 February 2022).
- Rosegrant, M.W. Water Resources in the Twenty-First Century: Challenges and Implications for Action; International Food Policy Research Institute (IFPRI): Washington, DC, USA, 1997. [Google Scholar]
- Katz, R.W.; Brown, B.G. Extreme events in a changing climate: Variability is more important than averages. Clim. Change 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Schwabe, K.A.; Kan, I.; Knapp, K.C. Drainwater Management for Salinity Mitigation in Irrigated Agriculture. Am. J. Agric. Econ. 2006, 88, 133–149. [Google Scholar] [CrossRef]
- Long, S.P.; Ort, D.R. More than taking the heat: Crops and global change. Curr. Opin. Plant Biol. 2010, 13, 240–247. [Google Scholar] [CrossRef]
- Gorjian, S.; Singh, R.; Shukla, A.; Mazhar, A.R. Chapter 6-On-farm applications of solar PV systems. In Photovoltaic Solar Energy Conversion; Gorjian, S., Shukla, A., Eds.; Academic Press: New York, NY, USA, 2020; pp. 147–190. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Jha, S.K.; Mittal, R.K.; Vashishtha, S. Assessment of floating solar PV (FSPV) potential and water conservation: Case study on Rajghat Dam in Uttar Pradesh, India. Energy Sustain. Dev. 2022, 66, 287–295. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, Y.; Sadeghi, M.; Horton, R.; Ren, T. Measurement and estimation of evapotranspiration in a maize field: A new method based on an analytical water flux model. Agric. Water Manag. 2024, 295, 108764. [Google Scholar] [CrossRef]
- Rong, Y.; Dai, X.; Wang, W.; Wu, P.; Huo, Z. Dependence of evapotranspiration validity on shallow groundwater in arid area-a three years field observation experiment. Agric. Water Manag. 2023, 286, 108411. [Google Scholar] [CrossRef]
- Shao, R.; Zhang, B.; He, X. Implementation of Dynamic Effective Rooting Depth in Evapotranspiration Model Deepens Understanding of Evapotranspiration Partitioning Under Soil Moisture Gradients in China. Water Resour. Res. 2022, 58, e2022WR032962. [Google Scholar] [CrossRef]
- Karbasi, M.; Jamei, M.; Ali, M.; Malik, A.; Chu, X.; Farooque, A.A.; Yaseen, Z.M. Development of an enhanced bidirectional recurrent neural network combined with time-varying filter-based empirical mode decomposition to forecast weekly reference evapotranspiration. Agric. Water Manag. 2023, 290, 108604. [Google Scholar] [CrossRef]
- Feng, J.; Wang, W.; Xu, F.; Wang, S. Evaluating the ability of deep learning on actual daily evapotranspiration estimation over the heterogeneous surfaces. Agric. Water Manag. 2024, 291, 108627. [Google Scholar] [CrossRef]
- Talib, A.; Desai, A.R.; Huang, J.; Griffis, T.J.; Reed, D.E.; Chen, J. Evaluation of prediction and forecasting models for evapotranspiration of agricultural lands in the Midwest U.S. J. Hydrol. 2021, 600, 126579. [Google Scholar] [CrossRef]
- Luo, B.; Liu, X.; Zhang, F.; Guo, P. Optimal management of cultivated land coupling remote sensing-based expected irrigation water forecasting. J. Clean. Prod. 2021, 308, 127370. [Google Scholar] [CrossRef]
- Pande, C.B.; Egbueri, J.C.; Costache, R.; Sidek, L.M.; Wang, Q.; Alshehri, F.; Din, N.M.; Gautam, V.K.; Chandra Pal, S. Predictive modeling of land surface temperature (LST) based on Landsat-8 satellite data and machine learning models for sustainable development. J. Clean. Prod. 2024, 444, 141035. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zheng, J.; Zhang, F. Medium-range forecasting of daily reference evapotranspiration across China using numerical weather prediction outputs downscaled by extreme gradient boosting. J. Hydrol. 2021, 601, 126664. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; de Marinis, G. Advanced evapotranspiration forecasting in Central Italy: Stacked MLP-RF algorithm and correlated Nystrom views with feature selection strategies. Comput. Electron. Agric. 2024, 220, 108887. [Google Scholar] [CrossRef]
- Troncoso-García, A.R.; Brito, I.S.; Troncoso, A.; Martínez-Álvarez, F. Explainable hybrid deep learning and Coronavirus Optimization Algorithm for improving evapotranspiration forecasting. Comput. Electron. Agric. 2023, 215, 108387. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Ahmadi, A.; Daccache, A.; Sadegh, M.; Snyder, R.L. Statistical and deep learning models for reference evapotranspiration time series forecasting: A comparison of accuracy, complexity, and data efficiency. Comput. Electron. Agric. 2023, 215, 108424. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Gao, H.; Zhangzhong, L.; Zheng, W.; Chen, G. How can agricultural water production be promoted? a review on machine learning for irrigation. J. Clean. Prod. 2023, 414, 137687. [Google Scholar] [CrossRef]
- Taguta, C.; Dirwai, T.L.; Senzanje, A.; Sikka, A.; Mabhaudhi, T. Sustainable irrigation technologies: A water-energy-food (WEF) nexus perspective towards achieving more crop per drop per joule per hectare. Environ. Res. Lett. 2022, 17, 073003. [Google Scholar] [CrossRef]
- Chapagain, K.; Babel, M.S.; Karthe, D.; Stamm, J. Integrated assessment of water–energy–food nexus: Conceptual framework and application to the Ping River basin, Thailand. Int. J. Water Resour. Dev. 2024, 40, 284–318. [Google Scholar] [CrossRef]
- Zahedi, R.; Yousefi, H.; Aslani, A.; Ahmadi, R. System dynamic model of water, energy and food nexus for policy implementation. Appl. Water Sci. 2024, 14, 213. [Google Scholar] [CrossRef]
- El Mghouchi, Y.; Chham, E.; Zemmouri, E.M.; El Bouardi, A. Assessment of different combinations of meteorological parameters for predicting daily global solar radiation using artificial neural networks. Build. Environ. 2019, 149, 607–622. [Google Scholar] [CrossRef]
- Chakraborty, K.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Forecasting the behavior of multivariate time series using neural networks. Neural Netw. 1992, 5, 961–970. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; p. 794. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Abellán, J.; Masegosa, A.R. Bagging Decision Trees on Data Sets with Classification Noise. In Foundations of Information and Knowledge Systems; Link, S., Prade, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 248–265. [Google Scholar] [CrossRef]
- Lesaffre, E.; Marx, B.D. Collinearity in generalized linear regression. Commun. Stat. Theory Methods 1993, 22, 1933–1952. [Google Scholar] [CrossRef]
- Najibi, F.; Apostolopoulou, D.; Alonso, E. Enhanced performance Gaussian process regression for probabilistic short-term solar output forecast. Int. J. Electr. Power Energy Syst. 2021, 130, 106916. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A Review on Linear Regression Comprehensive in Machine Learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Hastie, T.J. Generalized Additive Models. In Statistical Models in S; Routledge: London, UK, 1992. [Google Scholar]
- Vovk, V. Kernel Ridge Regression. In Empirical Inference: Festschrift in Honor of Vladimir N. Vapnik; Schölkopf, B., Luo, Z., Vovk, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 105–116. [Google Scholar] [CrossRef]
- Liu, X.-Q.; Gao, F. Linearized Ridge Regression Estimator in Linear Regression. Commun. Stat. Theory Methods 2011, 40, 2182–2192. [Google Scholar] [CrossRef]
- Gürel, A.E.; Ağbulut, Ü.; Bakır, H.; Ergün, A.; Yıldız, G. A state of art review on estimation of solar radiation with various models. Heliyon 2023, 9, e13167. [Google Scholar] [CrossRef]
- Udristioiu, M.T.; EL Mghouchi, Y.; Yildizhan, H. Prediction, modelling, and forecasting of PM and AQI using hybrid machine learning. J. Clean. Prod. 2023, 421, 138496. [Google Scholar] [CrossRef]
- Çiftçi, E.; Khanlari, A.; Sözen, A.; Aytaç, İ.; Tuncer, A.D. Energy and exergy analysis of a photovoltaic thermal (PVT) system used in solar dryer: A numerical and experimental investigation. Renew. Energy 2021, 180, 410–423. [Google Scholar] [CrossRef]
- Misha, S.; Abdullah, A.L.; Tamaldin, N.; Rosli, M.A.M.; Sachit, F.A. Simulation CFD and experimental investigation of PVT water system under natural Malaysian weather conditions. Energy Rep. 2020, 6, 28–44. [Google Scholar] [CrossRef]






| Period | Location | Latitude (Degrees) | Longitude (Degrees) | Altitude (m) | Average Evapotranspiration (mm) | Average Precipitation (mm) | Average Solar Radiation Intensity (kWh/m2/day) | Average Ambient Temperature (°C) | Average Humidity (%) | Average Wind Speed (m/s) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2016–2020 | AIT AMIRA | 30.17 | −9.48 | 84 | 4.03 | 0.09 | 5.82 | 17.53 | 76.93 | 20.03 |
| 2015–2020 | AIT MELLOUL | 30.33 | −9.50 | 21 | 3.54 | 0.24 | 4.86 | 18.34 | 79.91 | 13.34 |
| 2015–2020 | AOULOUZ | 30.70 | −8.15 | 735 | 3.84 | 0.10 | 4.66 | 19.38 | 59.93 | 14.52 |
| 2016–2020 | KENITRA | 34.30 | −6.60 | 14 | 1.89 | 1.02 | 2.33 | 17.06 | 81.74 | 14.10 |
| 2018–2020 | RIBAT-LKHEIR | 34.05 | −6.76 | 75 | 4.56 | 1.03 | 5.86 | 16.09 | 61.42 | 12.80 |
| 2016–2020 | SIDI SLIMAN | 34.26 | −5.92 | 37 | 3.73 | 0.79 | 4.79 | 17.86 | 73.32 | 13.02 |
| 2016–2020 | SOUK LARBAA | 33.97 | −6.61 | 37 | 4.27 | 0.99 | 5.99 | 18.04 | 73.81 | 12.52 |
| 2019–2020 | TAFILALET—ARREFOUD | 31.43 | −4.23 | 813 | 6.15 | 0.14 | 6.75 | 25.58 | 24.96 | 7.40 |
| 2019–2020 | TAFILALET—GOULMIMA | 31.69 | −4.95 | 1024 | 6.29 | 0.22 | 6.84 | 23.42 | 28.49 | 9.97 |
| 2016–2020 | TEMSIA | 30.36 | −9.41 | 48 | 4.21 | 0.41 | 5.99 | 18.09 | 80.51 | 14.31 |
| 2015–2020 | TAROUDANT | 30.46 | −8.86 | 30 | 4.53 | 0.18 | 5.66 | 19.02 | 65.52 | 16.56 |
| Input | Variable |
|---|---|
| Input1 | P (mm) |
| Input2 | Tmin (°C) |
| Input3 | Tavr (°C) |
| Input4 | Tmax (°C) |
| Input5 | Rhmin (%) |
| Input6 | Rhavr (%) |
| Input7 | Rhmax (%) |
| Input8 | H (kW/m2) |
| Input9 | Ws (km/h) |
| Input10 | Wd (degrees) |
| Output | ETo (mm) |
| Model | Description | Key Features and Highlights | Reference |
|---|---|---|---|
| Artificial Neural Networks (ANNs) | ML models inspired by the brain, composed of layers of interconnected neurons. Include input, hidden, and output layers. | Inspired by biology, uses backpropagation. Suited for various tasks. | [39] |
| Decision Trees (DTs) | Hierarchical models with nodes representing decisions based on feature values. Simple and interpretable. | Used for classification, regression, rule extraction, and anomaly detection. | [40] |
| Support Vector Machine (SVM) | Supervised algorithm that finds a hyperplane to separate classes with maximum margin. | Effective in high-dimensional spaces; used for classification and regression. | [41] |
| Extreme Learning Machine (ELM) | Neural network with a single hidden layer; weights from input to hidden layer are random. Fast training. | Faster alternative to traditional training; random weights in a hidden layer. | [42] |
| Extreme Gradient Boosting (XGBoost) | Gradient boosting ensemble algorithm that sequentially adds trees to correct errors. | High accuracy and efficiency; widely used in ML competitions. | [43] |
| Random Forest (RF) | Ensemble method of decision trees using bagging and random feature selection. | Robust, handles high-dimensional data; used in many domains. | [44] |
| Tree Bagger (TreeBag) | Ensemble of bagged decision trees trained on bootstrap samples. | Reduces variance and improves prediction through averaging. | [45] |
| Generalised Linear Regression (GLR) | Extends linear regression to handle non-normal response variables using a link function. | Flexible for different distributions; suitable for generalised tasks. | [46] |
| Gaussian Process Regression (GPR) | Non-parametric probabilistic model defining a distribution over functions for regression. | Models uncertainty; predictions are probabilistic. | [47] |
| Linear Regression (LR) | Predicts a continuous outcome from one or more input variables using a linear approach. | Simple, interpretable, and widely used historically and across disciplines. | [48] |
| Generalised Additive Model (GAM) | Extends GLMs to include nonlinear additive effects for each predictor. | Captures nonlinear relationships while maintaining interpretability. | [49] |
| Kernelised Ridge Regression (KRR) | Combines ridge regression with kernel trick to handle nonlinearity. | Regularisation + kernel transformation; suited for nonlinear regression. | [50] |
| Linear Ridge Regression (LRR) | Linear regression with L2 regularisation. Has a closed-form solution for model coefficients. | Controls overfitting; analytically solvable. | [51] |
| Solar Flux | Improvement Rate | |||
|---|---|---|---|---|
| 800 W/m2 | 1000 W/m2 | 800 W/m2 | 1000 W/m2 | |
| PV module | 13.93% | 13.37% | --- | --- |
| Scaled PVT | 14.95% | 14.71% | 7.32% | 10.02% |
| Coiled PVT | 14.34% | 14.67% | 2.94% | 9.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Mghouchi, Y.; Udristioiu, M.T. Enhancing Agricultural Sustainability Through Intelligent Irrigation Using PVT Energy Applications: Implementing Hybrid Machine and Deep Learning Models. Agriculture 2025, 15, 906. https://doi.org/10.3390/agriculture15080906
El Mghouchi Y, Udristioiu MT. Enhancing Agricultural Sustainability Through Intelligent Irrigation Using PVT Energy Applications: Implementing Hybrid Machine and Deep Learning Models. Agriculture. 2025; 15(8):906. https://doi.org/10.3390/agriculture15080906
Chicago/Turabian StyleEl Mghouchi, Youness, and Mihaela Tinca Udristioiu. 2025. "Enhancing Agricultural Sustainability Through Intelligent Irrigation Using PVT Energy Applications: Implementing Hybrid Machine and Deep Learning Models" Agriculture 15, no. 8: 906. https://doi.org/10.3390/agriculture15080906
APA StyleEl Mghouchi, Y., & Udristioiu, M. T. (2025). Enhancing Agricultural Sustainability Through Intelligent Irrigation Using PVT Energy Applications: Implementing Hybrid Machine and Deep Learning Models. Agriculture, 15(8), 906. https://doi.org/10.3390/agriculture15080906







