Simulating the Interconnected Eastern Mediterranean–Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast
Abstract
:1. Introduction
2. Materials and Methods
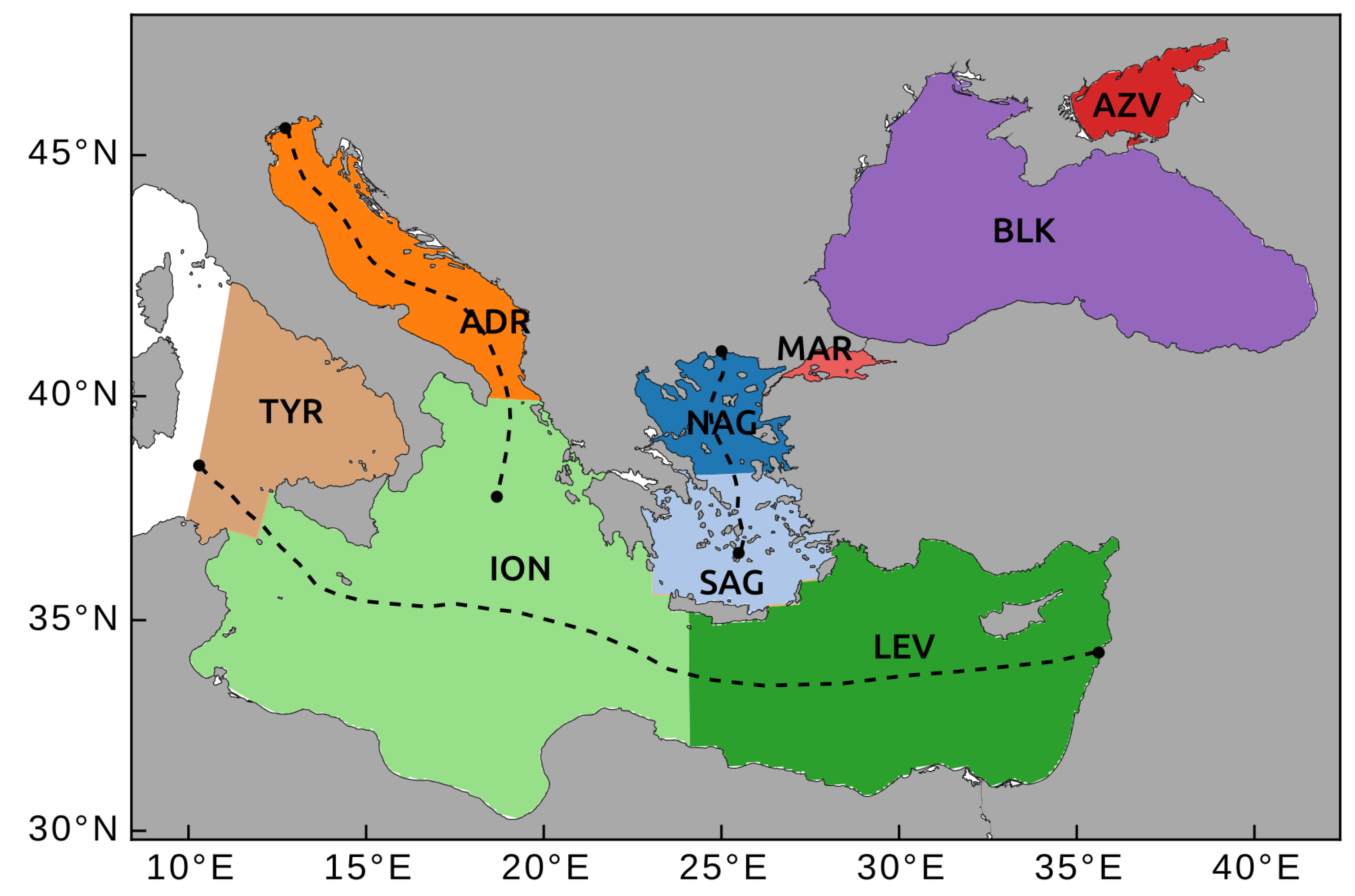
2.1. Domain Selection and Model Setup
2.2. Realistic Forcing
2.3. Validation Datasets
3. Results
3.1. Sea Surface Temperature
3.2. Sea Surface Elevation
3.3. Water Exchange and Properties at the Straits
3.4. General Circulation
3.5. Column Structure—Profiles
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sverdrup, H.; Johnson, M.W.; Fleming, R.H. The Oceans Their Physics, Chemistry, and General Biology; Prentice-Hall: New York, NY, USA, 1942; Available online: https://publishing.cdlib.org/ucpressebooks/view?docId=kt167nb66r (accessed on 1 May 2022).
- Pinardi, N.; Özsoy, E.; Latif, M.A.; Moroni, F.; Grandi, A.; Manzella, G.; Strobel, F.D.; Lyubartsev, V. Measuring the Sea: Marsili’s Oceanographic Cruise (1679–80) and the Roots of Oceanography. J. Phys. Oceanogr. 2018, 48, 845–860. [Google Scholar] [CrossRef]
- Astraldi, M.; Balopoulos, S.; Candela, J.; Font, J.; Gacic, M.; Gasparini, G.; Manca, B.; Theocharis, A.; Tintoré, J. The role of straits and channels in understanding the characteristics of Mediterranean circulation. Prog. Oceanogr. 1999, 44, 65–108. [Google Scholar] [CrossRef]
- Sannino, G.; Herrmann, M.; Carillo, A.; Rupolo, V.; Ruggiero, V.; Artale, V.; Heimbach, P. An eddy-permitting model of the Mediterranean Sea with a two-way grid refinement at the Strait of Gibraltar. Ocean Model. 2009, 30, 56–72. [Google Scholar] [CrossRef]
- Dietrich, D.E.; Tseng, Y.H.; Medina, R.; Piacsek, S.A.; Liste, M.; Olabarrieta, M.; Bowman, M.J.; Mehra, A. Mediterranean Overflow Water (MOW) simulation using a coupled multiple-grid Mediterranean Sea/North Atlantic Ocean model. J. Geophys. Res. Ocean. 2008, 113, C07027. [Google Scholar] [CrossRef] [Green Version]
- Malanotte-Rizzoli, P.; Manca, B.B.; D’Alcala, M.R.; Theocharis, A.; Brenner, S.; Budillon, G.; Ozsoy, E. The Eastern Mediterranean in the 80s and in the 90s: The big transition in the intermediate and deep circulations. Dyn. Atmos. Ocean. 1999, 29, 365–395. [Google Scholar] [CrossRef]
- Roether, W.; Klein, B.; Manca, B.B.; Theocharis, A.; Kioroglou, S. Transient Eastern Mediterranean deep waters in response to the massive dense-water output of the Aegean Sea in the 1990s. Prog. Oceanogr. 2007, 74, 540–571. [Google Scholar] [CrossRef]
- Tragou, E.; Petalas, S.; Mamoutos, I. Air–Sea Interaction: Heat and Fresh-Water Fluxes in the Aegean Sea; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–21. [Google Scholar] [CrossRef]
- Zervakis, V.; Georgopoulos, D.; Drakopoulos, P.G. The role of the North Aegean in triggering the recent Eastern Mediterranean climatic changes. J. Geophys. Res. Ocean. 2000, 105, 26103–26116. [Google Scholar] [CrossRef]
- Gertman, I.; Pinardi, N.; Popov, Y.; Hecht, A. Aegean Sea Water Masses during the Early Stages of the Eastern Mediterranean Climatic Transient (1988–1990). J. Phys. Oceanogr. 2006, 36, 184–1859. [Google Scholar] [CrossRef]
- Vervatis, V.; Skliris, N.; Sofianos, S.S. INTER-annual/decadal variability of the north Aegean Sea hydrodynamics over 1960–2000. Mediterr. Mar. Sci. 2014, 15, 696–705. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; Barbopoulos, K. High resolution simulations on the North Aegean Sea seasonal circulation. Ann. Geophys. 2003, 21, 251–265. [Google Scholar] [CrossRef] [Green Version]
- Kourafalou, V.; Tsiaras, K. A nested circulation model for the North Aegean Sea. Ocean Sci. 2007, 3, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Androulidakis, Y.S.; Krestenitis, Y.N.; Kourafalou, V.H. Connectivity of North Aegean circulation to the Black Sea water budget. Cont. Shelf Res. 2012, 48, 8–26. [Google Scholar] [CrossRef]
- Kanarska, Y.; Maderich, V. Modelling of seasonal exchange flows through the Dardanelles Strait. Estuar. Coast. Shelf Sci. 2008, 79, 449–458. [Google Scholar] [CrossRef]
- Sannino, G.; Sözer, A.; Özsoy, E. A high-resolution modelling study of the Turkish Straits System. Ocean Dyn. 2017, 67, 397–432. [Google Scholar] [CrossRef]
- Sözer, A.; Özsoy, E. Modeling of the Bosphorus exchange flow dynamics. Ocean Dyn. 2017, 67, 321–343. [Google Scholar] [CrossRef]
- Aydoğdu, A.; Pinardi, N.; Özsoy, E.; Danabasoglu, G.; Gürses, O.; Karspeck, A. Circulation of the Turkish Straits System under interannual atmospheric forcing. Ocean Sci. 2018, 14, 999–1019. [Google Scholar] [CrossRef] [Green Version]
- Ilicak, M.; Federico, I.; Barletta, I.; Mutlu, S.; Karan, H.; Ciliberti, S.A.; Clementi, E.; Coppini, G.; Pinardi, N. Modeling of the Turkish Strait System Using a High Resolution Unstructured Grid Ocean Circulation Model. J. Mar. Sci. Eng. 2021, 9, 769. [Google Scholar] [CrossRef]
- Somot, S.; Sevault, F.; Déqué, M.; Crépon, M. 21st century climate change scenario for the Mediterranean using a coupled atmosphere–ocean regional climate model. Glob. Planet. Change 2008, 63, 112–126. [Google Scholar] [CrossRef] [Green Version]
- Mavropoulou, A.M.; Vervatis, V.; Sofianos, S. The Mediterranean Sea overturning circulation: A hindcast simulation (1958–2015) with an eddy-resolving (1/36) model. Deep Sea Res. Part I Oceanogr. Res. Pap. 2022, 187, 103846. [Google Scholar] [CrossRef]
- Soto-Navarro, J.; Jordá, G.; Amores, A.; Cabos, W.; Somot, S.; Sevault, F.; Macías, D.; Djurdjevic, V.; Sannino, G.; Li, L.; et al. Evolution of Mediterranean Sea water properties under climate change scenarios in the Med-CORDEX ensemble. Clim. Dyn. 2020, 54, 2135–2165. [Google Scholar] [CrossRef] [Green Version]
- Sein, D.V.; Mikolajewicz, U.; Gröger, M.; Fast, I.; Cabos, W.; Pinto, J.G.; Hagemann, S.; Semmler, T.; Izquierdo, A.; Jacob, D. Regionally coupled atmosphere-ocean-sea ice-marine biogeochemistry model ROM: 1. Description and validation. J. Adv. Model. Earth Syst. 2015, 7, 268–304. [Google Scholar] [CrossRef]
- Ferrarin, C.; Bellafiore, D.; Sannino, G.; Bajo, M.; Umgiesser, G. Tidal dynamics in the inter-connected Mediterranean, Marmara, Black and Azov seas. Prog. Oceanogr. 2018, 161, 102–115. [Google Scholar] [CrossRef]
- Napolitano, E.; Iacono, R.; Palma, M.; Sannino, G.; Carillo, A.; Lombardi, E.; Pisacane, G.; Struglia, M.V. MITO: A new operational model for the forecasting of the Mediterranean sea circulation. Front. Energy Res. 2022, 10, 941606. [Google Scholar] [CrossRef]
- Sannino, G.; Carillo, A.; Iacono, R.; Napolitano, E.; Palma, M.; Pisacane, G.; Struglia, M. Modelling present and future climate in the Mediterranean Sea: A focus on sea-level change. Clim. Dyn. 2022, 59, 357–391. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res. Ocean. 2003, 108, 3090. [Google Scholar] [CrossRef] [Green Version]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Hogg, A.M.; Ivey, G.N.; Winters, K.B. Hydraulics and mixing in controlled exchange flows. J. Geophys. Res. Ocean. 2001, 106, 959–972. [Google Scholar] [CrossRef]
- Sannino, G.; Carillo, A.; Artale, V. Three-layer view of transports and hydraulics in the Strait of Gibraltar: A three-dimensional model study. J. Geophys. Res. Ocean. 2007, 112, C03010. [Google Scholar] [CrossRef] [Green Version]
- Maderich, V.; Konstantinov, S.; Kulik, A.; Oleksiuk, V. Laboratory modelling of the water exchange through the sea straits. OKEANOLOGIYA 1998, 38, 665–672. [Google Scholar]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015, 2, 331–345. [Google Scholar] [CrossRef]
- Martinho, A.S.; Batteen, M.L. On reducing the slope parameter in terrain-following numerical ocean models. Ocean Model. 2006, 13, 166–175. [Google Scholar] [CrossRef] [Green Version]
- Beckmann, A.; Haidvogel, D. Numerical simulation of flow around a tall isolated seamount. Part I: Problem formulation and model accuracy. J. Phys. Oceanogr. 1993, 23, 1736–1753. [Google Scholar] [CrossRef]
- Haney, R.L. On the Pressure Gradient Force over Steep Topography in Sigma Coordinate Ocean Models. J. Phys. Oceanogr. 1991, 21, 610–619. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Galperin, B.; Kantha, L.H.; Hassid, S.; Rosati, A. A Quasi-equilibrium Turbulent Energy Model for Geophysical Flows. J. Atmos. Sci. 1988, 45, 55–62. [Google Scholar] [CrossRef]
- Allen, J.S.; Newberger, P.A.; Federiuk, J. Upwelling Circulation on the Oregon Continental Shelf. Part I: Response to Idealized Forcing. J. Phys. Oceanogr. 1995, 25, 1843–1866. [Google Scholar] [CrossRef]
- Kantha, L.; Clayson, C. Numerical Models of Oceans and Oceanic Processes. Int. Geophys. Ser. 1994, 66, 940. [Google Scholar]
- Smolarkiewicz, P.K.; Margolin, L.G. MPDATA: A Finite-Difference Solver for Geophysical Flows. J. Comput. Phys. 1998, 140, 459–480. [Google Scholar] [CrossRef] [Green Version]
- Chapman, D. Numerical Treatment of Cross-Shelf Open Boundaries in a Barotropic Coastal Ocean Model. J. Phys. Oceanogr. 1985, 15, 1060–1075. [Google Scholar] [CrossRef]
- Marchesiello, P.; McWilliams, J.C.; Shchepetkin, A. Open boundary conditions for long-term integration of regional oceanic models. Ocean Model. 2001, 3, 1–20. [Google Scholar] [CrossRef]
- Flather, R. A tidal model of the northwest European continental shelf. Mem. Soc. R. Sci. Liege 1976, 6, 141–164. [Google Scholar]
- Mason, E.; Molemaker, J.; Shchepetkin, A.F.; Colas, F.; McWilliams, J.C.; Sangrà, P. Procedures for offline grid nesting in regional ocean models. Ocean Model. 2010, 35, 1–15. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Rogers, D.P.; Edson, J.B.; Young, G.S. Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment. J. Geophys. Res. Ocean. 1996, 101, 3747–3764. [Google Scholar] [CrossRef] [Green Version]
- Paulson, C.A.; Simpson, J.J. Irradiance Measurements in the Upper Ocean. J. Phys. Oceanogr. 1977, 7, 952–956. [Google Scholar] [CrossRef]
- Pinardi, N.; Zavatarelli, M.; Adani, M.; Coppini, G.; Fratianni, C.; Oddo, P.; Simoncelli, S.; Tonani, M.; Lyubartsev, V.; Dobricic, S.; et al. Mediterranean Sea large-scale low-frequency ocean variability and water mass formation rates from 1987 to 2007: A retrospective analysis. Prog. Oceanogr. 2015, 132, 318–332. [Google Scholar] [CrossRef]
- Simoncelli, S.; Fratianni, C.; Pinardi, N.; Grandi, A.; Drudi, M.; Oddo, P.; Dobricic, S. Mediterranean Sea Physical Reanalysis (CMEMS MED-Physics). 2019. Available online: https://www.cmcc.it/mediterranean-sea-physical-reanalysis-cmems-med-physics (accessed on 1 February 2020).
- Maillard, C.; Balopoulos, E.; The MEDAR Group. Recent advances in oceanographic data management of the Mediterranean and Black Seas: The MEDAR/MEDATLAS 2002 data base. The colour of Ocean Data. In Proceedings of the Internatinal Symposium on Oceanographic Data and Information Management with Special Attention to Biological Data, Brussels, Belgium, 25–27 November 2002. [Google Scholar]
- Simoncelli, S.; Schaap, D.; Schlitzer, R. SeaDataNet—Mediterranean Sea—Temperature and Salinity Observation Collection V2. 2015. Available online: https://sextant.ifremer.fr/record/8c3bd19b-9687-429c-a232-48b10478581c/ (accessed on 24 January 2019).
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Venice System, Symposium on the Classification of Brackish Waters, Venice, April 8–14. Arch. Oceanogr. Limnol. 1958, 11, 1–248.
- Bellafiore, D.; Ferrarin, C.; Maicu, F.; Manfè, G.; Lorenzetti, G.; Umgiesser, G.; Zaggia, L.; Levinson, A.V. Saltwater Intrusion in a Mediterranean Delta Under a Changing Climate. J. Geophys. Res. Ocean. 2021, 126, e2020JC016437. [Google Scholar] [CrossRef]
- Pisano, A.; Buongiorno Nardelli, B.; Tronconi, C.; Santoleri, R. The new Mediterranean optimally interpolated pathfinder AVHRR SST Dataset (1982–2012). Remote Sens. Environ. 2016, 176, 107–116. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Tronconi, C.; Pisano, A.; Santoleri, R. High and Ultra-High resolution processing of satellite Sea Surface Temperature data over Southern European Seas in the framework of MyOcean project. Remote Sens. Environ. 2013, 129, 1–16. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Colella, S.; Santoleri, R.; Guarracino, M.; Kholod, A. A re-analysis of Black Sea surface temperature. J. Mar. Syst. 2010, 79, 50–64. [Google Scholar] [CrossRef]
- EU Copernicus Marine Service. Altimeter Satellite Gridded Sea Level Anomalies (SLA) Computed with Respect to a Twenty-Year 2012 Mean. Product SEALEVEL_EUR_PHY_L4_MY_008_068. Available online: https://data.marine.copernicus.eu/product/SEALEVEL_EUR_PHY_L4_MY_008_068/description (accessed on 21 November 2021).
- Maderich, V.; Ilyin, Y.; Lemeshko, E. Seasonal and interannual variability of the water exchange in the Turkish Straits System estimated by modelling. Mediterr. Mar. Sci. 2015, 16, 444–459. [Google Scholar] [CrossRef] [Green Version]
- Mamoutos, I.; Zervakis, V.; Tragou, E.; Karydis, M.; Frangoulis, C.; Kolovoyiannis, V.; Georgopoulos, D.; Psarra, S. The role of wind-forced coastal upwelling on the thermohaline functioning of the North Aegean Sea. Cont. Shelf Res. 2017, 149, 52–68. [Google Scholar] [CrossRef]
- Mamoutos, I.G.; Potiris, E.; Tragou, E.; Zervakis, V.; Petalas, S. A high-resolution numerical model of the North Aegean Sea aimed at climatological studies. J. Mar. Sci. Eng. 2021, 9, 1463. [Google Scholar] [CrossRef]
- Jarosz, E.; Teague, W.J.; Book, J.W.; Beşiktepe, S.T. Observed volume fluxes and mixing in the Dardanelles Strait. J. Geophys. Res. Ocean. 2013, 118, 5007–5021. [Google Scholar] [CrossRef] [Green Version]
- Beşiktepe, S.T. Density Currents in the Two-Layer Flow: An Example of Dardanelles Outflow. Oceanol. Acta 2003, 26, 243–253. [Google Scholar] [CrossRef] [Green Version]
- Beşiktepe, S.T.; Sur, H.I.; Özsoy, E.; Latif, M.A.; Oğuz, T.; Ünlüata, U. The circulation and hydrography of the Marmara Sea. Prog. Oceanogr. 1994, 34, 285–334. [Google Scholar] [CrossRef]
- Ciliberti, S.A.; Jansen, E.; Coppini, G.; Peneva, E.; Azevedo, D.; Causio, S.; Stefanizzi, L.; Creti’, S.; Lecci, R.; Lima, L.; et al. The Black Sea Physics Analysis and Forecasting System within the Framework of the Copernicus Marine Service. J. Mar. Sci. Eng. 2022, 10, 48. [Google Scholar] [CrossRef]
- Lima, L.; Masina, S.; Ciliberti, S.A.; Peneva, E.L.; Cretí, S.; Stefanizzi, L.; Lecci, R.; Palermo, F.; Coppini, G.; Pinardi, N.; et al. Black Sea Physical Reanalysis (CMEMS BS-Currents). 2020. Available online: https://www.cmcc.it/black-sea-physical-reanalysis-cmems-bs-currents (accessed on 20 July 2021).
- Kassis, D.; Korres, G. Recent hydrological status of the Aegean Sea derived from free drifting profilers. Mediterr. Mar. Sci. 2021, 22, 347–361. [Google Scholar] [CrossRef]
- Andersen, O.; Scharroo, R. Range and geophysical corrections in coastal regions: And implications for mean sea surface determination. In Coastal Altimetry; Vignudelli, S., Kostianoy, A., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 103–146. [Google Scholar]
- Ponte, R.M.; Ray, R.D. Atmospheric pressure corrections in geodesy and oceanography: A strategy for handling air tides. Geophys. Res. Lett. 2002, 29, 6-1–6-4. [Google Scholar] [CrossRef]
- Vervatis, V.; Sofianos, S.; Skliris, N.; Somot, S.; Lascaratos, A.; Rixen, M. Mechanisms controlling the thermohaline circulation pattern variability in the Aegean–Levantine region. A hindcast simulation (1960–2000) with an eddy resolving model. Deep Sea Res. Part Oceanogr. Res. Pap. 2013, 74, 82–97. [Google Scholar] [CrossRef]
















| Basin/Location | Min. | Average | Max. |
|---|---|---|---|
| North Aegean Sea | 1.29 | 1.85 | 2.78 |
| South Aegean Sea | 2.29 | 3.05 | 4.15 |
| Ionian Sea | 2.05 | 4.43 | 7.34 |
| Levantine Sea | 2.56 | 3.80 | 5.61 |
| Black Sea | 1.49 | 2.49 | 3.64 |
| Dardanelles/Bosphorus | 1.21 | 1.39 | 1.45 |
| Overall | 1.21 | 3.05 | 7.34 |
| Basin | SST (°C) | Bias (°C) | RMSE (°C) | Pearson’s R (De-Seasoned) |
|---|---|---|---|---|
| Aegean Sea | 19.37 | 0.46 | 0.808 | 0.824 |
| Adriatic Sea | 18.62 | 0.66 | 0.952 | 0.852 |
| Ionian Sea | 20.86 | 0.58 | 0.802 | 0.790 |
| Levantine Sea | 21.55 | 0.40 | 0.771 | 0.783 |
| Black Sea | 15.79 | 0.76 | 1.310 | 0.808 |
| Overall | 19.61 | 0.55 | 0.891 | 0.804 |
| Basin | Bias (m) | RMSE (m) | Pearson’s R | ||
|---|---|---|---|---|---|
| Seasonal | De-Seasoned | Seasonal | De-Seasoned | ||
| Aegean Sea | 0.012 | 0.053 | 0.035 | 0.692 | 0.652 |
| Adriatic Sea | 0.012 | 0.049 | 0.031 | 0.702 | 0.641 |
| Ionian Sea | 0.012 | 0.048 | 0.026 | 0.722 | 0.636 |
| Levantine Sea | 0.012 | 0.052 | 0.032 | 0.680 | 0.616 |
| Black Sea | 0.009 | 0.069 | 0.057 | 0.494 | 0.590 |
| Overall | 0.011 | 0.043 | 0.027 | 0.690 | 0.701 |
| (All Flows in ) | EMBS Simulation | Box-Model | Observations | ||||
|---|---|---|---|---|---|---|---|
| Period | Location/Layer | Mean | StD | Mean | StD | Mean | StD |
| Bosp. Upper | 15.7 | 9.4 | 13.9 | 4.5 | — | — | |
| Bosp. Lower | 4.0 | 4.6 | 5.6 | 2.3 | — | — | |
| Bosp. Net | 11.8 | 12.1 | 8.4 | 6.8 | — | — | |
| 1985–2009 | |||||||
| Dard. Upper | 27.6 | 13.7 | 23.9 | 3.6 | — | — | |
| Dard. Lower | 15.6 | 5.8 | 15.7 | 4.1 | — | — | |
| Dard. Net | 12.0 | 11.2 | 8.3 | 6.8 | — | — | |
| Dard. Upper | 29.4 | 12.2 | 23.2 | 3.5 | 37.8 | 16.4 | |
| 2008–2009 | Dard. Lower | 15.1 | 5.3 | 16.6 | 4.6 | 32.8 | 13.4 |
| Dard. Net | 14.4 | 10.7 | 6.6 | 7.7 | 5.0 | 23.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petalas, S.; Tragou, E.; Mamoutos, I.G.; Zervakis, V. Simulating the Interconnected Eastern Mediterranean–Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast. J. Mar. Sci. Eng. 2022, 10, 1786. https://doi.org/10.3390/jmse10111786
Petalas S, Tragou E, Mamoutos IG, Zervakis V. Simulating the Interconnected Eastern Mediterranean–Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast. Journal of Marine Science and Engineering. 2022; 10(11):1786. https://doi.org/10.3390/jmse10111786
Chicago/Turabian StylePetalas, Stamatios, Elina Tragou, Ioannis G. Mamoutos, and Vassilis Zervakis. 2022. "Simulating the Interconnected Eastern Mediterranean–Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast" Journal of Marine Science and Engineering 10, no. 11: 1786. https://doi.org/10.3390/jmse10111786
APA StylePetalas, S., Tragou, E., Mamoutos, I. G., & Zervakis, V. (2022). Simulating the Interconnected Eastern Mediterranean–Black Sea System on Climatic Timescales: A 30-Year Realistic Hindcast. Journal of Marine Science and Engineering, 10(11), 1786. https://doi.org/10.3390/jmse10111786









