Load Resistance Factor for Vertical Caisson Breakwater in Korea
Abstract
:1. Introduction
2. PSF vs. LRFD
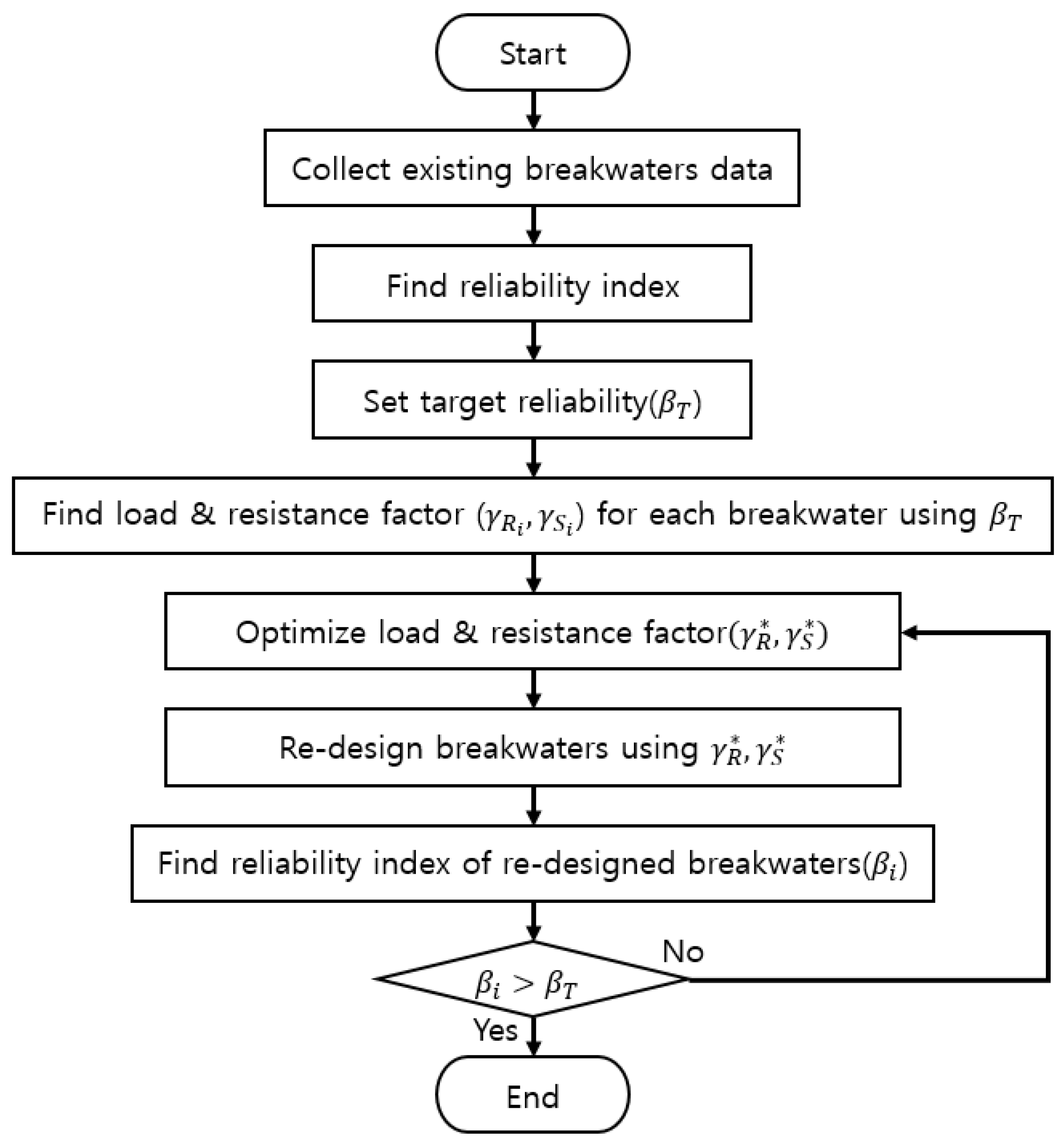
3. Load Resistance Factor Calibration Procedure
4. Reliability Analysis of Breakwater
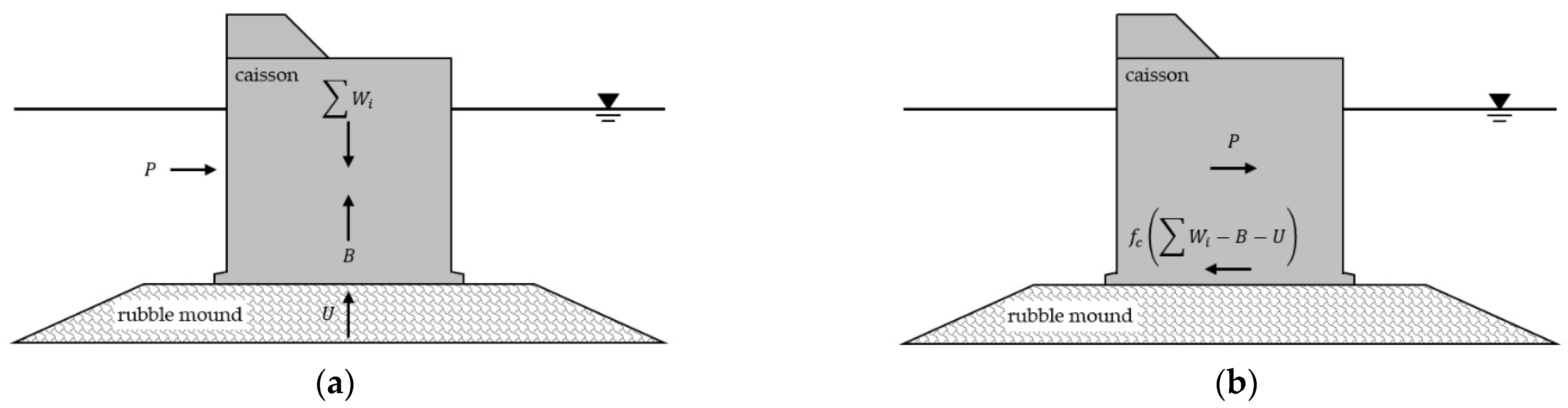
4.1. Failure Modes and Limit States
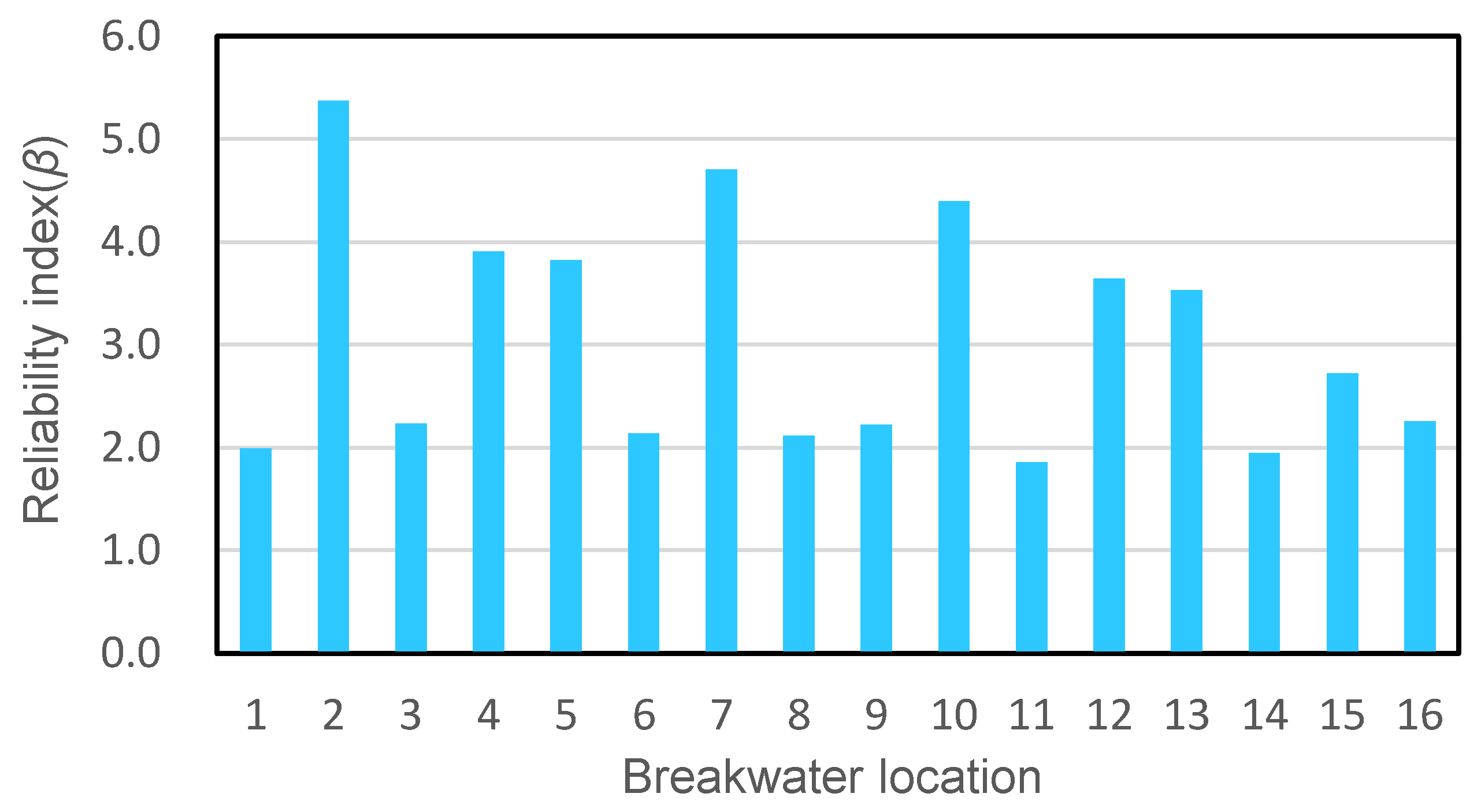
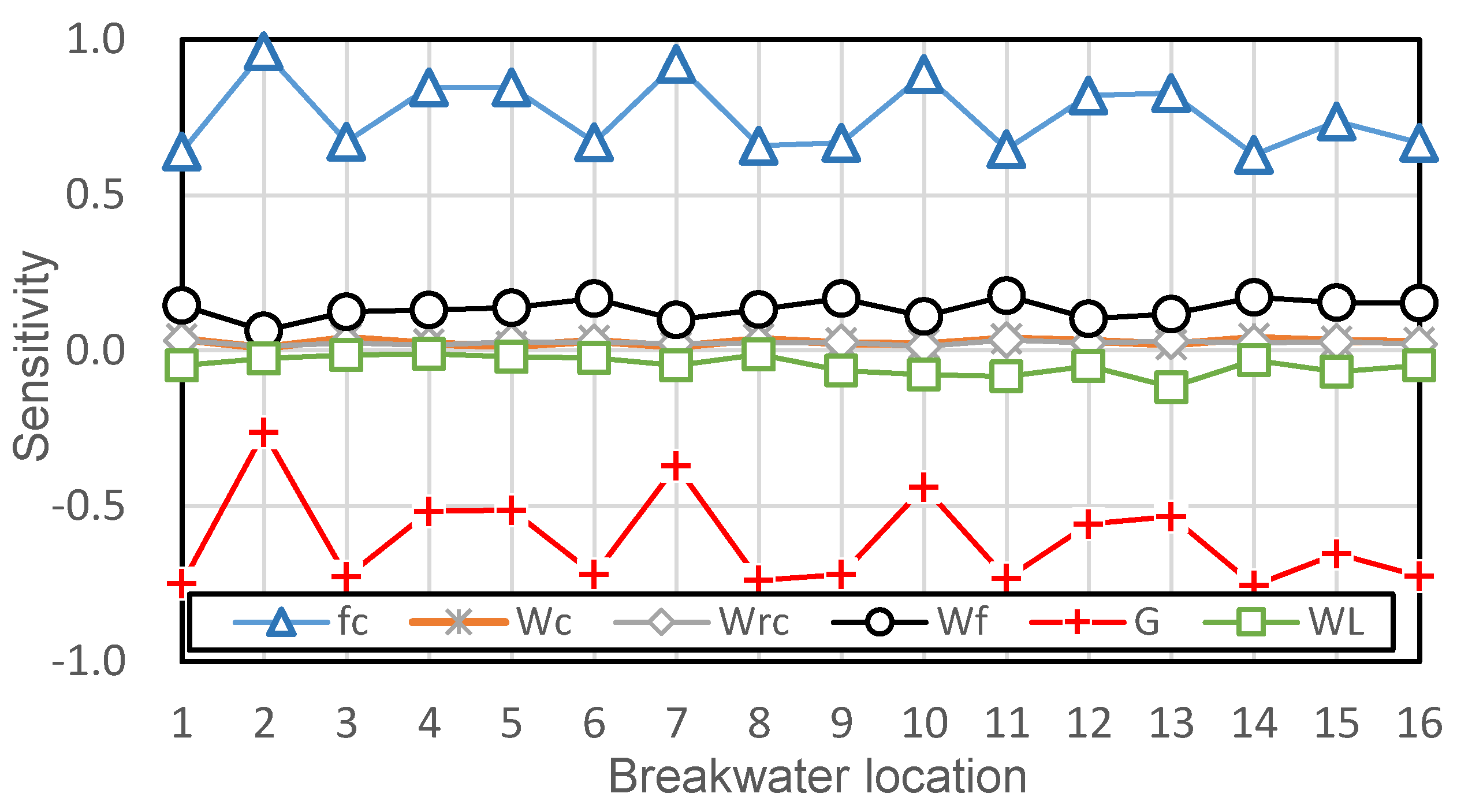
4.2. Reliability Analysis
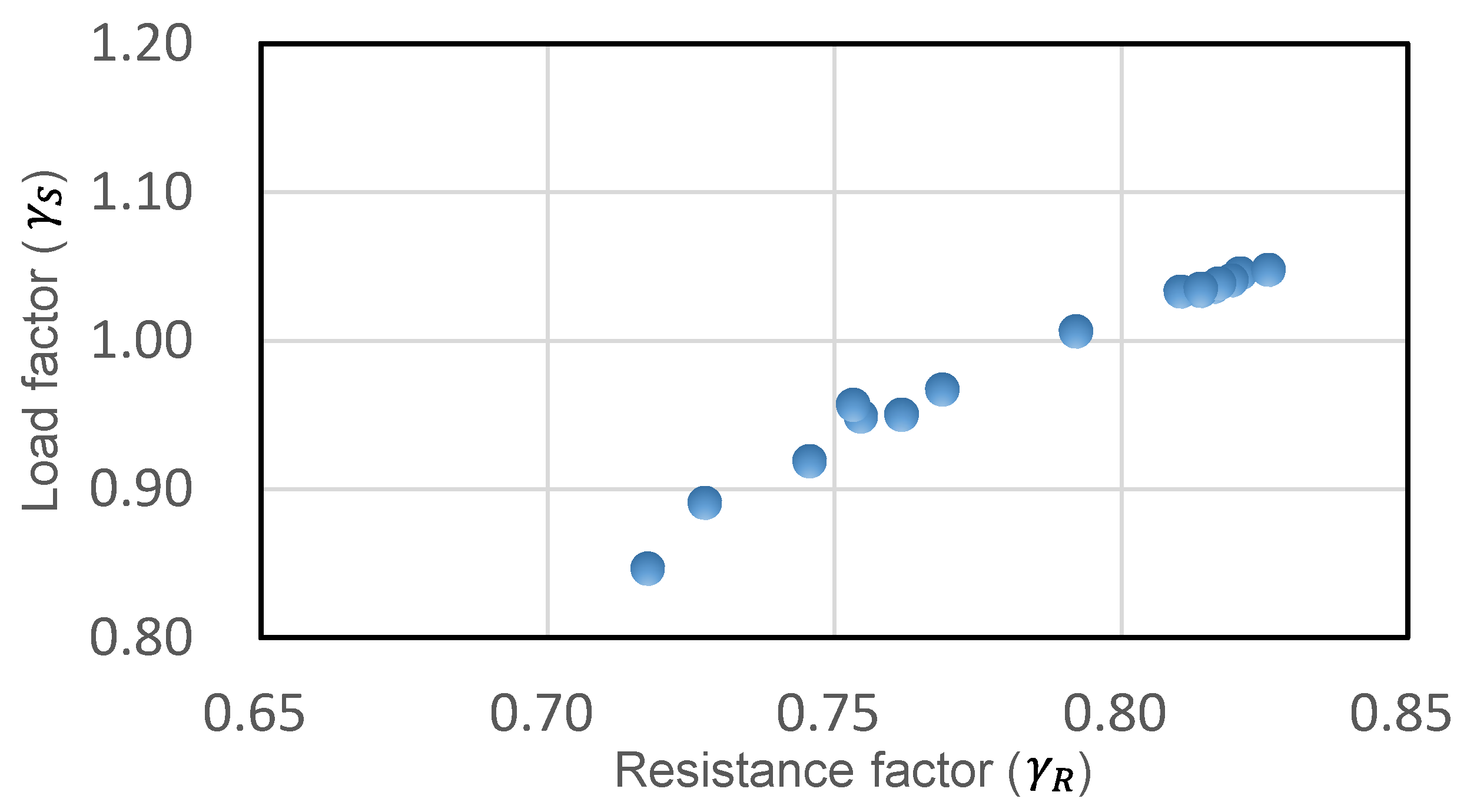
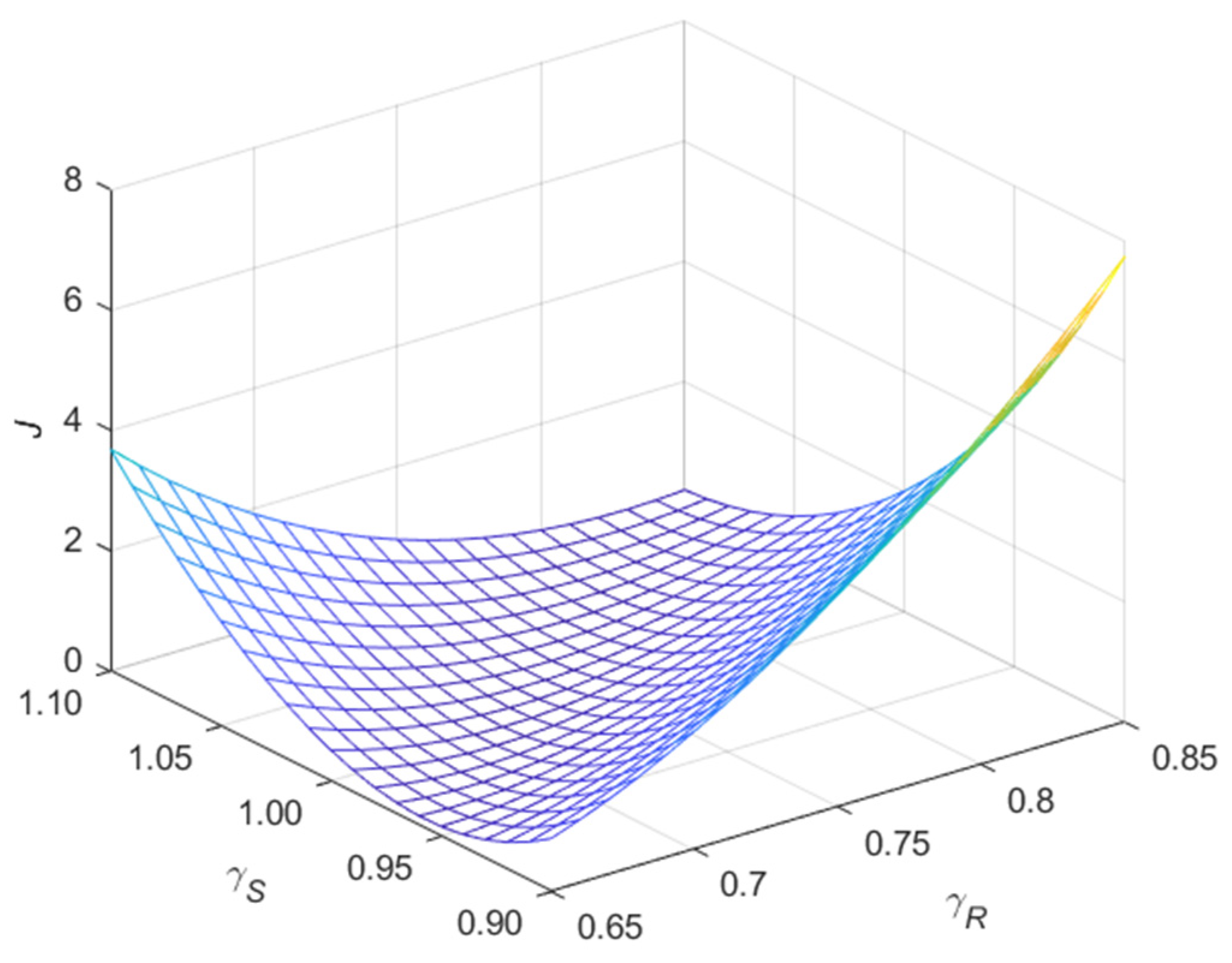
5. Code Calibration
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Safety factor | |
| Friction coefficient between caisson and rubble mound | |
| Weight of material i(i = c for concrete, rc for reinforced concrete, f for filler), kN | |
| Buoyancy, kN | |
| Unit weight of seawater, kN/m3 | |
| Water level, m | |
| Depth to bottom of caisson, m | |
| Caisson width, m | |
| Volume of front and rear heel, m3 | |
| Uplift force, kN | |
| Design value of uplift force, kN | |
| Horizontal wave force, kN | |
| Design value of horizontal wave force, kN | |
| Probability of failure | |
| Target probability of failure | |
| Limit state function of failure mode i(i = s for sliding, o for overturning mode) | |
| Probability density function | |
| Design random variable | |
| Reliability index | |
| Target reliability index | |
| Target reliability index for sliding failure mode | |
| Target reliability index for overturning failure mode | |
| Cumulative density function of standard normal random variable | |
| Partial safety factor of design variable | |
| Resistance factor | |
| Resistance factor for breakwater i | |
| Load factor | |
| Load factor for breakwater i | |
| Moment arm of self-weight, m | |
| Moment arm of buoyancy, m | |
| Moment arm of uplift force, m | |
| Moment arm of horizontal load, m | |
| Uncertainty of wave pressure by Goda’s formula | |
| Sensitivity of limit state function with respect to | |
| Standard deviation of | |
| Mean of | |
| Characteristic value of | |
| Weight of the cost by reliability index | |
| Weight of the cost by load resistance factor | |
| Number of breakwaters used in code calibration | |
| Apparent safety factor |
References
- PIANC. Analysis of Rubble Mound Breakwaters; PIANC: Brussels, Belgium, 1992. [Google Scholar]
- Melby, J.A.; Mlakar, P.F. Reliability Assessment of Breakwater; Technical Report of US Army Corps of Engineers (CHL-97-7); US Army Corps: Washington, DC, USA, 1997. [Google Scholar]
- US Army Corps of Engineers. Coastal Engineering Manual (CEM), Chapter 6: Reliability Based Design of Coastal Structures; US Army Corps: Washington, DC, USA, 2006.
- Japanese Harbor Society. Harbor Facilities Design Code and Commentaries; Japanese Harbor Society: Tokyo, Japan, 2007. [Google Scholar]
- Japanese Harbor Society. Harbor Facilities Design Code and Commentaries; Japanese Harbor Society: Tokyo, Japan, 2018. [Google Scholar]
- Sørenson, J.D.; Kroon, I.B.; Faber, M.H. Optimal reliability code calibration. Struct. Saf. 1994, 15, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Burcharth, H.F.; Sørensen, J.D. Design of vertical wall caisson breakwaters using partial safety factors. In Proceedings of the 26th Conference on Coastal Engineering, New York, NY, USA, 22–26 June 1998. [Google Scholar]
- Nagao, T. Reliability Based Design Method for Caisson Type Quay Walls; Research Report No. 2; National Institute of Land and Infrastructure Management: Tokyo, Japan, 2001. [Google Scholar]
- Yoshioka, T.; Nagao, T. Level 1 Reliability Based Design Method for Gravity Type Breakwaters; Research Report No. 20; National Institute of Land and Infrastructure Management: Tokyo, Japan, 2005. [Google Scholar]
- Sato, T.; Takenobu, M.; Miyata, M. A Basic Study of the Level 1 Reliability Design Method for Gravity-Type Breakwater; Techincal Note No. 922; National Institute of Land and Infrastructure Management: Tokyo, Japan, 2016. [Google Scholar]
- Takano, H.; Takenobu, M.; Miyata, M.; Sato, T. A Study of the Level 1 Reliability Design Method for Gravity-Type Breakwater with Slope; Techincal Note No. 995; National Institute of Land and Infrastructure Management: Tokyo, Japan, 2017. [Google Scholar]
- Kawamata, H.; Takenobu, M.; Miyata, M. A Basic Study of the Level 1 Reliability based Design Method of Circular Slip Failure Verification by Modified Fellenius’ Method; Techincal Note No. 955; National Institute of Land and Infrastructure Management: Tokyo, Japan, 2017. [Google Scholar]
- Kim, S.W.; Suh, K.D. Evaluation of target reliability indices and partial safety factors for sliding of caisson breakwaters. J. Coast. Res. 2011, 21, 622–626. [Google Scholar]
- Lee, C.E.; Kim, S.W.; Park, D.H.; Suh, K.D. Target reliability of caisson sliding of vertical breakwater based on safety factors. Coast. Eng. 2012, 60, 167–173. [Google Scholar] [CrossRef]
- Doan, N.S.; Huh, J.; Mac, V.H.; Kim, D.H.; Kwak, K. Calibration of Load and Resistance Factors for Breakwater Foundations under the Earthquake Loading. Sustainability 2021, 13, 1730. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Kim, D.H. Code Calibration of Load Resistance Factor for Limit State Design of Vertical Breakwater Caisson. In Proceedings of the Korean Society of Coast. & Ocean Engineers, Pyeong-Chang, Korea, 31 December 2019. [Google Scholar]
- Hasofer, A.M.; Lind, N.C. Exact and Invariant Second Moment Code Format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
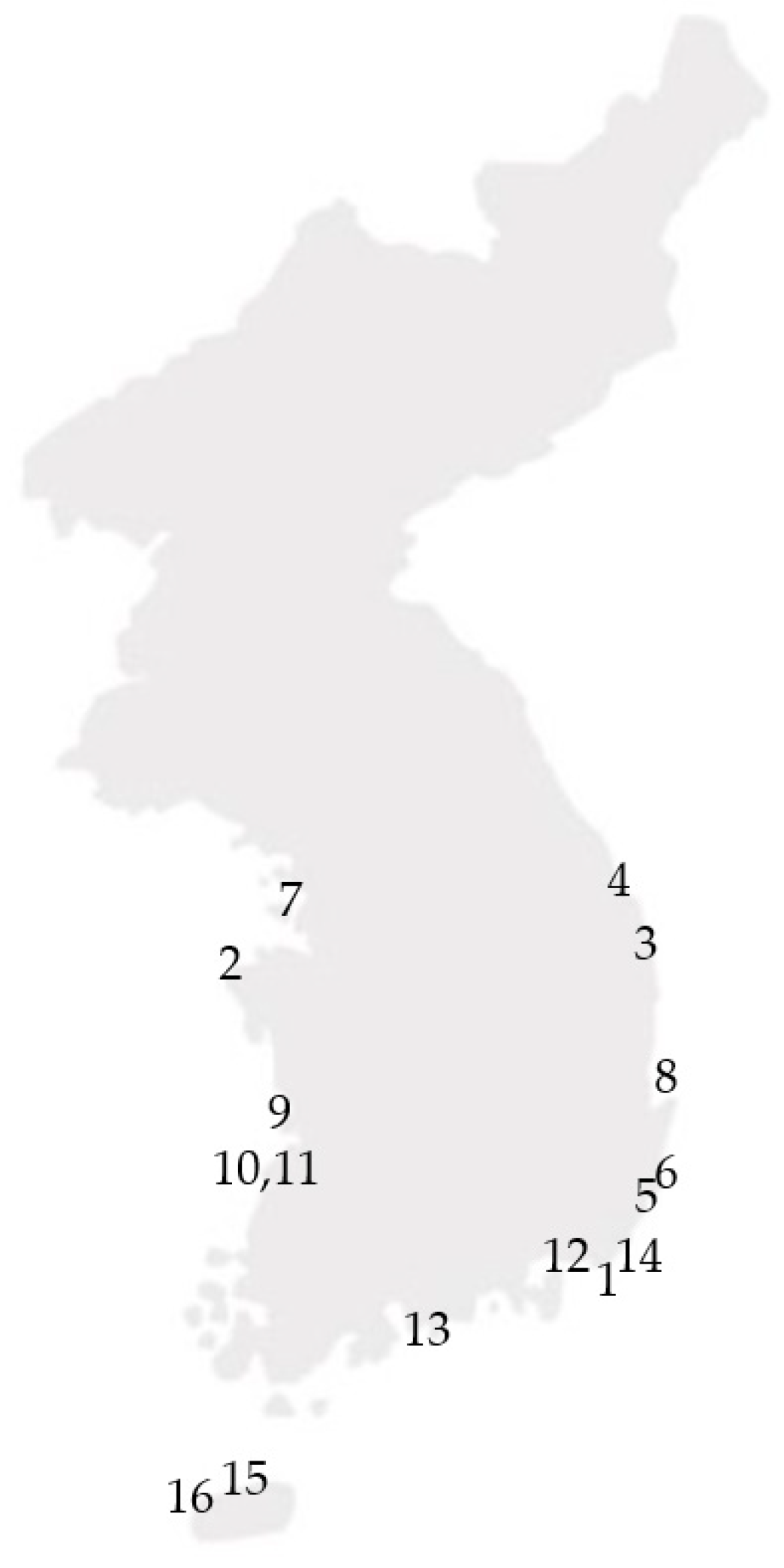


| No | Name | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Gamcheon | 1696.73 | 1500.44 | 3371.6 | 1673.88 | 760.44 | 17.0 | 1.28 | 5.7 | 13.0 | 1.165 |
| 2 | Daesan | 622.66 | 947.74 | 2265.85 | 301.20 | 38.30 | 9.0 | 8.26 | 1.8 | 10.0 | 4.157 |
| 3 | Donghae | 2152.71 | 1341.11 | 3364.56 | 1828.64 | 818.90 | 19.2 | 0.39 | 0 | 10.5 | 1.275 |
| 4 | Okgye | 1569.89 | 1370.87 | 4766.92 | 1247.36 | 494.55 | 18.0 | 0.45 | 3.15 | 15.0 | 2.076 |
| 5 | Onsan | 505.4 | 1134.17 | 2560.46 | 668.67 | 179.18 | 12.0 | 0.61 | 2.0 | 13.5 | 2.025 |
| 6 | Ulsan | 1308.38 | 1098.9 | 3526.02 | 1490.88 | 530.70 | 15.0 | 0.66 | 2.6 | 15.0 | 1.190 |
| 7 | Incheon | 473.45 | 907.33 | 1946.6 | 369.57 | 37.67 | 8.0 | 9.27 | 2.2 | 9.0 | 2.860 |
| 8 | Pohang | 1029.98 | 704.11 | 1841.76 | 970.69 | 436.56 | 13.6 | 0.246 | 0 | 8.0 | 1.226 |
| 9 | Gunsan | 1081.23 | 1284.1 | 3792.07 | 1554.57 | 645.53 | 16.0 | 7.246 | 1.7 | 6.5 | 1.246 |
| 10 | SMG1 | 2088.66 | 1338.46 | 7381.17 | 1247.06 | 444.48 | 17.7 | 7.41 | 1.35 | 11.0 | 3.365 |
| 11 | SMG2 | 1150.13 | 1049.68 | 3532.5 | 1156.36 | 335.03 | 13.5 | 7.41 | 1.35 | 9.5 | 1.573 |
| 12 | MD | 984.72 | 808.4 | 1653.72 | 637.65 | 277.96 | 12.0 | 2.23 | 0 | 7.0 | 1.908 |
| 13 | Yeosu | 379.82 | 618.39 | 1134.95 | 406.36 | 52.03 | 7.0 | 5.4 | 1.7 | 5.9 | 1.844 |
| 14 | Jodo | 2208.65 | 1411.15 | 4752.35 | 2017.99 | 978.11 | 20.0 | 1.44 | 5.0 | 15.5 | 1.146 |
| 15 | Jeju | 2099.94 | 2003.94 | 5279.12 | 2027.67 | 625.54 | 20.0 | 3.83 | 3.2 | 15.0 | 1.434 |
| 16 | Aeweol | 2277.28 | 1779.03 | 6406.18 | 2819.41 | 1292.03 | 23.4 | 2.858 | 5.0 | 10.5 | 1.255 |
| Symbol | Bias Factor | COV | Symbol | Bias Factor | COV |
|---|---|---|---|---|---|
| 1.06 | 0.15 | 1.02 | 0.04 | ||
| 1.02 | 0.02 | 1.00 | 0.05/0.12/0.20 | ||
| 0.98 | 0.02 | 0.74 | 0.239 |
| Sliding | Overturning | ||||||
|---|---|---|---|---|---|---|---|
| 1.80 | 0.0359 | 0.85 | 0.97 | 1.141 | 0.94 | 1.06 | 1.128 |
| 1.90 | 0.0287 | 0.81 | 0.95 | 1.173 | 0.95 | 1.10 | 1.158 |
| 2.00 | 0.0228 | 0.78 | 0.94 | 1.205 | 0.90 | 1.07 | 1.189 |
| 2.10 | 0.0179 | 0.80 | 0.99 | 1.238 | 0.91 | 1.11 | 1.220 |
| 2.20 | 0.0139 | 0.77 | 0.98 | 1.273 | 0.92 | 1.15 | 1.250 |
| 2.30 | 0.0107 | 0.75 | 0.98 | 1.307 | 0.86 | 1.10 | 1.279 |
| 2.40 | 0.0082 | 0.76 | 1.02 | 1.342 | 0.87 | 1.14 | 1.310 |
| 2.50 | 0.0062 | 0.73 | 1.01 | 1.384 | 0.88 | 1.18 | 1.341 |
| 2.60 | 0.0047 | 0.74 | 1.05 | 1.419 | 0.84 | 1.15 | 1.369 |
| 2.70 | 0.0035 | 0.70 | 1.02 | 1.457 | 0.85 | 1.19 | 1.400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, I.-G.; Kim, D.-H. Load Resistance Factor for Vertical Caisson Breakwater in Korea. J. Mar. Sci. Eng. 2022, 10, 468. https://doi.org/10.3390/jmse10040468
Lee I-G, Kim D-H. Load Resistance Factor for Vertical Caisson Breakwater in Korea. Journal of Marine Science and Engineering. 2022; 10(4):468. https://doi.org/10.3390/jmse10040468
Chicago/Turabian StyleLee, Il-Geun, and Dong-Hyawn Kim. 2022. "Load Resistance Factor for Vertical Caisson Breakwater in Korea" Journal of Marine Science and Engineering 10, no. 4: 468. https://doi.org/10.3390/jmse10040468
APA StyleLee, I.-G., & Kim, D.-H. (2022). Load Resistance Factor for Vertical Caisson Breakwater in Korea. Journal of Marine Science and Engineering, 10(4), 468. https://doi.org/10.3390/jmse10040468






