Design and Reconfiguration of Multicomponent Hydrodynamic Manipulation Devices with Arbitrary Complex Structures
Abstract
:1. Introduction
2. Description and Application of the Numerical Theory
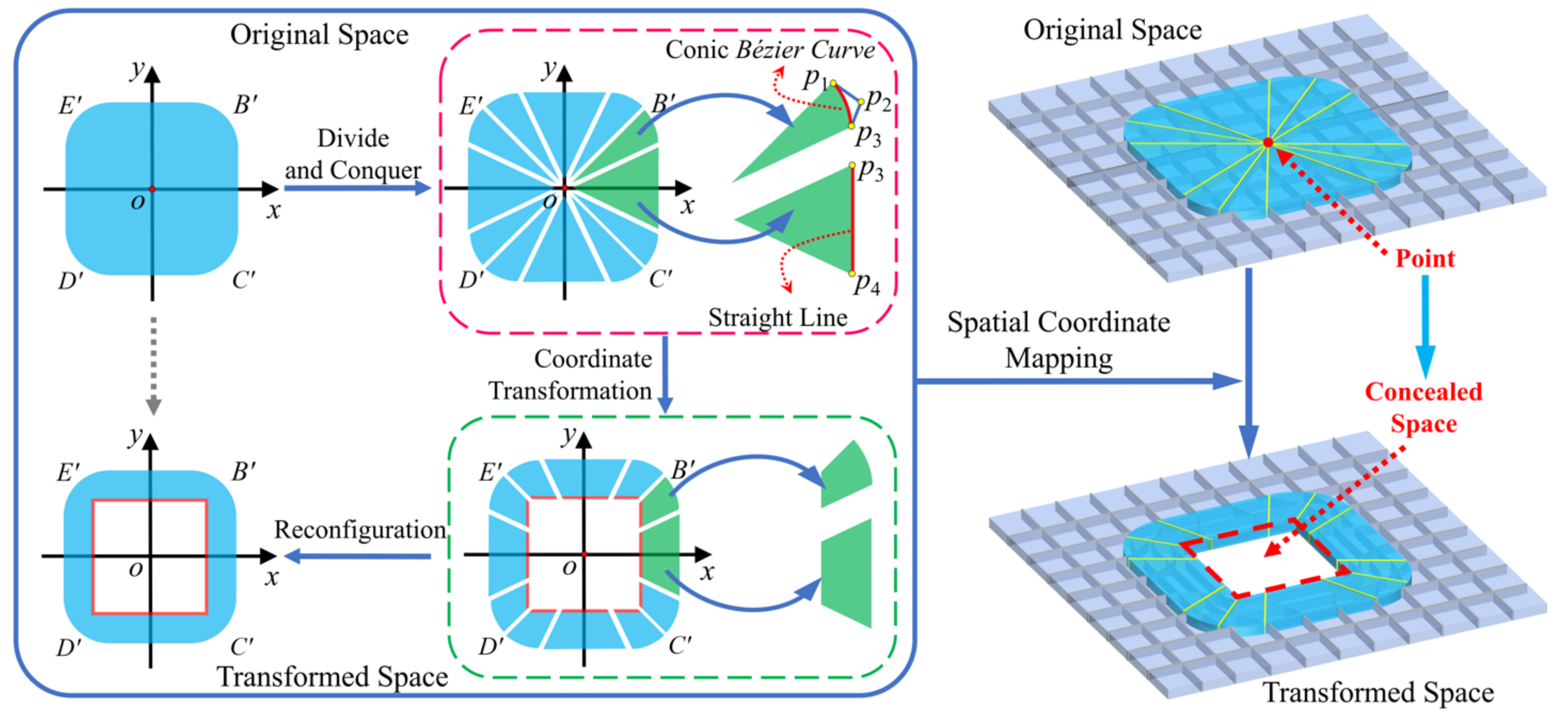
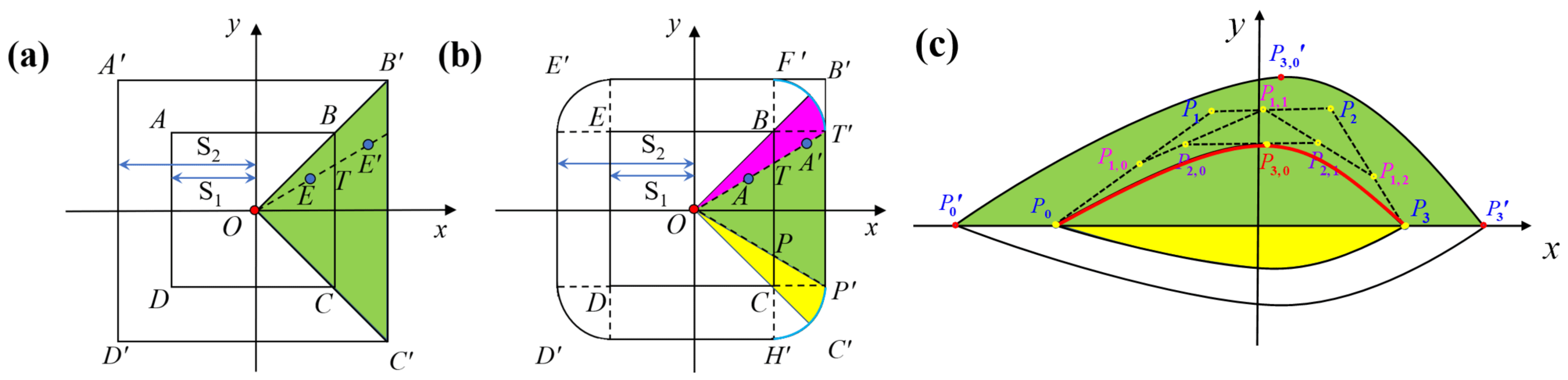
2.1. Divide-and-Conquer Strategy to Construct Arbitrary Geometries
2.2. Numerical Theory Validation and Model Building
3. Results and Discussion
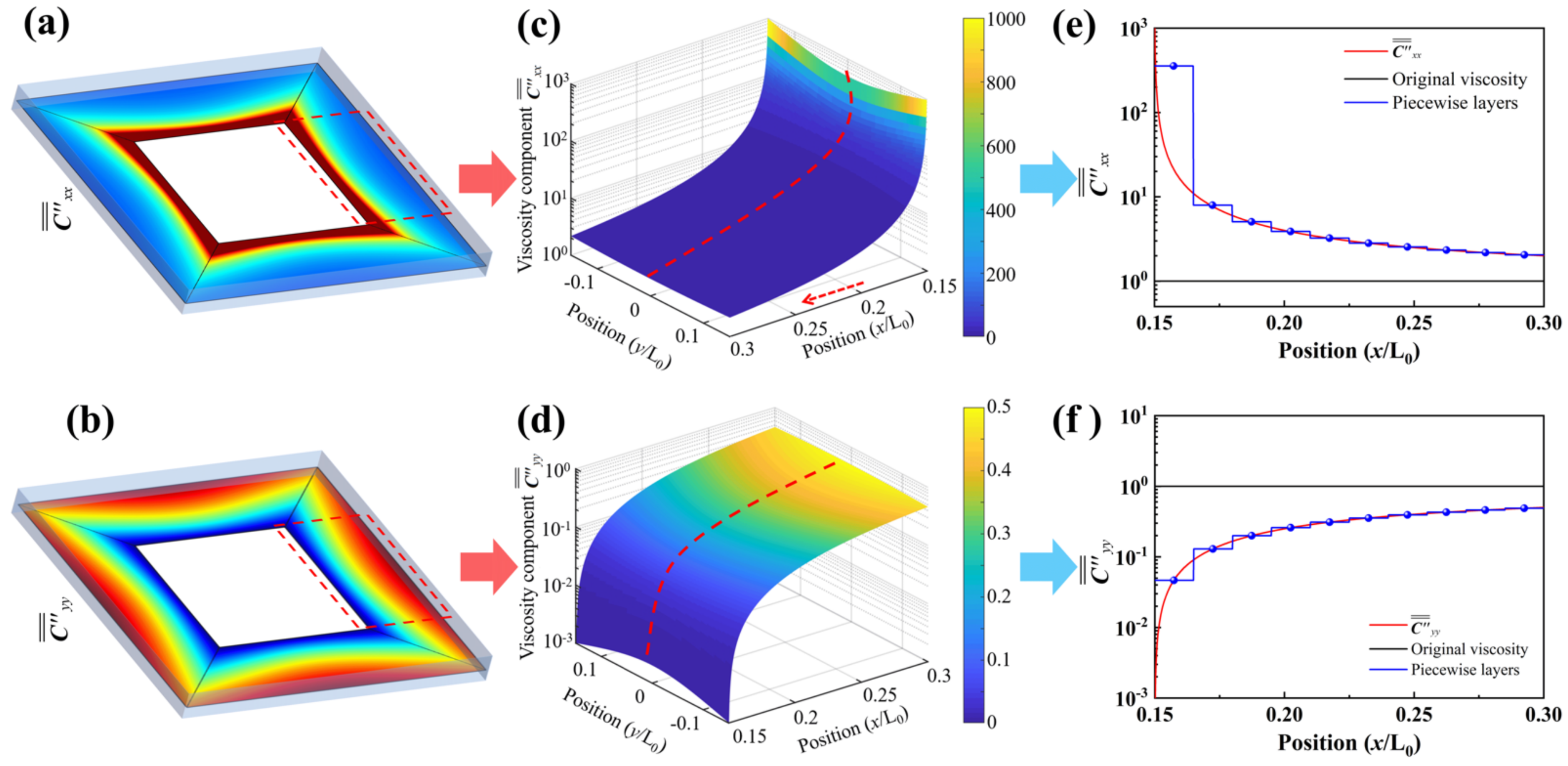
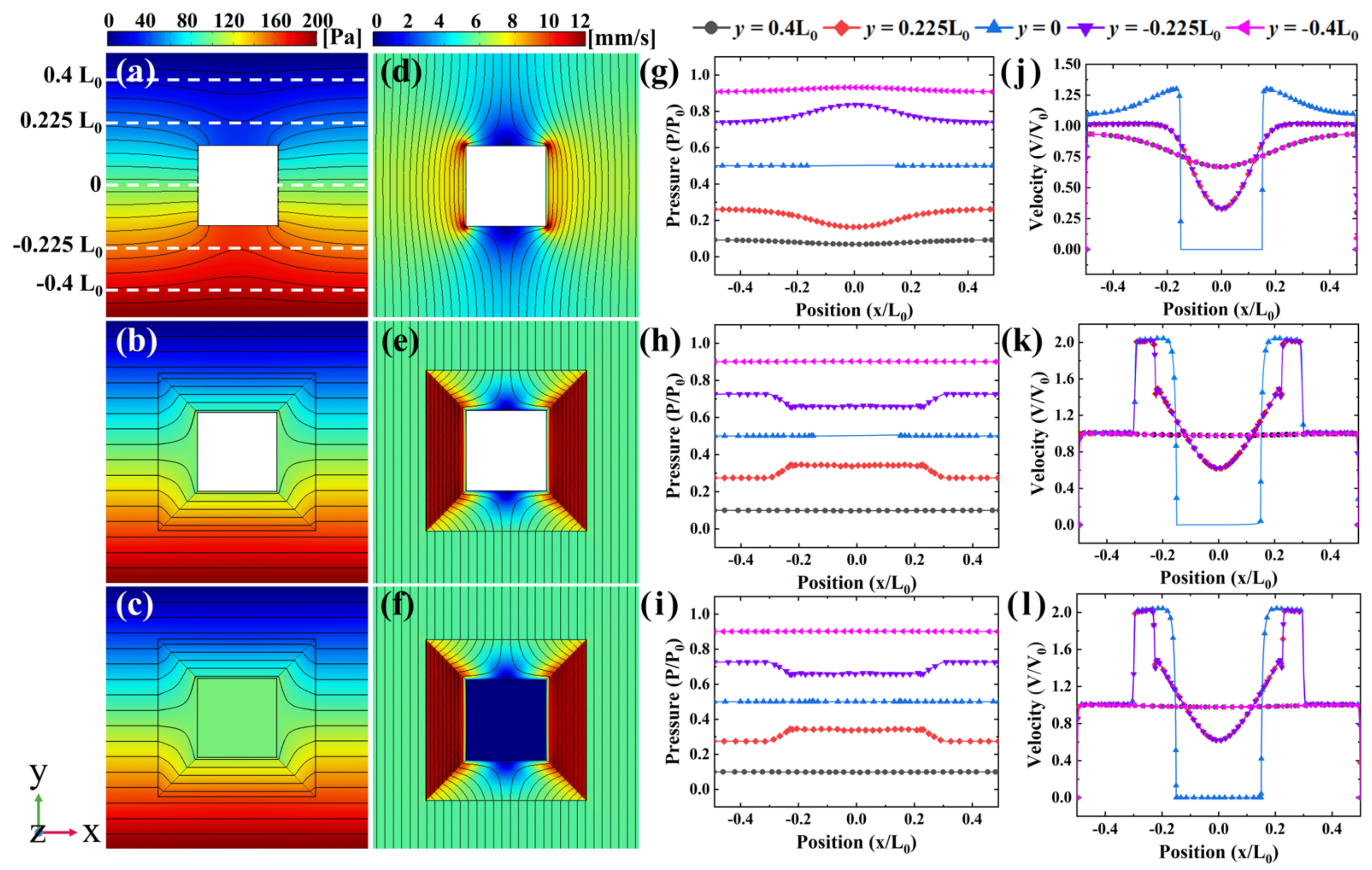
3.1. Analytical Result for the Square Cloak
3.2. Analytical Result for the Square Cylindrical Fillet Cloak
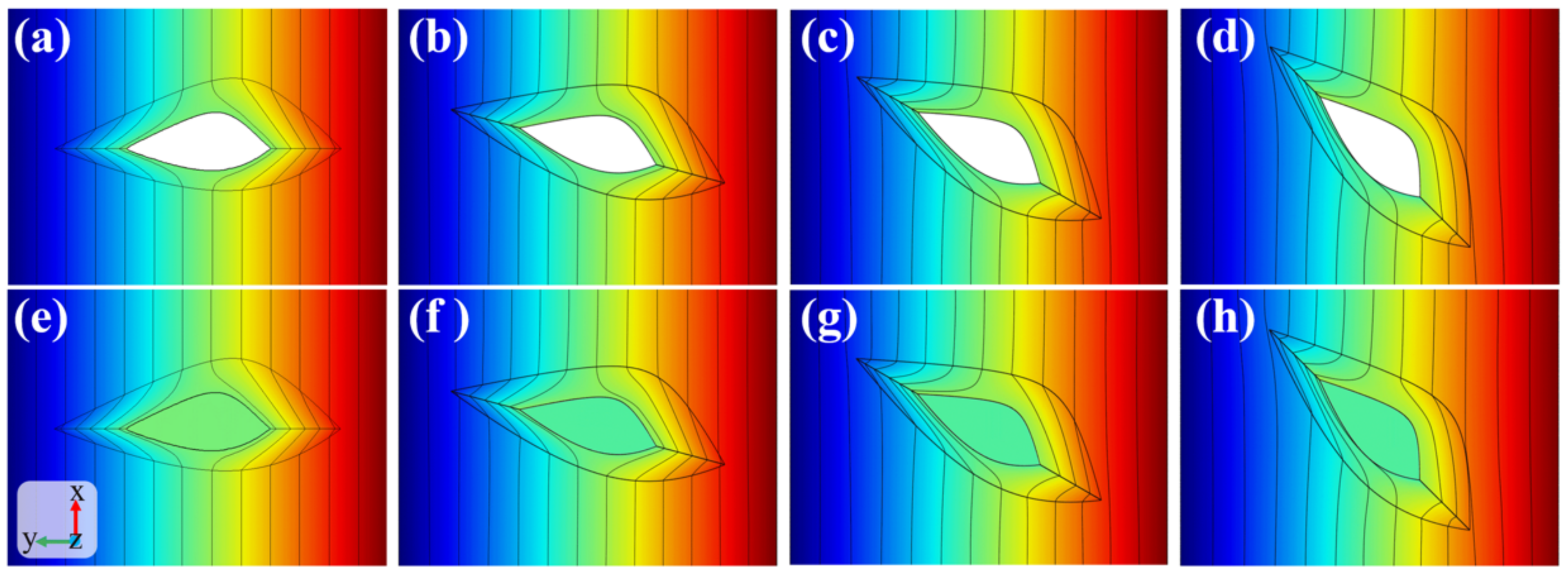
3.3. Analytical Result for the Asymmetric Streamline Body
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alben, S.; Shelley, M.; Zhang, J. Drag reduction through self-similar bending of a flexible body. Nature 2002, 420, 479–481. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Jiao, Z.; Song, Y.; Liu, C.; Wang, H.; Yan, Y. Experimental investigations on drag-reduction characteristics of bionic surface with water-trapping microstructures of fish scales. Sci. Rep. 2018, 8, 12186. [Google Scholar] [CrossRef]
- Stevens, M.; Merilaita, S. Animal camouflage: Current issues and new perspectives. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 423–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cronin, T.W. Camouflage: Being invisible in the open ocean. Curr. Biol. 2016, 26, R1179–R1181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, S.; Zhu, P.; Zheng, H.; Zhan, H.; Chen, C.; Li, J.; Wang, L.; Yao, X.; Liu, Y.; Wang, Z. Three-dimensional capillary ratchet-induced liquid directional steering. Science 2021, 373, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [Green Version]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, Z. Superlenses to overcome the diffraction limit. Nat. Mater. 2008, 7, 435–441. [Google Scholar] [CrossRef]
- Cui, T.J.; Smith, D.R.; Liu, R. Metamaterials: Theory, Design, and Applications; Springer: New York, NY, USA, 2010; ISBN 9781441905727. [Google Scholar]
- Xu, Y.; Fu, Y.; Chen, H. Planar gradient metamaterials. Nat. Rev. Mater. 2016, 1, 16067. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Chen, H. Conformal transformation optics. Nat. Photonics 2014, 9, 15–23. [Google Scholar] [CrossRef]
- Qian, C.; Chen, H. A perspective on the next generation of invisibility cloaks—Intelligent cloaks. Appl. Phys. Lett. 2021, 118, 180501. [Google Scholar] [CrossRef]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation optics and metamaterials. Nat. Mater. 2010, 9, 387–396. [Google Scholar] [CrossRef]
- Cai, W.; Shalaev, V.M. Optical Metamaterials; Springer: New York, NY, USA, 2009; ISBN 9781441911506. [Google Scholar]
- Chen, H.; Hou, B.; Chen, S.; Ao, X.; Wen, W.; Chan, C.T. Design and experimental realization of a broadband transformation media field rotator at microwave frequencies. Phys. Rev. Lett. 2009, 102, 1–4. [Google Scholar] [CrossRef]
- Li, J.; Pendry, J.B. Hiding under the Carpet: A new strategy for cloaking. Phys. Rev. Lett. 2008, 101, 203901. [Google Scholar] [CrossRef] [Green Version]
- Huangfu, J.; Xi, S.; Kong, F.; Zhang, J.; Chen, H.; Wang, D.; Wu, B.I.; Ran, L.; Kong, J.A. Application of coordinate transformation in bent waveguides. J. Appl. Phys. 2008, 104, 014502. [Google Scholar] [CrossRef]
- Jiang, W.X.; Cui, T.J.; Zhou, X.Y.; Yang, X.M.; Cheng, Q. Arbitrary bending of electromagnetic waves using realizable inhomogeneous and anisotropic materials. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 78, 066607. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, H.; Zhang, J.; Ran, L.; Kong, J.A. Design and analytical full-wave validation of the invisibility cloaks, concentrators, and field rotators created with a general class of transformations. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 125127. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.; Ruan, Z.; Qiu, M. Cylindrical invisibility cloak with simplified material parameters is inherently visible. Phys. Rev. Lett. 2007, 99, 233901. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Narayana, S.; Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 2012, 108, 214303. [Google Scholar] [CrossRef]
- Schittny, R.; Kadic, M.; Guenneau, S.; Wegener, M. Experiments on transformation thermodynamics: Molding the flow of heat. Phys. Rev. Lett. 2013, 110, 195901. [Google Scholar] [CrossRef] [Green Version]
- Dai, G.; Shang, J.; Huang, J. Theory of transformation thermal convection for creeping flow in porous media: Cloaking, concentrating, and camouflage. Phys. Rev. E 2018, 97, 022129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeung, W.S.; Mai, V.P.; Yang, R.J. Cloaking: Controlling thermal and hydrodynamic fields simultaneously. Phys. Rev. Appl. 2020, 13, 064030. [Google Scholar] [CrossRef]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Cummer, S.A.; Popa, B.I.; Schurig, D.; Smith, D.R.; Pendry, J.; Rahm, M.; Starr, A. Scattering theory derivation of a 3D acoustic cloaking shell. Phys. Rev. Lett. 2008, 100, 24301. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Chan, C.T. Acoustic cloaking and transformation acoustics. J. Phys. D Appl. Phys. 2010, 43, 113001. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, C.; Fang, N. Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 2011, 106, 24301. [Google Scholar] [CrossRef]
- Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. Metamaterials beyond electromagnetism. Reports Prog. Phys. 2013, 76, 126501. [Google Scholar] [CrossRef]
- Yang, J.; Li, Z.; Xin, X.; Gao, X.; Yuan, X.; Wang, Z.; Yu, Z.; Wang, X.; Zhou, J.; Dong, S. Designing electromechanical metamaterial with full nonzero piezoelectric coefficients. Sci. Adv. 2019, 5, eaax1782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bückmann, T.; Thiel, M.; Kadic, M.; Schittny, R.; Wegener, M. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun. 2014, 5, 4130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bückmann, T.; Kadic, M.; Schittny, R.; Wegener, M. Mechanical cloak design by direct lattice transformation. Proc. Natl. Acad. Sci. USA 2015, 112, 4930–4934. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urzhumov, Y.A.; Smith, D.R. Fluid flow control with transformation media. Phys. Rev. Lett. 2011, 107, 74501. [Google Scholar] [CrossRef]
- Zareei, A.; Alam, M.R. Cloaking in shallow-water waves via nonlinear medium transformation. J. Fluid Mech. 2015, 778, 273–287. [Google Scholar] [CrossRef]
- Park, J.; Youn, J.R.; Song, Y.S. Hydrodynamic metamaterial cloak for drag-free flow. Phys. Rev. Lett. 2019, 123, 74502. [Google Scholar] [CrossRef]
- Zou, S.; Xu, Y.; Zatianina, R.; Li, C.; Liang, X.; Zhu, L.; Zhang, Y.; Liu, G.; Liu, Q.H.; Chen, H.; et al. Broadband waveguide cloak for water waves. Phys. Rev. Lett. 2019, 123, 74501. [Google Scholar] [CrossRef]
- Boyko, E.; Bacheva, V.; Eigenbrod, M.; Paratore, F.; Gat, A.D.; Hardt, S.; Bercovici, M. Microscale hydrodynamic cloaking and shielding via electro-osmosis. Phys. Rev. Lett. 2021, 126, 184502. [Google Scholar] [CrossRef]
- Pang, H.; You, Y.; Feng, A.; Chen, K. Hydrodynamic manipulation cloak for redirecting fluid flow. Phys. Fluids 2022, 34, 053603. [Google Scholar] [CrossRef]
- Park, J.; Song, Y.S. Laminar flow manipulators. Extrem. Mech. Lett. 2020, 40, 100908. [Google Scholar] [CrossRef]
- Park, J.; Song, Y.S. Assembling hydrodynamic cloaks to conceal complex objects from drag. J. Fluids Struct. 2020, 98, 103136. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, H.; You, Y.; Li, T.; Chen, K.; Sheng, L. Design and Reconfiguration of Multicomponent Hydrodynamic Manipulation Devices with Arbitrary Complex Structures. J. Mar. Sci. Eng. 2022, 10, 861. https://doi.org/10.3390/jmse10070861
Pang H, You Y, Li T, Chen K, Sheng L. Design and Reconfiguration of Multicomponent Hydrodynamic Manipulation Devices with Arbitrary Complex Structures. Journal of Marine Science and Engineering. 2022; 10(7):861. https://doi.org/10.3390/jmse10070861
Chicago/Turabian StylePang, Haixiang, Yunxiang You, Tingqiu Li, Ke Chen, and Li Sheng. 2022. "Design and Reconfiguration of Multicomponent Hydrodynamic Manipulation Devices with Arbitrary Complex Structures" Journal of Marine Science and Engineering 10, no. 7: 861. https://doi.org/10.3390/jmse10070861
APA StylePang, H., You, Y., Li, T., Chen, K., & Sheng, L. (2022). Design and Reconfiguration of Multicomponent Hydrodynamic Manipulation Devices with Arbitrary Complex Structures. Journal of Marine Science and Engineering, 10(7), 861. https://doi.org/10.3390/jmse10070861






