Analyzing the Inlet Gas Void Fraction on the Flow Characteristics for a Multiphase Pump Based on Cavitation Cases
Abstract
:1. Introduction
2. Computational Model and Method of Multiphase Pump
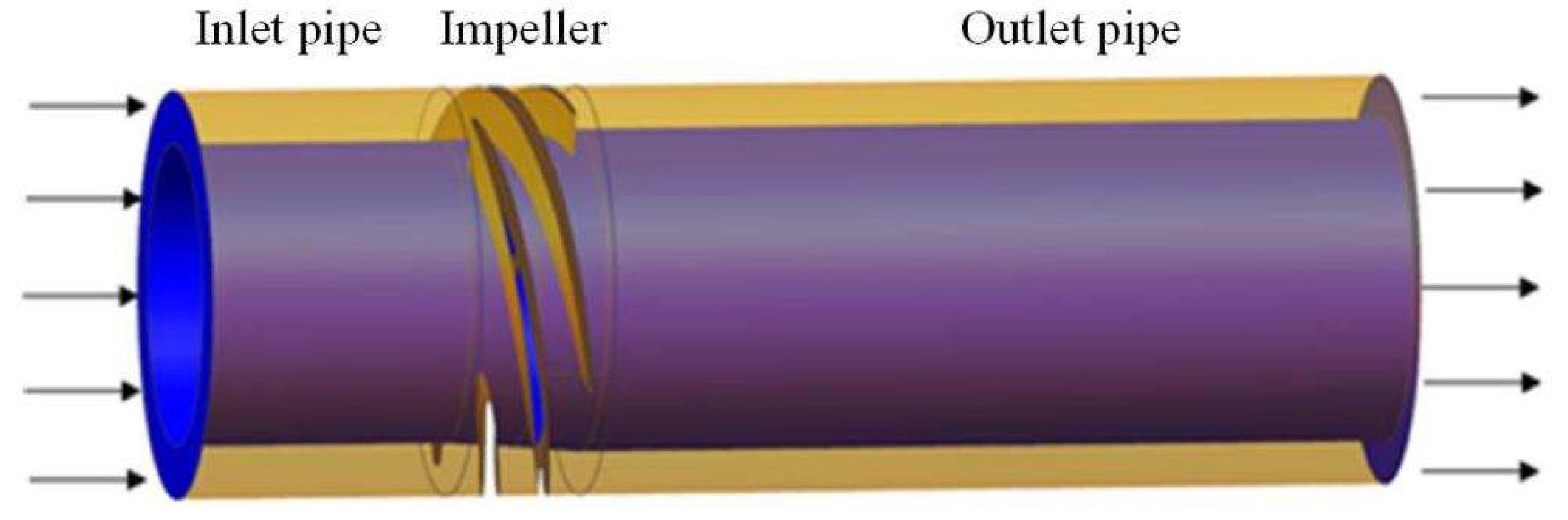
2.1. Computational Model
2.2. Numerical Simulation Theory
2.2.1. Turbulence Model
2.2.2. Multiphase Flow Model
2.2.3. Cavitation Model
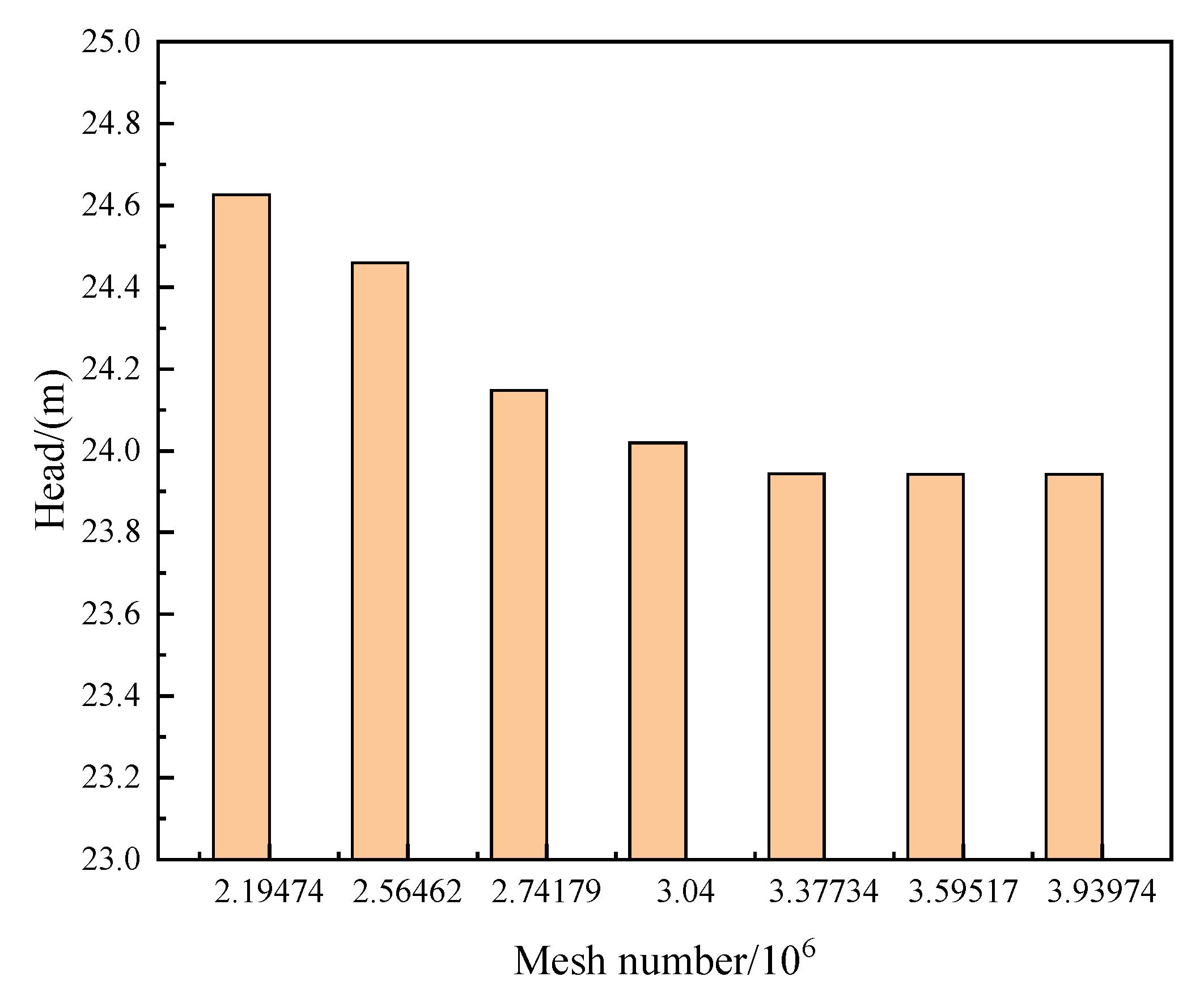
2.3. Mesh and Independent Verification
2.4. Boundary Condition Settings
3. Experimental Rig and Numerical Verification
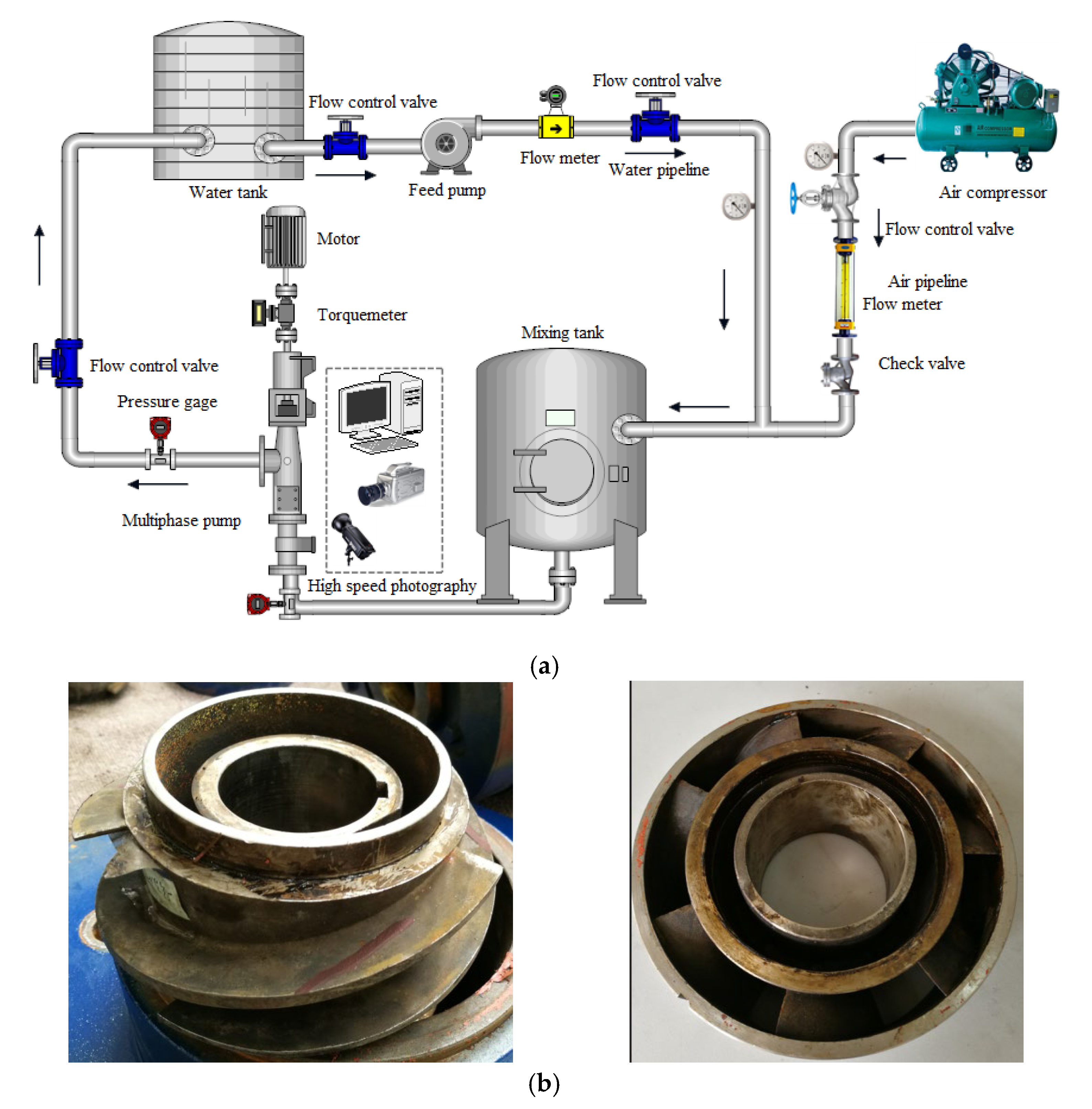
3.1. Experimental Rig
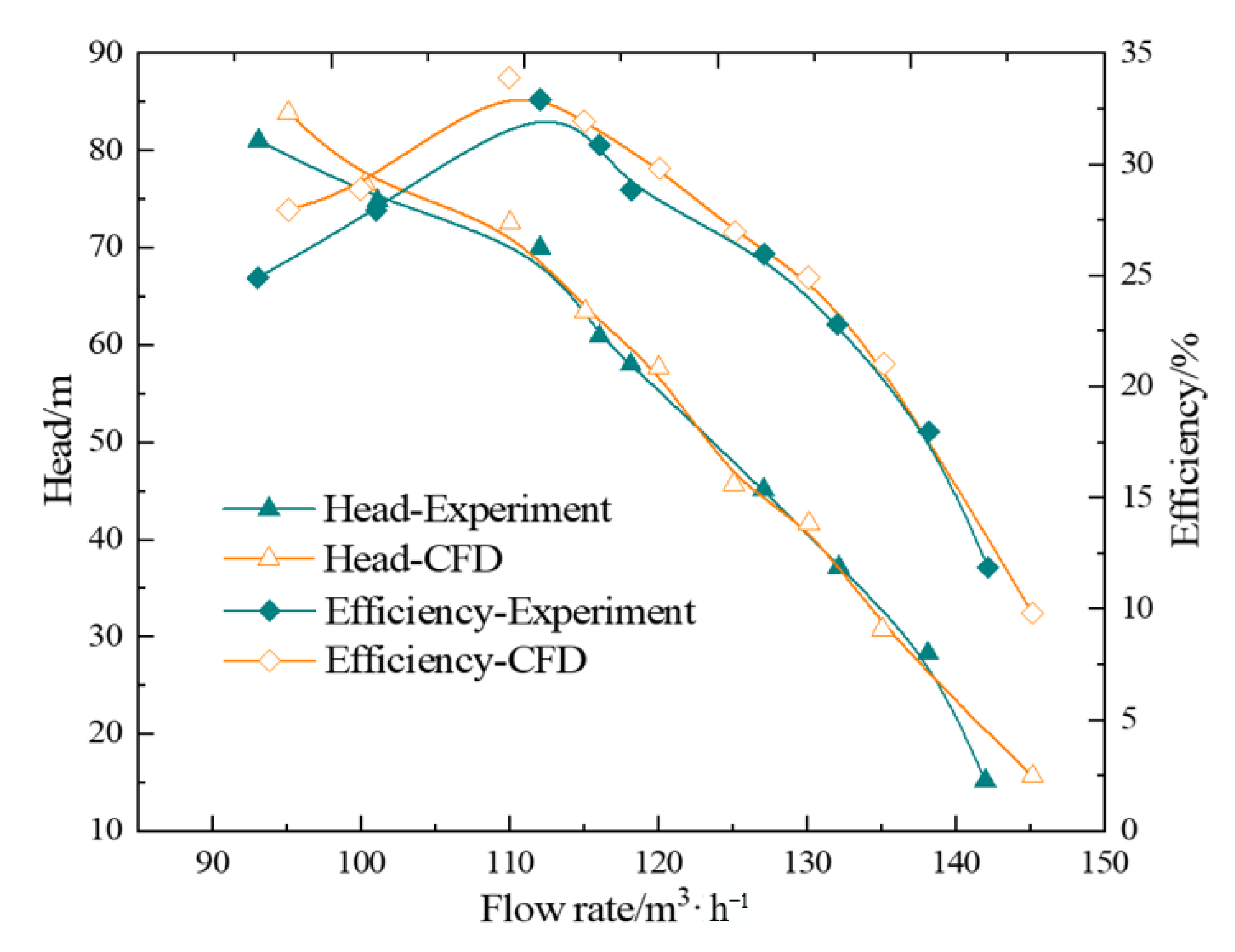
3.2. Numerical Verification
4. Results and Discussion
4.1. Cavitation Characteristic Prediction
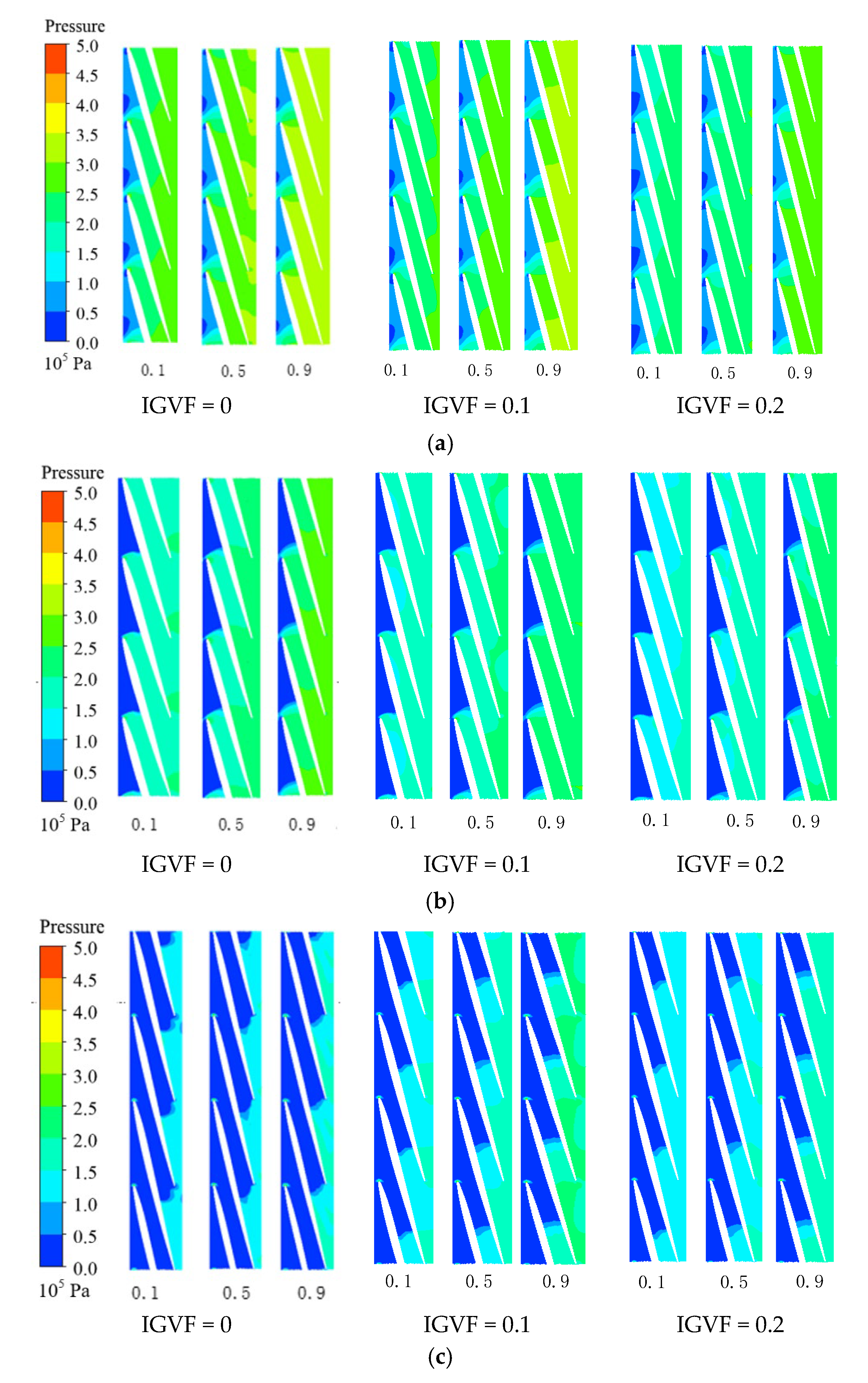
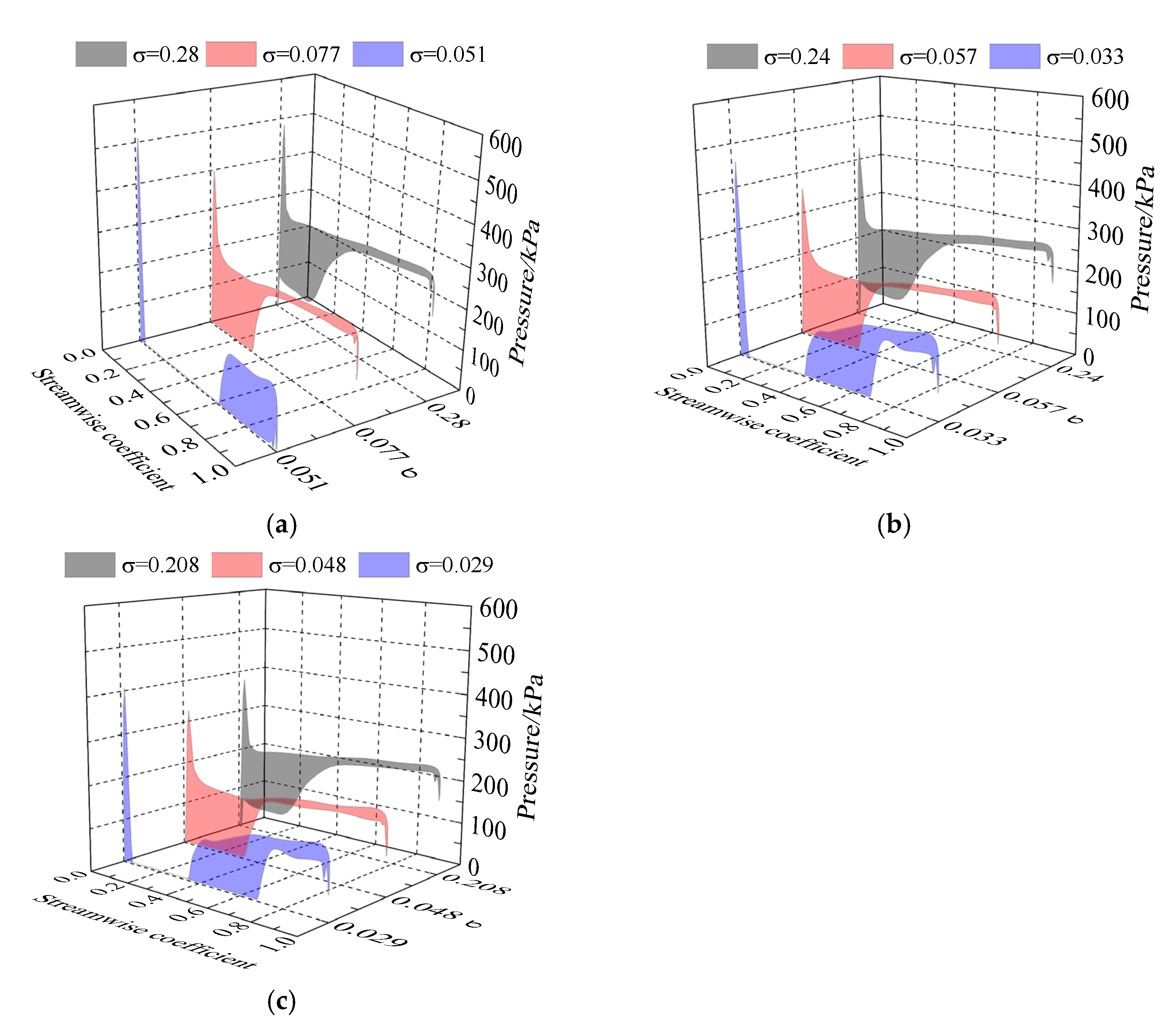
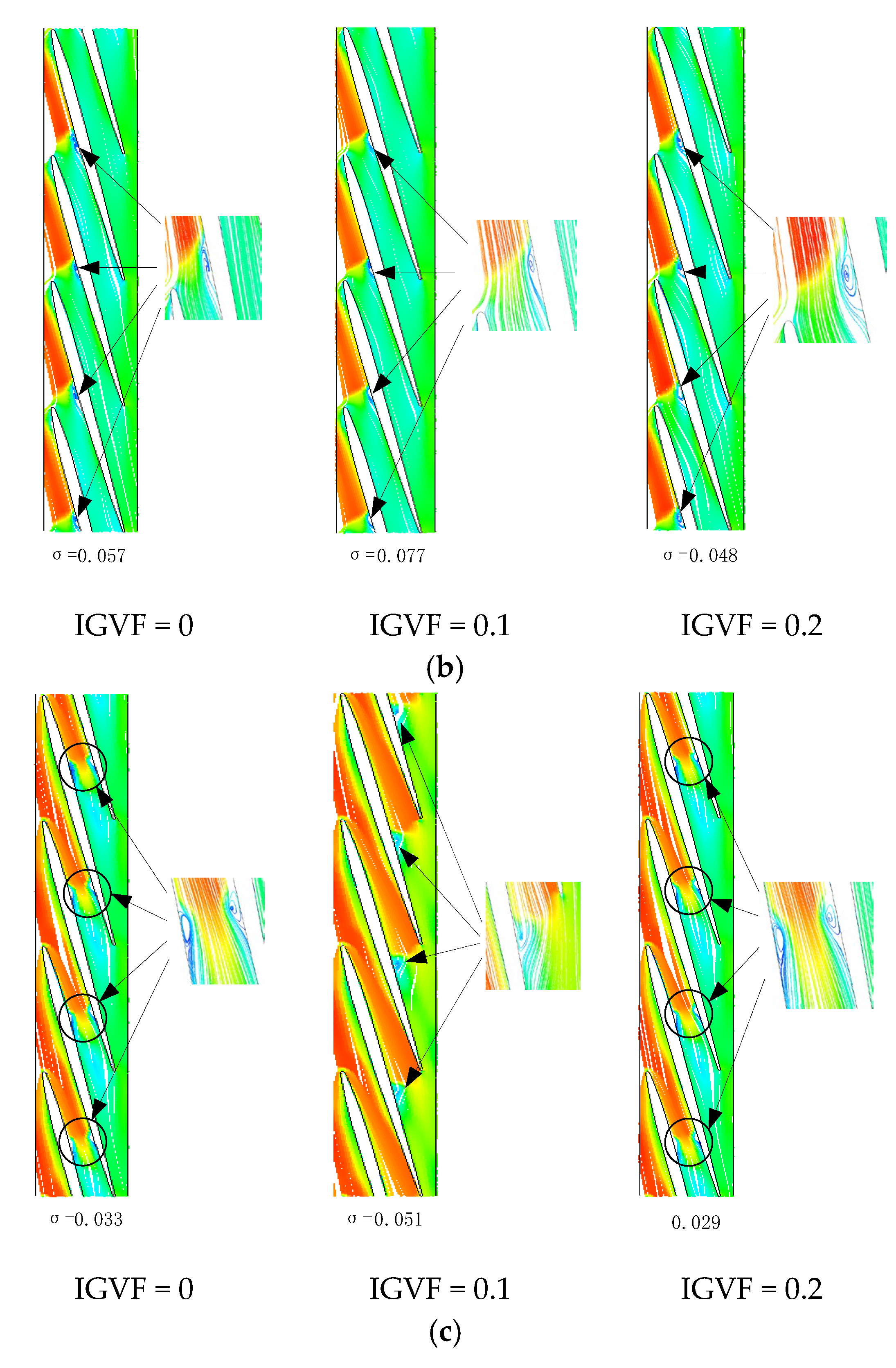
4.2. Effect of IGVF on Pressure Characteristics at Cavitation Case
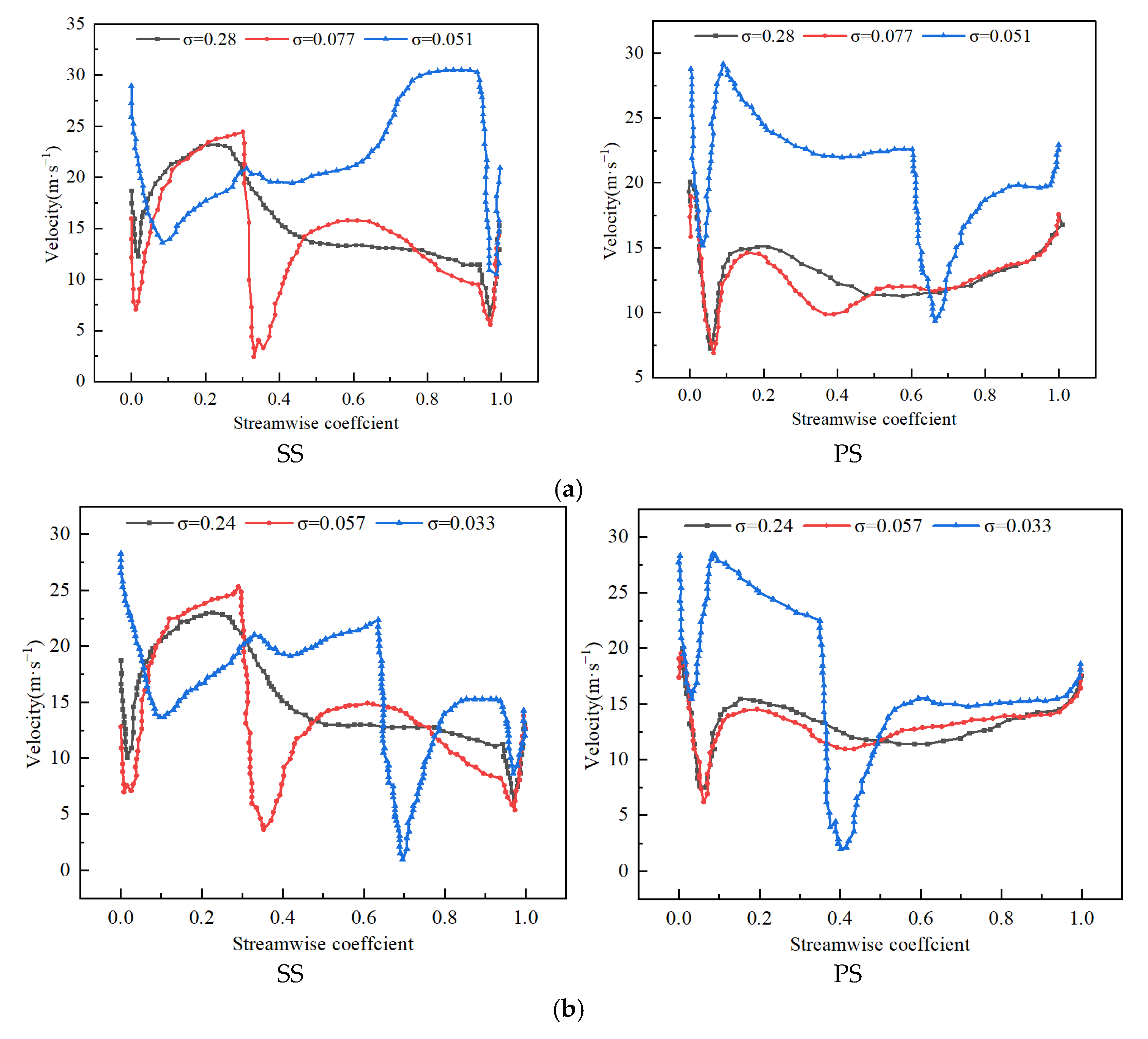
4.3. Effect of IGVF on Velocity Characteristics at Cavitation Case
5. Conclusions
- (1)
- The increase of IGVF and the development of cavitation reduce the pressure in the impeller flow passage, and the pressure corresponding to the bubbles drops sharply to about the saturated vapor pressure. When the bubbles extend to the blade PS, the load near the cavitation intersection area is reduced to 0. The load on the end of the bubbles between the PS and SS increases, and the pressure gradient at the end of the bubbles is very large.
- (2)
- As the cavitation coefficient decreases, the relative velocity near the cavitation becomes larger due to the squeezing effect of the bubbles. Due to the large pressure gradient at the end of the bubbles, the kinetic energy of the fluid is not enough to overcome the effect of the reverse pressure gradient, resulting in a backflow vortex.
- (3)
- As the blade span increases, the relative velocity in the cavitation region gradually increases. Because the pressure gradient at the end of the cavitation region is large, a low-velocity region occurs at the end of the cavitation zone. To further avoid the cavitation phenomenon, a convex structure can be set on the blade to improve the flow state in the pump.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Tan, L.; Xu, Y.; Cao, S. Optimization design method of multi-stage multiphase pump based on Oseen vortex. J. Pet. Sci. Eng. 2020, 184, 106532. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Influence of viscosity on energy performance and flow field of a multiphase pump. Renew. Energy 2020, 162, 1151–1160. [Google Scholar] [CrossRef]
- Sano, T.; Wakai, T.; Reclari, M.; Xu, Y.; Cao, S. Investigation of internal flow pattern of a multiphase axial pump. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 062058. [Google Scholar] [CrossRef]
- Shi, G.; Wang, S.; Xiao, Y.; Liu, Z.; Li, H.; Liu, X. Effect of cavitation on energy conversion characteristics of a multiphase pump. Renew. Energy 2021, 177, 1308–1320. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Zhang, J.; Zhu, J. Flow pattern recognition inside a rotodynamic multiphase pump via developed entropy production diagnostic model. J. Pet. Sci. Eng. 2020, 194, 107467. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J.; Zhu, H.; Cai, S.; Wang, J. 3D Blade Hydraulic Design Method of the Rotodynamic Multiphase Pump Impeller and Performance Research. Adv. Mech. Eng. 2014, 6, 803972. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, S.; Zhu, H.; Zhang, Y. Experimental investigation of the flow at the entrance of a rotodynamic multiphase pump by visualization. J. Pet. Sci. Eng. 2015, 126, 254–261. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, S.; Sano, T.; Wakai, T.; Reclari, M. Experimental Investigation on Transient Pressure Characteristics in a Helico-Axial Multiphase Pump. Energies 2019, 12, 461. [Google Scholar] [CrossRef] [Green Version]
- Han, W.; Li, X.; Su, Y.; Su, M.; Li, R.; Zhao, Y. Effect of Thickness Ratio Coefficient on the Mixture Transportation Characteristics of Helical–Axial Multiphase Pumps. Appl. Sci. 2020, 10, 345. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Hu, Q.; Wang, H.; Jiang, Q.; Shi, G. Characteristics of unsteady excitation induced by cavitation in axial-flow oil–gas multiphase pumps. Adv. Mech. Eng. 2018, 10, 168781401877126. [Google Scholar] [CrossRef]
- Huan, Y.-Y.; Liu, Y.-Y.; Li, X.-J.; Zhu, Z.-C.; Qu, J.-T.; Zhe, L.; Han, A.-D. Experimental and numerical investigations of cavitation evolution in a high-speed centrifugal pump with inducer. J. Hydrodyn. 2021, 33, 140–149. [Google Scholar] [CrossRef]
- Lomakin, V.; Bibik, O. Numerical prediction of the gas content effect on the cavitation characteristics of the pump using the simplified Rayleigh-Plesset equation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 492, 012037. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.-J.; Feng, Z.-P. Two-dimensional analysis of cavitating flows in a centrifugal pump using a single-phase Reynolds averaged Navier—Stokes solver and cavitation model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 783–791. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Q.; Huang, R.; Cao, S. Numerical simulation of unsteady flow in multiphase rotodynamic pumps. J. Drain. Irrig. Mach. Eng. 2013, 31, 284–288. [Google Scholar]
- Zhang, J.; Cai, S.; Zhu, H.; Yang, K.; Qiang, R. Numerical Investigation of Compressible Flow in a Three-stage Helico-axial Multiphase Pump. Trans. Chin. Soc. Agric. Mach. 2014, 45, 89–95. [Google Scholar]
- Yang, X.; Xia, Y.; Jin, L.; Cao, F. Experimental Study on Pumping Behavior of Twin-Screw Multiphase Pump. J. Xi’an Jiaotong Univ. 2013, 47, 30–35. [Google Scholar]
- Ma, X.; Zhao, J.; Shao, L. Study on the Performance of Oil-gas Pump by Varying the Blade Number. Fluid Mach. 2009, 37, 24–27. [Google Scholar]
- Yang, X.; Hu, C.C.; Qu, Z.C. Theoretical and experimental study of a synchronal rotary multiphase pump at very high inlet gas volume fractions. Appl. Therm. Eng. 2017, 110, 710–719. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Cai, S.; Li, Y. Visualization study of gas–liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump. Exp. Therm. Fluid Sci. 2016, 70, 125–138. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, S.; Zhu, H. Experimental Study of Gas-Liquid Two-Phase Flow Pattern in a Helico-Axial Multiphase Pump by Visualization. J. Eng. Thermophys. 2015, 36, 1937–1941. [Google Scholar]
- Shi, Y.; Zhu, H.; Zhang, J. Experiment and numerical study of a new generation three-stage multiphase pump. J. Pet. Sci. Eng. 2018, 169, 471–484. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, K.Y. Analysis and Optimization of a Vaned Diffuser in a Mixed Flow Pump to Improve Hydrodynamic Performance. J. Fluids Eng. 2012, 134, 071104–071113. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Pet. Sci. Eng. 2018, 162, 588–601. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.; Zhu, B. Numerical Study of Pressure Fluctuation in a Gas- Liquid Two-Phase Mixed-Flow Pump. Energies 2017, 10, 634. [Google Scholar] [CrossRef] [Green Version]
- Ge, M.; Zhang, G.; Petkovek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.; Petkovek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Shi, G.; Li, H.; Liu, X.; Wang, B. Transport performance improvement of a multiphase pump for gas–liquid mixture based on the orthogonal test method. Processes 2021, 9, 1402. [Google Scholar] [CrossRef]
- Wang, C.; Yang, F.; Nguyen, V.; Vo, N. CFD analysis and optimum design for a centrifugal pump using an effectively artificial intelligent algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Nguyen, V.T.T.; Vo, T.M.N. Centrifugal Pump Design: An Optimization. Eurasia Proc. Sci. Technol. Eng. Math. 2022, 17, 136–151. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, B.; Wang, Z.; Wang, F. Optimization design for an impeller of the multiphase rotodynamic pump handling gas-liquid two-phase flow. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 236, 09576509221098223. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, H.C.; Yoon, J.Y.; Lee, K.; Choi, Y. Multi objective optimization of a multiphase pump for offshore plants. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting, Chicago, IL, USA, 3–7 August 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. 46223. [Google Scholar]
- Liu, M.; Tan, L.; Cao, S. Design method of controllable blade angle and orthogonal optimization of pressure rise for a multiphase pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Zhang, X.; Chen, Y.; Gong, Y.; Li, H.; Huang, S. A Method for the Integrated Optimal Design of Multiphase Pump Based on the Sparse Grid Model. Processes 2022, 10, 1317. [Google Scholar] [CrossRef]
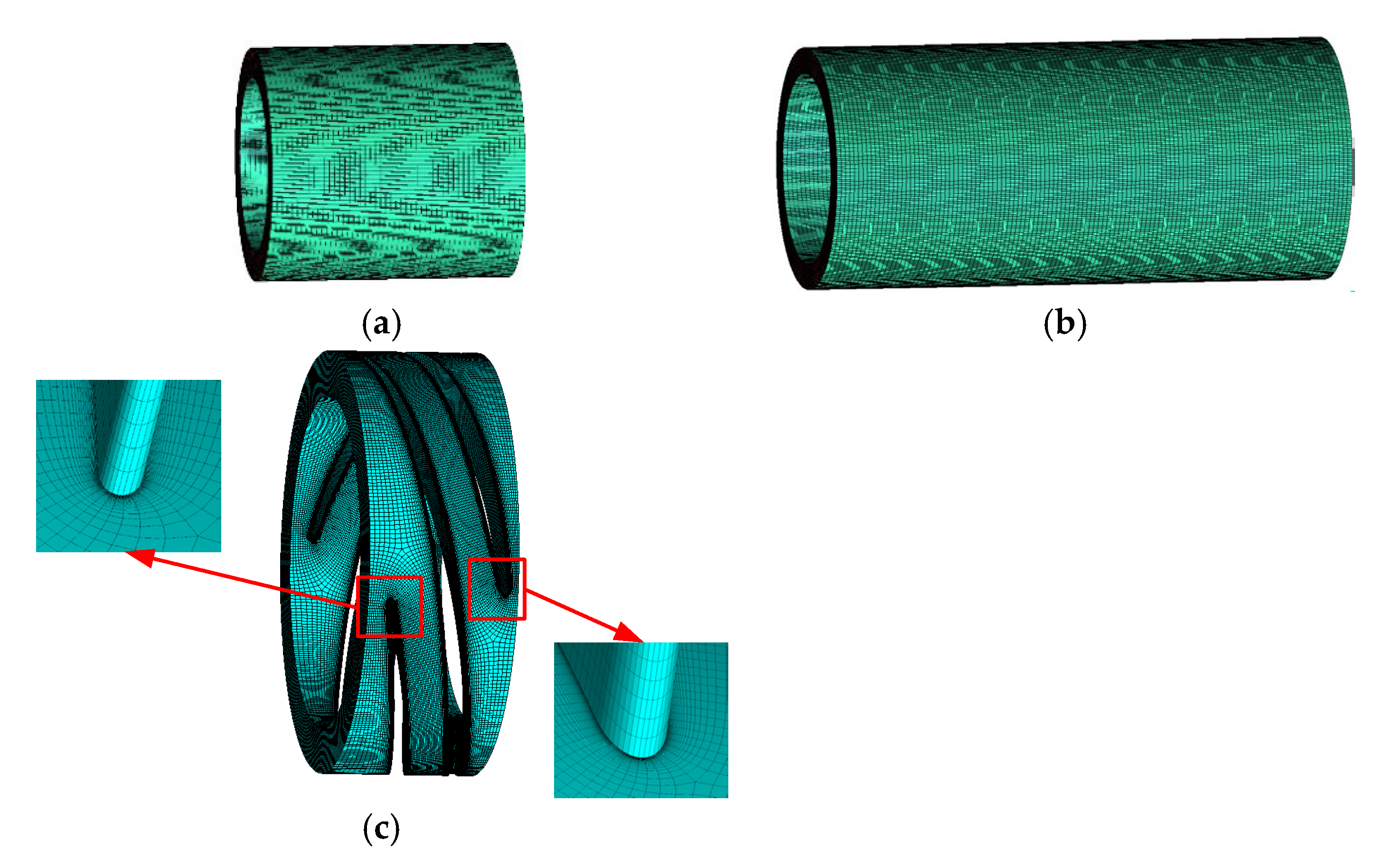




| Computational Domain | Max Angle | Max Warp | Skew | Aspect Ratio | Quality |
|---|---|---|---|---|---|
| Inlet pipe | 90.0377~108.284 | 0~0.416 | 0.80~0.99 | 0.00091~0.99 | 0.95 |
| Impeller | 90.002~121.61 | 0~2.46 | 0.68~1 | 0.0018~0.99 | 0.48 |
| Outlet pipe | 90.001~119.16 | 0~0.27 | 0.688~1 | 0.0006~0.99 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Wen, H.; Shi, G.; Wang, S. Analyzing the Inlet Gas Void Fraction on the Flow Characteristics for a Multiphase Pump Based on Cavitation Cases. J. Mar. Sci. Eng. 2023, 11, 130. https://doi.org/10.3390/jmse11010130
Lv W, Wen H, Shi G, Wang S. Analyzing the Inlet Gas Void Fraction on the Flow Characteristics for a Multiphase Pump Based on Cavitation Cases. Journal of Marine Science and Engineering. 2023; 11(1):130. https://doi.org/10.3390/jmse11010130
Chicago/Turabian StyleLv, Wenjuan, Haigang Wen, Guangtai Shi, and Shan Wang. 2023. "Analyzing the Inlet Gas Void Fraction on the Flow Characteristics for a Multiphase Pump Based on Cavitation Cases" Journal of Marine Science and Engineering 11, no. 1: 130. https://doi.org/10.3390/jmse11010130
APA StyleLv, W., Wen, H., Shi, G., & Wang, S. (2023). Analyzing the Inlet Gas Void Fraction on the Flow Characteristics for a Multiphase Pump Based on Cavitation Cases. Journal of Marine Science and Engineering, 11(1), 130. https://doi.org/10.3390/jmse11010130





