An Inequality Indicator for High-Resistance Connection Fault Diagnosis in Marine Current Turbine
Abstract
:1. Introduction
2. PMSM Model and Current Model under HRC Condition
2.1. PMSM Model under HRC Condition
2.2. Current Model under HRC Condition
3. Feature of Long-Wavelength Swells
4. An Inequality Indicator for HRC Fault Diagnosis
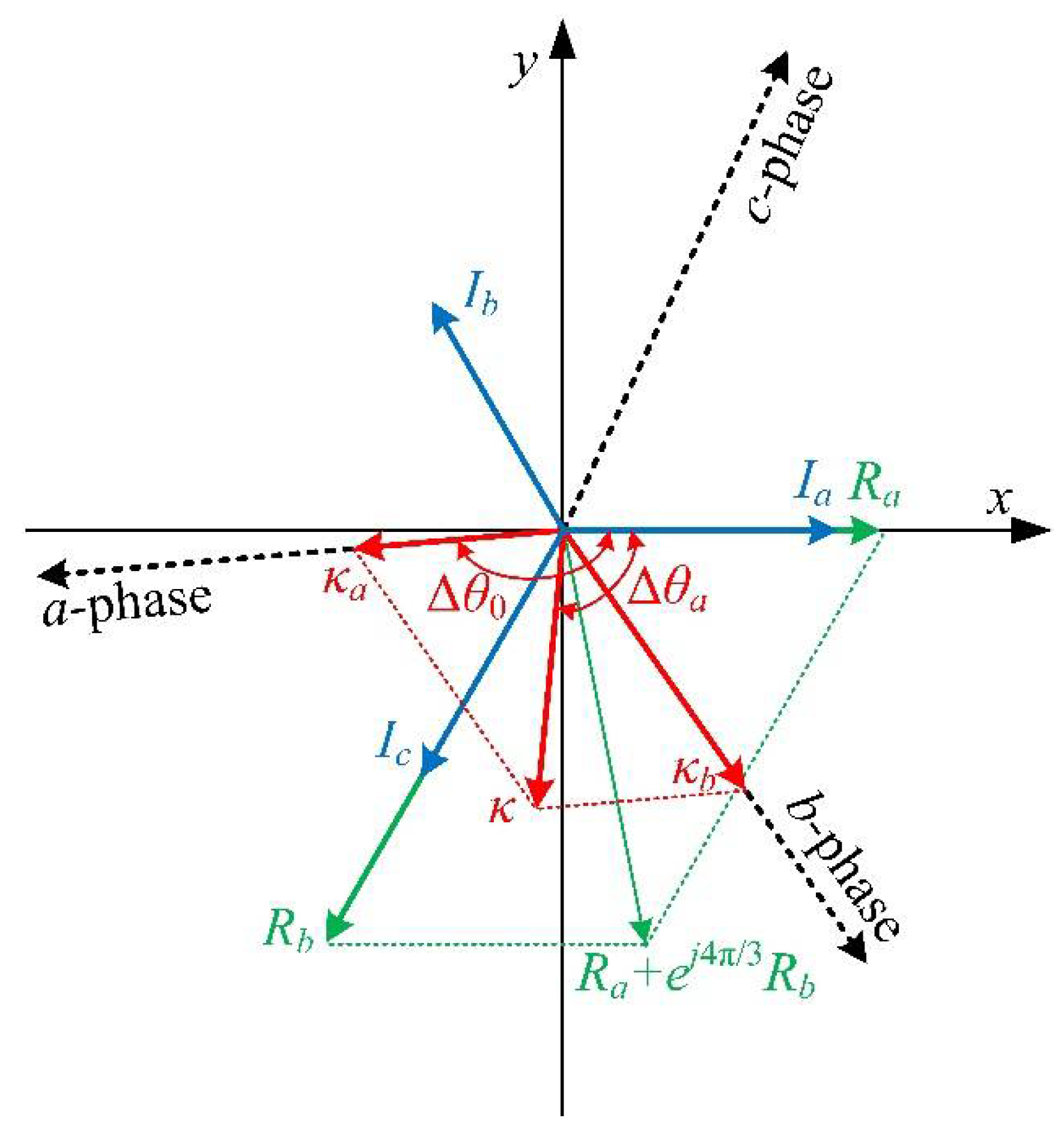
4.1. The Inequality Indicator
4.2. Diagnostic Mechanism of Inequality Indicator
4.3. Robustness of Inequality Indicator
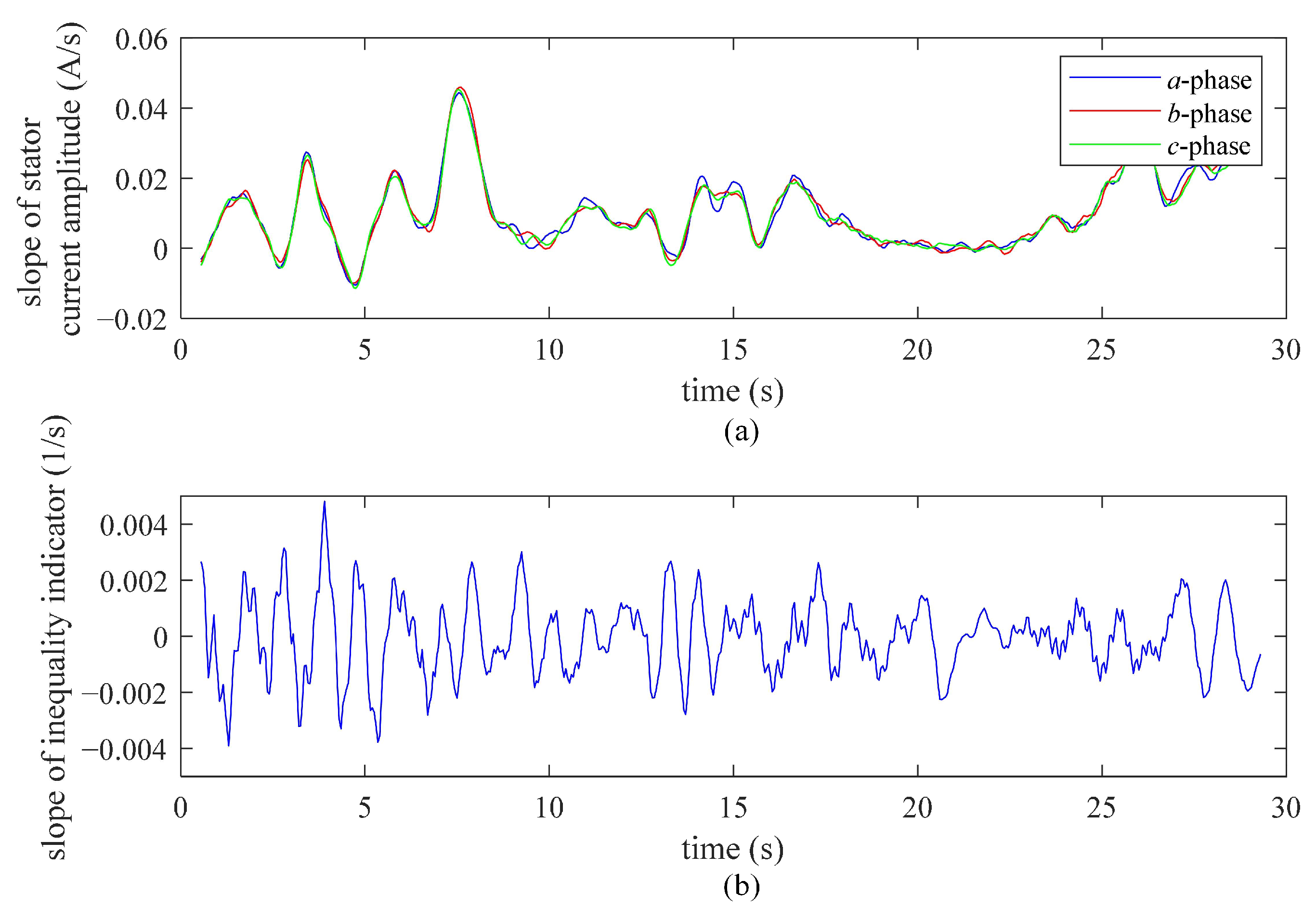
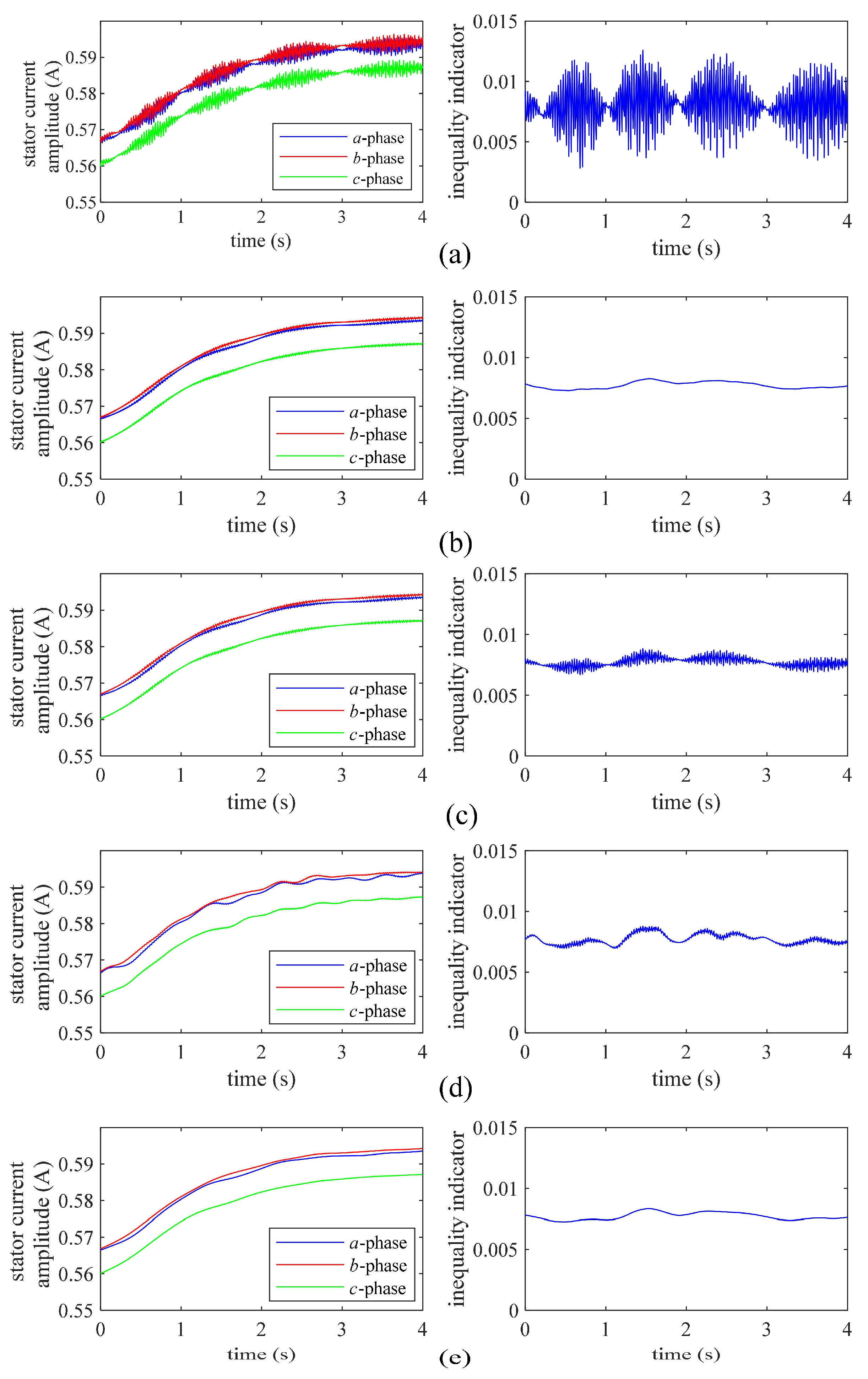
4.4. Filtering for Improving Diagnostic Accuracy
5. Experimental Results and Discussions
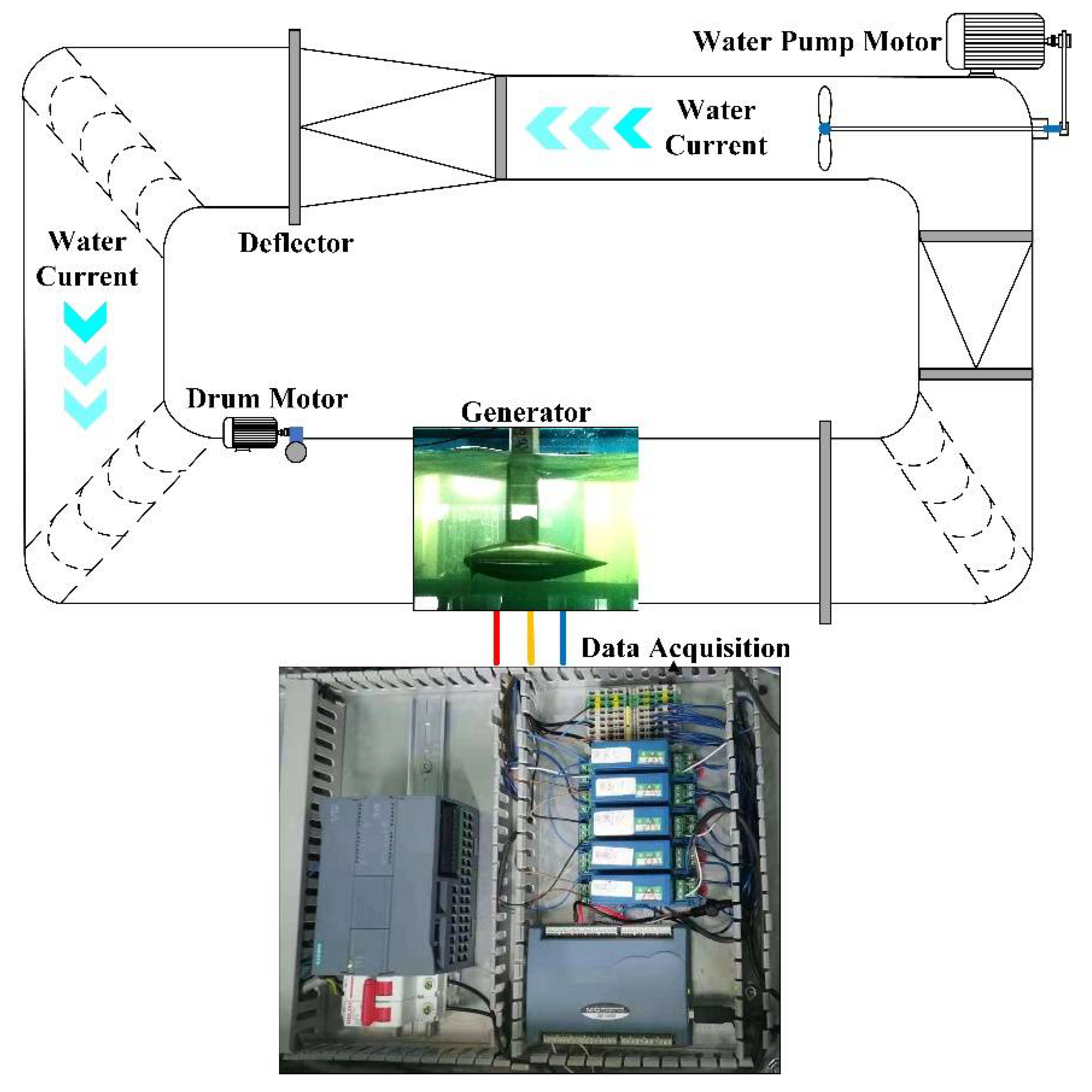
5.1. Experimental Setup and Practical Considerations
5.2. Test for Robustness of Inequality Indicator
5.3. Test for Improving Diagnostic Accuracy
5.4. Experimental Result of Diagnosis
5.5. The Performance of Inequality Indicator with Silght Current Imbalance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lo Brutto, O.A.; Barakat, M.R.; Guillou, S.S.; Thiebot, J.; Gualous, H. Influence of the wake effect on electrical dynamics of commercial tidal farms: Application to the alderney race (France). IEEE Trans. Sustain. Energy 2018, 9, 321–332. [Google Scholar] [CrossRef]
- Pham, H.; Bourgeot, J.; Benbouzid, M.E.H. Comparative investigations of sensor fault-tolerant control strategies performance for marine current turbine applications. IEEE J. Ocean. Eng. 2018, 43, 1024–1036. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A. Fuzzy passivity-based linear feedback current controller approach for PMSG-based tidal turbine. Ocean Eng. 2020, 218, 108156. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.; Frédéric Charpentier, J.; Scuiller, F.; Tang, T. A review of energy storage technologies for marine current energy systems. Renew. Sustain. Energy Rev. 2013, 18, 390–400. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Wang, T.; Zhou, F.; Shi, M. An adaptive single neural control for variable step-size P&O MPPT of marine current turbine system. China Ocean Eng. 2021, 35, 750–758. [Google Scholar] [CrossRef]
- Ben Elghali, S.E.; Benbouzid, M.; Ahmed-Ali, T.; Charpentier, J.F. High-order sliding mode control of a marine current turbine driven doubly-fed induction generator. IEEE J. Ocean. Eng. 2010, 35, 402–411. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.B.; Scuiller, F.; Charpentier, J.F.; Benbouzid, M.E.; Tang, T.H. Power control of a nonpitchable PMSG-based marine current turbine at overrated current speed with flux-weakening strategy. IEEE J. Ocean. Eng. 2015, 40, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Xie, T.; Wang, T.Z.; He, Q.Q.; Diallo, D.; Claramunt, C. A review of current issues of marine current turbine blade fault detection. Ocean Eng. 2020, 218, 108194. [Google Scholar] [CrossRef]
- Hsu, C.C.; Yang, S.C. Permanent-magnet machine flux and torque response under the influence of turn fault. IEEE Trans. Ind. Electron. 2020, 67, 169–179. [Google Scholar] [CrossRef]
- Hall, S.; Marquez-Fernandez, F.J.; Alakula, M. Dynamic magnetic model identification of permanent magnet synchronous machines. IEEE Trans. Energy Convers. 2017, 32, 1367–1375. [Google Scholar] [CrossRef]
- Obeid, N.H.; Battiston, A.; Boileau, T.; Nahid-Mobarakeh, B. Early intermittent interturn fault detection and localization for a permanent magnet synchronous motor of electrical vehicles using wavelet transform. IEEE Trans. Transp. Electrif. 2017, 3, 694–702. [Google Scholar] [CrossRef]
- Eker, M.; Akar, M. Eccentricity fault diagnosis in a permanent magnet synchronous motor under nonstationary speed conditions. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Karami, M.; Bin Mariun, N.; Ab-Kadir, M.; Misron, N.; Radzi, M. Motor current signature analysis-based non-invasive recognition of mixed eccentricity fault in line start permanent magnet synchronous motor. Electr. Power Compon. Syst. 2021, 49, 133–145. [Google Scholar] [CrossRef]
- Ma, C.G.; Gao, Y.J.; Degano, M.; Wang, Y.Y.; Fang, J.G.; Gerada, C.; Zhou, S.S.; Mu, Y.Y. Eccentric position diagnosis of static eccentricity fault of external rotor permanent magnet synchronous motor as an in-wheel motor. IET Electr. Power Appl. 2020, 14, 2263–2272. [Google Scholar] [CrossRef]
- Zhao, K.H.; Leng, A.J.; Zhou, R.R.; Dai, W.K.; Wu, S.C.; Li, T. Demagnetization fault reconstruction for six-phase permanent magnet synchronous motor by improved super-twisting algorithm-based sliding-mode observer. Measurement 2021, 172, 10895. [Google Scholar] [CrossRef]
- Krichen, M.; Elbouchikhi, E.; Benhadj, N.; Chaieb, M.; Benbouzid, M.; Neji, R. Motor current signature analysis-based permanent magnet synchronous motor demagnetization characterization and detection. Machines 2020, 8, 35. [Google Scholar] [CrossRef]
- Li, W.L.; Feng, G.D.; Li, Z.; Tjong, J.; Kar, N.C. Multireference frame based open-phase fault modeling and control for asymmetrical six-phase interior permanent magnet motors. IEEE Trans. Power Electron. 2021, 36, 11712–11725. [Google Scholar] [CrossRef]
- Song, Z.F.; Zhou, F.J.; Yu, Y.; Zhang, R.; Hu, S.Y. Open-phase fault-tolerant predictive control strategy for open-end-winding permanent magnet synchronous machines without postfault controller reconfiguration. IEEE Trans. Ind. Electron. 2021, 68, 3770–3781. [Google Scholar] [CrossRef]
- Mohammed, H.H.M.; Zhengyou, H.; Ling, F.; Yujia, D. A cumulative standard deviation sum based method for high resistance fault identification and classification in power transmission lines. Prot. Control Mod. Power Syst. 2018, 3, 30. [Google Scholar]
- Yun, J.; Cho, J.; Lee, S.B.; Yoo, J.Y. Online detection of high-resistance connections in the incoming electrical circuit for induction motors. IEEE Trans. Ind. Appl. 2009, 45, 694–702. [Google Scholar] [CrossRef]
- Hang, J.; Ren, X.X.; Tang, C.Y.; Tong, M.H.; Ding, S.C. Fault-tolerant control strategy for five-phase PMSM drive system with high-resistance connection. IEEE Trans. Transp. Electrif. 2021, 7, 1390–1400. [Google Scholar] [CrossRef]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 2013, 59, 1–12. [Google Scholar] [CrossRef] [Green Version]
- de la Barrera, P.M.; Bossio, G.R.; Leidhold, R. Online voltage sensorless high-resistance connection diagnosis in induction motor drives. IEEE Trans. Ind. Electron. 2015, 62, 4374–4384. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.Z.; Cheng, M.; Zhang, B.F.; Ding, S.C. High-resistance connection detection in permanent magnet synchronous machine using zero-sequence current component. IEEE Trans. Power Electron. 2016, 31, 4710–4719. [Google Scholar] [CrossRef]
- Yun, J.; Lee, K.; Lee, K.W.; Lee, S.B.; Yoo, J.Y. Detection and classification of stator turn faults and high-resistance electrical connections for induction machines. IEEE Trans. Ind. Appl. 2009, 45, 666–675. [Google Scholar] [CrossRef]
- Zarri, L.; Mengoni, M.; Gritli, Y.; Tani, A.; Filippetti, F.; Serra, G.; Casadei, D. Detection and localization of stator resistance dissymmetry based on multiple reference frame controllers in multiphase induction motor drives. IEEE Trans. Ind. Electron. 2013, 60, 3506–3518. [Google Scholar] [CrossRef]
- de la Barrera, P.M.; Bossio, G.R.; Solsona, J.A. High-resistance connection detection in induction motor drives using signal injection. IEEE Trans. Ind. Electron. 2014, 61, 3563–3573. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Gritli, Y.; Serra, G.; Filippetti, F.; Casadei, D. Online detection of high-resistance connections in multiphase induction machines. IEEE Trans. Power Electron. 2015, 30, 4505–4513. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Hang, J.; Ding, S.C.; Cheng, M. Online diagnosis and localization of high-resistance connection in PMSM with improved fault indicator. IEEE Trans. Power Electron. 2017, 32, 3585–3594. [Google Scholar] [CrossRef]
- Hang, J.; Yan, D.D.; Xia, M.J.; Ding, S.C.; Wang, Q.J. Quantitative fault severity estimation for high-resistance connection in PMSM drive system. IEEE Access 2019, 7, 26855–26866. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Ding, S.C.; Hua, W.; Wang, Q.J. A DC-flux-injection method for fault diagnosis of high-resistance connection in direct-torque-controlled PMSM drive system. IEEE Trans. Power Electron. 2020, 35, 3029–3042. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Park, Y.; Lee, S.B. High-resistance fault control in permanent magnet synchronous motors. IEEE-Asme Trans. Mechatron. 2020, 25, 271–281. [Google Scholar] [CrossRef]
- Hu, R.G.; Wang, J.B.; Mills, A.; Chong, E.; Sun, Z.G. Detection and classification of turn fault and high resistance connection fault in permanent magnet machines based on zero sequence voltage. IEEE Trans. Power Electron. 2020, 35, 1922–1933. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.B.; Ding, S.C.; Huang, Y.R.; Wang, Q.J. A model-based strategy with robust parameter mismatch for online HRC diagnosis and location in PMSM drive system. IEEE Trans. Power Electron. 2020, 35, 10917–10929. [Google Scholar] [CrossRef]
- Abosh, A.H.; Zhu, Z.Q.; Ren, Y. Cascaded direct torque control of unbalanced PMSM with low torque and flux ripples. IEEE Trans. Power Electron. 2018, 33, 1740–1749. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Wang, T.Z.; Diallo, D. An active disturbance rejection sensorless control strategy based on sliding mode observer for marine current turbine. ISA Trans. 2022, 124, 403–410. [Google Scholar] [CrossRef] [PubMed]
- Willems, J.L. Reflections on apparent power and power factor in nonsinusoidal and polyphase situations. IEEE Trans. Power Deliv. 2004, 19, 835–840. [Google Scholar] [CrossRef]
- Saleh, S.A.; Aljankawey, A.S.; Meng, R.; Meng, J.; Diduch, C.P.; Chang, L. Antiislanding protection based on signatures extracted from the instantaneous apparent power. IEEE Trans. Power Electron. 2014, 29, 5872–5891. [Google Scholar] [CrossRef]
- Milne, I.A.; Sharma, R.N.; Flay, R.; Bickerton, S. Characteristics of the turbulence in the flow at a tidal stream power site. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120196. [Google Scholar] [CrossRef]
- Sababheh, M.; Furuichi, S.; Heydarbeygi, Z.; Moradi, H.R. On the arithmetic-geometric mean inequality. J. Math Inequal. 2021, 15, 1255–1266. [Google Scholar] [CrossRef]
- Yuce, E.; Minaei, S.; Tokat, S. Root-mean-square measurement of distinct voltage signals. IEEE Trans. Instrum. Meas. 2007, 56, 2782–2787. [Google Scholar] [CrossRef]



| Turbine Parameters | Value | PMSM Parameters | Value |
|---|---|---|---|
| Twist angle | 3.4°~25.2° | Pole-pair | 8 |
| Blade chord | 0.6 m | Flux linkage | 0.1775 Wb |
| Number of blades | 3 | Resistance | 3.3 Ω |
| Water density | 1024 kg/m3 | d axis inductance | 11.873 mH |
| damping | 1 × 10−6 m2/s | q axis inductance | 11.873 mH |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Additional resistance (Ω) | b-phase | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.3 | 1.4 |
| c-phase | 0 | 0.2 | 0.3 | 0.6 | 0.8 | 1.2 | 1.5 | 0 | 0 | |
| Case | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Additional resistance (Ω) | b-phase | 1.7 | 0.3 | 0.6 | 0.8 | 1.0 | 0.3 | 0.5 | 0.7 | 0.9 |
| c-phase | 0 | 0.6 | 0.6 | 0.6 | 0.6 | 1.2 | 1.2 | 1.2 | 1.2 | |
| Window Function | Dispersion Coefficient | Margin Factor |
|---|---|---|
| No weight | 0.2881 | 1.7897 |
| Hanning window | 0.0491 | 1.1529 |
| Hamming window | 0.0653 | 1.2005 |
| Flap top window | 0.0756 | 1.2821 |
| Blackman window | 0.0523 | 1.1729 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Range | 2.9 × 10−4 | 2.9 × 10−4 | 3.6 × 10−4 | 3.2 × 10−4 | 7.8 × 10−4 | 7.7 × 10−4 | 3.3 × 10−4 | 3.9 × 10−4 | 4.4 × 10−4 |
| Case | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Range | 7.0 × 10−4 | 6.4 × 10−4 | 3.8 × 10−4 | 5.1 × 10−4 | 4.4 × 10−4 | 3.3 × 10−4 | 3.1 × 10−4 | 8.3 × 10−4 | 5.0 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Wang, T.; Amirat, Y.; Tang, Y. An Inequality Indicator for High-Resistance Connection Fault Diagnosis in Marine Current Turbine. J. Mar. Sci. Eng. 2023, 11, 97. https://doi.org/10.3390/jmse11010097
Jia D, Wang T, Amirat Y, Tang Y. An Inequality Indicator for High-Resistance Connection Fault Diagnosis in Marine Current Turbine. Journal of Marine Science and Engineering. 2023; 11(1):97. https://doi.org/10.3390/jmse11010097
Chicago/Turabian StyleJia, Dongxu, Tianzhen Wang, Yassine Amirat, and Yunjie Tang. 2023. "An Inequality Indicator for High-Resistance Connection Fault Diagnosis in Marine Current Turbine" Journal of Marine Science and Engineering 11, no. 1: 97. https://doi.org/10.3390/jmse11010097
APA StyleJia, D., Wang, T., Amirat, Y., & Tang, Y. (2023). An Inequality Indicator for High-Resistance Connection Fault Diagnosis in Marine Current Turbine. Journal of Marine Science and Engineering, 11(1), 97. https://doi.org/10.3390/jmse11010097








