A Distributed Intelligent Buoy System for Tracking Underwater Vehicles

Abstract

Underwater vehicles play a crucial role in various underwater applications, such as data collection in underwater sensor networks, target detection and tracking, and underwater pipeline monitoring. Real-time acquisition of their states, particularly their location and velocity, is vital for their operation and navigation. Consequently, the development of a remote tracking system to monitor these states is essential. In this paper, we propose a system that can track the underwater vehicle’s location and velocity. We take a systematic approach that encompasses the system architecture, system composition, signal processing, and mobility state estimation. We present the system architecture and define its components, along with their relationships and interfaces. The beacon signal employed in the system features dual-hyperbolic-frequency-modulated (HFM) waveform and an OFDM symbol with cyclic prefix (CP). Based on this beacon signal, we demonstrate how signal processing techniques are utilized to precisely determine the time of arrival and reduce false alarm rates in underwater acoustic channels affected by impulsive noise. Additionally, we explain how the CP-OFDM symbol is used to measure the Doppler scaling factor and transmit essential information for localization and velocity estimation purposes. Utilizing the measurements obtained through signal processing, least squares estimators are used for estimating both the location and velocity. To validate the effectiveness of our approach, we implement the system and conduct field trials. Two separate experiments were conducted in which the diagonal lengths of the square topology were designed to be 1000 m and 800 m. The minimum/maximum root mean square error of localization in the first and second experiment is 2.36/2.91 m and 1.47/2.49 m, respectively. And the minimum/maximum root mean square error of velocity estimation in the first and second experiment is 0.16/0.47 m/s and 0.21/0.76 m/s, respectively. Results confirm the effectiveness of the proposed method in estimating the location and velocity of the underwater vehicle. Overall, this paper provides a practical and effective design of a system to track the location and velocity of underwater vehicles. By leveraging the proposed system, signal processing, and mobility state estimation methods, our work offers a systematic solution. And, the successful field experiment serves as evidence of the feasibility and effectiveness of the proposed system, making it a valuable contribution to the field of tracking underwater vehicles.

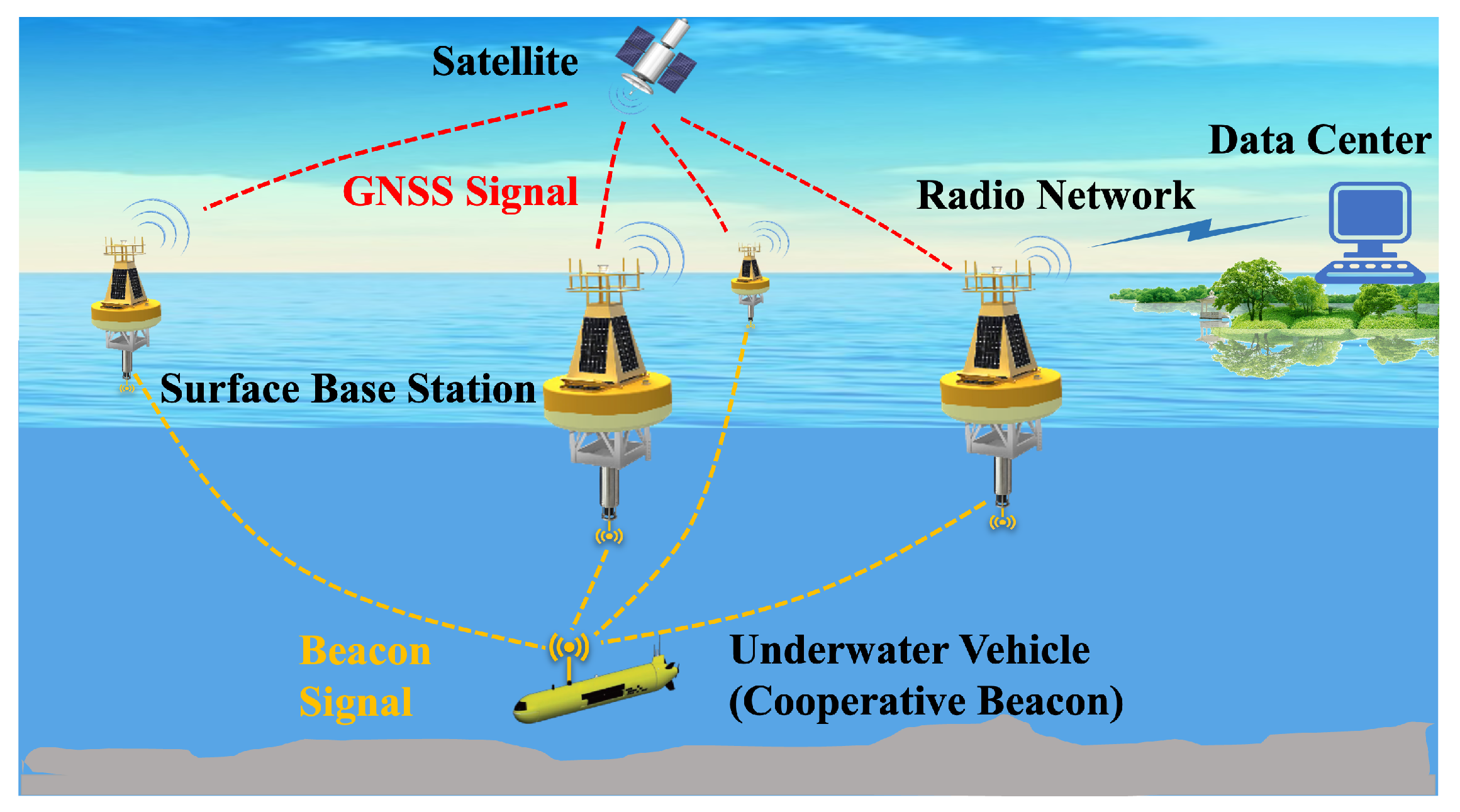
1. Introduction

The harsh underwater environment presents numerous challenges to manned operations. Consequently, many applications are switching to underwater unmanned platforms, such as autonomous underwater vehicles (AUVs) or remote control vehicles (rovs), to execute tasks that are difficult and dangerous for humans to undertake, thereby facilitating underwater applications, such as data collections in underwater wireless sensor networks (UWSNs) [1,2], target detection and tracking [3], and underwater pipeline monitoring [4].

There is a need to track the vehicles’ status, particularly the location and velocity, constantly. For example, during an operation, the vehicle’s real-time status needs to be readily available to the vehicle owner and operator to know where the vehicle is and where it is going. In addition, this information is also important to the vehicle’s navigation system when the calibration of the inertial sensor is needed [5,6,7]. In terrestrial environments, the GNSS (Global Navigation Satellite System) signal can be used to eliminate the accumulated error of the inertial sensor. However, it is not the case underwater, where the GNSS signals do not travel well. Therefore, the location and velocity estimation have to be obtained in a different manner.

In this paper, we present a distributed intelligent buoy system (DIBS) for tracking the underwater vehicle’s location and velocity. We explain the design of such a system from three aspects. The first aspect concerns the design of system architecture, its components, and the relationships among them. The second aspect involves the signal processing methods employed by the system. In this aspect, we primarily focus on the techniques for signal detection, time of arrival (ToA) estimation, and the Doppler scaling factor estimation from the signal. And the final aspect is about how the results of signal processing are leveraged for estimating the location and velocity of underwater vehicle.

Within DIBS, there are three main components: the cooperative beacon (CB), the surface base station (SBS), and the data center (DC). Each of the vehicles in the system carries a beacon, which actively and periodically broadcasts the beacon signal. A set of SBSs passively listen to the beacon signal. Upon receiving, the SBS performs estimation of ToA and Doppler scaling factor. These measurements are then forwarded to the DC. Finally, the DC gathers the measurements obtained from all SBSs and estimates the vehicle’s location and velocity.

Due to the consideration of accuracy, we employ ranging-based localization and Doppler-based velocity estimation, requiring signal processing methods to estimate the ToA and the Doppler scaling factor about the received signal. To facilitate the estimation, a beacon signal comprising dual-hyperbolic-frequency-modulated (HFM) waveform and an OFDM symbol with cyclic prefix (CP) is employed. Based on this signal, the ToA of beacon signal is effectively estimated by using the Page test statistic. Additionally, estimation of Doppler scaling factor can be conveniently achieved by leveraging the null subcarriers within the CP-OFDM symbol. In addition to its use for estimating the ToA and Doppler scale, there are several other reasons that contribute to our employment of this beacon signal. Firstly, the underwater environment is prone to impulsive noise, leading to false alarms which result in anomalous ranging data. To address this, we employ a dual-HFM structure, with the second HFM acting as a redundancy. Additionally, the CP-OFDM symbol transmitted after the dual-HFM structure ensures that only signals with a matched pattern are considered as beacon signals, further mitigating false alarms. Finally, in centralized localization, when the maximum propagation delay is longer than the period between two successive beacon signals, it is hard to decide which set of measurements belongs to the same epoch. Thus, further processing needs to be performed on the measurements. To enhance efficiency, we modulate the epoch number into the CP-OFDM symbol, allowing the DC to determine which set of measurements belong to the same epoch in a more straightforward manner.

With the determined ToA and Doppler scaling factor from the SBS, localization and velocity estimation are performed at DC. We form least squares estimators for underwater vehicle location and velocity. The location is estimated using a time difference of arrival (TDoA) method, while the velocity is estimated by utilizing the Doppler scaling factors.

The main contributions of this paper are:

• In this paper, we present the design and implementation of a self-contained, fully integrated and practical solution for underwater vehicle’s location and velocity. Detailed information about the overall architecture of the system, system components, the functionality definitions of each component, the relationships and interfaces between them, as well as the underlying signal processing and mobility estimation methods are given.
• Through the employment of a signal comprising a dual-HFM and a CP-OFDM symbol, we achieve efficient ToA and Doppler scale estimation while reducing the false alarms. Additionally, essential information is modulated in the CP-OFDM symbol, thereby enhancing the efficiency of location and velocity estimation process.
• To verify the effectiveness of our purposed system, experiments are conducted at Dapeng Bay, Shenzhen. Within the test area, four SBSs are deployed, which forms a four-grid square topology. The experiment results are compared with the ground truth obtained from the GNSS receiver. And, the results show the feasibility and effectiveness of our proposed system.

The rest of the paper is arranged as follows: Section 2 reviews the existing works related to the design of remote tracking systems for the underwater vehicle mobility state. Section 3 outlines the system architecture, while Section 4 provides a detailed description of our signal processing and mobility state estimation methods. Section 5 presents our field test results, and in Section 6, we draw our conclusions.

2. Related Work

DIBS is designed for underwater vehicle mobility state estimation, where the mobility state includes location and velocity, thus resulting in related research that can be broadly categorized into two topics: location estimation and velocity estimation. Accordingly, the review of relevant work is split into two parts, each focused on either location or velocity estimation.

Location estimation. The localization of underwater vehicle can be accomplished with two kinds of methods: range-based and non-range-based [8]. The focus of this paper is the range-based approach. Under such an approach, a correlation is established between the measured range and the underwater vehicle’s location. Two types of algorithms can be used to resolve the location of underwater vehicle, namely the iterative-based algorithm [9] and the closed-form algorithm [10]. The iterative-based algorithm resolves underwater vehicle’s location as a nonlinear least squares problem and is solved using an iterative approach. Conversely, the closed-form algorithm links measurements directly to the underwater vehicle’s location through a set of equations.

As stated in [11], underwater localization systems are typically classified into ultra-short baseline, short baseline, and long baseline. The long baseline system, which utilizes multiple base stations to provide redundant measurements and ensure system reliability, generally offers superior localization accuracy and wider area coverage. Long baseline systems can be deployed on the seafloor or carried by buoys, depending on the intended application. It can be challenging to calibrate the exact geodetic coordinates of base stations deployed underwater. To address this, a common practice is to continually ranging the base stations using vessels equipped with GPS and hydrophones at various locations [12].

Given its superior accuracy and coverage, the long baseline system is deemed more appropriate for establishing the desired system. Considering the need for flexible deployment and to avoid intricate calibration processes, the SBS-based long baseline system is a preferred choice. The GPS intelligent buoy (GIB) system [13,14] is a design that features surface buoys which serve as a platform carrying base station.The buoys are commonly equipped with GPS receivers, thus their precise location can be acquired. Therefore, underwater nodes can determine their geodetic coordinates by performing localization with surface buoys as reference points. The GIB system’s flexibility allows it for easy deployment to different areas.

Apart from the works related to GIB, which give a broad overview about the surface-buoy-based localization system, many research studies which focus on how to perform precise localization with the SBS have been conducted. In the system proposed in [15], a set-membership approach is utilized to localize underwater vehicles. Ranging results between the base station and the underwater vehicle are used to determine a set of ring-shaped regions centered on the base station. The intersection points of the rings form a rectangle whose interior represents the possible location of the underwater vehicle. As the number of base stations increases, the iterative reduction of the possible location of the underwater vehicle results in a computationally intensive method.

In [16], the author propose a GIB-based localization system for underwater vehicles in which vehicles synchronize with the base station and periodically transmit beacon signals. The system employs the ToA method to localize underwater vehicles while encoding depth information in the two consecutive pulse intervals of the signal.

Passive localization methods based on the TDoA are proposed in [17,18]. In [17], during localization, the number of measurements may not be sufficient to meet localization requirements due to the influence of acoustic channels. To overcome this, the authors proposed two modified methods, whereby the first employs buffered messages to construct a virtual node to predict virtual arrival times, and the second utilizes motion information and an extended Kalman filter (EKF) to estimate the location of the underwater vehicle. In [18], a three-stage method for target localization is proposed, where the non-linear equations of localization are transformed into the pseudolinear equations by introducing nuisance variables, and the estimated location of the unknown source is further optimized by improving the estimation accuracy of the interference variable. A similar system is proposed in [19], in which an EKF method is employed to predict the motion of the underwater vehicle. Apart from directly ranging, the work in [20] proposes a received signal-strength-indication (RSSI)-based method for indoor localization scenarios. A least-squares curve fitting is designed to estimate the critical radio propagation parameters of the transmit power and path loss exponent. Then, the resulting signal strength is converted to range, and a trilateration method is adopted for localization. Finally, a Bayesian filter is applied to improve the localization accuracy.

Apart from the localization method proposed for different scenarios, researches have been conducted to deal with the ranging noise and range ambiguity problem. To deal with range measurements that are degraded by noise and outliers, a method is proposed which applies graph partitioning for range-measurement outlier rejection in [21], aiming to aid the navigation of AUVs. The range ambiguity problem occurs when the period between successive beacon signals is shorter than the maximum propagation delay of the beacon signal to a distant surface buoy. To resolve the ambiguity, a method is proposed that utilized a designed OFDM waveform to mitigate the range ambiguities dedicated to a synthetic-aperture radar case in [22].

Velocity estimation. The remote tracking of an underwater vehicle’s velocity can be achieved with the help of Doppler scaling factor estimation. Prior studies on Doppler scaling factor estimation can be found in [23,24]. Studies like [25,26] have proposed velocity estimation methods that rely on estimated Doppler scaling factors.

To estimated Doppler scaling factors in underwater multicarrier systems, methods have been proposed which rely on the scaling in time of transmitted signals and the inherent characteristics of the OFDM symbol [23,24]. In [23], a Doppler scale estimation technique that utilizes the null subcarrier of a CP-OFDM symbol is proposed. The proposed method estimates the Doppler scaling factor through a two-step algorithm. The first step involves resampling the received signal, which compensates the majority of Doppler shift. The resulting signal can be considered as affected by frequency-independent Doppler shift. In the second step, a channel frequency offset (CFO) estimation is conducted on the output signal in the first step to make more accurate compensation. In [24], a Doppler estimation method based on the embedded repetition pattern is proposed. The transmitted signal contains a repetition pattern that may undergo changes due to unknown factor(s) when transmitted through a channel affected by the Doppler effect and consequently, the repetition period changed. A filter bank with each branch having a possible value of changed period is proposed. The branch with the highest correlation metric with the incoming signal is regarded as the best match.

Upon the estimation of Doppler scaling factors, velocity estimation can be conducted accordingly. A GIB-based system is proposed in [25], which uses a closed-form algorithm to estimate the underwater vehicle’s velocity with at least two base stations. The input to the algorithm consists of a Doppler shift measurement of the received signal and information about the location of the base stations. However, this paper does not mention the signal processing method on how to extract the Doppler scaling factor on which the accuracy of the speed estimation heavily depends. Additionally, the experimental results do not report the algorithm’s performance at different signal-to-noise ratios.

Apart from utilizing the SBS, in [26], a multiple AUV-assisted velocity estimation method is proposed that combines the location and velocity information of at least three neighboring AUVs and the radial velocity produced from the estimation of Doppler scaling factor. The estimation process consists of a data acquisition phase and a closed-form algorithm that determines underwater vehicle’s velocity in three dimensions.

In addition to the aforementioned works, there are some studies that estimate underwater vehicle location and velocity simultaneously. As proposed in [27], an algebraic solution for target location and velocity is given, which is shown to achieve the Cramér–Rao lower bound for Gaussian TDoA and FDoA noise at moderate noise level before the thresholding effect occurs. In [28], a closed-form estimator of target location and velocity is proposed, as in [27]. The accuracy of the estimation achieves the Cramér–Rao lower bound at a sufficiently high noise level before the threshold effect occurs.

To summarize, previous works on system designs based on surface base stations are not directly applicable to our intended system because they lack specific methods for location and velocity estimation. Furthermore, studies on location and velocity estimation either focus on only one aspect or neglect the signal processing methods at the physical layer and the design considerations for achieving a system. Therefore, this paper takes the perspective of designing a tracking system for underwater vehicle and presents a systematic design that includes the system architecture as well as the signal processing methods and mobility state estimation method. To mitigate the false alarm rate in underwater environment and enhance the estimation efficiency, a signal comprising dual-HFM and a CP-OFDM symbol is employed. This signal enables efficient estimation of ToA and Doppler scaling factor. Moreover, essential information is modulated into the CP-OFDM symbol, thereby enhancing the efficiency of estimating the mobility state of underwater vehicles.

3. System Overview

Figure 1 depicts the system architecture primarily consisting of a DC, SBSs, and CB attached to an underwater vehicle. During operation, the vehicle maneuvering within the deployment area and the CB will periodically broadcast a beacon signal. The SBS continuously monitors the incoming signals, and upon receiving the beacon signal, the SBS estimates the ToA and the Doppler scaling factor of the received signal. These two parameters are then transmitted via radio network to the DC. The DC acts as the fusing center, utilizing the received data to estimate the vehicle’s location and velocity. The DC can be a shore-based station, cloud-based server, or a center SBS, depending on the application. Correspondingly, the communication between the DC and SBS can be either through the 4G networks or a radio ad hoc network.

The above gives a broad overview about the architecture and workflow of this system; we now elaborate the individual structure of each component in the following subsections.

3.1. Structure of Data Center

The diagram of the DC is shown in Figure 2. Localization and velocity estimation are performed here. As mentioned before, depending on the application, the DC can either be a shore-based station, cloud-based server, or a center SBS, and estimation results can be returned either to the SBS or underwater vehicle, stored in a database, or fed to a display monitor. The workflow of the DC is as follows: First, upon collection of packets containing estimated parameters from SBSs, it performs localization and velocity estimation, and then results are delivered to a sink, depending on the application. Second, commands or packets can also be generated and transmitted through the RF module.

3.2. Structure of Cooperative Beacon

As shown in Figure 3, the CB contains a digital signal processor (DSP), pressure gauge, and an acoustic transducer. The DSP in the CB serves to build signal according to the employed signal structure. The digital signal is converted to an analog signal, then amplified and emitted by the transducer. The pressure gauge is utilized to acquire the depth of underwater vehicles and depth of the CB, and the mobility state estimation epoch number is encoded into the acoustic signal.

3.3. Structure of Surface Base Station

As shown in Figure 4, the SBS is a platform that comprises a power supply system, base station gateway (GW), DSP, RF module, GNSS receiver, and hydrophone. In order to introduce the SBS more clearly, we first describe the internal workflow of the SBS and then introduce the specific functions of each component. There are two workflows inside the SBS; we term the first as uplink workflow, which is related to the acoustic signal recorded from the hydrophone. And the second one is termed the downlink workflow, which is related to the commands and packets sent by the DC. To describe the first workflow, we begin with the recorded acoustic signal by the hydrophone. The recorded acoustic signal will be amplified and then provided to the DSP, where the signal processing algorithm is performed. After processing, the estimated ToA and Doppler scaling factor are delivered through RS-232 to the GW. Upon receiving, the GW builds a packet containing the estimated parameters and real-time coordinates of the SBS, which is then transmitted by the GW through the RF module to the DC. As for the second workflow, it is nearly a reverse of the first one. The DC generates commands or packets and then transmits them through radio network to the SBS. Upon receiving, the messages contained in commands or packets will be decapsulated, and action will be taken by the GW or DSP according to the indication in payload.

With the understanding of the inside workflow, we give the individual function of every component:

• Power supply system: Provides power to the whole system.
• Hydrophone: Listens and detects the acoustic signal.
• GNSS receiver: Provides real-time coordinates of the SBS. Additionally, it provides a pulse per second (PPS) signal to the DSP, which is used by the DSP as a clock source. The detail about time synchronization of the SBS will be explained in Section 4.
• RF module: Our system performs localization and velocity estimation in a centralized fashion; thus, the individual information from each SBS needs to be delivered to the DC. The medium is a radio network; depending on the application, it could be the 4G LTE networks or radio ad hoc networks.
• DSP: The term DSP here does not just refer to the narrow definition of a microprocessor, it is a broad concept that comprises microprocessor, related circuits, and signal processing algorithms. The function of the DSP is related to the process of the acoustic signal, determining the ToA and Doppler scaling factor, which will be used in localization and velocity estimation.
• GW: The most important function of the GW is as a data relay station that transits messages between the DSP and the DC. It receives signal processing results from the DSP, and then encapsulates these results into a packet, which will be transmitted to the DC for further processing. Additionally, it receives commands or packets from the DC, and then performs actions based on the commands or forwards the packets to the DSP. As shown in Figure 4, in addition to serving as a data relay station, the GW also receives real-time coordinates from the GNSS receiver, and the coordinates will be used in localization.

4. Parameter Estimation

The previous section gives the system architecture and its components. In this section, we develop a synthesis method consisting of three main parts: time synchronization of the DSP, signal parameter estimation, and underwater vehicle mobility state parameter estimation. Time synchronization of the DSP is a prerequisite in achieving precise mobility state estimation, and we will elaborate on the philosophy and rationale of time synchronization of the DSP in the following section. Signal parameter estimation is primarily conducted at the SBS and involves the estimation of the signal’s ToA and Doppler scaling factor. These two parameters are the input for the mobility state parameter estimation, which is performed at the DC. Based on the ToA and Doppler scaling factor estimated at each SBS, the DC estimates the underwater vehicle’s location and velocity. For localization of underwater vehicles, we adopted a TDoA method, removing the need for clock synchronization between the SBS and CB, which simplifies the system’s implementation. Based on the localization result, we estimate the underwater vehicle’s velocity vector by the radial velocity produced from the Doppler scaling factor of each SBS. In the subsequent section, we will dive into each part and give the detailed procedures.

Moreover, we would like to clarify that the SBS is a platform comprised of a variety of devices, such as the DSP, the GW, and the hydrophone, etc. Thus, the DSP, the GW, and the SBS physically belong to the same system. Consequently, in subsequent sections, we will use the DSP, the GW, and the SBS interchangeably.

4.1. Time Synchronization of the DSP

In this section, we will discuss two topics related to the time synchronization of the DSP. The first topic involves partial time synchronization, while the second topic provides a method called time reference acquisition to correct clock offset between the DSPs.

The precise synchronization of the DSPs is essential for accurate acoustic localization using TDoA. The DSPs can be synchronized with a master DSP by transmitting an acoustic signal, as was previously discussed in the literature [29,30]. However, these approaches can be inefficient. Our system relies on the SBS, which is capable of radio communication (through the RF module). An alternative approach is to synchronize all the DSPs to UTC time using the network time protocol (NTP). But internet access may not always be available, and thus synchronization through NTP is not a universally applicable method. Given the challenges described above, to achieve DSP synchronization, a two-step approach is developed.

The first step is as follows. A hybrid clock source is developed incorporating PPS signal and oscillator output. The GNSS receiver provides a synchronized PPS signal output across all receivers, and its accuracy of synchronization can meet our requirement [31]. The PPS output is chosen as one of the clock sources, connected to the DSP’s general-purpose input/output (GPIO), and the DSP continuously counts the number of received PPS signals from the time of system bootup.

PPS output with a frequency of 1 Hz is inadequate for localization and necessitates an additional clock source with a higher frequency. Many DSPs are equipped with a built-in crystal oscillator (BXO) that provides a 1 kHz clock source. To address the frequency limitations of PPS, we combine the PPS and BXO output to produce a hybrid clock source, and an intuitive illustration of the proposed clock source structure is shown in Figure 5. The output of this resulting clock source is named clock-tick counting (CTC) and is accurate to the millisecond level. Two variables, named $C_{int}$ and $C_{frac}$, are initialized to zero at the DSP bootup. Whenever a PPS signal is received, $C_{int}$ is increased by 1, and whenever a BXO pulse is received, $C_{frac}$ is also increased by 1. The term $C_{int}$, which is abbreviated from “CTC integer part”, is a variable that stores the value of how many PPS signals have been received since the DSP bootup. Likewise, the term $C_{frac}$, which is abbreviated from “CTC fractional part”, is a variable that stores the value of how many BXO outputs have been received since the DSP bootup. By combining $C_{int}$ and $C_{frac}$, we can produce CTC as $C_{int}+C_{frac}/1000$, which is a variable with both integer and fractional parts. Therefore, CTC is a decimal number that represents how much time has elapsed since the DSP bootup. As depicted in Figure 5, $C_{frac}$ is reset to 0 every time a PPS is received since the induced clock drift of the common low-cost BXO must be considered. By resetting $C_{frac}$ every time, a PPS is received, the output of BXO is only valid within a second. Thus, in a relatively short period, the error induced by clock drift of the BXO is limited.

The DSPs’ CTC only begins counting when they boot up. As a result, different bootup times of the DSP lead to numerically different CTC values, which can be seen as a clock offset between each DSP. Consequently, we consider the DSPs to be partially synchronized. Under this partially synchronized clock, the integer part of the DSPs’ CTCs are simultaneously incremented, but the exact values of the integer part of the CTCs are not identical across the DSPs, which can be considered as clock offset. As for the fractional part, since it is set to zero every time a PPS signal is received, the fractional part of the CTC can be regarded as synchronized, which implies that there is no offset between the fractional part of the CTC in each DSP, meaning that it is not affected by the different bootup times.

The next step is to address the challenge of partial synchronization among the DSPs, which we have named time reference acquisition. The most straightforward approach to determine the time offset between the DSPs is for each DSP to sample its own CTC simultaneously, then transmitting these values to a DC for comparison. In order to simultaneously sample the CTC at each DSP, the DC sends commands sequentially to each DSP through the radio network to request their current CTC. Although each command may experience different queuing and network delays, the divergence is not significant. Therefore, nearly simultaneous CTC samples can be obtained from each DSP. Since the fractional part of the CTC is synchronized, we do not consider this part of collected CTCs in time reference acquisition, and this is accomplished by applying a $floor$ operation to each CTC. Following this, offset determination can be achieved by simply comparing the CTCs from a selected reference DSP with other DSPs. The floored CTC of the DSP n will be denoted as $C_n$, so the offset can be calculated as follows:

$$\begin{array}{cc}\hfill {\mathbf{C}}_{\mathbf{ref}}& =[C_2-C_1,C_3-C_1,\dots ,C_N-C_1]\hfill \\ \hfill & =[C_{2,1},C_{3,1},\dots ,C_{N,1}]\hfill \end{array}$$

(1)

where ${\mathbf{C}}_{\mathbf{ref}}$ represents the clock offset between the reference DSP to other DSPs. $C_{i,j}$ denotes the clock offset between the DSP i to a reference DSP j, while the DSP 1 is selected as the reference DSP in Equation (1). As mobility state estimation is carried out at the DC, only the DC needs to be aware of the offsets, meaning that the offsets do not need to be returned to the DSPs.

4.2. Parameter Estimation Methods

This section provides the method for parameter estimation, which can be divided into two types: signal parameters estimation and underwater vehicle’s mobility state parameter estimation. Therefore, two types of estimations are involved: signal parameter estimation and mobility state estimation. Signal parameter estimation is performed by the DSP in the SBS. Upon receiving a beacon signal broadcasted by the CB, the DSP performs the estimation of the ToA and the Doppler scaling factor of the received signal. Additionally, the demodulation of the CP-OFDM symbol is carried out to obtain the information (depth and mobility state estimation epoch number) required for localization. Following this, estimated parameters and decoded information are encapsulated by the GW in a state information packet (SIP) and uploaded to the DC. The DC then performs mobility state estimation with a collection of the DSPs’ SIPs, which yields the underwater vehicle’s location and velocity. These procedures are illustrated intuitively in Figure 6. The entire period of completing the aforementioned steps is referred to as a state estimation epoch. The epoch number is a self-augmented scalar that is modulated in the broadcasted beacon signal by the CB, and the reasons for the modulation are as follows. In the case of centralized localization, all data are gathered and processed at the DC. When the coverage area of the SBSs is large, the propagation delay of the beacon signal to the SBSs located far from the CB might exceed the beacon signal’s broadcasting interval. When a ToA measurement taken by an SBS located at a greater distance from the CB is delivered to the DC, two or more ToA measurements taken by the same SBS located closer to the CB may have already been received by the DC. Considering the potential loss of beacon signals and in the absence of prior knowledge regarding the underwater vehicle’s location, determining which ToAs belong to the same epoch becomes challenging. Further processing should be undertaken to deal with this problem. To enhance the efficiency of this process, we modulate the epoch number into the CP-OFDM symbol.

Since this is a long baseline system with each SBS only equipped with a single hydrophone, the depth measurement cannot be performed by individual SBS. Thus, the CB is integrated with a pressure gauge and the depth information is modulated into the CP-OFDM symbol.

4.2.1. Signal Processing

The structure of the beacon signal is illustrated in Figure 7. It consists of dual-HFM signals and a CP-OFDM symbol. The dual-HFM signals are utilized for signal detection and estimation of the ToA, while the null subcarriers of the CP-OFDM symbol enables estimation of the Doppler scaling factor. In addition, the CP-OFDM symbol encodes the underwater vehicle’s depth and mobility state estimation epoch number information into the data subcarriers. The signal processing involves two main stages: first, detecting the signal and estimating its arrival time, and second, estimating the Doppler scaling factor and decoding the data from the data subcarriers of the CP-OFDM symbol.

• Signal detection and ToA estimation

The initial step involves detecting the presence of a beacon signal in the incoming signal and subsequently estimating its arrival time, i.e., ToA. To accomplish this task, a detector utilizing the Page’s test [32,33] is implemented, which serves to detect dual-HFM signals and estimate the arrival time simultaneously.

We will first explain the rationale behind using dual-HFM signals before detailing the detection procedures. In the presence of impulsive noise, a single HFM design may not perform well due to false alarm. This is because impulsive noise can also generate high correlation peaks with the local replica (the single HFM) in the matched filter output, leading to incorrect detection. To overcome this issue, we employ a dual-HFM design. The concept is simple: since a single HFM is vulnerable to impulsive noise, we use an additional HFM as a redundancy to perform a double-check, ensuring that the incoming signal is indeed the desired signal, which reduces the false alarm rate.

For a single HFM signal with duration T, start frequency $f_1$, and end frequency $f_2$, it can be represented as follows [34]:

$$s\left(t\right)=A\left(t\right)exp\left[j\frac{2\pi }{b}ln\left(1+b{f}_{1}t\right)\right],0\le t\le T$$

(2)

where $b=\frac{f_1 - f_2}{f_1{f}_{2}T}$, and $A\left(t\right)$ denotes the rectangular envelope. The corresponding received signal can then be represented as $r\left(t\right)=s(t-{\tau }_0)$, where ${\tau }_0$ denotes the propagation delay, and the time reference t is from the receiving end perspective. The received signal is match filtered with a local replica of the transmitted signal $s\left(t\right)$, and the resulting output is denoted as $y\left(t\right)=r\left(t\right)\ast s\left(t\right)$, where ${}^{\prime }{\ast }^{\prime }$ denotes the convolution. We take the discrete-time counterpart of matched filter output $y\left(t\right)$ as $y\left[n\right]$, where $t=n{T}_s$ and $T_s=1/f_s$ as the sampling interval, while $f_s$ is the sampling frequency.

The diagram of the detector is shown in Figure 8. The Page test statistic of the first and second HFM is running in parallel, and input of the first and second PTS is $y\left[n\right]$ and $y[N_G+n]$, respectively. The $N_G=G_{HFM}/T_s$ represents the samples between two HFMs. And $G_{HFM}$ is the interval bewteen two HFMs, as shown in Figure 7. As in [32], the data sequence is fed into the Page test sequentially. The statistical results are combined to make a decision about whether a beacon signal is presented. There are two pieces of information contained in the detector output. The detection state is a declaration of the presence of a beacon signal, and detection is announced only if both statistical results of two PTSs cross a preset threshold. Alongside the detection state, an estimated signal start time $n_s$ is also outputted, which is the ToA of the beacon signal. After determining the ToA, a corresponding CTC can be decided, which will then be used for localization.

• Doppler estimation

Following the detection of the beacon signal, Doppler scaling factor estimation is performed using the null subcarriers of the CP-OFDM symbol. As demonstrated in previous works [23,24], a rough estimation of the Doppler scaling factor can be obtained by estimation of the time scaling of the received signal. Since the employed signal structure only consists of a preamble and an OFDM symbol, we rely primarily on the null subcarriers for Doppler scaling factor estimation, adopting a hybrid method inspired by previous works [23,24].

The core of the algorithm lies in the frequency offset induced by the Doppler shift, which results in the breakdown of orthogonality between subcarriers within the CP-OFDM symbol, causing inter-carrier interference and making the null subcarriers’ energy non-zero. The Doppler scaling factor estimation consists of two steps: first, a set of resamplings is applied to the received signal, each with a different resampling factor, followed by identifying which resampling factor minimizes the total energy of null subcarriers. The identified factor is regarded as a coarse estimation of the Doppler shift. With the first processing step, we can produce the radial speed through the estimated Doppler shift. As mentioned before, essential information is modulated into the CP-OFDM symbol. Thus, Doppler shift must be further reduced through fine-tuning to mitigate inter-carrier interference, enabling the correct demodulation of CP-OFDM symbol. In other words, after resampling, a residual Doppler shift remains. To further mitigate the residual Doppler shift, a grid search for a frequency shift that minimizes the total energy of null subcarriers is conducted. The diagram of Doppler scale estimation and compensation is shown in Figure 9.

Assuming there are $K_0$ subcarriers, the duration of OFDM symbol is $T_0$. The frequency spacing of the OFDM symbol is $\Delta f=1/T_0$ and the occupied bandwidth is $B=K_0/T_0$. The transmitted signal in baseband can be expressed as

$$x_{tx}\left(t\right)=\sum _{k\in S}^{}s\left[k\right]e^{j2\pi \frac{k}{T_0}t}g\left(t\right),t\in [0,T_0]$$

(3)

where, $S=\left\{-\frac{K_0}{2},\dots ,\frac{K_0}{2}-1\right\}$, and $s\left[k\right]$ is the symbol transmitted by the kth subcarrier, $g\left(t\right)$ is a window function of width $T_0$. The transmitted signal in passband can be expressed as

$$\begin{array}{cc}\hfill {\tilde{x}}_{tx}\left(t\right)& =Re\left\{e^{j2\pi f_{c}t}\sum _{k\in S}^{}s\left[k\right]e^{j2\pi \frac{k}{T_0}t}g\left(t\right)\right\}\hfill \end{array}$$

(4)

The received passband signal taking into account only the effect of Doppler can be expressed as

$${\tilde{y}}_{rx}\left(t\right)=Re\left\{e^{j2\pi f_c(t+at-\tau )}\sum _{k\in S}s\left[k\right]e^{j2\pi \frac{k}{T_o}(t+at-\tau )}g(t+at-\tau )\right\}$$

(5)

where the Dopper scaling factor is defined as $a=v/c$, v is the radial speed between sender and receiver, c is the signal propagation speed, and $\tau$ is the propagation delay. The baseband received signal $y_{rx}\left(t\right)$ is related to ${\tilde{y}}_{rx}\left(t\right)$ as ${\tilde{y}}_{rx}\left(t\right)=Re\left\{y_{rx}\left(t\right)e^{j2\pi f_{c}t}\right\}$. Thus, $y_{rx}\left(t\right)$ can be expressed as

$$\begin{array}{cc}\hfill y_{rx}\left(t\right)& =e^{j2\pi f_c(at-\tau )}\sum _{k\in S}s\left[k\right]e^{j2\pi \frac{k}{T_0}(t+at-\tau )}g(t+at-\tau )\hfill \\ \hfill & =e^{j2\pi f_{c}at}\sum _{k\in S}s\left[k\right]e^{j2\pi \frac{k}{T_0}(t+at)}g(t+at-\tau )e^{-j2\pi f_k\tau }\hfill \end{array}$$

(6)

where $f_k=f_c+k/T_0$ represents the kth subcarrier’s frequency in passband. The $y_{rx}\left(t\right)$ is fed into the Doppler estimation and compensation process, as shown in Figure 9. To perform the coarse estimation, a series of resamplings of $y_{rx}\left(t\right)$ is executed, each with a different resampling factor. After each resampling, the total energy of null subcarriers is calculated. The resampled signal can be expressed as

$$y_{rx}\left(\frac{t}{1+\widehat{a}}\right)=e^{j2\pi f_c\frac{a}{1+\widehat{a}}t}\sum _{k\in S}s\left[k\right]e^{j2\pi \frac{k}{T_0}\frac{1+a}{1+\widehat{a}}t}g(\frac{1+a}{1+\widehat{a}}t-\tau )e^{-j2\pi f_k\tau }$$

(7)

where $\widehat{a}$ represents a candidate resampling factor. We denote the resampling factor that gives the minimum total energy on all null subcarriers as b, and the estimated radial speed from the SBS n is derived as

$$v_n=b\ast c$$

(8)

After resampling, the $y_{rx}\left(\frac{t}{1 + b}\right)$ is fed into the next step to reduce the Doppler shift further. Within this step, a grid search is performed, which finds the proper frequency shift $f_m$ that further minimizes null subcarriers’ energy. The cost function to be minimized is expressed as

$$\widehat{f_m}=\underset{f_m}{argmin}\sum _{k\in S_N}{\left|e^{j2\pi f_{m}t}{y}_{rx}\left(\frac{t}{1+b}\right)\right|}^2$$

(9)

where $S_N$ represents the set of null subcarriers. With this two-step processing, the Doppler shift can be compensated properly, and the resulting signal can be expressed as

$$z\left(t\right)=e^{j2\pi \widehat{f_m}t}{y}_{rx}\left(\frac{t}{1+b}\right)$$

(10)

• Demodulation

After the Doppler estimation and compensation have been completed, the break of orthogonality between subcarriers of $y_{rx}\left(t\right)$ is well mitigated, allowing the data on the CP-OFDM symbol to be demodulated through normal processes. It is important to note that a complete OFDM system may also include channel coding and channel equalization and other sophisticated processing, which are not described in detail as they are not the primary focus of this paper.

4.2.2. Location Estimation

Before diving into the mobility state estimation, we make a clarification that, since the pressure gauge is integrated into the CB, the localization and velocity estimation can be conducted in two-dimensional space without loss of generality. Now, we give details about the localization method. After performing ToA estimation and Doppler scaling factor estimation, the DSP encapsulates the necessary information into a SIP. The structure of the SIP is given in Figure 10.

The explanation of each field in SIP is as follows:

• SBS ID: A unique identifier assigned to each SBS.
• Epoch: A number that represents the current mobility state estimation epoch.
• Timestamp: The timestamp attached to the SIP immediately after detection of a beacon signal, representing the ToA of the beacon signal.
• Coordinate: the SBS’s coordinate from the GNSS receiver’s output sampled immediately after detection of a beacon signal.
• Depth: The depth of the underwater vehicle encoded in the beacon signal. It is measured using the pressure gauge integrated into the CB.
• Speed: The Doppler speed estimated from the received beacon signal at the SBS.

We need to mention here again that the Epoch and Depth information is both demodulated from the CP-OFDM symbol. Upon receiving, values of Timestamp belonging to the same mobility state estimation epoch are put into a measurement matrix, as shown in Equation (11), where the SBS 1 is selected as the reference SBS.

$$\mathbf{x}=c\ast \left|\begin{array}{c}{(\tilde{t}}_{r,2}-C_{2,1})-{\tilde{t}}_{r,1}\\ \dots \\ {(\tilde{t}}_{r,N}-C_{N,1})-{\tilde{t}}_{r,1}\end{array}\right|$$

(11)

For simplicity, we assume the reference SBS here is the same as that in the time reference acquisition process. And the c represents the speed of sound underwater, ${\tilde{t}}_{r,n}$ is the value of the Timestamp from the SBS n, and $C_{n,1}$ is the time offset between the SBS n and the reference SBS in Equation (1).

The least squares is used to estimate the underwater vehicle’s location $\mathit{\theta }=[x,y]$. The range differences from the CB to the reference SBS and the other SBSs are expressed in the form of a matrix as follows:

$$d\left(\mathit{\theta }\right)=\left|\begin{array}{c}∥\mathit{\theta }-{\mathbf{b}}_{\mathbf{2}}∥-∥\mathit{\theta }-{\mathbf{b}}_{\mathbf{1}}∥\\ \dots \\ ∥\mathit{\theta }-{\mathbf{b}}_{\mathbf{N}}∥-∥\mathit{\theta }-{\mathbf{b}}_{\mathbf{1}}∥\end{array}\right|$$

(12)

where ${\mathbf{b}}_{\mathbf{n}}=[x_n,y_n]$ is the coordinates of the SBS n. Thus, the cost function can be written as

$$r\left(\mathit{\theta }\right)={\left[d\left(\mathit{\theta }\right)-\mathbf{x}\right]}^T\left[d\right(\mathit{\theta })-\mathbf{x}]$$

(13)

where T denotes transpose. Observe that, in order to enhance accuracy, we take all measurements from the same epoch into the least-squares estimator for localization. The estimation of the underwater vehicle’s location can be expressed as

$$\widehat{\mathit{\theta }}=[\widehat{x},\widehat{y}]=\underset{\mathit{\theta }}{argmin}r\left(\mathit{\theta }\right)$$

(14)

This is a nonlinear least squares problem that can be solved by the commonly used iterative optimization method [35]. And in our implementation, the Levenberg–Marquardt (LM) algorithm is adopted since it is robust.

Localization in our proposed system requires at least three measurements. If the number of measurements is fewer, the system cannot provide localization results. However, in such cases, a prediction-based method (e.g.,EKF [36]) may be employed instead.

4.2.3. Velocity Estimation

Upon the completion of localization, the velocity estimation is conducted. The method for velocity estimation is detailed in the following. From the description of the CB in the previous section, we know that the CB is integrated with a pressure gauge, indicating that the vertical velocity could be produced by the differences between successive samplings of depth. Thus, the estimation of velocity is performed in the two-dimensional plane. The underwater vehicle’s velocity can be expressed as

$$\mathbf{V}={\left[V_x{V}_y\right]}^T$$

(15)

The procedure for velocity estimation is depicted in Figure 11, which has been simplified for clarity by only depicting three SBSs.

As shown in Figure 11, the velocity vector of the underwater vehicle can be produced from the individual radial velocities. With the underwater vehicle’s location already estimated, the estimation of the underwater vehicle’s velocity is equivalent to finding a velocity vector that coincides as closely as possible with each radial velocity.

The estimated underwater vehicle’s location is $\widehat{\mathit{\theta }}$; then, the directional vector from each SBS to the underwater vehicle can be expressed as

$${\mathbf{D}}_{\mathbf{n}}=\frac{\left({\mathbf{b}}_{\mathbf{n}}-\widehat{\mathit{\theta }}\right)}{∥{\mathbf{b}}_{\mathbf{n}}-\widehat{\mathit{\theta }}∥}$$

(16)

let $\mathbf{D}={[{\mathbf{D}}_{\mathbf{1}}^T,{\mathbf{D}}_{\mathbf{2}}^T,\dots ,{\mathbf{D}}_{\mathbf{N}}^T]}^T$. The Doppler speed (radial speed) measured at each SBS is expressed as a vector as follows:

$$\mathbf{v}={[v_1,v_2,\dots ,v_N]}^T$$

(17)

where $v_n$ is the individual radial speed measured from each SBS as in Equation (8). Then, the estimation of underwater vehicle’s velocity can be performed by a linear least squares estimator. Since radial velocity is the projection of the underwater vehicle’s velocity on each directional vector, combining the above two equations, we can obtain the following relation:

$$\mathbf{v}=\mathbf{D}·\mathbf{V}+{\mathbf{n}}_{\mathbf{v}}$$

(18)

where ${\mathbf{n}}_{\mathbf{v}}$ denotes white Gaussian noise. Since this is a linear system, the estimator of $\mathbf{V}$ is expressed as

$$\widehat{\mathbf{V}}={({\mathbf{D}}^T·\mathbf{D})}^{-1}·{\mathbf{D}}^T·\mathbf{v}$$

(19)

5. Field Results and Analysis

To evaluate the performance of the proposed system, field tests were conducted at Dapeng Bay, Shenzhen, China, in May 2023. The depth of the experiment area is around 10 m. According to the sound velocity profiler (SVP) output, the variation of sound speed from the surface to the bottom is limited, and 1530.37 m/s is taken as the effective sound speed.

5.1. Setup

In the experiment, we mounted a single CB on a pole, attached the pole to the port side of a boat, and lowered it to a fixed depth of 3 m, as shown in Figure 12a,b. In other words, the CB was located underwater and traveled with the boat. This is to simulate a CB-equipped underwater vehicle. The advantage of this method is that it is easy to acquire the real-time coordinates using a GNSS receiver. These coordinates can then serve as the ground truth of the underwater vehicle’s location. Besides, all equipment of the SBS is contained in a waterproof box, as shown in Figure 12c.

In the experiment area, the SBSs were deployed to form a square. The coordinates of the SBSs are shown in Figure 13, where the yellow pins and green pins represent their coordinates in two different experiments. During the experiment, the CB broadcasted the signal at an interval of approximately 1.4 s.

The center frequency of the beacon signal is 24 kHz, and the bandwidth is 3 kHz. Within the CP-OFDM symbol, the entire bandwidth is divided into 1024 subcarriers: 224 data subcarriers, 672 pilot subcarriers, and 128 null subcarriers.

5.2. Results

Two separate experiments were conducted, and a total of 1139 results were collected. In these two experiments, the diagonal distance of the square topology is designed to be 1000 m and 800 m, respectively. Using the received signal from each SBS, we performed post-processing to estimate the channel response and calculate the effective SNR. A sample signal’s spectrogram and estimated channel response is shown in Figure 14.

Figure 15 displays the distribution of received signals’ SNR from all the SBSs. The step size of the x-axis is 1 dB, and each dot in the figure represents all SNRs within a 1 dB range of its x-axis coordinates.

5.2.1. Localization Results

In each experiment, we adopted a random way-point method to simulate the movement of the underwater vehicle, with an average speed of approximately 1.69 m/s. The trajectories were recorded by the GNSS receiver as ground truth. During each experiment, 729 and 410 localization results were collected respectively.

As depicted in Figure 16, there are four SBSs deployed, with the fourth SBS acting as redundancy and used to improve accuracy, even though three SBSs are sufficient for localization using TDoA. The estimated trajectories are converted to a Cartesian coordinate system, with +x eastward and +y northward. In most of the epochs, there were at least three SIPs received at the DC. But there were still 33 and 61 epochs in each experiment that the received SIPs were not adequate to perform mobility state estimation. The trajectories depicted in Figure 16 represent the localization results from epochs in which at least three SIPs were received. As shown in Figure 16, the ground truth is represented in a red solid line, and the estimated trajectories are represented by blue triangles. In Figure 16a,c, the overall estimated trajectories are depicted. To provide a clearer visualization of the estimated trajectories, Figure 16b,d present magnified views of the segments of estimated trajectories, and the magnified areas are indicated by green boxes in Figure 16a,c.

Estimated locations are compared with the ground truth of the CB, and the comparison between the estimated location and the true location can be performed directly. Apart from localization error, the TDoA estimation errors are also given and can be used to demonstrate the performance of TDoA estimation, i.e., the effectiveness of signal detection and the ToA estimation method. To derive the error of TDoA, we first obtain the TDoAs from a reference SBS to other SBSs in each epoch. The SBS whose SIP arrived at the DC first is selected as the reference SBS. With the true location of the SBSs and CB in the corresponding epoch, the TDoA error can be calculated as

$$Error\left(TDoA\right)=d\left(\theta \right)-\mathbf{x}$$

(20)

where the $\mathbf{x}$ is from Equation (11) and $d\left(\theta \right)$ is from Equation (12), and the $\theta$ here should be the true location from the output of the GNSS receiver atop the CB. Within each epoch, we then calculate the root mean square (RMS) of TDoA error as follow

$$RMS\left(Error\left(TDoA\right)\right)=\sqrt{\frac{{\sum }_{i=1}^{N_i}{e}_i^2}{N_i}}=R_{E\_tdoa}$$

(21)

where the $N_i$ is the number of SIPs received in this epoch, and the $e_i$ is the ith element in the vector $Error\left(TDoA\right)$.

The root mean square error (RMSE) is calculated as

$$RMSE=\sqrt{\frac{{\sum }_{m=1}^{M_i}{E}_m^2}{M_i}}$$

(22)

it represents the RMS error over $M_i$ epochs of mobility state estimation. And the $E_m$ could represent localization error, velocity estimation error, or $R_{E\_tdoa}$.

Apart from showing the localization errors observed from the experiments, to demonstrate the system’s resilience to exceptional circumstances, such as the loss of signal or an SBS failure, we re-perform localization with only three SBSs’ SIPs collected in the experiments. Since there were four SBSs deployed in our experiments, at most four SIPs were supposed be received within an epoch. To simulate the situation that only three SIPs exist, we randomly drop a SIP from a certain SBS, leaving only three SIPs for localization. But, if only three SIPs were received in a particular epoch, we did not drop any SIPs and we used the original localization result directly.

As shown in Figure 17, both the RMS of $R_{E\_tdoa}$ and the RMS of localization error are depicted with respect to the sequence of epochs in which at least three SIPs are received. We denote the localization results obtained from the original experiments as ‘ALL’, and the results obtained by re-localization with three SBSs as ‘THREE’. The re-localization with three SBSs is performed 1000 times, and THREE is obtained by averaging 1000 RMS errors of re-localization. Based on the obtained results, in the 1000 m square experiment, ALL demonstrates RMS of localization errors ranging from 2.36 m (minimum) to 2.91 m (maximum), while THREE shows RMS of localization errors ranging from 2.48 m (minimum) to 3.28 m (maximum). In the 800 m experiment, ALL yields RMS of localization errors ranging from 1.47 m (minimum) to 2.49 m (maximum), whereas THREE results in errors ranging from 2.31 m (minimum) to 2.83 m (maximum). From Figure 17 and the statistical results, it is evident that the results of THREE, ALL, and RMS of $R_{E\_tdoa}$ have similar variation trends. And as the results of THREE suggest, when there are only three SBSs, the accuracy of localization is decreased compared with ALL, and ALL shows consistently better localization accuracy than THREE in both experiments.

5.2.2. Velocity Estimation Results

This section presents the results of the velocity estimation. It was performed in two-dimensions, since the depth variation can be measured from the pressure gauge integrated into the CB. And the vertical velocity can be derived from the difference between consecutive depth measurements relative to the mobility state estimation interval. The ground truth of the velocity was obtained from the output of the GNSS. The GNSS receiver provides data at a frequency of 1 Hz. Considering that the CB’s velocity does not change significantly, we assume its velocity remained unchanged during a single estimation epoch. The RMS of velocity estimation error in each experiment is depicted in Figure 18. Notably, in both the 1000 m and 800 m experiments, we observe similar RMSs of velocity estimation error between ALL and THREE. Specifically, in the 1000 m experiment, the RMS of velocity estimation error of ALL ranges from 0.16 m/s (minimum) to 0.47 m/s (maximum), while THREE yields results ranging from 0.14 m/s (minimum) to 0.50 m/s (maximum). Furthermore, in the 800 m experiment, the RMS of velocity estimation error of ALL varies from 0.21 m/s (minimum) to 0.76 m/s (maximum), and the results of THREE range from 0.22 m/s (minimum) to 0.72 m/s (maximum). Based on Figure 18 and the statistical results, we observe that the velocity estimation error of ALL and THREE did not differ significantly in both experiments. One possible reason is as follows: We employ localization results for velocity estimation, but the differences between the localization result of ALL and THREE may not be significant enough to induce notable deviations in velocity estimation results in our experiments.

6. Conclusions

In this paper, we propose a distributed intelligent buoy system to track the location and velocity of an underwater vehicle, facilitating applications such as remote monitoring and navigation of underwater vehicles. We present a systematic approach that consists of the system architecture, system composition, signal processing, and mobility state estimation. We provide a comprehensive description of the overall architecture of the system and its individual components. To address the false alarms and enhance efficiency, a beacon signal consisting of a dual-HFM signal and a CP-OFDM symbol is employed. Based on this signal, we can obtain efficient detection and ToA estimation by Page test statistics. Subsequently, we estimate the Doppler scale through CP-OFDM, along with a fine compensation for the Doppler shift. Additionally, the CP-OFDM modulates essential information, thereby enhancing the efficiency in estimating the location of the underwater vehicle. For the underwater vehicle’s mobility state estimation, we utilize the results obtained from ToA, Doppler scale estimation, and the demodulated information from CP-OFDM. The field test was conducted at Dapeng Bay, Shenzhen, China. From the experiment results, the effectiveness of our proposed system can be verified, serving as a proof of the feasibility of the proposed system for tracking underwater vehicles.